Let \(G\) be a simple connected molecular graph with vertex set \(V(G)\) and edge set \(E(G)\). One important modification of classical Zagreb index, called hyper Zagreb index \(HM(G)\) is defined as the sum of squares of the degree sum of the adjacent vertices, that is, sum of the terms \({[{{d}_{G}}(u)+{{d}_{G}}(v)]^2}\) over all the edges of \(G\), where \(d_G(v)\) denote the degree of the vertex \(u\) of \(G\). In this paper, the hyper Zagreb index of certain bridge and chain graphs are computed and hence using the derived results we compute the hyper Zagreb index of several classes of chemical graphs and nanostructures.
In theoretical chemistry different molecular structures are often modeled using molecular graphs. Molecular graphs are actually a graphical representation of molecular structure through vertices and edges so that each vertex corresponds to atoms and the edges represents the bonds between them. Graph theory provides an important tool called molecular graph-based structure-descriptor or more commonly topological index to correlate the physico-chemical properties of chemical compounds with their molecular structure. A topological index is a numeric amount derived from a molecular graph which characterize the topology of the molecular graph and is invariant under automorphism. Thus a topological index \(Top(G)\) of a graph \(G\) is a number such that, for each graph \(H\) isomorphic to \(G\), \(Top(G)=Top(H)\). The concept of topological index was first originated by Wiener, while he was chipping away at boiling point of paraffin. In this paper, we are concerned with molecular graphs, that is, the graphs which are simple, connected and having no directed or weighted edges. Let \(G\) be such a graph with vertex set \(V9G)\) and edge set \(E(G)\). Let the number of vertices and edges of \(G\) will be denoted by \(n\) and \(m\) respectively. Also let the edge connecting the vertices \(u\) and \(v\) is denoted by \(uv\). The degree of a vertex \(v\), is the number of first neighbors of \(v\) and is denoted by \(d_G(v)\). Among different types of topological indices, the first and second Zagreb indices are most important topological indices in study of structure property correlation of molecules and have received a lot of attention in mathematical as well as chemical literature. The First and Second Zagreb Index was first introduced by Gutman et al. [1] and are defined as \[{{M}_{1}}(G)=\sum\limits_{v\in V(G)}{{{d}_{G}}{{(v)}^{2}}}=\sum\limits_{uv\in E(G)}{[{{d}_{G}}(u)+{{d}_{G}}(v)]}\] and \[{{M}_{2}}(G)=\sum\limits_{uv\in E(G)}{{{d}_{G}}(u){{d}_{G}}(v)}.\] These two Zagreb indices are among the oldest molecular structure descriptors and have been extensively studied both with respect to mathematical and chemical point of view (see [2, 3, 4, 5, 6, 7]).
Different modification, generalization and extension of Zagreb indices have been introduced and studied by many researchers. One such modified version of Zagreb index called hyper Zagreb index, was introduced by Shirdel et al. in [8], which is defined as \[{HM}(G)=\sum\limits_{uv\in E(G)}{[{{d}_{G}}(u)+{{d}_{G}}(v)]^2}.\] There are various study of this index in recent literature (see [9, 10, 11, 12]).
We know that, a bridge or a chain graphs is the composite graphs formed from \(d\) number of different graphs \(\{G_i\}_{i=1}^n\) by connecting them in proper sense. Thus different relationship for various topological indices can be established between the whole molecular graph with their components \(\{G_i\}_{i=1}^n\). Also, it is interestingly found that many important molecular graphs and nanostructure are composed of some isomorphic subgraphs. So the expressions of different topological indices can be obtained by considering some special cases of bridge and chain graphs. In this paper, we consider two types of bridge graphs and a chain graph. There are some other studies in this direction for some topological indices also Azari et al. in [13] derived some explicit expression of first and second Zagreb indices of bridge and chain graphs. In [14], the present author studied forgotten topological index or F-index of bridge and chain graphs with there respective applications. Mansour and Schork in [15] and [16] respectively calculated PI index, Szeged index, Wiener, hyper-Wiener, detour and hyper-detour indices of different bridge and chain graphs where as they studied vertex PI index and Szeged index of bridge graphs in [17]. Li et al. in [18] calculated the vertex PI index and Szeged index of chain graphs.
In this study, first we derive different expressions for bridge and chain graphs which are composition of the graphs denoted by \(G_i\) , for \(i=1,2,…,d\) which are not necessarily isomorphic. Hence, we calculate the relations when all \(G_i\) are isomorphic. Finally using these relations, we find hyper Zagreb index of some special chemical graphs and nanostructure.
Lemma 3.1. The degree of the vertices of \(B_1\) is given by \[{{d}_{{{B}_{1}}}}(v) = \left\{ \begin{array}{ll} {{d}_{{{G}_{i}}}}(u),~if~u\in V({{G}_{i}})-\{v_i\}\\[2mm] v_1+1,~if~u=v_1\\[2mm] v_i+2~if~u=v_i,~2\leq i\leq d-1\\[2mm] v_d+1,~if~u=v_d. \end{array}\right.\] where \(v_i=d_{G_i}(v_i)\), for \(1\leq i\leq d\)
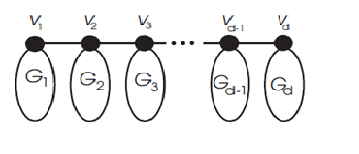
Theorem 3.2. The hyper Zagreb index of the bridge graph \(B_1\) ,\(d\ge 2\), is given by \begin{eqnarray*} HM(B_1)&=&\sum\limits_{{i=1}}^{d}HM(G_i)+6\sum\limits_{{i=2}}^{d-1}v_i^2+20\sum\limits_{{i=3}}^{d-2}v_i+2\sum\limits_{{i=1}}^{d-1}v_iv_{i+1}+4\sum\limits_{{i=2}}^{d-1}\delta_{G_i}(v_i)\\ &&+3(v_1^2+v_d^2)+7(v_1+v_d)+18(v_2+v_{d-1})+2(\delta_{G_1}(v_1)\\ &&+\delta_{G_d}(v_d))+16d-30, \end{eqnarray*} where, \(v_i=d_{G_i}(v_i),~ for ~1\leq i\leq d.\)
Proof. From the construction of the bridge graph \(B_1\), the edge set of \(B_1\) is given by \[E(B_1)=E(G_1)\cup E(G_2)\cup …\cup E(G_d)\cup \{v_iv_{i+1}: 1\leq i\leq (d-1)\}.\] Now to calculate \(HM(B_1)\), we use lemma 3.1 and partition the total sum into the following sums. First we consider the sum \(S_1(B_1)\) over the edges \(ab\in E(G_1)\). \begin{eqnarray*} S_1(B_1)&=&\sum\limits_{ab\in E(G_1)}[d_{B_1}(a)+d_{B_1}(b)]^2\\ &=&\sum\limits_{ab\in E(G_1); a,b\neq v_1}[d_{G_1}(a)+d_{G_1}(b)]^2\\ &&+\sum\limits_{ab\in E(G_1); a\in V(G_1),b=v_1}[d_{G_1}(a)+(d_{G_1}(v_1)+1)]^2\\ &=&\sum\limits_{ab\in E(G_1); a,b\neq v_1}[d_{G_1}(a)+d_{G_1}(b)]^2\\ &&+\sum\limits_{ab\in E(G_1); a\in V(G_1),b=v_1}[d_{G_1}(a)+d_{G_1}(b)]^2\\ &&+\sum\limits_{ab\in E(G_1); a\in V(G_1),b=v_1}[1+2(d_{G_1}(a)+d_{G_1}(v_1))]\\ &=&HM(G_1)+d_{G_1}(v_1)+2\delta_{G_1}(v_1)+2d_{G_1}(v_1)^2. \end{eqnarray*} Next we consider the sum \(S_2(B_1)\) over the edges \(ab\in E(G_d)\). \begin{eqnarray*} S_2(B_1)&=&\sum\limits_{ab\in E(G_d)}[d_{B_1}(a)+d_{B_1}(b)]^2\\ &=&\sum\limits_{ab\in E(G_d);a,b\neq v_d}[d_{G_d}(a)+d_{G_d}(b)]^2\\ &&+\sum\limits_{ab\in E(G_d);a\in V(G_d),b=v_d}[d_{G_d}(a)+(d_{G_d}(v_d)+1)]^2\\ &=&\sum\limits_{ab\in E(G_d);a,b\neq v_d}[d_{G_d}(a)+d_{G_d}(b)]^2\\ &&+\sum\limits_{ab\in E(G_d);a\in V(G_d),b=v_d}[d_{G_d}(a)+d_{G_d}(v_d)]^2\\ &&+\sum\limits_{ab\in E(G_d);a\in V(G_d),b=v_d}[2(d_{G_d}(a)+d_{G_d}(v_d))+1)]\\ &=&HM(G_d)+d_{G_d}(v_d)+2\delta_{G_d}(v_d)+2d_{G_d}(v_d)^2. \end{eqnarray*} Similarly, the third sum \(S_3(B_1)\) is taken over the edges \(ab\in E(G_i)\), for \(i=2,3,…,(d-1)\). \begin{eqnarray*} S_3(B_1)&=&\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_1)}[d_{B_1}(a)+d_{B_1}(b)]^2\\ &=&\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_1);a,b\neq v_i}[d_{G_i}(a)+d_{G_i}(b)]^2\\ &&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_1);a\in V(G_i),b=v_i}[d_{G_i}(a)+(d_{G_i}(b)+2)]^2\\ &=&\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_1);a,b\neq v_i}[d_{G_i}(a)+d_{G_i}(b)]^2\\ &&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_1);a\in V(G_i),b=v_i}[d_{G_i}(a)+d_{G_i}(v_i)]^2\\ &&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_1);a\in V(G_i),b=v_i}[4+4(d_{G_i}(a)+d_{G_i}(v_i))]\\ &=&\sum\limits_{i=2}^{d-1}HM(G_i)+4\sum\limits_{i=2}^{d-1}d_{G_i}(v_i)^2+4\sum\limits_{i=2}^{d-1}d_{G_i}(v_i)+4\sum\limits_{i=2}^{d-1}\delta_{G_i}(v_i). \end{eqnarray*} Finally the contribution \(S_4(B_1)\) of all the edges \(v_iv_{i+1}\), for \(i=1,2,…,(d-1)\) is given by \begin{eqnarray*} S_4(B_1)&=&\sum\limits_{i=1}^{d-1}\sum\limits_{ab=v_iv_{i+1}}[d_{B_1}(a)+d_{B_1}(b)]^2\\ &=&[(d_{G_1}(v_1)+1)+(d_{G_1}(v_2)+2)]^2\\ &&+\sum\limits_{i=2}^{d-2}[(d_{G_i}(v_i)+2)+d_{G_{i+1}}(v_{i+1})+2)]^2\\ &&+[(d_{G_{d-1}}(v_{d-1})+2)+(d_{G_d}(v_d)+1)]^2\\ &=&(v_1+v_2+3)^2+\sum\limits_{i=2}^{d-2}(v_i+v_{i+1}+4)^2+(v_{d-1}+v_d+3)^2\\ &=&2\sum\limits_{i=2}^{d-1}v_i^2+16\sum\limits_{i=3}^{d-1}v_i+2\sum\limits_{i=1}^{d-1}v_iv_{i+1}+(v_1^2+v_d^2)+6(v_1+v_d)\\ &&+14(v_2+v_{d-1})+16d-30. \end{eqnarray*} Hence combining the contributions \(S_1(B_1)\), \(S_2(B_1)\), \(S_3(B_1)\) and \(S_4(B_1)\), we get the desired result.
Let \(v\) is a vertex of a graph \(G\), and \(G_i=G\) and \(v_i=v\) for \(i=1,2,…,d\), then using above Theorem 3.2 we directly get the following:Corollary 3.3. The hyper Zagreb index of the bridge graph \[B_1=B_1(G,G,…,G,v,v,…,v),~~d\ge 2,~ is~ given~ by\] \[HM(B_1)=dHM(G)+8(d-1)v^2+10(2d-3)v+4(d-1)\delta_G(v)+16d-30\] where \(v=d_G(v)\).
Another kind of bridge graph of \(\{G_i\}_{i=1}^d\) with respect to the vertices \(\{v_i,w_i\}_{i=1}^d\) is denoted by \[B_2=B_2(G_1,G_2,…,G_d; v_1,w_1,v_2,w_2,…,v_d,w_d),\] which is the graph obtained from \(G_1,G_2,…,G_d\) by connecting the vertices \(w_i\) and \(v_{i+1}\) by an edge for all \(i=1,2,…,d-1.\) The bridge graph \(B_2\) is shown in the Figure 2. Similarly the following Lemma is the direct consequence of the definition of \(B_2\).Lemma 3.4. The degree of the vertices of \(B_2\) is given by \[{{d}_{{{B}_{2}}}}(u) = \left\{ \begin{array}{ll} {{d}_{{{G}_{1}}}}(u),~if~u\in V({{G}_{1}})-\{w_1\},\\[2mm] d_{G_d}(u),~if~u\in V(G_d)-\{v_d\},\\[2mm] d_{G_i}(u),~if~u\in V(G_i)-\{v_i,w_i\},~2\leq i\leq d-1\\[2mm] w_i+1,~if~u=w_i,~1\leq i\leq d-1,\\[2mm] v_i+1,~if~u=v_i,~2\leq i\leq d, \end{array}\right.\] where \(v_i=d_{G_i}(v_i)\), \(w_i=d_{G_i}(w_i)\), for \(1\leq i\leq d\).
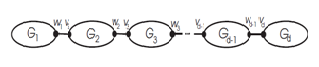
Theorem 3.5. The hyper Zagreb index of the bridge graph \(B_2\), \(d\ge 2\), is given by \begin{eqnarray*} HM(B_2)&=&\sum\limits_{i=1}^2 HM(G_i)+\sum\limits_{i=1}^{d-1}[3w_i^2+5w_i+2\delta_{G_i}(w_i)]\\ &&+\sum\limits_{i=1}^{d-1}[3v_i^2+5v_i+2\delta_{G_i}(v_i)]+2\sum\limits_{i=1}^{d-1}v_iw_i+4(d-1) \end{eqnarray*} where \(v_i=d_{G_i}(v_i)\), \(w_i=d_{G_i}(w_i)\); \(v_i\) and \(w_i\) are not adjacent, for \(1\leq i\leq d\).
Proof. From the construction of the bridge graph \(B_2\), the edge set of \(B_2\) is given by \(E(B_2)=E(G_1)\cup E(G_2)\cup …\cup E(G_d)\cup \{v_iv_{i+1}: 1\leq i\leq (d-1)\}.\) Now to calculate \(HM(B_2)\), we use Lemma 3.4 and partition the total sum into the following sums. First we consider the sum \(S_1(B_2)\) over the edges \(ab\in E(G_1)\). \begin{eqnarray*} S_1(B_2)&=&\sum\limits_{ab\in E(G_1)}[d_{B_2}(a)+d_{B_2}(b)]^2\\ &=&\sum\limits_{ab\in E(G_1); a,b\neq w_1}[d_{G_1}(a)+d_{G_1}(b)]^2\\ &&+\sum\limits_{ab\in E(G_1); a\in V(G_1),b=w_1}[d_{G_1}(a)+(d_{G_1}(w_1)+1)]^2\\ &=&\sum\limits_{ab\in E(G_1); a,b\neq w_1}[d_{G_1}(a)+d_{G_1}(b)]^2\\ &&+\sum\limits_{ab\in E(G_1); a\in V(G_1),b=w_1}[d_{G_1}(a)+d_{G_1}(w_1)]^2\\ &&+\sum\limits_{ab\in E(G_1); a\in V(G_1),b=w_1}[1+2(d_{G_1}(a)+d_{G_1}(w_1))]\\ &=&HM(G_1)+d_{G_1}(w_1)+2\delta_{G_1}(w_1)+2d_{G_1}(w_1)^2. \end{eqnarray*} Next we consider the sum \(S_2(B_1)\) over the edges \(ab\in E(G_d)\). \begin{eqnarray*} S_2(B_2)&=&\sum\limits_{ab\in E(G_d)}[d_{B_2}(a)+d_{B_2}(b)]^2\\ &=&\sum\limits_{ab\in E(G_d);a,b\neq v_d}[d_{G_d}(a)+d_{G_d}(b)]^2\\ &&+\sum\limits_{ab\in E(G_d);a\in V(G_d),b=v_d}[d_{G_d}(a)+(d_{G_d}(v_d)+1)]^2\\ &=&\sum\limits_{ab\in E(G_d);a,b\neq v_d}[d_{G_d}(a)+d_{G_d}(b)]^2\\ &&+\sum\limits_{ab\in E(G_d);a\in V(G_d),b=v_d}[d_{G_d}(a)+d_{G_d}(v_d)]^2\\ &&+\sum\limits_{ab\in E(G_d);a\in V(G_d),b=v_d}[2(d_{G_d}(a)+d_{G_d}(v_d))+1)]\\ &=&HM(G_d)+d_{G_d}(v_d)+2\delta_{G_d}(v_d)+2d_{G_d}(v_d)^2. \end{eqnarray*} Similarly, the third sum \(S_3(B_2)\) is taken over the edges \(ab\in E(G_i)\), for \(i=2,3,…,(d-1)\). \begin{eqnarray*} S_3(B_2)&=&\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i)}[d_{B_2}(a)+d_{B_2}(b)]^2\\ &=&\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a,b\neq v_i,w_i}[d_{G_i}(a)+d_{G_i}(b)]^2\\ &&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq w_i}[d_{G_i}(a)+(d_{G_i}(b)+1)]^2\\ &&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq v_i}[d_{G_i}(a)+(d_{G_i}(b)+1)]^2\\ &&+\sum\limits_{i=2}^{d-1}[(d_{G_i}(v_i)+1)+(d_{G_i}(w_i)+1)]^2\\ &=&\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a,b\neq v_i,w_i}[d_{G_i}(a)+d_{G_i}(b)]^2\\ &&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq w_i}[d_{G_i}(a)+(d_{G_i}(v_i)]^2\\ &&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq v_i}[d_{G_i}(a)+(d_{G_i}(w_i)]^2\\ &&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq w_i}[1+2(d_{G_i}(a)+d_{G_i}(v_i))]\\ &&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq v_i}[1+2(d_{G_i}(a)+d_{G_i}(w_i))]\\ &=&\sum\limits_{i=2}^{d-1}HM(G_i)+\sum\limits_{i=2}^{d-1}[2d_{G_i}(v_i)^2+d_{G_i}(v_i)+2\delta_{G_i}(v_i)\\ &&+2d_{G_i}(w_i)^2+d_{G_i}(w_i)+2\delta_{G_i}(w_i)]. \end{eqnarray*} Finally, the contribution \(S_4(B_2)\) of all the edges \(w_iv_{i+1}\), for \(i=2,3,…,(d-1)\) is calculated as follows \begin{eqnarray*} S_4(B_2)&=&\sum\limits_{i=1}^{d-1}\sum\limits_{ab=w_iv_{i+1}}[d_{B_1}(a)+d_{B_1}(b)]^2\\ &=&\sum\limits_{i=2}^{d-2}[(d_{G_i}(w_i)+1)+d_{G_i}(v_{i+1})+1)]^2\\ &=&\sum\limits_{i=2}^{d-2}(w_i+v_{i+1}+4)^2\\ &=&\sum\limits_{i=2}^{d-1}[w_i^2+v_{i+1}^2+2w_iv_{i+1}+4w_i+4v_{i+1}+4]. \end{eqnarray*} Now combining the contributions \(S_1(B_2)\), \(S_2(B_2)\), \(S_3(B_2)\) and \(S_4(B_2)\), we get the desired expression.
Let, \(u\) and \(v\) are two vertices of a graph \(G\), and \(G_i=G\), \(v_i=v\) and \(w_i=w\) for all \(i=1,2,…,d\). Then using above Theorem 3.5 we directly get the following:Corrolary 3.6. The hyper Zagreb index of the bridge graph \(B_2\), \(d\ge 2\), is given by \[F(B_2)=dF(G)+3(d-1)(v^2+w^2+v+w)+2(d-1)\] where \(v=d_G(v)\), \(w=d_G(w)\) and \(v\), \(w\) are not adjacent.
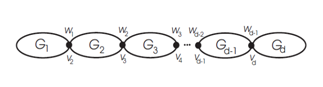
Lemma 4.1. The degree of the vertices of \(B_2\) is given by \[{d}_C(v) = \left\{ \begin{array}{ll} {{d}_{{{G}_{1}}}}(v),~if~v\in V({{G}_{1}})-\{w_1\},\\[2mm] d_{G_d}(v),~if~v\in V(G_d)-\{v_d\},\\[2mm] d_{G_i}(v),~if~v\in V(G_i)-\{v_i,w_i\},~2\leq i\leq d-1\\[2mm] w_i+v_i+1,~if~u=w_i=v_{i+1},~1\leq i\leq d-1,\\ \end{array}\right.\] where \(v_i=d_{G_i}(v_i)\), \(w_i=d_{G_i}(w_i)\), for \(1\leq i\leq d\).
In the following theorem, we now calculate hyper Zagreb index of chain graph \(C\).Theorem 4.2. The hyper Zagreb index of the Chain graph \(C\), \(d\ge 2\), is given by \begin{eqnarray*} HM(C)&=&\sum\limits_{i=1}^d HM(G_i)+\sum\limits_{i=2}^{d-1}[w_{i-1}^2v_i+2w_{i-1}\delta_{G_i}(v_i)+2w_{i-1}v_i^2]\\ &&+\sum\limits_{i=2}^{d-1}[w_iv_{i+1}^2+2v_{i+1}\delta_{G_i}(w_i)+2v_{i+1}w_i^2]+w_1v_2^2+2v_2\delta_{G_1}(w_1)\\ &&+2v_2w_1^2+w_{d-1}^2v_d+2w_{d-1}\delta_{G_d}(v_d)+2w_{d-1}v_d^2. \end{eqnarray*} where \(v_i=d_{G_i}(v_i)\), \(w_i=d_{G_i}(w_i)\); \(v_i\) and \(w_i\) are not adjacent, for \(1\leq i\leq d\).
Proof.
Using definition of F-index and Lemma 4.1, we procedure as follows:
First, we have the sum \(S_1(C)\) over the edges \(ab\in E(G_1)\) as follows
\begin{eqnarray*}
S_1(C)&=&\sum\limits_{ab\in E(G_1)}[d_C(a)+d_C(b)]^2\\
&=&\sum\limits_{ab\in E(G_1); a,b\neq w_1}[d_{G_1}(a)+d_{G_1}(b)]^2\\
&&+\sum\limits_{ab\in E(G_1); a\in V(G_1),b=w_1}[d_{G_1}(a)+(d_{G_1}(w_1)+d_{G_2}(v_2))]^2\\
&=&\sum\limits_{ab\in E(G_1); a,b\neq w_1}[d_{G_1}(a)+d_{G_1}(b)]^2\\
&&+\sum\limits_{ab\in E(G_1); a\in V(G_1),b=w_1}[d_{G_1}(a)+d_{G_1}(w_1)]^2\\
&&+\sum\limits_{ab\in E(G_1); a\in V(G_1),b=w_1}[d_{G_2}(v_2)^2+2d_{G_2}(v_2)(d_{G_1}(a)+d_{G_1}(w_1))]\\
&=&HM(G_1)+d_{G_2}(v_2)^2d_{G_1}(w_1)+2d_{G_2}(v_2)\delta_{G_1}(w_1)+2d_{G_2}(v_2)d_{G_1}(w_1)^2.
\end{eqnarray*}
Similarly we have the sum \(S_2(C)\) over the edges \(ab\in E(G_d)\).
\begin{eqnarray*}
S_2(C)&=&\sum\limits_{ab\in E(G_d)}[d_{C}(a)+d_{C}(b)]^2\\
&=&\sum\limits_{ab\in E(G_d);a,b\neq v_d}[d_{G_{d}}(a)+d_{G_d}(b)]^2\\
&&+\sum\limits_{ab\in E(G_d);a\in V(G_d),b=v_d}[d_{G_d}(a)+(d_{G_{d-1}}(w_{d-1})+d_{G_d}(v_d))]^2\\
&=&\sum\limits_{ab\in E(G_d);a,b\neq v_d}[d_{G_d}(a)+d_{G_d}(b)]^2\\
&&+\sum\limits_{ab\in E(G_d);a\in V(G_d),b=v_d}[d_{G_d}(a)+d_{G_d}(v_d)]^2\\
&&+\sum\limits_{ab\in E(G_d);a\in V(G_d),b=v_d}[2d_{G_{d-1}}(w_{d-1})(d_{G_d}(a)+d_{G_d}(v_d))\\
&&+d_{G_{d-1}}(w_{d-1})^2]\\
&=&HM(G_d)+d_{G_{d-1}}(w_{d-1})^2d_{G_d}(v_d)+2d_{G_{d-1}}(w_{d-1})\delta_{G_d}(v_d)\\
&&+2d_{G_{d-1}}(w_{d-1})d_{G_d}(v_d)^2.
\end{eqnarray*}
The third sum \(S_3(C)\) is taken over the edges \(ab\in E(G_i)\), for \(i=2,3,…,(d-1)\).
\begin{eqnarray*}
S_3(C)&=&\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i)}[d_{C}(a)+d_{C}(b)]^2\\
&=&\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a,b\neq v_i,w_i}[d_{G_i}(a)+d_{G_i}(b)]^2\\
&&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq w_i,b=v_i}[d_{G_{i-1}}(w_{i-1})+(d_{G_i}(v_i)]^2\\
&&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq v_i,b=w_i}[d_{G_i}(a)+(d_{G_i}(w_i)+d_{G_{i+1}}(v_{i+1}))]^2\\
&&+\sum\limits_{i=2}^{d-1}[(d_{G_i}(v_i)+d_{G_{i-1}}(w_{i-1}))+(d_{G_i}(w_i)+d_{G_{i+1}}(v_{i+1}))]^2\\
&=&\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a,b\neq v_i,w_i}[d_{G_i}(a)+d_{G_i}(b)]^2\\
&&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq w_i}[d_{G_i}(a)+(d_{G_i}(v_i)]^2\\
&&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq v_i}[d_{G_i}(a)+(d_{G_i}(w_i)]^2\\
&&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq w_i}[d_{G_{i-1}}(w_{i-1})^2+2d_{G_{i-1}}(w_{i-1})(d_{G_i}(a)+d_{G_i}(v_i))]\\
&&+\sum\limits_{i=2}^{d-1}\sum\limits_{ab\in E(G_i);a\neq v_i}[d_{G_{i+1}}(v_{i+1})^2+2d_{G_{i+1}}(v_{i+1})(d_{G_i}(a)+d_{G_i}(w_i))]\\
&=&\sum\limits_{i=2}^{d-1}HM(G_i)+\sum\limits_{i=2}^{d-1}[2d_{G_i}(v_i)^2+d_{G_i}(v_i)+2\delta_{G_i}(v_i)\\
&&+2d_{G_i}(w_i)^2+d_{G_i}(w_i)+2\delta_{G_i}(w_i)].
\end{eqnarray*}
Now combining the sums \(S_1(C)\), \(S_2(C)\) and \(S_3(C)\) the desired result follows.
Corollary 4.3. The hyper Zagreb index of the chain graph \(C\), \(d\ge 2\), is given by \[HM(C)=dHM(G)+(d-1)[(3vw(v+w)+2(w\delta_G(v)+v\delta_G(w))]\] where \(v=d_G(v)\), \(w=d_G(w)\) and \(v\), \(w\) are not adjacent.
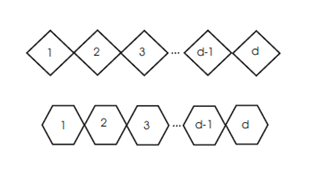
Example 5.1. First we consider a particular bridge graph, denoted by \[T_{d,n}=G_d(C_n,v)=B_1(C_n,C_n,…,C_n;v,v,…,v)(d-times),\] where \(v\) is an arbitrary vertex of degree 2 of \(C_n\) (see Figure 4). Applying Corollary 3.3, and after direct calculation we get the following \[HM(T_{d,n})=16nd+104d-138.\]
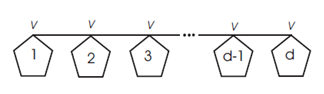
Example5.2. Let us now consider another particular bridge graph, denoted by \[B_d=G_d(P_3,v)=B_1(P_3,P_3,…,P_3;v,v,…,v)(d-times)\], where \(v\) is the middle vertex of degree 2 of the path graph \(P_3\) (see Figure 5). Applying Corollary 3.3 and after direct calculation we get the following \[HM(B_d)=114d-130.\]
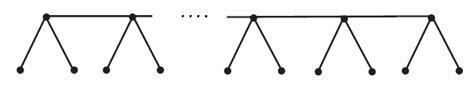
Example 5.3. Let us now consider a particular bridge graph, denoted by \[A_{d,m}=G_d(P_m,v)=B_1(P_m,P_m,…,P_m;v,v,…,v)(d-times)\], where \(v\) is the vertex of degree 1 of \(P_m\) (see Figure 6). Applying Corollary 3.3 and after direct calculation we get the following \[HM(A_{d,m})=16md+22d-76.\] Note that, the square comb lattice graph \(C_q(N)\) with open ends, is the bridge graph \(A_{n,n}\), where \(N=n^2\) is the total number of vertices.
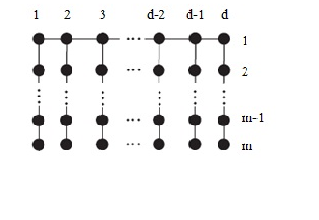
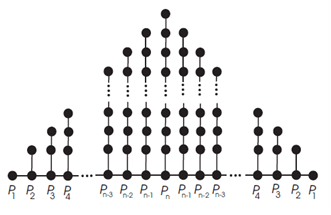
Example 5.4. Now we consider a particular bridge graph called the van Hove comb lattice graph \(CvH(N)\) with open ends. This graph can be represented as the bridge graph \[B_1(P_1,P_2,..,P_{n-1},P_n,P_{n-1},..,P_2,P_1;v_{1,1},v_{1,2},..,v_{1,n-1},v_{1,n},v_{1,n-1},..,\\v_{1,2},v_{1,1})\], where for \(2\leq i\leq n\), \(v_{1,i}\) is the first vertex of degree one of the path graph \(P_i\) and \(v_{1,1}\) is the single vertex of degree zero of the path \(P_1\) (Figure 7). So, using Corollary 3.1, we get, after calculation \[HM(CvH(N)=16n^2+44n-106.\]
Example 5.5. Next consider the molecular graph of the nanostar dendrimers \(D_n\)(as shown in Figure 8). This graph is equivalent to the bridge graph \[B_2(G,G,…,G;v,w,v,w,…,v,w)~ (n-times),\] where \(G\) is the graph given in Figure 9 and \(v\) and \(w\) are vertices of degree 2. Thus applying Corollary 3.6, we get \[HM(D_n)=450n+72(n-1)=522n-72\].
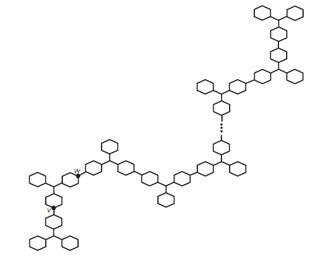
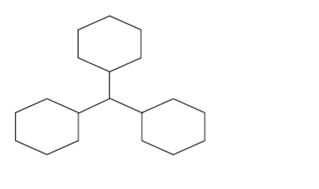
Example 5.6. The polyphenyl chain of \(h\) hexagon is said to be an ortho-\((O_h)\), meta-\((M_h)\) and para-\((L_h)\), if all its internal hexagons are ortho-hexagons, meta-hexagons and para-hexagons respectively. The polyphenyl chain \(O_h\), \(M_h\) and \(L_h\) may be considered as the second type of bridge graph \[B_2(C_6,C_6,…,C_6;v,w,v,w,…,v,w)\]. Here \(C_6\) is the cycle graph where every vertex is of degree two (i.e. \(v=w=2\)). The ortho-, meta-, para-polyphenyl chain of hexagons is given in Figure 10. So, using Corollary 3.6, we get from direct calculation \[HM(M_h)=HM(L_h)=96h+72(h-1)=168h-72.\] Also, applying Corollary 3.6, we get \[HM(O_h)=200h-138.\]
https://pisrt.org/wp-content/uploads/2018/01/10thgraph.png
Example 5.7. The spiro-chain of the graph \(G=C_n(k,l)\) is the chain graph \[C(G,G,…,G;v,w,v,w,…,v,w)\] where \(k\) and l are numbers of vertices \(v\) and \(w\) respectively. The spiro-chain of \(C_4\) and \(C_6\) are shown in Figure 11. The spiro-chain of \(d\) number of \(C_n(k,l)\) is denoted by \(S_d(C_n(k,l))\). Thus applying Corollary 4.3, we get \[HM(S_d(C_n(k,l)))=16nd+80d-80.\]