We introduce the generalized von Neumann-Jordan constant of a quasi-Banach space \(X\). Also, the quasi-Hilbert characteristic is introduced. An attempt has been made to investigate the relationship between them. At the end, a characterization of uniformly non-square is given.
In general, the study of the geometric property of a Banach space is not easy. Alternatively one can do this with the help of some reasonable geometric constants or moduli. These geometric constants may seem simple, but they were proved to be powerful tools for studying the geometric structure of Banach spaces. Several results on the Jordan-von Neumann constant (which is usually called the von Neumann-Jordan constant) of a Banach space \(X\), denoted by \(C_{NJ}(X)\), have recently been obtained by the authors [1,2], (we also refer to [3,4] for the classical results). To some extent, this constant is closely related to the parallelogram rule.
Because some basic tools are missing, we don’t have a lot of results about quasi-Banach spaces, some good results have been obtained by the authors [5,6,7]. Although the geometric properties of quasi-Banach spaces are difficult to study and different from Banach spaces, we can also describe it quantitatively. The most common way to create these descriptions is to define a real function and an appropriate constant closely related to it, depending on the spatial structure under consideration. Some geometric constants on quasi-Banach spaces have also been studied. These moduli are a taste of the shape of the unit sphere in space and whether the space has some geometric properties. The most recent research work with these moduli are investigated by [8,9,10].
In this paper, we introduce a new coefficient \(C_{NJ} (a,X)\) generalizing the von Neumann-Jordan constant and its properties. Additionally, the characteristics of quasi-Hilbert and its relationship with the modulus of convexity have also been discussed. Also, our analysis found an equivalence condition about uniformly non-square.
Definition 1.[11]
A quasi-norm on \(\Vert \cdot\Vert\) on vector space \(X\) over a field \(K\) \((\mathbb{R} \text { or } \mathbb{C})\) is a map \(X\longrightarrow [0, \infty)\) with the properties:
The Jordan-von Neumann constant of a Banach space \(X\), \(C_{NJ(X)}\) is defined by \[C_{\mathrm{NJ}}(X)=\sup \left\{\frac{\|x+y\|^{2}+\|x-y\|^{2}}{2\left(\|x\|^{2}+\|y\|^{2}\right)}: x, y \in X, \text { not both zero }\right\}.\] Now, we collect some properties about von Neumann-Jordan constant (see [1,12]):
Definition 2. Let \(X\) be a quasi-Banach space. Define \[C_{\mathrm{NJ}}(X)=\sup \left\{\frac{\|x+y\|^{2}+\|x-y\|^{2}}{2C^2\left(\|x\|^{2}+\|y\|^{2}\right)}: x, y \in X, \text { not both zero }\right\}.\]
Theorem 1. Let X be a quasi-Banach space. Then \[\frac{1}{C^2}\leq C_{NJ}(X)\leq2.\]
Proof. Let \(x\neq0,y=0\), then clearly \[\lim\limits_{y\rightarrow 0}\frac {\|x+y\|^2+\|x-y\|^2}{2C^2(\|x\|^2+\|y\|^2)}=\frac{\Vert x\Vert^2+\Vert x\Vert^2}{2C^2\Vert x\Vert^2}=\frac{1}{C^2}.\] We have \[C_{\mathrm{NJ}}(X)\geq\frac{1}{C^2}.\] On the other hand, \(\Vert x+y\Vert\leq C(\Vert x\Vert+\Vert y\Vert)\), so we have\(\Vert x+y\Vert^2\leq2C^2\Vert x\Vert^2+2C^2\Vert y\Vert^2\). In the same way, we have \(\Vert x-y\Vert^2\leq2C^2\Vert x\Vert^2+2C^2\Vert y\Vert^2\). We then obtain \[\frac{\Vert x+y\Vert^2+\Vert x-y\Vert^2}{2C^2\Vert x\Vert^2+2C^2\Vert y\Vert^2}\leq\frac{2C^2\Vert x\Vert^2+2C^2\Vert y\Vert^2+2C^2\Vert x\Vert^2+2C^2\Vert y\Vert^2}{2C^2\Vert x\Vert^2+2C^2\Vert y\Vert^2}=2.\] Thus \[C_{NJ} (X)\leq2.\] So \(\frac{1}{C^2}\leq C_{NJ} (X)\leq2\).
The generalization of the Jordan-von Neumann constant of \(X\) (see [13]) is defined by
\[ C_{\mathrm{NJ}}(a, X)=\sup \left\{\frac{\|x+y\|^{2}+\|x-z\|^{2}}{2\|x\|^{2}+\|y\|^{2}+\|z\|^{2}}\right. x, y, z \in X \text { not all zero } \text { and }\|y-z\| \leq a\|x\|\bigg\}. \] Now, we are going to study a more generalized von Neumann-Jordan constant \(C_{\mathrm{NJ}}(a, X)\) in a quasi-Banach space.Definition 3. Let \(X\) be a quasi-Banach space. Define \[ C_{\mathrm{NJ}}(a, X)=\sup \left\{\frac{\|x+y\|^{2}+\|x-z\|^{2}}{2C^2\|x\|^{2}+C^2\|y\|^{2}+C^2\|z\|^{2}}\right.: x, y, z \in X \text { not all zero } \\ \text { and }\|y-z\| \leq a\|x\|\bigg\}. \]
Theorem 2. Let \(X\) be quasi-Banach space, then for any \(a\geq0\) we have \[ \frac{1}{C^2}+\frac{4 a}{4C^2+C^2a^{2}} \leq C_{\mathrm{NJ}}(a, X) \leq 2. \]
Proof. For this, we take any \(x\in S_X\) and put \(y=\frac{a}{2}x=-z\), we then have \(y-z=ax\) and so, \[ \begin{aligned} C_{\mathrm{NJ}}(a, X) & \geq \frac{\|x+y\|^{2}+\|x-z\|^{2}}{2C^2\|x\|^{2}+C^2\|y\|^{2}+C^2\|z\|^{2}}=\frac{(1+\frac{a}{2})^{2}\|x\|^{2}+(1+\frac{a}{2})^{2}\|x\|^{2}}{2C^2\|x\|^{2}+2C^2\left(a^{2} / 4\right)\|x\|^{2}} \\ &=\frac{2(1+\frac{a}{2})^{2}}{2C^2\left(1+\frac{a^2}{4}\right)}=\frac{4+4 a+a^{2}}{4C^2+C^2a^{2}}=\frac{1}{C^2}+\frac{4 a}{4C^2+C^2a^{2}}. \end{aligned} \] Next, we show that \(C_{NJ}(a, X) \leq 2\). By the triangle inequality, we have \[ \begin{aligned}\|x+y\|^{2}+\|x-z\|^{2} & \leq\left(C^2\|x\|^{2}+2C\|x\|\|y\|+C^2\|y\|^{2}\right)+\left(C^2\|x\|^{2}+2C\|x\|\|z\|+C^2\|z\|^{2}\right) \\ & \leq\left(2C^2\|x\|^{2}+2C^2\|y\|^{2}\right)+\left(2C^2\|x\|^{2}+2C^2\|z\|^{2}\right) \\ &=4C^2\|x\|^{2}+2C^2\|y\|^{2}+2C^2\|z\|^{2}. \end{aligned} \] From which it is clear that \(C_{NJ}(a,X) \leq 2\).
The classical result by Jordan and von Neumann states the following criterium for checking when the norm derives from an inner product.
Theorem 3. ([4]) Let \((X, \Vert \cdot \Vert)\) be a real normed linear space. Then \(\Vert \cdot \Vert\) derives from an inner product if and only if the parallelogram law holds, i.e., \[\|x+y\|^{2}+\|x-y\|^{2}=2\|x\|^{2}+2\|y\|^{2}\] for all \(x,y \in X\).
There exist some modifications of Theorem 3, where the sign of equality is replaced by one of the inequality signs, or where the condition is satisfied for unit vectors only.
Theorem 4. [14] Let \((X, \Vert \cdot \Vert)\) be a real normed linear space. Then \(\Vert \cdot \Vert\) derives from an inner product if and only if \[\|x+y\|^{2}+\|x-y\|^{2} \sim 2\|x\|^{2}+2\|y\|^{2}\] for all \(x,y \in X\), where \(\sim\) stands either for \(\leq\) or \(\geq\).
Theorem 5. [15] Let \((X, \Vert \cdot \Vert)\) be a real normed linear space. Then \(\Vert \cdot \Vert\) derives from an inner product if and only if \[\|u+v\|^{2}+\|u-v\|^{2} \sim 4\] for all \(u,v \in S_X\), where \(\sim\) stands for one of the signs \(=\), \(\leq\) or \(\geq\).
As we all known, in a Banach space \(C_{NJ}(X)=1\) if and only if \(X\) is Hilbert space. In quasi-Banach spaces, we give a similar definition.
Definition 4. Let \(X\) be a quasi-Banach space, we call it quasi-Hilbert characteristic if for any \(x,y\in S_X\), we have \[\Vert x+y\Vert^2+\Vert x-y\Vert^2\leq 4C^2,\] where \(C\) is the modulus of concavity of the quasi-norm \(\Vert\cdot\Vert\).
Example 1. Let \(X=\mathbb{R}^2\) with the \(l_{\frac{1}{2}}\) norm \(\displaystyle\|x\|=\left(\sum_{i=1}^{2}\left|x_{i}\right|^{\frac{1}{2}}\right)^{2}\) for \(x=(x_1,x_2)\in \mathbb{R}^2\), we call it \(\mathbb{R}^{\frac{1}{2}}\) space. It has no quasi-Hilbert characteristic.
Proof. For \(x,y\in S_X\), \(x=(x_1,x_2)\), \(y=(y_1,y_2)\), we have
\[\|x\|=\left(\left|x_{1}\right|^{\frac{1}{2}}+\left|x_{2}\right|^{\frac{1}{2}}\right)^{2}=\left|x_{1}\right|+\left|x_{2}\right|+2\left(\left|x_{1}\right| \cdot\left|x_{2}\right|\right)^{\frac{1}{2}},\]
\[\|y\|=\left(\left|y_{1}\right|^{\frac{1}{2}}+\left|y_{2}\right|^{\frac{1}{2}}\right)^{2}=\left|y_{1}\right|+\left|y_{2}\right|+2\left(\left|y_{1}\right| \cdot\left|y_{2}\right|\right)^{\frac{1}{2}}\]
and
\[\|x+y\|=\left(\left|x_{1}+y_{1}\right|^{\frac{1}{2}}+\left|x_{2}+y_{2}\right|^{\frac{1}{2}}\right)^{2}=\left|x_{1}+y_{1}\right|+\left|x_{1}+y_{2}\right|+2\left(\left|x_{1}+y_{1}\right| \cdot\left|x_{2}+y_{2}\right|\right)^{\frac{1}{2}}.\]
So we can get
\[2\left|x_{1}+y_{1}\right|^{\frac{1}{2}} \cdot\left|x_{2}+y_{2}\right|^{\frac{1}{2}} \leq\|x \|+\| y \|\]
and
\[\left|x_{1}+y_{1}\right|+\left|x_{2}+y_{2}\right| \leq\|x \|+\| y \|.\]
Then we have
\[\Vert x+y\Vert\leq 2(\Vert x\Vert +\Vert y\Vert) .\]
According to the proof of Theorem 1, we have
\[\Vert x\pm y\Vert^2\leq 2\cdot2^2(\Vert x\Vert^2+\Vert y\Vert^2).\]
So we have
\[\Vert x+y\Vert^2+\Vert x-y\Vert^2\leq 2\cdot(2\sqrt2)^2(\Vert x\Vert^2+\Vert y\Vert^2)=4(2\sqrt2)^2=8C^2.\]
When \(x=(1,0)\), \(y=(0,1)\), the equality holds. Since \(2\sqrt2\neq2\), \(\mathbb{R}^{\frac{1}{2}}\) has no quasi-Hilbert characteristic.
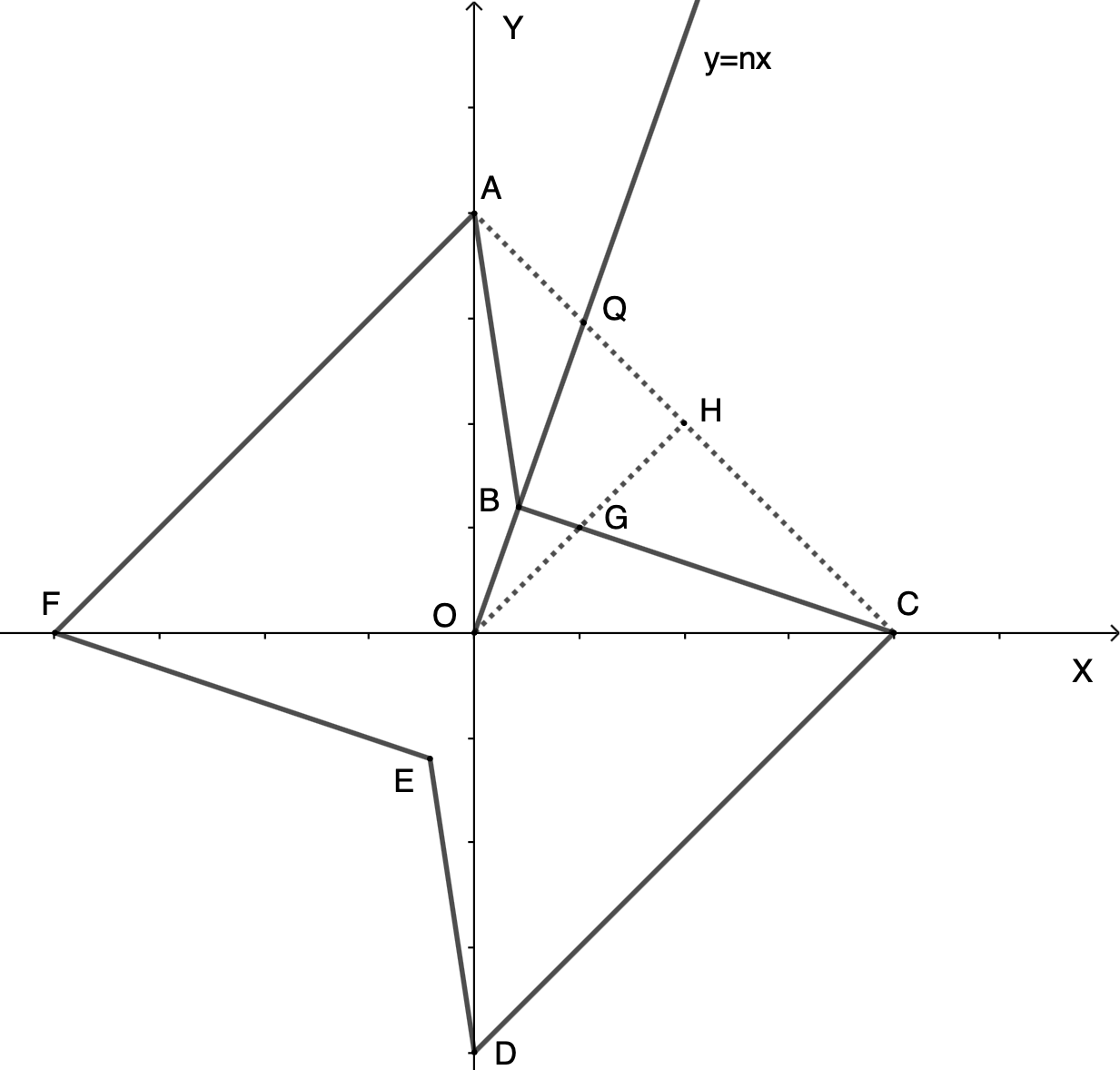
Example 2. An example of a quasi-Banach space is \((\mathbb R^2,\mu_B)\) whose unit ball is exactly the set of all the vectors inside polygon as shown in Figure 1, this figure is symmetric about the origin . The Minkowski functional \(\mu_B\) induced by the set polygon is a quasi-norm on \(R^2\), i.e. \((\mathbb{R}^2,\mu_B)\) is quasi-Banach space. For line \( y=nx\), its intersection with \(AC\) is \(Q\). \(H\) is the midponit of \(A\). Assume \(OQ=l_1\), \(OB=l_2\), here \(l_1>l_2\). According to the fact, We have \(C=\max_{\lambda \in [0,1]\atop x,y\in S_X} \Vert \lambda x+(1-\lambda)y\Vert\), here \(C\) is the modulus of concavity of the quasi-norm \(\Vert\cdot\Vert\). Based on geometric properties we have \(\max \Vert \lambda x+(1-\lambda)y\Vert=\frac{l_1}{l_2}=\Vert \overrightarrow{O Q}\Vert\), so we have \(C=\frac{l_1}{l_2}\). On the other hand, \(\forall x,y\in S_X\), we have \(\Vert \frac{x+y}{2}\Vert\leq\Vert \frac{\overrightarrow {O A}+\overrightarrow {O C} }{2}\Vert=\Vert \overrightarrow {O H}\Vert=\frac{OH}{OG}\), and \(OH=\frac{\sqrt 2}{2}\), \(OG=\frac{\sqrt 2 nl_2}{nl_2+(n+1)l_2-l_2}\), so we have \(\frac{OH}{OG}=\frac{nl_2+(n+1)l_2-l_2}{2nl_2}\). As long as \(l_2\) is small enough and \(n\) is large enough, we have \(\frac{OH}{OG}\leq\frac{l_1}{\sqrt 2\cdot l_2}=\frac{C}{\sqrt 2}\), then we have \(\Vert\frac{x+y}{2} \Vert\leq \frac{C}{\sqrt2}, \forall x,y \in S_X\). So \[ \Vert x+y\Vert^2+\Vert x-y\Vert^2\leq4C^2 \] it has quasi-Hilbert characteristic.
Definition 5.[8] The modulus of convexity of a quasi-Banach space \(X\) is defined as \[\delta(\epsilon)=\inf \left\{1-\left\|\frac{x+y}{2 C}\right\|: x,y \in S_X,~ \left\|\frac{x-y}{C}\right\| = \epsilon\right \}, \quad 0 \leq \epsilon \leq 2.\]
Theorem 6. Let \(X\) be a quasi-Banach space is quasi-Hilbert characteristic, we have \[ \delta_{X}(\epsilon)\geq1-\frac{1}{C} \sqrt{C^2-\frac{\epsilon^{2} C^{2}}{4}} .\]
Proof. Let \(x,y \in X\) with \(\Vert x\Vert = 1\), \(\Vert y\Vert = 1\) and \( \frac{\left\|x-y\right\|}{C}=\epsilon \). Since it has quasi-Hilbert characteristic, \[\Vert x+y\Vert^2+\Vert x-y\Vert^2\leq 4C^2.\] Thus \[ \begin{aligned}\left\|x+y\right\|^{2} &\leq4C^2-\left\|x-y\right\|^{2} \\ &=4C^2-\epsilon^{2} C^{2}. \end{aligned} \] Hence \[ \left\|x+y\right\|\leq\sqrt{4C^2-\epsilon^{2} C^{2}} .\] Thus we have \[ 1-\frac{\left\|x+y\right\|}{2 C}\geq1-\frac{\sqrt{4C^2-\epsilon^{2} C^{2}}}{2 C}. \] Which implies that \[ \inf \left\{1-\frac{\left\|x+y\right\|}{2 C}\right\}\geq1-\frac{1}{C} \sqrt{C^2-\frac{\epsilon^{2} C^{2}}{4}} .\] Hence, we get \[ \delta_{X}(\epsilon)\geq1-\frac{1}{C} \sqrt{C^2-\frac{\epsilon^{2} C^{2}}{4}} .\] This completes the proof.
Definition 6. Let \(X\) be a quasi-Banach space. Define \[E(X)=\sup\Bigg\{\frac{\Vert x+y\Vert^2+\Vert x-y\Vert^2}{C^2}:x,y\in S_X\Bigg\}.\] The following proposition can be found in [16], and we get the same result for quasi-Banach spaces.
Proposition 1. Let \(X\) be a Banach space, one has the following equality: \[ E(X)=\sup \left\{\epsilon^{2}+4\left(1-\delta_{X}(\epsilon)\right)^{2}: \epsilon \in[0,2]\right\}. \]
Theorem 7. Let \(X\) be a quasi-Banach space, one has the following equality: \[E(X)=\sup \left\{\epsilon^{2}+4\left(1-\delta_{X}(\epsilon)\right)^{2}: \epsilon \in[0,2]\right\}.\]
Proof. Take \(x\in S_X,y\in S_X\), and \(\Vert \frac{x-y}{C}\Vert=\epsilon\). It follows from the definition of \(E(X)\), that \[E(X) \geq \frac{C^2\epsilon^{2}+\|x+y\|^{2}}{C^2}.\] Thus we have \[\begin{aligned}1-\frac{\|x+y\|}{2C} &\geq 1-\frac{\sqrt{ C^2{E(X)-C^2\epsilon^{2}}}}{2C}\\&=1-\frac{\sqrt{E(X)-\epsilon^{2}}}{2}.\end{aligned}\] From the definition of \(\delta(\epsilon)\), we have that \[\begin{aligned}E(X) \geq \sup \left\{\epsilon^{2}+4\left(1-\delta(\epsilon)\right)^{2}\right\}.\end{aligned}\] On the other hand for every \(x, y \in S_X, \delta(\frac{\|x-y\|}{C}) \leq 1-\|x+y\| / 2C\), which implies that \[\begin{aligned}\|x+y\|^{2}+\|x-y\|^{2} & \leq C^2\epsilon^{2}+4C^2\left(1-\delta(\frac{\|x-y\|}{C})\right)^{2} \\ & \leq C^2\epsilon^{2}+4C^2\left(1-\delta(\epsilon)\right)^{2} .\end{aligned}\] Hence \(E(X) \leq \sup \left\{\epsilon^{2}+4\left(1-\delta(\epsilon)\right)^{2}\right\}\). So we obtain the desired equality.
Definition 7.[9] The modulus of uniform smoothness of a quasi-Banach space \(X\) is defined as \[ \rho_{1}(\epsilon)=\sup \left\{1-\frac{\|x+y\|}{2C}: x, y \in S_{X},\frac{\|x-y\|}{C}=\epsilon\right\}.\]
Definition 8.Let \(X\) be a quasi-Banach space. Define \[f(X)=\inf \left\{\frac {\|x+y\|^{2}+\|x-y\|^{2}}{C^2}: x, y \in S_{X}\right\}.\]
Theorem 8. Let \(X\) be a quasi-Banach space, one has the following equality: \[f(X)=\inf \{\epsilon^{2}+4\left(1-\rho_{1}(\epsilon)\right)^{2}: \epsilon \in[0,2]\} .\]
Proof. Take \(x\in S_X,y\in S_X\), and \(\frac{\Vert x-y\Vert}{C}=\epsilon\). It follows from the definition of \(f(X)\), that \[f(X) \leq \frac{C^2\epsilon^{2}+\|x+y\|^{2}}{C^2}.\] Thus we have \[\begin{aligned}1-\frac{\|x+y\|}{2C} &\leq 1-\frac{\sqrt{C^2f(X)-C^2\epsilon^{2}}}{2C}\\&=1-\frac{\sqrt{f(X)-\epsilon^{2}}}{2}.\end{aligned}\] From the definition of \(\rho_1(\epsilon)\), we have that \[f(X) \leq \inf \left\{\epsilon^{2}+4\left(1-\rho_{1}(\epsilon)\right)^{2}\right\}.\] On the other hand for every \(x, y \in S_X, \rho_{1}(\|x-y\|) \geq 1-\|x+y\| / 2C\), which implies that \[\begin{aligned}\|x+y\|^{2}+\|x-y\|^{2} & \geq C^2\epsilon^{2}+4C^2\left(1-\rho_{1}(\|x-y\|)\right)^{2} \\ & \geq C^2\epsilon^{2}+4C^2\left(1-\rho_{1}(\epsilon)\right)^{2}. \end{aligned}\] Hence \(f(X) \geq \inf \left\{\epsilon^{2}+4\left(1-\rho_{1}(\epsilon)\right)^{2}\right\}\). So we obtain the desired equality.
Now, we are going to introduce a special von Neumann-Jordan constant, and get some relationship with property of uniformly non-square.
Definition 9. Let \(X\) be a quasi-Banach space. Define \[C_{N J}^{\prime}(X)=\sup\Bigg\{\frac{\Vert x+y\Vert^2+\Vert x-y\Vert^2}{4C^2}:x\in B_X,y\in B_X\Bigg\} .\]
Definition 10.[10] A quasi-Banach space \(X\) is said to be uniformly non-square if there exists a positive number \(\delta< 2\) such that for any \(x,y\in S_X\), we have \[ \min \left(\left\|\frac{x+y}{C}\right\|,\left\|\frac{x-y}{C}\right\|\right) \leq \delta. \]
Theorem 9. For \(p \in (1, \infty)\). A quasi-Banach space \(X\) is uniformly non-square if and only if there exists \(\delta \in (0, 1)\) such that for any \(x, y \in X\), we have \[C_{N J}^{\prime}(X) \leq(2-\delta) \frac{\left\|x\right\|^{2}+\left\|y\right\|^{2}}{2}. \]
Proof. Let \(X\) be an uniformly non-square quasi-Banach space and on contrary assume that inequality is not hold. Therefore for every positive integer \(n\), there exists \(x_n\) and \(y_n\) in \(X\) such that \[ \frac{\Vert x_n+y_n\Vert^2+\Vert x_n-y_n\Vert^2}{4C^2}>\left(2-\frac{1}{n}\right) \frac{\left\|x_{n}\right\|^{2}+\left\|y_{n}\right\|^{2}}{2}. \] Let \(x_n \in S_X\) and \(y_n \in B_X =\{x\in X:\Vert x\Vert\leq1\}\) for all \(n\). Without loss of generality we assume that \({\Vert y_n\Vert}\) converges to some \(\gamma\), where \(0 \leq \gamma \leq 1\) we have \[ \begin{aligned}\left(2-\frac{1}{n}\right) \frac{1+\left\|y_{n}\right\|^{2}}{2} &<\left\|\frac{x_{n}+y_{n}}{2 C}\right\|^{2}+\left\|\frac{x_{n}-y_{n}}{2 C}\right\|^{2} \\ & \leq 2\left(\frac{C\left(\left\|x_{n}\right\|^{2}+\left\|y_{n}\right\|^{2}\right)}{2 C}\right)^{2} \\ &=2\left(\frac{1+\left\|y_{n}\right\|^{2}}{2}\right)^2 \\ & \leq 2\left(\frac{1+\left\|y_{n}\right\|}{2}\right)^2. \end{aligned} \] According the function \(f(\gamma)=\gamma^2\) is convex, which leads \[ (1+\gamma)^{2}=\left(2 \cdot \frac{1+\gamma}{2}\right)^{2} \leq 2^{2}\left(\frac{1+\gamma^{2}}{2}\right)=2\left(1+\gamma^{2}\right). \] Letting \(n \rightarrow \infty\), we obtain \[ \frac{(1+\gamma)^{2}}{1+\gamma^{2}}=2 \quad\text{then we have}\quad \gamma=1. \] Therefore \[ \left\|\frac{x_{n}+y_{n}}{2 C}\right\|^{2}+\left\|\frac{x_{n}-y_{n}}{2 C}\right\|^{2} \longrightarrow 2. \] This contradicts to the fact that \(X\) is uniformly non-square.
Conversely, suppose that
\[ \left\|\frac{x_{1}+x_{2}}{2 C}\right\|^{2}+\left\|\frac{x_{1}-x_{2}}{2 C}\right\|^{2} \leq(2-\delta) \frac{\left\|x_{1}\right\|^{2}+\left\|x_{2}\right\|^{2}}{2}. \] In particularly, let \(x_1,x_2\in S_X\) we have \[ \left\|\frac{x_{1}+x_{2}}{2 C}\right\|^{2}+\left\|\frac{x_{1}-x_{2}}{2 C}\right\|^{2} \leq(2-\delta). \] Which implies that \[ \min \left\{\left\|\frac{x_{1}+x_{2}}{C}\right\|,\left\|\frac{x_{1}-x_{2}}{ C}\right\|\right\} \leq2\left(1-\frac{\delta}{2}\right)^{\frac{1}{2}}. \] Hence \(X\) is uniformly non-square. This completes the proof.