Reachability results in labelled \(t\)-ary trees

1. Introduction

Mathematical trees (and their natural counterparts) have been studied for a very long time. In this work, we consider labelled \(t\)-ary trees, i.e. these are rooted trees embedded in the plane such that each vertex has a degree of at most \(t\) and the vertex set is \([n]:=\{1,2,\ldots,n\}\). Here, a degree of a vertex is the number of edges that come out of a vertex if the edges are oriented away from the root. Trees treated here have local orientation [1], i.e. the edges are oriented from a vertex of lower label towards a vertex of higher label. A vertex \(v\) is said to be reachable from a vertex \(i\) if there is an oriented path from vertex \(i\) to vertex \(v\) and we say that a path \(p\) has length \(\ell\) if there are \(\ell\) edges on the path. All paths are oriented. A vertex in which there is no edge that is oriented away from it is called a sink.

We note that in any labelled tree on \(n\) vertices, only one vertex (i.e itself) is reachable from vertex \(n\) since it is always a sink. It is also clear that many vertices can be reached from vertex \(1\) than from any other vertex. The vertices with the same parent are called siblings. Since the siblings are linearly ordered, they are always drawn in a left-right pattern where the leftmost sibling is referred to as first child. At level \(\ell\), the left most child of all the siblings is the eldest child. A left most path refers to a sequence of edges joining eldest children at each level in a plane tree. The corresponding results for ordinary trees and noncrossing trees were obtained in the PhD thesis [2]. Using the aforementioned statistics, Nyariaro and Okoth [3] worked on the corresponding results for ordered trees. From now henceforth, \(t\)-ary trees will be referred to as trees.

The paper is organized as follows: In §2, we obtain the number of these trees as enumerated by path lengths, number of sinks and number of leaf sinks. Enumeration by left most paths and first children is considered in §3. Finally, we use non-first children and non-leaves to enumerate the trees in §4. We derive most of our results by means of generating functions and Lagrange Inversion Formula [4].

2. Enumeration by path lengths, sinks and leaf sinks

The aim of this section is to find the average number of vertices, sinks and leaf sinks in labelled trees of order \(n\) that are reachable from a root of label \(i\).

Proposition 1. There are

labelled trees on \([n]\) such that vertex \(j\), of degree \(d\) and at length \(\ell\geq 0\), is reachable from root \(i\).

Proof. Let \(T(x)\) be the generating function of unlabelled trees such that \(x\) marks the number of non-root vertices. It follows that \(T(x)=(1+xT(x))^t\). Consider a tree rooted at \(i\) and having a path of length \(\ell\) terminating at a vertex of degree \(d\). There are \(\ell+1\) vertices in this path. The trees with such a path can be decomposed as shown in Figure 1.

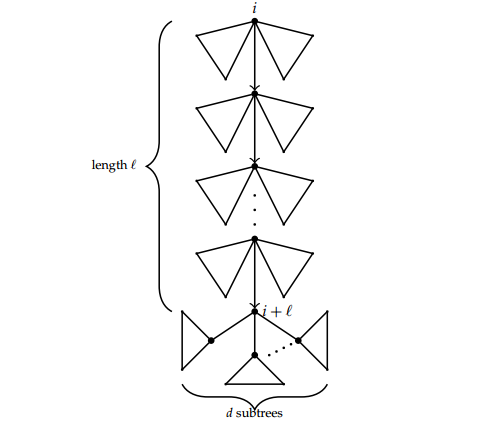
We therefore have the generating function for these trees as \[(xT(x)^2)^{\ell}x(xT(x))^d=x^{\ell+d+1}T(x)^{2\ell +d}.\] We need to extract the coefficient of \(x^{n}\) in the generating function. Set \(xT(x)=S(x)\) so that the generating function becomes \(x^{-\ell+1}S(x)^{2\ell+d}\). We also have \(S(x)=x(1+S(x))^t.\)

By Lagrange Inversion Formula, we obtain

\begin{align*} [x^n]x^{\ell+d+1}T(x)^{2\ell +d}&=[x^n]x^{-\ell+1}S(x)^{2\ell +d} =[x^{n+\ell-1}]S(x)^{2\ell +d}\\ &=\frac{2\ell+d}{n+\ell-1}[s^{n-\ell-d-1}](1+s)^{t(n+\ell-1)}\\ &=\frac{2\ell+d}{n+\ell-1}[s^{n-\ell-d-1}]\sum_{i\geq 0}{t(n+\ell-1)\choose i}s^{i}\\ &=\frac{2\ell+d}{n+\ell-1}{t(n+\ell-1)\choose n-\ell-d-1}. \end{align*}

This formula counts the number of unlabelled trees with a path of length \(\ell\) starting at the root and ending at a vertex of degree \(d\). There are \({t\choose d}\) possible positions for the children of the terminating vertex. Lets consider a path of length \(\ell\) starting at root \(i\) and ending at vertex \(j.\) There are \(\binom{j-i-1}{\ell-1}\) such paths. Once the \(\ell+1\) vertices on the path are labelled, there are \((n-\ell-1)!\) choices for labels of the vertices which are not on the path. Putting everything together, we obtain the required formula.

We remark that Equation (1) also gives the number of vertices of label \(j\) with degree \(d\) that are reachable from root \(i\) in \(\ell\) steps in all labelled trees of order \(n\). A number of corollaries follow for example by summing over all \(d\), we obtain the following corollary:

Corollary 1. The total number of labelled trees on \(n\) vertices such that vertex \(j\) is reachable from root \(i\) in \(\ell\geq 0\) steps is given by \begin{align*} \dfrac{(2\ell+1)(n-\ell-1)!}{n+\ell}{j-i-1\choose \ell-1} {t(n+\ell)\choose n-\ell-1}. \end{align*}

Corollary 2.The total number of labelled trees on \(n\) vertices such that vertex \(j\) is reachable from the root in \(\ell\geq 0\) steps is given by

Proof. The result follows by summing over all \(i\) in Equation (1).

Similarly, summing over all \(j\) in Equation (1), we obtain:

Corollary 3. There are

paths of length \(\ell\geq 0\) starting at the root in labelled trees of order \(n\).

By substituting for \(\ell=1\) and \(i=1\) in Equation (3), we obtain:

Corollary 4. There are a total of \(\frac{3n!}{n^2+n}{tn+t\choose n-2}\) children of root \(1\) in all labelled trees of order \(n.\)

By summing over all \(j\) in Equation (2) or by summing over all \(i\) in Equation (3) we arrive at the total number of paths of length \(\ell\) in labelled trees on \([n]\) whose formula is given by If \(\ell=0\) in Equation (4), we recover the formula, \((n-1)!{tn\choose n-1}\), for the number of labelled trees on \(n\) vertices. By substituting for \(\ell=1\) in Equation (4), we obtain:

Corollary 5. There are a total of \(\frac{3n!}{2n+2}{tn+t\choose n-2}\) children of the root in all labelled trees of order \(n.\)

Corollary 6. The average number of vertices, at length \(\ell\geq 0\), that are reachable from the root in a random labelled tree is \((2\ell+1)/(t^{\ell}(\ell+1)!)\).

Proof. By dividing Equation (4) by \((n-1)!{tn\choose n-1}\), the number of labelled trees on \(n\) vertices, we obtain

as the average number of vertices that can be reached from the root in labelled trees of order \(n\). Now, let \[A=\dfrac{2\ell+1}{(\ell+1)!}\cdot\dfrac{(t(n+\ell)-1)(t(n+\ell)-2)\cdots (t(n+\ell)-(n-\ell-2))n(n-1)\cdots (n-\ell)}{n(tn-1)(tn-2)\cdots (tn-n+2)},\] so that \begin{align*} \lim_{n\rightarrow \infty}A&=\dfrac{2\ell+1}{(\ell+1)!}\cdot\lim_{n\rightarrow \infty}\dfrac{t^{n-\ell-2}n^{n-\ell-2}n^{\ell+1 }+\cdots}{t^{n-2}n^{n-1}+\cdots}=\dfrac{2\ell+1}{(\ell+1)!}\cdot\lim_{n\rightarrow \infty}\dfrac{n^{n-1}+\cdots}{t^{\ell}n^{n-1}+\cdots}\\ &=\dfrac{2\ell+1}{(\ell+1)!}\cdot\dfrac{1}{t^{\ell}}\cdot\lim_{n\rightarrow \infty}\dfrac{1+\cdots}{1+\cdots}=\dfrac{2\ell+1}{(\ell+1)!}\cdot\dfrac{1}{t^{\ell}}. \end{align*} This completes the proof.

From Equation (4), we get the total number of reachable vertices in these trees of order \(n\) as \begin{align*} n!\sum_{\ell=0}^{n-1}\dfrac{(2\ell+1)}{(\ell+1)!(n+\ell)} {t(n+\ell)\choose n-\ell-1}. \end{align*} We now enumerate the trees by sinks:

Proposition 2. The number of labelled trees on \([n]\) such that a sink \(j\), of degree \(d\) and at length \(\ell\geq 0\), is reachable from root \(i\) is given by,

Proof. From the proof of Proposition 1, it follows that there are \begin{align*} \frac{2\ell+d}{n+\ell-1}{t(n+\ell-1)\choose n-\ell-d-1} \end{align*} unlabelled trees with a path of length \(\ell\) starting at the root such that the terminating vertex has degree \(d\). Lets consider a path of length \(\ell\) starting at root \(i\) and ending at vertex \(j.\) There are \(\binom{j-i-1}{\ell-1}\) such paths. Since vertex \(j\) is a sink of degree \(d\), the labels of the \(d\) vertices must be less than \(j\). Thus there are \({j-\ell-1\choose d}\) choices for these labels. There are \({t}\choose {d}\) possible positions for children of final vertex. Once the \(\ell+1\) vertices on the path and the \(d\) children of \(j\) are labelled, there are \((n-\ell-d-1)!\) choices for other labels in the tree. Collecting everything, we arrive at the required formula.

It is worthwhile to note Equation (6) also gives the number of sinks of label \(j\) with degree \(d\) that are reachable from root \(i\) in \(\ell\) steps in all labelled trees of order \(n\). Again a number of corollaries follow. By summing over all \(d\), we obtain that

Corollary 7. The total number of sinks of degree \(d\) that are reachable from vertex \(i\) in \(\ell\) steps in labelled trees of order \(n\) is given by \begin{align*} {(n-\ell-d-1)!}\frac{2\ell+d}{n+\ell-1}\sum_{j=\ell+i}^{n}{\begin{pmatrix}{j-i-1}\\{\ell-1}\end{pmatrix}}\begin{pmatrix}{j-\ell-1}\\{d}\end{pmatrix}{{t}\choose {d}}\begin{pmatrix}{t(n+\ell-1}\\{n-d-\ell-1}\end{pmatrix}. \end{align*}

Proof. We obtain the formula by summing over all \(j\) in Equation (6).

Corollary 8. The total number of labelled trees with \(n\) vertices such that root \(i\) is a sink of degree \(d\) is given by:

Proof. The result follows by setting \(\ell=0\) and \(j=i\) in Equation (6).

Corollary 9. The total number of labelled trees of order \(n\) with root sinks of degree \(d\) is given by:

Proof. The result follows by summing over all \(i\) in Equation (7).

The following result is immediate by setting \(\ell=1\) in Equation (6).

Corollary 10. Irrespective of the label of the root, the number of children of the root labelled \(j\) and having degree \(d\), in labelled trees on \(n\) vertices is given by:

Summing over all \(j\) in Equation (9), we obtain the number of children of the root which are sinks of degree \(d\), in trees of order \(n\) as \begin{equation*} {(n-d-2)!}\frac{2+d}{n}\begin{pmatrix}{n-d-1}\\{d+1}\end{pmatrix}{{t}\choose{d}}\begin{pmatrix}{tn}\\{n-d-2}\end{pmatrix}. \end{equation*}

Corollary 11. The average number of root sinks of degree \(d\) in a random tree of order \(n\) is

Proof. Diving the total number of labelled trees of order \(n\) with root sinks of degree \(d\) (Equation (8)), by the total number of labelled trees we get, \begin{align*} \frac{{(n-d-1)!}\frac{d}{n-1}\begin{pmatrix}{n}\\{d+1}\end{pmatrix}\displaystyle{t\choose d}\begin{pmatrix}{t(n-1)}\\{n-d-1}\end{pmatrix}}{\frac{n!}{n}\begin{pmatrix}{tn}\\{n-1}\end{pmatrix}}, \end{align*} as the average number of root sinks of degree \(d\) in a random plane tree on \(n\) vertices. The result follows by simplification and tending \(n\) to infinity.

Setting \(d=0\) in Equation (10) we get that the average number of root sinks of degree \(0\) is zero. This implies that there is no leaf sink which is also a root.

For the remainder of this section, we enumerate the trees by leaf sinks. The following result follows by setting \(d=0\) in Equation (6). However, to show the decomposition of trees with a leaf sink, we shall construct the proof.

Corollary 12. The number of labelled trees on \([n]\) such that vertex \(j\) is a leaf sink reachable from vertex \(i\) in \(\ell \) steps is given by

Proof. Let \(T(x)\) be the generating function of unlabelled trees such that \(x\) marks the number of non-root vertices. Consider a tree rooted at vertex \(i\) and having a path of length \(\ell\) starting at \(i\) and ending at \(i+\ell\). Let vertex \(i+\ell\) be a leaf sink. The path decomposes the tree into right an left subtrees up to length \(\ell\). Such trees are pictorially represented in Figure 2.

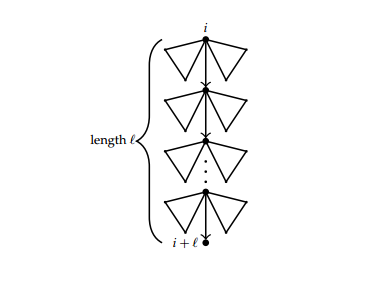
The generating function for these trees is thus \((xT(x)^{2})^{\ell}x=x^{\ell+1}T(x)^{2\ell}.\) We set \(xT(x)=S(x)\) and use Lagrange Inversion Formula to obtain

\begin{align*} [x^n]x^{\ell+1}T(x)^{2\ell}=[x^{n+\ell-1}]S(x)^{2\ell}&=\frac{2\ell}{n+\ell-1}[s^{n-\ell-1}](1+s)^{t(n+\ell-1)}\\ &=\frac{2\ell}{n+\ell-1}[s^{n-\ell-1}]\sum_{i\geq{0}}{t(n+\ell-1)\choose i}s^i\\ &=\frac{2\ell}{n+\ell-1}{t(n+\ell-1)\choose n-\ell-1}. \end{align*} Consider a path of length \(\ell\) starting from vertex \(i\) and terminating at vertex \(j\). There are \({j-i-1 \choose \ell-1}\) such paths. Once \(\ell+1\) vertices on the path have been labelled, there are \((n-\ell-1)!\) choices for labels of the vertices which are not on the path. Therefore, putting everything together we obtain the desired formula.

Summing over all \(j\) in Equation (11), we obtain the result below:

Corollary 13. There are

paths of length \( \ell\geq{0}\) starting at root \(i\) and ending at a leaf sink in a labelled tree of order \(n\).

Corollary 14. The total number of labelled trees on \(n\) vertices such that vertex \(j\) is a leaf sink reachable from the root in \(\ell\geq{0}\) steps is given by

Proof. We obtain the desired result by summing over all \(i\) in Equation (12).

Moreover, summing over all \(\ell\) in Equation (13) we obtain the following result:

Corollary 15. The number of leaf sinks in a labelled tree of order \(n\) that are reachable from the root is given by \begin{align*} n!\sum_{\ell=0}^{n-1}\frac{2\ell}{(\ell+1)!(n+\ell-1)}{t(n+\ell-1)\choose n-\ell-1}. \end{align*}

Corollary 16. The average number of leaf sinks that are reachable from the root in \(\ell\) steps in a random tree of order \(n\) is given by: \begin{align*} \frac{2\ell}{(\ell+1)!t^\ell}\,. \end{align*}

Proof. The result follows by dividing Equation (13) by \((n-1)!{tn\choose n-1}\), and tending \(n\to\infty\).

3. Enumeration by left most paths and first children

In this section, we obtain the number of trees with a given number of first children and also with a left most path of a given length.

Proposition 3. The number of labelled trees of order \(n\) in which there is a left most path of length \(\ell\) from root \(i\) to vertex \(j\) is given by

Proof. Let \(T(x)\) be the generating function for unlabelled trees, where vertex \(x\) marks the number of non-root vertices. Consider a tree rooted at vertex \(i\) and having a path of length \(\ell\) terminating at vertex \(\ell+1\). There are \(\ell+1\) vertices on the path. These trees are represented pictorially as shown in Figure 3.

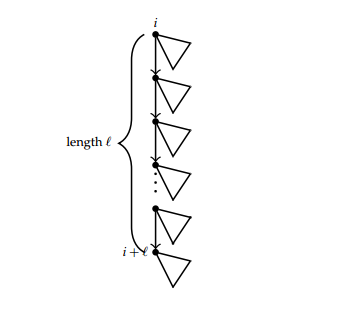
The generating function for the trees is therefore expressed as \(x^{\ell+1}T(x)^{\ell+1}.\) Since \(T(x)=(1+xT(x))^{t}\), we set \(xT(x)=S(x)\), and making use of Lagrange Inversion formula, we get

\begin{align*} [x^{n}]x^{\ell+1}T(x)^{\ell+1}=[x^{n}]S(x)^{\ell+1}&=\frac{\ell+1}{n}{[s^{n-\ell-1}]}(1+s)^{tn} =\frac{\ell+1}{n}[s^{n-\ell-1}]\sum_{i\geq{0}} {tn \choose i} s^{i} =\frac{\ell+1}{n}{tn \choose n-\ell-1}. \end{align*} As before, there are \(\displaystyle{j-i-1 \choose \ell-1}\) choices for paths of length \(\ell\) between vertices \(i\) and \(j\). Once \(\ell+1\) vertices on the path have been labelled, there are \((n-\ell-1)!\) ways of labelling the remaining vertices which are not on the path. Thus, having everything altogether we obtain Formula (14).

Corollary 17. The number of labelled trees on \(n\) vertices with a left most path of length \(\ell\) from vertex \(i\) is given by

Proof. The desired formula is obtained by summing over all \(j\) in Equation (14).

The following result follows by summing over all \(i\) in Equation (15).

Corollary 18. The number of labelled trees of order \(n\) in which there is a left most path of length \(\ell\) from the root is given by

Corollary 19. The number of labelled trees of order \(n\) in which there is a left most path starting form the root is given by \begin{align*} (n-1)!\sum_{\ell=0}^{n-1}\frac{1}{\ell!}{tn\choose n-\ell-1}. \end{align*}

Proof. We obtain the required formula by summing over all \(\ell\) in Equation (16).

Corollary 20. The average number of trees on \(n\) vertices with a left most path of length \(\ell\) from the root is given by \(\frac{1}{\ell! t^{\ell}}\).

Proof. The result follows by dividing Equation (16) by \((n-1)!{tn\choose n-1}\), and tending \(n\to\infty\).

Proposition 4. The number of labelled trees of order \(n\) rooted at vertex \(i\) in which there is a left most path of length \(\ell\) such that the final vertex \(j\) is a leaf sink is given by

Proof. Let \(T(x)\) be the generating function of a trees where \(x\) marks non-root vertices. Now, consider a tree rooted at vertex \(i\) such that there is a left most path of length \(\ell\) starting at root \(i\) and ending at vertex \(i+\ell\) which is also a leaf sink. The path decomposes the tree into right subtrees only up to length \(\ell\). The final vertex, being a leaf sink, has no subtree attached to it. See Figure 4 for the decomposition.

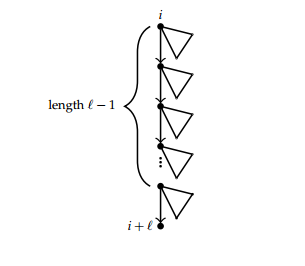
Therefore, the generating function of the above tree is given by \(x^{\ell+1}T(x)^{\ell}.\) As already seen in this paper, we set \(xT(x)=S(x)\) so that \(x^{\ell+1}T(x)^{\ell}= xS(x)^{\ell} \) and we use Lagrange Inversion Formula to extract the coefficient of \(x^n\) in the generating function:

\begin{align*} [x^{n}]x^{\ell+1}T(x)^{\ell}=[x^{n-1}]S(x)^{\ell}&=\frac{\ell}{n-1}[s^{n-\ell-1}](1+s)^{t(n-1)} =\frac{\ell}{n-1}[s^{n-\ell-1}]\sum_{i\geq{0}} {t(n-1) \choose i}s^{i} =\frac{\ell}{n-1}{t(n-1) \choose n-\ell-1}. \end{align*} The result follows by choosing the labels for the vertices on the path and for the vertices which are not on the path.

By summing of all \(j\) in Equation (17), we obtain the following result.

Corollary 21. There are

labelled trees of order \(n\) with a left most path of length \(\ell\) with vertex \(i\) as a root and final vertex \(j\) as a leaf sink.

Also, summing over all \(i\) in Equation (18), we obtain the following result.

Corollary 22. The number of labelled trees of order \(n\) in which there is a left most path of length \(\ell\) from the root and a final vertex as a leaf sink is given by

Corollary 23. The number of labelled trees of order \(n\) in which there is a left most path starting from the root and ending at a leaf sink is given by \begin{align*} \frac{n!}{n-1}\sum_{\ell=0}^{n-1} \frac{\ell}{(\ell+1)!} {t(n-1)\choose n-\ell-1}. \end{align*}

Proof. The result is immediate by summing over all \(\ell\) in Equation (19).

Proposition 5. The number of labelled trees on \(n\) vertices with vertex \(i\) as a root and vertex \(j\) as a first child at level \(\ell\) is given by

Proof. Let \(T(x)\) be the generating function of trees where \(x\) marks non-root vertices. Consider tree with a path of length \(\ell\) starting from vertex \(i\) and terminating at vertex \(i+\ell\) which is also a first child. The path decomposes the tree into left and right subtrees up to length \(\ell-1\). Since vertex \(i+\ell\) is a first child then its parent has no left subtrees. Moreover, vertex \(i+\ell\) has a subtree attached to it, which can possibly be empty. The tree is represented as in Figure 5.

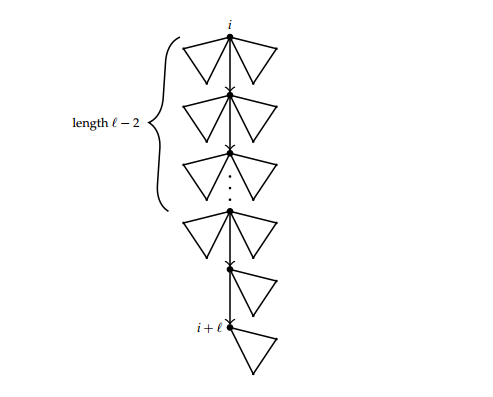
The generating function for the number of these tree is thus \((xT(x)^{2})^{\ell-1}(xT(x))^{2}=x^{\ell+1}T(x)^{2\ell}\). We set \(xT(x)=S(x)\) and apply Lagrange Inversion Formula to obtain

\begin{align*} [x^{n}]x^{\ell+1}T(x)^{2\ell}=[x^{n+\ell-1}]S(x)^{2\ell}&=\frac{2\ell}{n+\ell-1}[s^{n-\ell-1}](1+s)^{t(n+\ell-1)}\\ &=\frac{2\ell}{n+\ell-1}[s^{n-\ell-1}]\sum_{i\geq{0}}{t(n+\ell-1) \choose i}s^{i}\end{align*} \begin{align*}&=\frac{2\ell}{n+\ell-1}{t(n+\ell-1)\choose {n-\ell-1}}. \end{align*} The number of choices for a path of length \(\ell\) between vertex \(j\) and vertex \(i\) is \(j-i-1\choose \ell-1\). Once the \(\ell+1\) vertices along the path have been labelled, then the remaining vertices can be labelled in \((n-\ell-1)!\) ways. Therefore, by putting all the terms together we obtain the desired closed formula.

Corollary 24. The number of first children at level \(\ell\) that are reachable from vertex \(i\) in a labelled tree of order \(n\) is given by

Proof. We sum over all \(j\) in Equation (20) to obtain the desired result.

Corollary 25. The number of first children at level \(\ell\) that are reachable from the root in a labelled tree on \(n\) vertices is

Proof. The required formula follows by summing over all \(i\) in Equation (21).

By summing over all \(\ell\) in Equation (22), we obtain the following result.

Corollary 26. There are \begin{align*} n!\sum_{\ell=0}^{n-1}\frac{2\ell}{(\ell+1)!(n+\ell-1)}{t(n+\ell-1)\choose n-\ell-1} \end{align*} first children in labelled tree of order \(n\) that are reachable from the root.

Corollary 27. The average number of first children at level \(\ell\) in a random labelled tree is given by \(\frac{2\ell}{(\ell+1)!t^{\ell}}.\)

Proof. The required formula is arrived at by dividing Equation (22) by \((n-1)!{tn \choose {n-1}}\) and tending \(n\) to infinity.

Remark 1. It is worth noting that the generating function for the number of trees with a leaf sink at length \(\ell\) from the root is the same as the generating function for the trees with a first child at length \(\ell\). Thus the results are quite the same.

4. Enumeration by non-first children and non-leaves

In this section, we enumerate trees by number of reachable non-first children and non-leaves.

Proposition 6. The number of labelled trees on \([n]\) in which vertex \(i\) is a root such that there is a path of length \(\ell\) starting at \(i\) and terminating at vertex \(j\) which is also a non-first child is given by

Proof. Consider a tree rooted at vertex \(i\) with a path of length \(\ell\) from the root to vertex \(i+\ell\) which is non-first child. This path decomposes the tree into left and right subtrees up to step \(\ell\). Moreover, since vertex \(i+\ell\) is a non-first child, there must be an elder sibling of \(i+\ell\). Vertex \(i+\ell\) can have a subtree attached to it, which is possibly empty. This decomposition is represented by Figure 6.

The generating function for these trees is thus \((xT(x)^{2})^{\ell}xT(x)xT(x)=x^{\ell+2}T(x)^{2\ell+2}\), where \(T(x)\) is the generating function for unlabelled rooted trees with \(x\) marking non-root vertices. We set \(xT(x)=S(x)\) and apply Lagrange Inversion Formula to obtain

\begin{align*} [x^{n}]x^{\ell+2}T(x)^{2\ell+2}=[x^{n+\ell}]S(x)^{2\ell+2}&=\frac{2\ell+2}{n+\ell}[s^{n-\ell-2}(1+s)^{t(n+\ell)}\end{align*}\begin{align*} &=\frac{2\ell+2}{n+\ell}[s^{n-\ell-2}]\sum_{i\geq{0}}{t(n+\ell)\choose i}s^{i}\\ &=\frac{2\ell+2}{n+\ell}{t(n+\ell)\choose n-\ell-2}. \end{align*} There are \(j-i-1 \choose \ell-1\) choices for paths of length \(\ell\) between vertex \(i\) to vertex \(j\). Once the \(\ell+1\) vertices on the path have been labelled, the remaining vertices can be labelled in \((n-\ell-1)!\) ways. Thus putting everything together we obtain the desired formula.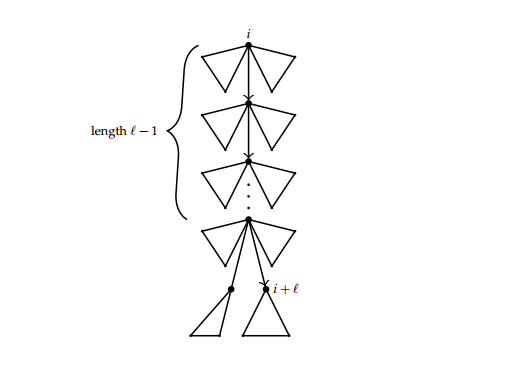

The next result follows by summing over all \(j\) in Equation (23).

Corollary 28. The total number of labelled trees of order \(n\) such that a non-first child at length \(\ell\) is reachable from a root \(i\) is given by

Summing over all \(i,\) in (24) we obtain:

Corollary 29. The total number of labelled trees on \(n\) vertices such that a non-first child at length \(\ell\) is reachable from the root is given by

Similarly, by summing over all \(\ell\) in Equation (25), we find that

Corollary 30. There are \begin{align*} 2n!\sum_{\ell=0}^{n-1}\frac{1}{\ell!(n+\ell)}{t(n+\ell)\choose n-\ell-2} \end{align*} labelled trees with a non-first child at level \(\ell\) that is reachable from the root.

Corollary 31. The average number of non-first children at level \(\ell\) in a random tree is given by \(\frac{2}{\ell!t^{\ell}}\).

Proof. Dividing Equation (25) by \((n-1)! {tn \choose {n-1}}\), we obtain the average number of non-first children that are reachable from the root at length \(\ell\) in trees of order \(n\). Now, simplifying the average and tending \(n\) to infinity we arrive at the required formula.

We now enumerate the trees by the number of non-leaves.

Proposition 7. The number of labelled trees on \([n]\) in which vertex \(i\) is a root such that there is a path of length \(\ell\) starting at \(i\) and terminating at a non-leaf vertex \(j\) is given by the formula,

Proof. Consider a tree rooted at vertex \(i\) with a path of length \(\ell\) from the root to vertex \(i+\ell\) which is non-leaf. This path decomposes the tree into left and right subtrees up to step \(\ell\). Moreover, since vertex \(i+\ell\) is a non-leaf, there must be a subtree of \(i+\ell\) which may be empty and a subtree, rooted at a child of \(i+\ell\). This subtree may also be empty. The decomposition is therefore given by Figure 7.

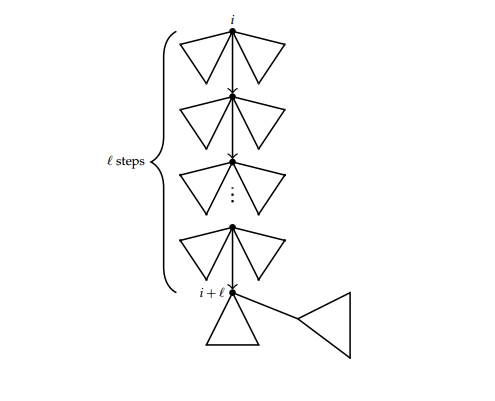
The generating function for the trees is thus \((xT(x)^{2})^{\ell}xT(x)xT(x)=x^{\ell+2}T(x)^{2\ell+2}\), where \(T(x)\) is the generating function for unlabelled rooted trees with \(x\) marking non-root vertices. The required result therefore follows by applying Lagrange Inversion formula, upon setting \(xT(x)=S(x)\), and giving the number of choices for the labels on the path and those that are not on the path.

Remark 2. The number of trees with a non-leaf vertex \(j\) which is reachable at length \(\ell\) from a root \(i\) have similar generating functions (though different decompositions) as for the case of non-first children. The results in the case of non-first children therefore hold for non-leaf vertices.

Author Contributions:

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest

“The authors declare no conflict of interest”.