Certain topological indices of Basava wheel windmill graph

1. Introduction

A topological index, also known as a connectivity index in the field of chemical graph theory, is a form of molecular descriptor that is derived based on the molecular graph of a chemical compound. Topological indices are involved in the construction of quantitative structure-activity relationships (QSARs), in which the biological activity or other attributes of molecules are associated with their chemical structure.

Throughout this paper, we have considered only finite, connected, undirected graph without loops and multiple edges of \(n\) vertices and \(m\) edges and is called \((n,m)\) graph. We denote vertex set as \(V(G)\) and edge set as \(E(G)\) of graph \(G\), respectively. For a graph \(G\), the degree of a vertex \(v\) is the number of edges incident to \(v\) and is denoted by \(d_G(v)\). For unexplained graph terminology and notation refer [1,2].

Definition 1.[1] The wheel graph is a graph obtained from a cycle graph \(C_{n-1}\) by adding a new vertex which is adjacent to the vertices of a cycle \(C_{n-1}\). That is \(W_n=K_1+C_{n-1}\) is a graph with \(n\) vertices and \(2(n-1)\) edges.

Now a days, topological indices are extensively used in mathematical chemistry. Among them, first and second Zagreb indices of a graph \(G\) were defined by Gutman and Trinajsti\(\acute{c}\) [3] in 1972 as, The first Zagreb index of a graph \(G\) [4] can also be defined as, The forgotten topological index or F-index of a graph \(G\) was introduced by Furtula and Gutman [5] as, The first hyper-Zagreb index of a graph \(G\) was introduced by Shirdel et al., in [6] as, The second hyper-Zagreb index of a graph \(G\) was introduced by Farahani et al., in [7] as, The harmonic index of a graph \(G\) was introduced by Fajtlowicz in [8] as, The Randic index or product connectivity index of a graph \(G\) was proposed by Randic in [9] as, The sum connectivity index of a graph \(G\) was defined in [10] as, The general Randic index of a graph \(G\) was defined as, The general sum connectivity index of a graph \(G\) was defined as, The above two topological indices were proposed in [3,11].

The atom-bond connectivity index of a graph \(G\) was defined in [12] as,

The geometric-arithmetic index of a graph \(G\) was defined in [13] as, The symmetric division deg index of graph \(G\) [14] is defined as, The concept of Sombor index \((SO)\) of a graph \(G\) was recently introduced by Gutman in [15] as, Further, we have extend to the new degree based topological indices of general \(SK_{\alpha}\) and general \(SK^{\alpha}_1\) indices of a graph \(G\).

The general \(SK_{\alpha}\) index of a graph \(G\) is defined as,

For \(\alpha=1\), we get, the \(SK_1(G)\) index of a graph \(G\) [16], which is defined as, For \(\alpha=2\), we get, the \(SK_2\) index of a graph \(G\) [16], which is defined as, The general \(SK^{\alpha}_1(G)\) index of a graph \(G\) is defined as, For \(\alpha=1\), we get, the \(SK^{1}_1\) index of a graph \(G\) [16], which is defined as, For \(\alpha=2\), we get, the \(SK^{2}_1(G)\) index of a graph \(G\), which is defined as, In the literature review, many researchers are studied on windmill graphs, see for example, [17,18]. Recently Kulli et al., [19,20] proposed two windmill graphs which are Kulli cycle and Kulli path windmill graphs. Motivated by this, we have proposed the Basava wheel windmill graph, which is defined as below;

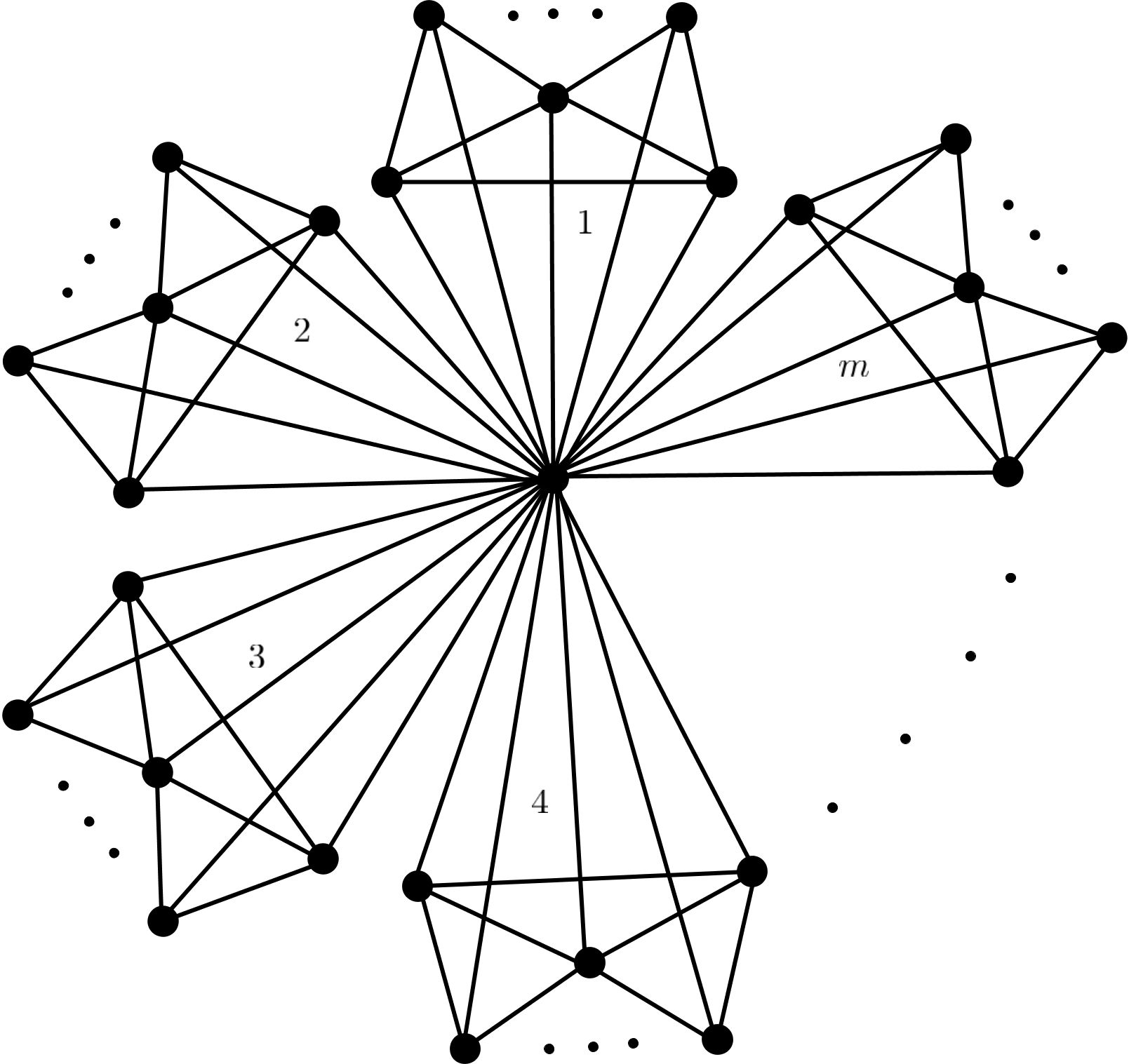
Definition 2. The Basava wheel windmill graph \(W^{(m)}_{n+1}\) is the graph obtained by taking \(m\geq 2\) copies of the graph \(K_1+W_{n}\) for \(n\geq 4\) with a vertex \(K_1\) in common. This graph is shown in Figure-1. The Basava wheel windmill graph \(W^{(m)}_{4+1}\) is a french windmill graph \(F^{(m)}_{5}\).

Let \(G\) be the Basava wheel windmill \(W^{(m)}_{n+1}\) graph. The graph \(G\) has \(mn+1\) vertices and \(3mn-2m\) edges, \(m\geq 2\), \(n\geq 4\). Then there are three types of vertices as given in Table 1. Also there are four types of edges as given in Table 2.

Table 1. Vertex partition of Basava wheel windmill \(W^{(m)}_{n+1}\) graph.

\(d_G(v)\)	\(4\)	\(n\)	\(mn\)
Number of vertices	\(m(n-1)\)	\(m\)	\(1\)

Table 2. Edge partition of Basava wheel windmill \(W^{(m)}_{n+1}\) graph.

\((deg_{G}(u), deg_{G}(v))\)	\((4,4)\)	\((4,n)\)	\((4,mn)\)	\((n,mn)\)
Number of edges	\(m(n-1)\)	\(m(n-1)\)	\(m(n-1)\)	\(m\)

2. Degree based topological indices of the Basava wheel windmill graph

Theorem 1. The F-index of Basava wheel windmill graph is \[F(W^{(m)}_{n+1})=64m(n-1)+mn^3(1+m^2).\]

Proof. By using the definition of F-index and Table 1, we obtain \begin{eqnarray*} F(G) &=& {\sum\limits_{v\in V(G)} {d_G(v)^3}}\\ &=& \sum\limits_{v\in V_4} {4^3}+\sum\limits_{v\in V_n} {n^3}+\sum\limits_{v\in V_{mn}} {(mn)^3}\\ &=& 64\times m(n-1)+n^3 \times m+(mn)^3\\ &=& 64m(n-1)+mn^3+m^3n^3\\ &=& 64m(n-1)+mn^3(1+m^2). \end{eqnarray*}

Theorem 2. The harmonic index of Basava wheel windmill graph is \[H(W^{(m)}_{n+1})=2m(n-1)\bigg[\frac{1}{8}+\frac{1}{4+n}+\frac{1}{4+mn}\bigg]+\frac{2m}{n+mn}.\]

Proof. By using the definition of harmonic index and Table 2, we obtain \begin{eqnarray*} H(G) &=& {\sum_{uv\in E(G)}{\frac{2}{d_G(u)+d_G(v)}}}\\ &=&\sum_{uv\in E_8}{\frac{2}{4+4}} +\sum_{uv\in E_{4+n}}{\frac{2}{4+n}}+\sum_{uv\in E_{4+mn}}{\frac{2}{4+mn}}+\sum_{uv\in E_{n+mn}}{\frac{2}{n+mn}}\\ &=&\frac{2}{8}\times m(n-1)+\frac{2}{4+n}\times m(n-1)+\frac{2}{4+mn}\times m(n-1)+\frac{2}{n+mn}\times m\end{eqnarray*}\begin{eqnarray*} &=&m(n-1)\Bigg[\frac{2}{8}+\frac{2}{4+n}+\frac{2}{4+mn}\Bigg]+\frac{2m}{n+mn}\\ &=&2m(n-1)\bigg[\frac{1}{8}+\frac{1}{4+n}+\frac{1}{4+mn}\bigg]+\frac{2m}{n+mn}. \end{eqnarray*}

Theorem 3. The Randi\(\acute{c}\) index of Basava wheel windmill graph is \[\chi(W^{(m)}_{n+1})=m(n-1)\bigg[\frac{1}{4}+\frac{1}{2\sqrt{n}}+\frac{1}{2\sqrt{mn}}\bigg]+\frac{\sqrt{m}}{n}.\]

Proof. By using the definition of Randi\(\acute{c}\) index and Table 2, we obtain \begin{eqnarray*} \chi(G) &=& {\sum_{uv\in E(G)}{\frac{1}{\sqrt{d_G(u)d_G(v)}}}}\\ &=&\sum_{uv\in E_8}{\frac{1}{\sqrt{4\times4}}} +\sum_{uv\in E_{4+n}}{\frac{1}{\sqrt{4\times n}}}+\sum_{uv\in E_{4+mn}}{\frac{1}{\sqrt{4\times mn}}}+\sum_{uv\in E_{n+mn}}{\frac{1}{\sqrt{n\times mn}}}\\ &=&\frac{1}{4}\times m(n-1)+\frac{1}{2\sqrt{n}}\times m(n-1)+\frac{1}{2\sqrt{mn}}\times m(n-1)+\frac{1}{n\sqrt{m}}\times m \\ &=&m(n-1)\Bigg[\frac{1}{4}+\frac{1}{2\sqrt{n}}+\frac{1}{2\sqrt{mn}}\Bigg]+\frac{m}{n\sqrt{m}}\\ &=&m(n-1)\bigg[\frac{1}{4}+\frac{1}{2\sqrt{n}}+\frac{1}{2\sqrt{mn}}\bigg]+\frac{\sqrt{m}}{n}. \end{eqnarray*}

Theorem 4. The general Randi\(\acute{c}\) index of Basava wheel windmill graph is \[\chi^{\alpha}(W^{(m)}_{n+1})=4^{\alpha}m(n-1)\big(4^{\alpha}+n^{\alpha}+(mn)^{\alpha}\big)+m^{\alpha+1}n^{2\alpha}.\]

Proof. By using the definition of general Randi\(\acute{c}\) index and Table 2, we obtain \begin{eqnarray*} \chi^{\alpha}(G) &=& {\sum_{uv\in E(G)}{[d_G(u)d_G(v)]}^{\alpha}}\\ &=&\sum_{uv\in E_8}{[4\times4]^{\alpha}}+\sum_{uv\in E_{4+n}}{[4\times n]^{\alpha}}+\sum_{uv\in E_{4+mn}}{[4\times mn]^{\alpha}}+\sum_{uv\in E_{n+mn}}{[n\times mn]^{\alpha}}\\ &=&16^{\alpha}\times m(n-1)+{(4n)}^{\alpha}\times m(n-1)+{(4mn)}^{\alpha}\times m(n-1)+{(mn^2)}^{\alpha}\times m \\ &=&m(n-1)\Big[16^{\alpha}+{(4n)}^{\alpha}+{(4mn)}^{\alpha}\Big]+m(m^{\alpha}n^{2\alpha})\\ &=&4^{\alpha}m(n-1)\big(4^{\alpha}+n^{\alpha}+(mn)^{\alpha}\big)+m^{\alpha+1}n^{2\alpha}. \end{eqnarray*}

By using the Theorem 4, we establish the following results;

Corollary 5. The second Zagreb index of Basava wheel windmill graph is \[M_2(W^{(m)}_{n+1})=5m^2n^2+4mn^2-4m^2n+12mn-16m.\]

Corollary 6. The second hyper Zagreb index of Basava wheel windmill graph is \[HM_2(W^{(m)}_{n+1})=16m(n-1)\big[16+n^2(1+m^2)\big]+m^3n^4.\]

Theorem 7. The sum connectivity index of Basava wheel windmill graph is \[X(W^{(m)}_{n+1})=m(n-1)\bigg[\frac{1}{2\sqrt{2}}+\frac{1}{\sqrt{4+n}}+\frac{1}{\sqrt{4+mn}}\bigg]+\frac{m}{\sqrt{n(m+1)}}.\]

Proof. By using the definition of sum connectivity index and Table 2, we obtain \begin{eqnarray*} X(G)&=&{\sum_{uv\in E(G)}{\frac{1}{\sqrt{d_G(u)+d_G(v)}}}}\\ &=&\sum_{uv\in E_8}{\frac{1}{\sqrt{4+4}}} +\sum_{uv\in E_{4+n}}{\frac{1}{\sqrt{4+n}}}+\sum_{uv\in E_{4+mn}}{\frac{1}{\sqrt{4+mn}}}+\sum_{uv\in E_{n+mn}}{\frac{1}{\sqrt{n+mn}}}\\ &=&\frac{1}{\sqrt{4+4}}\times m(n-1)+\frac{1}{\sqrt{4+n}}\times m(n-1)+\frac{1}{\sqrt{4+mn}}\times m(n-1)+\frac{1}{\sqrt{n+mn}}\times m \\ &=&m(n-1)\bigg[\frac{1}{2\sqrt{2}}+\frac{1}{\sqrt{4+n}}+\frac{1}{\sqrt{4+mn}}\bigg]+\frac{m}{\sqrt{n(m+1)}}. \end{eqnarray*}

Theorem 8. The general sum connectivity index of Basava wheel windmill graph is \[X^{\alpha}(W^{(m)}_{n+1})=m(n-1)\big[8^{\alpha}+(4+n)^{\alpha}+(4+mn)^{\alpha}\big]+m(n+mn)^{\alpha}.\]

Proof. By using the definition of general sum connectivity index and Table 2, we obtain \begin{eqnarray*} X^{\alpha}(G) &=& {\sum_{uv\in E(G)}{[d_G(u)+d_G(v)]}^{\alpha}}\\ &=&\sum_{uv\in E_8}{[4+4]^{\alpha}}+\sum_{uv\in E_{4+n}}{[4+n]^{\alpha}}+\sum_{uv\in E_{4+mn}}{[4+mn]^{\alpha}}+\sum_{uv\in E_{n+mn}}{[n+mn]^{\alpha}}\\ &=&8^{\alpha}\times m(n-1)+{(4+n)}^{\alpha}\times m(n-1)+{(4+mn)}^{\alpha}\times m(n-1)+{(n+mn)}^{\alpha}\times m \\ &=&m(n-1)\big[8^{\alpha}+(4+n)^{\alpha}+(4+mn)^{\alpha}\big]+m(n+mn)^{\alpha}. \end{eqnarray*}

By using the Theorem 8, we establish the following results.

Corollary 9. The first Zagreb index of Basava wheel windmill graph is \[M_1(W^{(m)}_{n+1})=16m(n-1)+mn^2(m+1).\]

Corollary 10. The first hyper Zagreb index of Basava wheel windmill graph is \[HM_1(W^{(m)}_{n+1})=m(n-1)\big[96+n^2+8n+m^2n^2+8mn\big]+mn^2+m^3n^2+2m^2n^2.\]

Theorem 11. The atom-bond connectivity index of Basava wheel windmill graph is \[ABC(W^{(m)}_{n+1})=\frac{m(n-1)}{2}\bigg[\frac{\sqrt{6}}{2}+\sqrt{\frac{n+2}{n}}+\sqrt{\frac{mn+2}{mn}}\bigg]+{\frac{m}{n}}\sqrt{\frac{mn+n-2}{m}}.\]

Proof. By using the definition of atom-bond connectivity index and Table 2, we obtain \begin{eqnarray*} ABC(G)&=&\sum\limits_{uv\in E(G)}{\sqrt\frac{d_G(u)+d_G(v)-2}{d_G(u)d_G(v)}}\\ &=&\sum\limits_{uv\in E_8}{\sqrt\frac{4+4-2}{4\times4}}+\sum\limits_{uv\in E_{4+n}}{\sqrt\frac{4+n-2}{4\times n}}+\sum\limits_{uv\in E_{4+mn}}{\sqrt\frac{4+mn-2}{4\times mn}} +\sum\limits_{uv\in E_{n+mn}}{\sqrt\frac{n+mn-2}{n\times mn}}\\ &=&\sqrt\frac{6}{16}\times m(n-1)+\sqrt\frac{n+2}{4n}\times m(n-1)+\sqrt\frac{mn+2}{4mn}\times m(n-1)+\sqrt\frac{mn+n-2}{mn^2}\times m\end{eqnarray*}\begin{eqnarray*} &=&m(n-1)\bigg[\frac{\sqrt{6}}{4}++\frac{1}{2}\sqrt{\frac{n+2}{n}}+\frac{1}{2}\sqrt{\frac{mn+2}{mn}}\bigg]+\frac{m}{n}\sqrt{\frac{mn+n-2}{m}}\\ &=&\frac{m(n-1)}{2}\bigg[\frac{\sqrt{6}}{2}+\sqrt{\frac{n+2}{n}}+\sqrt{\frac{mn+2}{mn}}\bigg]+\frac{m}{n}\sqrt{\frac{mn+n-2}{m}}. \end{eqnarray*}

Theorem 12. The Geometric-arithmetic index of Basava wheel windmill graph is \[GA(W^{(m)}_{n+1})=m(n-1)\bigg[1+\frac{4\sqrt{n}}{4+n}+\frac{4\sqrt{mn}}{4+mn}\bigg]+\frac{2m\sqrt{m}}{1+m}.\]

Proof. By using the definition of Geometric-arithmetic index and Table 2, we obtain \begin{eqnarray*} GA(G)&=&\sum\limits_{uv\in E(G)}\frac{2\sqrt{d_G(u)d_G(v)}}{d_G(u)+d_G(v)}\\ &=&\sum\limits_{uv\in E_8}\frac{2\sqrt{4\times4}}{4+4}+\sum\limits_{uv\in E_{4+n}}\frac{2\sqrt{4\times n}}{4+n}+\sum\limits_{uv\in E_{4+mn}}\frac{2\sqrt{4\times mn}}{4+mn} +\sum\limits_{uv\in E_{n+mn}}\frac{2\sqrt{n\times mn}}{n+mn}\\ &=&{\frac{2\sqrt{16}}{8}}\times m(n-1)+\frac{2\sqrt{4n}}{4+n}\times m(n-1)+\frac{4\sqrt{mn}}{4+mn}\times m(n-1)+\frac{2\sqrt{mn^2}}{n+mn}\times m\\ &=&m(n-1)\bigg[1+\frac{4\sqrt{n}}{4+n}+\frac{4\sqrt{mn}}{4+mn}\bigg]+\frac{2mn\sqrt{m}}{n+mn}\\ &=&m(n-1)\bigg[1+\frac{4\sqrt{n}}{4+n}+\frac{4\sqrt{mn}}{4+mn}\bigg]+\frac{2m\sqrt{m}}{1+m}. \end{eqnarray*}

Theorem 13. The Symmetric division deg index of Basava wheel windmill graph is \[SDD(W^{(m)}_{n+1})=1+m^{2}+m(n-1)\bigg[2+\frac{16+n^2}{4n}+\frac{16+(mn)^2}{4mn}\bigg].\]

Proof. By using the definition of Symmetric division deg index and Table 2, we obtain \begin{eqnarray*} SDD(G)&=&\sum\limits_{uv\in E(G)}\frac{d^2_G(u)+d^2_G(v)}{d_G(u)d_G(v)}\\ &=&\sum\limits_{uv\in E_8}\frac{4^2+4^2}{4\times 4}+\sum\limits_{uv\in E_{4+n}}\frac{4^2+n^2}{4\times n}+\sum\limits_{uv\in E_{4+mn}}\frac{4^2+(mn)^2}{4\times mn} +\sum\limits_{uv\in E_{n+mn}}\frac{n^2+(mn)^2}{n\times mn}\\ &=&\frac{16+16}{16}\times m(n-1)+\frac{16+n^2}{4n}\times m(n-1)+\frac{16+(mn)^2}{4mn}\times m(n-1)+\frac{n^2+(mn)^2}{mn^2}\times m\\ &=&m(n-1)\bigg[\frac{32}{16}+\frac{16+n^2}{4n}+\frac{16+(mn)^2}{4mn}\bigg]+\frac{n^2(1+m^2)}{n^2}\\ &=&1+m^{2}+m(n-1)\bigg[2+\frac{16+n^2}{4n}+\frac{16+(mn)^2}{4mn}\bigg]. \end{eqnarray*}

Theorem 14. The Sombor index of Basava wheel windmill graph is \[SO(W^{(m)}_{n+1})=m(n-1)\big[4\sqrt{2}+\sqrt{16+n^2}+\sqrt{16+m^2n^2}\big]+mn\sqrt{1+m^2}.\]

Proof. By using the definition of Sombor index and Table 2, we obtain \begin{eqnarray*} SO(G)&=&{\sum_{uv\in E(G)}{\sqrt{d_G(u)^2+d_G(v)^2}}}\end{eqnarray*}\begin{eqnarray*} &=&\sum_{uv\in E_8}{\sqrt{4^2+4^2}}+\sum_{uv\in E_{4+n}}{\sqrt{4^2+n^2}}+\sum_{uv\in E_{4+mn}}{\sqrt{4^2+(mn)^2}} +\sum_{uv\in E_{n+mn}}{\sqrt{n^2+(mn)^2}}\\ &=&\sqrt{32}\times m(n-1)+\sqrt{16+n^2}\times m(n-1)+\sqrt{16+(mn)^2}\times m(n-1) +\sqrt{n^2+(mn)^2}\times m \\ &=&m(n-1)\big[4\sqrt{2}+\sqrt{16+n^2}+\sqrt{16+m^2n^2}\big]+mn\sqrt{1+m^2}. \end{eqnarray*}

Theorem 15. The general \(SK_{\alpha}\) index of Basava wheel windmill graph is \[SK_{\alpha}(W^{(m)}_{n+1})=\frac{1}{2^{\alpha}}\bigg[m(n-1)\bigg(8^{\alpha}+(4+n)^{\alpha}+(4+mn)^{\alpha}\bigg)+m(n+mn)^{\alpha}\bigg].\]

Proof. By using the definition of general \(SK_{\alpha}\) index and Table 2, we obtain \begin{eqnarray*} SK_{\alpha}(G)&=&\sum\limits_{uv\in E(G)}\bigg(\frac{d_G(u)+d_G(v)}{2}\bigg)^{\alpha}\\ &=&\sum\limits_{uv\in E_8}\bigg(\frac{4+4}{2}\bigg)^{\alpha}+\sum\limits_{uv\in E_{4+n}}\bigg(\frac{4+n}{2}\bigg)^{\alpha}+\sum\limits_{uv\in E_{4+mn}}\bigg(\frac{4+mn}{2}\bigg)^{\alpha}+\sum\limits_{uv\in E_{n+mn}}\bigg(\frac{n+mn}{2}\bigg)^{\alpha}\\ &=&\bigg(\frac{4+4}{2}\bigg)^{\alpha} \times m(n-1)+\bigg(\frac{4+n}{2}\bigg)^{\alpha}\times m(n-1)+\bigg(\frac{4+mn}{2}\bigg)^{\alpha}\times m(n-1)+\bigg(\frac{n+mn}{2}\bigg)^{\alpha}\times m\\ &=&m(n-1)\bigg[\bigg(\frac{8}{2}\bigg)^{\alpha}+\bigg(\frac{4+n}{2}\bigg)^{\alpha}+\bigg(\frac{4+mn}{2}\bigg)^{\alpha}\bigg]+m\bigg(\frac{n+mn}{2}\bigg)^{\alpha}\\ &=&\frac{m(n-1)}{2^{\alpha}}\bigg[8^{\alpha}+(4+n)^{\alpha}+(4+mn)^{\alpha}\bigg]+\frac{m(n+mn)^{\alpha}}{2^{\alpha}}\\ &=&\frac{1}{2^{\alpha}}\bigg[m(n-1)\bigg(8^{\alpha}+(4+n)^{\alpha}+(4+mn)^{\alpha}\bigg)+m(n+mn)^{\alpha}\bigg]. \end{eqnarray*}

By using the Theorem 15, we establish the following results.

Corollary 16. The \(SK_1\) index of Basava wheel windmill graph is \[SK_1(W^{(m)}_{n+1})=\frac{1}{2}\bigg[m(n-1)(16+n+mn)+mn(1+m)\bigg].\]

Corollary 17. The \(SK_2\) index of Basava wheel windmill graph is \[SK_2(W^{(m)}_{n+1})=\frac{1}{4}\bigg[m(n-1)\bigg(64+(4+n)^{2}+(4+mn)^{2}\bigg)+m(n+mn)^{2}\bigg].\]

Theorem 18. The general \(SK^{\alpha}_{1}\) index of Basava wheel windmill graph is \[SK^{\alpha}_{1}(W^{(m)}_{n+1})=2^{\alpha}m(n-1)\big[4^{\alpha}+n^{\alpha}+(mn)^{\alpha}\big]+\frac{m(mn^2)^{\alpha}}{2^\alpha}\]

Proof. By using the definition of general \(SK^{\alpha}_{1}\) index and Table 2, we obtain \begin{eqnarray*} SK^{\alpha}_{1}(G)&=&\sum\limits_{uv\in E(G)}\bigg(\frac{d_G(u)d_G(v)}{2}\bigg)^{\alpha}\\ &=&\sum\limits_{uv\in E_8}\bigg(\frac{4\times4}{2}\bigg)^{\alpha}+\sum\limits_{uv\in E_{4+n}}\bigg(\frac{4\times n}{2}\bigg)^{\alpha}+\sum\limits_{uv\in E_{4+mn}}\bigg(\frac{4\times mn}{2}\bigg)^{\alpha}+\sum\limits_{uv\in E_{n+mn}}\bigg(\frac{n\times mn}{2}\bigg)^{\alpha}\\ &=&m(n-1)\bigg[\bigg(\frac{16}{2}\bigg)^{\alpha}+\bigg(\frac{4n}{2}\bigg)^{\alpha}+\bigg(\frac{4mn}{2}\bigg)^{\alpha}\bigg]+m\bigg(\frac{mn^2}{2}\bigg)^{\alpha}\end{eqnarray*}\begin{eqnarray*} &=&m(n-1)\bigg[8^{\alpha}+(2n)^{\alpha}+(2mn)^{\alpha}\bigg]+\frac{m(mn^2)^{\alpha}}{2^{\alpha}}\\ &=&2^{\alpha}m(n-1)\big[4^{\alpha}+n^{\alpha}+(mn)^{\alpha}\big]+\frac{m(mn^2)^{\alpha}}{2^\alpha}. \end{eqnarray*}

By using the Theorem 18, we establish the following results.

Corollary 19. The \(SK^{1}_1\) index of Basava wheel windmill graph is \[SK^{1}_1(W^{(m)}_{n+1})=m(n-1)(8+2n+2mn)+\frac{m^2n^2}{2}.\]

Corollary 20. The \(SK^{2}_1\) index of Basava wheel windmill graph is \[SK^{2}_1(W^{(m)}_{n+1})=m(n-1)(64+4n^2+4m^2n^2)+\frac{m^3n^4}{4}.\]

3. Comparison of topological indices of some chemical drugs

We have considered three chemical drugs, which are chloroquine, hydroxychloroquine and remdesiver [21]. Chloroquine is an antiviral drug, which is used to prevent and treat malaria. It’s also used to treat protozoa-induced liver infections (extraintestinal amebiasis) and coronavirus patients (COVID-19). Hydroxychloroquine is also antiviral drug, which has also have similar activity to that of chloroquine. The U. S. Food and Drug Administration (FDA) approved to treat autoimmune conditions such as systemic lupus erythematosus in adults, chronic discoid lupus erythematosus and rheumatoid arthritis. Remdesivir is used to treat the coronavirus patients (COVID-19). Table 3 shows the exact values of topological indices of chloroquine, hydroxychloroquine and remdesiver. These values are useful to planning the effective use of these drugs in medical field.

Table 3. Topological indices (TI’s) of chloroquine, hydroxychloroquine and remdesiver.

\({TI’s} \backslash {Chemical \; drugs}\)	<b>Chloroquine</b>	<b>Hydroxychloroquine</b>	<b>Remdesiver</b>
\(M_1(G)\)	106	110	216
\(M_2(G)\)	120	124	257
\(F(G)\)	262	270	586
\(HM_1(G)\)	502	518	1100
\(HM_2(G)\)	700	716	1493
\(H(G)\)	10.2999	10.7999	18.6380
\(\chi(G)\)	9.8179	10.3179	19.5080
\(X(G)\)	10.8376	11.3376	20.1485
\(ABC(G)\)	16.7007	17.4078	31.6111
\(GA(G)\)	22.3751	23.3751	21.1418
\(SDD(G)\)	51.6666	53.6666	104.6666
\(SO(G)\)	76.6907	79.5191	157.8076
\(SK_{1}(G)\)	53	55	108
\(SK_2(G)\)	125.5	129.5	275
\(SK^{1}_1(G)\)	60	62	128.5
\(SK^{2}_1(G)\)	175	179	440.75

4. Conclusion

We have presented here, few theoretical results on the some degree based topological indices. In this paper, we have proposed new graph transformation, is Basava wheel windmill graph. And also we have proposed two topological indices, namely, general \(SK_{\alpha}\) and general \(SK^{\alpha}_1\) indices, using these indices we can obtain physio-chemical properties of molecular graphs. The SK, \(SK_1\) and \(SK_2\) indices are corollary of this proposed indices. Further we have investigated these topological indices of chloroquine, hydroxychloroquine and remdesiver.

Acknowledgments

The second author is supported by Directorate of Minorities, Government of Karnataka, Bangalore, through M.Phil/Ph.D fellowship-2019-20:No.DOM/Ph.D/M.Phil/FELLOWSHIP/CR-01/2019-20 dated \(15^{th}\) October \(2019\).

Author Contributions

All authors contributed equally in this paper. All authors read and approved the final version of this paper.

Conflicts of Interest

“The author declares no conflict of interest”.

Data Availability

No data is required for this research.

Funding Information

No funding is available for this research.