We study analytical solutions of a bi-dimensional low-mass gaseous disc slowly rotating around a central mass and submitted to small radial periodic perturbations. Hydrodynamics equations are solved for the equilibrium and perturbed configurations. A wave-like equation for the gas-perturbed specific mass is deduced and solved analytically for several cases of exponents of the power law distributions of the unperturbed specific mass and sound speed. It is found that, first, the gas perturbed specific mass displays exponentially spaced maxima, corresponding to zeros of the radial perturbed velocity; second, the distance ratio of successive maxima of the perturbed specific mass is a constant depending on disc characteristics and, following the model, also on the perturbation’s frequency; and, third, inward and outward gas flows are induced from zones of minima toward zones of maxima of perturbed specific mass, leading eventually to the possible formation of gaseous annular structures in the disc. The results presented may be applied in various astrophysical contexts to slowly rotating thin gaseous discs of negligible relative mass, submitted to small radial periodic perturbations.
Discs play an important role in astrophysics (see e.g., [1]).
Protostellar discs are found around certain categories of young stars. Dynamical accretion discs intervene in the feeding process of massive stars by less massive ones in some binary systems. Galaxies have often the shape of a disc surrounding a central bulge. Planetary rings form discs around giant planets. Furthermore, it is generally believed that the planetary system and the regular satellite systems originate from disc-shaped nebulae surrounding the proto-Sun and the giant proto-planets.
The disc stage is thus an important step in some systems’ evolution. Depending on disc and central mass characteristics and on their mutual relative importance, different kind of structures may appear in discs: bars, spiral arms, and rings. Theories of disc dynamical evolution in an astrophysical context may be applied to other situations, for example, the theory of spiral density waves of galactic arms was successfully applied to models of planetary rings (see e.g., [2]).
Characteristics of a disc that may influence its evolution are self-gravity, thermal pressure, interaction with magnetic fields, rotation and viscosity.
In this paper, we show that annular rings may appear under certain circumstances in slowly rotating thin low mass gaseous discs submitted to small radial perturbations, where self-gravitation, viscous, magneto-hydrodynamics effects and azimuthal perturbations can be neglected. We study the behaviour of a nebular disc taken away from equilibrium by small radial periodic perturbations, extending the classical Jeans’ model of an uncompressible isothermal stationary nebula submitted to perturbations. Although initially intended for protoplanetary discs, the results of the investigations presented here can be applied to any thin gaseous disc that can be described by the model considered. Hypotheses on the model are discussed in section 2. We consider in section 3 a differentially rotating thin gaseous axisymmetric nebula undergoing polytropic transformations of index \(\gamma\) and departing from equilibrium because of small radial periodic perturbations. Physical characteristics of the nebular disc are supposed continuous and have power law dependencies on the radial distance \(r\), in particular for the specific mass \(\rho\sim r^{d}\) and sound speed \(c\sim r^{\frac{s}{2}}\). Equations describing the hydrodynamic model are solved for the equilibrium and perturbed configurations, where the perturbations are assumed small enough for the equations to be linearized. A wave-like equation is deduced for the nebula perturbed gas specific mass and expressions of the gas radial velocity and specific mass flux momentum are found in function of the gas specific mass. Looking for solutions yielding annular gaseous structures to appear in the disc, these equations are solved analytically in Section 4 for two particular models (\(d=0\) and \(d<2\left(2\gamma-1\right)\); \(s=2\)) and for three general cases, the first with \(d=\left(s-2\right)\); \(s<2\) for small frequencies, and a particular case with \(s=-1\) and \(d=-3\), called the standard model; the second with \(d=(s-2)/2\); and the third for \(d=s/(\gamma-1)\), called the polytropic model, with a complete solution for the particular values \(\gamma=3/2\), \(d=-3\) and \(s=-1\). For each case, expressions of the distance ratios \(\beta\) of the maxima of the perturbed gas specific mass are also deduced. Profiles of the perturbed specific mass and velocity are presented in Section 5 and the possible formation of annular structures are discussed. We are not aware of previous similar general analytical resolutions, although particular cases were treated in [3].
This paper is a reworked excerpt of [4].
The mass of a primeval nebula is a key factor in deciding on its later evolution: either the nebula mass is large, typically greater than or close to the central mass, and sub-regions of the nebula of large specific mass may undergo local collapse, or the primeval nebula mass is low, typically a few percents of the central mass and gravitational instabilities may never develop in this case [5]. In some theories of protoplanetary nebula formation (see e.g., [6]), viscous friction plays an important role in inducing an inward flow of accretion material onto the central primary and causing the conversion of kinetic into thermal energy to be the dominant heat source ([7]).
However, the epoch at which the viscous friction becomes the predominant effect is critical in a nebula history. After an initial collapse phase, a low mass rotating nebula can achieve a stationary equilibrium without considering turbulent friction ([8]).
On the other hand, an axisymmetric equilibrium configuration was shown to be unstable against non-axisymmetric perturbations, the result being a binary system ([9,10]).
Furthermore, friction processes are not always able to produce a central object surrounded by a disc-shaped nebula ([7]). Therefore, it is reasonable to assume, within the low mass nebula hypothesis, that there was a period in a nebula history during which the viscous friction may not have been the predominant process governing the disc evolution, independently of further evolution where the viscous effects may have become predominant. The problem of transfer of angular momentum from the central mass to outer parts of the disc is not addressed here, as it depends on viscous processes (see e.g., [11]).
We consider the model of a disc-shaped gaseous nebular disc of mass \(M_{d}\) in a slow rotation around a central mass \(M^{*}\), supposed spherical. The disc mass is negligible in front of the central mass \(M_{d}<<M^{*}\) and the disc thickness is small compared to its radius. The nebula is assumed to be composed of gas only, the presence of nebular dust being neglected. Self-gravitation, magneto-hydrodynamics and viscous effects in the disc are not considered (although, the viscous force is included in the general equations of section 3, but neglected further in section 4).
The effects of small periodic radial perturbations on the disc are studied, without any coupling to non-radial perturbations. This last hypothesis is somehow controversial as there is a large body of work (see e.g, [12-15] and references therein) that consider coupling between radial and azimuthal perturbations, typically through the Coriolis force. However, for slowly rotating discs, i.e., for which the angular frequency of rotation \(\Omega\) is smaller than the perturbation periodic angular frequency \(\omega\), with \(\Omega<<\omega\), the error committed by ignoring the azimuthal perturbations would be small. Although this approximation is strictly speaking incorrect, as we will be interested further in the radial distributions of the perturbed variables, the small azimuthal effects are ignored in a first approach in this study. Nevertheless, the nebula model equations are deduced for the radial, azimuthal and vertical components, and we show that azimuthal perturbations are negligible for a slowly rotating disc and vertical perturbations are non-existent for an inviscid disc.
The motion of the gas of specific mass \(\rho\) is described in spatial Eulerian coordinates by the vectorial Navier-Stokes equation, which relates for an unit volume of gas, the inertia force (sum of the time derivative, denoted by an upper dot, of the vectorial velocity \(\boldsymbol{v}\) and the advection term), the gradients of the pressure \(p\) and the gravitational potential \(V\), and the viscous forces \[\rho\dot{\boldsymbol{v}}+\rho\left(\boldsymbol{v}\cdot\nabla\right)\boldsymbol{v}+\nabla p+\rho\nabla V=\rho\nu\boldsymbol{\Delta}\boldsymbol{v}\label{eq:1}, \tag{1}\] where \(\nu\) is the kinematic viscosity, \(\nabla\) and \(\boldsymbol{\Delta}\) the gradient and vectorial Laplacian operators. This equation is complemented by the continuity and Poisson equations \[\dot{\rho}+\nabla\cdot\left(\rho\boldsymbol{v}\right)=0\label{eq:2}, \tag{2}\] \[\Delta V=4\pi G\rho\label{eq:3}, \tag{3}\] where \(\nabla\cdot\) and \(\Delta\) are the divergence and scalar Laplacian operators and \(G\) the gravitational constant. The disc gravitational potential is neglected in front of the central mass gravitational potential and the viscosity \(\nu\) is assumed constant in the disc.
At dynamic equilibrium, the stationary model is described by \[\rho_{o}\left(\boldsymbol{v_{0}}\cdot\nabla\right)\boldsymbol{v_{0}}+\nabla p_{0}+\rho_{0}\nabla V_{0}=\rho_{0}\nu\boldsymbol{\Delta}\boldsymbol{v_{0}}\label{eq:4}, \tag{4}\] \[\nabla\cdot\left(\rho_{0}\boldsymbol{v}_{0}\right)=0\label{eq:5}, \tag{5}\] \[\Delta V_{0}=4\pi G\rho_{0}\label{eq:6}, \tag{6}\] where the index \(0\) denotes the equilibrium characteristics. Allowing for small radial periodic perturbations to take the model away from equilibrium, the linearized perturbed equations read, after simplification by the equilibrium equations (4) to (6), \[\ rho_{0}\dot{\boldsymbol{v_{1}}}+\rho_{0}\left(\left(\boldsymbol{v_{1}}\cdot\nabla\right)\boldsymbol{v_{0}}+\left(\boldsymbol{v_{0}}\cdot\nabla\right)\boldsymbol{v_{1}}\right)+\rho_{1}\left(\boldsymbol{v_{0}}\cdot\nabla\right)\boldsymbol{v_{0}} +\nabla p_{1}+\rho_{1}\nabla V_{0}=\rho_{0}\nu\boldsymbol{\Delta}\boldsymbol{v_{1}}+\rho_{1}\nu\boldsymbol{\Delta}\boldsymbol{v_{0}}\label{eq:7}, \tag{7}\]
\[\ dot{\rho_{1}}+\nabla\cdot\left(\rho_{1}\boldsymbol{v_{0}}\right)+\nabla\cdot\left(\rho_{0}\boldsymbol{v_{1}}\right)=0\label{eq:8}, \tag{8}\] \[\Delta V_{1}=4\pi G\rho_{1}\label{eq:9}, \tag{9}\] where indexes \(1\) denote the perturbed characteristics. As the model is plane and axisymmetric, these equations are solved in a cylindrical polar reference frame. Considering that the equilibrium characteristics depend only on the radial distance \(r\) and that the perturbed characteristics depend on \(r\) and on the time \(t\), the equilibrium and perturbed gas vectorial velocities are written respectively \[\begin{aligned} \boldsymbol{v_{0}} & =\left(0,v_{0}\left(r\right),0\right)\\ \boldsymbol{v_{1}} & =\left(v_{1}\left(r,t\right),u_{1}\left(r,t\right),w_{1}\left(r,t\right)\right). \end{aligned}\] At dynamical equilibrium, the radial and azimuthal components of the Navier-Stokes equation (4) and the Poisson equation (6) read, with the prime sign \(^{\prime}\) denoting \(\partial\,/\partial r\), \[\ frac{\rho_{o}v_{0}^{2}}{r}-p_{0}^{\prime}-\rho_{0}V_{0}^{\prime}=0\label{eq:10}, \tag{10}\]
\[\ rho_{0}\nu\left(v_{0}^{\prime\prime}+\frac{v_{0}^{\prime}}{r}-\frac{v_{0}}{r^{2}}\right)=0\label{eq:11}, \tag{11}\]
\[V_{0}^{\prime\prime}+\frac{V_{0}^{\prime}}{r}=4\pi G\rho_{0}\label{eq:12}. \tag{12}\] The Navier-Stokes equations (7) for the perturbed radial component reads \[ \rho_{0}\dot{v_{1}}-\frac{v_{0}}{r}\left(\rho_{1}v_{0}+2\rho_{0}u_{1}\right)+p_{1}^{\prime}+\rho_{0}V_{1}^{\prime}+\rho_{1}V_{0}^{\prime}=\rho_{0}\nu\left(v_{1}^{\prime\prime}+\frac{v_{1}^{\prime}}{r}-\frac{v_{1}}{r^{2}}\right)\label{eq:13}. \tag{13}\] The second and third terms of (13) can be simplified as\(\rho_{1}v_{0}>>2\rho_{0}u_{1}\) (see Appendix A), yielding \[\rho_{0}\dot{v_{1}}-\rho_{1}\frac{v_{0}^{2}}{r}+p_{1}^{\prime}+\rho_{0}V_{1}^{\prime}+\rho_{1}V_{0}^{\prime}=\rho_{0}\nu\left(v_{1}^{\prime\prime}+\frac{v_{1}^{\prime}}{r}-\frac{v_{1}}{r^{2}}\right)\label{eq:13-1}. \tag{14}\] The Navier-Stokes equations (7) for the perturbed azimuthal and vertical components become
\[ \rho_{0}\dot{u_{1}}+\rho_{0}v_{1}\left(v_{0}^{\prime}+\frac{v_{0}}{r}\right)=\rho_{1}\nu\left(v_{0}^{\prime\prime}+\frac{v_{0}^{\prime}}{r}-\frac{v_{0}}{r^{2}}\right)+\rho_{0}\nu\left(u_{1}^{\prime\prime}+\frac{u_{1}^{\prime}}{r}-\frac{u_{1}}{r^{2}}\right)\label{eq:14}, \tag{15}\]
\[\ rho_{0}\dot{w_{1}}=\rho_{0}\nu\left(w_{1}^{\prime\prime}+\frac{w_{1}^{\prime}}{r}\right)\label{eq:14-1}. \tag{16}\] The continuity and Poisson equations (8) and (9) read \[\ dot{\rho_{1}}+\frac{\rho_{0}v_{1}}{r}+\rho_{0}^{\prime}v_{1}+\rho_{0}v_{1}^{\prime}=0\label{eq: 15}, \tag{17}\] \[V_{1}^{\prime\prime}+\frac{V_{1}^{\prime}}{r}=4\pi G\rho_{1}\label{eq:16}. \tag{18}\] This set of equations is completed by a gas state equation. The nebula gas is approximated by a perfect gas undergoing polytropic transformations of index \(\gamma\), assumed to be constant throughout the disc. Denoting the local sound speed by \(c\), the pressure at equilibrium reads \[p_{0}=\frac{c_{0}^{2}\rho_{0}}{\gamma}\label{eq:17}. \tag{19}\] Using the gas polytropic relation, \(p\,/\rho^{\gamma}=constant\), the linearized perturbed pressure reads \[ p_{1}=\frac{c_{0}^{2}\rho_{1}}{\gamma}+2\frac{c_{0}c_{1}\rho_{0}}{\gamma}=c_{0}^{2}\rho_{1}\label{eq:18}. \tag{20}\] Expressions of the gas circular velocity at equilibrium are found from the radial and azimuthal components of the Navier-Stokes equation (10) and (11) and are given in Appendix B.
Solving for the gas perturbed specific mass \(\rho_{1}\) and perturbed radial velocity \(v_{1}\), the equation (14), with (10), (19) and (20), reads \[\ dot{v_{1}}+\frac{c_{0}^{2}}{\rho_{0}}\left(\rho_{1}^{\prime}+\rho_{1}\left(\left(\frac{\gamma-1}{\gamma}\right)\frac{\left(c_{0}^{2}\right)^{\prime}}{c_{0}^{2}}-\frac{\rho_{0}^{\prime}}{\gamma\rho_{0}}\right)\right)+V_{1}^{\prime} =\nu\left(v_{1}^{\prime\prime}+\frac{v_{1}^{\prime}}{r}-\frac{v_{1}}{r^{2}}\right)\label{eq:19}. \tag{21}\] Taking the time derivative of (17) and introducing (18) and (21) yield \[\ ddot{\rho_{1}}-c_{0}^{2}\left(\rho_{1}^{\prime\prime}+\rho_{1}^{\prime}\left(\left(\frac{2\gamma-1}{\gamma}\right)\frac{\left(c_{0}^{2}\right)^{\prime}}{c_{0}^{2}}-\frac{\rho_{0}^{\prime}}{\gamma\rho_{0}}+\frac{1}{r}\right)\right.\nonumber \\ \left.+\rho_{1}\left(\left(\frac{\gamma-1}{\gamma}\right)\frac{\left(c_{0}^{2}\right)^{\prime\prime}}{c_{0}^{2}}+\frac{\left(c_{0}^{2}\right)^{\prime}}{c_{0}^{2}}\left(\left(\frac{\gamma-1}{\gamma}\right)\frac{1}{r}-\frac{\rho_{0}^{\prime}}{\gamma\rho_{0}}\right)\right.\right.\nonumber \\ \left.\left.-\frac{1}{\gamma\rho_{0}}\left(\rho_{0}^{\prime\prime}+\rho_{0}^{\prime}\left(\frac{1}{r}-\frac{\rho_{0}^{\prime}}{\rho_{0}}\right)\right)+\frac{4\pi G\rho_{0}}{c_{0}^{2}}\right)\right)\nonumber \\ =\rho_{0}^{\prime}V_{1}^{\prime}-\frac{1}{r}\frac{\partial}{\partial r}\left(r\rho_{0}\nu\left(v_{1}^{\prime\prime}+\frac{v_{1}^{\prime}}{r}-\frac{v_{1}}{r^{2}}\right)\right)\label{eq:20}. \tag{22}\] The specific mass flux radial momentum \(\varPhi\) is defined as \[\varPhi=r\rho_{0}v_{1},\] and its behaviour is given by the continuity equation (17) \[\dot{\rho_{1}}+\frac{1}{r}\frac{\partial}{\partial r}\left(r\rho_{0}v_{1}\right)=\dot{\rho_{1}}+\frac{\varPhi^{\prime}}{r}=0\label{eq:21}. \tag{23}\]
It seems hopeless to try to find an analytical solution to the third order differential equation (22) in \(v_{1}\) and \(\rho_{1}\). However, a wave-like equation in \(\rho_{1}\) with a mass term can be found if one neglects the right side of (22): the gas is assumed of low viscosity such as the viscous friction can be neglected in front of the pressure gradient and of the central mass gravitational gradient and secondly, the product of the radial derivatives of the unperturbed specific mass \(\rho_{0}\) and of the perturbed gravitational potential \(V_{1}\) is shown to be small (see Appendix C) and can be neglected \(\rho_{0}^{\prime}V_{1}^{\prime}\approx0\). Using notations of [3], the equilibrium characteristics are written with power law dependencies on the radial distance \(r\). With the dimensionless variable \(R\), one defines \[\ R=\frac{r}{r_{c}}\,\,\,;\,\,\rho_{0}=\rho_{c}R^{d}\,\,\,;\,\,c_{0}^{2}=c_{c}^{2}R^{s}, \tag{24}\] where \(r_{c}\) is a reference distance corresponding to the disc inner radius, \(\rho_{c}\) and \(c_{c}\) are the nebula reference specific mass and sound speed at the disc inner edge. The exponents \(d\) and \(s\) depend on the nebula physical models and are addressed further. The homogeneous equation (22) becomes \[ \ddot{\rho_{1}}-\frac{R^{s}}{A^{2}}\left(\rho_{1}^{\prime\prime}+\left(2s+1-\frac{d+s}{\gamma}\right)\frac{\rho_{1}^{\prime}}{R} +\left(B^{2}R^{d+2-s}+s\left(s-\frac{d+s}{\gamma}\right)\right)\frac{\rho_{1}}{R^{2}}\right)=0\label{eq:23}, \tag{25}\] with, from now on, the prime sign \(^{\prime}\) denoting \(\partial\,/\partial R\) and where \[A^{2}=\frac{r_{c}^{2}}{c_{c}^{2}}\,\,\,;\,\,B^{2}=\frac{4\pi G\rho_{c}r_{c}^{2}}{c_{c}^{2}}\] are constants. Posing \[ \rho_{1}\left(R,t\right) =D\left(R\right)\Theta\left(t\right)\label{eq:24}, \tag{26}\] \[\ v_{1}\left(R,t\right) =U\left(R\right)\varXi\left(t\right)\label{eq:24-1}, \tag{27}\] \[\ varPhi\left(R,t\right) =\Phi\left(R\right)\Psi\left(t\right)\label{eq:24-2}, \tag{28}\] and choosing \(-\omega^{2}\) as separating constant (\(\omega\) real), for periodic perturbations that do not grow exponentially with time, (25) yields \[\begin{equation} \ddot{\Theta}\left(t\right)+\omega^{2}\Theta\left(t\right)=0 ,\tag{29} \end{equation}\] \[\ D^{\prime\prime}+\left(2s+1-\frac{d+s}{\gamma}\right)\frac{D^{\prime}}{R}+ \left(B^{2}R^{d+2-s}+\omega^{2}A^{2}R^{2-s}+s\left(s-\frac{d+s}{\gamma}\right)\right)\frac{D}{R^{2}}=0\label{eq:26}. \tag{30}\] The perturbed continuity equation (17) yields, with \(\kappa\) as a separating constant \[\dot{\Theta}\left(t\right)-\kappa\Xi\left(t\right)=0\,\,\,;\,\,\Psi\left(t\right)=\Xi\left(t\right)\label{eq:27}, \tag{31}\] \[\ U\left(R\right)=-\kappa\frac{r{c}}{\rho_{c}}R^{-\left(d+1\right)}\int D\left(R\right)R\,dR\label{eq:28}, \tag{32}\] \[\Phi\left(R\right)=r_{c}\rho_{c}R^{d+1}U\left(R\right)=-\kappa r_{c}^{2}\int D\left(R\right)R\,dR\label{eq:29}, \tag{33}\] showing that \(\Phi\left(R\right)\) is strongly dependent on the behaviour of the radial perturbed velocity.
The solutions of (26) and (30) for the time-dependent part of \(\rho_{1}\) and \(v_{1}\) are \[ Theta\left(t\right)=C\sin\left(\omega t+\varphi\right)\label{eq:30}, \tag{34}\] \[ \Xi\left(t\right)=\Psi\left(t\right)=\frac{C}{\kappa}\omega\cos\left(\omega t+\varphi\right)\label{eq:30-1}, \tag{35}\] with \(C\) and \(\varphi\) constants to be determined by initial conditions.
The solutions (34) show that the time dependent parts of the gas perturbed specific mass \(\Theta\left(t\right)\) and velocity \(\varXi\left(t\right)\) have the same frequency and the same initial phase but they are out of phase by \(\pi/2\), for \(\kappa\) positive, while the time dependent part of the specific mass flux radial momentum \(\Psi\left(t\right)\) is identical to the one of the gas perturbed velocity \(\varXi\left(t\right)\). The type of solution of equation (30) and hence the radial behaviour of \(\rho_{1}\), \(v_{1}\) and \(\varPhi\) depend on the exponents \(d\) and \(s\) of the \(\rho_{0}\) and \(c_{0}\) radial distributions. Searching in the next sections for analytical solutions of the equation (30) for annular structures to appear in the disc, we solve these equations (30), (32) and (33) for certain values of \(d\) and \(s\).
Two boundary conditions are given: first, at the disc inner edge, for \(R=1\), the nebula perturbed specific mass must equal a parameter \(\rho_{c1}^{*}\left(t\right)\) independent of disc physical characteristics, but that can depend on the time \(t\), and second, for increasing \(R\), the nebula perturbed specific mass must decrease and vanish far away from the central mass, for \(R>>1\), for all time \(t\).
The solutions for the perturbed azimuthal and vertical velocity components are given in Appendix D.
We consider first the unrealistic case of an uncompressible nebula (\(d=0\)) with a sound speed increasing linearly with the distance (\(s=2\)). This first case is purely theoretical, as for a nebula with constant specific mass undergoing polytropic transformations, the sound speed should be constant. The equation (30) becomes then a simple Euler type equation \[ \label{eq:31} D^{\prime\prime}+\left(\frac{5\gamma-2}{\gamma}\right)\frac{D^{\prime}}{R} +\left(B^{2}+\omega^{2}A^{2}+4\left(\frac{\gamma-1}{\gamma}\right)\right)\frac{D}{R^{2}}=0. \tag{36}\] Under the condition \[B^{2}+\omega^{2}A^{2}+4\left(\frac{\gamma-1}{\gamma}\right)>1\] yielding \[\omega^{2}>\frac{c_{c}^{2}}{r_{c}^{2}}\left(\frac{4-3\gamma}{\gamma}\right)-4\pi G\rho_{c}\label{eq:32}, \tag{37}\] and with the first boundary condition and posing \[y=\sqrt{B^{2}+\omega^{2}A^{2}+\frac{3\gamma-1}{\gamma}}\] the solution of (36) reads \[D=\frac{\rho_{c1}^{*}}{R}\cos\left(y\ln\left(R\right)\right)\label{eq:33}, \tag{38}\] where \(\ln\) is the Napier logarithm function. The radial terms of the perturbed velocity and of the specific mass flux radial momentum are found from (32) and (33) \[\ U =-\kappa\frac{\rho_{c1}^{*}}{\rho_{c}}\frac{r_{c}}{y^{2}+1}R\cos\left(y\ln\left(R\right)-\arctan\left(y\right)\right)\label{eq:34}, \tag{39}\] \[ \Phi =-\kappa\rho_{c1}^{*}\frac{r_{c}^{2}}{y^{2}+1}R^{2}\cos\left(y\ln\left(R\right)-\arctan\left(y\right)\right)\label{eq:35}. \tag{40}\] The extrema (maxima and minima) of \(D\) are found from \[D^{\prime}=-\frac{\rho_{c1}^{*}\sqrt{y^{2}+1}}{R^{2}}\cos\left(y\ln\left(R\right)-\arctan\left(y\right)\right)=0\label{eq:36}, \tag{41}\] The zeros of \(D\) (38), \(U\)(39), \(\Phi\) (40) and \(D^{\prime}\) (41) are given by \[\ R=\alpha_{1}\left(\beta_{1}^{\backprime}\right)^{n}, \tag{42}\] \[\alpha_{1}=\exp\left(\frac{\pi/2+\varphi_{1}}{y}\right)\,\,\,;\,\,\beta_{1}^{\backprime}=\exp\left(\frac{\pi}{y}\right)\label{eq:37-1}, \tag{43}\] and \(n\) non-negative integers, \(\varphi_{1}=0\) for \(D\) and \(\varphi_{1}=\arctan\left(y\right)\) for \(U\), \(\Phi\) and \(D^{\prime}\). The initial spatial phase between \(D\) and \(U\) is \(\arctan\left(y\right)=\pi/2\), provided that \(y\) is large enough within the condition (37), while there is no initial phase between \(U\) (or \(\Phi\)) and \(D^{\prime}\). The distance ratio of two successive maxima of \(D\), for \(D^{\prime\prime}<0\), is \[\beta_{1}=\left(\beta_{1}^{\backprime}\right)^{2}=\exp\left(\frac{2\pi}{\frac{r_{c}}{c_{c}}\sqrt{\omega^{2}+4\pi G\rho_{c}+\frac{c_{c}^{2}}{r_{c}^{2}}\left(\frac{3\gamma-4}{\gamma}\right)}}\right)\label{eq:38}, \tag{44}\] which, from (37), is a real constant depending on the nebula characteristics \(r_{c}\), \(c_{c}\), \(\rho_{c}\), \(\gamma\) and on the perturbations circular frequency \(\omega\). Note that the condition (37) is equivalent to the dispersion relation in the classical Jeans problem (see e.g., [16]) with, for \(\omega^{2}=0\), critical wave number and wavelength \[\ k_{crit}=\frac{\sqrt{4\pi G\rho_{c}}}{c_{c}}=\frac{\sqrt{\frac{4-3\gamma}{\gamma}}}{r_{c}}\,\,\,;\,\,\lambda_{crit}=2\pi r_{c}\sqrt{\frac{\gamma}{4-3\gamma}}\label{eq:39}. \tag{45}\] The relation (37) ensures that the perturbations do not grow exponentially with time.
In this second case, the sound speed increases linearly with the radial distance and the specific mass depends on the radial distance, with the conditions that \(d\) must be non-null and smaller than \(2(2\gamma-1)\). The Eq. (30) becomes \[\ D^{\prime\prime}+\left(\frac{5\gamma-\left(d+2\right)}{\gamma}\right)\frac{D^{\prime}}{R} +\left(B^{2}R^{d}+\omega^{2}A^{2}+2\left(\frac{2\gamma-\left(d+2\right)}{\gamma}\right)\right)\frac{D}{R^{2}}=0, \tag{46}\] which is a Bessel type equation, whose general solution reads \[D=K_{1}R^{\left(\left(d+2\right)/2\gamma\right)-2}Z_{\nu}\left(z\right),\label{eq:41} \tag{47}\] where \(Z_{\nu}\left(z\right)\) is the Bessel function of first kind with \(z\) the argument and \(\nu\), from now on, the order \[z=\frac{2}{d}B\,R^{d/2}\,\,\,;\,\,\nu=\frac{2}{d}\sqrt{\left(\frac{d+2}{2\gamma}\right)^{2}-\omega^{2}A^{2}},\label{eq:42} \tag{48}\] and \(K_{1}\) is a constant determined by the first boundary condition \[K_{1}=\frac{\rho_{c1}^{*}}{Z_{\nu}\left(\frac{2}{d}B\right)}.\] For circular frequencies \(\omega\) such that \[\omega>\frac{d+2}{2\gamma A}=\left(\frac{d+2}{2\gamma}\right)\frac{c_{c}}{r_{c}},\label{eq:43} \tag{49}\] the order \(\nu\) is a pure imaginary, \(\nu=jy\) with \(j=\sqrt{-1}\) and, from now on, \[y=\frac{2}{d}\sqrt{\omega^{2}A^{2}-\left(\frac{d+2}{2\gamma}\right)^{2}}.\] The function \(Z_{\nu}\left(z\right)\) takes complex values and reads generally [17] \[Z_{\nu}\left(z\right)=\left(\frac{z}{2}\right)^{\nu}\sum_{k=0}^{\infty}\frac{\left(-1\right)^{k}\left(\frac{z}{2}\right)^{2k}}{k!\,\Gamma\left(\nu+k+1\right)},\label{eq:44} \tag{50}\] where \(\Gamma\) is the Legendre Gamma function. Writing \[ \Gamma\left(k+1+jy\right)=h_{k}\exp\left(j\eta_{k}\right)\] \[h_{k}=k!\prod_{n=0}^{\infty}\frac{1}{\sqrt{\frac{y^{2}}{\left(k+1+n\right)^{2}}+1}}, \tag{51}\] \[\eta_{k}=y\Psi\left(k+1\right) +\sum_{n=0}^{\infty}\left(\frac{y}{\left(k+1+n\right)}-\arctan\left(\frac{y}{\left(k+1+n\right)}\right)\right),\] where \(\Psi\) is the digamma function, the Bessel function of imaginary order reads \[Z_{\nu}\left(z\right)=\sum_{k=0}^{\infty}C_{1k}\left(\frac{z}{2}\right)^{2k}\exp\left(j\left(y\ln\left(\frac{z}{2}\right)-\eta_{k}\right)\right),\label{eq:46} \tag{52}\] with \[C_{1k}=\exp\left(q\right)\frac{\left(-1\right)^{k}}{k!\,h_{k}},\] where \(q=0\) if \(d>0\) and \(q=-\pi y\) if \(d<0\) and where, from now on, \(z\) has to be replaced by its absolute value \[\left|z\right|=\frac{2}{\left|d\right|}B\,R^{d/2}.\] Taking the real part of (52), the relation (47) reads \[\ D =K_{1}R^{\left(\left(d+2\right)/2\gamma\right)-2}\sum_{k=0}^{\infty}\left[C_{1k}\left(\frac{z}{2}\right)^{2k}\cos\left(y\ln\left(\frac{z}{2}\right)-\eta_{k}\right)\right].\label{eq:47} \tag{53}\] The second boundary condition, decreasing \(D\) for increasing \(R\), restricts the exponent of \(R\), giving the initial condition on \(d\), \(d<2(2\gamma-1)\), \(d\neq0\).
The radial terms of the perturbed velocity and of the specific mass flux momentum become, from (32) and (33), \[\ U =-\kappa K_{1}\frac{r_{c}}{\rho_{c}}R^{\left(\left(d+2\right)/2\gamma\right)-\left(d+1\right)}\sum_{k=0}^{\infty}\left[C_{2k}\left(\frac{z}{2}\right)^{2k}\sin\left(y\ln\left(\frac{z}{2}\right)-\eta_{k}+\tau_{k}\right)\right],\label{eq:48} \tag{54}\] \[ \Phi =-\kappa K_{1}r_{c}^{2}R^{\left(d+2\right)/2\gamma}\sum_{k=0}^{\infty}\left[C_{2k}\left(\frac{z}{2}\right)^{2k}\sin\left(y\ln\left(\frac{z}{2}\right)-\eta_{k}+\tau_{k}\right)\right],\label{eq:49} \tag{55}\] with \[\begin{aligned} C_{2k} & =\frac{2C_{1k}}{\sqrt{\left(kd+\frac{d+2}{2\gamma}\right)^{2}+\left(\frac{yd}{2}\right)^{2}}},\\ \tau_{k} & =\arctan\left(\frac{2}{yd}\left(kd-\frac{d+2}{2\gamma}\right)\right). \end{aligned}\] The extrema of \(D\) are solutions of \[\ D^{\prime} =-K_{1}R^{\left(\left(d+2\right)/2\gamma\right)-3}\sum_{k=0}^{\infty}\left[C_{3k}\left(\frac{z}{2}\right)^{2k} \sin\left(y\ln\left(\frac{z}{2}\right)-\eta_{k}+\mu_{k}\right)\right]=0,\label{eq:50} \tag{56}\] \[\tan\left(y\ln\left(\frac{z}{2}\right)\right)=\frac{\sum_{k=0}^{\infty}C_{3k}\left(\frac{z}{2}\right)^{2k}\sin\left(\eta_{k}-\mu_{k}\right)}{\sum_{k=0}^{\infty}C_{3k}\left(\frac{z}{2}\right)^{2k}\cos\left(\eta_{k}-\mu_{k}\right)},\label{eq:51} \tag{57}\] with \[\begin{aligned} C_{3k} & =C_{1k}\sqrt{\left(2-kd-\frac{d+2}{2\gamma}\right)^{2}+\left(\frac{yd}{2}\right)^{2}},\\ \mu_{k} & =\arctan\left(\frac{2}{yd}\left(2-kd-\frac{d+2}{2\gamma}\right)\right). \end{aligned}\] The zeros of \(U\) and \(\Phi\) are found like in (57) with \(C_{3k}\) and \(\mu_{k}\) replaced by \(C_{2k}\) and \(\tau_{k}\). It seems that there are no simple analytical solutions to (57). However, for small arguments \((z/2)<<1\) , i.e., \[\frac{4\pi G\rho_{c}r_{c}^{2}}{dc_{c}^{2}}R^{d}<<1,\label{eq:52} \tag{58}\] one finds similar solutions for \(D\) (53), \(U\) (54), \(\Phi\) (55) and \(D^{\prime}\) (56), in the form \[\tan\left(y\ln\left(\frac{z}{2}\right)\right)\approx\tan\left(\kappa\right)\] with \(\kappa\) constant, as the first term for \(k=0\) in the series of (57) predominates, yielding \(\kappa=\eta_{0}\) for \(D\), \(\kappa=\left(\eta_{0}-\tau_{0}\right)\) for \(U\) and \(\Phi\), and \(\kappa=\left(\eta_{0}-\mu_{0}\right)\) for \(D^{\prime}\).
The zeros of \(D\) (53), \(U\) (54), \(\Phi\) (55) and \(D^{\prime}\) (56) are then given by \[\ R=\alpha_{2}\left(\beta_{2}^{\backprime}\right)^{n};\label{eq:53} \tag{59}\] \[ \alpha_{2}=\left(\frac{\left|d\right|}{B}\right)^{2/d}\exp\left(\frac{2\left(\eta_{0}+\phi_{2}\right)}{dy}\right)\,\,\,;\,\,\beta_{2}^{\backprime}=\exp\left(\frac{2\pi}{dy}\right),\label{eq:53-1} \tag{60}\] \(n\) being non-negative integers and \(\phi_{2}=\pi/2\) for \(D\), \(\phi_{2}=-\tau_{0}\) for \(U\) and \(\Phi\), and \(\phi_{2}=-\mu_{0}\) for \(D^{\prime}\). Provided that \(y\) is large enough within the condition (49), one has \(\tau_{0}<<1\) and \(\mu_{0}<<1\). The initial phase between \(D\) and \(U\) is \(\left(\pi/2\right)-\tau_{0}\approx\left(\pi/2\right)\), while the initial phase between \(U\) (or \(\Phi\)) and \(D^{\prime}\) is \(\left(\mu_{0}-\tau_{0}\right)\approx0\). The distance ratio of two successive maxima of \(D\) is \[\beta_{2}=\left(\beta_{2}^{\backprime}\right)^{2}=\exp\left(\frac{2\pi}{\sqrt{\omega^{2}\frac{r_{c}^{2}}{c_{c}^{2}}-\frac{c_{c}^{2}}{r_{c}^{2}}\left(\frac{d+2}{2\gamma}\right)^{2}}}\right),\label{eq:54} \tag{61}\] which, from (49), is a real constant depending on nebula reference characteristics and on \(\omega\).
The third case is more general and considers the two exponents linked by the relation \(d=s-2\) with the restrictions \(d\neq0\) (\(s\neq2\)) and \(d>(2\gamma-1)/\left(1-\gamma\right)\). The Eq. (30) becomes \[\ D^{\prime\prime}+\left(2d+5-\frac{2\left(d+1\right)}{\gamma}\right)\frac{D^{\prime}}{R}+ \left(B^{2}+\frac{\omega^{2}A^{2}}{R^{d}}+\left(d+2\right)\left(d+2-\frac{2\left(d+1\right)}{\gamma}\right)\right)\frac{D}{R^{2}}=0,\label{eq:55} \tag{62}\] which is another Bessel type differential equation, whose solutions are \[D=K_{2}R^{\left(\left(d+1\right)/\gamma\right)-\left(d+2\right)}Z_{\nu}\left(z\right),\label{eq:56} \tag{63}\] where the argument \(z\) and the order \(\nu\) are now \[z=\frac{2}{\left|d\right|}\omega AR^{\left|d\right|/2}\,\,\,;\,\,\nu=\frac{2}{\left|d\right|}\sqrt{\left(\frac{d+1}{\gamma}\right)^{2}-B^{2}},\label{eq:57} \tag{64}\] with \(K_{2}\) a constant determined by the first boundary condition \[K_{2}=\frac{\rho_{c1}^{*}}{Z_{\nu}\left(\frac{2}{\left|d\right|}\omega A\right)}.\] Under the condition \[B^{2}>\left(\frac{d+1}{\gamma}\right)^{2}.\] yielding \[\frac{4\pi G\rho_{c}r_{c}^{2}}{c_{c}^{2}}>\left(\frac{d+1}{\gamma}\right)^{2}\label{eq:58}, \tag{65}\] the order \(\nu\) is a pure imaginary, \(\nu=jy\), with from now on \[y=\frac{2}{\left|d\right|}\sqrt{B^{2}-\left(\frac{d+1}{\gamma}\right)^{2}}.\] Writing the Bessel functions of imaginary order as in (52), with \(q=0\) in \(C_{1k}\), the solution (63) becomes \[\ D =K_{2}R^{\left(\left(d+1\right)/\gamma\right)-\left(d+2\right)}\sum_{k=0}^{\infty}\left[C_{1k}\left(\frac{z}{2}\right)^{2k} \cos\left(y\ln\left(\frac{z}{2}\right)-\eta_{k}\right)\right].\label{eq:59} \tag{66}\] The second boundary condition is fulfilled by the restriction on the exponent of \(R\) (with \(\gamma>1\)).
The radial parts of the perturbed velocity and of the specific mass flux momentum read, from (32) and (33), \[\ U =-\kappa K_{2}\frac{r_{c}}{\rho_{c}}R^{\left(\left(d+1\right)/\gamma\right)-\left(2d+1\right)}\sum_{k=0}^{\infty}\left[C_{4k}\left(\frac{z}{2}\right)^{2k}\sin\left(y\ln\left(\frac{z}{2}\right)-\eta_{k}+\theta_{k}\right)\right],\label{eq:60} \tag{67}\] \[\ Phi =-\kappa K_{2}r_{c}^{2}R^{\left(\left(d+1\right)/\gamma\right)-d}\sum_{k=0}^{\infty}\left[C_{4k}\left(\frac{z}{2}\right)^{2k} \sin\left(y\ln\left(\frac{z}{2}\right)-\eta_{k}+\theta_{k}\right)\right].\label{eq:61} \tag{68}\] Like in the previous section, the extrema of \(D\) are solutions of \[\ D^{\prime} =-K_{2}R^{\left(\left(d+1\right)/\gamma\right)-\left(d+3\right)}\sum_{k=0}^{\infty}\left[C_{5k}\left(\frac{z}{2}\right)^{2k}\sin\left(y\ln\left(\frac{z}{2}\right)-\eta_{k}+\sigma_{k}\right)\right]=0,\label{eq:62} \tag{69}\] \[\tan\left(y\ln\left(\frac{z}{2}\right)\right)=\frac{\sum_{k=0}^{\infty}C_{5k}\left(\frac{z}{2}\right)^{2k}\sin\left(\eta_{k}-\sigma_{k}\right)}{\sum_{k=0}^{\infty}C_{5k}\left(\frac{z}{2}\right)^{2k}\cos\left(\eta_{k}-\sigma_{k}\right)},\label{eq:63} \tag{70}\] with \[\begin{aligned} C_{5k} & =C_{1k}\sqrt{\left(d+2-\frac{d+1}{\gamma}-k\left|d\right|\right)^{2}+\left(\frac{yd}{2}\right)^{2}},\\ \sigma_{k} & =\arctan\left(\frac{2}{y\left|d\right|}\left(d+2-\frac{d+1}{\gamma}-k\left|d\right|\right)\right). \end{aligned}\] The zeros of \(U\) and \(\Phi\) are found like in (70) with \(C_{4k}\) and \(\theta_{k}\) replacing \(C_{5k}\) and \(\sigma_{k}\).
For small arguments \((z/2)<<1\), i.e., \[\omega<<\left|d\right|\frac{c_{c}}{r_{c}}R^{-\left|d\right|/2}\label{eq:64}, \tag{71}\] one finds similar solutions for \(D\) (66), \(U\) (67), \(\Phi\) (68) and \(D^{\prime}\) (69) like in the previous case, as (70) is equal to a constant, \(\tan\left(\kappa\right)\), with \(\kappa=\eta_{0}\) for \(D\), \(\kappa=\left(\eta_{0}-\theta_{0}\right)\) for \(U\) and \(\Phi\), and \(\kappa=\left(\eta_{0}-\sigma_{0}\right)\) for\(D^{\prime}\).
The zeros of \(D\) (66), \(U\) (67), \(\Phi\) (68) and \(D^{\prime}\) read \[\ R=\alpha_{3}\left(\beta_{3}^{\backprime}\right)^{n};\label{eq:65} \tag{72}\] \[ \alpha_{3}=\left(\frac{\left|d\right|}{\omega A}\right)^{2/\left|d\right|}\exp\left(\frac{2\left(\eta_{0}+\phi_{3}\right)}{\left|d\right|y}\right)\,\,\,;\,\,\beta_{3}^{\backprime}=\exp\left(\frac{2\pi}{\left|d\right|y}\right),\label{eq:65-1} \tag{73}\] with \(n\) non-negative integers, \(\phi_{3}=\pi/2\) for \(D\), \(\phi_{3}=-\theta_{0}\) for \(U\) and \(\Phi\), and \(\phi_{3}=-\sigma_{0}\) for \(D^{\prime}\). Provided that \(y\) is large enough within the condition (65), one has \(\theta_{0}<<1\) and \(\sigma_{0}<<1\) . The initial phase between \(D\) and \(U\) (or \(\Phi\)) is \(\pi/2-\theta_{0}\approx\pi/2\), while the initial phase between \(U\) (or \(\Phi\)) and \(D^{\prime}\) is \(\left(\sigma_{0}-\theta_{0}\right)\approx0\).
The distance ratio of two successive maxima of \(D\) is \[\beta_{3}=\left(\beta_{3}^{\backprime}\right)^{2}=\exp\left(\frac{2\pi}{\sqrt{4\pi G\rho_{c}\frac{r_{c}^{2}}{c_{c}^{2}}-\left(\frac{d+1}{\gamma}\right)^{2}}}\right),\label{eq:66} \tag{74}\] which, from (65), is a real constant depending on the reference characteristics but independent of \(\omega\). The period of the small perturbations must be larger than a minimum value \[P_{m}=\frac{2\pi}{\left|d\right|}\frac{r_{c}}{c_{c}}\left(R_{max}\right)^{\left|d\right|/2}\label{eq:67}, \tag{75}\] deduced from the condition (71) applied to the whole range of radial distances of a nebula (\(R_{max}\) is the ratio of the disc outer to inner radii).
We mention an interesting particular case, called the standard model, of the general case \(d=(s-2)\) above. One writes the gravitational potential in the unperturbed disc as a power law distribution in \(R\) (= \(r/r_{c}\)) \[V_{0}=V_{c}R^{\upsilon},\label{eq:68} \tag{76}\] where \(V_{c}\) is the gravitational potential of the central mass \(M^{*}\) (the gravitational potential of the disc is neglected as \(M_{d}<<M^{*}\)) and \(\upsilon\) is an exponent to be defined by physical models. Replacing in the Poisson equation at equilibrium (12) with (24) yields successively \[ \frac{\upsilon^{2}V_{c}}{r_{c}^{2}}R^{\upsilon-2}=4\pi G\rho_{c}R^{d},\label{eq:69} \tag{77}\] \[\ V_{c}=\frac{4\pi G\rho_{c}r_{c}^{2}}{\upsilon^{2}}=\frac{3GM_{c}}{\upsilon^{2}r_{c}},\label{eq:70} \tag{78}\] for \(d=\upsilon-2\) and with \(M_{c}=\left(4\pi/3\right)r_{c}^{3}\rho_{c}\), the mass of the homogeneous sphere of specific mass \(\rho_{c}\) and radius \(r_{c}\).
We make the hypothesis for the standard model that the reference distance \(r_{c}\) of the disc inner edge can be approximated by the central body unperturbed external radius \(r_{c}^{*}\) \[r_{c}\approx r_{c}^{*},\label{eq:71} \tag{79}\] (superscript \(^{*}\) denotes central body characteristics). Noting the central body mean specific mass by \(\rho^{*}\), identifying \(V_{c}\) in (78) with the gravitational potential of the central mass \(M^{*}\) yields \[\rho_{c}=\frac{\upsilon^{2}}{3}\rho^{*}.\label{eq:72} \tag{80}\] In the simplest case, the gravitational potential of a spherical body is given by (76), with \(\upsilon=-1\). The condition (78) yields then \(d=-3\) and, from (80), the nebula reference specific mass \(\rho_{c}\) is one third of the mean specific mass of the central body.
On the other hand, within the perfect gas approximation, the sound speed distribution (24) follows the gas temperature radial distribution in the disc, which can be represented by a power law relation of exponent \(\zeta\) \[c_{c}^{2}R^{s}=\frac{\gamma\Re}{\mu}T_{c}R^{\zeta}\label{eq:73}, \tag{81}\] with \(\Re\) the perfect gas constant, \(\mu\) the gas molecular mass and \(T_{c}\) a reference temperature at the disc inner edge, that can be approximated for example by the central body effective temperature. The radial behaviour of the temperature in a nebula is model dependent. Considering only the central body luminosity as the dominant source of energy heating the nebula (the gas viscosity is neglected), the temperature gradient is adiabatic with \(\zeta=-1\) for an optically thick nebula [18], yielding \(s=-1\).
We define the standard model of a disc as the case with \(\upsilon=-1\), \(d=-3\) and \(s=-1\), and it can be solved with these values by the general case \(d=(s-2)\) above. The distance ratio of maxima of the gas perturbed specific mass distribution writes then, from (74), \[\beta_{st.mod.}=\exp\left(\frac{2\pi c_{c}}{\sqrt{\frac{GM^{*}}{r_{c}}-\left(\frac{2c_{c}}{\gamma}\right)^{2}}}\right).\label{eq:74} \tag{82}\] The condition (65) ensures that this ratio is a real constant.
This simple standard model can be useful as a first approximation model, provided that the disc mass \(M_{d}\) calculated with the value (80) of \(\rho_{c}\) fulfills the initial condition \(M_{d}<<M^{*}\). Let’s note also that in the above approximation, the value \(\rho_{c1}^{*}\left(t\right)\) that the nebula perturbed specific mass has to match at the disc inner edge (first boundary condition) can be approximated by the perturbed specific mass of the central body at its outer edge, for \(r=r_{c}^{*}=r_{c}\) or \(R=1\), at the epoch \(t\). (Strictly speaking, one should consider the central body external perturbed radius \(r_{c1}^{*}=r_{c}^{*}+\xi\left(r_{c}^{*},t\right)\), where \(\xi\left(r_{c}^{*},t\right)\) is the radial displacement of the central body outer edge at \(r=r_{c}^{*}\) due to small perturbations at the epoch \(t\), yielding \(R_{c1}=r_{c1}^{*}/r_{c}^{*}=1+\xi/r_{c}^{*}\); but if the displacements are small in front of the central body unperturbed radius (\(\xi<<r_{c}^{*}\)), one has \(R_{c1}\approx R_{c}=1\)).
We consider a fourth case where the exponents \(d\) and \(s\) are linked by the relation \(d=(s-2)/2\). The equation (30) reads \[\ D^{\prime\prime}+\left(4d+5-\frac{3d+2}{\gamma}\right)\frac{D^{\prime}}{R}+\left(\omega^{2}A^{2}R^{-2d}+B^{2}R^{-d}+2\left(d+1\right)\left(2\left(d+1\right)-\left(\frac{3d+2}{\gamma}\right)\right)\right)\frac{D}{R^{2}}=0.\label{eq:4-1} \tag{83}\] Substituting the variable \(R\) for \[z=j\left(\frac{2}{d}\omega AR^{-d}\right)\] with \(j=\sqrt{-1}\), yields a confluent hypergeometric equation \[\ z^{2}\frac{\partial^{2}D}{\partial z^{2}}-\frac{1}{d}\left(3d+4-\left(\frac{3d+2}{\gamma}\right)\right)z\frac{\partial D}{\partial z}-\left(\frac{z^{2}}{4}+ j\frac{B^{2}}{2d\omega A}z-\left(2\frac{d+1}{d}\right)^{2}\left(1-\frac{3d+2}{2\gamma\left(d+1\right)}\right)\right)D=0.\label{eq:5-1} \tag{84}\] With \(d\neq-2/\left(3+i\gamma\right)\) for all integers \(i\), (84) has a complex solution ([17,19,20]) \[\ D_{C} =R^{-\frac{1}{2}\left(3d+4-\left(\frac{3d+2}{\gamma}\right)\right)}\exp\left(\frac{-z}{2}\right) \left(K_{1}z^{\frac{1}{2}\left(1+\left(\frac{3d+2}{d\gamma}\right)\right)}\phi_{1}+K_{2}z^{\frac{1}{2}\left(1-\left(\frac{3d+2}{d\gamma}\right)\right)}\phi_{2}\right)\label{eq:6-1}, \tag{85}\] with \(K_{1}\) and \(K_{2}\) constants and where \(\phi_{1}=\phi\left(a_{1},b_{1},z\right)\) and \(\phi_{2}=\phi\left(a_{2},b_{2},z\right)\) are Kummer confluent hypergeometric function of arguments \[\begin{aligned} a_{1} & =\frac{1}{2}\left(1+\frac{3d+2}{d\gamma}\right)+jy\,\,\,;\,\,b_{1}=1+\frac{3d+2}{d\gamma};\\ a_{2} & =\frac{1}{2}\left(1-\frac{3d+2}{d\gamma}\right)+jy\,\,\,;\,\,b_{2}=1-\frac{3d+2}{d\gamma}, \end{aligned}\] where \[y=\frac{B^{2}}{d\omega A\left(\frac{3d+2}{\gamma}-\left(3d+4\right)\right)}.\] For \(b_{1}\) and \(b_{2}\) non null and different from negative integers, the Kummer function \(\phi\) expands for both sets of arguments as [21] \[ \phi\left(a,b,z\right) =\Gamma\left(\nu\right)\left(\frac{z}{4}\right)^{-\nu}\exp\left(\frac{z}{2}\right) \sum_{k=0}^{\infty}\frac{\left(-1\right)^{k}\left(2\nu\right)_{k}\left(b-2a\right)_{k}}{k!\left(b\right)_{k}}\,I_{\nu+k}\left(\frac{z}{2}\right),\label{eq:7-1} \tag{86}\] where \(\Gamma\) is the Legendre Gamma function, \((x)_{k}\) are Pochhammer polynomials, \[(x)_{k}=\prod_{q=0}^{k-1}(x+q)\,\,\,;\,\,(x)_{0}=1,\] and \(I_{\nu+k}\) is the complex valued hyperbolic Bessel function of order \(\left(\nu+k\right)\), with \(\nu\) either of \[\begin{aligned} \nu_{1} & =\left(b_{1}-a_{1}-\frac{1}{2}\right)=\frac{3d+2}{2d\gamma}-jy,\\ \nu_{2} & =\left(b_{2}-a_{2}-\frac{1}{2}\right)=-\frac{3d+2}{2d\gamma}+jy. \end{aligned}\] Developing the complex coefficients \(H_{k}\) of \(I_{\nu+k}\) in (86) as in Appendix A, \(D_{C}\) (85) becomes \[\ D_{C} =CR^{-2\left(d+1\right)+\left(\frac{3d+2}{2\gamma}\right)}\frac{z}{4}jy\left(K_{1}C_{1}\sum_{k=0}^{\infty}\left(H_{1k}I_{\nu_{1}+k}\left(\frac{z}{2}\right)\right) +K_{2}C_{2}\sum_{k=0}^{\infty}\left(H_{2k}I_{\nu_{2}+k}\left(\frac{z}{2}\right)\right)\right),\label{eq:8-1} \tag{87}\] where \[\begin{aligned} & C=\sqrt{\frac{\omega A}{d}}\exp\left(j\frac{\pi}{4}\right),\\ & C_{1}=2^{1+\frac{3d+2}{d\gamma}}\Gamma\left(\nu_{1}\right),\\ & C_{2}=2^{1-\frac{3d+2}{d\gamma}}\Gamma\left(\nu_{2}\right) \end{aligned}\] are complex constants. Simple analytical expressions of zeros and extrema of the real part of \(D_{C}\) (87) were not found. However, for small arguments \(z\), \(\left(\left|z\right|/2\right)<<1\), i.e. for small frequencies \[\omega<<\left|d\right|\frac{c_{c}}{r_{c}}R^{-\left|d\right|}\label{eq:9-1}, \tag{88}\] where vertical bars denote the absolute value, the terms other than the first in the convergent series of (86) can be neglected. By the multiplication theorem [22], the hyperbolic Bessel function reduces then to \[\ I_{\nu}\left(\frac{z}{2}\right) \approx\left(\frac{z}{4}\right)^{-\nu}\sum_{m=0}^{\infty}\sum_{n=0}^{\infty}\frac{\left(-1\right)^{m}}{m!n!\Gamma\left(\nu-m+n+1\right)} =\left(\frac{z}{4}\right)^{-\nu}\frac{G\left(\nu\right)}{\nu\Gamma\left(\nu\right)},\label{eq:10-1} \tag{89}\] where terms of second order were neglected in front of unity and where \(G(\nu)\) is a complex function developed in Appendix F. The relation (86) reads now \[\phi\left(a,b,z\right)=\frac{G\left(\nu\right)}{\nu}\left(\frac{z}{4}\right)^{-2\nu}\exp\left(\frac{z}{2}\right).\label{eq:11-1} \tag{90}\] The complex solution (87), written for the variable \(R\), becomes \[\ D_{C}= \left(K_{1}\varLambda R^{-2\left(d+1\right)+\frac{3d+2}{\gamma}}+K_{2}MR^{-2\left(d+1\right)}\right) \exp\left(2jy\ln\left(\frac{2}{\left|d\right|}\omega AR^{-d}\right)\right),\label{eq:12-1} \tag{91}\] where \(\varLambda=\left|\varLambda\right|\exp\left(j\lambda\right)\) and \(M=\left|M\right|\exp\left(j\mu\right)\) are complex constants depending on \(y\), \(\nu\) and \(G(\nu)\) (see Appendix F). The real part of (91) reads as the sum of two terms \[\ D_{R}=K_{1}\left|\varLambda\right|R^{-2\left(d+1\right)+\frac{3d+2}{\gamma}}\cos\left(2y\ln\left(\frac{2}{\left|d\right|}\omega AR^{-d}\right)+\lambda\right)+K_{2}\left|M\right|R^{-2\left(d+1\right)}\cos\left(2y\ln\left(\frac{2}{\left|d\right|}\omega AR^{-d}\right)+\mu\right).\label{eq:13-1-1} \tag{92}\] Due to the second boundary condition (decrease of \(D\) for increasing \(R\)), either the first or the second or both terms of (92) should be considered for the general solution, depending on the respective values of \(d\) and \(\gamma\) as indicated in Table 1.
| \(d>-1\) | \(d\leq-1\) | ||
| \(\gamma<\frac{3}{2}\) | \(d<\frac{2\left(\gamma-1\right)}{3-2\gamma}\) | Both parts | \(K_2=0\) |
| \(d\geq\frac{2\left(\gamma-1\right)}{3-2\gamma}\) | \(K_1=0\) | __ | |
| \(\gamma=\frac{3}{2}\) | all values of \(d\) | Both parts | \(K_2=0\) |
| \(\gamma>\frac{3}{2}\) | \(d\leq\frac{2\left(\gamma-1\right)}{3-2\gamma}\) | __ | No decrease |
| \(d>\frac{2\left(\gamma-1\right)}{3-2\gamma}\) | Both parts | \(K_2=0\) |
Without loss of generality in the resolution, we consider from now on only the case \(s<0\) and \(d<-1\), yielding \(K_{2}=0\) in (92), the other constant \(K_{1}\) being fully determined by the first boundary condition.
The perturbed radial velocity \(U\) and the specific mass flux momentum \(\varPhi\) read, from (32) and (33), \[\ U =-\kappa K_{1}C_{3}\frac{r_{c}}{\rho_{c}}R^{-\left(3d+1\right)+\frac{3d+2}{\gamma}} \sin\left(2y\ln\left(\frac{2}{\left|d\right|}\omega AR^{-d}\right)+\lambda+\zeta\right),\label{eq:14-1-1} \tag{93}\] \[ \varPhi =-\kappa K_{1}C_{3}r_{c}^{2}R^{-2d+\frac{3d+2}{\gamma}} \sin\left(2y\ln\left(\frac{2}{\left|d\right|}\omega AR^{-d}\right)+\lambda+\zeta\right)\label{eq:15}, \tag{94}\] with \[\begin{aligned} & C_{3}=\frac{\left|\varLambda\right|}{\sqrt{\left(\frac{3d+2}{\gamma}-2d\right)^{2}+\left(-2dy\right)^{2}}},\\ & \zeta=\arctan\left(\frac{\frac{3d+2}{\gamma}-2d}{-2dy}\right). \end{aligned}\] The extrema (minima and maxima) of \(D_{R}\) are found from \[\ D_{R}^{\prime} =-K_{1}C_{4}R^{-2\left(d+3\right)+\frac{3d+2}{\gamma}} \sin\left(2y\ln\left(\frac{2}{\left|d\right|}\omega AR^{-d}\right)+\lambda+\xi\right)=0\label{eq:16-1}, \tag{95}\] with \[\begin{aligned} & C_{4}=\left|\varLambda\right|\sqrt{\left(\frac{3d+2}{\gamma}-2\left(d+1\right)\right)^{2}+\left(2dy\right)^{2}},\\ & \xi=\arctan\left(\frac{\frac{3d+2}{\gamma}-2\left(d+1\right)}{2dy}\right). \end{aligned}\] The zeros of \(D_{R}\) (92), \(U\) (93), \(\varPhi\) (94) and \(D_{R}^{\prime}\) (95) read in this fourth case \[\ R=\alpha_{4}\left(\beta_{4}^{\backprime}\right)^{n},\label{eq:17-1} \tag{96}\] \[ \alpha_{4}=\left(\frac{2}{\left|d\right|}\omega A\right)^{\frac{1}{d}}\exp\left(\frac{\lambda+\varphi_{4}}{2\left|d\right|y}\right)\,\,\,;\,\,\beta_{4}^{\backprime}=\exp\left(\frac{\pi}{2\left|d\right|y}\right), \tag{97}\] \(n\) being non-negative integers and \(\varphi_{4}=\left(\pi/2\right)\) for\(D_{R}\), \(\varphi_{4}=\zeta\) for \(U\) and \(\varPhi\), and \(\varphi_{4}=\xi\) for \(D_{R}^{\prime}\). Provided that \(\omega A\) is small enough, within the condition (88), one has \(y>>1\), yielding \(\zeta<<1\) and \(\xi<<1\). The initial phase between \(D\) and \(U\) is \(\left(\pi/2\right)-\zeta\approx\left(\pi/2\right)\), while the initial phase between \(U\) (or \(\varPhi\)) and \(D^{\prime}\) is \((\xi-\zeta)\approx0\).
The distances ratio of two successive maxima of \(D\) is \[\beta_{4}=\left(\beta_{4}^{\backprime}\right)^{2}=\exp\left(\frac{\left(3d+4-\frac{3d+2}{\gamma}\right)\omega c_{c}}{4\pi G\rho_{c}r_{c}}\right)\label{eq:18-1}, \tag{98}\] which is a real constant depending on the perturbations angular frequency \(\omega\) and the disc reference characteristics. The period of the perturbations must be larger than a minimum value \[P_{m}=\frac{2\pi}{\left|d\right|}\frac{r_{c}}{c_{c}}R_{max}^{d}\label{eq:19-1}, \tag{99}\] deduced from the condition (88) applied to the whole range of radial distances of the disc (\(R_{max}\) is the ratio of the outer and inner radii of the disc).
In the previous section, we considered the exponents \(d\) and \(s\) taking particular values or linked by non-causal relations. However, a relation between \(d\) and \(s\) can be found if one considers that the specific mass and sound speed are fully governed by polytropic processes in the disc. Considering the two polytropic relations between the pressure \(p\), the specific mass \(\rho\) and the sound speed \(c\) \[p=\frac{c^{2}\rho}{\gamma}\,\,\,;\,\,p\rho^{-\gamma}=\text{constant},\label{eq:20-1} \tag{100}\] one has successively, with the power law radial distributions \(\rho_{0}=\rho_{c}R^{d}\) and \(c_{0}^{2}=c_{c}^{2}R^{s}\), \[\ c^{2}\rho^{1-\gamma}=c_{c}^{2}\rho_{c}^{1-\gamma}R^{s+d\left(1-\gamma\right)}=\text{constant},\label{eq:21-1} \tag{101}\] \[ s+d\left(1-\gamma\right)=0\,\,\,\text{or}\,\,\gamma=1+\frac{s}{d}.\label{eq:22-1} \tag{102}\] Replacing \(\gamma\) for \(s\) and \(d\) in the Eq. (30) yields \[\ D^{\prime\prime}+\left(2s+1-d\right)\frac{D^{\prime}}{R}+ \left(B^{2}R^{d+2-s}+\omega^{2}A^{2}R^{2-s}+s\left(s-d\right)\right)\frac{D}{R^{2}}=0,\label{eq:23-1} \tag{103}\] which becomes a differential Schrödinger type equation by posing \[D=\frac{Y}{\sqrt{R^{2s+1-d}}}\] yielding \[Y^{\prime\prime}+\left(B^{2}R^{d-s}+\omega^{2}A^{2}R^{-s}-\left(\frac{d^{2}-1}{4}\right)R^{-2}\right)Y=0.\label{eq:24-1-1} \tag{104}\] An approximate solution to this equation can be found by the Wentzel-Kramers-Brillouin (WKB) theory [23]. Considering the case of small frequencies such as \[\omega A<<B^{2}\,\,\,\text{or}\,\,\omega<<4\pi G\frac{\rho_{c}r_{c}}{c_{c}}\label{eq:25-1}, \tag{105}\] one poses \(\epsilon=\omega AB^{-2}\) with \(\epsilon<<1\). The Eq. (104) reads then \[ \epsilon^{2}Y^{\prime\prime} =\left(-\omega^{2}A^{2}\epsilon^{2}R^{-s}-\omega A\epsilon R^{d-s}+\epsilon^{2}\left(\frac{d^{2}-1}{4}\right)R^{-2}\right)Y =Q\left(R\right)Y.\label{eq:26-1} \tag{106}\] Let us consider the three following functions of \(R\) \[ S_{0}\left(R\right) =\intop^{R}\sqrt{Q(x)}dx\,;\,\,S_{1}\left(R\right)=-\frac{\ln\left(Q\left(R\right)\right)}{4};\label{eq:27-1} \tag{107}\] \[\ S_{2}\left(R\right) =\intop^{R}\left(\frac{QQ^{\prime\prime}-\frac{5}{4}\left(Q^{\prime}\right)^{2}}{8Q^{\frac{5}{2}}}\right)dx,\label{eq:27-2} \tag{108}\] where the first two functions (107) are referred to respectively as the eikonal function and the transport function and where \(Q^{\prime}=dQ(x)/dx\).
If \(Q(R)\neq0\) in the range of interest of \(R\) (i.e., \(1\leq R\leq R_{max}\)) and under the conditions \[\epsilon S_{2}\left(R\right)<<S_{1}\left(R\right)<<\frac{S_{0}\left(R\right)}{\epsilon}\,\,\,;\,\,\epsilon S_{2}\left(R\right)<<1\label{eq:28-1}, \tag{109}\] the leading orders in the WKB physical optics approximation to the exact solutions in \(Y\) and \(D\) reads generally \[ Y\left(R\right) =K_{3}\exp\left(\frac{S_{0}\left(1,R\right)}{\epsilon}+S_{1}\left(R\right)\right) +K_{4}\exp\left(-\frac{S_{0}\left(1,R\right)}{\epsilon}+S_{1}\left(R\right)\right),\label{eq:29-1} \tag{110}\] \[\ D\left(R\right) =R^{-\left(2s+1-d\right)/2}\left(K_{3}\exp\left(\frac{S_{0}\left(1,R\right)}{\epsilon}+S_{1}\left(R\right)\right)+K_{4}\exp\left(-\frac{S_{0}\left(1,R\right)}{\epsilon}+S_{1}\left(R\right)\right)\right)\label{eq:30-1-1}, \tag{111}\] with \(K_{3}\) and \(K_{4}\) constants determined by the boundary conditions and where \(S_{0}\left(1,R\right)\) is the eikonal function on the interval \(\left[1,R\right]\). Strictly speaking, the above equality sign should be replaced by an asymptotic equality sign. The eikonal function \(S_{0}\left(1,R\right)\) reads \[\ S_{0}\left(1,R\right)=\intop_{1}^{R}\sqrt{Q\left(x\right)}dx =j\omega A\epsilon\intop_{1}^{R}\sqrt{x^{-s}+\frac{1}{\omega A\epsilon}x^{d-s}-\left(\frac{d^{2}-1}{4\omega^{2}A^{2}}\right)x^{-2}}dx =j\omega A\epsilon\intop_{1}^{R}\frac{\sqrt{T\left(x\right)}}{x}dx\label{eq:31-1}, \tag{112}\] with \[T\left(x\right)=x^{2-s}+\frac{1}{\omega A\epsilon}x^{2+d-s}-\left(\frac{d^{2}-1}{4\omega^{2}A^{2}}\right).\label{eq:32-1} \tag{113}\] The integral (112) has to be evaluated for specific values of \(d\) and \(s\). This evaluation involves most of the time elliptic integrals, which makes it uneasy.
In most nebula models, the gas specific mass and sound speed are decreasing outward from the central body, with the exponents \(d\) and \(s\) taking negative values and \(s\) usually in the order of or close to \(-1\). We consider here the particular polytropic case with \(s=-1\) and \(d=-2\), yielding \(\gamma=3/2\). Cases for other values of \(d\), \(s\) and \(\gamma\) can be solved similarly. The integral (112) reads \[S_{0}\left(1,R\right)=j\left(\frac{\omega A\epsilon}{3}I_{1}+\frac{2}{3}I_{2}-\frac{3\epsilon}{4\omega A}I_{3}\right)\label{eq:33-1}, \tag{114}\] with \[\ I_{1}=\intop_{1}^{R}\frac{3x^{2}+\frac{1}{\omega A\epsilon}}{\sqrt{T\left(x\right)}}dx\,\,\,;\,\,I_{2}=\intop_{1}^{R}\frac{dx}{\sqrt{T\left(x\right)}}\label{eq:33-2}, \tag{115}\] \[\ I_{3}=\intop_{1}^{R}\frac{dx}{x\sqrt{T\left(x\right)}}.\label{eq:33-3} \tag{116}\] The cubic trinomial \(T\left(x\right)\) (113) has a single real root and, neglecting terms in \(\epsilon^{2}\) and of higher order, it becomes \[T\left(x\right)=\left(x-\frac{3\epsilon}{4\omega A}\right)\left(x^{2}+\frac{3\epsilon}{4\omega A}x+\frac{1}{\omega A\epsilon}\right).\label{eq:34-1} \tag{117}\] Posing \[C_{5}=\sqrt{\frac{1}{\omega A\epsilon}+\frac{9}{8}\left(\frac{\epsilon}{\omega A}\right)^{2}}\] one substitutes \(\left(x-\frac{3\epsilon}{4\omega A}\right)\) for \(C_{5}z\) in integral \(I_{2}\) and for \(C_{5}z^{2}\) in integral \(I_{3}\) in (115). The integrals in (115) are evaluated under the two following conditions \[\frac{\omega A}{B}R<<1\,\,\,;\,\,B^{2}R>>\frac{3}{4}\label{eq:35-1}, \tag{118}\] in the range \(1\leq R\leq R_{max}\), showing also that the real root of the trinomial \(T\left(x\right)\) (117) is outside the range of interest of \(R\), fulfilling the condition \(Q(R)\neq0\). The other conditions (109) to apply the WKB theory are verified in Appendix C.
Under the above two conditions, \(I_{2}\) and \(I_{3}\) become [24] \[\ I_{2} =\frac{1}{\sqrt{C_{2}}}\left(F\left(\boldsymbol{\varphi}\left(R\right),k\right)-F\left(\boldsymbol{\varphi}\left(1\right),k\right)\right)\label{eq:36-2}, \tag{119}\] \[I_{3} =\frac{1}{\sqrt{\left(C_{2}\right)^{3}}}\left(\left(F\left(\boldsymbol{\varphi}\left(R\right),k\right)-2E\left(\boldsymbol{\varphi}\left(R\right),k\right)\right)\right.\] \[\left.-\left(F\left(\boldsymbol{\varphi}\left(1\right),k\right)-2E\left(\boldsymbol{\varphi}\left(1\right),k\right)\right)\right)\] \[ -\frac{2}{C_{2}}\left(\frac{1}{R-\frac{3\epsilon}{4\omega A}+C_{2}}\sqrt{\frac{R^{2}+\frac{3\epsilon}{4\omega A}R+\frac{1}{\omega A\epsilon}}{R-\frac{3\epsilon}{4\omega A}}}\right.\] \[\left.-\left(\frac{1}{1-\frac{3\epsilon}{4\omega A}+C_{2}}\sqrt{\frac{1+\frac{3\epsilon}{4\omega A}+\frac{1}{\omega A\epsilon}}{1-\frac{3\epsilon}{4\omega A}}}\right)\right), \tag{120}\] where \(F\) and \(E\) are the incomplete elliptic integrals of the first and second kinds of argument and modulus \[ \boldsymbol{\varphi}\left(R\right) =2\arctan\left(\frac{1}{C_{2}}\sqrt{R-\frac{3\epsilon}{4\omega A}}\right) \approx2\arctan\left(\sqrt{\frac{\omega A}{B}R}\right),\label{eq:38-1} \tag{121}\] \[\ k= \sqrt{\frac{1}{2}-\frac{9\epsilon}{16\omega A\sqrt{C_{2}}}}\approx\frac{1}{\sqrt{2}},\label{eq:39-1} \tag{122}\] where the conditions (118) were used, yielding also \(C_{2}=\frac{B}{\omega A}\). Replacing in (120), (121) and in (115), (114) yields eventually \[S_{0}\left(1,R\right)=j\epsilon\left(s_{0R}-s_{01}\right)\label{eq:40-1}, \tag{123}\] with \[\ s_{0R} =\left(\frac{2}{3}\sqrt{\frac{B^{3}}{\omega A}}-\frac{3}{4}\sqrt{\frac{\omega A}{B^{3}}}\right)F\left(\boldsymbol{\varphi}\left(R\right),k\right) +\frac{3}{2}\sqrt{\frac{\omega A}{B^{3}}}E\left(\boldsymbol{\varphi}\left(R\right),k\right) +\frac{\sqrt{\left(\omega A\right)^{2}R^{3}+B^{2}R-\frac{3}{4}}\left(\frac{2}{3}+\frac{3}{2}\frac{B^{3}}{\omega A}\right)}{\left(B^{2}R-\frac{3}{4}\right)\left(B^{2}R-\frac{3}{4}+\frac{B^{3}}{\omega A}\right)}\label{eq:41-1}, \tag{124}\] and a similar relation for \(s_{01}\) with \(R=1\) .
The incomplete elliptic integrals \(F\) and \(E\) are evaluated after an ascending Landen transformation, yielding the new argument and modulus and the transformed expressions of \(F\) and \(E\) to be \[ \boldsymbol{\varphi}_{t}=\frac{1}{2}\left(\boldsymbol{\varphi}+\arcsin\left(k\sin\boldsymbol{\varphi}\right)\right) \approx\frac{1}{2}\arcsin\left(2\left(1+\frac{1}{\sqrt{2}}\right)\sqrt{\frac{\omega A}{B}R}\right),\label{eq:42-1} \tag{125}\] \[\ k_{t}=\frac{2\sqrt{k}}{1+k}\approx\frac{2^{\frac{5}{4}}}{1+\sqrt{2}}\approx0.9852,\label{eq:43-1} \tag{126}\] \[\ F\left(\boldsymbol{\varphi}\left(R\right),k\right)=\frac{2}{1+k}F\left(\boldsymbol{\varphi_{t}}\left(R\right),k_{t}\right),\label{eq:44-1} \tag{127}\] \[\ E\left(\boldsymbol{\varphi}\left(R\right),k\right)=\left(1+k\right)E\left(\boldsymbol{\varphi_{t}}\left(R\right),k_{t}\right) +\left(1-k\right)F\left(\boldsymbol{\varphi_{t}}\left(R\right),k_{t}\right) -\frac{\left(1+k\right)\tan\boldsymbol{\varphi}}{2+\frac{\sec\boldsymbol{\varphi}\left(1+\frac{1}{k^{2}}\right)\sqrt{1-k^{2}}}{\cos\boldsymbol{\varphi}+\sqrt{\frac{1}{k^{2}}-\sin^{2}\boldsymbol{\varphi}}}}.\label{eq:45-1} \tag{128}\] As \(k_{t}\) is close to unity, one can use the expansions [24] \[\ F\left(\boldsymbol{\varphi_{t}}\left(R\right),k_{t}\right)=\frac{2}{\pi}\boldsymbol{K^{\prime}}\ln\left(\tan\left(\frac{\boldsymbol{\varphi}_{t}}{2}+\frac{\pi}{4}\right)\right) -\sin\boldsymbol{\varphi}_{t}\sec^{2}\boldsymbol{\varphi}_{t}\left(a_{0}-\frac{2}{3}a_{1}\tan^{2}\boldsymbol{\varphi}_{t}+…\right)\label{eq:46-1}, \tag{129}\] \[\ E\left(\boldsymbol{\varphi_{t}}\left(R\right),k_{t}\right)=\frac{2}{\pi}\boldsymbol{E^{\prime}}\ln\left(\tan\left(\frac{\boldsymbol{\varphi}_{t}}{2}+\frac{\pi}{4}\right)\right) +\sin\boldsymbol{\varphi}_{t}\sec^{2}\boldsymbol{\varphi}_{t}\left(b_{0}-\frac{2}{3}b_{1}\tan^{2}\boldsymbol{\varphi}_{t}+…\right),\label{eq:47-1} \tag{130}\] where \[\boldsymbol{K^{\prime}}=\boldsymbol{K}\sqrt{1-k_{t}^{2}}\,\,\,;\,\,\boldsymbol{E^{\prime}}=\boldsymbol{E}\sqrt{1-k_{t}^{2}}\] are the complete integrals of the first and second kinds and \(a_{0},a_{1},…,b_{0},b_{1},…\) are decreasing coefficients, functions of \(k_{t}\). As \(k_{t}\approx0.9852\), \(\boldsymbol{K^{\prime}}\approx\boldsymbol{E^{\prime}}\approx\pi/2\) within \(7.5\times10^{-3}\), \(a_{0}\approx7.5\times10^{-3}\), \(a_{1}\approx10^{-4}\), \(b_{0}\approx-7.5\times10^{-3}\), etc … , yielding \[\ F\left(\boldsymbol{\varphi_{t}}\left(R\right),k_{t}\right) ; \approx E\left(\boldsymbol{\varphi_{t}}\left(R\right),k_{t}\right) \approx\ln\left(\frac{1}{2}\left(1+\frac{1}{\sqrt{2}}\right)\sqrt{\frac{\omega A}{B}R}\right).\label{eq:48-1} \tag{131}\] Replacing in (127), (128) and (124) and using conditions (118) to neglect small terms, it yields \[\ s_{0R} =W\ln\left(\frac{1}{2}\left(1+\frac{1}{\sqrt{2}}\right)\sqrt{\frac{\omega A}{B}R}\right) +\frac{2}{3}\sqrt{\left(\omega A\right)^{2}R^{3}+B^{2}R-\frac{3}{4}}\label{eq:49-1}, \tag{132}\] and similarly for \(s_{01}\) for \(R=1\), with \(W=W(\omega,A,B)\) \[\ W =\frac{8}{3}\left(1-\frac{1}{\sqrt{2}}\right)\sqrt{\frac{B^{3}}{\omega A}}+3\sqrt{\frac{\omega A}{2B^{3}}} \approx\frac{8}{3}\left(1-\frac{1}{\sqrt{2}}\right)\sqrt{\frac{B^{3}}{\omega A}}\label{eq:50-1}, \tag{133}\] under the conditions (118).
The complex perturbed specific mass \(D_{C}\) (35) and its real part read \[\ D_{C}=\frac{B}{\sqrt{j\omega A}\sqrt[4]{\left(\omega A\right)^{2}R^{3}+B^{2}R-\frac{3}{4}}} \left(K_{3}\exp\left(j\left(s_{0R}-s_{01}\right)\right)+K_{4}\exp\left(-j\left(s_{0R}-s_{01}\right)\right)\right),\label{eq:51-1} \tag{134}\] \[\ D_{R}=\frac{K_{5}B\cos\left(s_{0R}-s_{01}-\kappa\right)}{\sqrt{\omega A}\sqrt[4]{\left(\omega A\right)^{2}R^{3}+B^{2}R-\frac{3}{4}}}\label{eq:52-1}, \tag{135}\] with \[K_{5}=\sqrt{K_{3}^{2}+K_{4}^{2}}\,\,\,;\,\,\kappa=\arctan\left(\frac{K_{3}-K_{4}}{K_{3}+K_{4}}\right).\] The extrema of \(D_{R}\) are solutions of \[D_{R}^{\prime}=-\frac{K_{5}C_{6}\sin\left(s_{0R}-s_{01}-\kappa+\tau\right)}{\sqrt[4]{\left(\omega A\right)^{2}R^{3}+B^{2}R-\frac{3}{4}}}=0\label{eq:53-1-1}, \tag{136}\] with \[\begin{aligned} & C_{6}=\frac{4}{3}\left(1-\frac{1}{\sqrt{2}}\right)\frac{B^{\frac{5}{2}}}{\omega A},\\ & \tau=\arctan\left(\frac{3}{8}\left(1+\frac{1}{\sqrt{2}}\right)\sqrt{\frac{\omega A}{B^{3}}}\right), \end{aligned}\] where the conditions (118) were used to neglect small terms. The zeros and extrema of \(D_{R}\) are given by \[\ \frac{1}{2}\left(1+\frac{1}{\sqrt{2}}\right)\sqrt{\frac{\omega A}{B}R}\exp\left(\frac{2}{3}\frac{\sqrt{\left(\omega A\right)^{2}R^{3}+B^{2}R-\frac{3}{4}}}{W}\right) =\exp\left(\frac{s_{01}+\varphi_{5}+\kappa}{W}\right)\exp\left(\frac{\pi n}{W}\right),\label{eq:54-1} \tag{137}\] where \(n\) are non-negative integers and \(\varphi_{5}=\pi/2\) for \(D_{R}\) and \(\varphi_{5}=-\tau\) for \(D_{R}^{\prime}\). The exponential term in the above left hand side part reduces to \[ \exp\left(\frac{2}{3}\frac{\sqrt{\left(\omega A\right)^{2}R^{3}+B^{2}R-\frac{3}{4}}}{W}\right) \approx\exp\left(\frac{1}{2}\left(1+\frac{1}{\sqrt{2}}\right)\sqrt{\frac{\omega A}{B}R}\right)\label{eq:55-1}, \tag{138}\] under the conditions (118), and it can be neglected when multiplied by its argument, small by (118). The zeros and extrema of \(D_{R}\) are then given in good approximation by \[\ R=\alpha_{5}\left(\beta_{5}^{\backprime}\right)^{n},\label{eq:56-1}, \tag{139}\] \[ \alpha_{5}=16\left(\frac{3}{2}-\sqrt{2}\right)\frac{B}{\omega A}\exp\left(\frac{2\left(s_{01}+\varphi_{5}+\kappa\right)}{W}\right),\label{eq:56-2} \tag{140}\] \[ \beta_{5}^{\backprime}=\exp\left(\frac{2\pi}{W}\right).\label{eq:56-3} \tag{141}\] The perturbed radial velocity \(U\) and the specific mass flux radial momentum \(\varPhi\) are found from (32) and (33), with (135). However, their evaluation requires the resolution of a new elliptic integral. To avoid this and as there are no zeros due to the transport function \(S_{1}(R)\) (in the 4-th root of the trinomial term in \(R\)) in (135), we evaluate \(U\) and \(\varPhi\) by neglecting \(S_{1}(R)\). This is the geometrical optics approximation, which gives the most rapidly varying component (controlling factor) of the leading behaviour of the exact solution. In the geometrical optics (g.o.) approximation, the real part of the complex perturbed specific mass (135) reduces then to \[D_{R\,g.o.}=K_{5}\frac{B}{\sqrt{\omega A}}\cos\left(s_{0R}-s_{01}-\kappa\right).\label{eq:57-1} \tag{142}\] Under the conditions (118), the term \(s_{0R}\) (132) can be written approximately \[\ s_{0R} \approx W\left(\ln\left(\frac{1}{2}\left(1+\frac{1}{\sqrt{2}}\right)\sqrt{\frac{\omega A}{B}R}\right)+\frac{1}{2}\left(1+\frac{1}{\sqrt{2}}\right)\sqrt{\frac{\omega A}{B}R}\right)\label{eq:58-1}, \tag{143}\] as was already done in (138). The radial velocity \(U\) and the specific mass flux radial momentum \(\varPhi\) read then in the geometrical optics approximation \[\ U_{g.o.} =-\kappa K_{5}C_{7}\frac{r_{c}}{\rho_{c}}R^{3}\sin\left(s_{0R}-s_{01}-\kappa+\sigma\right),\label{eq:59-1} \tag{144}\] \[\ varPhi_{g.o.} ; =-\kappa K_{5}C_{7}r_{c}^{2}R^{2}\sin\left(s_{0R}-s_{01}-\kappa+\sigma\right),\label{eq:60-1} \tag{145}\] with \[\begin{aligned} & C_{7}=\frac{2B}{\sqrt{\omega A\left(W^{2}+16\right)}},\\ & \sigma=\arctan\left(3\left(1+\frac{1}{\sqrt{2}}\right)\sqrt{\frac{\omega A}{B^{3}}}\right), \end{aligned}\] showing that their zeros are given like the zeros and extrema of \(D_{R}\) with \(\beta_{5}^{\backprime}\) (139) and \(\varphi_{5}=-\sigma\) in \(\alpha_{5}\) (139).
By the condition (105), one has \(\sigma<<1\) and \(\tau<<1\). The initial phase between \(D\) and \(U\) (or \(\varPhi\)) is \(\left(\pi/2\right)-\sigma\approx\pi/2\), while the initial phase between \(U\) (or \(\varPhi\)) and \(D^{\prime}\) is \(\left(\tau-\sigma\right)\approx0\).
Let us note that, in the physical optics approximation, retaining the term \(S_{1}(R)\) in \(D_{R}\) would change the amplitudes of \(U\) and \(\varPhi\) (by the addition of decreasing terms in \(R\) in front of the sin function) and it would change the coefficient of \(\sqrt{\omega A/B^{3}}\) and add negligible terms in the argument of the \(\arctan\) of \(\sigma\). But the distance ratio of two successive zeros of \(U\) (or \(\varPhi\)) is unaffected and is still given by \(\beta_{5}^{\backprime}\) (139) in both WKB approximations.
The distances ratio of two successive maxima of \(D\) is given by \[\beta_{5}=\left(\beta_{5}^{\backprime}\right)^{2}\label{eq:62-1}, \tag{146}\] with \[ \beta_{5} =\exp\left(\frac{\pi}{\frac{2\left(\sqrt{2}-1\right)r_{c}}{3\sqrt{2\omega}c_{c}}\left(4\pi G\rho_{c}\right)^{\frac{3}{4}}+\frac{3c_{c}}{4r_{c}}\sqrt{\frac{\omega}{2}}\left(4\pi G\rho_{c}\right)^{-\frac{3}{4}}}\right) \approx\exp\left(\frac{3\pi\left(\sqrt{2}+1\right)c_{c}\sqrt{\omega}}{\sqrt{2}r_{c}\left(4\pi G\rho_{c}\right)^{\frac{3}{4}}}\right),\label{eq:63-1} \tag{147}\] where the approximated value of \(W\) (133) is used in (147). The distances ratio \(\beta_{5}\) is a constant, function of the perturbations angular frequency \(\omega\) and of the disc reference characteristics. The period of the small perturbations must be larger than a minimum value \(P_{m}\), which is the greatest of the two values that can be deduced from the two conditions (105) and (118) on \(\omega\), applied to the whole range of radial distances up to \(R_{max}\), yielding
\[P_{m}=\frac{c_{c}}{2G\rho_{c}r_{c}}\,\,\,\text{or}\,\,\,P_{m}=\sqrt{\frac{\pi}{G\rho_{c}}}R_{max}.\label{eq:64-1} \tag{148}\]
For all the cases considered, the spatial part of the perturbed specific mass \(D\) has a sign opposite to the signs of its radial derivative \(D^{\prime}\), of the radial perturbed velocity \(U\) and of the specific mass flux radial momentum \(\Phi\). The functions \(U\) and \(\Phi\) have an initial phase difference of approximately \(\pi/2\) with respect to the function \(D\). The zeros of \(U\) correspond to the extrema of \(D\) and vice-versa. For increasing \(R\), \(U\) and \(\Phi\) are positive (respectively negative) between successive minima and maxima (respectively successive maxima and minima) of \(D\), as shown in Figure 1. This configuration yields radial outward flows of gas between successive minima and maxima of \(D\) and radial inward flows of gas between successive maxima and minima. The extrema amplitudes of \(D\) and \(D^{\prime}\) decrease for increasing \(R\), while the extrema amplitudes of \(U\) and \(\Phi\) increase for increasing \(R\), although less for \(\Phi\) than for \(U\) in the case \(d=(s-2)\). The nebular gas, flowing outward (respectively inward) with a positive (respectively negative) radial velocity \(U\), may accumulate in annular rings centered on circular orbits with radii corresponding to the distances of the maxima of the gas perturbed specific mass, depleting the zones of minima of perturbed specific mass.
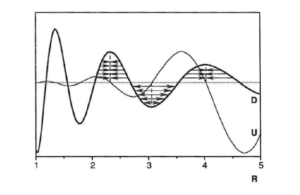
In a rotating nebula containing dust, the solid particles experience an inward drift due to the gas drag caused by the difference of the gas circular velocity and the Keplerian orbital velocity, the former being less than the latter [25]. Smaller particles are more affected by the gas drag than larger ones. Particles on eccentric orbits encounter gas of variable density, causing circularization of their orbit. If a radial velocity is superimposed onto the gas circular velocity, solid particles experience an additional radial drag causing the orbit of smaller particles to decay more (respectively less) rapidly in the case of inward (respectively outward) gas flow, larger particles being less affected. The nebular dust is dragged along with the gas, causing the orbit’s eccentricity of particles to change, favouring collision and accretion (see e.g., [26]). This process would eventually result in an accumulation of solid particles dragged along with the gas, near zones of maxima of gas perturbed specific mass. A more detailed analysis of the dynamical gas/particle interactions would confirm this but is outside the scope of this paper.
A wave-like equation of perturbed specific mass deduced for thin slowly rotating low mass gaseous discs undergoing small radial periodic perturbations and disregarding non-radial perturbations has been solved for several cases of exponents \(d\) and \(s\) of the equilibrium radial power law distributions of specific mass \(\rho\sim r^{d}\) and sound speed \(c\sim r^{\frac{s}{2}}\), namely for two particular models (\(d=0\) and \(d<2\left(2\gamma-1\right)\); \(s=2\)) and for three general cases, the first for \(d=\left(s-2\right)\); \(s<2\) for small frequencies, and a particular case with \(s=-1\) and \(d=-3\), called the standard model; the second for \(d=(s-2)/2\); and the third for \(d=s/(\gamma-1)\), called the polytropic model, with a complete solution for the particular values \(\gamma=3/2\), \(d=-3\) and \(s=-1\).
For all these cases, similar conclusions are reached concerning the spatial part functions of perturbed specific mass \(D\), of its derivative \(D^{\prime}\), of the perturbed radial velocity \(U\) and of the specific mass flux radial momentum \(\varPhi\), namely that, first, \(D\) has a sign opposite to the signs of \(D^{\prime}\), \(U\) and \(\varPhi\); second, the functions \(D^{\prime}\), \(U\) and \(\varPhi\) are in phase and have an initial phase difference of approximately \(\pi/2\) with respect to the function \(D\); third, the zeros of \(U\) corresponds to the extrema of \(D\) and vice-versa; and finally, for increasing \(R\), the functions \(U\) and \(\varPhi\) are positive (respectively negative) between successive minima and maxima (respectively successive maxima and minima) of \(D\). This situation yields radial outward flows of gas between successive minima and maxima of \(D\) and radial inward flows of gas between successive maxima and minima of \(D\), that would eventually form annular structures of gas, with axial radii corresponding to the distances of maxima of the gas perturbed specific mass. Furthermore, the maxima of the gas perturbed specific mass are found to be exponentially spaced for all cases and their distances ratios are constants depending on disc characteristics and on the angular frequency of the perturbations. These results can be applied to protoplanetary and proto-satellite discs. A lower limit on orders of magnitudes of time scales can be deduced for the case \(d=(s-2)\) from the condition (75) on the period of the perturbations. For the standard model, minimum periods depend on dimensions of the central mass and are in the order of several \(10^{3}\) years for protostellar discs similar to what the protoplanetary disc around the proto-Sun may have been and in the order of several \(10^{-1}\) year for giant planets proto-satellite discs.
The specific mass flux due to the radial periodic perturbation can be divided in two parts. The radial part is due to the perturbed radial velocity \(v_{1}\) and reads \(\rho_{0}v_{1}\) while the azimuthal part has two components, the first one due to the azimuthal velocity at equilibrium \(v_{0}\) multiplied by the perturbed specific mass \(\rho_{1}\) and the second one due to the perturbed azimuthal velocity \(u_{1}\) multiplied by the specific mass \(\rho_{0}\) at equilibrium, that is \(\rho_{1}v_{0}+\rho_{0}u_{1}\). We show here that the contribution of the second term \(\rho_{0}u_{1}\) to the azimuthal specific mass flux is in fact much smaller than the first one \(\rho_{1}v_{0}\) and can be neglected.
We show first that \(u_{1}\) is much smaller than \(v_{0}\). Under the hypothesis of purely axisymmetric radial perturbations, all perturbed variables are functions of the radius \(r\) and time \(t\). So, the perturbed azimuthal velocity \(u_{1}\) depends only on \(r\) and \(t\) and not on the azimuthal angle \(\theta\). Therefore, \(u_{1}\)does not appear in the continuity equation. However, we still can find a relation between \(u_{1}\) and \(v_{0}\).
The perturbed azimuthal velocity \(u_{1}\) is related to the radial perturbed velocity \(v_{1}\) by the Coriolis effect. With \(\Omega\) the norm of the nebula rotation angular velocity vector \(\boldsymbol{\Omega}\) pointing upward, the Coriolis acceleration vector has a norm \(-2\Omega v_{1}\) and is in the azimuthal direction of \(v_{0}\) if \(v_{1}\) is directed radially inward and in the opposite azimuthal direction of \(v_{0}\) if \(v_{1}\) is directed radially outward. As the perturbations are purely radial and periodic, let \(\omega\) be the angular frequency and the perturbed radial position \(r_{1}=\varepsilon\sin\left(\omega t\right)\), with the amplitude \(\varepsilon\) much smaller than the radial position \(\varepsilon<<r\), then the perturbed radial velocity reads \(v_{1}=\varepsilon\omega\cos\left(\omega t\right)\leq\varepsilon\omega\), yielding a periodically changing Coriolis acceleration \(a_{c1}=-2\Omega\varepsilon\omega\cos\left(\omega t\right)\).
The perturbed azimuthal velocity \(u_{1}\) is then in the order of \(u_{1}\approx\int a_{c1}dt=-2\Omega\varepsilon\sin\left(\omega t\right)\leq2\Omega\varepsilon\). The azimuthal velocity at equilibrium \(v_{0}\) is in the order of, or less than, \(\Omega r\) (see Appendix B). Then the ratio \[\frac{u_{1}}{v_{0}}\leq\frac{2\Omega\varepsilon}{\Omega r}=\frac{2\varepsilon}{r}<<1,\label{eq:A1} \tag{149}\] and the azimuthal velocity during perturbation is \(v_{0}+u_{1}=v_{0}\left(1+\frac{u_{1}}{v_{0}}\right)\approx v_{0}\).
Furthermore, as the perturbations are periodic, the second term of the azimuthal specific mass flux is \(\rho_{0}u_{1}=-2\rho_{0}\Omega\varepsilon\sin\left(\omega t\right)\) and is varying relatively fast as \(\omega>>\Omega\), i.e., its azimuthal direction changes sense relatively quickly between opposite and along the unperturbed velocity \(v_{0}\). Its average contribution \(\left\langle \rho_{0}u_{1}\right\rangle\) over a period \(T=\frac{2\pi}{\omega}\) is therefore small in front of the larger contribution of the first term \(\rho_{1}v_{0}\) and can be neglected. That is \(\rho_{1}v_{0}+2\left\langle \rho_{0}u_{1}\right\rangle =\rho_{1}v_{0}\left(1+2\frac{\left\langle \rho_{0}u_{1}\right\rangle }{\rho_{1}v_{0}}\right)\approx\rho_{1}v_{0}\).
Solving for the gas velocity \(v_{0}\) at equilibrium within the hypothesis that the kinematic viscosity is negligible (\(\nu=0\)), the azimuthal component of the Navier-Stokes equation (11) yields \[v_{0}^{\prime\prime}+\frac{v_{0}^{\prime}}{r}-\frac{v_{0}}{r^{2}}=f_{v}(r)\label{eq:B1}, \tag{150}\] with the notation \("^{\,\prime}"=\partial\,/\partial r\) and where \(f_{v}(r)\) is an unspecified function of \(r\), giving in general \[v_{0}=C_{1}\frac{1}{r}+C_{2}r+F_{v}(r)\label{eq:B2}, \tag{151}\] with \[F_{v}(r)=\frac{2}{r^{2}}\int\left(\intop f_{v}(r)dr\right)rdr,\] and \(C_{1}\) and \(C_{2}\) constants determined by boundary conditions. If the viscosity \(\nu\) is non-null, then obviously \(f_{v}(r)\) and \(F_{v}(r)\) have to be nil in (150) and (151). For \(r\rightarrow\infty\), the gas circular velocity has to stay within finite values, yielding theoretically \(C_{2}=0\). Another expression of the gas circular velocity \(v_{0}\) at equilibrium is found from the radial component of the Navier-Stokes equation (10). Using (19) and (24), it yields \[v_{0}=\sqrt{\frac{GM^{*}}{r}+\frac{c_{c}^{2}}{r_{c}^{s}}\left(\frac{s+d}{\gamma}\right)r^{s}},\label{eq:B3} \tag{152}\] where \(s\) and \(d\) are usually negative. For the gas circular velocity \(v_{0}\) to be real, the Keplerian velocity has to be greater than the velocity induced by the gas gradient pressure, which is usually the case in real nebulae ([25]). The relations (151) and (152) are complementary in describing the radial profile of the circular gas velocity at equilibrium. For \(\nu\neq0\) (\(F_{v}(r)=0\)) and noting generally \(v_{0}\left(r\right)\sim r^{p}\), the value \(p=+1\) (\(C_{1}=0\)) gives the rotation velocity of a solid, and approximately of a fluid with high viscosity, at a constant angular speed. A value \(p=-1\) (\(C_{2}=0\)) describes the rotation of a perfect gas, and approximately of a fluid with low viscosity. The value \(p=-1/2\) corresponds to a Keplerian rotation. A value \(p=s/2\) describes the rotation of a gas dominated by thermal pressure. The gas circular velocity profile in a real nebula is at least a combination of the three first cases, as observed in the galaxies’ rotation curves [27,28]: highly viscous fluid near the central mass (\(v_{0}\left(r\right)\) \(\approx\) linear relation), lesser viscous fluid further from the centre (\(v_{0}\left(r\right)\) \(\approx\) inverse linear relation) and, after a transition region, approximate Keplerian rotation in the external regions (\(v_{0}\left(r\right)\) \(\approx\) inverse root square relation).
One can neglect \(\rho_{0}^{\prime}V_{1}^{\prime}\) in (22) if small displacements occur due to small radial perturbations. Assuming that a fluid element is displaced from vectorial positions \(x\) to \(x+\xi\left(x\right)\), where \(\xi\left(x\right)\) is a small displacement, vectorial function of \(x\), the perturbed specific mass at \(x\) reads
\[\rho_{1}\left(x\right)=-\nabla.\left(\rho_{0}\xi\right),\label{eq:C1} \tag{153}\] where the specific mass in the divergence operator is replaced by the unperturbed specific mass as it is multiplied by the small quantity \(\xi\) ([29,30]). Assuming that \(\rho_{1}\) and \(\xi\) depend only on \(r\) in a cylindrical polar referential, \(\xi=\left(\xi\left(r\right),0,0\right)\)), the relation (153) reads \[\rho_{1}\left(r\right)=\frac{-1}{r}\frac{\partial\left(r\rho_{0}\xi\right)}{\partial r},\label{eq:C2} \tag{154}\] and from (9) and (6), with the notation \("^{\,\prime}"=\partial\,/\partial r\), \[V_{1}^{\prime}=\frac{4\pi G}{r}\int\rho_{1}r\,dr=-4\pi G\rho_{0}\xi.\label{eq:C3} \tag{155}\] The product \(\rho_{0}^{\prime}V_{1}^{\prime}\) in (22) reads then, with (24), \[\rho_{0}^{\prime}V_{1}^{\prime}=-4\pi Gd\rho_{c}^{2}R^{2d-1}\left(\frac{\xi}{r_{c}}\right)\label{eq:C4}, \tag{156}\] showing that it can be neglected if the small displacement \(\xi\) is small enough in comparison with the central mass radius \(r_{c}\).
The perturbed azimuthal velocity is found from (15) and reads now
\[\dot{u_{1}}+\frac{v_{1}}{r_{c}}\left(v_{0}^{\prime}+\frac{v_{0}}{R}\right)=0\label{eq:D1}, \tag{157}\] yielding successively, with (26) and (34), \(\kappa_{1}\) as (negative) separating constant, and using \(u_{1}=0\) at \(t=0\) as initial condition, \[\ u_{1} =\frac{\kappa_{1}}{r_{c}}\left(v_{0}^{\prime}+\frac{v_{0}}{R}\right)\int v_{1}dt\nonumber \\ =\frac{\kappa_{1}}{r_{c}}\left(v_{0}^{\prime}+\frac{v_{0}}{R}\right)U\left(R\right)\int\varXi\left(t\right)dt\nonumber \\ =\frac{\kappa_{1}C}{\kappa r_{c}}\omega\left(v_{0}^{\prime}+\frac{v_{0}}{R}\right)U\left(R\right)\int\cos\left(\omega t\right)dt\nonumber \\ =\frac{\kappa_{1}C}{\kappa r_{c}}\left(v_{0}^{\prime}+\frac{v_{0}}{R}\right)U\left(R\right)\sin\left(\omega t\right)\label{eq:D2}, \tag{158}\] showing that the perturbed azimuthal velocity \(u_{1}\) is periodic by nature.
The perturbed vertical velocity (116) reads now \(\dot{w_{1}}=0\), yielding with \(w_{1}=0\) at \(t=0\) as an initial condition, that the perturbed vertical velocity is nil at all time, \(w_{1}=0\).
The \(k\)-th complex coefficient of the hyperbolic Bessel functions in the series of (86) reads \[H_{k}=\frac{\left(-1\right)^{k}\left(2\nu\right)_{k}\left(b-2a\right)_{k}}{k!\,\left(b\right)_{k}},\label{eq:A1-1} \tag{159}\] where \(\left(x\right)_{k}\) are Pochhammer polynomials. This expression can be written \(H_{k}=H_{Rk}+jH_{Ik}\) by posing \(a=a_{R}+ja_{I}\) and by developing the Pochhammer polynomials, yielding \[\ H_{Rk} =T_{k}\left(P_{Rk}Q_{Rk}-P_{Ik}Q_{Ik}\right)\label{eq:A2}, \tag{160}\] \[\ H_{Ik} =T_{k}\left(P_{Rk}Q_{Ik}-P_{Ik}Q_{Rk}\right)\label{eq:A2-1}, \tag{161}\] with \[P_{Rk}=\sum_{m=0}^{L_{R}}\left(\sum_{q=2m}^{k}\left(-1\right)^{m+q}\left(_{2m}^{q}\right)S_{k}\left(q\right)a_{R}^{q-2m}a_{I}^{2m}\right)\label{eq:A3}, \tag{162}\] \[Q_{Rk}=\sum_{m=0}^{L_{R}}\left(-1\right)^{m}\left|S_{k}\left(2m\right)\right|a_{I}^{2m}\label{eq:A4}, \tag{163}\] \[\ P_{Ik}= \sum_{m=0}^{L_{I}}\left(\sum_{q=2m+1}^{k}\left(-1\right)^{m+q}\left(_{2m+1}^{q}\right)S_{k}\left(q\right)a_{R}^{q-\left(2m+1\right)}a_{I}^{2m+1}\right)\label{eq:A5}, \tag{164}\] \[Q_{Ik}=\sum_{m=0}^{L_{I}}\left(-1\right)^{m}\left|S_{k}\left(2m+1\right)\right|a_{I}^{2m+1}\label{eq:A6}, \tag{165}\] \[T_{k}=\frac{\left(-1\right)^{k}}{k!\sum_{m=0}^{k}\left|S_{k}\left(m\right)\right|b^{m}}\label{eq:A7}, \tag{166}\] where \(\left(_{2m}^{q}\right)\) are the binomial coefficients, \(\left|S_{k}\left(m\right)\right|\) is the absolute value of the Stirling numbers of the first kind and \(L_{R}=L_{I}=k/2\) for \(k\) even and \(L_{R}=\left(k-1\right)/2\), \(L_{I}=\left(k+1\right)/2\) for \(k\) odd.
Writing \(\nu=\nu_{R}+j\nu_{I}\), with \[\nu_{R}=\frac{3d+2}{2d\gamma}\,\,\,;\,\,\nu_{I}=-y=\frac{-B^{2}}{\omega Aa\left(\frac{3d+2}{\gamma}\right)-\left(3d+4\right)},\label{eq:B1-1} \tag{167}\] the term \(G\left(\nu\right)\) in (89) can be written \(G\left(\nu\right)=G_{R}+jG_{I}\) with, for \(\nu_{1}\), \[G_{1R}=\sum_{m=0}^{\infty}\frac{1}{m!}\left(\sum_{n=0}^{m}P_{n}+\sum_{n=m+1}^{\infty}\frac{T_{n}}{C_{n}}\right)\label{eq:B2-1}, \tag{168}\] \[G_{1I}=\sum_{m=0}^{\infty}\frac{1}{m!}\left(\sum_{n=0}^{m}Q_{n}+\sum_{n=m+1}^{\infty}\frac{W_{n}}{C_{n}}\right)\label{eq:B3-1}, \tag{169}\] \[P_{n}=\frac{1}{n!}\sum_{p=0}^{L_{1}}\sum_{q=2p}^{m-n}\left(-1\right)^{p-n}\left(_{2p}^{q}\right)\left(S_{m-n}\left(q\right)\right)\nu_{R}^{q-2p}\nu_{I}^{2p}\label{eq:B4}, \tag{170}\] \[\ Q_{n}= \frac{1}{n!}\sum_{p=0}^{L_{2}}\sum_{q=2p+1}^{m-n}\left(-1\right)^{p-n}\left(_{2p+1}^{q}\right)\left(S_{m-n}\left(q\right)\right)\nu_{R}^{q-2p-1}\nu_{I}^{2p+1}\label{eq:B5} , \tag{171}\] \[\ T_{n}= \sum_{p=0}^{L_{3}}\sum_{q=2p}^{n-m}\left(-1\right)^{m+p+q}\left(_{2p}^{q}\right)\left(S_{n-m}\left(q\right)\right)\left(\nu_{R}+1\right)^{q-2p}\nu_{I}^{2p}\label{eq:B6}, \tag{172}\] \[\ W_{n}=\sum_{p=0}^{L_{4}}\sum_{q=2p+1}^{n-m}\left[\left(-1\right)^{m+p+q+1}\left(_{2p+1}^{q}\right)\left(S_{n-m}\left(q\right)\right) \left(\nu_{R}+1\right)^{q-2p-1}\nu_{I}^{2p+1}\right]\label{eq:B7}, \tag{173}\] \[C_{n}=n!\left(T_{n}^{2}+W_{n}^{2}\right)\label{eq:B8}, \tag{174}\] with \(L_{1}=L_{2}=-L_{3}=-L_{4}=\left(m-n\right)/2\) for \(\left(m-n\right)\) even and \(L_{1}=-L_{4}=\left(m-n-1\right)/2\) and \(L_{2}=-L_{3}=\left(m-n+1\right)/2\) for \(\left(m-n\right)\) odd.
Similar relations are found for \(\nu_{2}\) replacing \(\nu_{R}\) by \(-\nu_{R}\).
The complex constants in (91) read \(\varLambda=\left|\varLambda\right|\exp\left(j\lambda\right)\) and \(M=\left|M\right|\exp\left(j\mu\right)\) with \[\left|\varLambda\right|=2^{2\left(\frac{3d+2}{\gamma d}\right)}\sqrt{\left(\frac{2}{\left|d\right|}\omega A\right)^{\frac{\left(\gamma-3\right)d+2}{\gamma d}}}\exp\left(-\pi y\right)\frac{\left|G_{1}\right|}{\left|\nu_{1}\right|}\label{eq:B9}, \tag{175}\] \[\lambda=\frac{\pi}{4}\left(\frac{\left(\gamma-3\right)d+2}{\gamma d}\right)-4y\ln\left(2\right)+\arg\left(G_{1}\right)-\arg\left(\nu_{1}\right)\label{eq:B10}, \tag{176}\] \[\left|M\right|=2^{-2\left(\frac{3d+2}{\gamma d}\right)}\sqrt{\left(\frac{2}{\left|d\right|}\omega A\right)^{\frac{\left(\gamma+3\right)d+2}{\gamma d}}}\exp\left(-\pi y\right)\frac{\left|G_{2}\right|}{\left|\nu_{2}\right|}\label{eq:B11}, \tag{177}\] \[\mu=\frac{\pi}{4}\left(\frac{\left(\gamma+3\right)d+2}{\gamma d}\right)-4y\ln\left(2\right)+\arg\left(G_{2}\right)-\arg\left(\nu_{2}\right)\label{eq:B12}, \tag{178}\] where \(\left|G\right|\) and \(\arg\left(G\right)\) are the modulus and the argument of the complex valued function \(G\left(\nu\right)\).
We verify the conditions (109) of application of the WKB physical optics approximation for the moduli \[\left|\epsilon S_{2}\left(R\right)\right|<<\left|S_{1}\left(R\right)\right|<<\left|\frac{S_{0}\left(R\right)}{\epsilon}\right|\,\,\,;\,\,\left|\epsilon S_{2}\left(R\right)\right|<<1\label{eq:C1-1}, \tag{179}\] with \[ \left|\frac{S_{0}}{\epsilon}\right|=W\ln\left(2\left(1+\frac{1}{\sqrt{2}}\right)\sqrt{\frac{\omega A}{B}R}\right)+\frac{2}{3}\sqrt{\left(\omega A\right)^{2}R^{3}+B^{2}R-\frac{3}{4}}\label{eq:C2-1}, \tag{180}\] \[\ \left|S_{1}\right|=\frac{1}{4}\sqrt{\pi^{2}+\left(\ln\left(\left(\frac{\omega A}{RB^{2}}\right)^{2}\left(\left(\omega A\right)^{2}R^{3}+B^{2}R-\frac{3}{4}\right)\right)\right)^{2}}\label{eq:C3-1}, \tag{181}\] \[\left|\epsilon S_{2}\right|=\frac{1}{32}\intop^{R}\left(\frac{4\left(-2B^{2}x+\frac{9}{2}\right)\left(\left(\omega A\right)^{2}x^{3}+B^{2}x-\frac{3}{4}\right)}{x\left(\left(\omega A\right)^{2}x^{3}+B^{2}x-\frac{3}{4}\right)^{\frac{5}{2}}}+\frac{5\left(\left(\omega A\right)^{2}x^{3}+B^{2}x\right)^{2}+15\left(\left(\omega A\right)^{2}x^{3}-B^{2}x+\frac{3}{4}\right)}{x\left(\left(\omega A\right)^{2}x^{3}+B^{2}x-\frac{3}{4}\right)^{\frac{5}{2}}}\right)dx, \tag{182}\] and \(W\) is given by (133). The first condition (179) reads \[\left|\frac{S_{0}\left(R\right)}{\epsilon}\right|-\left|S_{1}\left(R\right)\right|>>0.\label{eq:C5} \tag{183}\] One easily verifies that the left hand side of the inequality tends towards positive infinity either when taking the limit for \(R\rightarrow+\infty\) with \(\epsilon\) constant or when taking the limit for \(\epsilon\rightarrow0\) (or \(\omega\rightarrow0\)) with \(R\) constant. The verification of the second and third conditions implies the solution of the uneasy elliptic integral (182). One can get some insights into the verification of these two conditions without solving (182), although, strictly speaking, this method is not exactly rigorous. Looking at the behaviour of the dominant terms, we take the limit for \(\epsilon\rightarrow0\) (or \(\omega\rightarrow0\)) under the integral sign, which yields \[\left|\epsilon S_{2}\right| \approx\frac{1}{8}\left(\int^{R}\frac{-2B^{2}dx}{\sqrt{\left(B^{2}x-\frac{3}{4}\right)^{3}}}+\frac{3}{4}\int^{R}\frac{dx}{x\sqrt{\left(B^{2}x-\frac{3}{4}\right)^{3}}}+\frac{5}{4}\int^{R}\frac{B^{4}x}{\sqrt{\left(B^{2}x-\frac{3}{4}\right)^{5}}}dx\right)\label{eq:C6}, \tag{184}\] which solves easily in \[\left|\epsilon S_{2}\right| \approx\left|\frac{1}{16}\left(\frac{5}{4}\frac{1}{\sqrt{\left(B^{2}R-\frac{3}{4}\right)^{3}}}+\frac{1}{\sqrt{B^{2}R-\frac{3}{4}}}-\frac{1}{2\sqrt{3}}\arctan\left(\frac{1}{\sqrt{\frac{4}{3}B^{2}R-1}}\right)\right)\right|.\label{eq:C7} \tag{185}\] The second condition, for \(\epsilon\rightarrow0\) (or \(\omega\rightarrow0\)), is always satisfied, provided that \(B^{2}R\neq3/4\) for all \(R\), as \(\left|S_{1}\right|\rightarrow+\infty\). The third condition is also satisfied provided that \(B^{2}R>>3/4\) for all \(R\), which is the condition (118). Taking now the limit for \(R\rightarrow+\infty\) in (185) yields that \(\left|\epsilon S_{2}\right|\rightarrow0\), which satisfies both the second and third conditions (179).
Shu, F. H. (1984). In Greenberg, R., & Brahic, A. (Eds.), Planetary Rings (p. 513). University of Arizona Press.
Nowotny, E. (1979). The Moon and the Planets, 21, 257.
Pletser, V. (1990). On exponential distance relations in planetary and satellite systems, observations and origin, Ph.D. Thesis, Physics Department, Faculty of Sciences, Catholic University of Louvain, Louvain-la-Neuve, Belgium. Retrieved from https://www.researchgate.net/publication/257927392.
Lin, D. N. C. (1986). In Kivelson, M. G. (Ed.), The Solar System: Observations and Interpretations (p. 28). Prentice-Hall.
Black, D. C., & Matthews, M. S. (Eds.). (1985). Protostars and Planets II. University of Arizona Press.
Morfill, G. E., Tschamuter, W., & Volk, H. J. (1985). In Black, D. C., & Matthews, M. S. (Eds.), Protostars and Planets II (p. 493). University of Arizona Press.
Bodenheimer, P., & Tscharnuter, W. M. (1979). Astronomy and Astrophysics, 74, 288.
Rozyczka, M., Tscharnuter, W. M., Winkler, K. H., & Yorke, H. W. (1980a). Astronomy and Astrophysics, 83, 118.
Rozyczka, M., Tscharnuter, W. M., & Yorke, H. W. (1980b). Astronomy and Astrophysics, 83, 347.
Cassen, P., Shu, F. H., & Terebey, S. (1985). In Black, D. C., & Matthews, M. S. (Eds.), Protostars and Planets II (p. 448). University of Arizona Press.
Goldreich, P., & Tremaine, S. (1979). The Astrophysical Journal, 233, 857.
Blumenthal, G. R., Yang, L. T., & Lin, D. N. C. (1984). The Astrophysical Journal, 287, 774.
Lin, D. N. C., Papaloizou, J. C. B., & Savonije, G. J. (1990). The Astrophysical Journal, 364, 326.
Lubow, S. H., & Pringle, J. E. (1993). The Astrophysical Journal, 409, 360.
Tscharnuter, W. M. (1985). In Lucas, R., Omont, A., & Stora, R. (Eds.), Birth and Infancy of Stars (p. 601). Elsevier.
Jahnke-Emde-Losch. (1966). Tafeln Höherer Funktionen. B. G. Teubner Verlagsgesellschaft.
Pollack, J. B., Grossman, A. S., Moore, R., & Grasboke, H. C. (1977). Icarus, 30, 111.
Kamke, E. (1943). Differentialgleichungen (2nd ed.). Akademische Verlagsgesellschaft Seeker & Warburg.
Whittaker, E. T., & Watson, G. N. (1927). A Course of Modern Analysis (4th ed.). Cambridge University Press.
Slater, L. J. (1965). In Abramowitz, M., & Stegun, I. (Eds.), Handbook of Mathematical Functions (p. 503). Dover Publications.
Olver, F. W. J. (1965). In Abramowitz, M., & Stegun, I. (Eds.), Handbook of Mathematical Functions (p. 355). Dover Publications.
Bender, C. M., & Orszag, S. A. (1978). Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.
Gradshteyn, I. S., & Ryzhik, I. M. (1965). Tables of Integrals, Series, and Products (A. Jeffrey, Ed.). Academic Press.
Weidenschilling, S. J. (1977). Monthly Notices of the Royal Astronomical Society, 180, 57.
Brahic, A. (1977). Astronomy and Astrophysics, 54, 895.
Shapley, H. (1972). Galaxies. Harvard University Press.
Bowers, R., & Deeming, T. (Eds.). (1984). Astrophysics Vol. II: Interstellar Matter and Galaxies. Jones and Bartlett Publishers.
Chandrasekhar, S. (1969). Ellipsoidal Figures of Equilibrium. Yale University Press.
Binney, J., & Tremaine, S. (1987). Galactic Dynamics. Princeton University Press.