The Boolean logic of subsets, usually presented as `propositional logic,’ is considered as being “classical” while intuitionistic logic and the many sublogics and off-shoots are “non-classical.” But there is another mathematical logic, the logic of partitions, that is at the same mathmatical level as Boolean subset logic since subsets and quotient sets (partitions or equivalence relations) are dual to one another in the category-theoretic sense. Our purpose here is to explore the notions of implication and negation in that other mathematical logic of partitions.
Today, the ‘classical’ form of logic is seen as the Boolean logic of subsets usually presented as the special case of propositional logic (i.e., the logic of subsets \(0\) and \(1\) of the one element set \(1\)). Other related logics, such as intuitionistic logic (e.g., the logic of the open subsets of a topological space) are considered as non-classical. But there is another recently developed and little-known logic that is at the same mathematical level of fundamentality as subset logic and is thus ‘classical’ in that nontemporal sense. Since the development of category theory starting in the middle of the twentieth century, it has been known that the concept of a subset has a category-theoretic dual in the notion of a quotient set (or, equivalently, a partition or equivalence relation). F. William Lawvere calls the generalization of a subset a “part” and “The dual notion (obtained by reversing the arrows) of ‘part’ is the notion of partition.” [1, p. 85] The simplest illustration of this is the fact that given a set function \(f:X\rightarrow Y\), the image of \(f\) is a subset \(f\left( X\right) \subseteq Y\) of the codomain \(Y\) and the inverse-image \(\left\{ f^{-1}\left( y\right) \neq\emptyset:y\in Y\right\}\) is a partition on the domain \(X\). Hence, it should be expected that there is a logic of partitions ([2, 3]) dual to the Boolean logic of subsets. And since subsets and quotient sets are at the same basic level from the mathematical point of view, partition logic is more of a dual sibling to subset logic rather than being another ‘non-classical’ off-shoot of the classical subset logic.
Our purpose here is briefly present the basics of partition logic that suffice to explore the role of negation and implication in that logic. A partition \(\pi=\left\{ B,B^{\prime},…\right\}\) on a set \(U\) is a set of non-empty subsets \(B\), \(B^{\prime}\),… (“blocks”) of \(U\) where the blocks are mutually exclusive (the intersection of distinct blocks is empty) and jointly exhaustive (the union of the blocks is \(U\)). An equivalence relation is a binary relation \(E\subseteq U\times U\) that is reflexive, symmetric, and transitive. Every equivalence relation on a set \(U\) determines a partition on \(U\) where the equivalence classes are the mutually exclusive and jointly exhaustive blocks of the partition. Conversely, every partition on a set determines an equivalence relation on the set; two elements are equivalent if they are in the same block of the partition. The notions of a partition on a set and an equivalence relation on a set are thus interdefinable. Indeed, equivalence relations and partitions are often considered as the “same” as in the conventional practice (not used here) of defining the “lattice of partitions” as the lattice of equivalence relations [4].
For the purposes of partition logic, it is important to consider the complementary binary relation to an equivalence relation. A partition relation (also called an apartness relation) \(R\subseteq U\times U\) is irreflexive (i.e., \(\left( u,u\right) \not \in R\) for any \(u\in U\)), symmetric (i.e., \(\left( u,u^{\prime}\right) \in R\) implies \(\left( u^{\prime},u\right) \in R\)), and anti-transitive in the sense that if \(\left( u,u^{\prime}\right) \in R\), then for any \(a\in U\), either \(\left( u,a\right) \in R\) or \(\left( a,u^{\prime}\right) \in R\) (i.e., \(U\times U-R=R^{c}\) is transitive). Thus as binary relations, equivalence relations and partition relations are complementary. That is, \(E\subseteq U\times U\) is an equivalence relation if and only if (iff) \(E^{c}\subseteq U\times U\) is a partition relation.
A distinction of a partition is an ordered pair \(\left( u,u^{\prime }\right)\) of elements of \(U\) in distinct blocks of the partition. The set of distinctions (abbreviated “dits”) of a partition is the ditset
\[\operatorname{dit}\left( \pi\right) =\left\{ \left( u,u^{\prime}\right) :\exists B,B^{\prime}\in\pi;B\neq B^{\prime};u\in B;u^{\prime}\in B^{\prime }\right\} .\]
Similarly an indistinction or indit of a partition is an ordered pair of elements in the same block of the partition so:
\[\operatorname{indit}\left( \pi\right) =\left\{ \left( u,u^{\prime }\right) :\exists B\in\pi;u,u^{\prime}\in B\right\} = {\displaystyle\bigcup\limits_{B\in\pi}} B\times B=U\times U-\operatorname{dit}\left( \pi\right) .\]
The indit set of a partition is the equivalence relation defined by the partition, and the ditset of a partition is the complementary partition relation defined by the partition.
If \(\sigma=\left\{ C,C^{\prime},…\right\}\) is another partition on \(U\), then the partial order of refinement is defined by:
\[\sigma\precsim\pi \text{ (read:} \pi \text{ refines } \sigma \text{ or } \sigma \text{ is refined by }\pi) \text{ if }\forall B\in\pi,\exists C\in\sigma \text{ such that } B\subseteq C.\]
Note that if \(\sigma\precsim\pi\), then for any \(C\in\sigma\), there is a set of blocks of \(\pi\) whose union is \(C\). The most refined partition on \(U\) is the discrete partition \(\mathbf{1}=\left\{ \left\{ u\right\} \right\} _{u\in U}\) whose blocks are all singletons. It is the top or maximal element in the refinement partial order. The least refined partition is the indiscrete partition (nicknamed the ‘blob’) \(\mathbf{0}=\left\{ U\right\}\) whose only block is \(U\) itself. It is bottom or minimal element in the refinement partial order. The join \(\pi \vee\sigma\) (least upper bound) of \(\pi\) and \(\sigma\) is the partition whose blocks are the non-empty intersections of the blocks of \(\pi\) and \(\sigma\):
\[\pi\vee\sigma=\left\{ B\cap C\neq\emptyset:B\in\pi;C\in\sigma\right\} .\]
To define the meet \(\pi\wedge\sigma\) (greatest lower bound) of \(\pi\) and \(\sigma\), we define an equivalence relation on \(U\) that is generated by \(u\sim u^{\prime}\) if \(u\) and \(u^{\prime}\) are in the same block of \(\pi\) or \(\sigma\). Thus if two blocks of \(\pi\) and \(\sigma\) overlap (non-empty intersection) then all the elements of the two blocks are equated and so forth for any finite sequence of overlapping blocks. Hence a block of the meet partition, i.e., an equivalence class of that equivalence relation, is a precise union of blocks of \(\pi\) and a union of blocks of \(\sigma\), and is the smallest such union. These definitions of refinement, join, and meet turn the set \(\Pi\left( U\right)\) of partitions on \(U\) into a lattice. The notion of refinement between partitions is equivalent to inclusion between their corresponding ditsets or partition relations, i.e., \(\sigma\precsim\pi\) iff \(\operatorname{dit}\left( \sigma\right) \subseteq\operatorname{dit}\left( \pi\right)\), so the lattice of partitions on \(U\) can be represented as the isomorphic lattice of partition relations on \(U\times U\). But it should be carefully noted that what many textbooks call the “lattice of partitions” is really the opposite lattice of equivalence relations, e.g., Birkhoff [4] or Grätzer [5], where the join and meet are interchanged.
The lattice of partitions (in either presentation) was known and studied in the nineteenth century by Richard Dedekind and others. But no other operations on partitions besides join and meet were defined throughout the twentieth century.
“Equivalence relations are so ubiquitous in everyday life that we often forget about their proactive existence. Much is still unknown about equivalence relations. Were this situation remedied, the theory of equivalence relations could initiate a chain reaction generating new insights and discoveries in many fields dependent upon it.
This paper springs from a simple acknowledgement: the only operations on the family of equivalence relations fully studied, understood and deployed are the binary join \(\vee\) and meet \(\wedge\) operations” [6, p. 445].
Hence the development of partition logic depended on defining at least implication \(\sigma\Rightarrow\pi\), and then all the other logical (i.e., Boolean) operations on partitions, e.g., [7].
There are at least four equivalent ways to define the implication operation \(\sigma\Rightarrow\pi\) on partitions. The most intuitive and useful set-of-blocks definition will be used here. The implication partition \(\sigma\Rightarrow\pi\) is like the partition \(\pi\) except that every block \(B\in\pi\) that is contained in some block \(C\in\sigma\) is replaced by singletons of its elements. Such an ‘atomized’ or discretized block \(B\) might be denoted \(\mathbf{1}_{B}\) as the local \(B\)-version of the discrete partition \(\mathbf{1}\). If a block \(\ B\in\pi\) is not contained in any block of \(\sigma\), then it remains the same which might be denoted \(\mathbf{0}_{B}\) as the local \(B\)-version of the indiscrete partition \(\mathbf{0}\). Hence the implication partition \(\sigma\Rightarrow\pi\) functions as an indicator or characteristic function with blocks \(\mathbf{1}_{B}\) or \(\mathbf{0}_{B}\) according to whether or not \(B\) was contained in a block of \(\sigma\). With the implication operation, we could refer to \(\Pi\left( U\right)\) as the algebra of partitions on \(U\) instead of just the lattice of partitions.
Both subset logic and partition logic have their corresponding lattices with the join and meet operations based on their respective partial orders of inclusion and refinement. What is the intuition about the implication operation to go beyond the join and meet operations? The idea of the implication is that it is an operation on two elements in the lattice so that if the result is the top of the lattice, then those two elements are related by the partial order (the ‘antecendent’ is lower than or equal to the ‘consequent’ in the partial order). Thus in the case of the lattice of subsets, the implication or conditional operation takes subsets \(S,T\subseteq U\) to the subset \(S\supset T:=S^{c}\cup T\). And if that subset equals the top of the lattice \(U\), then the partial order holds between those two subsets, i.e., \(S\supset T=U\) iff \(S\subseteq T\). The same thing holds for the implication operation in the lattice of partitions. If all the blocks of \(\pi\) are atomized or discretized, i.e., \(\sigma\Rightarrow\pi=\mathbf{1}\), then \(\sigma\precsim\pi\) and vice versa. Thus we might say intuitively that the implication of two elements in the lattice is another lattice element that indicates the extent to which those two elements stand in the partial order to one another. Thus even if \(\sigma\Rightarrow\pi\) is not the top of the lattice, if we ‘restrict’ the implication to the antecedent, i.e., \(\sigma\wedge\left( \sigma\Rightarrow\pi\right)\), then we get a lattice element that does stand in the partial order to the consequent, i.e., \(\left[ \left( \sigma\wedge\left( \sigma\Rightarrow\pi\right) \right) \Rightarrow\pi\right] =\mathbf{1}\), and thus modus ponens is a validity in both logics.
With the implication operation, the (absolute) negation of \(\sigma\) can be defined as \(\lnot\sigma:=\sigma\Rightarrow\mathbf{0}\). But the more interesting (relative) \(\pi\)-negation of \(\sigma\) is defined as: \(\overset{\pi}{\lnot}\sigma:=\sigma\Rightarrow\pi\), so the \(\pi\)-negation of \(\sigma\) is just another way of considering the implication \(\sigma\Rightarrow\pi\).
The equivalence relation corresponding to the indiscrete partition \(\mathbf{0}\) is the universal relation \(U\times U\). For any two equivalence relations \(E,E^{\prime}\subseteq U\times U\), if \(E\cup E^{\prime}=U\times U\), then \(E=U\times U\) or \(E^{\prime}=U\times U\). This is essentially the standard result of graph theory that the complement of any disconnected graph is connected [8, p. 30]. Since the indiscrete partition has no distinctions, i.e., \(\operatorname{dit}\left( \mathbf{0}\right) =\emptyset\), the complementary form of that result is that for any two partitions \(\sigma,\pi\), if \(\operatorname{dit}\left( \sigma\right) \cap \operatorname{dit}\left( \pi\right) =\emptyset\), then \(\operatorname{dit}% \left( \sigma\right) =\emptyset\) or \(\operatorname{dit}\left( \pi\right) =\emptyset\), i.e., \(\sigma=\mathbf{0}\) or \(\pi=\mathbf{0}\). An alternative form of the result is useful to understand the negation \(\sigma\Rightarrow \mathbf{0}\).
Theorem 1 (Common-Dits Theorem). Any two non-empty ditsets overlap, i.e., have some dits in common.
Proof. Let \(\pi\) and \(\sigma\) be any two partitions on \(U\) with non-empty dit sets, i.e., \(\pi\not =\mathbf{0}\not =\sigma\). We need to show that \(\operatorname*{dit}\left( \pi\right) \cap\operatorname*{dit}% \left( \sigma\right) \not =\emptyset\). Since \(\sigma\) is not the blob \(\mathbf{0}\), consider two elements \(u\) and \(u^{\prime}\) distinguished by \(\sigma\) but identified by \(\pi\) [otherwise \(\left( u,u^{\prime}\right) \in\operatorname*{dit}\left( \pi\right) \cap\operatorname*{dit}\left( \sigma\right)\) and we are finished]. Since \(\pi\) is also not the blob, there must be a third element \(u^{\prime\prime}\) not in the same block of \(\pi\) as \(u\) and \(u^{\prime}\).
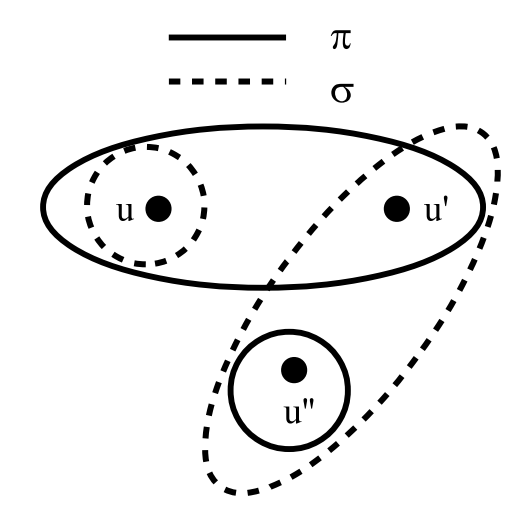
But since \(u\) and \(u^{\prime}\) are in different blocks of \(\sigma\), the third element \(u^{\prime\prime}\) must be distinguished from one or the other or both in \(\sigma\). Hence \(\left( u,u^{\prime\prime}\right)\) (as in Figure 1) or \(\left( u^{\prime},u^{\prime\prime}\right)\) must be distinguished by both partitions and thus must be in \(\operatorname*{dit}% \left( \pi\right) \cap\operatorname*{dit}\left( \sigma\right)\). ◻
This means that for any two non-blob partitions \(\pi\) and \(\sigma\) on \(U\), there is always a pair of elements \(u,u^{\prime}\in U\) that are in different blocks of both partitions. This result is perhaps particularly striking if we take \(\pi\) and \(\sigma\) to be atomic partitions, namely, partitions with only two blocks. For any two ways to divide the elements of \(U\) (\(\left\vert U\right\vert \geq2\)) into two parts, there is always a pair of elements separated by both divisions.
Since intuitionistic logic is the most developed logic aside from Boolean logic, it is often suggestive to compare the ditsets of partition logic with the open sets in the topological representation of intuitionistic logic, i.e., of a Heyting algebra (also called a pseudo-Boolean algebra or Brouwer algebra). The negation of an open set is the largest open set disjoint from the given set. But now we see that there is no non-empty ditsets disjoint from any given non-empty ditset. Hence intuitively the negation of any partition \(\sigma\neq\mathbf{0}\), is the partition \(\mathbf{0}\) with an empty ditset. The definition \(\lnot\sigma:=\sigma\Rightarrow\mathbf{0}\) gives the same result since the only block \(U\) in \(\mathbf{0}=\left\{ U\right\}\) is not contained in any block of \(\sigma\neq\mathbf{0}\). And when \(\sigma=\mathbf{0}%\), then \(\lnot\mathbf{0}=\mathbf{0}\Rightarrow\mathbf{0}=\mathbf{1}\) since \(U\subseteq U\) so it is discretized in the implication. That is why the absolute negation \(\lnot\sigma\) is of less interest than the relative negation \(\overset{\pi}{\lnot}\sigma=\sigma\Rightarrow\pi\) which is simply the partition implication.
For subsets \(R,S,T\subseteq U\), the set implication or conditional \(S\supset T\) in subset logic can also be characterized by a category-theoretic adjunction:
\[R\cap S\subseteq T \text{ iff } R\subseteq(S\supset T).\]
Since \(S\supset T\) is clearly the maximal subset to satisfy that characterization, we could define:
\[S\supset T:=\cup\left\{ R:R\cap S\subseteq T\right\} .\]
The partition implication \(\sigma\Rightarrow\pi\) can be similarly characterized in partition logic substituting ditsets for subsets [2]. For a third partition \(\tau=\left\{ D,D^{\prime},…\right\}\), the characterization is:
\[\operatorname{dit}\left( \tau\right) \cap\operatorname{dit}\left( \sigma\right) \subseteq\operatorname{dit}\left( \pi\right) \text{ iff }\tau\precsim\sigma\Rightarrow\pi.\]
Since any intersection of equivalence relations is an equivalence relation, any union of their complements, the partition relations or ditsets, is also a ditset. Hence we have a second definition of the partition implication by:
\[\operatorname{dit}\left( \sigma\Rightarrow\pi\right) :=\cup\left\{ \operatorname{dit}\left( \tau\right) :\operatorname{dit}\left( \tau\right) \cap\operatorname{dit}\left( \sigma\right) \subseteq\operatorname{dit} \left( \pi\right) \right\} .\]
Another way to define the partition implication or any Boolean operation on partitions is the graph-theoretic method [7]. Let \(K\left( U\right)\) be the complete undirected loop-free graph on \(U\). The links \(u-u^{\prime}\) corresponding to dits of a partition, i.e., \(\left( u,u^{\prime}\right) \in\operatorname*{dit}\left( \pi\right)\), of a partition are labelled with the ‘truth value’ \(T_{\pi}\) and the links corresponding to indits \(\left( u,u^{\prime}\right) \in\operatorname*{indit}% \left( \pi\right)\) are labelled with the ‘truth value’ \(F_{\pi}\). Given two partitions \(\pi\) and \(\sigma\), each link in the complete graph \(K\left( U\right)\) is labelled with a pair of truth values. Then to define any binary Boolean operation \(\pi\#\sigma\), one evaluates those two truth values on each link of \(K\left( U\right)\) according to that binary operation to obtain either \(T_{\pi\#\sigma}\) or \(F_{\pi\#\sigma}\) on that link. Then we obtain the graph \(G\left( \pi\#\sigma\right)\) for that operation by deleting all the links with the truth value \(T_{\pi\#\sigma}\) so that only the \(F_{\pi\#\sigma }\) links remain. Those \(F_{\pi\#\sigma}\) links then generate an equivalence relation on \(U\) whose blocks are the connected components of the graph \(G\left( \pi\#\sigma\right)\). Those connected components or equivalence classes are the partition \(\pi\#\sigma\) on \(U\).
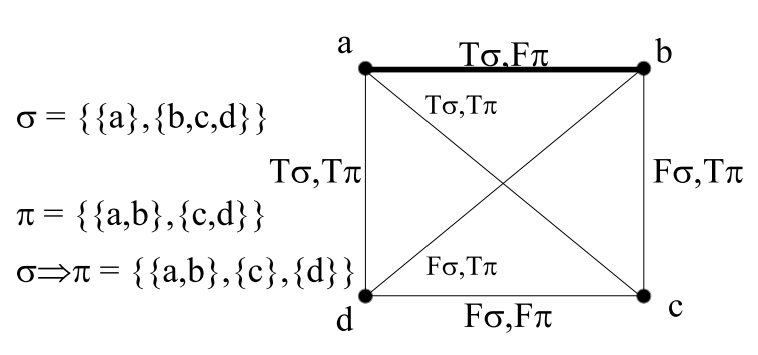
Specializing to the implication operation \(\sigma\Rightarrow\pi\), the links retained in \(G\left( \sigma\Rightarrow\pi\right)\) are the links labelled with \(T_{\sigma}\) and \(F_{\pi}\) since that combination is the only one to be evaluated to \(F_{\sigma\Rightarrow\pi}\) in the truth table for implication (or conditional). The connected components in that graph \(G\left( \sigma \Rightarrow\pi\right)\) are the blocks in the partition implication \(\sigma\Rightarrow\pi\).
Example 1. Let \(U=\left\{ a,b,c,d\right\}\) so that \(K(U)=K_{4}\) is the complete graph on four points. Let \(\sigma=\left\{ \left\{ a\right\} ,\left\{ b,c,d\right\} \right\}\) and \(\pi=\left\{ \left\{ a,b\right\} ,\left\{ c,d\right\} \right\}\) so we see immediately from the usual definition, that the \(\pi\)-block of \(\left\{ c,d\right\}\) will be discretized while the \(\pi\)-block of \(\left\{ a,b\right\}\) will remain whole so the partition implication is \(\sigma\Rightarrow\pi=\left\{ \left\{ a,b\right\} ,\left\{ c\right\} ,\left\{ d\right\} \right\}\). After labelling the links in \(K\left( U\right)\), we see that only the \(a-b\) link has the \(F_{\sigma \Rightarrow\pi}\) ‘truth value’ so the graph \(G\left( \sigma\Rightarrow \pi\right)\) has only that \(a-b\) link (thickened in Figure 2). Then the connected components of \(G\left( \sigma\Rightarrow\pi\right)\) give the same partition implication \(\sigma\Rightarrow\pi=\left\{ \left\{ a,b\right\} ,\left\{ c\right\} ,\left\{ d\right\} \right\}\).
Another equivalent way to define partition implication is to mimic the subset definition using ditsets except for the fact that Boolean subset operations on ditsets do not necessarily lead to ditsets. By the analogy with the interior operation on subsets of a topological space, the interior \(\operatorname*{int}% \left( S\right)\) of an arbitrary subset \(S\subseteq U\), where \(U\) is a topological space, is the largest open set contained in \(S\). The interior \(\operatorname*{int}\left( S\right)\) can also be defined as the complement of the (topological) closure of the complement, i.e., \(\left( \overline {S^{c}}\right) ^{c}\). Similarly, we could start with any subset \(S\subseteq U\times U\), and define the interior of \(S\) as the largest ditset contained in \(S\). It could be constructed by first taking the complement \(S^{c}\) in \(U\times U\) and then its reflexive, symmetric, and transitive closure \(\overline{S^{c}}\) which is just the intersection of all the equivalence relations containing \(S^{c}\). Then the complement is the interior: \(\operatorname*{int}\left( S\right) :=\left( \overline{S^{c}}\right) ^{c}%\). This partition-theoretic closure operation is not a topological closure operation, e.g., since the intersection of two ditsets is not necessarily a ditset, whereas the intersection of two open sets is open.
We can now use this interior operation to mimic the subset-logic definition of the implication: \(S\supset T:=S^{c}\cup T\). Hence to define the ditset \(\operatorname{dit}\left( \sigma\Rightarrow\pi\right)\), we first form \(\operatorname{dit}\left( \sigma\right) ^{c}\cup\operatorname{dit}\left( \pi\right)\) but that is not a ditset, so the definition is:
\[\operatorname{dit}\left( \sigma\Rightarrow\pi\right) =\operatorname*{int} \left[ \operatorname{dit}\left( \sigma\right) ^{c}\cup\operatorname{dit} \left( \pi\right) \right] .\]
Like the graph-theoretic definition, this approach can also be used for the other operations. The interior operation isn’t needed for the ditset treatment of the join since \(\operatorname{dit}\left( \sigma\vee\pi\right) =\operatorname{dit}\left( \sigma\right) \cup\operatorname{dit}\left( \pi\right)\), but the meet could be defined as \(\operatorname{dit}\left( \sigma\wedge\pi\right) =\operatorname*{int}\left[ \operatorname{dit}\left( \sigma\right) \cap\operatorname{dit}\left( \pi\right) \right]\).
Thus we have four definitions of the partition implication \(\sigma \Rightarrow\pi\) that are equivalent.
To study relative negation, we take the ‘consequence’ \(\pi\) as fixed and then let the ‘antecedent’ \(\sigma\) vary in the \(\pi\)-negation \(\overset{\pi}{\lnot }\sigma:=\sigma\Rightarrow\pi\). Another suggestion from intuitionistic logic is that the negated elements in a Heyting algebra form a Boolean algebra. In partition logic, this is trivially true for absolute negation since the negated elements form the two-element Boolean algebra. And it is also true for the relative \(\pi\)-negation as was suggested by viewing the implication \(\sigma\Rightarrow\pi\) as an indicator or characteristic function for the inclusion of the blocks of \(\pi\) in the blocks of \(\sigma\). And the double \(\pi\)-negation \(\overset{\pi}{\lnot}\overset{\pi}{\lnot}\sigma=\left( \sigma\Rightarrow\pi\right) \Rightarrow\pi\) just interchanges the \(\mathbf{0}_{B}\) and \(\mathbf{1}_{B}\) so \(\pi\)-negation is like the usual negation of a subset represented by its indicator function (i.e., negation interchanges the zero-one values).1 Thus the triple \(\pi\)-negation is the same as the single \(\pi\)-negation. For another partition \(\tau=\left\{ D,D^{\prime},…\right\}\), the join \(\overset{\pi}{\lnot}\sigma\vee\overset{\pi}{\lnot}\tau=\left( \sigma \Rightarrow\pi\right) \vee\left( \tau\Rightarrow\pi\right)\) would have \(B\) discretized, i.e., turned into \(\mathbf{1}_{B}\), iff \(B\) is contained in a block \(C\in\sigma\) or \(B\) is contained in a block \(D\in\tau\), so it acts like the Boolean join or disjunction: \(\mathbf{0}_{B}\vee\mathbf{1}% _{B}=\mathbf{1}_{B}\vee\mathbf{0}_{B}=\mathbf{1}_{B}\vee\mathbf{1}% _{B}=\mathbf{1}_{B}\) and \(\mathbf{0}_{B}\vee\mathbf{0}_{B}=\mathbf{0}_{B}\). Similarly, the meet \(\overset{\pi}{\lnot}\sigma\wedge\overset{\pi}{\lnot}% \tau=\left( \sigma\Rightarrow\pi\right) \wedge\left( \tau\Rightarrow \pi\right)\) would have \(B\) discretized, i.e., turned into \(\mathbf{1}_{B}\) iff \(B\) is contained in a block \(C\in\sigma\) and \(B\) is contained in a block \(D\in\tau\), so it acts like the Boolean conjunction. Thus all the partitions over \(U\) in the form of a \(\pi\)-negation \(\overset{\pi}{\lnot }\sigma=\sigma\Rightarrow\pi\) form a Boolean algebra \(\mathcal{B}_{\pi}\) with \(\pi=\overset{\pi}{\lnot}\mathbf{1}\) as the bottom element and \(\mathbf{1}% =\pi\Rightarrow\pi\) as the top element. Since all the \(\pi\)-negated partitions (also called \(\pi\)-regular partitions) refine \(\pi\), the Boolean algebra \(\mathcal{B}_{\pi}\) is contained in the upper segment \(\left[ \pi ,\mathbf{1}\right]\) and might be called the Boolean core \(\mathcal{B}_{\pi}\) of \(\left[ \pi,\mathbf{1}\right]\).
There is another construction of \(\mathcal{B}_{\pi}\) based on the fact that singleton blocks in \(\pi\) are already atomized so the implication \(\sigma\Rightarrow\pi\) essentially ignores the singletons of \(\pi\). Those singletons are always contained in some block of \(\sigma\) so they should be discretized into singletons, but they are already singletons. If we let \(\pi_{ns}\) stand for the set of non-singleton blocks of \(\pi\), then every \(\pi\)-negated formula \(\sigma\Rightarrow\pi\) is characterized by the set of non-singleton blocks \(B\in\pi_{ns}\) that were discretized, i.e., were assigned \(\mathbf{1}_{B}\) instead of \(\mathbf{0}_{B}\) by the implication \(\sigma \Rightarrow\pi\) viewed as an indicator function (for inclusion of blocks of \(\pi\) in blocks of \(\sigma\)). Then it is easily seen that the powerset Boolean algebra \(\wp\left( \pi_{ns}\right)\) on the set of non-singleton blocks of \(\pi\) is (anti-)isomorphic to the Boolean core \(\mathcal{B}_{\pi}\), i.e.,
\[\wp\left( \pi_{ns}\right) \cong\mathcal{B}_{\pi}.\]
Thus, we also have: \(\wp\left( \pi\right) \cong\mathcal{B}_{\pi }\times {\textstyle\prod\nolimits_{\left\{ u\right\} \in\pi}} 2\), where \(2=\left\{ 0,1\right\}\).
The single \(\pi\)-negation \(\overset{\pi}{\lnot}\sigma\), the double \(\pi\)-negation \(\overset{\pi}{\lnot}\overset{\pi}{\lnot}\sigma\), and the excluded middle \(\sigma\vee\overset{\pi}{\lnot}\sigma\) are all partitions of special interest. The non-singleton blocks of \(\overset{\pi}{\lnot}\sigma\) are the blocks \(B\in\pi\) that intersect two or more blocks of \(\sigma\). Thus the non-singleton blocks of the double \(\pi\)-negation \(\overset{\pi}{\lnot }\overset{\pi}{\lnot}\sigma\) are the blocks \(B\in\pi\) that are contained in blocks of \(\sigma\) so \(\sigma\Rightarrow\overset{\pi}{\lnot}\overset{\pi }{\lnot}\sigma\) is a partition tautology and \(\sigma\precsim\overset{\pi }{\lnot}\overset{\pi}{\lnot}\sigma\). The double \(\pi\)-negation \(\overset{\pi }{\lnot}\overset{\pi}{\lnot}\sigma\) can be thought of as the \(\pi\)-closure of any \(\sigma\) inside of \(\mathcal{B}_{\pi}\). Since \(\pi\precsim\overset{\pi}{\lnot}\overset{\pi}{\lnot}\sigma\), we also have that \(\sigma\vee\pi\precsim\overset{\pi}{\lnot}\overset{\pi}{\lnot}\sigma\).
Moreover, since the non-singleton blocks of \(\overset{\pi}{\lnot}\sigma\) intersect two or more blocks of \(\sigma\), the blocks (always non-singleton unless otherwise specified) in the excluded middle partition \(\sigma \vee\overset{\pi}{\lnot}\sigma\) are all (strictly) smaller than the blocks of \(\pi\) so \(\pi\precsim\sigma\vee\overset{\pi}{\lnot}\sigma\) and thus \(\sigma\vee\pi\precsim\sigma\vee\overset{\pi}{\lnot}\sigma\). And since the blocks of \(\sigma\vee\overset{\pi}{\lnot}\sigma\) are strictly smaller than the blocks of \(\pi\), no blocks of \(\pi\) are discretized in its \(\pi\)-negation, i.e., \(\overset{\pi}{\lnot}\left( \sigma\vee\overset{\pi}{\lnot }\sigma\right) =\pi\). Thus the double \(\pi\)-negation of the excluded-middle partition is \(\mathbf{1}\), i.e., \(\overset{\pi}{\lnot}\overset{\pi}{\lnot }\left( \sigma\vee\overset{\pi}{\lnot}\sigma\right)\) is a partition tautology. While the excluded middle partition \(\sigma\vee\overset{\pi}{\lnot }\sigma\) is not (in general) equal to \(\mathbf{1}\) (i.e., is not in general a partition tautology) and is not even in \(\mathcal{B}_{\pi}\), it could be said to be \(\pi\)-dense in \(\mathbf{1}\) since its \(\pi\)-closure is \(\mathbf{1}\).
Since both the excluded middle partition \(\sigma\vee\overset{\pi}{\lnot}% \sigma\) and the double \(\pi\)-negation partition \(\overset{\pi}{\lnot }\overset{\pi}{\lnot}\sigma\) refine \(\sigma\vee\pi\), their meet (greatest lower bound) \(\left( \sigma\vee\overset{\pi}{\lnot}\sigma\right) \wedge\overset{\pi}{\lnot}\overset{\pi}{\lnot}\sigma\) must also refine \(\sigma\vee\pi\). Moreover, that is an equality since the blocks of \(\sigma \vee\overset{\pi}{\lnot}\sigma\) are the non-empty intersections \(C\cap B\) for \(C\in\sigma\) and \(B\in\pi\) where \(B\) is not contained in any \(C\in\sigma\), and the blocks of \(\overset{\pi}{\lnot}\overset{\pi}{\lnot}\sigma\) are the blocks \(B\) contained in some \(C\in\sigma\). Those non-singleton blocks are all disjoint, so there are no overlaps in the meet operation. Hence those blocks remain the same in the meet and they are precisely the blocks of the join \(\sigma\vee\pi\), i.e.,
\[\sigma\vee\pi=\left( \sigma\vee\overset{\pi}{\lnot}\sigma\right) \wedge\overset{\pi}{\lnot}\overset{\pi}{\lnot}\sigma.\]
Since there are partition operations corresponding to all the Boolean operations [7], we can just write logical formulas using those logical operations without first specifying whether the variables stand for subsets or partitions (or open subsets as in the intuitionistic case) with the corresponding operations. Thus we can directly compare the valid formulas in the different logics.
In the Boolean logic of subsets, a valid formula (or subset tautology) is a formula (N.B., a formula, not a proposition) where no matter what subsets of the universe set \(U\) (where \(\left\vert U\right\vert \geq1\)) are substituted for the variables, the whole formula evaluates to \(U\), the top of the Boolean algebra of subsets on \(U\). The fact that the same set of valid formulas is obtained if one only considers the two subsets of the one-element universe \(U=1\) is a theorem of subset logic (which was known to Boole). But today most, if not all, textbooks unfortunately ignore subset logic and present only that special case where \(U=1\), “propositional logic,” and then define a valid formula as a proposition that is a truth-table tautology. That common misconception that Boolean logic is just about propositions (or zero-one entities) rather than subsets seems to have retarded the development of the dual logic of partitions (since subsets have a dual, i.e., quotient sets or partitions, while propositions do not). Valid formulas in intuitionistic logic may be defined similarly with open subsets substituted for arbitrary subsets.
In the logic of partitions on \(U\), a valid formula or partition tautology is a formula where no matter what partitions on the universe \(U\) (where \(\left\vert U\right\vert \geq2\)) are substituted for the variables, the whole formula evaluates to the discrete partition \(\mathbf{1}\), the top of the algebra of partitions on \(U\).2 The usual focus on the propositional interpretation of logic leads to the usual assumption that a tautology is a valid statement or proposition. But in subset or partition logic, a tautology is a formula so that no matter what subsets or partitions respectively are substituted for the variables, then the result is the subset or partition that is the top of the respective lattice. The variables and formulas constructed from the variables do not stand for propositions but for subsets or partitions.
There is a simple way to see that all partition tautologies are also subset tautologies, i.e., valid formulas of subset logic. Consider the partition algebra \(\Pi\left( 2\right)\) on the two-element set \(2=\left\{ 0,1\right\}\). It has only two partitions, the discrete partition \(\mathbf{1}=\left\{ \left\{ 0\right\} ,\left\{ 1\right\} \right\}\) where \(0\) and \(1\) are distinguished, and the indiscrete partition \(\mathbf{0}=\left\{ \left\{ 0,1\right\} \right\}\) where they are not distinguished. The partition operations, such as join, meet, and implication, applied to those two partitions could be described in “truth tables” since \(\mathbf{0}\) and \(\mathbf{1}\) are the only partitions on \(2\). And those truth tables are the same as the Boolean subset operations on the two subsets of the one-element set. Hence we have an isomorphism between the partition algebra \(\Pi\left( 2\right)\) on \(2\) and the power-set Boolean algebra \(\wp\left( 1\right) =2\) for \(1\) as the one-element set.3 Now consider any formula that is a valid formula in partition logic. Since it evaluates to \(\mathbf{1}\) for all partitions on any \(U\) where \(\left\vert U\right\vert \geq2\), it does that for \(U=2\), but then the isomorphism \(\Pi\left( 2\right) \cong\wp\left( 1\right)\) means that the same formula will be a truth table tautology in \(\wp\left( 1\right)\) and thus it is a valid formula for subset logic in general. Hence all partition tautologies are subset tautologies. But the inclusion is strict. For instance, the law of excluded middle \(\sigma\vee\lnot\sigma=\sigma\vee\left( \sigma\Rightarrow \mathbf{0}\right)\) is not a partition tautology since for any \(\sigma \neq\mathbf{0}\), \(\mathbf{1}\), \(\sigma\Rightarrow\mathbf{0}=\mathbf{0}\), and \(\sigma\vee\lnot\sigma=\sigma\vee\mathbf{0}=\sigma\neq\mathbf{1}\).
The Boolean core \(\mathcal{B}_{\pi}\) of the upper segment \(\left[ \pi,\mathbf{1}\right]\) for any partition \(\pi\), provides a way to ‘automatically’ generate partition tautologies. Since \(\mathcal{B}_{\pi}\) is a Boolean algebra, any Boolean tautology comprised of \(\pi\)-negated partitions will also be a partition tautology. For instance, the law of excluded middle in \(\mathcal{B}_{\pi}\) has the form \(\overset{\pi}{\lnot}\sigma\vee \overset{\pi}{\lnot}\overset{\pi}{\lnot}\sigma\) which is the “weak law of excluded middle” in partition logic. It is a partition validity since it is a Boolean tautology that evaluates to \(\mathbf{1}\) no matter what partitions on \(U\) are substituted for \(\pi\) and \(\sigma\).
Conversely, given any formula using the connectives of \(\vee\), \(\wedge\), \(\Rightarrow\), and the constants of \(\mathbf{0}\) and \(\mathbf{1}\), its single \(\pi\)-negation transform is obtained by replacing each atomic variable \(\sigma\) by its single \(\pi\)-negation \(\overset{\pi }{\lnot}\sigma=\sigma\Rightarrow\pi\) and by replacing the constant \(\mathbf{0}\) by \(\pi\). The binary operations \(\vee\), \(\wedge\), and \(\Rightarrow\) as well as the constant \(\mathbf{1}\) all remain the same. For instance, the single \(\pi\)-negation transform of the excluded middle formula \(\sigma\vee\lnot\sigma=\sigma\vee\left( \sigma\Rightarrow\mathbf{0}\right)\) is the partition tautology of the weak law of excluded middle for \(\pi\)-negation:
\[\left( \sigma\Rightarrow\pi\right) \vee\left( \left( \sigma\Rightarrow \pi\right) \Rightarrow\pi\right) =\overset{\pi}{\lnot}\sigma\vee \overset{\pi}{\lnot}\overset{\pi}{\lnot}\sigma.\]
Then the single \(\pi\)-negation transform of any classical tautology will still be a tautology but now expressed in \(\mathcal{B}_{\pi}\) and thus it is also a partition tautology. Thus all partition tautologies are ordinary Boolean logic tautologies, and any ordinary subset tautology transforms into a partition tautology via the single \(\pi\)-negation transform.
The weak law of excluded middle \(\overset{\pi}{\lnot}\sigma\vee\overset{\pi }{\lnot}\overset{\pi}{\lnot}\sigma\) is also an example of a partition tautology that is not an intuitionistic validity. And accumulation \(\pi\Rightarrow\left( \sigma\Rightarrow\left( \pi\wedge\sigma\right) \right)\) is valid in intuitionistic logic but not in partition logic. Since the lattice of partitions is the standard example of a non-distributive lattice while intuitionistic logic or Heyting algebras are distributive, the distributive laws are also examples of formulas that are valid in intuitionistic logic but not in partition logic. Thus there is no inclusion either way between partition and intuitionistic tautologies.
Since partition lattices and their non-distributivity were known to Dedekind and some other European mathematicians such as Ernest Schröder, it was an embarrassing moment in American mathematics when the philosopher-mathematican, Charles Saunders Peirce, claimed to prove the distributivity of all lattices [12] but omitted the ‘proof’ as being too tedious. Europeans soon besieged him with examples of partition lattices including the simplest non-trivial one on a three-element set \(U=\left\{ a,b,c\right\}\).
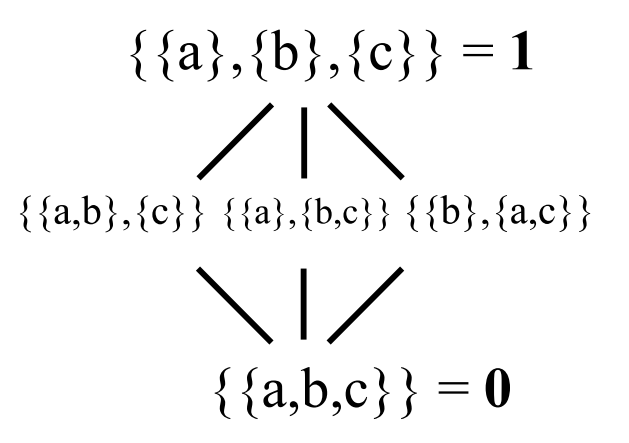
Taking the three middle partitions, \(\pi=\left\{ \left\{ a,b\right\} ,\left\{ c\right\} \right\}\), \(\sigma=\left\{ \left\{ a\right\} ,\left\{ b,c\right\} \right\}\), and \(\tau=\left\{ \left\{ b\right\} ,\left\{ a,c\right\} \right\}\), then: \(\pi\vee\left( \sigma\wedge\tau\right) =\pi\vee\mathbf{0}=\pi\) and \(\left( \pi\vee \sigma\right) \wedge\left( \pi\vee\tau\right) =\mathbf{1}\wedge \mathbf{1}=\mathbf{1}\). If Peirce had known about the partition implication and the Boolean core \(\mathcal{B}_{\pi}\), then he could at least have pointed out that the Boolean core \(\mathcal{B}_{\pi}\) for any \(\pi\) is distributive, and moreover any partition \(\varphi\in\left[ \pi,\mathbf{1}\right]\) distributes across the Boolean core in the sense that:
\[\begin{aligned} \varphi\vee\left( \overset{\pi}{\lnot}\sigma\wedge\overset{\pi}{\lnot} \tau\right) & =\left( \varphi\vee\overset{\pi}{\lnot}\sigma\right) \wedge\left( \varphi\vee\overset{\pi}{\lnot}\tau\right) \\ \varphi\wedge\left( \overset{\pi}{\lnot}\sigma\vee\overset{\pi}{\lnot} \tau\right) & =\left( \varphi\wedge\overset{\pi}{\lnot}\sigma\right) \vee\left( \varphi\wedge\overset{\pi}{\lnot}\tau\right) \text{.} \end{aligned}\]
Our purpose has been to develop the notions of negation and implication (relative negation) in the logic of partitions. Since partition relations (ditsets) and equivalence relations (indit sets) are complementary in \(U\times U\), every result in the logic of partitions has a complementary-dual result in the logic of equivalence relations so the latter is not really a different logic but a complementary way to view partition logic. There is a similar complementary-duality in intuitionistic logic between Heyting algebras (modelled by the open subsets of a topological space) and co-Heyting algebras [13] (modelled by the closed subsets).4 Intuitionistic logic makes the symmetry-breaking choice to deal with Heyting algebras rather than co-Heyting algebras, and we have made the similar choice to develop the logic of partitions rather than the (‘anti-isomorphic’) logic of equivalence relations. For instance, the complementary-dual to the implication operation on partitions is the difference or subtraction operation on equivalence relations. The partition logic tautology of modus ponens has the customary form: \(\left( \sigma\wedge\left( \sigma\Rightarrow\pi\right) \right) \Rightarrow\pi\), whereas the corresponding formula in the dual logic of equivalence relations is the unfamiliar \(\pi-\left( \sigma\vee\left( \pi-\sigma\right) \right)\). Hence we have made no independent development of the equivalence relation notions of difference or of negation as “difference from \(U\times U\).”
No new logical operations on partitions, aside from join and meet, were defined throughout the twentieth century. The definition of the partition implication (or relative negation) in any of the many equivalent ways was the key to the development of the full logic of partitions. Why the delay? One reason is perhaps the fact that partition lattices are so general that any partition tautology or identity involving just the lattice operations and top and bottom, e.g., \(\mathbf{1}\wedge\pi=\pi\) or \(\mathbf{0}\vee\pi=\pi\), are in fact identities that hold on all such lattices [15]. Thus the logic of general set partitions only becomes of independent interest by moving beyond the lattice operations on partitions. Alternatively, one could develop a ‘logic’ of equivalence relations sticking with only the lattice operations but specializing to certain types of equivalence relations [16]. But the main reason for the delay seems to be that the Boolean logic of subsets was and is presented in only the special case of the logic of propositions. And propositions, unlike subsets, do not have a category-theoretic dual concept. Hence twentieth century mathematical logicians were not even looking for the dual logic of quotient sets, equivalence relations, or partitions.
Much of the modern development in “logic” is focused on the propositional interpretation of the variables which is a special case of the general logic of subsets of some given universe \(U\) (where \(U=2=\left\{ 0,1\right\}\) or \(\left\{ F,T\right\}\) in the propositional case). Then attention has been focused on the many variations and sublogics of the Boolean logic of subsets. Partition logic is not about propositions at all and it is not a variation or sublogic of the Boolean logic of subsets. Partition logic is the category-theoretic dual to subset logic, and it is coequal to subset logic from the purely mathematical point of view (see, for instance, [17]). Hence our focus has been to address the topic of implication and negation in this little-known form of logic that is the mathematical coequal twin or dual to the Boolean logic of subsets.
This is also true of the relative negated elements \(b\Rightarrow a\) in a Heyting algebra \(H\) since they are the negated elements in the upper segment \(\uparrow a=\left\{ b\in H:a\leq b\right\}\) which is also a Heyting algebra [9, p.15].↩︎
A system of semantic tableaus for partition logic is given in [2] but there is today no known Hilbert-style axiom system for the partition tautologies.↩︎
There is essentially only one distinction in \(\Pi\left( 2\right)\) (between \(0\) and \(1\)). This is why when Spencer Brown [10] develops, in a rather esoteric way, the primary algebra of “the distinction,” it turns out to be the two element Boolean algebra \(\wp\left( 1\right)\) [11].↩︎
Our approach here is entirely semantic (i.e., no axiom system for partition logic) so there would seem to be no analogue of bi-intuitionistic or Heyting-Brouwer logic [14] since no partition relations are also equivalence relations–except in the ‘waste case’ of the empty partition on the empty set where both the ditset and indit set are empty.↩︎
Lawvere, F. W., & Rosebrugh, R. (2003). Sets for Mathematics. Cambridge, UK: Cambridge University Press.
Ellerman, D. (2010). The Logic of Partitions: Introduction to the Dual of the Logic of Subsets. Review of Symbolic Logic, 3(2), 287–350.
Ellerman, D. (2014). An Introduction to Partition Logic. Logic Journal of the IGPL, 22(1), 94–125.
Birkhoff, G. (1948). Lattice Theory. New York, NY: American Mathematical Society.
Grätzer, G. (2003). General Lattice Theory (2nd ed.). Boston, MA: Birkhäuser Verlag.
Britz, T., Mainetti, M., & Pezzoli, L. (2001). Some operations on the family of equivalence relations. In H. Crapo & D. Senato (Eds.), Algebraic Combinatorics and Computer Science: A Tribute to Gian-Carlo Rota (pp. 445–459). Milan: Springer.
Ellerman, D. (2019). A Graph-Theoretic Method to Define Any Boolean Operation on Partitions. The Art of Discrete and Applied Mathematics, 2(2), #P2.02. https://doi.org/10.26493/2590-9770.1259.9d5
Wilson, R. J. (1972). Introduction to Graph Theory. London, UK: Longman.
Borceux, F. (1994). Handbook of Categorical Algebra 3: Categories of Sheaves. Cambridge, UK: Cambridge University Press.
Spencer Brown, G. (1972). Laws of Form. New York, NY: The Julian Press.
Banaschewski, B. (1977). On G. Spencer Brown’s laws of form. Notre Dame Journal of Formal Logic, 18(3), 507-509.
Peirce, C. S. (1880). On the Algebra of Logic. American Journal of Mathematics, 13(1), 15–57.
Lawvere, F.W. (1991). Intrinsic Co-Heyting Boundaries and the Leibniz Rule in Certain Toposes. In A. Carboni, M. C. Pedicchio, & G. Rosolini (Eds.), Category Theory (Como 1990), LNM 1488 (pp. 279–297). Springer-Verlag.
Rauszer, C. (1974). A Formalization of the Propositional Calculus of H-B Logic. Studia Logica, 33(1), 23–34.
Whitman, P. M. (1946). Lattices, equivalence relations, and subgroups. Bulletin of the American Mathematical Society, 52, 507–522.
Finberg, D., Mainetti, M., & Rota, G.-C. (1996). The Logic of Commuting Equivalence Relations. In A. Ursini & P. Agliano (Eds.), Logic and Algebra (pp. 69–96). New York, NY: Marcel Dekker.
Ellerman, D. (2020). How Category Theory Works: The Elements & Distinctions Analysis of the Morphisms, Duality, and Universal Constructions in Sets. ArXiv.Org. https://arxiv.org/abs/2007.05733