A two-strain model of the transmission dynamics of herpes simplex virus (HSV) with treatment is formulated as a deterministic system of nonlinear ordinary differential equations. The model is then analyzed qualitatively, with numerical simulations provided to support the theoretical results. The basic reproduction number \(R_0\) is computed with \(R_0=\text{max}\lbrace R_1, R_2 \rbrace\) where \(R_1\) and \(R_2\) represent respectively the reproduction number for HSV1 and HSV2. We also compute the invasion reproductive numbers \(\tilde{R}_1\) for strain 1 when strain 2 is at endemic equilibrium and \(\tilde{R}_2\) for strain 2 when strain 1 is at endemic equilibrium. To determine the relative importance of model parameters to disease transmission, sensitivity analysis is carried out. The reproduction number is most sensitive respectively to the contact rates \(\beta_1\), \(\beta_2\) and the recruitment rate \(\pi\). Numerical simulations indicate the co-existence of the two strains, with HSV1 dominating but not driving out HSV2 whenever \(R_1 > R_2 > 1\) and vice versa.
Herpes simplex virus (HSV) is one of the most highly widespread sexually transmitted infections [1]. Lowestein confirmed the infectious nature of the HSV experimentally in 1919. In the years 1920s and 1930s, it was found that the HSV also infects the central nervous system [2]. The two strains of the disease are, HSV1 mostly known as cold sores and HSV2 also known as genital herpes. Both strains are transmitted sexually, however, HSV1 can also be transmitted non-sexually through contact with the fluid of an infected person. Looker et al., [3] estimated that about 417 million individuals with 267 million women inclusive age \(15-49\) have HSV2 infections worldwide, with the highest prevalence of 87% in Africa. Although South-East Asia and western pacific regions have a low prevalence of HSV2, they contribute significant amount to the global prevalence due to high population size. Fisman et al., [4] in their study on future dimensions and cost of HSV2 in the United States found that the prevalence of infection among individuals from age \(15-39\) years was projected to increase \(39%\) in men and \(49%\) in women by 2025.
In order to mitigate the spread and global socio-economic burden, mathematical modeling is an important tool that can provide insight into the long-term dynamics of a disease. It helps to simplify complex disease systems and has been a catalyst for decision making. Indeed, modeling has also been useful to present possible future outcomes of current trends and potential decision by policy makers. Some individuals infected with HSV are undiagnosed or do not display any physical symptoms. Latency is one of the major characteristics of the HSV [5,6,7]. Immunocompromised individuals with HSV stand a higher risk of acquiring HIV [8,9], and it has been found that HSV2 epidemics can more than double the peak of HIV incidence [8]. In fact, a key characteristic of HIV infection is poor control of herpes virus infections, which reactivate from latency and cause opportunistic infections in immunocompetent individuals [10].
Symptoms associated with HSV1 are tingling, itching or pains and sore throat which lead to blisters appearing on the face leading to sores, while in the case of HSV2, it appears on the genital areas [11,12] with associated symptoms such as headache, nerve pains, itching, lower abdominal pains, urinary difficulties, yeast infections, vaginal discharge, fever and open sores. Though HSV symptoms are mostly mild, there are other severity associated with such as ocular herpes which affects the eye leading to blindness; encephalitis also comes about as a result of being infected in the brain leading to death [13]. There is a reactivation after the latent infection to cause one or more rounds of the disease. And this reactivation can occur when infected individuals become sexually active again, weak immune system and inadequate or lack of treatment. Because there is currently neither complete treatment nor HSV vaccine, HSV which is a a life-long sexually-transmitted infection has no complete cure and an infected individual would live with it until death [14]. However, there are type-specific serology testing in the absence of symptoms which helps to determine the particular strain of the virus [15], and palliative treatment is administered to infected individuals to help get rid of the sores, reduce the risk of transmission as well as minimize the number and intensity of within host outbreaks. A study by the American College of Obstetricians and Gynecologists currently recommended the use of suppressive therapy to decrease transmission in discordant couples [16]. A comparison of two of these suppression drugs noted their effectiveness in decreasing both symptomatic and sub-clinical viral shedding [17,18].
Mathematical modeling is a useful tool to explore complex real life issue and guide experimental strategies and decision making [19]. Mathematical models of multiple strains of diseases such as HIV/AIDS, influenza and malaria have received much attention compared to HSV [20,21,22,23]. Nuno et al., [24] investigated the dynamics of a two-strain influenza with isolation and determined threshold conditions for the co-existence of the two strains. Because HSV treatement is only palliative, Schiffer et al., [25] developed a mathematical model to help optimize drug dose selection in clinical practice. To the best of our knowledge, a model that investigates conditions under which one strain of the virus would dominate or persist alone has not yet been considered. It is expected that this study will help fill the gap on HSV strains co-dynamics and provide a platform to further investigate if one strain could dominate and potentially drive the other to extinction.
The rest of this paper is organized as follows: The model formulation and the underlying assumptions are provided in \(§\)2. Theoretical analysis of the model is provided in \(§\)3. In \(§\)4, graphical representations generated (using the python programming language) to support the theoretical results are provided. \(§\)5 is the conclusion.
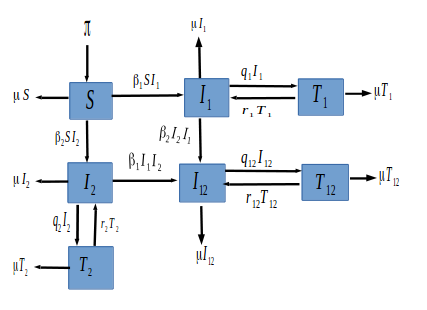
We formulate a simple HSV transmission dynamics model of the 2 HSV strains in the presence of treatment. Our model partitions the total population at any time \(t\) denoted by \( N(t)\) into seven epidemiological states depending on individuals disease status. The fully susceptible class denoted by \(S(t)\). The class of individuals who have come in contact with the HSV virus strain 1 and are infectious is denoted by \(I_{1}(t)\), and those in contact with the HSV2 virus and infectious is denoted by \(I_{2}(t)\). Individuals affected with the two strains are grouped in the \(I_{12}(t)\) class. The \(I_{1}(t)\) class of individuals who are on palliative treatment move to the \(T_1(t)\) class, and those in \(I_2(t)\) under palliative treatment move to the \(T_2(t)\) class. Individuals co-infected with both HSV1 and HSV2 strain \(I_{12}(t)\) under treatment move to the \(T_{12}(t)\) class.
Individuals are recruited into the susceptible compartment at a constant rate \(\pi\). Individuals in each compartment die naturally at a rate \(\mu\). Since there is no cure for HSV, treatment is just for relief and to reduce individual infectiousness. We assume no simultaneous infections by both strains. Susceptible individuals progress into \(I_{1}\) class at a transmission rate of \(\beta_1\) and to \(I_{2}\) class at a transmission rate of \(\beta_2\). Individuals in the \(I_{1}\) move to the \(T_{1}\) class and those in the \(I_{2}\) move to the \(T_{2}\) class at a treatment rate of \(q_{1}\) and \(q_{2}\) respectively or enter into the dual infection class at the rate of \(\beta_{2}\) and \(\beta_{1}\) respectively. The infected individuals with both diseases move to the \(T_{12}\) class at a rate of \(q_{12}\). Because treatment is not permanent, relapse is common, thus from the treatment class, the disease can re-activate at a rate \(r_{1}\), \(r_{2}\) and \(r_{12}\) into the \(I_{1}\), \(I_{2}\) and \(I_{12}\) class respectively. The description of the model variables and parameters are summarized in Table 1. Figure 1 gives a graphical interpretation of our proposed model based on the above description and assumptions.
| Description | Value | Reference | |
|---|---|---|---|
| Parameter | |||
| \(\beta_1\) | Transmission rate for individuals with HSV1 | \(0.007(0.001-0.03)yr^{-1}\) | Assumed |
| \(\beta_2\) | Transmission rate for individuals with HSV2 | \(0.001(0.001-0.03)yr^{-1}\) | [26] |
| \(\mu\) | natural death rate | \(0.019(0.015-0.02)yr^{-1}\) | [27] |
| \(r_1\) | Reactivation rate of HSV1 | \(0.6\) | Assumed |
| \(r_2\) | Reactivation rate of HSV2 | \(0.6\) | Assumed |
| \(r_{12}\) | Reactivation rate of both HSV1 and HSV2 | \(0.6\) | Assumed |
| \(q_{12}\) | Treatment rate of both HSV1 and HSV2 | \(0.45(0-1.0)yr^{-1}\) | Assumed |
| \(q_{1}\) | Treatment rate of HSV1 | \(0.45(0-1.0)yr^{-1}\) | Assumed |
| \(q_{2}\) | Treatment rate of HSV2 | \(0.45(0-1.0)yr^{-1}\) | [28] |
| \(\pi\) | Recruitment rate | \(0.3yr^{-1}\) | Assumed |
| Variable | |||
| \(I_1(t)\) | Individuals infected with HSV1 | ||
| \(I_2(t)\) | Individuals infected with HSV2 | ||
| \(I_{12}(t)\) | Individuals infected with both HSV1 and HSV2 | ||
| \(T_1(t)\) | Individuals infected with HSV1 and receiving treatment | ||
| \(T_2(t)\) | Individuals infected with HSV2 and receiving treatment | ||
| \(T_{12}(t)\) | Co-infected individuals receiving treatment |
From the aforementioned, we established the following non-linear ordinary differential equations given by system (1)
Since model 1 describe the dynamics of a human population, all state variables should be positive for the model to be epidemiological meaningful. Thus the following Lemma holds.
Lemma 1. The feasible set of model system (1) is given by \[\Omega = \left\lbrace \left( S, I_{1}, I_{2}, I_{12}, T_{1}, T_{2}, T_{12} \right) \in R^{7}_{+} : S+I_{1}+I_{2}+I_{12}+T_{1}+T_{2}+T_{12} \leq \frac{\pi}{\mu} \right\rbrace, \] which is bounded, positively invariant and attracting for all \(t\geq 0.\)
The disease-free equilibrium of model system (1) is given by \begin{align*} E_0 &= \left( \frac{\pi}{\mu}, 0, 0, 0, 0, 0, 0 \right). \end{align*} Using the next generation matrix method of van den Driessche and Watmough [29], compute the basic reproduction number, which represents the expected number of secondary cases produced by a typical infected individual during its entire period of infectiousness in a completely susceptible population when a single infected individual is introduced [29].First, re-arrange the equations according to the infected compartments \(I_{1}(t), I_{2}(t), I_{12}(t), T_1,T_2,T_{12}\) .
Theorem 1. The disease-free equilibrium of our system (1) is locally asymptotically stable if \(R_0 1\).
Proof. The proof is investigated by the linearization method. The Jacobian matrix associated with the model system (1) at the disease-free equilibrium is given by
Theorem 2. The fixed point \(E_0\) is a globally stable point of model system (1) provided \(R_0< 1\).
Proof. Consider \(F(X,0)=[\pi – \mu S]\), \begin{align*} A = \begin{bmatrix} \frac{\beta_1 \pi}{\mu}-\beta_1 I_2 – (q_{1}+\mu) & -\beta_1 I_1 & 0 & r_1 &0 &0\\ -\beta_2 I_1 & \frac{\beta_2 \pi}{\mu}-\beta_2 I_1 – (q_2 + \mu) & 0 & r_2 & 0 & 0 \\ \beta_1 I_2 + \beta_2 I_2 & \beta_1 I_1 + \beta_2 I_1& -q_{12} + \mu & 0 & 0 & r_{12}\\ q_1 & 0 & 0 & -(r+\mu) & 0 & 0 \\ 0 & q_2 & 0 & 0 & -(r_2 + \mu) & 0\\ 0 & 0 & q_{12} & 0 & 0 & -(r_{12} + \mu) \end{bmatrix} \end{align*} and \begin{align*} \hat{G}(X,Y) = \begin{bmatrix} \beta_1 I_1 \bigg(\dfrac{\pi}{\mu} – \dfrac{S}{N} \bigg)\\ \beta_2 I_2 \bigg(\dfrac{\pi}{\mu} – \dfrac{S}{N} \bigg) \end{bmatrix}\geq 0 \end{align*} and \(0\) for \(I_{12}, T_1, T_2, T_{12}\) respectively. Therefore \(\hat{G}(X,Y)\geq 0\) for all \((X,Y)\in \Omega\) implies that \(\mathbb{E}_0\) is globally asymptotically stable for \(R_0 < 1\).
This equilibrium makes biological sense only when \(R_1 > 1\). Note that \(E_1\) partitions the population into parts, that is \(\dfrac{1}{R_1}\) uninfected which we observed from the \(s^*\) term. Also, a portion of the population represented by \(\dfrac{\pi}{\mu}\) remains in that class until death. The other parts are \(\dfrac{\mu}{\beta_1}\) and \(\dfrac{q_1}{\beta_1 \mu(\mu+r_1)}\).
When there is no infection with strain 1, that is when \(I_1^* = 0\), a second single-strain equilibrium is given by \[E_2 = (s^*, 0, i^*_2, 0, 0, t^*_2,0),\] where \(s^* = \dfrac{\pi}{\mu} \dfrac{1}{R_2},\)   \(\dfrac{\mu [R_2 – 1]}{\beta_2}\) and \(t^*_2 = \dfrac{q_2 \mu^2[R_2-1]}{\beta_2\mu^3(\mu+r_2)}.\) This equilibrium makes biological sense only when \(R_2>1\).
We further consider the invasion reproductive number \(\tilde{R}_2\). It is the ability of strain \(2\) to invade the susceptible population at \(E_1\). To determine \(\tilde{R}_2\), we follow a similar approach using the next generation matrix method. The \(\mathcal{F}_2\) matrix is given by the new infection terms in the equations \(I^{\prime}_{2}, I^{\prime}_{12}, T^{\prime}_{2}, T^{\prime}_{12}\) and the \(\mathcal{V}_2\) matrix consists of the remainder of the terms in those equations. Thus, we obtain
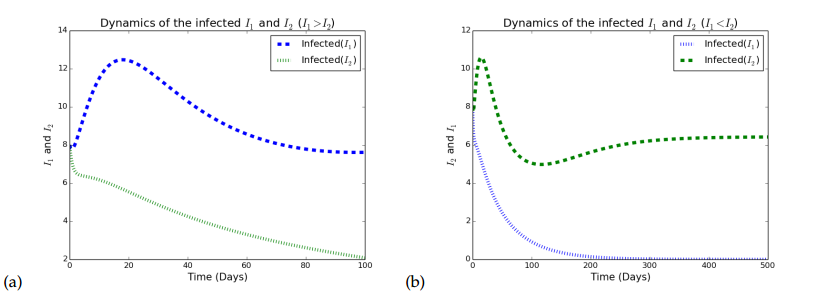
\begin{align*} \mathcal{F}_2 – \mathcal{V}_2 = \begin{pmatrix} \dfrac{\beta_2 \tilde{I_2} S}{N} \\[5pt] \dfrac{\beta_2\tilde{I_2} I_1}{N} \\[5pt] 0 \\[5pt] 0 \end{pmatrix} – \begin{pmatrix} \dfrac{\beta_1 I_2\tilde{I}_1}{N} + (q_2 + \mu)I_2 – r_2 T_2 \\[5pt] -\dfrac{\beta_1 \tilde{I}_1 I_2}{N} – r_{12}T_{12} + (q_{12}+\mu)I_{12}\\[5pt] -q_2I_2 + (r_2+\mu)T_2 \\[5pt] -q_{12}I_{12} + (r_{12}+\mu)T_{12} \end{pmatrix}. \end{align*} We then compute the Jacobian of the following \(F_2\) and \(V_2\) at strain \(2\) to obtain \begin{align*} F_2 & = \begin{pmatrix} \beta_2 S^{*} & \beta_2 S^{*} & 0 & 0 \\[5pt] \beta_2 I^{*}_{1} & \beta_2 I_1^{*} & 0 & 0 \\[5pt] 0 & 0 & 0 & 0 \\[5pt] 0 & 0 & 0 & 0 \end{pmatrix}\quad \text{and} \quad V_2 = \begin{pmatrix} \beta_1 I_1^{*} + q_2 + \mu & 0 & -r_2 & 0 \\[5pt] -\beta_1 I_{1}^{*} & (q_{12} + \mu) & 0 & -r_{12}\\[5pt] -q_2 & 0 & r_2+\mu & 0 \\[5pt] 0 & -q_{12} & 0 & r_{12}+\mu \end{pmatrix}. \end{align*} The dominant eigenvalue of the matrix which is determined by \(F_1V_1^{-1}\) and is the invasion reproductive number \(\tilde{R}_2\) is given by \begin{align*} \tilde{R}_2 = \frac{\beta_2}{\mu} \bigg[ \frac{\textbf{M} + \textbf{N} + {\left(\textbf{O} + \textbf{P} + {\left(\beta_{2} \mu^{2} + \beta_{2} \mu q_{12} + \beta_{2} \mu r_{12}\right)} r_{2}\right)} S}{\mu^{3} + \mu^{2} q_{12} + \textbf{Q} + {\left(\mu^{2} + \mu q_{12}\right)} q_{2} + {\left(\mu^{2} + \mu q_{2}\right)} r_{12} + {\left(\mu^{2} + \mu q_{12} + \mu r_{12}\right)} r_{2}} \bigg], \end{align*} where \begin{align*} \textbf{M} & = {\left(\beta_{1} \mu^{2} + \beta_{1}\mu r_{12} + {\left(\beta_{1}\mu + \beta_{1} r_{12}\right)} r_{2}\right)} I_{1}^{2}, \\[5pt] \textbf{N} &= {\left(\mu^{3} + \mu^{2} q_{2} + {\left(\mu^{2} +\mu q_{2}\right)} r_{12} + {\left(\mu^{2} + \mu r_{12}\right)} r_{2}\right)} I_{1}, \\[5pt] \textbf{O} & = \mu^{3} + \mu^{2} q_{12} + \mu^{2} r_{12}, \\[5pt] \textbf{P} & = {\left(\beta_{1} \mu^{2} + \beta_{1} \mu r_{12} + {\left(\beta_{1}\mu + \beta_{1}r_{12}\right)} r_{2}\right)} I_{1}, \\[5pt] \textbf{Q} & = {\left(\beta_{1} \mu^{2} + \beta_{1} \mu q_{12} + \beta_{1} \mu r_{12} + {\left(\beta_{1} \mu + \beta_{1} q_{12} + \beta_{1} r_{12}\right)} r_{2}\right)} I_{1}. \end{align*} After some algebraic manipulations, \(\tilde{R}_2\) can further be expressed as \begin{align*} \tilde{R}_2 = R_2\dfrac{\mu(a_1)}{\pi(\mu+r_2)}\dfrac{s^*\mu q_{12}(\mu+r_2\beta_2)+(\mu+r_{12})(\mu+r_2)i^{*^2}_1\beta_1+i^*_1(\mu q_2 +(\mu+r_2)(\mu+s^*\beta_1))+s^*\mu(\mu+r_2\beta_2))}{(\mu+q_{12}+r_{12})(\mu q_2+(\mu+r_2)(\mu+i^*\beta_1))} \end{align*} where \(a_1 = \mu+q_2+r_2\) and \(s^*, i^*_1\) is defined in \(E_1\). Similarly, \(\tilde{R}_2\) is essentially \(R_2\) multiplied by a term representing an altered vulnerability to infection with strain \(2\).Figure 2 depicts the graphical representation of infectious individuals with HSV1 and HSV when either \(R_1>1>R_2\) Figure 2(a) or \(R_2>1>R_1\) Figure 2(b). In Figure 2(a), strain 1 dominates while in Figure 2(b), strain 2 dominates.
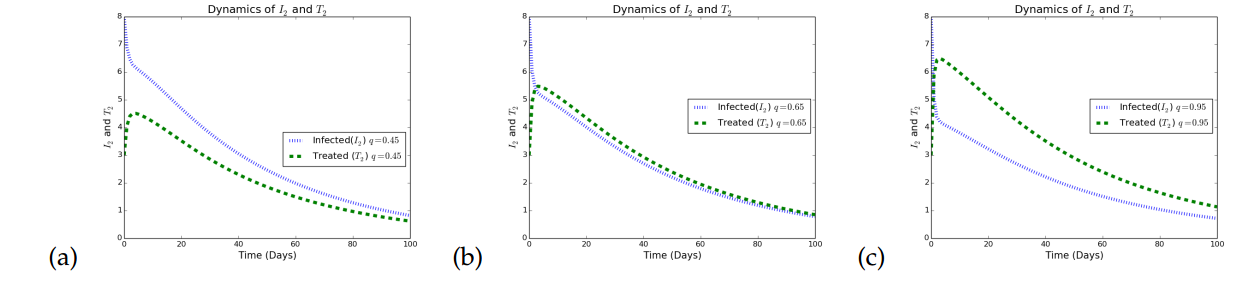
Next, we illustrate the effects of increasing treatment rates on the dynamics of population with HSV1 and HSV2 in Figure 3.
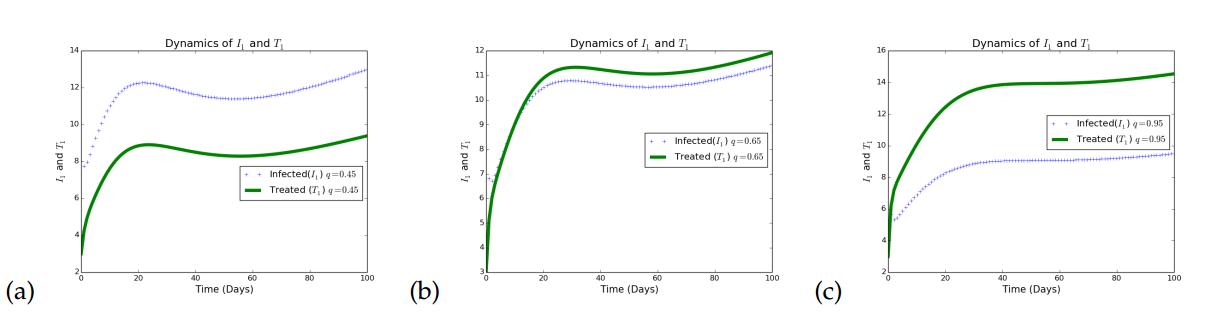
Figure 3 illustrates the effects of increasing treatment as a control strategy in a given population. In Figure 3(a), it is observed that when treatment rates with respect to HSV1 is small, the infected individuals increases. In Figure 3(b), the treatment rates for HSV1 infection is increased to a very reasonable value (\(0.65\)) and it is observed that although there is a reduction in the number of infected individuals, the impact is minimal. The treatment rate for the HSV1 is further increased to a reasonably high value (\(0.95\)) and it is observed that the infection persists, but at a lower rate. Thus, treatment only minimizes the rate of transmitting HSV strain 1, but does not eradicate it, which agrees with what is know about this disease that treatment is only palliative.
Simulations in Figure 4 illustrates the effects of increasing treatment as a control strategy in a given population. In Figure 4(a), it is observed that when treatment rates with respect to HSV2 is small, the infected individuals increases. In Figure 4(b) the treatment rate for HSV2 infection was increased to a very reasonable value (\(0.65\)) and it is observed that although there is a reduction in the number of infected individuals the impact is not that great. The treatment rate for the HSV2 was further increased to a reasonably high value (\(0.95\)) and it is observed that the infection persists but at a lower rate. Again, treatment only minimizes the rate of transmitting HSV strain 2, but does not eradicate it, which agrees with what is know about HSV that treatment only palliative.
Using sage programming language, we derive the following:
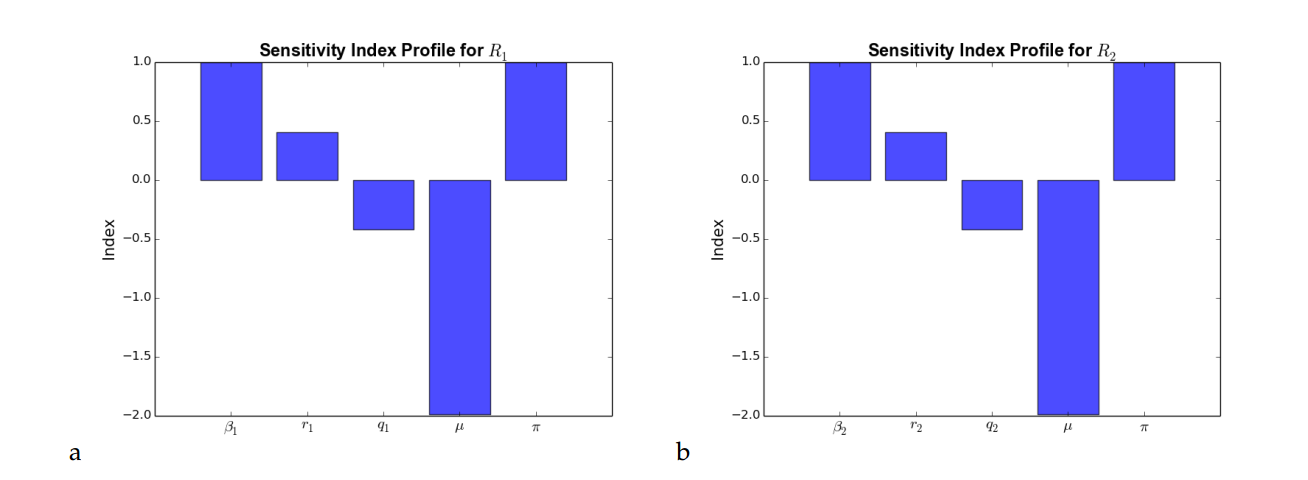
\begin{align*} \beta_1 &=\newcommand{\Bold}[1]{\mathbf{#1}}\frac{{\left(\mu \pi + \pi r_{1}\right)} \beta_{1}}{\beta_{1} \mu \pi + \beta_{1} \pi r_{1}},\\ r_1 &=\newcommand{\Bold}[1]{\mathbf{#1}}-\frac{{\left(\mu^{3} + \mu^{2} q_{1} + \mu^{2} r_{1}\right)} {\left(\frac{{\left(\beta_{1} \mu \pi + \beta_{1} \pi r_{1}\right)} \mu^{2}}{{\left(\mu^{3} + \mu^{2} q_{1} + \mu^{2} r_{1}\right)}^{2}} – \frac{\beta_{1} \pi}{\mu^{3} + \mu^{2} q_{1} + \mu^{2} r_{1}}\right)} r_{1}}{\beta_{1} \mu \pi + \beta_{1} \pi r_{1}},\\ q_1 &=\newcommand{\Bold}[1]{\mathbf{#1}}-\frac{\mu^{2} q_{1}}{\mu^{3} + \mu^{2} q_{1} + \mu^{2} r_{1}},\\ \\ \mu &=\newcommand{\Bold}[1]{\mathbf{#1}}\frac{\mu{\left(\mu^{3} + \mu^{2} q_{1} + \mu^{2} r_{1}\right)} {\left(\frac{\beta_{1} \pi}{\mu^{3} + \mu^{2} q_{1} + \mu^{2} r_{1}} – \frac{{\left(\beta_{1} \mu \pi + \beta_{1} \pi r_{1}\right)} {\left(3 \, \mu^{2} + 2 \, \mu q_{1} + 2 \, \mu r_{1}\right)}}{{\left(\mu^{3} + \mu^{2} q_{1} + \mu^{2} r_{1}\right)}^{2}}\right)}}{\beta_{1} \mu \pi + \beta_{1} \pi r_{1}},\\ \pi &=\newcommand{\Bold}[1]{\mathbf{#1}}\frac{{\left(\beta_{1} \mu + \beta_{1} r_{1}\right)} \pi}{\beta_{1} \mu \pi + \beta_{1} \pi r_{1}},\\ \beta_2 &=\newcommand{\Bold}[1]{\mathbf{#1}}\frac{{\left(\mu \pi + \pi r_{2}\right)} \beta_{2}}{\beta_{2} \mu \pi + \beta_{2} \pi r_{2}},\\ r_2 &=\newcommand{\Bold}[1]{\mathbf{#1}}-\frac{{\left(\mu^{3} + \mu^{2} q_{2} + \mu^{2} r_{2}\right)} {\left(\frac{{\left(\beta_{2} \mu \pi + \beta_{2} \pi r_{2}\right)} \mu^{2}}{{\left(\mu^{3} + \mu^{2} q_{2} + \mu^{2} r_{2}\right)}^{2}} – \frac{\beta_{2} \pi}{\mu^{3} + \mu^{2} q_{2} + \mu^{2} r_{2}}\right)} r_{2}}{\beta_{2} \mu \pi + \beta_{2} \pi r_{2}},\\ q_2 &=\newcommand{\Bold}[1]{\mathbf{#1}}-\frac{\mu^{2} q_{2}}{\mu^{3} + \mu^{2} q_{2} + \mu^{2} r_{2}}. \end{align*} Then, using the parameter values \(\beta_1 = 0.007\), \(\beta_2 = 0.001\), \(r_1= 0.6\), \(r_2= 0.6\), \(q_1 = 0.45\), \(q_1 = 0.45\), \(\mu = 0.019\), \(\pi = 0.3\), we compute the sensitivity indices of \(R_1\) and \(R_2\) which are summarized in Tables 2 and 3.| Parameter | Sensitivity index |
|---|---|
| \(\beta_1\) | \(1.00000\) |
| \(r_1\) | \(0.408033 \) |
| \(q_1\) | \(-0.42095\) |
| \(\mu \) | \(-1.98708\) |
| \(\pi \) | \(1.00000\) |
| Parameter | Sensitivity index |
|---|---|
| \(\beta_2\) | \(1.00000\) |
| \(r_2\) | \(0.408033 \) |
| \(q_2\) | \(-0.42095\) |
| \(\mu \) | \(-1.98708\) |
| \(\pi \) | \(1.00000\) |
From Tables 2 and 3, the sensitivity index with positive sign indicate that the value of the reproduction numbers \(R_1\) and \(R_2\) increase when the corresponding parameters increase while the parameters with negative signs indicate that, for an increase in the corresponding parameters, there is a decrease in the value of the reproduction numbers \(R_1\) and \(R_2\). Using the model parameter values in Table 1, we graphically represent the sensitivity index profile of the reproduction numbers \(R_1\) and \(R_2\).
From Figure 5(a) and Figure 5(b), it can be observed that \(\beta_1\), \(\beta_2\) and \(\pi\) have the highest influence on the reproduction number \(R_0\) followed by \(\mu\), \(q_1\) and \(q_2\). This implies that an increase in the contact rates \(\beta_1\), \(\beta_2\) and recruitment/inflow rate \(\pi\) will lead to a corresponding increase in the basic reproduction number. On the other hand, \(\mu\), \(q_2\) and \(q_1\) correlates negatively with the basic reproduction number as an increase in such parameters will lead to a corresponding decrease in the basic reproduction number.