Harmonic mixture weibull normal regression with applications in biomedicine

1. Introduction

The use of appropriate statistical models with sufficient flexibility in capturing data characteristics is crucial for gaining meaningful insights into essential aspects of real-world datasets. According to [1], the normal distribution remains one of the most widely used models in practical data analysis. In many applied research domains, the outcome of a dependent (response) variable is often influenced by predictor variables, such as sex and insulin concentration. Regression analysis is a fundamental statistical tool employed to study the effects of these predictor variables on a response variable.

Over the past decades, the classical normal regression model has been extensively utilized for analyzing symmetric datasets in biomedical research and other fields. However, empirical data in practical scenarios often exhibit characteristics such as heavy or light tails, asymmetry, or bimodality, which cannot be adequately modeled by the classical linear regression model. Moreover, the standard assumptions of classical regression analysis—homogeneity of error variances and normality of the error distribution—are frequently violated in real-world applications. Such violations can adversely affect the efficiency and reliability of estimators [1].

To address these limitations, numerous generalized normal distributions have been developed to produce generalized regression models. Examples include the complementary Topp-Leone geometric normal distribution [2], the folded normal distribution [3], and the new extended normal distribution [4]. Other studies have also utilized generalized normal distributions to create enhanced regression models [], among others.

In this study, we build on these advancements by presenting the Harmonic Mixture Weibull-Normal (HMWN) distribution developed by [11]. This distribution is utilized to construct efficient generalized regression models with residuals following the HMWN distribution. The motivations for employing the HMWN distribution include the following:

• To develop efficient generalized regression models capable of modeling bimodal data with varying complexities in medical studies.

• To produce generalized regression models suitable for both symmetric and asymmetric datasets in biomedical research.

• To create models capable of handling data with varying dispersion as well as constant dispersion.

• To construct efficient generalized regression models applicable to experimental design data in medical and biomedical studies.

The remainder of this article is structured as follows: Section 2 introduces the HMWN distribution, while Section 3 describes the maximum likelihood estimation method. Section 4 presents the results of simulation experiments. Sections 5 and 6 detail the newly developed generalized regression models and the experimental design model, respectively, based on the HMWN distribution. Empirical applications of the proposed models to practical biomedical datasets are discussed in Section 7, and Section 8 concludes the article.

2. HMWN Distribution

The probability density function (PDF) of the normal distribution and its corresponding cumulative distribution function (CDF) are respectively given by \[f\left(y\right)=\frac{1}{\sigma \sqrt{2\pi } } e^{-\frac{1}{2} \left(\frac{y-\mu }{\sigma } \right)^{2} } {\rm \; and\; }F\left(y\right)=\Phi \left(\frac{y-\mu }{\sigma } \right){\rm \; },y\in {\rm R},\] where \(\sigma >0\) is a scale parameter with \(-\infty <\mu <\infty\) being a location parameter and \(\Phi \left(.\right)\) being the CDF for the standard normal distribution.

The HMWN distribution developed by [11] is defined based on a new generalized family of distributions called Harmonic Mixture Weibull-Generated family of distributions. If a random variable \(Y\) follows the HMWN distribution, the PDF of the HMWN distribution and its corresponding CDF according to [11] are given respectively by \[\begin{aligned} \label{GrindEQ__1_} g\left(y\right)=&\beta \left[\Phi \left(\frac{y-\mu }{\sigma } \right)\right]^{\beta -1} \exp \left\{-\left(\frac{1}{2} \left(\frac{y-\mu }{\sigma } \right)^{2} +\alpha \left[\left[\Phi \left(\frac{y-\mu }{\sigma } \right)\right]^{-1} -1\right]^{-\beta } \right)\right\} \notag\\ &{\times \frac{\alpha \left(1-\theta \right)+\theta \exp \left\{-\left(\alpha -1\right)\left[\left[\Phi \left(\frac{y-\mu }{\sigma } \right)\right]^{-1} -1\right]^{-\beta } \right\}}{\sigma \sqrt{2\pi } \left[1-\Phi \left(\frac{y-\mu }{\sigma } \right)\right]^{\beta +1} \left[1-\theta \left(1-\exp \left\{-\left(\alpha -1\right)\left[\left[\Phi \left(\frac{y-\mu }{\sigma } \right)\right]^{-1} -1\right]^{-\beta } \right\}\right)\right]^{2} } ,{\rm \; }y\in {\rm R},} \end{aligned} \tag{1}\] and \[\begin{aligned} \label{GrindEQ__2_}G\left(y\right)=1-\frac{\exp \left\{-\alpha \left[\left[\Phi \left(\frac{y-\mu }{\sigma } \right)\right]^{-1} -1\right]^{-\beta } \right\}}{1-\theta \left[1-\exp \left\{-\left(\alpha -1\right)\left[\left[\Phi \left(\frac{y-\mu }{\sigma } \right)\right]^{-1} -1\right]^{-\beta } \right\}\right]} ,y\in {\rm R}, \end{aligned} \tag{2}\] where \(\beta >0\) is a shape parameter with \(u\in {\rm R}\) being a location parameter, \(\alpha >0,{\rm \; }0<\theta <1,{\rm \; }\sigma >0\) being scale parameters and \(\Phi \left(.\right)\) being the CDF for the standard normal distribution.

Thus, a random variable \(Y\sim {\rm HMWN}\left(\alpha ,\beta ,\theta ,\mu ,\sigma \right)\) has a PDF given by (1). The flexibility of the HMWN distribution is illustrated by the results of the density plots in Figure 1a, Figure 1b, Figure 1c and Figure 1d. The results of the plots establish the HMWN distribution as a very flexible model with desirable properties including different complexities of bimodality, asymmetry and symmetry shapes.

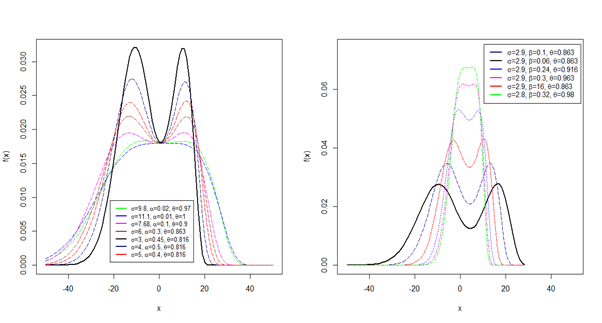
A standard normal random variable defined by \(Z={\left(x-\mu \right)\mathord{\left/ {\vphantom {\left(x-\mu \right) \sigma }} \right. } \sigma }\) has a PDF given by \[\begin{aligned} \label{GrindEQ__3_} g\left(z\right)=&\beta \left[\Phi \left(z\right)\right]^{\beta -1} \exp \left\{-\left(\frac{1}{2} \left(z\right)^{2} +\alpha \left[\left[\Phi \left(z\right)\right]^{-1} -1\right]^{-\beta } \right)\right\} \notag\\ & \times \frac{\alpha \left(1-\theta \right)+\theta \exp \left\{-\left(\alpha -1\right)\left[\left[\Phi \left(z\right)\right]^{-1} -1\right]^{-\beta } \right\}}{\sigma \sqrt{2\pi } \left[1-\Phi \left(z\right)\right]^{\beta +1} \left[1-\theta \left(1-\exp \left\{-\left(\alpha -1\right)\left[\left[\Phi \left(z\right)\right]^{-1} -1\right]^{-\beta } \right\}\right)\right]^{2} }. \end{aligned} \tag{3}\]

3. Estimation Method: Maximum Likelihood

Suppose the distribution of a random sample of size \(n\) with a sequence of independent observations \(x_{1} ,x_{2} ,…,x_{n} ,\) is that of the HMWN. Then, the total log-likelihood function is given by \[\begin{aligned} \label{GrindEQ__4_} \ell =&n\log \left(\beta \right)+\left(\beta -1\right)\sum _{i=1}^{n}\log \left[\Phi \left(z_{i} \right)\right] -\sum _{i=1}^{n}\left(\frac{1}{2} \left(z_{i} \right)^{2} +\alpha \left[\left[\Phi \left(z_{i} \right)\right]^{-1} -1\right]^{-\beta } \right) \notag \\ & +\sum _{i=1}^{n}\log \left\{\alpha \left(1-\theta \right)+\theta \exp \left[-\left(\alpha -1\right)\left\{\left[\Phi \left(z_{i} \right)\right]^{-1} -1\right\}^{-\beta } \right]\right\}-\sum _{i=1}^{n}\log \left(\sigma _{i} \right) -\frac{1}{2} \sum _{i=1}^{n}\log \left(2\pi \right) \notag \\& -\left(\beta +1\right)\sum _{i=1}^{n}\log \left[1-\Phi \left(z_{i} \right)\right]-2\sum _{i=1}^{n}\log \left\{1-\theta \left\{1-\exp \left[-\left(\alpha -1\right)\left\{\left[\Phi \left(z_{i} \right)\right]^{-1} -1\right\}^{-\beta } \right]\right\}\right\} , \end{aligned} \tag{4}\] where \(z_{i} =\frac{x_{i} -\mu }{\sigma } .\) By differentiating (4) with respect to \(\alpha ,\beta ,\theta {\rm \; and\; }\sigma\), \(U\left(\Psi \right)\)g representing the score vector is obtained by \(U\left(\Psi \right)=\frac{\partial \ell }{\partial \Psi } =\left(\frac{\partial \ell }{\partial \alpha } ,\frac{\partial \ell }{\partial \beta } ,\frac{\partial \ell }{\partial \theta } ,\frac{\partial \ell }{\partial \sigma } \right).\) By solving the system of likelihood equations \(\frac{\partial \ell }{\partial \Psi } =0,\) the maximum likelihood estimates (MLEs) of the unknown parameter vector \(\Psi\) are obtained. However, the system of likelihood equations does not have an explicit solution in closed form. Consequently, numerical procedures are applied using R software to obtain the MLEs. The Fisher information matrix estimated by \(J\left(\Psi \right)=\frac{\partial ^{2} \ell }{\partial _{i} \partial _{j} } {\rm \; for\; }\left(i,j=\alpha ,\beta ,\theta ,\sigma \right)\) can be used to construct asymptotic confidence intervals for the model parameters.

4. Results of Simulation Experiment

To evaluate the behaviour of the model coefficients obtained using the approach of maximum likelihood, simulation experiments were conducted. Thus, estimators of the HMWN distribution were used to perform Monte Carlo simulation studies. The simulation experiment was repeated 1000 times for each of different probability samples obtained from the HMWN distribution with 25, 50, 75, 100, 200, 300 and 600 being the sample sizes \(\left(n\right).\) Different values for the coefficients of the HMWN generalized model used in the simulation are given as \(\left(\mu ,\sigma ,\alpha ,\beta ,\theta \right)=\) I: (4.4, 2.8, 0.1, 0.33, 1.0), II: (0.8, 4.5, 0.01, 0.21, 0.9), III: (9.0, 3.0, 4.5, 0.2, 0.01) and IV: (0.5, 2.9, 0.1, 0.1, 0.863). Coverage probability (CP) as an assessment criterion was used to evaluate the behaviour of the estimated values of the model coefficients. Root mean square error (RMSE) in addition to average estimate (AE) as well as average bias (AB) was also used in assessing the behaviour of the estimated values of the model coefficients. Presented in Table 1 and Table 2 are the results of the simulation experimentation.

Table 1 Results of simulation experimentation

\(\rm Parameter\)	n	\(I:\left(4.4,{\rm ; }2.8,{\rm ; }0.1,{\rm ; }0.33,{\rm ; }1.0\right)\)				\(II:\left(0.8,{\rm ; }4.5,{\rm ; }0.01,{\rm ; }0.21,{\rm ; }0.9\right)\)
		CP	RMSE	AB	AE	CP	RMSE	AB	AE
\(\mu \)	25	0.9980	1.9122	1.5283	2.9752	0.9750	0.9237	0.7943	0.4345
	50	0.9670	1.4746	1.1629	3.2550	0.9790	0.9252	0.7524	0.4474
	75	0.9760	1.1484	0.9221	3.5005	0.9750	0.7842	0.6944	0.4489
	100	0.9660	1.0061	0.7890	3.6556	0.9810	0.7606	0.6611	0.5501
	200	0.9780	0.6533	0.5334	3.9028	0.9900	0.6631	0.5695	0.5965
	300	0.9680	0.5284	0.4247	4.0077	0.9900	0.5619	0.4826	0.6375
	600	0.9890	0.3874	0.3136	4.1107	0.9990	0.4800	0.4069	0.7680
\(\sigma \)	25	0.9900	1.3092	09857	2.4393	0.9950	2.1249	1.6100	4.8632
	50	0.9930	1.2230	0.8684	2.5877	0.9900	1.7127	1.3028	4.7279
	75	0.9780	0.9471	0.7295	2.5754	0.9880	1.4956	1.1146	4.6851
	100	0.9710	0.8782	0.6544	2.6078	0.9780	1.3274	1.0079	4.6290
	200	0.9680	0.5957	0.4770	2.6505	0.9710	0.9262	0.7116	4.6013
	300	0.9670	0.5054	0.4128	2.6523	0.9630	0.7610	0.6074	4.5984
	600	0.9720	0.3705	0.2968	2.6926	0.9640	0.5673	0.4499	4.5459
\(\alpha \)	25	0.8140	0.5885	0.4987	0.5462	0.9390	0.5226	0.4664	0.4746
	50	0.7950	0.5759	0.4906	0.5237	0.9320	0.5559	0.4731	0.3804
	75	0.7320	0.5655	0.4851	0.5149	0.9230	0.5527	0.4705	0.3477
	100	0.8860	0.5414	0.4775	0.5104	0.9140	0.5501	0.4629	0.2694
	200	0.9680	0.5359	0.4642	0.5077	0.8820	0.5684	0.4658	0.2047
	300	0.9880	0.5290	0.4432	0.4807	0.8600	0.5793	0.4713	0.1870
	600	0.9640	0.5258	0.4333	0.4672	0.8270	0.5861	0.4687	0.1627
\(\beta \)	25	0.9920	0.2174	0.1519	0.2830	0.9950	0.1651	0.1165	0.2576
	50	0.9910	0.1941	0.1360	0.2917	0.9930	0.1267	0.0940	0.2375
	75	0.9720	0.1520	0.1173	0.2962	0.9820	0.1099	0.0798	0.2272
	100	0.9760	0.1407	0.1050	0.3019	0.9650	0.0983	0.0730	0.2226
	200	0.9670	0.0957	0.0768	0.3046	0.9660	0.0680	0.0512	0.2149
	300	0.9840	0.0822	0.0676	0.3050	0.9610	0.0548	0.0437	0.2122
	600	0.9470	0.0612	0.0493	0.3113	0.9670	0.0409	0.0322	0.2114
\(\theta \)	25	0.9490	0.0240	0.7075	0.2925	0.9440	0.0161	0.4324	0.4719
	50	0.8310	0.0224	0.6419	0.3581	0.9810	0.0140	0.3571	0.5496
	75	0.8710	0.0211	0.5904	0.4096	0.9890	0.0135	0.3415	0.5653
	100	0.8920	0.0198	0.4560	0.4541	0.9920	0.0132	0.3216	0.5846
	200	0.9790	0.0174	0.4551	0.5449	0.9920	0.0129	0.3081	0.6003
	300	0.9870	0.0159	0.3939	0.6061	0.9990	0.0128	0.2959	0.6172
	600	0.9910	0.0145	0.3391	0.6609	0.9990	0.0126	0.2803	0.6306

From the results of both Table 1 and Table 2, most of the values for the CP are shown to revolve around a 0.95 nominal value. Also, the values of the RMSE decrease with an increasing sample size. Further, there is a decrease in the values of the AB as the sample size increases. With an increase in the sample size, it is also observed that the values of the AE converge to the true population values. By these characteristics, the maximum likelihood procedure proved to be very efficient in providing estimated values for the model coefficients. Asymptotically, the results also show that the estimators are consistent.

Table 2 Results of simulation experimentation

Parameter	n	\(III:{\rm ; }\left(9,{\rm ; }3.0,{\rm ; }4.5,{\rm ; }0.2,{\rm ; }0.01\right)\)				\(IV:{\rm ; }\left(0.5,{\rm ; }2.9,{\rm ; }0.1,{\rm ; }0.1,{\rm ; }0.863\right)\)
		\(CP\)	\(RMSE\)	\(AB\)	\(AE\)	\(CP\)	\(RMSE\)	\(AB\)	\(AE\)
\(\mu\)	25	0.7460	6.4051	6.0223	3.0009	0.9730	0.9330	0.6366	0.4595
	50	0.9950	5.1606	4.5708	4.5252	0.9770	0.6660	0.5268	0.4047
	75	0.8990	3.6888	3.0887	6.0992	0.9500	0.5935	0.4923	0.3900
	100	0.9800	3.0845	3.0008	6.1812	0.9800	0.5765	0.4595	0.3961
	200	0.9280	2.5845	2.1150	7.1951	0.9180	0.4515	0.3799	0.4117
	300	0.9910	2.1883	1.8039	7.5397	0.9180	0.4209	0.3523	0.4295
	600	0.9560	1.7396	1.4386	7.9226	0.9920	0.3291	0.2750	0.4495
\(\sigma\)	25	0.8810	1.4145	1.1765	2.3338	0.8640	2.0664	1.4032	4.1415
	50	0.9900	1.3903	1.1056	2.5038	0.9910	1.4486	1.0015	3.7512
	75	0.9200	1.1731	0.9407	2.5460	0.9180	1.1762	0.8310	3.5900
	100	0.9910	1.0765	0.9015	2.5573	0.9250	1.0167	0.7437	3.5123
	200	0.9180	0.9479	0.8070	2.5612	0.9950	0.6096	0.4496	3.2494
	300	0.9850	0.8319	0.7001	2.6024	0.9910	0.5306	0.3030	3.2090
	600	0.8730	0.6692	0.5495	2.6870	0.9680	0.3660	0.2823	3.1007
\(\alpha\)	25	0.9800	2.5477	2.3740	2.2368	0.9840	0.5165	0.4177	0.4984
	50	0.9170	2.1485	1.8780	3.0759	0.9450	0.4809	0.4064	0.3782
	75	0.9790	1.6971	1.4293	3.4498	0.9900	0.4745	0.4023	0.3081
	100	0.9900	1.4846	1.2230	3.6129	0.9100	0.4659	0.4018	0.2698
	200	0.9450	1.0157	0.8183	4.1574	0.8950	0.4541	0.4012	0.2114
	300	0.9870	0.8782	0.7175	4.3190	0.9850	0.4082	0.3900	0.2018
	600	0.9590	0.6675	0.5453	4.4263	0.9250	0.3980	0.3704	0.1935
\(\beta\)	25	0.8450	0.1873	0.1313	0.2439	0.9100	0.1552	0.1032	0.1975
	50	0.9780	0.1729	0.1259	0.2386	0.9910	0.1035	0.0697	0.1638
	75	0.9160	0.1621	0.1131	0.2363	0.9990	0.0818	0.0557	0.1498
	100	0.9890	0.1318	0.0999	0.2289	0.9720	0.0682	0.0482	0.1428
	200	0.8440	0.1051	0.0869	0.2240	0.9980	0.0406	0.0294	0.1246
	300	0.9940	0.0942	0.0782	0.2198	0.9250	0.0346	0.0259	0.1212
	600	0.8450	0.0738	0.0614	0.2138	0.9900	0.0237	0.0180	0.1140
\(\theta\)	25	0.9900	0.0296	0.3986	0.4037	0.9570	0.0151	0.4037	0.4688
	50	0.9350	0.0201	0.3652	0.3892	0.9730	0.0137	0.3439	0.5339
	75	0.9810	0.0186	0.3431	0.3396	0.9910	0.0131	0.3190	0.5579
	100	0.9890	0.0164	0.2939	0.3041	0.9850	0.0126	0.2994	0.5817
	200	0.7920	0.0133	0.2702	0.2812	0.9350	0.0121	0.2761	0.6044
	300	0.9750	0.0121	0.2648	0.2633	0.9990	0.0115	0.2499	0.6371
	600	0.7390	0.0109	0.2220	0.1017	0.9980	0.0106	0.2309	0.7466

5. The HMWN Regression Models

Let \(w_{i} =\left(w_{i1} ,…,w_{ik_{1} } \right)^{T}\)be a \(k\times 1\) vector of independent variables associated with the ith response variable \(y_{i} {\rm \; }\left(i=1,…,n_{o} \right)\). Let \(y_{i}\) be a response variable having the HMWN distribution. By utilizing the density function in (3), the HMWN generalized regression models are defined with the regression structure given as \[\begin{aligned} \label{e5}y_{i} =\mu _{i} +\sigma _{i} z_{i} , \end{aligned} \tag{5}\] where the random error \(z_{i} ={\left(y_{i} -\mu _{i} \right)\mathord{\left/ {\vphantom {\left(y_{i} -\mu _{i} \right) \sigma _{i} }} \right. } \sigma _{i} }\) has the standardized HMWN distribution. The parameters \(\mu _{i} {\rm \; and\; }\sigma _{i}\) are respectively given by \[\begin{aligned} \label{e6}\mu _{i} =\mu _{i} \left(\gamma _{1} \right){\rm \; \; \; \; \; \; and\; \; \; \; \; \; \; \; }\sigma _{i} =\sigma _{i} \left(\gamma _{2} \right), \end{aligned} \tag{6}\] where \(\gamma _{1} =\left(\gamma _{11} ,…,\gamma _{1k_{1} } \right)^{T}\) and \(\gamma _{2} =\left(\gamma _{21} ,…,\gamma _{2k_{2} } \right)^{T}\). For the location and dispersion parameters, the respective systematic components are \(\mu _{i} =w_{i}^{T} \gamma _{1}\) and \(f\left(\sigma _{i} \right)=\psi _{i} =u_{i}^{T} \gamma _{2}\). Thus, \(\mu =W\gamma _{1} ,\) \(\mu =\left(\mu _{1} ,…,\mu _{n_{0} } \right)^{T}\) and \(W=\left(w_{1} ,…,w_{n_{0} } \right)^{T}\) is a full rank \(n_{0} \times k_{1}\) matrix. \(f\left(.\right)\) denotes a link function for the dispersion parameter, \(u_{i} =\left(u_{i1} ,…,u_{ik_{2} } \right)^{T}\) is a vector of covariates with a linear function in \(f\left(\sigma _{i} \right)\) that gives a measure of variation associated with the \(i{\rm th}\) observed value. Thus, \(f\left(\sigma \right)=\psi =U\gamma _{2} ,\) \(\sigma =\left(\sigma _{1} ,…,\sigma _{n} \right)^{T}\), \(\psi =\left(\psi _{1} ,…,\psi _{n} \right)^{T}\) and \(U=\left(u_{1} ,…,u_{n} \right)^{T}\) is a \(n_{0} \times k_{2}\) full rank matrix. The dispersion covariates in \(U\) are but not necessarily regression covariates in \(W\). Functionally, \(\gamma _{1}\) and \(\gamma _{2}\) are independent and \(f(.)\) is a twice differentiable one-to-one function.

The Marshall-Olkin Weibull Normal (MOWN) regression model is a special case of HMWN regression when \(\alpha =0\). The MLEs of the parameter vector \(\left(\gamma _{1}^{T} ,\gamma _{2}^{T} ,\alpha ,\beta ,\theta \right)^{T}\) are obtained by utilizing (4). Residual analysis involving Cox-Snell residuals according to [12] is utilized in this study to assess the adequacy of the HMWN generalized regression models. For a given HMWN generalized regression model, the Cox-Snell residuals are defined by \[r_{i} =-\log \left\{S\left[y_{i} \left|\left(\hat{\gamma }_{1}^{T} ,\hat{\gamma }_{2}^{T} ,\hat{\alpha },\hat{\beta },\hat{\theta }\right)^{T} \right. \right]\right\},{\rm \; }i=1,2,…,n,\] where \(S\left(y_{i} \left|\left(\hat{\gamma }_{1}^{T} ,\hat{\gamma }_{2}^{T} ,\hat{\alpha },\hat{\beta },\hat{\theta }\right)^{T} \right. \right)\) is the survival function of the HMWN regression model. For a given data set therefore, a HMWN generalized regression model is said to provide an adequate fit if the distribution of its Cox-Snell residuals is that of the standard exponential.

6. HMWN Experimental Design Model

Experimental design models have been applied in many fields of enquiry including medical and biomedical studies. With the use of these models, the response variable is required to be normally distributed and hence symmetric. In some practical situations however, the data are skewed or bimodal and cannot be modelled by the classical experimental design models [7]. Thus, the HMWN experimental design model is proposed as a robust generalization to overcome these limitations.

In a completely randomized block design (CRBD), the experimental units randomly receive experimental dosages independently in the given blocks. Thus, this ensures a restriction on the randomization allowing for local control. This type of control should therefore be taken into consideration in the fitted statistical model [7]. In a given block \(q\), let \(y_{pq}\) represent the observation from the \(p^{th}\) treatment such that \(y_{pq}\) follows the HMWN distribution. By using the density function in (3), a HMWN CRBD model is defined with a control structure given in the form \[\begin{aligned} \label{GrindEQ__7_} y_{pq} =\mu +v_{p} +b_{q} +\sigma z_{pq} , \end{aligned} \tag{7}\] where \(\mu\) denotes the grand mean, the \(p^{th}\) treatment effect represented by \(v_{p}\) and the \(q^{th}\) block effect represented by \(b_{q}\) with \(z_{pq}\) being the random error having a distribution of the HMWN. Thus, \(p=1,…,P\) where \(P\) is the number of treatments and \(q=1,…,Q\) where \(Q\) is the number of blocks.

Consider a sample \(y_{11} ,…,y_{PQ}\) of size \(n=PQ\) drawn from a distribution of HMWN and let \(v=\left(v_{1} ,…,v_{P} \right)^{T}\) and \(b=\left(b_{1} ,…,b_{Q} \right)^{T}\). By adopting numerical procedures in R software, the MLEs of the vector of parameters \(\psi =\left(\mu ,v^{T} ,b^{T} ,\alpha ,\beta ,\theta \right)^{T}\) are obtained by maximizing (8). \[\begin{aligned} \label{GrindEQ__8_} \ell =&PQ\log \left(\beta \right)+\left(\beta -1\right)\sum _{p=1}^{P}\sum _{q=1}^{Q}\log \left[\Phi \left(z_{pq} \right)\right] -\sum _{p=1}^{P}\sum _{q=1}^{Q}\left\{\frac{1}{2} \left(z_{pq} \right)^{2} +\alpha \left[\left(\Phi \left(z_{pq} \right)\right)^{-1} -1\right]^{-\beta } \right\} \notag \\ & +\sum _{p=1}^{P}\sum _{q=1}^{Q}\log \left[\alpha \left(1-\theta \right)+\theta \exp \left\{-\left(\alpha -1\right)\left[\left(\Phi \left(z_{pq} \right)\right)^{-1} -1\right]^{-\beta } \right\}\right] -\sum _{p=1}^{P}\sum _{q=1}^{Q}\log \left(\sigma _{pq} \right) -\frac{1}{2} \sum _{p=1}^{P}\sum _{q=1}^{Q}\log \left(2\pi \right) \notag \\&-\left(\beta +1\right)\sum _{p=1}^{P}\sum _{q=1}^{Q}\log \left[1-\Phi \left(z_{pq} \right)\right] -2\sum _{p=1}^{P}\sum _{q=1}^{Q}\log \left[1-\theta \left(1-\exp \left\{-\left(\alpha -1\right)\left[\left(\Phi \left(z_{pq} \right)\right)^{-1} -1\right]^{-\beta } \right\}\right)\right], \end{aligned} \tag{8}\] where \(z_{pq} ={\left(y_{pq} -\mu -v_{p} -b_{q} \right)\mathord{\left/ {\vphantom {\left(y_{pq} -\mu -v_{p} -b_{q} \right) \sigma .}} \right. } \sigma .}\) A HMWN completely randomized design (CRD) model is obtained as a specialized case in the absence of a local control where \(b_{q} =0.\) To assess the quality of fit of the model for the HMWN CRD in terms of its adequacy, residual analysis involving Cox-Snell residuals according to [12] is utilized. For a HMWN experimental design model, the Cox-Snell residuals are defined by \[r_{i} =-\log \left\{S\left[y_{i} \left|\left(\hat{\mu },\hat{v}^{T} ,\hat{b}^{T} ,\hat{\sigma },\hat{\alpha },\hat{\beta },\hat{\theta }\right)^{T} \right. \right]\right\},{\rm \; }i=1,2,…,PQ,\] where \(S\left[y_{i} \left|\left(\hat{\mu },\hat{v}^{T} ,\hat{b}^{T} ,\hat{\alpha },\hat{\beta },\hat{\theta }\right)^{T} \right. \right]\) is the survival function of the HMWN CRD model. For a given data set, the complete randomized HMWN experimental design model is said to provide an adequate fit if the distribution of its Cox-Snell residuals is that of the standard exponential.

7. Applications

This section presents the use of practical data sets in illustrating the applications of the HMWN generalized models. The AIC representing Akaike Information Criterion is used to estimate the quality of the model fits. Consistent AIC (CAIC) and Schwarz Information Criterion (BIC) are also utilized as additional measures of model fit. The HMWN generalized models are then compared with some well-known models and the best performing model selected based on least values of the model fit measures.

7.1. First application: red cell folate data

A practical dataset on red cell folate levels, accessible in [13] and replicated in [1], was used to demonstrate the applicability of the HMWN generalized regression models. During an anesthesia procedure, patients undergoing cardiac bypass surgery were randomized into three ventilation procedure groups, and red cell folate measurements were recorded. The ventilation procedures are described as follows:

– **Ventilation Procedure I**: A mixture of 50% nitrous oxide and 50% oxygen was administered continuously for 24 hours \(\left({\rm N}_{2} {\rm O} + {\rm O}_{2}, {\rm \; 24\; h}\right)\).

– **Ventilation Procedure II**: A mixture of 50% nitrous oxide and 50% oxygen was administered only during the operation \(\left({\rm N}_{2} {\rm O} + {\rm O}_{2}, {\rm \; operation\; only}\right)\).

– **Ventilation Procedure III**: A 35-50% oxygen mixture without nitrous oxide was administered continuously for 24 hours \(\left({\rm O}_{2}, {\rm \; 24\; h}\right)\).

The folate concentration levels (\(\mu\)g/l), denoted by \(y_{i}\), were modeled as the response variable, while the ventilation procedure \(\left({\rm v}_{i}\right)\) served as the explanatory variable categorized into three levels (Ventilation Procedure I, Ventilation Procedure II, and Ventilation Procedure III). The three levels of \({\rm v}_{i}\) were encoded using dummy variables:

– Ventilation Procedure I: \(\left({\rm v}_{i1} = 0 \; \text{and} \; {\rm v}_{i2} = 0\right)\),

– Ventilation Procedure II: \(\left({\rm v}_{i1} = 1 \; \text{and} \; {\rm v}_{i2} = 0\right)\),

– Ventilation Procedure III: \(\left({\rm v}_{i1} = 0 \; \text{and} \; {\rm v}_{i2} = 1\right)\).

The regression model fitted to the dataset takes the form: \[y_{i} = \mu _{i} + \sigma _{i} z_{i},\] where \(\mu_{i} = \gamma_{10} + \gamma_{11} {\rm v}_{1} + \gamma_{12} {\rm v}_{2}\) and \(\sigma_{i} = \gamma_{20} + \gamma_{21} {\rm v}_{1} + \gamma_{22} {\rm v}_{2}\) are the location and dispersion parameters, respectively, in the HMWN regression model with varying dispersion. The variables \(z_{1}, z_{2}, \dots, z_{n}\) are independently distributed random variables with the density function specified in (3). The HMWN regression model with constant dispersion is a special case where \(\sigma_{i} = \sigma\).

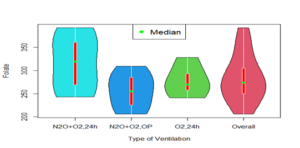
The performance of the HMWN generalized regression models was evaluated by comparison with two competitive models: the OLLG-N regression model with constant dispersion and the OLLGN regression model with varying dispersion, as developed in [1]. Table 3 presents descriptive statistics for the ventilation procedures and the overall red cell folate concentration levels. The minimum and maximum folate concentrations observed were 206 and 392 \(\mu\)g/l, respectively, with an overall mean of 283.23 \(\mu\)g/l. The coefficient of skewness (0.5853) and excess kurtosis (-0.4068) indicate that the overall folate concentration levels are right-skewed and platykurtic. The levels of skewness and kurtosis varied across the ventilation procedures.

These results demonstrate that classical linear regression models are unsuitable for this dataset due to the asymmetry in the response variable. However, the HMWN generalized regression models provided an adequate fit, highlighting their applicability for analyzing asymmetric data in biomedical studies.

Table 3 Descriptive Statistics for the red cell folate data

	Minimum	Mean	Skewness	Excess Kurtosis	Maximum
Overall folate levels	206.0000	283.2273	0.5853	-0.4068$$\sim$$	392.0000
N\(_2\)O+O\(_2\),24h	243.0000	316.6250	-0.0058	-1.5911	392.0000
N\(_2\)O+O\(_2\),op	206.0000	256.4444	-0.0697	-1.3287	309.0000
O\(_2\),24h	241.0000	278.0000	0.5029	-0.9931	328.0000

The results of the violin plot in Figure 1c show that the overall folate concentration levels are skewed to the right with some ventilation procedures showing some form of bimodality. The results further confirm that the data cannot be adequately modeled by the classical linear regression but can be modeled adequately using the HMWN generalized regression models.

Presented in Table 4 are the model fit measures of the generalized regression models fitted to the data on red cell folate concentrations. The AIC and the BIC reported least values for the HMWN generalized regression models compared with the other fitted generalized regression models. The results thus indicate that the HMWN generalized regression models provided a superior fitness capability than the OLLG-N generalized regression models.

Table 4 Measures of model fit for the red cell folate

Model	AIC	BIC
HMWN regression with varying dispersion	232.0619	240.8813
HMWN regression with constant dispersion	233.2760	241.4133
OLLG-N regression with varying dispersion	234.2000	243.0000
OLLG-N regression with constant dispersion	235.0000	241.6000

Estimated values for the coefficients of the HMWN generalized regression models with constant and varying dispersion are presented in Table 5. Using a significance level of 5%, the results showed the parameter \(\gamma _{11}\) to be statistically significant. The result therefore provided empirical evidence that Ventilation Procedure I had a statistically significant effect on the red cell folate concentration levels in the patients during the anaesthesia procedure. Again, the result further showed that the effect of Ventilation Procedure I differ significantly from that of Ventilation Procedure II.

Table 5 Estimated values for the coefficients of the fitted generalized regression models for the data on red cell folate concentrations

\(Model\)	\(Parameter\)	\(Estimate\)	\(Standard\; Error\)	\(P-Value\)
HMWN Regression with Varying Dispersion	\(\alpha \)	\(3.0198\times 10^-1 \)	\(\rm 1.1176\times 10^-1 \)	\(\rm 6.8890\times {\rm 10}^-3 \)
	\(\beta \)	\(1.4841\)	\(3.2914\times 10^-1 \)	\(6.5150\times 10^-6 \)
	\(\theta \)	\(2.0212\times 10^-3 \; \)	\(8.5446\times 10^-3 \)	\(8.1301\times 10^-1 \)
	\(\gamma _10\)	\(296.5550\)	\(3.7695\)	\(<2.2000\times 10^-16 \)
	\(\gamma _11\)	\(-64.7101\)	\(5.5879\)	\(<2.2000\times 10^-16 \)
	\(\gamma _12\)	\(-44.2504\)	\(7.7546\)	\(1.1540\times 10^-8 \)
	\(\gamma _20\)	\(113.6263\)	\(2.3128\)	\(<2.2000\times 10^-16 \)
	\(\gamma _21\)	\(-27.5977\)	\(4.6731\)	\(3.5130\times 10^-9 \)
	\(\gamma _22\)	\(-25.2431\)	\(6.0898\rm ; \)	\(3.3960\times 10^-5 \)
HMWN Regression with Constant Dispersion	\(\sigma \)	\(103.0343\)	\(2.4194\times 10^-1 \)	\(<2.2000\times 10^-16 \)
	\(\alpha \)	\(3.0307\times 10^-1 \)	\(1.2369\times 10^-1 \)	\(1.4280\; \times 10^-2 \)
	\(\beta \)	\(1.7039\)	\(3.6023\times 10^-1 \)	\(2.2460\times 10^-6 \)
	\(\theta \)	\(1.6343\; \times 10^-3 \)	\(6.8906\times 10^-3 \)	\(0.8122\)
	\(\gamma _10\)	\(312.1668\)	\(2.6117\; \)	\(<2.2000\times 10^-16 \)
	\(\gamma _11\)	\(-81.1948\)	\(13.6228\)	\(2.5190\times 10^-9 \)
	\(\gamma _12\)	\(-64.1245\)	\(12.2834\)	\(1.7850\times 10^-7 \)
	\(\beta _10\)	\(317.3760\)	\(9.7130\)	\(<0.0001\)
OLLG-N Regression with Varying Dispersion	\(\beta _11\)	\(-61.4500\)	\(10.2170\rm ; \)	\(\rm 0.00003\)
	\(\beta _12\)	\(-31.6260\)	\(15.2970\)	\(0.0570\)
	\(\beta _20\)	\(2.5250\)	\(0.6610\)	\(0.0010\)
	\(\beta _21\)	\(-0.3890\)	\(\rm 0.2270\)	\(\rm 0.1080\)
	\(\beta _22\)	\(-0.5220\)	\(0.2810\)	\(0.0840\)
	\(logit(\nu )\)	\(-2.1650\)	\(1.2860\)	\(-\)
	\(log(\tau )\)	\(-\rm 2.0880\)	\(\rm 1.1200\)	\(-\)
OLLG-N Regression with Constant Dispersion	\(\beta _20\)	\(320.1140\)	\(\rm 5.2920\rm ; \)	\(<0.0001\)
	\(\beta _21\)	\(-63.3280\)	\(18.6330\)	\(\rm 0.003\)
	\(\beta _22\)	\(-25.3060\)	\(\rm 27.8040; \)	\(0.3740\)
	\(\mathrm{log}\mathrm{}(\sigma )\)	\(2.3840\)	\(0.1140\rm ; \)	–
	\(logit(\nu )\)	\(-1.6520\)	\(\rm 1.1470\)	–
	\(log(\tau )\)	\(-1.9600\)	\(0.1960\rm ; \)	–

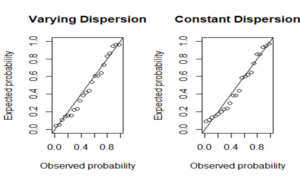
The adequacies of the HMWN regression models (both constant and varying dispersion) were evaluated through a residual analysis with the use of the Cox- Snell residuals. Residual analysis results presented in Figure 1d give a firm indication that the HMWN generalized regression models provided an adequate fit to the data and can be practically utilized to analyze data in biomedical research studies.

7.2. Second application: doses effects data

The second data set represents the effectiveness levels of different dosages of anthelmintic compound in the control of a parasite. Representing 5 treatments, 5 experimental dosages were examined through a completely randomized design experiment. Experimental dosage 1 and dosage 2 were defined as controls while 5%, 10% and 15% concentrations of a new drug were used to represent experimental dosages 3, 4 and 5 respectively. The experiment was replicated 6 times for each experimental dosage and the data are accessible through [7]. The effectiveness levels of the experimental dosages on the parasite control representing the response variable was modelled with the treatment factor \(\left({\rm v}_{i} \right)\) having five levels (experimental dosage 1 \(\left({\rm V}_{1} \right)\), experimental dosage 2 \(\left({\rm V}_{2} \right)\), experimental dosage 3 \(\left({\rm V}_{3} \right)\), experimental dosage 4 \(\left({\rm V}_{4} \right)\) and experimental dosage 5 \(\left({\rm V}_{5} \right)\)) defined by the following dummy variables: \({\rm V}_{1}\) \(\left({\rm v}_{i1} =0,{\rm v}_{i2} =0,{\rm v}_{i3} =0{\rm \; \; and\; v}_{i4} =0\right),\) \({\rm V}_{2}\) \(\left({\rm v}_{i1} =1,{\rm v}_{i2} =0,{\rm v}_{i3} =0{\rm \; \; and\; v}_{i4} =0\right),\) \({\rm V}_{3}\) \(\left({\rm v}_{i1} =0,{\rm v}_{i2} =1,{\rm v}_{i3} =0{\rm \; \; and\; v}_{i4} =0\right),\) \({\rm V}_{4}\) \(\left({\rm v}_{i1} =0,{\rm v}_{i2} =0,{\rm v}_{i3} =1{\rm \; \; and\; v}_{i4} =0\right),\) and \({\rm V}_{5}\) \(\left({\rm v}_{i1} =0,{\rm v}_{i2} =0,{\rm v}_{i3} =0{\rm \; \; and\; v}_{i4} =1\right).\) By setting \(b_{j} =0,\) the HMWN CRD model fitted to the data set is \[y_{i} =\mu _{i} +\sigma _{i} z_{i} ,\] where \(\mu _{i} =\mu +t_{11} v_{1} +t_{12} v_{2} +t_{13} v_{3} +t_{14} v_{4}\) and \(\sigma _{i}\) are the parameters of the HMWN CRD model and \(z_{1} ,{\rm \; }.{\rm \; }.{\rm \; }.,{\rm \; }z_{n}\) are independently distributed random variables with density function given in (3).

The competitiveness of the HMWN CRD model in practical applications was evaluated by comparing with other CRD models generated from gamma normal (GN) distribution by [6], odd log-logistic normal (OLLN) distribution by [7], Kumaraswamy normal (KN) distribution by [9], beta-normal (BN) distribution by [8] and skew-normal (SN) distribution by [14]. In Table 6, the descriptive statistics for the overall doses effect and for the different experimental dosage groups are presented. The least and the highest overall doses effect were observed to be 44.0000 and 3020 respectively. The overall average doses effect of the anthelmintic compound is also shown to be 1065.3667. The overall coefficient of skewness and excess kurtosis are shown to be 0.5270 and -1.3773 respectively which indicate that the overall doses effects are skewed to the right and platykurtic. The doses effects of the different experimental dosage groups also showed various levels of skewness and kurtosis. The asymmetric nature of the doses effects shows that whilst the HMWN experimental design model can adequately model the data, the classical experimental design models cannot adequately model the data.

Table 6 Descriptive Statistics of the doses data

Variable	Minimum	Maximum	Mean	Skewness	Excess Kurtosis
Overall Doses Effects	44.0000	3020.0000	1065.3667	0.5270	-1.3773\(\sim\)
Experimental dosage 1	1687.0000	3020.0000	2477.0000	-0.5016	-0.7453
Experimental dosage 2	1825.0000	2527.0000	2075.0000	0.7727	-0.9066
Experimental dosage 3	317.0000	842.0000	527.1667	0.3930	-0.9538
Experimental dosage 4	127.0000	227.0000	156.3333	1.1183	-0.1642
Experimental dosage 5	44.0000	193.0000	91.3333	1.3522	0.4724

In Figure 3, the anthelmintic compound’s overall doses effect on the parasite control is shown to exhibit positive asymmetry and bimodality in the violin plot with the effect level on the parasite control showing different forms of asymmetry across the different experimental dosages. The results further confirm that the data cannot be adequately modeled by the classical CRD model but can be modeled adequately using the HMWN CRD model.

Presented in Table 7 are the model fit measures of the generalized CRD models fitted to the data on anthelmintic compound doses. The AIC and CAIC as well as the BIC all reported least values for the HMWN CRD model compared with the other fitted generalized CRD models. The results thus indicate that the HMWN CRD model provided a superior performance in fitting the data than the other generalized CRD models.

Table 7 Measures of model fit for the data on anthelmintic doses

Design Model	AIC	CAIC	BIC
HMWN	421.2100	430.7100	431.1820
OLLN	424.7210	433.721	434.5300
SN	428.7210	437.7210	438.529
BN	430.1750	441.7540	441.3840
KN	430.1870	441.7660	441.3960
GN	428.4140	437.4140	438.2220

Estimated values for the coefficients of the fitted generalized CRD models are presented in Table 8. By applying the standard error procedure of test of significance of model coefficients, all the parameters of the HMWN CRD model are statistically significant except \(\theta\). The empirical results provided a significant evidence of differences between the experimental dosages in the parasite control.

Table 8 Estimated values of the coefficients of the fitted CRD generalized models for the data on doses effects

Model	Parameter	Estimate	Standard Error
HMWN Design model	\(\mu \)	\(1.1247\times 10^3 \)	\(2.0820\times 10^-3 \)
	\(t_2\)	\(-3.8179\times 10^2 \)	\(8.0457\times 10^-4 \)
	\(t_3\)	\(-1.9254\times 10^3 \)	\(1.2482\times 10^-3 \)
	\(t_4\)	\(-2.5002\times 10^3 \)	\(9.0656\times 10^-4 \)
	\(t_5\)	\(-1.1883\times 10^3 \)	\(3.0173\times 10^-4 \)
	\(\sigma \)	\(9.5181\times 10^3 \)	\(\rm 5.6226\times 10^-4 \)
	\(\alpha \)	\(7.6670\times 10^-2 \)	\(3.6742\times 10^-2 \)
	\(\beta \)	\(7.1819\rm ; \)	\(7.4463\times 10^-1 \)
	\(\theta \)	\(4.0013\times 10^-3 \)	\(5.6922\times 10^-3 \)
OLLN Design Model	\(\mu \)	\(2466.5220\)	\(\rm 110.2280\)
	\(t_2\)	\(-405.0100\)	\(\rm 146.8860\)
	\(t_3\)	\(-1949.3200\)	\(\rm 139.5390\)
	\(t_4\)	\(-2310.0070\)	\(\rm 131.5050\)
	\(t_5\)	\(-2375.4370\)	\(\rm 131.8170\)
	\(\sigma \)	\(1022.3570\)	\(\rm 343.8980\)
	\(\alpha\)	\(5.2310\)	\(\rm 7.0570\)
SN Design model	\(\mu \)	\(2384.5410\)	\(401.5300\)
	\(t_2\)	\(-392.2600\)	\(148.7730\)
	\(t_3\)	\(-1940.7960\)	\(\rm 153.7840\)
	\(t_4\)	\(-2305.9270\)	\(\rm 159.8830\)
	\(t_5\)	\(-2374.2070\)	\(\rm 159.6560\)
	\(\sigma \)	\(256.9020\)	\(\rm 115.7650\)
	\(\lambda \)	\(0.4390\)	\(\rm 1.9160\)
BN Design Model	\(\mu \)	\(2716.7250\)	\(\rm 1339.8500\)
	\(t_2\)	\(-371.0160\)	\(\rm 227.2530\)
	\(t_3\)	\(-1948.8120\)	\(\rm 273.2410\)
	\(t_4\)	\(-2335.5260\)	\(\rm 326.1370\)
	\(t_5\)	\(-2400.13200\rm ; \)	\(\rm 324.3050\)
	\(\sigma \)	\(\rm 355.7740\)	\(\rm 359.7750\)
	\(a\)	\(1.2880\)	\(\rm 3.2000\)
	\(b\)	\(\rm 3.1860; \)	\(\rm 10.1360\)
KN design model	\(\mu \)	\(2461.8950\)	\(\rm 3304.0300\)
	\(t_2\)	\(-394.7450\)	\(\rm 331.9290\)
	\(t_3\)	\(-1946.1060\)	\(\rm 418.9820\)
	\(t_4\)	\(-2318.2710\)	\(\rm 508.6730\)
	\(t_5\)	\(-2385.7000\)	\(\rm 505.4300\)
	\(\sigma \)	\(\rm 378.0430\)	\(\rm 1001.6830\)
	\(a\)	\(2.0340\)	\(\rm 17.5560\)
	\(b\)	\(\rm 2.3160\)	\(\rm 5.7390\)
GN design model	\(\mu \)	\(2625.1850\)	\(\rm 395.7940\)
	\(t_2\)	\(-388.8660\)	\(\rm 156.5170\)
	\(t_3\)	\(-1950.0100\)	\(\rm 169.3580\)
	\(t_4\)	\(-2322.0100\)	\(\rm 187.9410\)
	\(t_5\)	\(-2385.7000\)	\(\rm 187.2800\)
	\(\sigma \)	\(\rm 209.0470\)	\(\rm 87.0540\)
	\(a\)	\(0.5570\rm ; \)	\(\rm 0.7720\)

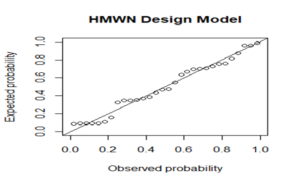
To assess the adequacy of the HMWN experimental design model, residual analysis was carried out using the Cox-Snell residuals. Diagnostic test results of the residual analysis presented in Figure 5 give a firm indication that the HMWN CRD model provided an adequate fit to the data and can be practically utilized to analyze data in biomedical research works.

Conclusion

Two Harmonic Mixture Weibull-Normal (HMWN) generalized regression models—one with varying dispersion and the other with constant dispersion—are proposed in this study. The relationships between the scale and location parameters and the covariates were defined using an identity link function. The utility of the HMWN generalized regression models was demonstrated through an application investigating the effect of different ventilation procedures on red cell folate concentration in patients undergoing anesthesia. The parameter estimates for both the constant and varying dispersion HMWN models provided significant empirical evidence of differences in red cell folate concentration between patients subjected to Ventilation Procedure I and Ventilation Procedure II. Moreover, empirical results established that the HMWN models offered a superior fit to the data compared to other competitive generalized regression models.

Additionally, this study proposes a novel experimental design model, referred to as the HMWN experimental design model. Its utility was illustrated through an application examining the effectiveness of varying dosages of an anthelmintic compound in controlling a parasite. The parameter estimates of the HMWN experimental design model provided strong empirical evidence of significant differences in the parasite control effects among the different dosages. Further results demonstrated that the HMWN experimental design model achieved a better fit to the data than competing experimental design models.

In summary, the HMWN generalized models, including the regression and experimental design variants, have been empirically validated as robust and practically applicable tools for analyzing biomedical data.