This paper proposes a new creative modification to the well-known standard Adomian decomposition method (ADM) in order to investigate various types of initial-value problems (IVPs) involving distinct kinds of fourth order ordinary differential equations (ODEs). We demonstrate that the singular point at \(x=0,\) therefore the form factor, could show up in several equations terms. Some non-linear numerical applications that have been studied and explained this method have confirmed its effectiveness and ability to find appropriate solutions for such equations. The outcomes we arrive at with this operator are reliable and converge faster than the exact solution.
]]ourth-order linear and non-linear initial-value problems (IVPs) serve as mathematical models for numerous real-life phenomena and are applied in various physical contexts. Some of these problems specifically address phenomena related to elastic stability, making their solutions highly significant in practical applications. Consequently, many researchers have developed and employed diverse mathematical techniques to solve such problems effectively.
Numerical methods for solving differential equations encompass a broad and active area of research. Techniques such as the Adomian decomposition method (ADM) [1], the differential transform method [2], the variational iteration method [3], and the homotopy method [4] have been widely explored. The ADM, introduced by George Adomian in the 1980s, has been extensively studied and applied, with numerous extensions and adaptations reported in the literature [1,5,6]. Modifications of the ADM to enhance accuracy and convergence, often termed the Modified Adomian Decomposition Method (MADM), have also been proposed [7-10] and applied to solving IVPs.
For example, E.U. Agom et al. [11] used the ADM to solve fourth-order linear differential equations, deriving a convergent series of analytical solutions and demonstrating the method’s high accuracy and reliability. Similarly, A.N. Kameradin and collaborators proposed a modified version of the ADM, which they found to converge more efficiently and rapidly to the exact solution compared to the original ADM [12]. Furthermore, A.M. Wazwaz et al. extended the Adomian method to tackle the Emden-Fowler equation of the fourth order, showcasing its versatility in solving various forms of this equation [13]. Numerous researchers have also studied singular equations with initial and boundary conditions of different orders [14-20].
The objective of this study is to apply a refined and efficient modification of the Adomian method to investigate various types of fourth-order ordinary differential equation IVPs. The effectiveness of the proposed approach is demonstrated through several illustrative examples, highlighting its rapid convergence to exact solutions and its potential for addressing complex problems.
We derive fourth-order ordinary differential equations using the formula \[\label{eq1} x^{-(\gamma+\eta)k}\frac{d^{mj}}{dx^{mj}}x^{(\gamma+\eta)k}e^{-(\gamma+\eta)bx}\frac{d^{nj}}{dx^{nj}}e^{(\gamma+\eta)bx}y=R(x,y),\tag{1}\] where \(k \geq 0\), \(b > 0\) is a real number, \(\gamma, \eta \in \{0, 1\}\), \(\gamma \neq \eta\), and \(R(x,y)\) is a given function of \(x\) and \(y\).
To obtain these fourth-order equations, we select \[mj+nj=4, \hspace{0.3cm} m, n \geq 1, \hspace{0.3cm} j=1, 2.\] This setup yields three distinct cases: \[m=3,\hspace{0.3cm} n=1,\hspace{0.3cm} j=1,\] \[m=1,\hspace{0.3cm} n=1,\hspace{0.3cm} j=2,\] and \[m=1,\hspace{0.3cm} n=3,\hspace{0.3cm} j=1.\]
Substituting \(m=3\), \(n=1\), \(j=1\), \(\gamma=1\), and \(\eta=0\) into Eq. (1), we obtain: \[\label{eq2} x^{-k}\frac{d^{3}}{dx^{3}}x^{k}e^{-bx}\frac{d}{dx}e^{bx}y=R(x,y).\tag{2}\] By computing the derivatives, we derive the first type of fourth-order singular equation as: \[\begin{aligned} x^{-k}\frac{d^{3}}{dx^{3}}x^{k}e^{-bx}\left(e^{bx}y' + be^{bx}y\right) &= x^{k}\frac{d^{4}y}{dx^{4}} + (3kx^{k-1} + bx^{k})\frac{d^{3}y}{dx^{3}}+ \left(3k(k-1)x^{k-2} + 3bkx^{k-1}\right)\frac{d^{2}y}{dx^{2}} \notag \\ &\quad+ \left(3k(k-1)(k-2)x^{k-3} + 3bk(k-1)x^{k-2}\right)\frac{dy}{dx}+ bk(k-1)(k-2)x^{k-3}y. \end{aligned}\tag{3}\]
The resulting fourth-order singular equation is: \[\begin{aligned} \left\{ \begin{array}{ll} \frac{d^{4}y}{dx^{4}} + \left(b + \frac{3k}{x}\right)\frac{d^{3}y}{dx^{3}} + \left(\frac{3bk}{x} + \frac{3k(k-1)}{x^{2}}\right)\frac{d^{2}y}{dx^{2}} + \left(\frac{3bk(k-1)}{x^{2}} + \frac{k(k-1)(k-2)}{x^{3}}\right)\frac{dy}{dx} + \frac{bk(k-1)(k-2)}{x^{3}}y = R(x,y), & x > 0, \\ y(0) = \delta, \; y'(0) = y''(0) = y'''(0) = 0. \end{array} \right. \end{aligned}\tag{4}\]
The singular point at \(x = 0\) appears four times with shape factors: \(3k\), \((3bk, 3k(k-1))\), \((3bk(k-1), k(k-1)(k-2))\), and \(bk(k-1)(k-2)\), associated with powers of \(x\), \((x, x^2)\), \((x^2, x^3)\), and \(x^3\), respectively. For \(k=1\), the fourth and fifth terms vanish. Similarly, for \(k=2\), the fifth term disappears.
Setting \(m=1\), \(n=1\), \(\gamma=1\), \(\eta=0\), and \(j=2\) in Eq. (1), we derive: \[\label{eq3} x^{-k}\frac{d^{2}}{dx^{2}}x^{k}e^{-bx}\frac{d^{2}}{dx^{2}}e^{bx}y=R(x,y).\tag{5}\] After computing the derivatives, the second type of fourth-order singular equation becomes: \[\begin{aligned} \left\{ \begin{array}{ll} \frac{d^{4}y}{dx^{4}} + \left(2b + \frac{2k}{x}\right)\frac{d^{3}y}{dx^{3}} + \left(b^2 + \frac{4kb}{x} + \frac{k(k-1)}{x^{2}}\right)\frac{d^{2}y}{dx^{2}} + \left(\frac{2b^2k}{x} + \frac{2bk(k-1)}{x^{2}}\right)\frac{dy}{dx} + \frac{b^2k(k-1)}{x^{2}}y = R(x,y), & x > 0, \\ y(0) = \delta_0, \; y'(0) = \delta_1, \; y''(0) = y'''(0) = 0. \end{array} \right. \end{aligned}\tag{6}\]
Here, \(\delta_0\) and \(\delta_1\) may be non-zero. The singular point at \(x = 0\) manifests as \(x\), \((x, x^2)\), \((x^2, x^3)\), and \(x^2\), with associated shape factors: \(2k\), \((4bk, k(k-1))\), \((2b^2k, 2bk(k-1))\), and \(b^2k(k-1)\), respectively. For \(k=1\), the fifth term vanishes.
In this final case, we set \(m=1\), \(n=3\), \(\gamma=0\), \(\eta=1\), and \(j=1\) in Eq. (1) to obtain: \[x^{-k}\frac{d}{dx}x^{k}e^{-bx}\frac{d^{3}}{dx^{3}}e^{bx}y=R(x,y).\tag{7}\] Upon simplification, the third type of fourth-order singular equation is: \[\begin{aligned} \left\{ \begin{array}{ll} \frac{d^{4}y}{dx^{4}} + \left(\frac{k}{x} + 3b\right)\frac{d^{3}y}{dx^{3}} + \left(\frac{3bk}{x} + 3b^2\right)\frac{d^{2}y}{dx^{2}} + \left(\frac{3b^2k}{x} + b^3\right)\frac{dy}{dx} + \frac{b^3k}{x}y = R(x,y), & x > 0, \\ y(0) = \delta_0, \; y'(0) = \delta_1, \; y''(0) = \delta_2, \; y'''(0) = 0. \end{array} \right. \end{aligned}\tag{8}\]
Here, \(\delta_0\), \(\delta_1\), and \(\delta_2\) may be non-zero. The singular point at \(x = 0\) appears only once as \(x\), with associated shape factors: \(k\), \(3bk\), \(3b^2k\), and \(b^3k\).
We now generalize singular and nonsingular equations for higher orders based on the derived results. Starting from: \[x^{-(\gamma+\eta)k}\frac{d^{mj}}{dx^{mj}}x^{(\gamma+\eta)k}e^{-(\gamma+\eta)bx}\frac{d^{nj}}{dx^{nj}}e^{(\gamma+\eta)bx}y=R(x,y),\tag{9}\] we formulate the higher-order generalized singular and nonsingular equations as: \[\begin{aligned} \sum_{r=0}^{mj+nj-j} & \binom{mj+nj-j}{r} \frac{1}{(x^{\gamma k} e^{\eta bx})} \big(x^{\gamma k} e^{\eta bx}\big)^{(mj+nj-j-r)} \left[ y^{(r+j)} + (2j-2) \frac{\big(e^{\gamma bx}\big)^{(j-1)}}{e^{\gamma bx}} y^{(r+j-1)} + \frac{\big(x^{\eta k} e^{\gamma bx}\big)^{(j)}}{x^{\eta k} e^{\gamma bx}} y^{(r)} \right] \nonumber \\ & = R(x, y) \end{aligned}\tag{10}\] with boundary conditions:
\[\label{eq9} y(0) = \delta_0, y'(0) = \delta_1, \dots, y^{(nj-1)}(0) = \delta_{nj-1}, y^{(nj)}(0) = \dots = y^{(mj+nj-1)}(0) = 0.\tag{11}\] The singular point \(x = 0\) appears \(mj\) times as \(x\), \((x, x^2)\), \((x^2, x^3)\), …, \((x^{mj-1}, x^{mj})\), with corresponding shape factors.
We now prove Eq. (11) by mathematical induction under the specified conditions.
Theorem 1. Let \(n\), \(m\), and \(j\) be positive integers. The following identity holds: \[\begin{aligned} \label{eq10} x^{-(\gamma+\eta)k} \frac{d^{mj}}{dx^{mj}} \left( x^{(\gamma+\eta)k} e^{-(\gamma+\eta)bx} \frac{d^{nj}}{dx^{nj}} \left( e^{(\gamma+\eta)bx} y \right) \right) = \sum_{r=0}^{mj+nj-j} \binom{mj+nj-j}{r} \frac{1}{x^{\gamma k} e^{\eta bx}}\nonumber\\ \times \left( x^{\gamma k} e^{\eta bx} \right)^{(mj+nj-j-r)} \left[ y^{(r+j)} + (2j-2) \frac{(e^{\gamma bx})^{(j-1)}}{e^{\gamma bx}} y^{(r+j-1)} + \frac{(x^{\eta k} e^{\gamma bx})^{(j)}}{x^{\eta k} e^{\gamma bx}} y^{(r)} \right]. \end{aligned}\tag{12}\]
Proof. by Mathematical induction, prove that the equation in (12) is correct under the conditions
\(\gamma=1\) and \(\eta=0,\)
\(\gamma=0\) and \(\eta=1.\)
If
\(\gamma=1\) and \(\eta=0,\)
then
\[\begin{aligned} \label{eq11} x^{-k}\frac{d^{mj}}{dx^{mj}}x^{k}e^{-bx}\frac{d^{nj}}{dx^{nj}}e^{bx}y =&\sum_{r=0}^{mj+nj-j}{mj+nj-j\choose{r}}\frac{1}{x^{ k}} (x^{ k} )^{(mj+nj-j-r)}\notag\\ &\times \left[ y^{(r+j)}+(2j-2)\frac{(e^{ bx})^{(j-1)}}{e^{ bx}} y^{(r+j-1)} +\frac{(e^{ bx})^{(j)}}{e^{ bx}}y^{(r)} \right]. \end{aligned}\tag{13}\] When \(m=3,\) \(j=1,\) in Eq. (13) get \[x^{-k} \frac{d^{3}}{dx^{3}} x^{k} e^{-bx} \frac{d^{n}}{dx^{n}} e^{bx}y =\sum_{r=0}^{n+2}{n+2\choose{r}}\frac{1}{x^{k}}(x^{k})^{(n+2-r)} \left[ y^{(r+1)}+\frac{(e^{bx})^{'}}{e^{bx}}y^{(r)} \right].\] Lift hand side is, \[\begin{aligned} x^{-k} \frac{d^{3}}{dx^{3}} x^{k} e^{-bx} \frac{d^{n}}{dx^{n}} e^{bx}y &= x^{-k} \frac{d^{3}}{dx^{3}} x^{k} e^{-bx}\bigg((e^{bx})^{(n)}y + \frac{n!}{(n-1)!}(e^{bx})^{(n-1)}y' \\ &\quad + \frac{n!}{2!(n-2)!}(e^{bx})^{(n-2)}y'' + \frac{n!}{3!(n-3)!}(e^{bx})^{(n-3)}y''' + \frac{n!}{4!(n-4)!}(e^{bx})^{(n-4)}y'''' + \dots\bigg) \\ &= x^{-k} \frac{d^{3}}{dx^{3}} \bigg(x^{k}\bigg(b^{n}y + nb^{n-1}y' + \frac{n(n-1)}{2!}b^{n-2}y'' \\ &\quad + \frac{n(n-1)(n-2)}{3!}b^{n-3}y''' + \frac{n(n-1)(n-2)(n-3)}{4!}y'''' + \dots\bigg)\bigg) \\ &= x^{-k} \sum_{r=0}^{3} \binom{3}{r} (x^{k})^{(3-r)} \bigg(b^{n}y + nb^{n-1}y' + \frac{n(n-1)}{2!}b^{n-2}y'' \\ &\quad + \frac{n(n-1)(n-2)}{3!}b^{n-3}y''' + \frac{n(n-1)(n-2)(n-3)}{4!}y'''' + \dots\bigg)^{(r)} \\ &= \frac{b^{n}k(k-1)(k-2)}{x^{3}} y + \bigg(\frac{nb^{n-1}k(k-1)(k-2)}{x^{3}} + \frac{3b^{n}k(k-1)}{x^{2}}\bigg)y' \\ &\quad + \bigg(\frac{3nb^{n-1}k(k-1)}{x^{2}} + \frac{3b^{n}k}{x}\bigg)y'' + \bigg(\frac{3nb^{n-1}k}{x} + b^{n}\bigg)y''' + \dots \end{aligned}\] Right hand side is, \[\begin{aligned} &\sum_{r=0}^{n+2} {n+2 \choose r} \frac{1}{x^k} (x^k)^{(2+n-r)} \Bigg[ y^{(r+1)} + \frac{(e^{bx})'}{e^{bx}} y^{(r)} \Bigg] \nonumber \\ &= {n+2 \choose 0} \frac{1}{x^k} (x^k)^{(2+n)} \big[y' + by\big] + {n+2 \choose 1} \frac{1}{x^k} (x^k)^{(1+n)} \big[y'' + by'\big] \nonumber \\ &\quad + {n+2 \choose 2} \frac{1}{x^k} (x^k)^{(n)} \big[y''' + by''\big] + {n+2 \choose 3} \frac{1}{x^k} (x^k)^{(n-1)} \big[y'''' + by'''\big] + \dots \nonumber \\ &= \frac{bk(k-1)\cdots(k-2-n+1)}{x^{2+n}} y \nonumber \\ &\quad + \left(\frac{k(k-1)\cdots(k-2-n+1)}{x^{2+n}} + \frac{b(2+n)k(k-1)\cdots(k-n)}{x^{n+1}}\right) y' \nonumber \\ &\quad + \left(\frac{(2+n)k(k-1)\cdots(k-n)}{x^{n+1}} + \frac{b(n+2)(n+1)k(k-1)\cdots(k-n+1)}{2!x^n}\right) y'' \nonumber \\ &\quad + \left(\frac{(n+2)(n+1)k(k-1)\cdots(k-n+1)}{2!x^n} + \frac{bn(n+2)(n+1)k(k-1)\cdots(k-n+2)}{3!x^{n-1}}\right) y''' + \dots \end{aligned}\tag{14}\] then the statement holds for \(m=3,\) \(j=1,\) \(n=1\).
Consider that Eq. (13) is hold for \(mj=p,\) that is \[\begin{aligned} x^{-k}\frac{d^{p}}{dx^{p}}x^{k}e^{-bx}\frac{d^{nj}}{dx^{nj}}e^{bx}y &= \sum_{r=0}^{p+nj-j} {p+nj-j \choose r} \frac{1}{x^{k}} (x^{k})^{(p+nj-j-r)} \nonumber \\ &\quad \times \left[ y^{(r+j)} + (2j-2) \frac{(e^{bx})^{(j-1)}}{e^{bx}} y^{(r+j-1)} + \frac{(e^{bx})^{(j)}}{e^{bx}} y^{(r)} \right]. \end{aligned}\tag{15}\]
Assume that the statement holds for \(mj=p+1,\) we use direct proof as \[\begin{aligned} x^{-k} \frac{d^{(p+1)}}{dx^{(p+1)}} x^{k} e^{-bx} \frac{d^{nj}}{dx^{nj}} e^{bx} y =& \sum_{r=0}^{p+1+nj-j} \binom{p+1+nj-j}{r} \frac{1}{x^{k}} \left( x^{k} \right)^{(p+1+nj-j-r)} \notag \\ & \times \left[ y^{(r+j)} + (2j-2) \frac{(e^{bx})^{(j-1)}}{e^{bx}} y^{(r+j-1)} \right. \left. + \frac{(e^{bx})^{(j)}}{e^{bx}} y^{(r)} \right]. \notag \end{aligned}\] Let \[\begin{aligned} x^{-k} \frac{d^{(p+1)}}{dx^{(p+1)}} \left( x^{k} e^{-bx} \frac{d^{(nj)}}{dx^{(nj)}} e^{bx} y \right) &= x^{-k} \frac{d^{p}}{dx^{p}} \left[ \frac{d}{dx} \left( x^{k} e^{bx} \frac{d^{(nj)}}{dx^{(nj)}} e^{bx} y \right) \right], \end{aligned}\] then \[\begin{aligned} &x^{-k} \frac{d^{p}}{dx^{p}} \bigg[x^{k} e^{-bx} \bigg( \frac{d^{(nj+1)}}{dx^{(nj+1)}} e^{bx} y \bigg) + \bigg(kx^{k-1}e^{-bx} – bx^{k} e^{-bx}\bigg) \frac{d^{nj}}{dx^{nj}} e^{bx} y \bigg] \\ &= x^{-k} \frac{d^{p}}{dx^{p}} x^{k} e^{-bx} \frac{d^{(nj)}}{dx^{(nj)}} e^{bx} y' + b x^{-k} \frac{d^{p}}{dx^{p}} x^{k} e^{-bx} \frac{d^{(nj)}}{dx^{(nj)}} e^{bx} y \\ &\quad + x^{-k} \frac{d^{p}}{dx^{p}} kx^{k-1} e^{-bx} \frac{d^{nj}}{dx^{nj}} e^{bx} y – b x^{-k} \frac{d^{p}}{dx^{p}} x^{k} e^{-bx} \frac{d^{(nj)}}{dx^{(nj)}} e^{bx} y \\ &= \sum_{r=0}^{p+nj-j} \binom{p+nj-j}{r} \frac{(x^{k})^{(p+nj-j-r)}}{x^{k}} \bigg[ y^{(r+1+j)} + (2j-2) \frac{(e^{bx})^{(j-1)}}{e^{bx}} y^{(r+j)} + \frac{(e^{bx})^{(j)}}{e^{bx}} y^{(r+1)} \bigg] \\ &\quad + \sum_{r=0}^{p+nj-j} \binom{p+nj-j}{r} \frac{(x^{k})^{(p+nj-j-r+1)}}{x^{k}} \bigg[ y^{(r+j)} + (2j-2) \frac{(e^{bx})^{(j-1)}}{e^{bx}} y^{(r+j-1)} + \frac{(e^{bx})^{(j)}}{e^{bx}} y^{(r)} \bigg] \\ &= \sum_{r=1}^{p+nj-j} \binom{p+nj-j}{r-1} \frac{(x^{k})^{(p+nj-j-r+1)}}{x^{k}} \bigg[ y^{(r+j)} + (2j-2) \frac{(e^{bx})^{(j-1)}}{e^{bx}} y^{(r+j-1)} \\ &\quad + \frac{(e^{bx})^{(j)}}{e^{bx}} y^{(r)} \bigg] + \sum_{r=1}^{p+nj-j} \binom{p+nj-j}{r} \frac{(x^{k})^{(p+nj-j-r+1)}}{x^{k}} \bigg[ y^{(r+j)} + (2j-2) \frac{(e^{bx})^{(j-1)}}{e^{bx}} y^{(r+j-1)} \\ &\quad + \frac{(e^{bx})^{(j)}}{e^{bx}} y^{(r)} \bigg] + \binom{p+nj-j}{0} \frac{1}{x^{k}} (x^{k})^{(p+nj-j+1)} \bigg[ y^{(j)} + (2j-2) \frac{(e^{bx})^{(j-1)}}{e^{bx}} y^{(j-1)} + \frac{(e^{bx})^{(j)}}{e^{bx}} y \bigg] \\ &= \sum_{r=0}^{p+1+nj-j} \binom{p+1+nj-j}{r} \frac{(x^{k})^{(p+1+nj-j-r)}}{x^{k}} \bigg[ y^{(r+j)} + (2j-2) \frac{(e^{bx})^{(j-1)}}{e^{bx}} y^{(r+j-1)} + \frac{(e^{bx})^{(j)}}{e^{bx}} y^{(r)} \bigg], \end{aligned}\] therefore \[\begin{aligned} x^{-k}\frac{d^{p}}{dx^{p}}x^{k}e^{-bx}\frac{d^{nj}}{dx^{nj}}e^{bx}y =& \sum_{r=0}^{p+nj-j} \binom{p+nj-j}{r} \frac{1}{x^k}(x^{k})^{(p+nj-j-r)} \notag \\ &\times \left[ y^{(r+j)} + (2j-2)\frac{(e^{bx})^{(j-1)}}{e^{bx}} y^{(r+j-1)} + \frac{(e^{bx})^{(j)}}{e^{bx}}y^{(r)} \right]. \end{aligned}\tag{16}\] If
\(\gamma=0\) and \(\eta=1.\)
then \[\begin{aligned} \label{eq12} x^{-k} \frac{d^{mj}}{dx^{mj}} \left( x^{k} e^{-bx} \frac{d^{nj}}{dx^{nj}} \left( e^{bx} y \right) \right) =& \sum_{r=0}^{mj+nj-j} \binom{mj+nj-j}{r} \frac{1}{e^{bx}} \left( e^{bx} \right)^{(mj+nj-j-r)}\nonumber\\ &\times\left[ y^{(r+j)}+(2j-2) y^{(r+j-1)} +\frac{(x^{ k})^{(j)}}{x^{ k}}y^{(r)} \right]. \end{aligned}\tag{17}\]
We prove a relationship in Eq. (17) is true for \(n=3,\) \(j=1,\) that is \[x^{-k} \frac{d^{m}}{dx^{m}} x^{k} e^{-bx} \frac{d^{3}}{dx^{3}} e^{bx}y =\sum_{r=0}^{m+2}{m+2\choose{r}}\frac{1}{e^{bx}}(e^{bx})^{(m+2-r)} \left[ y^{(r+1)}+\frac{(x^{k})^{'}}{x^{k}}y^{(r)} \right].\] Left hand side is, \[\begin{aligned} x^{-k} \frac{d^{m}}{dx^{m}} & x^{k} e^{bx} \frac{d^{3}}{dx^{3}} e^{bx} y = x^{-k} \frac{d^{m}}{dx^{m}} \left[ x^{k} \left( y''' + 3by'' + 3b^{2}y' + b^{3}y \right) \right], \\ &= x^{-k} \sum_{r=0}^{m} \binom{m}{r} (x^{k})^{(m-r)} \left( y''' + 3by'' + 3b^{2}y' + b^{3}y \right)^{(r)}, \\ &= x^{-k} \Big[ (x^{k})^{(m)} \left( y''' + 3by'' + 3b^{2}y' + b^{3}y \right) + m (x^{k})^{(m-1)} \left( y'''' + 3by''' + 3b^{2}y'' + b^{3}y' \right) \nonumber \\ &\quad + \frac{m(m-1)}{2!} (x^{k})^{(m-2)} \left( y''''' + 3by'''' + 3b^{2}y''' + b^{3}y'' \right) + \dots \Big], \\ &= x^{-k} \Big[ k(k-1)\cdots(k-m+1)x^{k-m} \left( y''' + 3by'' + 3b^{2}y' + b^{3}y \right) \nonumber \\ &\quad + m k(k-1)\cdots(k-m+2)x^{k-m+1} \left( y'''' + 3by''' + 3b^{2}y'' + b^{3}y' \right) \nonumber \\ &\quad + \frac{m(m-1)}{2!} k(k-1)\cdots(k-m+3)x^{k-m+2} \left( y''''' + 3by'''' + 3b^{2}y''' + b^{3}y'' \right) + \dots \Big], \\ &= \frac{b^{3}k(k-1)\cdots(k-m+1)}{x^{m}}y + \left( \frac{3b^{2}k(k-1)\cdots(k-m+1)}{x^{m}} + \frac{mb^{3}k(k-1)\cdots(k-m+2)}{x^{m-1}} \right)y' \nonumber \\ &\quad + \left( \frac{3bk(k-1)\cdots(k-m+1)}{x^{m}} + \frac{3b^{2}k(k-1)\cdots(k-m+2)}{x^{m-1}} \right)y'' \nonumber \\ &\quad + \left( \frac{k(k-1)\cdots(k-m+1)}{x^{m}} + \frac{3bk(k-1)\cdots(k-m+2)}{x^{m-1}} \right)y''' + \dots. \end{aligned}\] Right hand side is, \[\begin{aligned} \sum_{r=0}^{m+2} & {m+2 \choose r} \frac{1}{e^{bx}} (e^{bx})^{(m+2-r)} \left[ y^{(r+1)} + \frac{(x^k)'}{x^k} y^{(r)} \right] = b^{(m+2)} \left(y' + \frac{k}{x} y \right) \nonumber \\ & + (m+2) b^{(m+1)} \left(y'' + \frac{k}{x} y' \right) + \frac{(m+2)(m+1)}{2!} b^{(m)} \left(y''' + \frac{k}{x} y'' \right) \nonumber \\ & + \frac{(m+2)(m+1)m}{3!} b^{(m-1)} \left(y'''' + \frac{k}{x} y''' \right) + \dots, \nonumber \\ = & \, b^{(m+2)} \frac{k}{x} y + \left(b^{(m+2)} + (m+2) b^{(m+1)} \frac{k}{x} \right) y' \nonumber \\ & + \left((m+2) b^{(m+1)} + \frac{(m+2)(m+1)}{2!} b^{(m)} \frac{k}{x} \right) y'' \nonumber \\ & + \left(\frac{(m+2)(m+1)}{2!} b^{(m)} + \frac{(m+2)(m+1)m}{3!} b^{(m-1)} \frac{k}{x} \right) y''' \nonumber \\ & + \frac{(m+2)(m+1)m}{3!} b^{(m-1)} y'''' + \dots. \end{aligned}\tag{18}\] We note that Left hand side=Right hand side for \(n=3,\) \(m=1,\) \(j=1.\)
Now we must prove the following formula \[\begin{aligned} x^{-k} \frac{d^{mj}}{dx^{mj}} x^{k} e^{-bx} \frac{d^{(p+1)}}{dx^{(p+1)}}e^{bx}y =& \sum_{r=0}^{mj+p+1-j} {mj+p+1-j \choose r} \frac{1}{e^{bx}} \left( e^{ bx} \right)^{(mj+p+1-j-r)} \\ &\times\left[ y^{(r+j)} + (2j-2) y^{(r+j-1)} + \frac{(x^{ k})^{(j)}}{x^{ k}} y^{(r)} \right]. \end{aligned}\] Suppose that \[\begin{aligned} x^{-k} \frac{d^{mj}}{dx^{mj}} x^{k} e^{-bx} \frac{d^{p}}{dx^{p}} e^{bx} y =& \sum_{r=0}^{mj+p-j} {mj+p-j \choose r} \frac{1}{e^{bx}} \left( e^{ bx} \right)^{(mj+p-j-r)} \\ &\times \left[ y^{(r+j)} + (2j-2) y^{(r+j-1)} + \frac{(x^{ k})^{(j)}}{x^{ k}} y^{(r)} \right]. \end{aligned}\] Then \[\begin{aligned} x^{-k} \frac{d^{mj}}{dx^{mj}}& x^{k} e^{-bx} \frac{d^{(p+1)}}{dx^{(p+1)}}e^{bx} y = x^{-k} \frac{d^{mj}}{dx^{mj}} x^{k} e^{-bx} \frac{d^{p}}{dx^{p}}(e^{bx}y' + (e^{(bx)})' y), \\ &= x^{-k} \frac{d^{mj}}{dx^{mj}} x^{k} e^{-bx} \frac{d^{p}}{dx^{p}} e^{bx} y' + x^{-k} \frac{d^{mj}}{dx^{mj}} x^{k} e^{-bx} \frac{d^{p}}{dx^{p}} (e^{bx})' y, \\ &= \sum_{r=0}^{mj+p-j}{mj+p-j \choose r} \frac{1}{e^{bx}} (e^{bx})^{(mj+p-j-r)} \left[ y^{(r+j+1)} + (2j-2) y^{(r+j)} + \frac{(x^k)^{(j)}}{x^k} y^{(r+1)} \right] \\ &+ \sum_{r=0}^{mj+p-j}{mj+p-j \choose r} \frac{1}{e^{bx}} (e^{bx})^{(mj+p-j-r+1)} \left[ y^{(r+j)} + (2j-2) y^{(r+j-1)} + \frac{(x^k)^{(j)}}{x^k} y^{(r)} \right], \\ &= \sum_{r=1}^{mj+p-j}{mj+p-j \choose r-1} \frac{1}{e^{bx}} (e^{bx})^{(mj+p-j-r+1)} \left[ y^{(r+j)} + (2j-2) y^{(r+j-1)} + \frac{(x^k)^{(j)}}{x^k} y^{(r)} \right] \\ &+ \sum_{r=1}^{mj+p-j}{mj+p-j \choose r} \frac{1}{e^{bx}} (e^{bx})^{(mj+p-j-r+1)} \left[ y^{(r+j)} + (2j-2) y^{(r+j-1)} + \frac{(x^k)^{(j)}}{x^k} y^{(r)} \right], \\ &+ {mj+p-j \choose 0} \frac{1}{e^{bx}} (e^{bx})^{(mj+p-j+1)} \left[ y^{(j)} + (2j-2) y^{(j-1)} + \frac{(x^k)^{(j)}}{x^k} y \right], \\ &= \sum_{r=1}^{mj+p-j} \left[ {mj+p-j \choose r-1} + {mj+p-j \choose r} \right] \frac{(e^{bx})^{(mj+p-j-r+1)}}{e^{bx}} \\ &\quad \times \left[ y^{(r+j)} + (2j-2) y^{(r+j-1)} + \frac{(x^k)^{(j)}}{x^k} y^{(r)} \right] \\ &+ {mj+p-j \choose 0} \frac{1}{e^{bx}} (e^{bx})^{(mj+p-j+1)} \left[ y^{(j)} + (2j-2) y^{(j-1)} + \frac{(x^k)^{(j)}}{x^k} y \right], \\ &= \sum_{r=0}^{mj+p+1-j}{mj+p+1-j \choose r} \frac{(e^{bx})^{(mj+p+1-j-r)}}{e^{bx}} \left[ y^{(r+j)} + (2j-2) y^{(r+j-1)} + \frac{(x^k)^{(j)}}{x^k} y^{(r)} \right]. \end{aligned}\] Therefore \[\begin{aligned} x^{-k} \frac{d^{mj}}{dx^{mj}} x^{k} e^{-bx} \frac{d^{p}}{dx^{p}} e^{bx} y &= \sum_{r=0}^{mj+p-j} \binom{mj+p-j}{r} \frac{1}{e^{bx}} \left( e^{bx} \right)^{(mj+p-j-r)} \left[ y^{(r+j)} + (2j-2) y^{(r+j-1)} + \frac{(x^{k})^{(j)}}{x^{k}} y^{(r)} \right]. \end{aligned}\] ◻
We will analyze the singular-type equations using the Adomian Decomposition Method (ADM) [21,22], as previously mentioned. This approach is now well-established and widely used in the literature, as evidenced by works such as [23,24].
The ADM allows for the use of an infinite decomposition series, given by:
\[y(x) = \sum_{n=0}^{\infty} y_n(x),\tag{19}\] where the solution \(y(x)\) is expressed as an infinite series. The function \(R(x, y)\) is similarly expanded as: \[R(x, y) = \sum_{n=0}^{\infty} A_n,\tag{20}\] where the components \(y_n(x)\) of the solution \(y(x)\) are determined recursively. The terms \(A_n\) are the Adomian polynomials, defined by:
\[A_n = \frac{1}{n!} \frac{d^n}{d\lambda^n} \left[ R\left( \sum_{i=0}^{\infty} \lambda^i v_i \right) \right]_{\lambda = 0}, \quad n = 0, 1, 2, \dots.\tag{21}\] Practical algorithms for computing the Adomian polynomials are given by the following expressions: \[\begin{aligned} A_0 &= R(y_0), \\ A_1 &= y_1 R'(y_0), \\ A_2 &= y_2 R'(y_0) + \frac{1}{2!} y_1^2 R''(y_0), \\ A_3 &= y_3 R'(y_0) + y_1 y_2 R''(y_0) + \frac{1}{3!} y_1^3 R'''(y_0), \\ \vdots . \end{aligned}\]
Consider the fourth-order singular equation of the first kind:
\[\begin{aligned} \label{eq16} \left\{ \begin{array}{ll} \frac{d^{4}y}{dx^{4}} + \left( b + \frac{3k}{x} \right) \frac{d^{3}y}{dx^{3}} + \left( \frac{3bk}{x} + \frac{3k(k-1)}{x^2} \right) \frac{d^{2}y}{dx^{2}} + \left( \frac{3bk(k-1)}{x^2} + \frac{k(k-1)(k-2)}{x^3} \right) \frac{dy}{dx} + \frac{bk(k-1)(k-2)}{x^3} y = R(x, y), \quad x > 0, \\ y(0) = \delta, \, y'(0) = y''(0) = y'''(0) = 0. \end{array} \right. \end{aligned}\tag{22}\] This can be expressed in operator form as:
\[\label{eq17} L y = R(x, y),\tag{23}\] where \(L\) is the differential operator defined by:
\[\label{eq18} L y = x^{-k} \frac{d^3}{dx^3} \left( x^k e^{-bx} \frac{d}{dx} e^{bx} y \right),\tag{24}\] and its inverse is given by:
\[\label{eq19} L^{-1}(.) = e^{-bx} \int_0^x e^{bx} x^{-k} \int_0^x \int_0^x \int_0^x x^k (.) \, dx \, dx \, dx \, dx.\tag{25}\] If \(y'(0) = y''(0) = y'''(0) = 0\) and \(k \geq 0\), \(b > 0\), we have the following expression for the inverse operator applied to \(L y\):
\[\begin{aligned} L^{-1}(L y) &= e^{-bx} \int_0^x e^{bx} x^{-k} \int_0^x \int_0^x \int_0^x x^k \left( x^{-k} \frac{d^3}{dx^3} \left( x^k e^{-bx} \left( \frac{d}{dx} e^{bx} y \right) \right) \right) dx \, dx \, dx \, dx, \\ &= e^{-bx} \int_0^x e^{bx} x^{-k} \int_0^x \int_0^x \frac{d^2}{dx^2} \left( x^k e^{-bx} \left( \frac{d}{dx} e^{bx} y \right) \right) dx \, dx \, dx, \\ &= e^{-bx} \int_0^x e^{bx} x^{-k} \int_0^x \frac{d}{dx} \left( x^k e^{-bx} \left( \frac{d}{dx} e^{bx} y \right) \right) dx \, dx, \\ &= y(x) – y(0) e^{-bx}. \end{aligned}\] By applying \(L^{-1}\) to Eq. (23), we obtain:
\[\label{eq20} y(x) = \phi(x) + L^{-1}(R(x, y)),\tag{26}\] where \(\phi(x)\) is the solution of the homogeneous equation, i.e., \(L(\phi(x)) = 0\). The series solution for \(y(x)\) is then given by:
\[y_0 = \phi(x),\] \[y_n(x) = -L^{-1}(R(x, y)), \quad n \geq 0.\] From this formulation, we obtain the new fourth-order singular and nonsingular differential equation.
Put \(b=\frac{1}{4}\), \(k =4\) in Eq. (22) to get, \[\begin{aligned} \label{eq21}\left\{ \begin{array}{ll} y^{(4)}+ \left(\frac{1}{4}+\frac{12}{x}\right) y^{(3)}+\left(\frac{3}{x}+\frac{36}{x^2}\right)y^{(2)}+\left(\frac{24}{x^3}+\frac{9}{x^2}\right)y'+\frac{6}{x^3}y =R(x,y), \\ R(x,y)=\frac{3\,\left( 8 – 80\,x + 16\,x^2 + 60\,x^3 + 15\,x^4 + 9\,x^6 + 2\,x^8 \right) }{4\,x^3\, {\left( 1 + x^2 \right) }^{\frac{9}{2}}}+\frac{1}{{1 + x^2}}-y^2 ,& x > 0, \\ y(0)=1,y'(0)=0,y''(0)=-1,y'''(0)=0. \end{array}\right. \end{aligned}\tag{27}\] Using the exact solution of Eq. (27) is \(y(x)=\frac{1}{{\sqrt{1 + x^2}}}.\) Formula (27) can be rewrite as \[\label{eq22} Ly=e^{-\frac{1}{4}x} +\frac{3\,\left( 8 – 80\,x + 16\,x^2 + 60\,x^3 + 15\,x^4 + 9\,x^6 + 2\,x^8 \right) }{4\,x^3\, {\left( 1 + x^2 \right) }^{\frac{9}{2}}}+\frac{1}{{1 + x^2}}-y^2,\tag{28}\] such that \[L(.)=x^{-4}\frac{d^{3}}{dx^{3}}x^{4}e^{\frac{-x}{4}}\frac{d}{dx}e^{\frac{x}{4}}(.),\] and \[L^{-1}(.)=e^{\frac{-x}{4}} \int_{0}^{x}e^{\frac{x}{4}}x^{-4}\int_{0}^{x}\int_{0}^{x}\int_{0}^{x}x^{4}(.)dxdxdxdx.\] Now, applying \(L^{-1}\) on Eq. (28) we find \[y(x)=e^{-\frac{1}{4}x}+L^{-1}\left(\frac{3\,\left( 8 – 80\,x + 16\,x^2 + 60\,x^3 + 15\,x^4 + 9\,x^6 + 2\,x^8 \right) }{4\,x^3\,{\left( 1 + x^2 \right) }^{\frac{9}{2}}}+\frac{1}{{1 + x^2}}\right)-L^{-1}y^2.\] We use the recursive relation \[\begin{aligned} y_0 &=e^{-\frac{1}{4}x}+L^{-1}\left(\frac{3\,\left( 8 – 80\,x + 16\,x^2 + 60\,x^3 + 15\,x^4 + 9\,x^6 + 2\,x^8 \right) }{4\,x^3\,{\left( 1 + x^2 \right) }^{\frac{9}{2}}}+\frac{1}{{1 + x^2}}\right),\\ y_{n+1} &= L^{-1}A_n, n \ge 0, \end{aligned}\] where the non-linear term \(y^2\) is Adomian polynomials as the following \[A_0 = y^{2}_0,\] \[A_1 = 2y_0y_1,\] so the solution components are \[\begin{aligned} y_0 &= 1. – 0.5\,x^2 + 0.37619\,x^4 – 0.0000595238\,x^5 – 0.312828\,x^6 + 0.0000117217\,x^7 \\ &\quad + 0.273563\,x^8 – 3.49712 \times 10^{-6}\,x^9 – 0.246152\,x^{10}, \\ y_1 &= -0.00119048\,x^4 + 0.0000595238\,x^5 + 0.000328208\,x^6 – 0.0000117217\,x^7 \\ &\quad – 0.000126197\,x^8 + 3.51549 \times 10^{-6}\,x^9 + 0.0000582948\,x^{10}, \\ y_2 &= 3.00625 \times 10^{-7}\,x^8 – 1.83715 \times 10^{-8}\,x^9 – 1.07168 \times 10^{-7}\,x^{10}. \end{aligned}\] Consequently, the series solution is obtained. \[y=1. – 0.5\,x^2 + 0.375\,x^4 – 0.3125\,x^6 + 0.273438\,x^8 – 0.246094\,x^{10}+…,\] that leads to the exact solution \(y(x)=\frac{1}{{\sqrt{1 + x^2}}}\).
Put \(b= k =1\) in Eq. (22) to get, \[\begin{aligned} \label{eq23} \left\{ \begin{array}{ll} y^{(4)}+(1+\frac{3}{x})y^{(3)}+\frac{3}{x}y^{(2)} =R(x,y), R(x,y)=e^{3\,x}\,{\left( 1 – x \right) }^3 – \frac{e^x\,\left( 9 + 11\,x + 2\,x^2 \right) } {x} – y^3, & x > 0, \\ y(0)=1, y'(0)=0, y''(0)=-1, y'''(0)=-2. \end{array}\right. \end{aligned}\tag{29}\] The exact solution of Eq. (29) has the form \(y(x)=e^{x}\,{\left( 1 – x \right) .}\) We can rewrite Eq. (29) as below \[\label{eq24} Ly=e^{3\,x}\,{\left( 1 – x \right) }^3 – \frac{e^x\,\left( 9 + 11\,x + 2\,x^2 \right) } {x} – y^3,\tag{30}\] such that \(L(.)=x^{-1}\frac{d^{3}}{dx^{3}}xe^{-x}\frac{d}{dx}e^{x}(.),\) and \(L^{-1}(.)=e^{-x} \int_{0}^{x}e^{x}x^{-1}\int_{0}^{x}\int_{0}^{x}\int_{0}^{x}x(.)dxdxdxdx,\) by applying inverse differential operator to ((30)) get \[\begin{aligned} y(x) &= -\left( \frac{1 – e^x\,\left( 2 – x \right) } {e^x} \right) + L^{-1}\left(e^{3\,x}\,{\left( 1 – x \right) }^3 – \frac{e^x\,\left( 9 + 11\,x + 2\,x^2 \right) } {x}\right) – L^{-1} y^3, \\ y_0 &= -\left( \frac{1 – e^x\,\left( 2 – x \right) } {e^x} \right) + L^{-1}\left(e^{3\,x}\,{\left( 1 – x \right) }^3 – \frac{e^x\,\left( 9 + 11\,x + 2\,x^2 \right) } {x}\right), \\ y_{n+1} &= -L^{-1}A_n. \end{aligned}\] After the little of the operation we obtain the first few components of the solution \[\begin{aligned} y_{0} &= 1. – 0.5\,x^2 – 0.333333\,x^3 – 0.125\,x^4 – 0.0333333\,x^5 – 0.00694444\,x^6 \\ &\quad – 0.00119048\,x^7 – 0.000173611\,x^8 – 0.0000220459\,x^9 – 2.48016\,{10}^{-6}\,x^{10}, \\ y_{1} &= -0.0104167\,x^4 + 0.00208333\,x^5 + 0.00173611\,x^6 + 0.000432256\,x^7 \\ &\quad – 0.000193541\,x^8 – 0.000176908\,x^9 – 0.0000604342\,x^{10}, \\ y_{2} &= 0.0000116257\,x^8 – 2.66962\,{10}^{-6}\,x^9 – 2.62656\,{10}^{-6}\,x^{10}, \\ \vdots \\ y(x) &= y_{0} + y_{1} + y_{2} \\ &= 1. – 0.5\,x^2 – 0.333333\,x^3 – 0.135417\,x^4 – 0.03125\,x^5 \\ &\quad – 0.00520833\,x^6 – 0.00075822\,x^7 – 0.000355526\,x^8 \\ &\quad – 0.000201624\,x^9 – 0.0000655409\,x^{10} + \cdots \end{aligned}\]
| \(k = B = 1\) | \(k = 2, B = 0.5\) | |||||
|---|---|---|---|---|---|---|
| \(x\) | Exact | MADM | Error | Exact | MADM | Error |
| 0.0 | 1.00000 | 1.00000 | 0.000000 | 1.00000 | 1.00000 | 0.00000 |
| 0.1 | 0.9946538 | 0.9946538 | \(1.11 \times 10^{-16}\) | 0.9946538 | 0.9946538 | \(1.11 \times 10^{-16}\) |
| 0.2 | 0.9771222 | 0.9771222 | \(5.11 \times 10^{-15}\) | 0.9771222 | 0.9771222 | \(1.71 \times 10^{-13}\) |
| 0.3 | 0.9449011 | 0.9449011 | \(4.56 \times 10^{-13}\) | 0.9449011 | 0.9449011 | \(1.00 \times 10^{-11}\) |
| 0.4 | 0.8950948 | 0.8950948 | \(1.09 \times 10^{-11}\) | 0.8950948 | 0.8950948 | \(1.81 \times 10^{-10}\) |
| 0.5 | 0.8243606 | 0.8243606 | \(1.28 \times 10^{-10}\) | 0.8243606 | 0.8243606 | \(1.71 \times 10^{-9}\) |
| 0.6 | 0.7288475 | 0.7288475 | \(9.62 \times 10^{-10}\) | 0.7288475 | 0.7288475 | \(1.08 \times 10^{-8}\) |
| 0.7 | 0.6041258 | 0.6041258 | \(5.29 \times 10^{-9}\) | 0.6041258 | 0.6041258 | \(5.11 \times 10^{-8}\) |
| 0.8 | 0.4451081 | 0.4451082 | \(2.32 \times 10^{-8}\) | 0.4451081 | 0.4451083 | \(1.98 \times 10^{-7}\) |
| 0.9 | 0.2459603 | 0.2459603 | \(8.56 \times 10^{-8}\) | 0.2459603 | 0.2459603 | \(6.52 \times 10^{-7}\) |
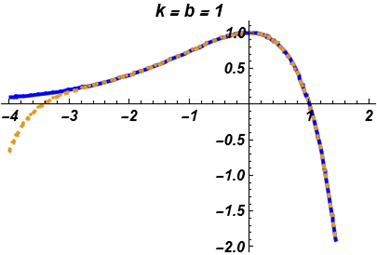
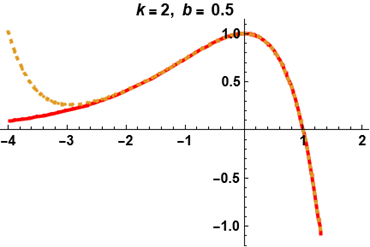
Put \(b=1\) \(K=0\) in Eq. (22) to get, \[\begin{aligned} \label{eq25} \left\{ \begin{array}{ll} y^{(4)}+y^{(3)} =R(x,y), \\ $$ R(x,y)=\left(\frac{1}{1 – x^2} + \frac{9 + 9\,x + 72\,x^2 – 3\,x^3 + 24\,x^4 – 6\,x^5}{{\left( 1 – x^2 \right) }^{\frac{9}{2}}}\right)-y^{2},$$ & x > 0, \\ y(0)=1, y'(0)=0, y''(0)=-1, y'''(0)=0, \end{array}\right. \end{aligned}\tag{31}\] with exact solution \[y(x)=\frac{1}{{\sqrt{1 – x^2}}} .\] \[\label{eq26} Ly=\left(\frac{1}{1 – x^2} + \frac{9 + 9\,x + 72\,x^2 – 3\,x^3 + 24\,x^4 – 6\,x^5}{{\left( 1 – x^2 \right) }^{\frac{9}{2}}}\right)-y^{2},\tag{32}\] where \(L(.)=\frac{d^{3}}{dx^{3}}e^{-x}\frac{d}{dx}e^{x}(.),\) and \(L^{-1}(.)=e^{-x} \int_{0}^{x}e^{x}\int_{0}^{x}\int_{0}^{x}\int_{0}^{x}(.)dxdxdxdx.\) By taking \(L^{-1}\) on Eq. (32) obtain \[y(x)=\frac{2 + x^2}{2}+L^{-1}\left(\frac{1}{1 – x^2} + \frac{9 + 9\,x + 72\,x^2 – 3\,x^3 + 24\,x^4 – 6\,x^5}{{\left( 1 – x^2 \right) }^{\frac{9}{2}}}\right)-L^{-1}y^{2},\] where \[y_{0}=\frac{2 + x^2}{2}+L^{-1}\left(\frac{1}{1 – x^2} + \frac{9 + 9\,x + 72\,x^2 – 3\,x^3 + 24\,x^4 – 6\,x^5}{{\left( 1 – x^2 \right) }^{\frac{9}{2}}}\right),\] \[y_{n+1}=-L^{-1}A_n,\] therefore the first few components of the solution \[\begin{aligned} y_{0} &= 1 + 0.5\,x^2 + 0.416667\,x^4 – 0.00833333\,x^5 + 0.316667\,x^6 – 0.000595238\,x^7 + 0.274107\,x^8 \nonumber \\ &\quad – 0.0000744048\,x^9 + 0.2463\,x^{10} + \cdots, \\ y_{1} &= -0.0416667\,x^4 + 0.00833333\,x^5 – 0.00416667\,x^6 + 0.000595238\,x^7 – 0.000719246\,x^8 \nonumber \\ &\quad + 0.0000854277\,x^9 – 0.000216876\,x^{10} + \cdots, \\ y_{2} &= 0.0000496032\,x^8 – 0.0000110229\,x^9 + 0.0000110229\,x^{10} + \cdots, \\ &\vdots \end{aligned}\] The series solution give exactly the exact solution as \[y(x)=y(x)=\frac{1}{{\sqrt{1 – x^2}}}.\]
The second kind of singular equation of fourth order \[\begin{aligned} \label{eq27}\left\{ \begin{array}{ll} \frac{d^{4}y}{dx^{4}}+\left(2b+\frac{2k}{x}\right)\frac{d^{3}y}{dx^{3}}+\left(b^2+\frac{4kb}{x}+\frac{k(k-1)}{x^{2}}\right)\frac{d^{2}y}{dx^{2}}+\left(\frac{2b^{2}k}{x}+\frac{2bk(k-1)}{x^{2}}\right)\frac{dy}{dx} +\left(\frac{b^{2}k(k-1)}{x^{2}}\right)y=R(x,y), & x > 0, \\ y(0)=\delta_0,y'(0)=\delta_1,y''(0)=y'''(0)=0. \end{array}\right. \end{aligned}\tag{33}\] \[\label{eq28} Ly=R(x,y),\tag{34}\] where \(L\) is differential operator defined by \[\label{eq29} Ly=x^{-k}\frac{d^{2}}{dx^{2}}x^{k}e^{-bx}\frac{d^{2}}{dx^{2}}e^{bx}y,\tag{35}\] and \[\label{eq30} L^{-1}(.)=e^{-bx}\int_{0}^{x} \int_{0}^{x}e^{bx}x^{-k}\int_{0}^{x}\int_{0}^{x}x^k(.)dxdxdxdx.\tag{36}\] If \(y''(0)=y'''(0)=0,\)and \(k\ge 0,\) \(b>0\) we have \[L^{-1}(Ly)=e^{-bx} \int_{0}^{x}\int_{0}^{x}e^{bx}x^{-k}\int_{0}^{x}\int_{0}^{x}x^k (x^{-k}\frac{d^{2}}{dx^{2}}x^{k}e^{-bx}\left(\frac{d^{2}}{dx^{2}}e^{bx}y\right))dxdxdxdx,\] \[=e^{-bx} \int_{0}^{x}\int_{0}^{x}e^{bx}x^{-k}\int_{0}^{x}\frac{d}{dx}x^{k}e^{-bx}\left(\frac{d^{2}}{dx^{2}}e^{bx}y\right)dxdxdx,\] after a simple operation we arrive to \[y(x)=y(0)(1+bx)e^{-bx}+y'(0)xe^{-bx}.\] Take \(L^{-1}\) on Eq. (35) obtain \[\label{eq31} y(x)=\delta(x)+L^{-1}(R(x,y)),\tag{37}\] therefore \[y_0=\delta(x),\] \[y_{n}=-L^{-1}(R(x,y)),ni\ge0,\] such that \(L(\delta(x)) = 0.\) Form this equation we get on the new fourth order singular and nonsingular differential equation.
Put \(b=\frac{1}{2}\), \(k =2\) in Eq. (33) to get, \[\begin{aligned} \label{eq32} \left\{ \begin{array}{ll} y^{(4)}+\left(1+\frac{4}{x}\right)y^{(3)}+\left(\frac{1}{4}+\frac{4}{x}+\frac{2}{x^{2}}\right)y^{(2)}+\left(\frac{1}{x}+\frac{2}{x^{2}}\right)y'+\frac{0.5}{x^2}y=R(x,y)\\ $$R(x,y)=\frac{2.\,x^3 + 25.\,e^{2\,x}\,\left( 0.292893 + x \right) \, \left( 1.70711 + x \right) }{x^2}-lny^2,$$ & x > 0, \\ y(0)=1,y'(0)=2,y''(0)=4,y'''(0)=8. \end{array}\right. \end{aligned}\tag{38}\] The exact solution is, \[y(x)=e^{2x}.\] Formula (38) can be rewrite as \[\label{eq33} Ly=({1 + \frac{x}{2}}){e^{\frac{-x}{2}}}+2xe^{\frac{-x}{2}}+\frac{2.\,x^3 + 25.\,e^{2\,x}\, \left( 0.292893 + x \right) \, \left( 1.70711 + x \right) }{x^2}-lny^2.\tag{39}\] Taking \(L^{-1}\) of Eq. (39)] we have \[y=({1 + \frac{x}{2}}){e^{\frac{-x}{2}}}+2xe^{\frac{-x}{2}}+L^{-1}\frac{2.\,x^3 + 25.\,e^{2\,x}\, \left( 0.292893 + x \right) \, \left( 1.70711 + x \right) }{x^2}-L^{-1}lny^2,\] hence \[y_0=({1 + \frac{x}{2}}){e^{\frac{-x}{2}}}+2xe^{\frac{-x}{2}}+L^{-1}\frac{2.\,x^3 + 25.\,e^{2\,x}\, \left( 0.292893 + x \right) \, \left( 1.70711 + x \right) }{x^2},\] \[\label{eq34} y_{n+1}=-L^{-1}A_n, n \ge 0,\tag{40}\] where \(A_i\) are Adomian polynomials given as \[A_0=lny^2{_0},\] \[A_1=\frac{2y_{1}}{y_{0}},\] therefore \[y_{1}=-L^{-1}A_0=-L^{-1}lny^2,\] \[y_{1}=-L^{-1}A_1=-L^{-1}\frac{2y_1}{y_0},\] hence \[\begin{aligned} y_0 &= 1. + 2.\,x + 2.\,x^2 + 1.33333\,x^3 + 0.666667\,x^4 + 0.271667\,x^5 + 0.0880556\,x^6 + 0.0254861\,x^7 \\ &\quad + 0.00634177\,x^8 + 0.00141145\,x^9 + 0.000282156\,x^{10} + \dots, \\ y_1 &= 4.76837\,{10}^{-7} + 1.93715\,{10}^{-7}\,x + 7.81962\,{10}^{-9}\,x^2 + 1.91328\,{10}^{-9}\,x^3 + 4.20188\,{10}^{-9}\,x^4 \\ &\quad – 0.01\,x^5 + 0.00166667\,x^6 – 0.000178572\,x^7 + 0.000014881\,x^8 – 2.96241\,{10}^{-6}\,x^9 + 2.9298\,{10}^{-6}\,x^{10} + \dots, \\ y_2 &= 3.8147\,{10}^{-6} – 1.66893\,{10}^{-6}\,x + 4.53981\,{10}^{-7}\,x^2 – 6.07684\,{10}^{-8}\,x^3 – 1.94625\,{10}^{-9}\,x^4 \\ &\quad + 6.0507\,{10}^{-9}\,x^5 – 2.48714\,{10}^{-9}\,x^6 + 6.62835\,{10}^{-10}\,x^7 – 1.28373\,{10}^{-10}\,x^8 \\ &\quad + 3.85804\,{10}^{-6}\,x^9 – 5.7356\,{10}^{-6}\,x^{10} + \dots. \end{aligned}\] This means that the solution in a series form given by \[\begin{aligned} y(x)=&y_0+y_1+y_2+…\\ =&1. + 2.\,x + 2.\,x^2 + 1.33333\,x^3 + 0.666667\,x^4 + 0.261667\,x^5 + 0.0897222\,x^6\\ &+ 0.0253075\,x^7 + 0.00635665\,x^8 + 0.00141235\,x^9 + 0.00027935\,x^{10}+…, \end{aligned}\] and in the closed form \[y(x)=e^{2x}.\]
Put \(b=k =1\) in Eq. (33) to get, \[\begin{aligned} \label{eq35}\left\{ \begin{array}{ll} y^{(4)}+(2+\frac{2}{x})y^{(3)}+(1+\frac{4}{x})y^{(2)}+\frac{2}{x}y' =R(x,y), \\ $$ R(x,y)={\left( -x^2 + \cos (x) \right) }^3 – \frac{8 + 6\,x + 4\,\cos (x) – 2\,x\,\sin (x)}{x}-y^3,$$ & x > 0, \\ y(0)=1,y'(0)=0,y''(0)=-3,y'''(0)=0. \end{array}\right. \end{aligned}\tag{41}\] Exact solution of Eq. (41) is \[y(x)=-x^2 + \cos (x).\] Using the differential operator \(L\) in Eq. (35) and \(L^{-1}\) in Eq. (36) of Eq. (41) we get \[\begin{aligned} y_{0} &= 1. – 1.5\,x^2 + 0.0555556\,x^4 – 0.00555556\,x^5 – 0.0075\,x^6 + 0.00187831\,x^7 + 0.0025874\,x^8 \\ &\quad – 0.000595553\,x^9 – 0.000488985\,x^{10} + \dots, \\ y_{1} &= -0.0138889\,x^4 + 0.00555556\,x^5 + 0.00611111\,x^6 – 0.00187831\,x^7 \\ &\quad – 0.00258031\,x^8 + 0.000603623\,x^9 + 0.000509411\,x^{10} + \dots, \\ y_{2} &= 0.0000177154\,x^8 – 8.07036 \times 10^{-6}\,x^9 – 0.0000207021\,x^{10} + \dots. \end{aligned}\] This means that the solution in a series form given by \[\begin{aligned} y(x)=&y_0+y_1+y_2+…\\ =&1. – 1.5\,x^2 + 0.0416667\,x^4 – 0.00138889\,x^6 + 0.0000248016\,x^8 – 2.75573\,{10}^{-7}\,x^{10}+…, \end{aligned}\] and in the closed form \(y(x)=-x^2 + \cos (x).\)
Put \(b=1\), \(k=0\) in Eq. (33) to get, \[\begin{aligned} \label{eq36} \left\{ \begin{array}{ll} y^{(4)}+2y^{(3)}+y^{(2)}=R(x,y) R(x,y)=\ln (e^{-x} + \frac{x}{e^x})-\ln y, & x > 0, \\ y(0)=1,y'(0)=0,y''(0)=-1,y'''(0)=2, \end{array}\right. \end{aligned}\tag{42}\] with exact solution \(y(x)=\left( \frac{1 + x}{e^x} \right).\)
\[\label{eq37} Ly=\ln (e^{-x} + \frac{x}{e^x})-\ln y,\] where \[L(.)=\frac{d^{2}}{dx^{2}}e^{-x}\frac{d^{2}}{dx^{2}}e^{x}(.),\] and \[L^{-1}(.)=e^{-x} \int_{0}^{x}\int_{0}^{x}e^{x}\int_{0}^{x}\int_{0}^{x}(.)dxdxdxdx.\] By taking \(L^{-1}\) on Eq. (43) we obtain \[y(x)=-\left( \frac{-1 – x}{e^x} \right)+L^{-1}(\ln (e^{-x} + \frac{x}{e^x})-\ln y,\] where \[y_{0}=-\left( \frac{-1 – x}{e^x} \right)+L^{-1}(\ln (e^{-x} + \frac{x}{e^x}),\] \[y_{n+1}=-L^{-1}A_{n},\] where \(A_i\) polynomials of Adomian taken form \[A_0=lny_{0},\] \[A_1=\frac{y_{1}}{y_{0}},\] therefore \[y_{1}=-L^{-1}A_0=-L^{-1}lny_0,\] \[y_{1}=-L^{-1}A_1=-L^{-1}\frac{y_1}{y_0},\] therefore the first few components of the solution \[\begin{aligned} y_0 &= 1. – 0.5\,x^2 + 0.333333\,x^3 – 0.125\,x^4 + 0.0333333\,x^5 – 0.00833333\,x^6 + 0.00198413\,x^7 \\ &\quad – 0.000496032\,x^8 + 0.00014881\,x^9 – 0.0000573192\,x^{10} + \cdots, \\ y_1 &= 0.00138889\,x^6 – 0.000793651\,x^7 + 0.000322421\,x^8 – 0.000126764\,x^9 + 0.0000551146\,x^{10} + \cdots, \\ y_2 &= -2.75573 \times 10^{-7}\,x^{10} + \cdots, \\ \vdots \\ y(x) &= y_0 + y_1 + y_2 + \cdots, \\ &= 1. – 0.5\,x^2 + 0.333333\,x^3 – 0.125\,x^4 + 0.0333333\,x^5 – 0.00694444\,x^6 + 0.00119048\,x^7 \\ &\quad – 0.000173611\,x^8 + 0.0000220459\,x^9 – 2.48016 \times 10^{-6}\,x^{10} + \cdots. \end{aligned}\] This leads us the exact solution \(y(x)=\left( \frac{1 + x}{e^x} \right).\)
The fourth-order singular equation of the third kind is given by: \[\begin{aligned} \label{eq38} \left\{ \begin{array}{ll} \frac{d^{4}y}{dx^{4}}+\left(\frac{k}{x}+3b\right)\frac{d^{3}y}{dx^{3}}+\left(\frac{3bk}{x}+3b^{2}\right)\frac{d^{2}y}{dx^{2}}+\left(\frac{3b^{2}k}{x}+b^{3}\right)\frac{dy}{dx}+\left(\frac{b^{3}k}{x}\right)y=R(x,y), & x > 0, \\ y(0)=\delta_0, \; y'(0)=\delta_1, \; y''(0)=\delta_2, \; y'''(0)=0. \end{array} \right. \end{aligned}\tag{44}\] The equation can be expressed compactly as: \[\label{eq39} Ly = R(x, y),\tag{45}\] where \(L\) is the differential operator defined as: \[\label{eq40} Ly = x^{-k}\frac{d}{dx}\left(x^{k}e^{-bx}\frac{d^{3}}{dx^{3}}\left(e^{bx}y\right)\right),\tag{46}\] and its inverse is given by: \[\label{eq41} L^{-1}(.) = e^{-bx}\int_{0}^{x}\int_{0}^{x} \int_{0}^{x}e^{bx}x^{-k}\int_{0}^{x}x^k(.) \,dx\,dx\,dx\,dx.\tag{47}\] Assuming \(y'''(0) = 0\), \(k \geq 0\), and \(b > 0\), applying \(L^{-1}\) to both sides yields: \[L^{-1}(Ly) = e^{-bx} \int_{0}^{x}\int_{0}^{x}\int_{0}^{x}e^{bx}x^{-k}\int_{0}^{x}x^k \left(x^{-k}\frac{d}{dx}\left(x^{k}e^{-bx}\frac{d^{3}}{dx^{3}}\left(e^{bx}y\right)\right)\right) \,dx\,dx\,dx\,dx.\] Simplifying further, we have: \[L^{-1}(Ly) = e^{-bx} \int_{0}^{x}\int_{0}^{x}\int_{0}^{x}\frac{d^{3}}{dx^{3}}\left(e^{bx}y\right) \,dx\,dx\,dx.\] After computation, \[y(x) = \left[y(0)(1+bx+b^{2}\frac{x^{2}}{2})+y'(0)(x+bx^{2})+y''(0)\left(\frac{x^{2}}{2}\right)\right]e^{-bx}.\] Applying \(L^{-1}\) to Eq. (45) gives: \[\label{eq42} y(x) = \aleph(x) + L^{-1}(R(x, y)),\tag{48}\] where \[y_0 = \aleph(x), \quad y_n = -L^{-1}(R(x, y)), \; n \geq 0,\] and \(L(\aleph(x)) = 0\).
From this formulation, we derive a new fourth-order singular and nonsingular differential equation.
Put \(b=1\), \(k =1\) in Eq. (44) to get, \[\begin{aligned} \label{eq43} \left\{ \begin{array}{ll} \frac{d^{4}y}{dx^{4}}+\left(\frac{1}{x}+3\right)\frac{d^{3}y}{dx^{3}}+\left(\frac{3}{x}+3\right)\frac{d^{2}y}{dx^{2}}+\left(\frac{3}{x}+1\right)\frac{dy}{dx}+\left(\frac{1}{x}\right)y=R(x,y), \\R(x,y)=\frac{4+2 x^2+24 x^3+3 x^4+12 x^5+7 x^6+3 x^7+2 x^8}{x \left(1+x^2\right)^{7/2}}-\ln y^{2},$$ & x > 0,\\ y(0)=1,y'(0)=0,y''(0)=1,y'''(0)=0. \end{array}\right. \end{aligned}\tag{49}\] The exact solution is \[y(x)=\sqrt{1 + x^2}.\] Which can be rewrite as \[\label{eq44} Ly=(1+x+x^{2})e^{-x}+\frac{4+2 x^2+24 x^3+3 x^4+12 x^5+7 x^6+3 x^7+2 x^8}{x \left(1+x^2\right)^{7/2}}-\ln y^{2},\tag{50}\] such that \[L(.)=x^{-1}\frac{d}{dx}xe^{-x}\frac{d^{3}}{dx^{3}}e^{x}(.),\] and \[L^{-1}(.)=e^{-x} \int_{0}^{x}\int_{0}^{x}\int_{0}^{x}e^{x}x^{-1}\int_{0}^{x}x(.)dxdxdxdx.\] Now, applying \(L^{-1}\) on Eq. (50) we find
\[y(x)=(1+x+x^{2})e^{-x}+L^{-1}(\frac{4+2 x^2+24 x^3+3 x^4+12 x^5+7 x^6+3 x^7+2 x^8}{x \left(1+x^2\right)^{7/2}}+\ln(1+x^{2}))-L^{-1}\ln y^{2},\] we use the recursive relation \[\begin{aligned} y_0 &= 1 + 0.5x^2 – 0.125x^4 + 0.0645833x^6 – 0.000892857x^7 – 0.0390873x^8 \\ &\quad + 0.000041336x^9 + 0.0273913x^{10} + \dots, \\ y_1 &= -0.0208333x^4 + 0.0125x^5 – 0.00625x^6 + 0.00188492x^7 – 0.000409226x^8 \\ &\quad + 0.0000702712x^9 – 0.0000107818x^{10} + \dots, \\ y_2 &= 0.000020668x^8 – 0.0000139755x^9 + 2.0569504283194747 \times 10^{-6}x^{10} + \dots. \end{aligned}\] The series solution is \[\begin{aligned} y(x)=&y_0+y_1+y_2+…\\ =&1 + 0.5 x^2 – 0.145833 x^4 + 0.0125 x^5 + 0.0583333 x^6 + 0.000992063 x^7 – 0.0394758 x^8 +…. \end{aligned}\]
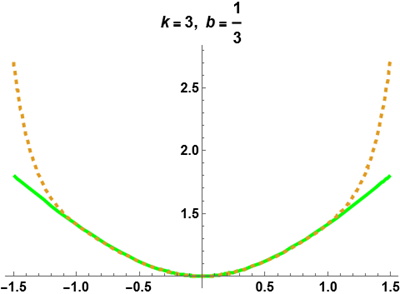
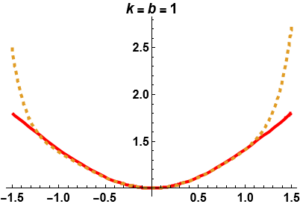
Put \(b=1\), \(k =0\) in Eq. (44) to get, \[\begin{aligned} \label{eq46} \left\{ \begin{array}{ll} y^{(4)} + 3y^{(3)} + 3y^{(2)} + y' = R(x,y),\\ R(x,y) = -24 + e^{-x^4 + x^5} + 48x + 144x^2 + 56x^3 + 5x^4 – e^{y}, & x > 0, \\ y(0) = y'(0) = y''(0) = y'''(0) = 0. \end{array} \right. \end{aligned}\tag{51}\]
The exact solution to this equation is \(y(x) = x^5 – x^4\). By applying the operator \(L\) from (47) and its inverse \(L^{-1}\) from Eq. (48) to Eq. (51), we obtain: \[y(x) = L^{-1}(-24 + e^{-x^4 + x^5} + 48x + 144x^2 + 56x^3 + 5x^4) – L^{-1}e^{y},\] where \[y_0 = L^{-1}(-24 + e^{-x^4 + x^5} + 48x + 144x^2 + 56x^3 + 5x^4),\] and \[y_{n+1} = -L^{-1}A_n, \quad n \geq 0.\] The terms \(A_n\) are Adomian polynomials corresponding to the nonlinear part \(e^{y}\), defined as follows: \[A_0 = e^{y_0}, \quad A_1 = y_1e^{y_0}, \quad \dots.\] For example: \[\begin{aligned} y_0 &= -0.958333x^4 + 0.975x^5 + 0.00833333x^6 – 0.00198413x^7 – 0.000223214x^8 + 0.00047123x^9, \\ y_1 &= -0.0416667x^4 + 0.025x^5 – 0.00833333x^6 + 0.00198413x^7 + 0.000198413x^8 – 0.000454696x^9, \\ y_2 &= 0.0000248016x^8 – 0.0000165344x^9, \end{aligned}\] and so on.
The series solution takes the form: \[y(x) = y_0 + y_1 + y_2 + \dots,\] which simplifies to: \[y(x) = -x^4 + x^5,\] leading to the exact solution \(y(x) = x^5 – x^4\).
In this study, we investigated three singular fourth-order differential equations with initial conditions using a novel modification of the Adomian decomposition method. This approach allowed us to derive a general formula that encompasses all three equations. From these foundational equations, we formulated various types of singular and nonsingular fourth-order differential equations. Through illustrative examples, we demonstrated the efficiency of this new modification and obtained results that are both highly accurate and closely aligned with the exact solutions.