This paper proposes an explicit numerical scheme based on Delannoy polynomials in conjunction with the tau method for solving the time-fractional diffusion equation involving the Caputo derivative. The proposed method constructs approximate solutions using shifted Delannoy polynomials as basis functions, allowing efficient and accurate treatment of the nonlocal nature of fractional derivatives. The method transforms the time-fractional diffusion problem into a system of algebraic equations, which can be solved explicitly. Several benchmark examples are provided to confirm the efficiency, accuracy, and applicability of the new scheme.
Time-fractional diffusion equations (TFDEs), which generalize classical diffusion processes using fractional-order derivatives, have gained substantial attention due to their capability to model memory-dependent phenomena such as subdiffusion in porous media, viscoelasticity, and anomalous transport in complex systems [1– 7]. The inclusion of a Caputo time-fractional derivative enables the incorporation of long-range temporal interactions, making these equations ideal for modeling real-world processes with hereditary effects.
Considerable progress has been achieved recently in the creation of spectral and collocation methods in order to resolve fractional and integral equations. For instance, modified Chebyshev–Galerkin approaches have been successfully implemented for higher-order boundary value problems [8], while Fermat polynomial-based collocation schemes have shown effectiveness in handling singular kernels in integral equations [9]. The third-kind Chebyshev polynomials have also been applied in the explicit solution of nonlinear fractional Duffing equations [10]. Researchers have extended spectral methods using Legendre derivatives for both differential and integral problems [11], and refined Galerkin techniques utilizing Bernoulli polynomials have demonstrated accuracy in higher-order differential systems [12]. High-accuracy modified spectral methods were developed for two-dimensional integral equations, offering improved convergence [13], and the fractional Newell-Whitehead-Segel equation has been treated using an approximate collocation scheme [14]. In the realm of metric space theory, fixed point theorems in \(G\)-metric spaces have been explored with applications [15]. For time-fractional PDEs, spectral approaches based on first-kind Chebyshev polynomials have been proposed for the Korteweg–de Vries–Burgers equation [16], while the Bagley–Torvik equation has been tackled using a fourth-kind Chebyshev operational tau method [17]. Notably, the modeling of human corneal geometry has been accomplished via a Caputo-fractional-based Chebyshev collocation algorithm [18], and Petrov–Galerkin schemes employing second-kind Chebyshev polynomials have been utilized in the Euler–Bernoulli beam context [19]. Time-fractional integro-differential equations with weak singularities have been studied using Chebyshev Petrov–Galerkin methods [20]. In the context of wave propagation, a spectral framework employing third-kind Chebyshev polynomials has been shown effective for solving hyperbolic telegraph equations in one and two dimensions [21]. Finally, Lucas polynomials have been applied in a Petrov–Galerkin scheme to address time-fractional diffusion equations, emphasizing flexibility and precision [22]. For more studies, see [23– 25].
Solving TFDEs analytically is often unfeasible, motivating the development of robust and efficient numerical techniques. Spectral methods, known for their exponential convergence properties for smooth solutions, are particularly suited for fractional problems due to their global approximation capabilities and their effectiveness in handling the nonlocality of fractional operators [26– 28]. Among these, the tau method and its variants offer a systematic framework for approximating solutions to differential equations via orthogonal polynomials [29, 30].
This work introduces a novel explicit tau-based spectral algorithm that employs shifted Delannoy polynomials for solving time-fractional diffusion equations. Delannoy polynomials, due to their orthogonality and computational tractability, serve as a powerful basis for spectral expansion. By leveraging their structural properties, we derive an efficient and stable numerical scheme that directly approximates the solution without the need for iterative solvers.
The following is a summary of this paper’s contributions:
We develop an explicit spectral scheme using shifted Delannoy polynomials tailored to time-fractional diffusion equations.
The method transforms the fractional PDE into a tractable system of algebraic equations using the tau framework.
Extensive numerical experiments demonstrate the accuracy and computational advantages of the proposed method.
The paper is organized as follows: §2 provides the necessary mathematical preliminaries, including properties of Delannoy polynomials and the Caputo derivative. §3 outlines the formulation of the explicit tau scheme. §4 presents numerical experiments. Lastly, §5 provides closing thoughts and recommendations for the future.
Definition 1.In Caputo’s sense, the fractional-order derivative of \(g \in C^{r}[0, \sigma]\), where \(r= \lceil \mu \rceil\) is defined as [1]: \[\label{e1} {D_{\sigma}^{\mu}}U(\sigma)=\frac{1}{\Gamma(r-\mu)}\int_{0}^{\sigma}(\sigma-t)^{r-\mu-1}U^{(r)}(t)\, dt,\quad \mu>0 ,\quad \sigma>0, \tag{1}\] where, \(r-1<\mu \leq r,\quad r\in \mathbb{N}.\)
Moreover, the following Caputo’s Properties are vital. \[ \label{e2} {D_{\sigma}^{\mu}}C =0,\ ( \textrm{for a constant \(C\)}),\ \tag{2}\] \[\label{e3} {D_{\sigma}^{\mu}}\,\sigma^\ell =\begin{cases} 0, \mbox{if }\ell\in{\mathbb{N}}_0 \quad and \quad \ell<\lceil \mu\rceil, \\ \frac{\ell\,!}{\Gamma(\ell+1-\mu)}\,\sigma^{\ell-\mu}, \mbox{if }\ell\in{\mathbb{N}}_0 \quad and \quad \ell\geq\lceil \mu\rceil, \end{cases} \tag{3}\] where \({\mathbb{N}}=\{1,2,\ldots\}\) and \({\mathbb{N}}_0=\{0,1,2,\ldots\}\).
The power formula of Delannoy polynomials is \[\label{power} \psi_i(z)=\sum\limits_{j=0}^i \binom{i}{j} \binom{i+j}{j}\,z^j. \tag{4}\]
The inversion formula is \[z^i=(i!)^2\sum_{m=0}^i \frac{(-1)^{i-m}\,(2m+1)}{(i-m)!\,(i+m+1)!}\,\psi_m(z). \tag{5}\]
Also, the orthogonality relation of \(\psi_r(z)\) is \[\label{eeeg} \int_{-1}^{0}\psi_r(z)\psi_s(z)\,d\,z = \frac{1}{2r+1} \delta_{r,s}, \tag{6}\] where \[\delta_{r,s}=\begin{cases} 1,& \mbox{if }r=s,\\ 0,& \mbox{if }r\not=s.\end{cases} \tag{7}\]
Now, define the shifted Delannoy polynomials \(\phi_i(z)=\psi_i(z-1)\) on the interval [0,1].
The orthogonality relation of \(\phi_i(z)\) is \[\label{ortho} \int_{0}^{1}\phi_r(z)\phi_s(z)\,d\,z = \frac{1}{2r+1} \delta_{r,s}. \tag{8}\]
The power form of \(\phi_i(z)\) is \[\phi_{i}(z)=\sum_{\tau=0}^i \frac{(-1)^{i+\tau}\,(i+\tau)!}{(i-\tau)!(\tau)!^2}z^{\tau}, \tag{9}\] and it’s inversion formula is \[\label{inversion} z^i=\sum\limits_{\tau=0}^r \frac{(-1)^{2\, \tau}\, (2\, \tau+1)\, \Gamma (r+1)^2 }{\Gamma (-\tau+r+1)\, \Gamma (\tau+r+2)}\,\phi_{\tau}(z). \tag{10}\]
Remark 1. Polynomials \(\psi_j(z)\) and \(\phi_j(z)\) are linked with shifted Legendre polynomials by the following formulas: \[ \psi_j(z)=P_j(2\,z+1),\ \tag{11}\] \[\phi_j(z)=P_j(2\,z-1). \tag{12}\]
Remark 2. The orthogonality relations (6) and (8) are direct results of the orthogonality relations of Legendre polynomials and their shifted ones [31, 32].
Assuming the following TFDE ([33, 34]): \[\label{e4} {D_{t}^{\alpha}}\xi(z,t)-\mu\,\xi_{zz}(z,t)=f(z,t), \quad 0<\alpha\leq1, \tag{13}\] controlled by \[ \label{e5} \xi(z,0)= g(z),\quad 0<z< 1,\ \tag{14}\] \[\label{e6} \xi(0,t)= h_{1}(t),\quad \xi(1,t)=h_{2}(t), \quad 0<t< 1, \tag{15}\] where \(\mu\) is a positive constant, \(g(z),\,h_{1}(t),\,h_{2}(t)\) are provided functions that are continuous and \(f(z,t)\) is the source term.
Now, define \[\label{e8} \mathcal{P}^{\mathcal{N}}={{span}}\{\phi_i(z)\,\phi_j(t):0\le i,j\le \mathcal{N}\}, \tag{16}\]
Consequently, we can infer that any function \(\xi^{\mathcal{N}}(z,t)\in \mathcal{P}^{\mathcal{N}}\) can be articulated as \[\label{e9} \xi^{\mathcal{N}}(z,t)=\sum_{i=0}^{\mathcal{N}}\sum_{j=0}^{\mathcal{N}}Q_{ij}\,\phi_i(z)\,\phi_j(t)= {\phi}(z)\, {Q}\, {\phi}(t)^{T}, \tag{17}\] where, \( {\phi}(z)=[\phi_0(z),\phi_1(z),\ldots,\phi_{\mathcal{N}}(z)],\) and \( {Q}=(Q_{ij})_{1\leq i,j\leq \mathcal{N}+1}\) is the unknown matrix of dimension \((\mathcal{N}+1)^2\).
The residual \(\mathbf{R}(z,t)\) of Eq. (13) in the subsequent format \[\label{e10} \mathbf{R}(z,t)={D_{t}^{\alpha}}\xi^{\mathcal{N}}(z,t)-\,\mu\,\xi^{\mathcal{N}}_{zz}(z,t)-f(z,t). \tag{18}\]
As the outcome of applying Tau method [35– 37],We obtain \[\label{e11} (\mathbf{R}(z,t)\,,\,\phi_r(z)\,\phi_s(t))=0,\quad 0\leq r\leq \mathcal{N}-2,\quad 0\leq s\leq \mathcal{N}-1. \tag{19}\]
Assume that \[ {F} =(f_{r,s})_{(\mathcal{N}-1)\times \mathcal{N} },\quad f_{rs}=( f(z,t)\,,\,\phi_r(z)\,\phi_s(t)), \ \tag{20}\] \[ {\mathcal{A}} = (a_{i,r})_{(\mathcal{N}+1)\times (\mathcal{N}-1)},\quad a_{i,r} =(\phi_i(z)\,,\, \phi_r(z)), \ \tag{21}\] \[ {\mathcal{B}} = (b_{j,s})_{(\mathcal{N}+1)\times \mathcal{N}},\quad b_{j,s} =(\phi_j(t)\,,\, \phi_s(t)), \ \tag{22}\] \[ {\mathcal{H}} = ({h}_{ir})_{(\mathcal{N}+1)\times (\mathcal{N}-1)},\quad {h}_{ir}=\left(\frac{d^2\,\phi_i(z)}{d\,z^2}\,,\, \phi_r(z)\right),\ \tag{23}\] \[ {\mathcal{K}} = (k_{j,s})_{(\mathcal{N}+1)\times \mathcal{N}},\quad k_{j,s}=\left({D_{t}^{\alpha}}\,\phi_j(t)\,,\, \phi_s(t)\right). \tag{24}\]
Therefore, Eq. (19) can be rephrased as \[\label{Sys1} \sum_{i=0}^{\mathcal{N}}\sum_{j=0}^{\mathcal{N}}Q_{ij}\,a_{i,r}\,k_{j,s}-\mu\,\sum_{i=0}^{\mathcal{N}}\sum_{j=0}^{\mathcal{N}}Q_{ij}\,h_{i,r}\,b_{j,s}=f_{r,s},\quad 0\leq r\leq \mathcal{N}-2,\quad 0\leq s\leq \mathcal{N}-1. \tag{25}\]
Or in matrix form as \[\label{e12} {\mathcal{A}}^{T}\, {{Q}}\, {\mathcal{K}}-\mu\, {\mathcal{H}}^{T} {{Q}}\, {\mathcal{B}}= {{F}}. \tag{26}\]
Furthermore, the conditions in (14) lead to \[\label{e13} \begin{split} &\sum_{i=0}^{\mathcal{N}}\sum_{j=0}^{\mathcal{N}}Q_{ij}\,a_{i,r}\,\phi_j(0)=(g(z)\,,\, \phi_r(z)),\quad 0\leq r\leq \mathcal{N},\\& \sum_{i=0}^{\mathcal{N}}\sum_{j=0}^{\mathcal{N}}Q_{ij}\,b_{j,s}\,\phi_i(0)=(h_{1}(t)\,,\, \phi_s(t)), \quad 0\leq s\leq \mathcal{N}-1,\\& \sum_{i=0}^{\mathcal{N}}\sum_{j=0}^{\mathcal{N}}Q_{ij}\,b_{j,s}\,\phi_i(1)=(h_{2}(t)\,,\, \phi_s(t)),\quad 0\leq s\leq \mathcal{N}-1. \end{split} \tag{27}\]
Now, an appropriate technique might be employed to solve the resultant algebraic system of equations of order \((\mathcal{N}+1)^{2}\), which includes Eqs. (26) and (27).
Theorem 1. The elements \(a_{i,r},\,b_{j,s},\,{h}_{i,r}\) and \(k_{i,r}\) in (25) are given by \[\label{e14}\left. \begin{split} &(1)\quad a_{i,r}=\frac{1}{2i+1} \delta_{i,r} \\&(2)\quad b_{j,s}=\frac{1}{2j+1} \delta_{j,s} \\&(3)\quad \begin{split} h_{i,r}=&\sum\limits_{j=2}^i \sum\limits_{n=0}^r \frac{j\, (j-1)\, \gamma_{j,i}\, \gamma_{n,r}}{j+n-1} \end{split} \\&(4)\quad k_{i,r}=\sum\limits_{j=1}^i \sum\limits_{n=0}^r \frac{j! \,\gamma_{j,i}\, \gamma_{n,r}}{\Gamma(j-\alpha+1 )\, (-\alpha +j+n+1)} \end{split}\right\} \tag{28}\] where \[\gamma_{j,i}=\sum\limits_{\tau=0}^i (-1)^{\tau-j} \binom{i}{\tau} \binom{i+\tau}{\tau} \binom{\tau}{j}. \tag{29}\]
Proof. The elements \(a_{i,r}\) and \(b_{j,s}\) are a directly results of the
orthogonality relation of \(\phi_r(z)\)
provided in (8),
To find the elements \(h_{i,r}\).
The application of power formula (4), we can write \[\phi_{i}(z)=\sum\limits_{j=0}^i \binom{i}{j} \,\binom{i+j}{j}\,(z-1)^j, \tag{30}\] it is able to be written after using relation \((z-1)^r=\sum\limits_{n=0}^r z^n (-1)^{r-n} \binom{r}{n},\) as \[\phi_{i}(z)=\sum\limits_{j=0}^i \sum\limits_{\ell=j}^i (-1)^{\ell-j}\, \binom{i}{\ell} \,\binom{i+\ell}{\ell} \,\binom{\ell}{j}\,z^j, \tag{31}\]
After extending, rearranging, and collecting related terms from the above equation, we obtain \[\phi_{i}(z)=\sum\limits_{j=0}^i \gamma_{j,i}\,z^j, \tag{32}\] where \[\gamma_{j,i}=\sum\limits_{\tau=0}^i (-1)^{\tau-j} \binom{i}{\tau} \binom{i+\tau}{\tau} \binom{\tau}{j}. \tag{33}\]
Based on the definition of \(h_{i,r}\), we van write
\[\begin{aligned} h_{i,r}=&\int_{0}^{1}\frac{d^2\,\phi_i(z)}{d\,z^2}\, \phi_r(z)\,dz=\sum\limits_{j=2}^i \sum\limits_{n=0}^r j\, (j-1)\, \gamma_{j,i} \gamma_{n,r}\,\int_0^1 z^{j+n-2} \, dz\notag\\ =&\sum\limits_{j=2}^i \sum\limits_{n=0}^r \frac{j\, (j-1)\, \gamma_{j,i}\, \gamma_{n,r}}{j+n-1}. \end{aligned} \tag{34}\]
To obtain \(k_{i,r}\), we use Definition 1 to get \[\begin{aligned} k_{i,r}&=\int_{0}^{1}{D_{t}^{\alpha}}\,\phi_i(t)\, \phi_r(t)\,dt\notag\\ &=\sum\limits_{j=1}^i \sum\limits_{n=0}^r \frac{j!\, \gamma_{j,i}\,\gamma_{n,r} }{(j-\alpha )!}\,\int_0^1 t^{-\alpha +j+n} \, dt\notag\\& =\sum\limits_{j=1}^i \sum\limits_{n=0}^r \frac{j! \,\gamma_{j,i}\, \gamma_{n,r}}{\Gamma(j-\alpha+1 )\, (-\alpha +j+n+1)}. \end{aligned} \tag{35}\]
This proves Theorem 1. ◻
Problem 1. [38] Consider \[{D_{t}^{\alpha}}\xi(z,t)-\xi_{zz}(z,t)=\frac{1}{\Gamma(2-\alpha)}\,t^{1-\alpha}\,z^2\,(1-z)+2\,t\,(3\,z-1), \quad 0<\alpha\leq1, \tag{36}\] controlled by \[\xi(z,0)=0,\quad 0<z< 1, \tag{37}\] and \[\xi(0,t)=\xi(1,t)=0, \quad 0<t< 1, \tag{38}\] where \(\xi(z,t)=t\,z^2\,(1-z)\) is the precise answer to this issue.
If we use the approach we suggested at \(\alpha=0.5\) for \(\mathcal{N}=3,\) We obtain the subsequent system. \[\begin{split} \frac{8\, Q_{0,1}}{3 \,\sqrt{\pi }}-12\, Q_{2,0}-\frac{8\, Q_{0,2}}{5 \,\sqrt{\pi }}+\frac{16 \,Q_{0,3}}{7 \,\sqrt{\pi }}&=\frac{1}{2}+\frac{1}{9 \sqrt{\pi }}, \frac{8\, Q_{0,1}}{15\, \sqrt{\pi }}-4 Q_{2,1}+\frac{8\, Q_{0,2}}{7\, \sqrt{\pi }}-\frac{16 Q_{0,3}}{45\, \sqrt{\pi }}\\& =\frac{1}{6}+\frac{1}{45 \sqrt{\pi }}, -\frac{8 \,Q_{0,1}}{105 \sqrt{\pi }}-\frac{12}{5} Q_{2,2}+\frac{8\, Q_{0,2}}{15\, \sqrt{\pi }}+\frac{304\, Q_{0,3}}{385 \sqrt{\pi }}\\& =-\frac{1}{315\, \sqrt{\pi }}, \frac{8\, Q_{1,1}}{9\, \sqrt{\pi }}-20\, Q_{3,0}-\frac{8\, Q_{1,2}}{15\, \sqrt{\pi }}+\frac{16\, Q_{1,3}}{21\, \sqrt{\pi }}\\&=\frac{1}{2}+\frac{1}{45 \sqrt{\pi }}, \frac{8\, Q_{1,1}}{45\, \sqrt{\pi }}-\frac{20}{3} Q_{3,1}+\frac{8\, Q_{1,2}}{21\, \sqrt{\pi }}-\frac{16 Q_{1,3}}{135\, \sqrt{\pi }}\\&=\frac{1}{6}+\frac{1}{225 \sqrt{\pi }}, -\frac{8 \,Q_{1,1}}{315 \sqrt{\pi }}-4 \,Q_{3,2}+\frac{8 \,Q_{1,2}}{45\, \sqrt{\pi }}+\frac{304\, Q_{1,3}}{1155\, \sqrt{\pi }}\\&=-\frac{1}{1575\, \sqrt{\pi }}. \end{split}\] \[\begin{split} Q_{0,0}-Q_{0,1}+Q_{0,2}-Q_{0,3}&=0,\\ Q_{1,0}- Q_{1,1}+ Q_{1,2}-\frac{1}{3} \,Q_{1,3}&=0,\\ Q_{2,0}- Q_{2,1}+ Q_{2,2}- Q_{2,3}&=0,\\ Q_{3,0}- Q_{3,1}+ Q_{3,2}- Q_{3,3}&=0,\\ Q_{0,0}-Q_{1,0}+Q_{2,0}-Q_{3,0}&=0,\\ Q_{0,1}-Q_{1,1}+ Q_{2,1}- Q_{3,1}&=0,\\ Q_{0,2}-Q_{1,2}+ Q_{2,2}- Q_{3,2}&=0,\\ Q_{0,0}+Q_{1,0}+Q_{2,0}+Q_{3,0}&=0,\\ Q_{0,1}+ Q_{1,1}+ Q_{2,1}+Q_{3,1}&=0,\\ Q_{0,2}+ Q_{1,2}+ Q_{2,2}+ Q_{3,2}&=0, \end{split}\] problem can be resolved by using Gauss elimination method to get
\[\begin{split} &Q_{0,0}\to \frac{1}{24},\; Q_{0,1}\to \frac{1}{24},\; Q_{0,2}\to 0,\; Q_{0,3}\to 0,\; Q_{1,0}\to \frac{1}{40},\; Q_{1,1}\to \frac{1}{40},\; Q_{1,2}\to 0,\; Q_{1,3}\to 0,\\& Q_{2,0}\to -\frac{1}{24},\; Q_{2,1}\to -\frac{1}{24},\; Q_{2,2}\to 0,\; Q_{2,3}\to 0,\; Q_{3,0}\to -\frac{1}{40},\; Q_{3,1}\to -\frac{1}{40},\; Q_{3,2}\to 0,\; Q_{3,3}\to 0, \end{split}\] and therefore \(\xi^{\mathcal{N}}(z,t)=t\,z^2\,(1-z)\), which is the precise answer.
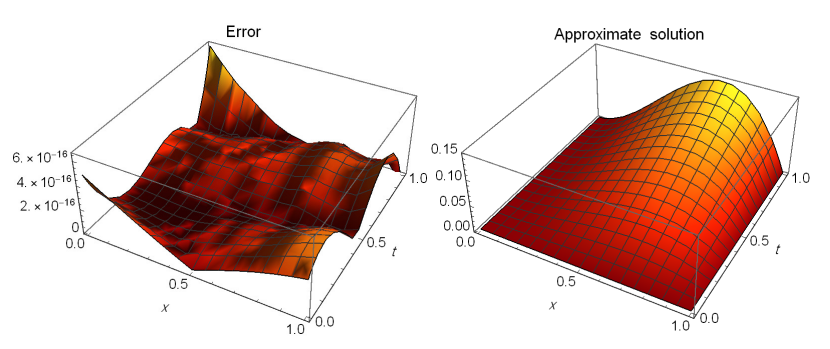
Additionally, Figure 1 illustrates the absolute errors (\(\mathcal{AE}\)) (left) and approximate solution (\(\mathcal{AS}\)) (right) for \(\alpha=0.75\) and \(\mathcal{N}=3\).
Problem 2. [39] Assuming \[{D_{t}^{\alpha}}\xi(z,t)-\mu\, \xi_{zz}(z,t)=t^3\, (z-1)\, z^4\,\frac{\Gamma (\alpha +4)}{6}-4\, z^2\, (5\, z-3)\, t^{\alpha +3}, \quad 0<\alpha\leq1, \tag{39}\] controlled by \[\xi(z,0)=e^z,\quad 0<z< 1, \tag{40}\] and \[\xi(0,t)=t^2+t+1,\quad \xi(1,t)=e \left(t^2+t+1\right), \quad 0<t< 1, \tag{41}\] where \(\xi(z,t)=\left(t^2+t+1\right) e^z\) is the analytic solution of this problem.
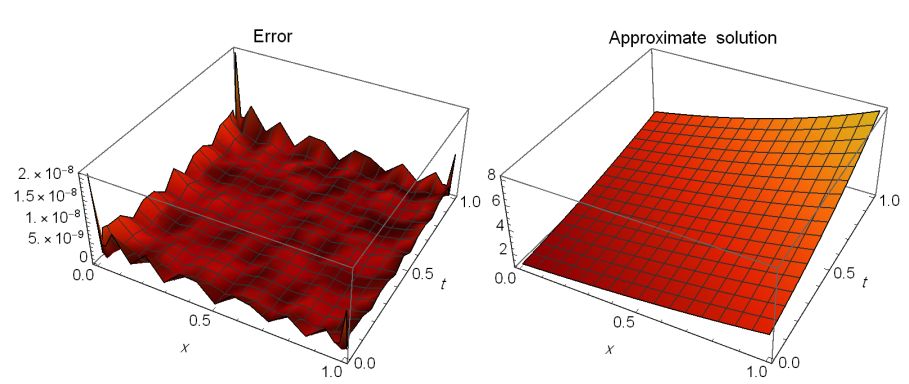
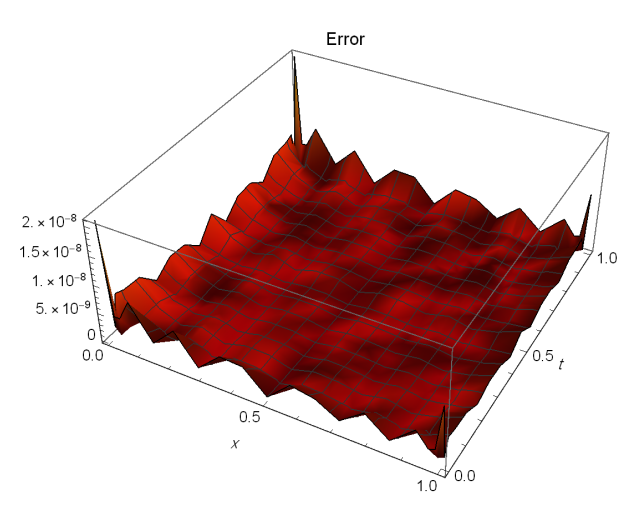
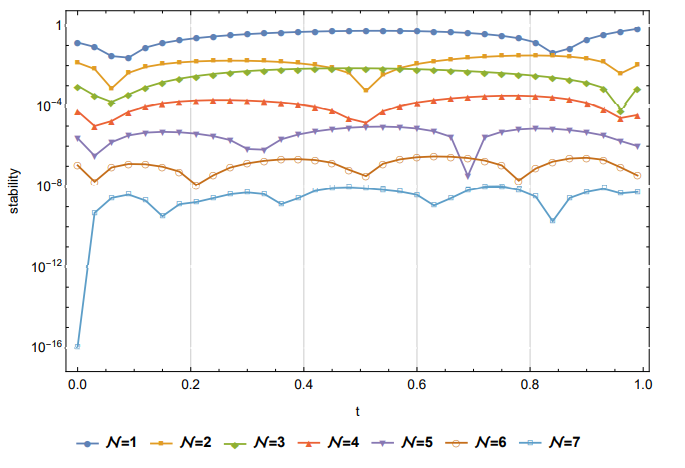
Table 1 compares the maximum \(\mathcal{AE}\) between our technique and that of [39] at various \(\alpha\) values when \(\mu=1\). Figure 2 illustrates the \(\mathcal{AE}\) (left) and \(\mathcal{AS}\) (right) for \(\alpha=0.75\) and \(\mathcal{N}=8\) when \(\mu=1\). Table 2 shows the \(\mathcal{AE}\) for \(\alpha=0.3\) and \(\mathcal{N}=8\) when \(\mu=1\). Figure 3 shows the \(\mathcal{AE}\) at \(\alpha=0.3\) and \(\mathcal{N}=8\) when \(\mu=2\). Finally, Figure 4 illustrates the stability \(|\xi^{\mathcal{N}+1}(z,t)-\xi^\mathcal{N}(z,t)|\) at \(z=t\) and different values of \(\mathcal{N}\) when \(\alpha=0.3\). These findings show that this method’s results are close to the exact solution.
| \(\alpha\) | Ref. [39] \((\mathcal{N}=64)\) | Proposed approach \((\mathcal{N} =8)\) |
|---|---|---|
| 0.25 | \(1.2889\times 10^{-5}\) | \(4.14712 \times 10^{-9}\) |
| 0.5 | \(1.1727\times 10^{-5}\) | \(2.07061 \times 10^{-9}\) |
| 0.75 | \(1.1645\times 10^{-5}\) | \(4.14649 \times 10^{-9}\) |
| \(z\) | \(t=0.2\) | \(t=0.5\) | \(t=0.8\) |
|---|---|---|---|
| 0.1 | \(9.92485\times 10^{-10}\) | \(1.28053\times 10^{-9}\) | \(1.01728\times 10^{-9}\) |
| 0.2 | \(1.3859\times 10^{-9}\) | \(1.79685\times 10^{-9}\) | \(1.49371\times 10^{-9}\) |
| 0.3 | \(1.26077\times 10^{-10}\) | \(1.67655\times 10^{-10}\) | \(1.48779\times 10^{-10}\) |
| 0.4 | \(1.17182\times 10^{-9}\) | \(1.52828\times 10^{-9}\) | \(1.32191\times 10^{-9}\) |
| 0.5 | \(5.85545\times 10^{-11}\) | \(7.65681\times 10^{-11}\) | \(5.56186\times 10^{-11}\) |
| 0.6 | \(1.05551\times 10^{-9}\) | \(1.37827\times 10^{-9}\) | \(1.20427\times 10^{-9}\) |
| 0.7 | \(1.91402\times 10^{-12}\) | \(2.99671\times 10^{-12}\) | \(2.37526\times 10^{-11}\) |
| 0.8 | \(9.63496\times 10^{-10}\) | \(1.25716\times 10^{-9}\) | \(1.07944\times 10^{-9}\) |
| 0.9 | \(6.59603\times 10^{-10}\) | \(8.53126\times 10^{-10}\) | \(6.84238\times 10^{-10}\) |
Problem 3. [38] Assuming \[{D_{t}^{\alpha}}\xi(z,t)-\xi_{zz}(z,t)= \left(4\,
\pi^2\, t^2+\frac{2\, t^{2-\alpha }}{\Gamma (3-\alpha )}\right)\,\sin
(2\, \pi\,z), \quad 0<\alpha\leq1, \tag{42}\] controlled by \[\xi(z,0)=0,\quad 0<z< 1, \tag{43}\] and \[\xi(0,t)=\xi(1,t)=0, \quad 0<t< 1, \tag{44}\]
where \(\xi(z,t)=t^{2}\,\sin(2\,\pi\,z)\)
constitutes the analytic solution to this problem.
Table 3 compares the maximum \(\mathcal{AE}\) between our technique and
that of [38] at
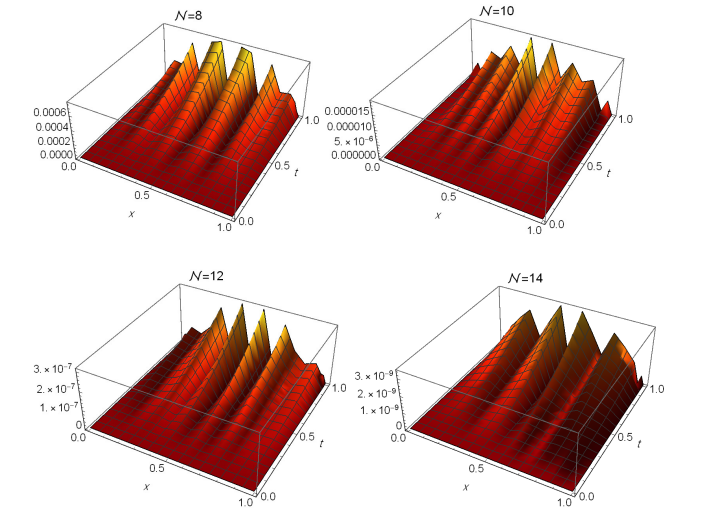
\(\alpha=0.5\). Figure 5 depicts the
maximum \(\mathcal{AE}\) at various
\(\mathcal{N}\) values for \(\alpha=0.5\). This image demonstrates the
advantage of adopting our strategy to obtain the maximum \(\mathcal{AE}\) for small values of \(\mathcal{N}.\) Table 4 shows the \(\mathcal{AE}\) at \(\alpha=0.9\) and \(\mathcal{N}=14\). It is clear that the
estimated and exact solutions are relatively close.
| Ref. [38] at \(\Delta t=0.001\) and \(M=64\) | Presented approach at \(\mathcal{N}=14\) |
|---|---|
| \(7.70\times 10^{-4}\) | \(8.03607 \times 10^{-10}\) |
| \(z\) | \(t=0.3\) | \(t=0.6\) | \(t=0.9\) |
|---|---|---|---|
| 0.1 | \(1.65467\times 10^{-9}\) | \(9.45648\times 10^{-10}\) | \(9.08267\times 10^{-11}\) |
| 0.2 | \(2.41125\times 10^{-9}\) | \(4.83308\times 10^{-10}\) | \(1.88788\times 10^{-9}\) |
| 0.3 | \(1.59463\times 10^{-9}\) | \(1.8858\times 10^{-9}\) | \(1.66441\times 10^{-9}\) |
| 0.4 | \(1.1292\times 10^{-9}\) | \(1.41938\times 10^{-10}\) | \(1.73461\times 10^{-9}\) |
| 0.5 | \(7.24165\times 10^{-11}\) | \(2.73845\times 10^{-10}\) | \(6.03381\times 10^{-10}\) |
| 0.6 | \(1.01843\times 10^{-9}\) | \(2.76671\times 10^{-10}\) | \(8.11171\times 10^{-10}\) |
| 0.7 | \(1.63854\times 10^{-9}\) | \(1.72031\times 10^{-9}\) | \(1.29951\times 10^{-9}\) |
| 0.8 | \(2.40511\times 10^{-9}\) | \(5.05605\times 10^{-10}\) | \(1.8508\times 10^{-9}\) |
| 0.9 | \(1.67916\times 10^{-9}\) | \(8.54546\times 10^{-10}\) | \(7.47452\times 10^{-11}\) |
This paper introduced an explicit Delannoy-tau spectral scheme for the numerical solution of the time-fractional diffusion equation with the Caputo derivative. By employing shifted Delannoy polynomials as basis functions, the method transforms the governing equation into a well-structured system of algebraic equations that can be solved without iterations. The proposed technique blends the precision of spectral approaches with the efficacy of explicit schemes, making it computationally attractive for large-scale or real-time simulations. Numerical examples confirm the precision and resilience of the approach. Future work may explore the application of the presented framework to multidimensional TFDEs, variable-order fractional models, and coupled systems arising in mathematical physics and engineering.
Podlubny, I. (1998). Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications (Vol. 198). Elsevier.
Xue, D., & Lu, B. (2024). Fractional calculus: High-Precision Algorithms and Numerical Implementations.
Srivastava, H. M. (2023). An introductory overview of special functions and their associated operators of fractional calculus. In Special Functions in Fractional Calculus and Engineering (pp. 1–35).
Youssri, Y. H., Ismail, M. I., & Atta, A. G. (2023). Chebyshev Petrov–Galerkin procedure for the time-fractional heat equation with nonlocal conditions. Physica Scripta, 99(1), 015251.
Moustafa, M., Youssri, Y. H., & Atta, A. G. (2023). Explicit Chebyshev Petrov–Galerkin scheme for time-fractional fourth-order uniform Euler–Bernoulli pinned–pinned beam equation. Nonlinear Engineering, 12(1), 20220308.
Ahmed, H. M. (2023). A new first finite class of classical orthogonal polynomials operational matrices: An application for solving fractional differential equations. Contemporary Mathematics, 4(4), 974–994.
Ahmed, H. M. (2024). Enhanced shifted Jacobi operational matrices of integrals: Spectral algorithm for solving some types of ordinary and fractional differential equations. Boundary Value Problems, 2024, Article 75.
Abdelhakem, M., Abdelhamied, D., El-Kady, M., & Youssri, Y. H. (2025). Two modified shifted Chebyshev–Galerkin operational matrix methods for even-order partial boundary value problems. Boundary Value Problems, 2025, Article 34.
Taema, M. A., Dagher, M. A., & Youssri, Y. H. (2025). Spectral collocation method via Fermat polynomials for Fredholm–Volterra integral equations with singular kernels and fractional differential equations. Palestine Journal of Mathematics, 14(2), 481–492.
Youssri, Y. H., Atta, A. G., Moustafa, M. O., & Abu Waar, Z. Y. (2025). Explicit collocation algorithm for the nonlinear fractional Duffing equation via third-kind Chebyshev polynomials. Iranian Journal of Numerical Analysis and Optimization, 15(2), 655–675.
Abbas, A. M., Youssri, Y. H., El-Kady, M., & Abdelhakem, M. (2025). Cutting-edge spectral solutions for differential and integral equations utilizing Legendre’s derivatives. Iranian Journal of Numerical Analysis and Optimization, 15(2), 655-675.
Touati Brahim, M. S., Youssri, Y. H., Alburaikan, A., Khalifa, H., & Radwan, T. (2025). A refined Galerkin approach for solving higher-order differential equations via Bernoulli polynomials. Fractals, 33(1), 2150001.
Abbas, A. M., Youssri, Y. H., El-Kady, M., & Abdelhakem, M. (2025). High-accuracy modified spectral techniques for two-dimensional integral equations. Journal of Computational and Applied Mechanics, 56(2), 364–379.
Atta, A. G., Abd-Elhameed, W. M., & Youssri, Y. H. (2025). Approximate collocation solution for the time-fractional Newell–Whitehead–Segel equation. Journal of Applied and Computational Mechanics, 11(2), 529–540.
Albeladi, G., Gamal, M., & Youssri, Y. H. (2025). G-metric spaces via fixed point techniques for \(\psi\)-contraction with applications. Fractal and Fractional, 9(3), 196.
Youssri, Y. H., Alnaser, L. A., & Atta, A. G. (2025). A spectral collocation approach for time-fractional Korteweg–de Vries–Burgers equation via first-kind Chebyshev polynomials. Contemporary Mathematics, 6(2), 1501–1519.
Taema, M. A., Zeen El Deen, M. R., & Youssri, Y. H. (2025). Fourth-kind Chebyshev operational tau algorithm for fractional Bagley–Torvik equation. Frontiers in Scientific Research and Technology, 2(1), 45–60.
Youssri, Y. H., & Atta, A. G. (2025). Adopted Chebyshev collocation algorithm for modeling human corneal shape via the Caputo fractional derivative. Contemporary Mathematics, 6(1), 1223–1238.
Youssri, Y. H., Abd-Elhameed, W. M., Elmasry, A. A., & Atta, A. G. (2025). An efficient Petrov–Galerkin scheme for the Euler–Bernoulli beam equation via second-kind Chebyshev polynomials. Fractal and Fractional, 9(2), 78.
Youssri, Y. H., & Atta, A. G. (2025). Chebyshev Petrov–Galerkin method for nonlinear time-fractional integro-differential equations with a mildly singular kernel. Journal of Applied Mathematics and Computing, 71, 3891–3911.
Sayed, S. M., Mohamed, A. S., Abo-Eldahab, E. M., & Youssri, Y. H. (2025). Spectral framework using modified shifted Chebyshev polynomials of the third-kind for numerical solutions of one- and two-dimensional hyperbolic telegraph equations. Boundary Value Problems, 2025, Article 7.
Abdelghany, E. M., Abd-Elhameed, W. M., Moatimid, G. M., Youssri, Y. H., & Atta, A. G. (2025). Petrov–Galerkin Lucas polynomials approach for solving the time-fractional diffusion equation. Mathematical Systems Science, 3(1), 3013.
Atta, A. G. (2024). Spectral collocation approach with shifted Chebyshev third-kind series approximation for nonlinear generalized fractional Riccati equation. International Journal of Applied and Computational Mathematics, 10(2), Article 59.
Abd-Elhameed, W. M., Youssri, Y. H., & Atta, A. G. (2024). Adopted spectral tau approach for the time-fractional diffusion equation via seventh-kind Chebyshev polynomials. Boundary Value Problems, 2024(1), Article 102.
Youssri, Y. H., Atta, A. G., Moustafa, M. O., & Abu Waar, Z. Y. (2025). Explicit collocation algorithm for the nonlinear fractional Duffing equation via third-kind Chebyshev polynomials. Iranian Journal of Numerical Analysis and Optimization, 15(2), 655–675.
Zayernouri, M., Wang, L.-L., Shen, J., & Karniadakis, G. E. (2024). In: Spectral and Spectral-Element Methods for Fractional Ordinary and Partial Differential Equations. Cambridge University Press.
Yüzbaşı, S. (2024). Fractional Bell collocation method for solving linear fractional integro-differential equations. Mathematical Sciences, 18(1), 29–40.
Jiang, W., & Gao, X. (2024). Review of collocation methods and applications in solving science and engineering problems. CMES-Computer Modeling in Engineering & Sciences, 140(1), 41-76.
Mostafazadeh, M., & Shahmorad, S. (2024). Convergence analysis of Jacobi spectral tau–collocation method in solving a system of weakly singular Volterra integral equations. Mathematics and Computers in Simulation, 223, 322–337.
Atta, A. G., & Youssri, Y. H. (2024). Enhanced spectral collocation Gegenbauer approach for the time-fractional Fisher equation. Mathematical Methods in the Applied Sciences, 47(18), 14173–14187.
Shen, J. (1994). Efficient spectral-Galerkin method I: Direct solvers of second- and fourth-order equations using Legendre polynomials. SIAM Journal on Scientific Computing, 15(6), 1489–1505.
Abdelhamid, D., Albalawi, W., Nisar, K. S., Abdel-Aty, A., Alsaeed, S., & Abdelhakem, M. (2023). Mixed Chebyshev and Legendre polynomials differentiation matrices for solving initial-boundary value problems. AIMS Mathematics, 8(10), 24609–24631.
Abd-Elhameed, W. M., Youssri, Y. H., & Atta, A. G. (2024). Adopted spectral tau approach for the time-fractional diffusion equation via seventh-kind Chebyshev polynomials. Boundary Value Problems, 2024(1), Article 102.
Moustafa, M., Youssri, Y. H., & Atta, A. G. (2024). Explicit Chebyshev–Galerkin scheme for the time-fractional diffusion equation. International Journal of Modern Physics C, 35(01), 2450002.
Abdelghany, E. M., Abd-Elhameed, W. M., Moatimid, G. M., Youssri, Y. H., & Atta, A. G. (2023). A tau approach for solving time-fractional heat equation based on the shifted sixth-kind Chebyshev polynomials. Symmetry, 15(3), 594.
Atta, A. G., Abd-Elhameed, W. M., Moatimid, G. M., & Youssri, Y. H. (2022). Modal shifted fifth-kind Chebyshev tau integral approach for solving heat conduction equation. Fractal and Fractional, 6(11), 619.
Abd-Elhameed, W. M., Youssri, Y. H., & Atta, A. G. (2024). Tau algorithm for fractional delay differential equations utilizing seventh-kind Chebyshev polynomials. Journal of Mathematical Modeling, 12(2), 277–299.
Sayevand, K., Yazdani, A., & Arjang, F. (2016). Cubic B-spline collocation method and its application for anomalous fractional diffusion equations in transport dynamic systems. Journal of Vibration and Control, 22(9), 2173–2186.
Zeng, F., & Li, C. (2017). A new Crank–Nicolson finite element method for the time-fractional subdiffusion equation. Applied Numerical Mathematics, 121, 82–95.