We construct a semigroup of composition operators on a subspace of the Dirichlet space of the upper half-plane. We then determine both the semigroup and spectral properties of the composition semigroup. Finally, we represent the resolvents of the infinitesimal generator as integral operators and obtain their norm and spectra.
Let \(\mathbb{C}\) be the complex plane. The open unit disk is the set, \(\mathbb{D} = \{z \in \mathbb{C} : |z| < 1\}\). Let \(w \in \mathbb{C}\) and \(\Im (w)\) be the imaginary part of \(w\). We denote the upper half-plane of \(\mathbb{C}\) by \(\mathbb{U} = \{w \in \mathbb{C} \mid \Im (w) > 0\}\). Also, the area Lebesgue measure on \(\mathbb{U}\) is denoted by \(d\mu_{\alpha}(w)\) . The function, \(\psi (z) = \frac{i(1+z)}{1-z}\) that maps \(\mathbb{D}\) conformally onto \(\mathbb{U}\) is known as the Cayley Transform and it is invertible. See [1] for more details.
Let \(\mathcal{H}(\Omega)\) be the Frétchet space of analytic functions \(f:\Omega \rightarrow \mathbb{C}\) endowed with topology of uniform convergence on compact subsets of \(\Omega\). For \(\alpha >-1\), the weighted Bergman space of \(\mathbb{U}\), \(L_{a}^2 (\mathbb{U}, \mu_{\alpha})\) is defined as \[\begin{equation*} L^{2}_{a}(\mathbb{U},\mu_{\alpha})=\left\{f\in\mathcal{H}(\mathbb{U}): \vert\vert\ f \vert\vert _{L^{2}_{a}(\mathbb{U},\mu_{\alpha})}= \left(\int_{\mathbb{U}}\vert f(w)\vert^{2}d\mu_{\alpha}(w)\right)^{\frac{1}{2}}< \infty\right\}, \end{equation*}\] and whenever \(\alpha = 0\) the growth condition is given by \[\begin{equation} \label{eqn : 13} |f(w)| \leq \frac{K\|f\|_{L^{2}_{a}(\mathbb{U},\mu_{0})}}{\Im (w)} \quad \text{for some constant } K, \forall f\in L_{a}^2 (\mathbb{U},\mu_{0}) . \end{equation} \tag{1}\]
For a more comprehensive detail on the theory of Bergman spaces, we refer to [1– 5].
For \(\alpha >-1\), the weighted Dirichlet space of the upper half-plane, \(\mathscr{D}_{\alpha}(\mathbb{U})\), is defined by \[\begin{equation*} \mathscr{D}_{\alpha}(\mathbb{U}) = \left\{f \in \mathcal{H}(\mathbb{U}) : \|f\|_{\mathscr{D}_{\alpha , 1}(\mathbb{U})} = \left(\int_{\mathbb{U}} |f'(w)|^2 d\mu_{\alpha}(w)\right)^{\frac{1}{2}} < \infty\right\} , \end{equation*}\]where \(\|\cdot\|_{\mathscr{D}_{\alpha, 1}(\mathbb{U})}\) is a seminorm on \(\mathscr{D}_{\alpha}(\mathbb{U})\) and the norm is given by \(\|f\|_{\mathscr{D}_{\alpha}(\mathbb{U})}^2 = |f(i)|^2 + \|f\|_{\mathscr{D}_{\alpha ,1}(\mathbb{U})}^2, \forall f \in \mathscr{D}_{\alpha}(\mathbb{U})\). Whenever \(\alpha = 0\) the growth condition of functions in \(\mathscr{D}_{0}(\mathbb{U})\) is given by \[\begin{equation} \label{eqn:11} |f(w)| \leq \|f\|_{\mathscr{D}_{0}(\mathbb{U})} \sqrt{1+\log \left( \frac{|w+i|^2}{4\Im(w)} \right)} \quad \forall f \in \mathscr{D}_{0}(\mathbb{U}). \end{equation} \tag{2}\]
A function \(f \in \mathscr{D}_{\alpha}(\mathbb{U})\) if and only if \(f' \in L_{a}^2 (\mathbb{U}, \mu_{\alpha})\). For \(\alpha > -1\), a closed subspace of \(\mathscr{D}_{\alpha}(\mathbb{U})\) that consists of functions that vanish at \(i\) is defined as \(\mathscr{D}_{\alpha}^{i}(\mathbb{U}) = \{ f \in \mathscr{D}_{\alpha}(\mathbb{U}) : f(i) = 0 \}\). The subspace \(\mathscr{D}_{\alpha}^{i}(\mathbb{U})\) is a Banach space with respect to \(\|\cdot\|_{\mathscr{D}_{\alpha}(\mathbb{U})}\). It suffices to check if \(\mathscr{D}_{\alpha}^{i}(\mathbb{U})\) is closed in \(\|\cdot\|_{\mathscr{D}_{\alpha}(\mathbb{U})}\). Indeed, if we let \(f_n\) to be a convergent sequence in \(\mathscr{D}_{\alpha}^{i}(\mathbb{U})\) and \(f\in \mathscr{D}_{\alpha}(\mathbb{U})\) such that \(f_n \to f \text{ as } n \to \infty\) in the Dirichlet norm, that is, \(\lim_{n \to \infty}\| f_n – f \|_{\mathscr{D}_{\alpha}(\mathbb{U})} = 0\) then this is equivalent to \[\begin{equation*} |(f_n – f)(i) | \to 0 \, \& \int_{\mathbb{U}} |(f_n – f)'(w) |^2 \, d\mu_{\alpha}(w) \to 0 \text{ as } n \to \infty. \end{equation*}\]
Since \(\forall n, f_n (i) = 0\) then \(\lim_{n \to \infty}\, f_n (i) = f(i) = 0\). Together with the assumption that \(f\in \mathscr{D}_{\alpha}(\mathbb{U})\), it follows that \(f \in \mathscr{D}_{\alpha}^{i}(\mathbb{U})\), as desired. The subspace, \(\mathscr{D}_{\alpha}^{i}(\mathbb{U})\) was also discussed in [4] and also considered in [5] where Schroderus used a version of the Paley-Wiener theorem for the weighted Dirichlet space as well as some spectral results to establish the relation \(\mathscr{D}_{\alpha}^{i}(\mathbb{U}) = L_a^2 (\mathbb{U},\mu_{\tau})\) with \(\tau = \alpha – 2\). See [4– 9] for more details on Dirichlet spaces.
Let \(X\) be an arbitrary Banach Space over \(\mathbb{C}\) and \(T\) be a closed linear operator on \(X\). The point spectrum of \(T\), \(\sigma_p (T) = \{\lambda \in \mathbb{C} : \lambda f = Tf , \text{ for some } 0 \neq f \in dom(T)\}\). The spectrum of \(T\), \(\sigma (T) = \{\lambda \in \mathbb{C} : (\lambda I – T)\quad \text{is not invertible}\}\). The resolvent set of \(T\), \(\rho(T) = \mathbb{C} \setminus \sigma(T)\). Moreover, \(r(T) = \sup \{|\lambda| : \lambda \in \sigma(T)\}\) defines the spectral radius of \(T\). For \(\lambda \in \rho(T)\), the operator \(R(\lambda,T) = (\lambda I – T)^{-1}\) is called the resolvent of \(T\) at \(\lambda\) or simply the resolvent operator. Details on the spectra of linear operators are found in [10– 12].
A semigroup, \((T_t)_{_{t \geq 0}}\), is said to be strongly continuous on \(X\) if \(\lim_{t \rightarrow 0^+}\|T_t f – f\|_{X} = 0, \quad \forall f \in X.\) For each \(f \in dom(\Gamma)\), the infinitesimal generator \(\Gamma\) of \((T_t)_{_{t \geq 0}}\) is defined by \[\begin{eqnarray*} \Gamma f = \lim_{t \rightarrow 0^+} \frac{T_{_t}f – f}{t} = \frac{\partial}{\partial t} (T_{_t}f – f) \Bigg| _{t=0}, \end{eqnarray*}\] and the domain of \(\Gamma\) is given by \[\begin{eqnarray*} \text{dom}(\Gamma) &=& \left\{ f \in X \mid \lim_{t \rightarrow 0^+} \frac{T_{_t}f – f}{t} \text{ exists} \right\}. \end{eqnarray*}\]
Defined as above, the infinitesimal generator \(\Gamma\) of a strongly continuous semigroup on \(X\), considered together with its domain \(\text{dom}(\Gamma)\), is a closed and densely defined operator that determines the semigroup uniquely, see for instance [11] or [12, Theorem 1.4]. If \((T_t)_{_{t \geq 0}}\) and \((T_t)_{_{t \leq 0}}\) are both semigroups of bounded linear operators on \(X\), then \((T_t)_{_{t \in \mathbb{R}}}\) is a group on \(X\). For details on the theory for semigroups, see [11, 12].
Let \(\varphi\) be a self map on \(\Omega\), then the composition operator, \(C_{\varphi}\), induced by \(\varphi\) and is acting on \(\mathcal{H}(\Omega)\) is defined by \(C_{\varphi} f = f \circ \varphi, \quad \forall f \in \mathcal{H}(\Omega).\)
The composition semigroup, \((C_{\varphi_t})_{t \geq 0}\), induced by a semigroup of self analytic maps, \((\varphi_{t})_{t \geq 0}\), and is acting on \(\mathcal{H}(\Omega)\) is defined by \(C_{\varphi_t}f = f \circ \varphi_t,\quad \forall f \in \mathcal{H}(\Omega).\)
The theory of composition semigroups on analytic spaces of the \(\mathbb{D}\) is given more comprehensively in [13, 14]. The study of composition semigroups on the analytic spaces of the upper half-plane was initiated by [15] on the Hardy space, and was extended in [16] to the Hardy and weighted Bergman spaces. On \(\mathscr{D}_{\alpha}(\mathbb{U})\), the composition semigroups have been partially considered by [9, 17, 18]. Despite this, the composition semigroup induced by the translation group on \(\mathscr{D}_{\alpha}(\mathbb{U})\) has not been studied. In this work we investigate the properties of the composition semigroup induced by the translation group on \(\mathscr{D}_{\alpha}(\mathbb{U})\), where \(\alpha = 0\).
The continuous groups of automorphisms of the upper half-plane are classified into three distinct groups [16], that is, the translation group, the scaling group and the rotation groups depending on the location of their fixed points. In this paper we consider the group of composition operators on \(\mathscr{D}_{0}(\mathbb{U})\) associated with the translation group of the form \(\varphi_t (w) = w+t\) for \(w\in \mathbb{U}\) where \(\varphi_t\) is a family of self analytic maps. Henceforth, we let \(C_{\varphi_t}= C_{t}\) and define the composition semigroup that is induced by \(\varphi_t (w)\) on \(\mathscr{D}_{0}(\mathbb{U})\) as \[\begin{equation*} C_{t}f(w)= f(w+t). \end{equation*}\]
We note that under composition, the operators \((C_{t})_{t \in \mathbb{R}}\) form a group on \(\mathscr{D}_{0}(\mathbb{U})\).
Theorem 1. The operator \(C_{t}\) fails to be an isometry on \(\mathscr{D}_{0}(\mathbb{U})\).
Proof. By norm definition, \[\begin{eqnarray} \|C_{t}f\|_{\mathscr{D}_{0}(\mathbb{U})}^2 &=& |f(i+t)|^2 + \int_{\mathbb{U}}|(f(w+t))'|^2 d\mu_0(w)\nonumber \\ \label{eqn:1} &=& |f(i+t)|^2 + \int_{\mathbb{U}}|f' (w+t)|^2 \, d\mu_0(w). \end{eqnarray} \tag{3}\]
By change of variables, let \(z = w + t\) then \(w = z – t\) which implies \(d\mu_0(w) = d\mu_0(z)\). Substituting into Eq. (3),
\[\begin{equation*} \|C_{t}f\|_{\mathscr{D}_{0}(\mathbb{U})}^2 = |f(i+t)|^2 + \int_{\mathbb{U}}|f'(z)|^2 \, d\mu(z) \neq \|f\|_{\mathscr{D}_{0}(\mathbb{U})}^2. \end{equation*}\] ◻
Remark 1. As a consequence of Theorem 1, we proceed with the approach employed in [9]. On \(\mathscr{D}_{0}^{i}(\mathbb{U})\), \(C_{t}f(i) = f(i+t) \neq 0\) meaning that \(C_{t}\) does not map \(\mathscr{D}_{0}^{i}(\mathbb{U})\) to itself as is expected for such semigroups. Therefore, we redefine \(C_{t}\) by applying a correction factor, that is, \[\begin{equation*} \label{eq:2} \hat{C}_{t}f(w) = f(w+t) – f(i+t) . \end{equation*}\]
At \(i\), \(\hat{C}_{t}f(i) = f(i+t) – f(i+t) = 0\) and therefore \(\hat{C}_{t} : \mathscr{D}_{0}^{i}(\mathbb{U}) \rightarrow \mathscr{D}_{0}^{i}(\mathbb{U})\).
We note that \(( \hat{C}_{t} )_{t \in \mathbb{R}}\) forms a group under composition on \(\mathscr{D}_{0}^{i}(\mathbb{U})\).
Proposition 1. The operator \(\hat{C}_{t}\) is a norm isometry on \(\mathscr{D}_{0}^{i}(\mathbb{U})\).
Proof. By the definition of the norm on \(\mathscr{D}_{0}^{i}(\mathbb{U})\), \[\begin{eqnarray} \|\hat{C}_{t} f\|_{\mathscr{D}_{0}^{i}(\mathbb{U})}^2 &=& \int_{\mathbb{U}} |(\hat{C}_{t}f) '(w)|^2 \, d\mu_0(w). \nonumber \\ &=&\int_{\mathbb{U}}|(f(w+t)-f(i+t))'|^2 d\mu_0(w). \nonumber \\ &=& \int_{\mathbb{U}}|f'(w+t)|^2 d\mu_0(w). \label{eqn:3} \end{eqnarray} \tag{4}\] Again we change the variables, if \(z = w+t\) then \(w=z-t\) which implies \(d\mu_0(w)=d\mu_0(z)\) and thus substituting in Eq. (4) gives, \[\begin{eqnarray*} \|\hat{C}_{t}f \|_{\mathscr{D}_{0}^{i}(\mathbb{U})}^2 = \int_{\mathbb{U}} |f'(z)|^2 d\mu_0(z) = \|f\|^2_{\mathscr{D}_{0}^{i}(\mathbb{U})}. \label{eqn:4} \end{eqnarray*}\] ◻
Proposition 2. The operator \(\hat{C}_{t}\) is strongly continuous on \(\mathscr{D}_{0}^{i}(\mathbb{U})\).
Proof. To prove that \(\hat{C}_{t}\) is strongly continuous it suffices to show that \(\forall f \in \mathscr{D}_{0}^{i}(\mathbb{U})\,\text{we have}\, \lim_{t\rightarrow 0^+}\|\hat{C}_{t} f – f\|_{\mathscr{D}_{0}^{i}(\mathbb{U})} = 0\).
Now, suppose \(t_n \rightarrow 0\) in \(\mathbb{R}\) and \(f \in \mathscr{D}_{0}^{i}(\mathbb{U}) = L_a^2 (\mathbb{U},\mu_{-2})\). Let \(f_{n} = \hat{C}_{t_{n}} f\), then \(f_{n}(w) \rightarrow f(w)\) uniformly on compact subsets of \(\mathbb{U}\) for each \(n\) with \(\|f_{n}\|_{L_a^2 (\mathbb{U},\mu_{-2})}=\|f\|_{L_a^2 (\mathbb{U},\mu_{-2})}\). If \(g_n = 2\left(|f|^2 + |f_{n}|^2\right) – |f-f_{n}|^2\), then \(g_n \geq 0\) and \(g_n (w)\rightarrow 4|f(w)|^2\), as \(n \rightarrow \infty\) on \(L_a^2 (\mathbb{U},\mu_{-2})\).
By Fatou’s lemma we have \[\begin{align*} \int_{\mathbb{U}} 4|f|^2 \, d\mu_{-2}(w) &= \int_{\mathbb{U}} \liminf_n g_n \, d\mu_{-2}(w) \\ &\leq \liminf_n \int_{\mathbb{U}} g_n \, d\mu_{-2}(w) \\ &= \liminf_n \int_{\mathbb{U}} 2\big(|f|^2 + |f_{n}|^2\big) – |f – f_{n}|^2 \, d\mu_{-2}(w) \\ &= \int_{\mathbb{U}} 2|f|^2 \, d\mu_{-2}(w) + \int_{\mathbb{U}} 2|f|^2 \, d\mu_{-2}(w) \\ &\qquad – \limsup_n \int_{\mathbb{U}} |f – f_{n}|^2 \, d\mu_{-2}(w) \\ &= 4 \int_{\mathbb{U}} |f|^2 \, d\mu_{-2}(w) – \limsup_n \int_{\mathbb{U}} |f – f_{n}|^2 \, d\mu_{-2}(w). \end{align*}\]
As a result, \(0 \leq -\limsup_n \int_{\mathbb{U}}|f-f_{n}|^2d\mu_{-2}(w) \leq 0,\) which implies that \(\limsup_n \int_{\mathbb{U}}|f-f_{n}|^2d\mu_{-2}(w) = 0.\) Therefore, \(\lim_n \|\hat{C}_{t_n} f – f \|_{L_a^2 (\mathbb{U},\mu_{-2})}^2 = 0.\) Consequently, \(\|\hat{C}_{t} f – f\|_{\mathscr{D}_{0}^{i}(\mathbb{U})} \rightarrow 0\) as \(t \rightarrow 0^+\) and therefore \(\hat{C}_{t}\) is strongly continuous on \(\mathscr{D}_{0}^{i}(\mathbb{U})\) as desired. ◻
Proposition 3. The infinitesimal generator, \(\Gamma : dom(\Gamma) \to \mathscr{D}_{0}^{i}(\mathbb{U})\), of \(\hat{C}_{t}\) is given by \[\Gamma f(w) = f'(w) – f'(i),\] with its domain given as \(dom(\Gamma) = \{ f \in \mathscr{D}_{0}^{i}(\mathbb{U}) : f' \in \mathscr{D}_{0}^{i}(\mathbb{U}) \}.\)
Proof. Let \(w \in \mathbb{U}\) and \(f \in dom(\Gamma)\) in \(\mathscr{D}_{0}^{i}(\mathbb{U})\) then by definition of the infinitesimal generator \(\Gamma\), \[\begin{eqnarray} \Gamma f(w) &=& \frac{\partial}{\partial t} \Big(f(w+t)-f(i+t)\Big)\Bigg|_{t=0} \nonumber \\ &=& f'(w+t)-f'(i+t) \Big|_{t=0} \nonumber \\ \label{eqn: generator} &=& f'(w)-f'(i). \end{eqnarray} \tag{5}\]
This proves that \(dom(\Gamma) \subseteq \{ f \in \mathscr{D}_{0}^{i}(\mathbb{U}) : f' \in \mathscr{D}_{0}^{i}(\mathbb{U}) \}\). To show the converse, let \(f \in \mathscr{D}_{0}^{i}(\mathbb{U})\) such that \(f' \in \mathscr{D}_{0}^{i}(\mathbb{U})\). By the Fundamental Theorem of Calculus, \[\begin{eqnarray*} \hat{C}_{t}f(w) – f(w) &=& \int_0^t \frac{\partial}{\partial s}(\hat{C}_{s}f(w))ds \\ &=& \int_0^t \frac{\partial}{\partial s}(f(w+s)-f(i+s))ds \nonumber \\ &=& \int_0^t f'(w+s)-f'(i+s)ds \\ &=& \int_0^t \hat{C}_{s} F(w) ds, \quad \text{ for } F(w) = f'(w) – f'(i) \in \mathscr{D}_{0}^{i}(\mathbb{U}). \end{eqnarray*}\]
Thus, \[\begin{eqnarray} \lim_{t \rightarrow 0^+} \frac{\hat{C}_{t}f(w) – f(w)}{t} &=& \lim_{t \rightarrow 0^+} \frac{1}{t} \int_0^t \hat{C}_{s} F(w) ds, \nonumber \end{eqnarray}\] where \(F(w) = f'(w) – f'(i) \in \mathscr{D}_{0}^{i}(\mathbb{U}).\) Strong continuity of \((\hat{C}_{s})_{s \in \mathbb{R}}\) implies that \(\frac{1}{t} \int_0^t \|\hat{C}_{s} F – F\|ds \rightarrow 0\) as \(t \rightarrow 0\). Therefore, \(dom(\Gamma) = \{ f \in \mathscr{D}_{0}^{i}(\mathbb{U}) \mid f' \in \mathscr{D}_{0}^{i}(\mathbb{U}) \}\), which concludes our proof. ◻
Lemma 1. For \(z \in \mathbb{U}\), a function \(f(z) = e^{i z} (z + i)^{-c} \in \mathscr{D}_{0}(\mathbb{U})\) if \(\frac{1}{2}<c< \infty\).
Proof. Let \(f(z)=e^{i z} (z + i)^{-c}\) then \[\begin{align*} f'(z) &= e^{i z} (z + i)^{-c} \left( -\frac{c}{z + i} + i \right). \end{align*}\]
For \(z=x+iy\) we have \[\begin{eqnarray*} |f'(z)|^2 & =& \frac{e^{-2y} \left[ x^2 + (c + y + 1)^2 \right]}{\left[ x^2 + (y + 1)^2 \right]^{c + 1}} \end{eqnarray*}\] and \[\begin{eqnarray*} \|f\|^2_{\mathscr{D}_{0,1}(\mathbb{U})} &=& \int_{0}^{\infty}\int_{-\infty}^{\infty} \frac{e^{-2y} \left[ x^2 + (c + y + 1)^2 \right]}{\left[ x^2 + (y + 1)^2 \right]^{c + 1}} dxdy, \end{eqnarray*}\] which is finite if \(\frac{1}{2}<c<\infty\). ◻
Theorem 2. Let \(\Gamma\) be the infinitesimal generator of \(\hat{C}_{t}\) given in Eq. (5), then the \(\sigma_p (\Gamma) = \emptyset\) and \(\sigma(\Gamma) = \{is :s\geq 0\}\).
Proof. Let \(\Gamma\) be the infinitesimal generator of \(\hat{C}_{{t}}\), and \(\lambda \in \mathbb{C}\) such that \(\lambda \in \sigma_p (\Gamma)\). Also, let \(f\) be the corresponding eigen function, then for some \(0 \neq f \in \mathscr{D}_{\alpha}^{i}(\mathbb{U})\) we have \[\begin{eqnarray} \lambda \in \sigma_p (\Gamma) &\Leftrightarrow & \lambda f= \Gamma f \nonumber \\ \label{eqn:8} &\Leftrightarrow & \lambda f(w) = f'(w) – f'(i). \end{eqnarray} \tag{6}\]
We solve Eq. (6). Let \(f'(i) = A\) then \(f'(w) – \lambda f(w) = A\). The integrating factor, \(I.F = e^{\int -\lambda dw} = e^{-\lambda w}\), which implies \[\begin{equation*} e^{-\lambda w} f(w) = A\int e^{-\lambda w} dw \Leftrightarrow f(w) = \frac{A}{-\lambda} + B e^{\lambda w} \end{equation*}\] where B is a constant of integration. By simple calculation we have that \(e^{\lambda w}\notin \mathscr{D}_{0}^{i}(\mathbb{U})\) therefore \(f(w) \notin \mathscr{D}_{0}^{i}(\mathbb{U})\). This implies \(\nexists\) such \(\lambda \in \mathbb{C}\) hence \(\sigma_p (\Gamma) = \emptyset\).
Next we calculate the spectrum, \(\sigma (\Gamma)\).
The spectral mapping theorem for semigroups asserts that, \(e^{t \sigma (\Gamma)} \subseteq \sigma(\hat{C}_{t})\). Since Proposition 1 holds we have \(\sigma(\hat{C}_{t}) \subseteq \partial \mathbb{D}\). This gives the relation, \(e^{t \sigma (\Gamma)} \subseteq \sigma(\hat{C}_{t}) \subseteq \partial \mathbb{D}\). Let \(\lambda \in \sigma(\Gamma)\), then \(|e^{\lambda t}| = 1\). This shows that \(e^{t \Re (\lambda)} = 1\) which means \(t \Re (\lambda) = 0\) implying \(\Re (\lambda) = 0\) and so \(\lambda \in i\mathbb{R}\) which shows \(\sigma(\Gamma) \subseteq i\mathbb{R}\).
Let \(\lambda = is \text{ for }s\geq 0\) and since \((\lambda I – \Gamma)f=h\) for \(h \in \mathscr{D}_{0}^{i}(\mathbb{U})\) we have \[\begin{eqnarray} &&\lambda f(w) = h(w) +f'(w) – f'(i) \nonumber \\ &\Leftrightarrow & \lambda f(w)-f'(w)= h(w) – f'(i) \nonumber \\ \label{eqn:10} &\Leftrightarrow & f'(w)-\lambda f(w)= f'(i) -h(w). \end{eqnarray} \tag{7}\]
If we let \(f'(i) = A\) and solve Eq. (7) by the integrating factor method we have, \[\begin{eqnarray} \label{eqn:14} (e^{-\lambda w} f(w))' &=& e^{-\lambda w} \left(A-h(w)\right). \end{eqnarray} \tag{8}\]
If \(h(w)=e^{\lambda w} (w + \lambda)^{-c} – e^{\lambda i } (i + \lambda)^{-c}\) for \(\frac{1}{2}<c<\infty\) then from Eq. (8) we have, \[\begin{eqnarray} f(w) &=& e^{\lambda w}\int (A+e^{\lambda i } (i + \lambda)^{-c})e^{-\lambda w} – (w + \lambda)^{-c})dw. \nonumber \end{eqnarray}\]
Let \(A+e^{\lambda i } (i + \lambda)^{-c} = B\) then \[\begin{eqnarray} \label{eqn:spec} f(w) &=& e^{\lambda w}\int (Be^{-\lambda w} – (w + \lambda)^{-c})dw \nonumber \\ &=& \begin{cases} \frac{-B}{\lambda} – e^{\lambda w} \frac{(w + \lambda)^{1 – c}}{1 – c} + Ke^{\lambda w}, & \text{if } c \ne 1, \\ \frac{-B}{\lambda} – e^{\lambda w}\ln(w + \lambda) + Ke^{\lambda w}, & \text{if } c = 1, \end{cases} \end{eqnarray} \tag{9}\] where \(K\) is a constant of integration. But \(\nexists\) such a \(K\) in either case of Eq. (9) such that \(f(w) \in \mathscr{D}_{0}^{i}(\mathbb{U})\). Therefore \(h \notin ran(\lambda I – \Gamma)\) and \(\{is :s\geq 0\} \subseteq \sigma(\Gamma)\).
For \(\Im(\lambda) < 0\), let \(f \in \mathcal{H}(\mathbb{U})\) be defined as \[\begin{equation} \label{eqn:15} f(w) =e^{\lambda w} \int_w^{\infty} e^{-\lambda z} (A – h(z)) dz. \end{equation} \tag{10}\]
Integrating Eq. (10) along the path \(z= w+\frac{\overline{\lambda}}{|\lambda|}t\) for \(0 \leq t \leq \infty\) implies \[\begin{eqnarray} \label{eqn:16} f(w) &=& \frac{\overline{\lambda}}{|\lambda|} \int_0^{\infty} e^{-|\lambda |t} \left(A – h\left(w+\frac{\overline{\lambda}}{|\lambda|}t\right)\right) dt, \end{eqnarray} \tag{11}\] which is absolutely convergent by the growth condition, Eq. (2), on \(\mathscr{D}_{0}^i(\mathbb{U})\). Eq. (11) is analytic, that is, \[\begin{eqnarray*} f'(w) &=& \frac{\overline{\lambda}}{|\lambda|} \int_0^{\infty} e^{-|\lambda |t} h'\left(w+\frac{\overline{\lambda}}{|\lambda|}t\right) dt, \end{eqnarray*}\] with \[\begin{eqnarray*} |f'(w)| &=& \left|\frac{\overline{\lambda}}{|\lambda|} \int_0^{\infty} e^{-|\lambda |t} h'\left(w+\frac{\overline{\lambda}}{|\lambda|}t\right) dt\right| \\ &\leq & \int_0^{\infty}e^{- |\lambda | t} \left|h'\left(w+\frac{\overline{\lambda}}{|\lambda|}t\right)\right|dt \\ &\leq & \frac{K\|h'\|_{L^{2}_{a}(\mathbb{U}, \mu_0)}}{\Im\left(w+\frac{\overline{\lambda}}{|\lambda |}t\right)}\int_0^{\infty}e^{-|\lambda | t}dt \\ &=& \frac{K\|h'\|_{L^{2}_{a}(\mathbb{U},\mu_0)}}{|\lambda |\Im\left(w+\frac{\overline{\lambda}}{|\lambda |}t\right)} < \infty, \end{eqnarray*}\] and note that \(f(w)\) as defined in Eq. (10) satisfies Eq. (8).
The upper norm bound of \(f\) on \(\mathscr{D}_{0}^{i}(\mathbb{U})\) is given by applying the integral version of Minkowski’s inequality [19], that is, \[\begin{eqnarray} \|f\|^2_{\mathscr{D}_{\alpha}^{i}(\mathbb{U})} &\leq & \int_0^{\infty}e^{- |\lambda | t} \int_{\mathbb{U}} \left|h'\left(w+\frac{\overline{\lambda}}{|\lambda|}t\right)\right|^2 \, d\mu(w) \, dt \nonumber \\ &\leq & \int_0^{\infty}e^{- |\lambda |t} \|h\|^2_{\mathscr{D}_{\alpha}^{i}(\mathbb{U})}\, dt \nonumber \\ &= & \frac{1}{|\lambda |}\|h\|^2_{\mathscr{D}_{\alpha}^{i}(\mathbb{U})}. \end{eqnarray} \tag{12}\]
Therefore, for \(\Im(\lambda) < 0\), the \(R(\lambda,\Gamma)\) exists with \(\|R(\lambda,\Gamma)\| \leq \frac{1}{|\lambda|}\) and thus the set \(\{is: s< 0\} \subseteq \rho(\Gamma)\). As a result we conclude that \(\sigma(\Gamma) = \{is :s\geq 0\}\), as claimed. ◻
Proposition 4. If \(\lambda \in \rho(\Gamma) \text{ and } h \in \mathscr{D}_{0}^{i}(\mathbb{U})\) then \[R(\lambda,\Gamma)h(w) = e^{\lambda w} \int_w^{\infty} e^{-\lambda z} \left( A – h(z) \right) dz,\] and \(R(\lambda,\Gamma): \mathscr{D}_{0}^{i}(\mathbb{U}) \to \mathscr{D}_{0}^{i}(\mathbb{U}).\)
Proof. Let \(h\in \mathscr{D}_{0}^{i}(\mathbb{U})\). If \(f = R(\lambda , \Gamma)h\), then \(f\) satisfies equation (8). Whenever \(\Im(\lambda) \geq 0 \text{ and }0 \leq t \leq \infty\), we integrate Eq. (8) along the path \(z=w+t\) if \(\Re(\lambda) > 0\) while if \(\Re(\lambda) < 0\) we integrate Eq. (8) along the path \(z=w-t\). In both cases we have \[\begin{eqnarray*} R(\lambda , \Gamma)h(w) = e^{\lambda w} \int_w^{\infty} e^{-\lambda z} \left( A – h(z) \right) dz. \end{eqnarray*}\]
Moreover, it’s clear that for any \(h\in \mathscr{D}_{0}^{i}(\mathbb{U})\), \(h(i) = 0\) and therefore obviously \(R(\lambda, \Gamma)h(i)=0\) implying that \(R(\lambda,\Gamma): \mathscr{D}_{0}^{i}(\mathbb{U}) \to \mathscr{D}_{0}^{i}(\mathbb{U}),\) as desired. ◻
Proposition 5. For \(\lambda \in \rho(\Gamma)\),
If \(\Re(\lambda) \neq 0 \text{ and } \Im(\lambda) \geq 0\), then \(\sigma (R(\lambda , \Gamma))\) is the arc from \(\frac{1}{\lambda}\) to \(0\) that contains the upper half of the circle \(\left| z – \frac{1}{2\Re(\lambda)} \right| = \frac{1}{|2\Re(\lambda)|}\).
If \(\Im(\lambda) < 0\), then \(\sigma (R(\lambda , \Gamma))\) is the arc from \(\frac{1}{\lambda}\) to \(0\) contained in the upper half of the circle \(\left| z – \frac{1}{2\Re(\lambda)} \right| = \frac{1}{|2\Re(\lambda)|}\).
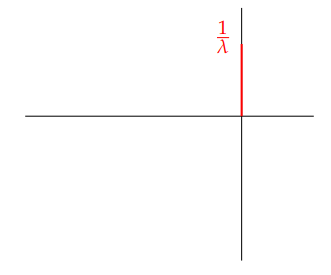
If \(\Re(\lambda) = 0\) then \(\sigma (R(\lambda , \Gamma))\) is the line on the imaginary axis from \(0\) to \(\frac{1}{\lambda}\).
Proof. The spectral mapping theorem for resolvents asserts that \[ \sigma (R(\lambda , \Gamma)) = \left\{ \frac{1}{\lambda – is} : s \geq 0 \right\} \cup \{0\} , \ \tag{13}\] \[\sigma_p (R(\lambda , \Gamma)) = \left\{ \frac{1}{\lambda – \emptyset} \right\} \cup \{0\} = \{0\}, \tag{14}\] and the spectral radius is given by \[\begin{eqnarray} r(R(\lambda , \Gamma)) = \sup \left\{ |\nu| : \nu\in \sigma (R(\lambda , \Gamma))\right\}. \end{eqnarray} \tag{15}\] Now,
1. Whenever \(\Im(\lambda) \geq 0\), the spectrum \(\sigma(R(\lambda , \Gamma) )\) is given as,
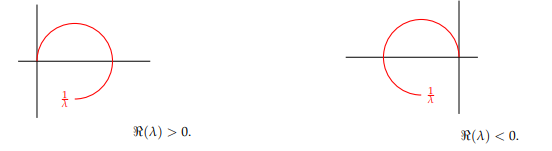
Also, by the Hille-Yosida Theorem and the spectral radius characterization we have \[\begin{eqnarray*} r(R(\lambda , \Gamma)) = \frac{1}{|\Re(\lambda)|} \leq \|R(\lambda , \Gamma)\| \leq \frac{1}{\Re(\lambda)}. \end{eqnarray*}\]
2. If \(\Im(\lambda) < 0\) and \(\Re(\lambda) \neq 0\), the spectrum \(\sigma(R(\lambda , \Gamma) )\) is given as,
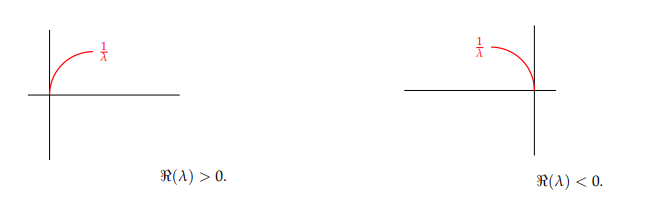
By the Hille-Yosida Theorem and the spectral radius characterization we have \[\begin{eqnarray*} r(R(\lambda , \Gamma)) = \frac{1}{|\lambda|} \leq \|R(\lambda , \Gamma)\| \leq \frac{1}{\Re(\lambda)}. \end{eqnarray*}\]
3. If \(\Re(\lambda) = 0\), then \(r(R(\lambda , \Gamma)) = \frac{1}{|\lambda|}\) and the spectrum \(\sigma(R(\lambda , \Gamma))\) is given as ◻
Zhu, K. (2007). Operator Theory in Function Spaces. Mathematical Surveys and Monographs, American Mathematical Society, Providence, RI.
Peloso, M. (2011). Classical Spaces of Holomorphic Functions. Lecture Notes.
Siskakis, A. G. (1987). Semigroups of composition operators on Bergman spaces. Bulletin of the Australian Mathematical Society, 35, 397–406.
Duren, P., Gallardo-Gutiérrez, E. A., & Montes-Rodríguez, A. (2007). A Paley-Wiener theorem for Bergman spaces with application to invariant subspaces. Bulletin of the London Mathematical Society, 39(3), 459–466.
Schroderus, R. (2017). Spectra of linear fractional composition operators on Hardy and weighted Bergman spaces of the half-plane. Journal of Mathematical Analysis and Applications, 447(2), 817–833.
El-Fallah, O., Kellay, K., Mashreghi, J., & Ransford, T. (2014). A Primer on the Dirichlet Space. Cambridge University Press, Cambridge Tracts in Mathematics.
Wanjiru, J. M., Bonyo, J. O., & Wattanga, I. S. (2022). Reproducing kernel for the classical Dirichlet space of the upper half plane. International Journal of Formal Sciences: Current and Future Research Trends, 15, 199–210.
Ross, W. T. (2006). The classical Dirichlet space. Contemporary Mathematics, 393, 171–197.
Oyugi, E. A., Bonyo, J. O., & Ambogo, D. O. (2023). Cesàro-type operator on the Dirichlet space of the upper half-plane. Communications in Advanced Mathematical Sciences, 6, 128–134.
Davies, E. B. (2007). Linear Operators and Their Spectra. Cambridge University Press, Cambridge Studies in Advanced Mathematics.
Pazy, A. (1970). Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Mathematical Sciences, Springer-Verlag, New York.
Engel, K. J., & Nagel, R. (2006). A Short Course on Operator Semigroups. Universitext, Springer, New York.
Siskakis, A. G. (1998). Semigroups of composition operators on analytic functions: A review. Contemporary Mathematics, 213, 229–252.
Siskakis, A. G. (1996). Semigroups of composition operators on Dirichlet spaces. Results in Mathematics, 30, 165–173.
Arvanitidis, A. G., & Siskakis, A. G. (2013). Cesàro operators on the Hardy spaces of the half-plane. Canadian Mathematical Bulletin, 56(2), 229–240.
Ballamoole, S., Bonyo, J. O., Miller, T. L., & Miller, V. G. (2016). Cesàro operators on the Hardy and Bergman spaces of the half-plane. Complex Analysis and Operator Theory, 10, 187–203.
Agwang, M. O., & Bonyo, J. O. (2020). Spectra of composition groups on the weighted Dirichlet space of the upper half-plane. Acta Mathematica Scientia, 40B, 1739–1752.
Wanja, M., Okello, I., & Bonyo, J. O. (2024). A class of integral operators on the Dirichlet space of the half-plane. (preprint).
Garnett, J. B. (2010). Bounded Analytic Functions. Graduate Texts in Mathematics. Springer, New York.