Degree based graph invariants for the molecular graph of Bismuth Tri-Iodide

The \(BiI_{3}\) is an inorganic compound which is the result of the reaction of iodine and bismuth, which inspired the enthusiasm for subjective inorganic investigations [1]. \(BiI_{3}\) is an excellent inorganic compound and is very useful in “qualitative inorganic analysis” [1, 2].

It was proved that $Bi$-doped glass optical strands are one of the most promising dynamic laser media. Different kinds of Bi-doped fiber strands have been created and have been used to construct Bi-doped fiber lasers and optical loudspeakers [3].

Layered \(BiI_{3}\) gemstones are considered to be a three-layered stack structure in which a plane of bismuth atoms is sandwiched between iodide particle planes to form a continuous \(I-Bi-I\) plane [4].

The periodic superposition of the diamond-shaped three layers forms \(BiI_{3}\) crystals with \(R\)-3 symmetry [5, 6]. A progressive stack of \(I-Bi-I\) layers forms a symmetric hexagonal structure [7] and jewel of \(BiI_{3}\) was integrated in [8].

In the unit cell (Figure 1), Main cycles are \(C_{4}^{1} ,C_{4}^{2}\) central cycles are \(C_{4}^{3} ,C_{4}^{6}\) and Base cycles are \(C_{4}^{4} ,C_{4}^{5}\)

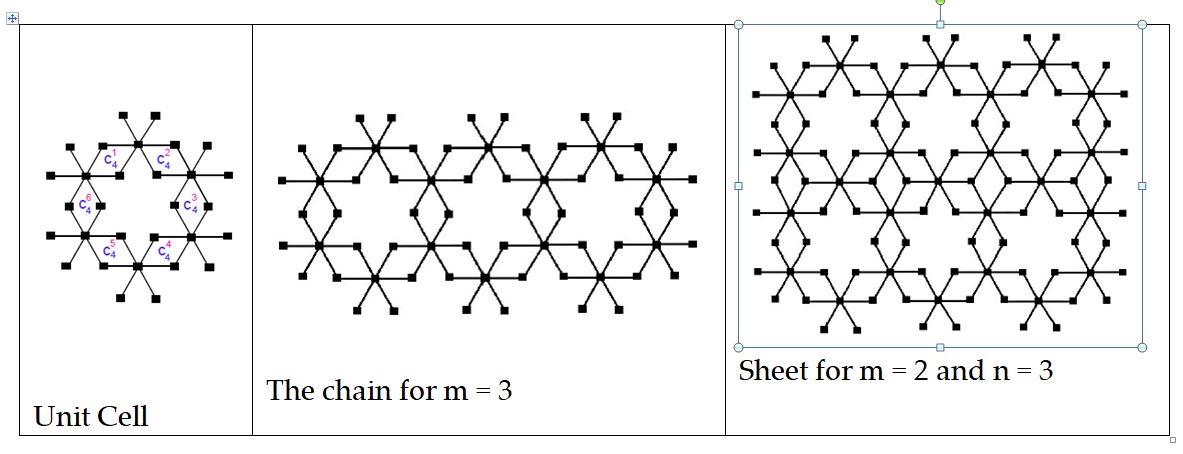
Mathematical chemistry is an area of research in chemistry in which mathematical tools are used to solve problems of chemistry. Chemical graph theory is an important area of research in mathematically chemistry which deals with topology of molecular structure such as the mathematical study of isomerism and the development of topological descriptors or indices. Infect, TIs are real numbers attached with graph networks and graph of chemical compounds and has applications in quantitative structure-property relationships. TIs remain invariant upto graph isomorphism and help to predict many properties of chemical compounds, networks and nanomaterials, for example, viscosity, boiling points, radius of gyrations, etc without going to lab [9, 10, 11, 12].

Other emerging field is Cheminformatics, in which we use QSAR and QSPR relationship to guess biological activity and chemical properties of nanomaterial and networks. In these investigations, some Physico-chemical properties and TIs are utilized to guess the behavior of chemical networks [13, 14, 15, 16, 17]. Like TIs, polynomials also fund considerable applications in network theory and chemistry, for example, Hosoya polynomial, which is also known as Wiener polynomial, introduced in [18] plays an important role in computation of distance-based TIs. M-polynomial [19] was defined in 2015 and plays a similar role in computation of numerous degree-based TIs [20, 21, 22, 23, 24]. The M-polynomial contains precious information about degree-based TIs and many TIs can be computed from this simple algebraic polynomial. The first TI was defined in 1947 by Weiner during studying boiling point of alkanes [25]. This index is now known as Weiner index. Thus Weiner established the framework of TIs and the Wiener index is initially the first and most concentrated TI [26, 27].

The other oldest TI is Randić index (RI), given by Milan Randić [28] in 1975. After the success of Randić index, in the year 1988, the generalized version of Randić index was introduced [29, 30]. This version attracts both the mathematicians and chemists [31]. Numerous numerical properties of this simple TI are studied in [32]. For comprehensive study about this index, the book [33] can be of great help.

The RI is a most mainstream regularly connected and most concentrated among all other TIs. Numerous research papers and text books, for example, [34, 35, 36] are published in different academic journals on this TI. Two surveys on RI was written by Milan Randi\'{c} [37, 38] and three more surveys are written on this TI by different scientists [39, 40 41]. The reason behind the success of such a simple TI is as yet a puzzle, although some conceivable clarifications were given.

After Randi\'{c} index, the most studied TIs are 1st Zagreb index (ZI) and 2nd ZI [42, 43, 44, 45, 46]. The modified 2nd ZI was defined in [47]. Another TI is symmetric division (SDI) [48], Harmonic index (HI) [49, 50], augmented ZI [51].

In this article, we compute general form of several degree-based topological indices for Bismuth Tri-Iodide chains and Bismuth Tri-Iodide sheets. For example we compute first and second multiplicative Zagreb indices, multiplicative atomic bond connectivity index, sum connectivity index, modify Randi\’c index, etc.

2. Basic definitions and Literature Review

In mathematical chemistry, precisely speaking, in chemical-graph-theory (CGT), a molecular graph and graph network is a simple and connected graph, in which atoms represents vertices and chemical bonds represents edges. We reserve \(G\) for simple connected graph, \(E\) for edge set and \(V\) for vertex set throughout the thesis. The degree of a vertex \(u\) of graph \(G\) is the number of vertices that are attached with \(u\) and is denoted by \(d_{v}\). With the help of TIs, many properties of molecular structure can be obtained without going to lab [52]. The reality is, many research paper has been written on computation of degree-based indices and polynomials of different molecular structure and networks but only few work has been done so far on distance based indices and polynomials. In this paper, we aim to compute multiplicative degree-based TIs. Some indices related to Wiener’s work are the first and second multiplicative Zagreb indices [53], respectively \[II_{1} \left(G\right)=\prod_{u\in V\left(G\right)}\left(d_{u} \right) ^{2} \] \[II_{2} \left(G\right)=\prod_{uv\in E\left(G\right)}d_{u} \cdot d_{v} \] and the Narumi-Katayama index [52] \[NK\left(G\right)=\prod_{u\in V\left(G\right)}d_{u} \] Like the Wiener index, these types of indices are the focus of considerable research in computational chemistry [54, 55, 56]. For example, in the year 2011, Gutman in [54] characterized the multiplicative Zagreb indices for trees and determined the unique trees that obtained maximum and minimum values for \(M_{1}(G)\) and \(M_{2}(G)\), respectively. Wang et al. in [57] extended the results of Gutman to the following index for k-trees, \[W_{1}^{s} \left(G\right)=\prod_{u\in V\left(G\right)}\left(d_{u} \right)^{s} .\] Notice that \(s = 1, 2\) is the Narumi-Katayama and Zagreb index, respectively. Based on the successful consideration of multiplicative Zagreb indices, Eliasi et al. [58] continued to define a new multiplicative version of the first Zagreb index as \[II_{1}^{*} \left(G\right)=\prod_{uv\in E\left(G\right)}\left(d_{u} +d_{v} \right) .\] Furthering the concept of indexing with the edge set, the first author introduced the first and second hyper-Zagreb indices of a graph [59]. They are defined as \[HII_{1} \left(G\right)=\prod_{uv\in E\left(G\right)}\left(d_{u} +d_{v} \right) ^{2} ,\] \[HII_{2} \left(G\right)=\prod_{uv\in E\left(G\right)}\left(d_{u} \cdot d_{v} \right)^{2} .\] In [60] Kulli et al. defined the first and second generalized Zagreb indices \[MZ_{1}^{a} \left(G\right)=\prod_{uv\in E\left(G\right)}\left(d_{u} +d_{v} \right) ^{\alpha} ,\] \[MZ_{2}^{a} \left(G\right)=\prod_{uv\in E\left(G\right)}\left(d_{u} \cdot d_{v} \right)^{\alpha} . \] Multiplicative sum connectivity and multiplicative product connectivity indices [61] are define as: \[SCII\left(G\right)=\prod_{uv\in E\left(G\right)}\frac{1}{\sqrt{d_{u} +d_{v} } } , \] \[PCII\left(G\right)=\prod_{uv\in E\left(G\right)}\frac{1}{\sqrt{d_{u} \cdot d_{v} } }. \] Multiplicative atomic bond connectivity index and multiplicative Geometric arithmetic index are defined as \[ABCII\left(G\right)=\prod_{uv\in E\left(\; G\right)}\sqrt{\frac{d_{u} +d_{v} -2}{d_{u} \cdot d_{v} } }, \] \[GAII\left(G\right)=\prod _{uv\in E\left(G\right)}\frac{2\sqrt{d_{u} \cdot d_{v} } }{d_{u} +d_{v} } ,\] \[GA^{a} II\left(G\right)=\prod _{uv\in E\left(G\right)}\left(\frac{2\sqrt{d_{u} \cdot d_{v} } }{d_{u} +d_{v} } \right) ^{\alpha}. \] Shigehalli and Kanabur [62] introduced following new degree-based topological indices:\\ Arithmetic-Geometric (AG1) index \(AG_{1} (G)=\sum_{uv\in E(G)}\frac{d_{u} +d_{v} }{2\sqrt{d_{u} d_{v} } } ,\) \(SK(G)=\sum_{uv\in E(G)}\frac{d_{u} +d_{v} }{2} ,\) \(AG_{1} (G)=\sum_{uv\in E(G)}\frac{d_{u} +d_{v} }{2\sqrt{d_{u} d_{v} } } ,\) \(SK_{2} (G)=\sum_{uv\in E(G)}\left(\frac{d_{u} +d_{v} }{2} \right)^{2}.\)

3. Computational Results

This section contains the main results. In this section we give formulae of multiplicative versions of degree-based TIs of Bismuth Tri-Iodide chains and Bismuth Tri-Iodide sheets. We also give formulae for some new degree-based TIs of Bismuth Tri-Iodide chains and Bismuth Tri-Iodide sheets.

3.1. Bismuth Tri-Iodide Chain

Theorem 1. Let \(G\) be the molecular graph of \(m-BiI_{3}\). Then

1. \(MZ_{1}^{\alpha} \left(G\right)=\left(7\right)^{\alpha (4p+8)} \times \left(8\right)^{\alpha (20p+4)} .\)
2. \(MZ_{2}^{\alpha} \left(G\right)=\left(2\right)^{\alpha (44p+16)} \times \left(3\right)^{\alpha (24p+12)} .\)
3. \(GA^{\alpha }II\left(G\right)=\left(\frac{2\sqrt{6} }{7} \right)^{\alpha (4p+8)} \times \left(\frac{\sqrt{3} }{2} \right)^{\alpha (20p+4)} .\)

Proof. Let \(G\) be the molecular graph of \(p-BiI_{3}\) bismuth tri-iodide chain. The edge set of \(p-BiI_{3}\) has following two partitions [1],
\(E_{1} =E_{\left\{1,6\right\}} =\left\{e=uv\in E\left(G\right) |d_{u} =1,\; d_{v} =6\right\},\)
\(E_{\left\{2,6\right\}} =\left\{e=uv\in E\left(G\right) |d_{u} =2,\; d_{v} =6\right\},\)
Such that
\(\left|E_{1} \left(G\right)\right|=4p+8,\)
\(\left|E_{2} \left(G\right)\right|=20p+4.\)
Now by definitions, we have

1. \begin{eqnarray*} MZ_{1}^{\alpha } \left(G\right)&=&\prod _{uv\in E\left(G\right)}\left(d_{u} +d_{v} \right) ^{\alpha } \\ &=&\left(1+6\right)^{\alpha (4p+8)} \times \left(2+6\right)^{\alpha (20p+4)} \\ & =&\left(7\right)^{\alpha (4p+8)} \times \left(8\right)^{\alpha (20p+4)} . \end{eqnarray*} 2. \begin{eqnarray*} MZ_{2}^{\alpha } \left(G\right)&=&\prod _{uv\in E\left(G\right)}(d_{u} \cdot d_{v} )^{\alpha }\\ &=&\left(1\times 6\right)^{\alpha \left(4p+8\right)} \times \left(2\times 6\right)^{\alpha (20p+4) }\\ &=&\left(2\times 3\right)^{\alpha (4p+8)} \times \left(4\times 3\right)^{\alpha (20p+4)} \\ &=&\left(2\right)^{\alpha (44p+16)} \times \left(3\right)^{\alpha (24p+12)}. \end{eqnarray*} 3. \begin{eqnarray*} GA^{\alpha } II\left(G\right)&=&\prod _{uv\in E\left(G\right)}\left(\frac{2\sqrt{d_{u} \cdot d_{v} } }{d_{u} +d_{v} } \right)^{\alpha } \\ &=&\left(\frac{2\sqrt{1\cdot 6} }{1+6} \right)^{\alpha (4p+8)} \times \left(\frac{2\sqrt{2\cdot 6} }{2+6} \right)^{\alpha (20p+8)} \\ &=& \left(\frac{2\sqrt{6} }{7} \right)^{\alpha (4p+8)} \times \left(\frac{\sqrt{3} }{2} \right)^{\alpha (20p+4)}. \end{eqnarray*}

Corollary 2. Let \(G\) be the molecular graph of \(p-BiI_{3}\). Then

1. \(MZ_{1} (G)=II_{2} \left(G\right){ =\; =}\left(2\right)^{44p+16} \times \left(3\right)^{24p+12} .\)
2. \(MZ_{2} (G)=II_{1}^{*} \left(G\right)=\left(7\right)^{4p+8} \times \left(8\right)^{20p+4} .\)
3. \(GAII\left(G\right){ \; =}\left(\frac{2\sqrt{6} }{7} \right)^{4p+8} \times \left(\frac{\sqrt{3} }{2} \right)^{20p+4} .\)

Proof. These results can be obtained immediately proved by taking \(\alpha =1\) in Theorem 1.

Corollary 3. Let \(G\) be the molecular graph of \(p-BiI_{3}\). Then

1. \(HII_{1} \left(G\right){ =}\left(7\right)^{2(4p+8)} \times \left(8\right)^{2(20p+4)} .\)
2. \(HII_{2} \left(G\right){ =}\left(2\right)^{88p+32} \times \left(3\right)^{48p+24} .\)

Proof. These results can be obtained immediately proved by taking \(\alpha =2\) in Theorem 1.

Corollary 4. Let \(G\) be the molecular graph of \(p-BiI_{3}\). Then

1. \(SCII\left(G\right)=\left(\frac{1}{\sqrt{7} } \right)^{4p+8} \times \left(\frac{1}{\sqrt{8} } \right)^{20p+4} .\)
2. \(PCII\left(G\right)=\left(\frac{1}{2} \right)^{22p+8} \times \left(\frac{1}{\sqrt{3} } \right)^{24p+12} .\)

Proof. These results can be obtained immediately proved by taking \(\alpha =-\frac{1}{2}\) in Theorem 1.

Theorem 5. Let \(G\) be the molecular graph of \(p-BiI_{3}\). Then \[ABCII\left(G\right)=\left(\sqrt{\frac{5}{6} } \right)^{4p+8} \times \left(\sqrt{\frac{1}{2} } \right)^{20p+4} .\]

Proof. Using the edge partition given in Theorem 1 and definition of multiplicative Atomic bond Connectivity index, we have \begin{eqnarray*}ABCII\left(G\right)&=&\prod _{uv\in E\left(G\right)}\sqrt{\frac{d_{u} +d_{v} -2}{d_{u} \cdot d_{v} } } \\ &=&\left(\sqrt{\frac{1+6-2}{1\cdot 6} } \right)^{4p+8} \times \left(\sqrt{\frac{2+6-2}{2\cdot 6} } \right)^{20p+4} \\\ &=&\left(\sqrt{\frac{5}{6} } \right)^{4p+8} \times \left(\sqrt{\frac{1}{2} } \right)^{20p+4} . \end{eqnarray*}

Theorem 6. Let \(G\) be the graph of \(p-BiI_{3}.\) Then

1. \(SC\left(G\right){ =}\left(\frac{4}{\sqrt{7} } +\frac{10}{\sqrt{2} } \right)p+\left(\frac{8}{\sqrt{7} } +\sqrt{2} \right).\)
2. \(AG_{1} \left(G\right){ =}\left(\frac{14}{\sqrt{6} } +\frac{40}{\sqrt{3} } \right)p+\left(\frac{28}{\sqrt{6} } +\frac{8}{\sqrt{3} } \right).\)
3. \(SK\left(G\right)=94p+44.\)
4. \(SK_{1} \left(G\right)=132p+48.\)
5. \(SK_{2} \left(G\right)=369p+162.\)
6. \(R’\left(G\right)=4p+2.\)

Proof. Using edge partition given in Theorem 1 and definitions, we have 1. \begin{eqnarray*} SC\left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{1}{\sqrt{d_{u} +d_{v} } } \\ &=&\frac{1}{\sqrt{7} } \left(4p+8\right)+\frac{1}{2\sqrt{2} } \left(20p+4\right) \\ &=&\left(\frac{4}{\sqrt{7} } +\frac{10}{\sqrt{2} } \right)p+\left(\frac{8}{\sqrt{7} } +\sqrt{2} \right). \end{eqnarray*} 2. \begin{eqnarray*} AG_{1} \left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{d_{u} +d_{v} }{2\sqrt{d_{u} \times d_{v} } } \\ &=&\frac{7}{2\sqrt{6} } \left(4p+8\right)+\left(20p+4\right)\frac{2}{\sqrt{3} } \\ &=&\left(\frac{14}{\sqrt{6} } +\frac{40}{\sqrt{3} } \right)p+\left(\frac{28}{\sqrt{6} } +\frac{8}{\sqrt{3} } \right). \end{eqnarray*} 3. \begin{eqnarray*} SK\left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{d_{u} +d_{v} }{2} \\ &=&\frac{7}{2} \left(4p+8\right)+4\left(20p+4\right) \\ &=&94p+44. \end{eqnarray*} 4. \begin{eqnarray*} SK_{1} \left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{d_{u} \times d_{v} }{2} \\ &=&3\left(4p+8\right)+6\left(20p+4\right)\\ &=&132p+48.\end{eqnarray*} 5. \begin{eqnarray*}SK_{2} \left(G\right)&=&\sum _{uv\in E\left(G\right)}\left(\frac{d_{u} +d_{v} }{2} \right) ^{2} \\ &=&\frac{49}{4} \left(4p+8\right)+16\left(20p+4\right) \\ &=&369p+162.\end{eqnarray*} 6. \begin{eqnarray*}R’\left(G\right)&=&\sum _{uv\in E\left(G\right)}\left(\frac{1}{\max \left\{d_{u} ,d_{v} \right\}} \right) \\ &=&\frac{1}{6} \left(4p+8\right)+\frac{1}{6} \left(20p+4\right) \\ &=&4p+2.\end{eqnarray*}

3.2. Bismuth Tri-Iodide sheet

In this section we compute several indices for Bismuth Tri-Iodide sheet.

Theorem 7. Let \(G\) be the molecular graph of \(BiI_{3} \left(p\times q\right)\). Then

1. \(MZ_{1}^{a} \left(G\right){ =}\left(7\right)^{\alpha (4p+4q+4)} \times \left(8\right)^{\alpha (12pq+8p+8q-4)} \times \left(9\right)^{\alpha (6pq-6q)} .\)
2. \(MZ_{2}^{a} \left(G\right)=\left(2\right)^{\alpha (30pq+20p+14q-4)} \times \left(3\right)^{\alpha (24pq+12p)} .\)
3. \({ GA}^{\alpha}{II}\left(G\right){ =}\left(\frac{2\sqrt{6} }{7} \right)^{\alpha (4p+4q+4)} \times \left(\frac{\sqrt{3} }{2} \right)^{\alpha (12pq+8p+8q-4)} \times \left(\frac{6\sqrt{2} }{9} \right)^{\alpha (6pq-6q)} .\)

Proof. Let \(G\) be the graph of \(BiI_{3} \left(p\times q\right)\) bismuth tri-iodide sheet. The edge set of \(BiI_{3} \left(p\times q\right)\) has following three partitions [1],
\(E_{1} =E_{\left\{1,6\right\}} =\left\{e=uv\in E\left(G\right){ |}d_{u} =1,\; d_{v} =6\right\},\)
\(E_{2} =E_{\left\{2,6\right\}} =\left\{e=uv\in E\left(G\right){ |}d_{u} =2,\; d_{v} =6\right\},\)
\(E_{3} =E_{\left\{3,6\right\}} =\left\{e=uv\in E\left(G\right){ |}d_{u} =3,\; d_{v} =6\right\},\)
such that
\(\left|E_{1} \left(G\right)\right|=4p+4q+4,\)
\(\left|E_{2} \left(G\right)\right|=12pq+8p+8q-4,\)
\(\left|E_{3} \left(G\right)\right|=6pq-6q.\)
Now by definition

1. \begin{eqnarray*}{ MZ}_{1}^{\alpha } \left(G\right)&=&\prod_{uv\in E\left(G\right)}\left(d_{u} +d_{v} \right)^{\alpha } \\ &=&\left(1+6\right)^{\alpha (4p+4q+4)} \times \left(2+6\right)^{\alpha (12pq+8p+8q-4)} \times \left(3+6\right)^{\alpha (6pq-6q)} \\ & =&\left(7\right)^{\alpha (4p+4q+4)} \times \left(8\right)^{\alpha (12pq+8p+8q-4)} \times \left(9\right)^{\alpha (6pq-6q)} . \end{eqnarray*} 2. \begin{eqnarray*}{ MZ}_{2}^{\alpha } \left(G\right)&=&\prod _{uv\in E\left(G\right)}(d_{u} \cdot d_{v} )^{\alpha } \\ &=&\left(6\right)^{\alpha (4p+4q+4)} \times \left(2\right)^{\alpha (12pq+8p+8q-4)} \times \left(3\right)^{\alpha (6pq-6q)} \\ &=&\left(2\right)^{\alpha (30pq+20p+14q-4)} \times \left(3\right)^{\alpha (24pq+12p)} .\end{eqnarray*} 3. \begin{eqnarray*} GA^{\alpha } II\left(G\right)&=&\prod _{uv\in E\left(G\right)}\left(\frac{2\sqrt{d_{u} \cdot d_{v} } }{d_{u} +d_{v} } \right)^{\alpha } \\ &=&\left(\frac{2\sqrt{1\cdot 6} }{1+6} \right)^{\alpha (4p+4q+4)} \times \left(\frac{2\sqrt{2\cdot 6} }{2+6} \right)^{\alpha (12pq+8p+8q-4)} \times \left(\frac{2\sqrt{3\cdot 6} }{3+6} \right)^{\alpha (6pq-6q)} \\ &=&\left(\frac{2\sqrt{6} }{7} \right)^{\alpha (4p+4q+4)} \times \left(\frac{\sqrt{3} }{2} \right)^{\alpha (12pq+8p+8q-4)} \times \left(\frac{6\sqrt{2} }{9} \right)^{\alpha (6pq-6q)} .\end{eqnarray*}

Corollary 8. Let \(G\) be the molecular graph of \(BiI_{3} \left(p\times q\right)\). Then

1. \(MZ_{1} (G)=II_{2} \left(G\right)=\left(2\right)^{30pq+20p+14q-4} \times \left(3\right)^{24pq+12p} .\)
2. \(MZ_{2} (G)=II_{1}^{*} \left(G\right){ =}\left(7\right)^{4p+4q+4} \times \left(8\right)^{12pq+8p+8q-4} \times \left(9\right)^{6pq-6q} .\)
3. \(GAII\left(G\right){ \; =}\left(\frac{2\sqrt{6} }{7} \right)^{4p+4q+4} \times \left(\frac{\sqrt{3} }{2} \right)^{12pq+8p+8q-4} \times \left(\frac{6\sqrt{2} }{9} \right)^{6pq-6q} .\)

Proof. These result can be obtained immediately proved by taking \(\alpha =1\) in Theorem 7.

Corollary 9. Let \(G\) be the molecular graph of \(BiI_{3} \left(p\times q\right)\). Then

1. \(HII_{1} \left(G\right){ =}\left(7\right)^{2(4p+4q+4)} \times \left(8\right)^{2(12pq+8p+8q-4)} \times \left(9\right)^{2(6pq-6q)} .\)
2. \(HII_{2} \left(G\right){ =}\left(2\right)^{4(15pq+10p+7q-2)} \times \left(3\right)^{24(2pq+p)} .\)

Proof. These result can be obtained immediately proved by taking \(\alpha =2\) in Theorem 7.

Corollary 10. Let \(G\) be the molecular graph of \(BiI_{3} \left(p\times q\right)\). Then

1. \(SCII\left(G\right)=\left(\frac{1}{\sqrt{7} } \right)^{4p+4q+4} \times \left(\frac{1}{\sqrt{8} } \right)^{12pq+8p+8q-4} \times \left(\frac{1}{\sqrt{9} } \right)^{6pq-6q} .\)
2. \(PCII\left(G\right){ =}\left(\frac{1}{\sqrt{2} } \right)^{30pq+20p+14q-4} \times \left(\frac{1}{\sqrt{3} } \right)^{24pq+12p} .\)

Proof. These result can be obtained immediately proved by taking \(\alpha =-\frac{1}{2}\) in Theorem 7.

Theroem 11. Let \(G\) be the molecular graph of \(BiI_{3} \left(p\times q\right)\). Then \[ABCII\left(G\right)=\left(\sqrt{\frac{5}{6} } \right)^{4p+4q+4} \times \left(\sqrt{\frac{1}{2} } \right)^{12pq+8p+8q-4} \times \left(\sqrt{\frac{7}{18} } \right)^{6pq-6q} .\]

Proof. \begin{eqnarray*} ABCII\left(G\right)&=&\prod _{uv\in E\left(G\right)}\sqrt{\frac{d_{u} +d_{v} -2}{d_{u} \cdot d_{v} } } \\ &=&\left(\sqrt{\frac{1+6-2}{1\cdot 6} } \right)^{4p+4q+4} \times \left(\sqrt{\frac{2+6-2}{2\cdot 6} } \right)^{12pq+8p+8q-4} \times \left(\sqrt{\frac{3+6-2}{3\cdot 6} } \right)^{6pq-6q} \\ &=&\left(\sqrt{\frac{5}{6} } \right)^{4p+4q+4} \times \left(\sqrt{\frac{1}{2} } \right)^{12pq+8p+8q-4} \times \left(\sqrt{\frac{7}{18} } \right)^{6pq-6q} . \end{eqnarray*}

Theroem 12. Let \(G\) be the graph of \(BiI_{3} \left(p\times q\right)\). Then

1. \(SC\left(G\right){ =}\left(\frac{6}{\sqrt{2} } +2\right)pq+\left(\frac{4}{\sqrt{7} } +\frac{4}{\sqrt{2} } \right)p+\left(\frac{4}{\sqrt{7} } +\frac{4}{\sqrt{2} } -2\right)q+\left(\frac{4}{\sqrt{7} } -\frac{2}{\sqrt{2} } \right).\)
2. \(AG_{1} \left(G\right){ =}\left(\frac{24}{\sqrt{3} } +\frac{9}{\sqrt{2} } \right)pq+\left(\frac{14}{\sqrt{6} } +\frac{16}{\sqrt{3} } \right)p+\left(\frac{14}{\sqrt{6} } +\frac{16}{\sqrt{3} } -\frac{9}{\sqrt{2} } \right)q+\left(\frac{14}{\sqrt{6} } -\frac{8}{\sqrt{3} } \right)\).
3. \(SK\left(G\right)=75pq+46p+19q-2.\)
4. \(SK_{1} \left(G\right)=126pq+60p+6q-12.\)
5. \(SK_{2} \left(G\right)=\frac{627}{2} pq+177p-\frac{111}{2} q-15.\)
6. \(R’\left(G\right)=3pq+2p+q.\)

Proof. Using the edge partition given in Theorem 7, we have

1. \begin{eqnarray*}SC\left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{1}{\sqrt{d_{u} +d_{v} } } \\ &=&\frac{1}{\sqrt{7} } \left(4p+4q+4\right)+\frac{1}{2\sqrt{2} } \left(12pq+8p+8q-4\right)+\frac{1}{3} \left(6pq-6q\right) \\ &=&\left(\frac{6}{\sqrt{2} } +2\right)pq+\left(\frac{4}{\sqrt{7} } +\frac{4}{\sqrt{2} } \right)p+\left(\frac{4}{\sqrt{7} } +\frac{4}{\sqrt{2} } -2\right)q+\left(\frac{4}{\sqrt{7} } -\frac{2}{\sqrt{2} } \right).\end{eqnarray*} 2. \begin{eqnarray*}AG_{1} \left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{d_{u} +d_{v} }{2\sqrt{d_{u} \times d_{v} } } \\ &=&\frac{7}{2\sqrt{6} } \left(4p+4q+4\right)+\left(12pq+8p+8q-4\right)\frac{2}{\sqrt{3} } +\left(6pq-6q\right)\frac{3}{2\sqrt{2} } \\ &=&\left(\frac{24}{\sqrt{3} } +\frac{9}{\sqrt{2} } \right)pq+\left(\frac{14}{\sqrt{6} } +\frac{16}{\sqrt{3} } \right)p+\left(\frac{14}{\sqrt{6} } +\frac{16}{\sqrt{3} } -\frac{9}{\sqrt{2} } \right)q+\left(\frac{14}{\sqrt{6} } -\frac{8}{\sqrt{3} } \right).\end{eqnarray*} 3. \begin{eqnarray*}SK\left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{d_{u} +d_{v} }{2} \\ &=&\frac{7}{2} \left(4p+4q+4\right)+4\left(12pq+8p+8q-4\right)+\frac{9}{2} \left(6pq-6q\right) \\ &=&75pq+46p+19q-2.\end{eqnarray*} 4. \begin{eqnarray*}SK_{1} \left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{d_{u} \times d_{v} }{2} \\ &=&3\left(4p+4q+4\right)+6\left(12pq+8p+8q-4\right)+9\left(6pq-6q\right) \\ &=&126pq+60p+6q-12.\end{eqnarray*} 5. \begin{eqnarray*}SK_{2} \left(G\right)&=&\sum _{uv\in E\left(G\right)}\left(\frac{d_{u} +d_{v} }{2} \right) ^{2} \\ &=&\frac{49}{4} \left(4p+4q+4\right)+16\left(12pq+8p+8q-4\right)+\frac{81}{4} \left(6pq-6q\right) \\ &=&\frac{627}{2} pq+177p-\frac{111}{2} q-15.\end{eqnarray*} 6. \begin{eqnarray*}R’\left(G\right)&=&\sum _{uv\in E\left(G\right)}\left(\frac{1}{\max \left\{d_{u} ,d_{v} \right\}} \right) \\ &=&\frac{1}{6} \left(4p+4q+4\right)+\frac{1}{6} \left(12pq+8p+8q-4\right)+\frac{1}{6} \left(6pq-6q\right) \\ &=&3pq+2p+q.\end{eqnarray*}

4. Conclusions

In the present article, we computed closed form of 17 degree-based TIs for Bismuth Tri-Iodide chain and sheet. TIs thus calculated for these Bismuth Tri-Iodides can help us to understand the physical features, chemical reactivity, and biological activities. In this perspective, a TIs can be viewed as a score work which maps each sub-atomic structure to a real number and is utilized as descriptors of the particle under testing. These outcomes can likewise have a crucial influence in the assurance of the importance of Bismuth Tri-Iodide. For instance, it has been proved that the first Zagreb index is straightforwardly related with all out \(\pi\)-electron energy. Additionally Randic index is helpful for deciding physio-chemical properties of alkanes as seen by scientific expert Melan Randic in 1975. He saw the relationship between’s the Randic index and a few physico–chemical properties of alkanes like, “enthalpies of formation, boiling points, chromatographic retention times, vapor pressure and surface areas” [52].

Competing Interests

The authors declare that they have no competing interests.