The main difficulty in dealing with the basic differential equations of fluid momentum is in choosing an appropriate problem-solving methodology. In addition, it is necessary to correct minor errors incurred by neglecting some losses. However, in many cases, such methodologies suffer from long processing time (P-time). Therefore, this article focuses on the truncation technique involving an unsteady Eyring-Powell fluid towards a shrinking wall. The governing differential equations are converted to the non-dimensional from through similarity variables. It is seen that the present system is totally convergent in 8th-order approximate solution together with \(\hbar=-0.875\).
Analyzing the rheological behavior of Eyring-Powell fluid models (at low and high shear rates), which can be easily deduced from the molecular theory of rarefied gases [1], is very important for pseudoplastic systems nowadays. Until recently, only such fluid flow problems, whether “steady” or “unsteady”, have been concerned with finding the velocity and temperature distribution through the use of some particular problem-solving methodologies [2,3,4,5,6,7,8,9,10,11]. However, from a mathematical viewpoint, it can be desirable to have a series expansion which converges in the semi-infinite intervals faster than a series expansion with a smaller interval of convergence. In this way, Khoshrouye Ghiasi and Saleh [12] employed a rather convergent feature of homotopy analysis method (HAM) by adding to the truncation technique, namely, tHAM, for solving the Falkner-Skan boundary value problem (FBVP) and spotting many errors. In fact, they could give rigorous proof of their observations showing how the P-time can be minimized without any loss of accuracy. Furthermore, it is to be mentioned here that some other types of technical problems [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] can be solved quite simply through this starting point.
Unlike many side benefits of the truncation technique, the lack of tHAM for solving many flow problems is pronounced yet. To this aim, an efficient tHAM for studying the laminar flow velocity distribution in an Eyring-Powell fluid model subjected to inclined magnetic field is developed here. The obtained results concerning the steady case are compared and validated with those simulations available in the open literature. It is shown that the tHAM can be considered as a powerful tool for deriving high-accuracy approximations.
According to the Eyring-Powell fluid model, the differential equations of mass and linear momentum conservation for the assumed flow pattern can be expressed as,
\begin{equation*} u_{,x}+v_{,y}=0, \end{equation*} \begin{equation*} \dot{u}+uu_{,x}+vv_{,y}=\left(v+\frac{1}{\rho\Gamma\Lambda}\right)u_{,yy}-\frac{1}{2\rho\Gamma\Lambda^3}u^{2}_{,y}u_{,yy}-\frac{\sigma \mathcal{B}^2sin^{2}\theta}{\rho}u, \end{equation*} with the boundary conditions \begin{equation*} u=U_{w}(x,t)=\frac{ax}{1-bt} \ \ \ \ , v=V(x,t) \ \ \ \ \text{at} \ \ \ \ y=0, \end{equation*} \begin{equation*} \ \ \ \ \ \ \ u\rightarrow 0, \ \ \ \ \ v\rightarrow 0, \ \ \ \ \ \ \ \text{as} \ \ \ \ \ \ y\rightarrow \infty, \end{equation*} where \(v\) is the kinematic viscosity, \(\rho\) is the density, \(\Gamma\) and \(\Lambda\) are the material constants, \(\sigma\) is the electrical conductivity and \(V(x,t)\) is the mass transfer rate. It is to be noted that the comma sign and dot-superscript followed by independent variables signify the partial derivative involving \(\frac{\partial}{\partial x}\)(or \(\frac{\partial}{\partial x}\) ) and differentiation with respect to the time , respectively.Introducing these variables \(\tau=y=\sqrt{\frac{a}{v(1-bt)}}\), \(u=\frac{ax}{1-bt}\varphi_{,\tau}\) and \(v=-\frac{av}{1-bt}\varphi\), the governing equations and associated boundary conditions are given by
\begin{equation*} (1+\lambda)\varphi_{,\tau\tau\tau}-\beta(\varphi_{,\tau}+\frac{1}{2}\tau\phi_{,\tau\tau})+\varphi\varphi_{,\tau\tau}-\varphi^{2}_{,\tau}-\lambda \delta \varphi^{2}_{,\tau\tau}\varphi_{,\tau\tau\tau}-\mathrm{M}^2sin^{2}\theta \varphi_{,\tau}=0 \end{equation*} \begin{equation*} \varphi=0, \ \ \ \ \varphi_{,\tau}=1, \ \ \ \ \text{at} \ \ \ \ \tau =0, \end{equation*} \begin{equation*} \varphi_{,\tau}=0 \ \ \ \ \ \ \ \ \ \ \ \ \text{as} \ \ \ \ \tau\rightarrow \infty, \end{equation*} where \(\lambda=\frac{1}{\rho\Gamma\Lambda}\) and \(\delta=\frac{a^3x^2}{2v\Lambda^2}\), are the Eyring-Powell fluid parameters, \(\beta=\frac{b}{a}\) is the unsteadiness parameter and \(\mathrm{M}=\sqrt{\frac{\sigma B^2}{\rho a}}\) is the magnetic field parameter.Here the dimensionless quantity skin friction coefficient \(C_{f}\) is defined as,
\begin{equation*} \sqrt{Re_{x}}C_{f}=[(1+\lambda)\varphi_{,\tau\tau}(0)-\frac{1}{3}\lambda\delta\varphi^{3}_{,\tau\tau}(0)], \end{equation*} where \(Re_{x}=\frac{U_{w}x}{v}\) is the local Reynolds number.To find a more explicit way of representing the th-order deformation Equation (2), it is required to express \(\frac{1}{j-1!}\hbar\mathcal{N}^{j-1}_{,q} [\varphi(\tau,q)]|_{q=0}\) by a linear combination of independent functions. With an inner product of any two independent functions in such a way that \(\psi_{m},\psi_{n}=\int^{\infty}_{0} (\tau)\psi_{m}(\tau)\psi_{n}(\tau)d\tau\) \(m\geq1\) and \(n\leq r\) [30] where \(k\) and \(\tau\) are the weight function and number of truncation, respectively. The Schmidt-Gram procedure [31] as well as the Kronecker delta functions can be applied to calculate \(r\). Therefore, \(\frac{1}{j-1!}\hbar\mathcal{N}^{j-1}_{,q} [\varphi(\tau,q)]|_{q=0}\) will be approximated by an orthonormal set of bases \(e_{1}, e_{2}, … e_{r}\) at each point \(\tau\). It is to be noted here that after making this substitution and then solving the \(p-\)th order deformation Equation (2), the th-order approximate solution is achieved by
\begin{equation*} \varphi_{p}=\sum^{p}_{j=0}\varphi_{j}(\tau). \end{equation*} In theory, the square residual error at the th-order of approximation can be defined as [32]; \begin{equation*} \Delta_{p}=\frac{1}{d+1}\sum^{d}_{l=0}\left(\mathcal{N}\left[\sum^{p}_{z=0}\varphi_{z}(\tau)\right]\right)^2. \end{equation*}| \(\lambda\) | \(\beta\) | \(\delta\) | \(\mathcal{M}\) | \(\theta\) |
|---|---|---|---|---|
| \(0.6\) | \(-0.5\) | \(0.1\) | \(0.2\) | \(45^{o}\) [1ex] |
| \(p\) | \(\hbar\) | \(\triangle_{p}\) | \(P-times(s)\) |
|---|---|---|---|
| \(5\) | \(-0.864\) | \(6.403 \times 10^{-9}\) | \(7.41\) |
| \(6\) | \(-0.871\) | \(5.179 \times 10^{-10}\) | \(15.66\) |
| \(7\) | \(-0.875\) | \(2.436 \times 10^{-11}\) | \(32.90\) |
| \(8\) | \(-0.875\) | \(2.436 \times 10^{-11}\) | \(73.75\) |
| \(9\) | \(-0.875\) | \(2.436 \times 10^{-11}\) | \(169.15\) |
| \(10\) | \(-0.875\) | \(2.436 \times 10^{-11}\) | \(406.24\) |
In view of the results given in Table 2, the 8th-order tHAM converges rapidly for \(\hbar=-0.875\). However, due to the loop-like behavior of the tHAM, the P-time is greatly enhanced by increasing the order of approximation. According to the case reported by Zhao et al. [33], the main idea behind the truncation technique is to reduce the computation of series expansion and P-time made of (two or more) independent functions with a given \(k\). Since the number of truncation can simply be calculated as \(k=40\) [12] therefore, the square residual error will be minimized.
| \(\lambda\) | \(\beta\) | \(\delta\) | \(\mathcal{M}\) | \(\theta\) | \([(1+\lambda)\varphi_{,\tau\tau}(0)-\frac{1}{3}\lambda\delta\varphi^{3}_{,\tau\tau}(0)]\) |
|---|---|---|---|---|---|
| \(0.6\) | \(-0.5\) | \(0.1\) | \(0.2\) | \(30^{o}\) | \(1.0191\) |
| \(0.7\) | \(0.9591\) | ||||
| \(0.8\) | \(0.9262\) | ||||
| \(0.8\) | \(-0.4\) | \(0.9280\) | |||
| \(-0.3\) | \(0.9516\) | ||||
| \(-0.2\) | \(0.9733\) | ||||
| \(0.8\) | \(-0.2\) | \(0.2\) | \(1.1170\) | ||
| \(0.3\) | \(1.1046\) | ||||
| \(0.4\) | \(1.1776\) | ||||
| \(0.8\) | \(-0.2\) | \(0.4\) | \(0.3\) | \(1.1046\) | |
| \(0.4\) | \(1.1053\) | ||||
| \(0.5\) | \(1.1061\) | ||||
| \(0.8\) | \(-0.2\) | \(0.4\) | \(0.5\) | \(45^{o}\) | \(0.9970\) |
| \(60^{o}\) | \(0.9811\) | ||||
| \(90^{o}\) | \(0.9684\) |
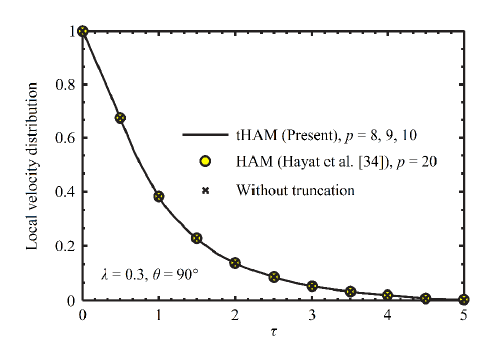
A comparison of the local velocity distribution obtained by different solution methodologies with geometric and physical properties \(\lambda=0.3\) and \(\theta=90^{o}\) is shown in Figure 1. According to this Figure 1, the 8th-order tHAM gives accurate answers compared to those findings reported by Hayat et al. [34]; however, the order of approximation in the case analyzed by Hayat et al. [21] is radically different. Furthermore, the local velocity distribution for the same system without using the truncation is consistent with the tHAM results, but instead takes more P-time to consistency (i.e., 996.43s). It is worth noting that, based on the results reported in Table 2 and Figure 1, although the square residual error should be taken to optimize the value of auxiliary parameter, the only way that the P-time can reduce appears in the combination of truncation technique with the HAM.
Table 3 investigates the variation of skin friction coefficient versus different geometric and physical properties presented in Section 2. It is seen that the skin friction coefficient enhances when \(\beta\), \(\delta\) and \(\mathcal{M}\) are increased in any case. In contrast to the previous observation, the skin friction coefficient is a diminishing function of \(\theta\) and \(\lambda\). Hence, one can conclude that such findings involved in Table 3 are particularly useful for developing thermodynamic characteristics of an Eyring-Powell fluid model with slip velocity at the wall.