Characterizing Trees with Minimal ABC Index with Computer Search: A Short Survey

1. Introduction

We consider non-trivial connected simple graphs only. Such a graph will be denoted by \(G=(V,E)\), where \(V=\{v_{0}, v_{1}, \cdots, v_{n-1}\}\) and are the vertex set and edge set of, respectively. If \(v_{i}v_{j}\in E\), then \(G-v_{i}v_{j}\) will denote the graph obtained from G by deleting the edge \(v_{i}v_{j}\). If, in turn, \(v_{i}v_{j} \notin E\), then \(G+v_{i}v_{j}\) will denote the graph obtained from \(G\) by adding the edge \(v_{i}v_{j}\).

Let \(P= u_{0}u_{1}\cdots u_{k-1}u_{k}\) be a path of length \(k\) in graph \(G\) with \(k\geq 1\), \(d(u_{0}) \geq 3\), \(d(u_{k}) \neq 2\), and \(d(u_{1})=d(u_{2})= \cdots =d(u_{k-1})=2\). If \(d(u_{k}) \geq 3\) then \(P\) is said to be an internal path of \(G\). If \(d(u_{k})=1\) then \(P\) is said to be a pendent path of \(G\).

Let \(d_{i}=d(v_{i})\) be the degree of \(v_{i}\), and \(\Delta =\Delta (G)\) the maximum degree of \(G\). A vertex of degree 1 is called a pendent vertex. \(\pi(G)=(d_{0}, d_{1}, \cdots, d_{n-1})\) is called the degree sequence of \(G\). Given a positive integer sequence \(\pi =(d_{0}, d_{1}, \cdots, d_{n-1})\), if there exists a connected graph \(G\) with \(\pi (G)=\pi\), then \(\pi\) is said to be a (graphic) degree sequence. In particular, if \(G\) is a tree, then \(\pi\) is called a tree degree sequence. Let \(\mathcal{C} (\pi)= \{G|G\) is connected and \(\pi(G)=\pi \}\), and \(\mathcal{T} (\pi)= \{T|T\) is a tree and \(\pi(T)=\pi \}\).

The ABC index of graph \(G=(V,E)\) is defined [1] as $$ABC(G)=\sum\nolimits_{v_{i}v_{j} \in E}\sqrt{(d_{i}+d_{j}-2)/(d_{i}d_{j})}.$$

This vertex-degree-based topological index turned out to be closely correlated with the heat of formation of alkanes [1], and a quantum-chemical explanation for its descriptive ability was provided in [2]. Gutman et al. [3] later confirmed that the ABC index could reproduce the heat of formation with accuracy comparable to that of high-level ab initio and DFT (MP2, B3LYP) quantum chemical calculations. Recently, a probabilistic interpretation of the generalized ABC index is provided by Estrada [4]. Due to these applications, there is an increased interest in the mathematical properties of the ABC index in the last few years (See [5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 29, 30, 31, 32, 33, 34, 35, 36]).

From a mathematical point of view, the first question that needs to answer is for which graphs this index assumes minimal and maximal values. It was proved [5, 6] that, the ABC index of a graph strictly increases with addition of edges. Hence among \(n\)-vertex connected graphs, the complete graph \(K_{n}\) uniquely maximizes the ABC index, and a graph with minimal ABC index is a tree. In [7] Furtula proved that, among \(n\)-vertex trees the star \(S_{n}\) uniquely maximizes the ABC index. Xing et al. [8] found some upper bounds for the ABC index in some classes of trees. However, the problem of characterizing \(n\)-vertex tree(s) with minimal ABC index is more elusive and remains open. In [9] Gutman et al. summarized the known results and coined the problem as the “ ABC index conundrum”. After [9] there are quite a few significant developments, in both mathematical and computational aspects. In the course of research computer search plays a non-negligible role. Namely, the research paradigm of repeating the procedure “Searching – Conjecturing – Proving” was applied: (a) Computer search for trees with minimal ABC index of order as large as possible by using their known properties; (b) Conjecture their properties based on the search results; (c) Prove or disprove the conjectures; (d) Go to (a). In the present paper, we will review the state of the art of the problem, as an update of [10]. In addition we intend to demonstrate that, the paradigm may be applicable to cope with other elusive problems of extremal graph characterization.

For convenience, in the rest of the paper, we refer a tree with minimal ABC index as a min- ABC tree, and the problem of characterizing \(n\)-vertex tree(s) with minimal ABC index as min- ABC tree problem. We also assume \(n\geq 10\).

2. A brute-force and a heuristic search, and the modulo 7 conjecture

In order to guess the general structure of min- ABC trees, Furtula et al. [10] firstly conducted a brute-force computer search. Their algorithm consists of two successive steps: (1) Generating the trees recursively; (2) Computing the ABC index for each generated tree and find its minimum value. Since the number of \(n\)-vertex trees increases rapidly with \(n\), though a computer grid with 400 CPUs was employed, the computation was just performed up to \(n=31\). One can refer to [11] for the search results. Few as the search results obtained in [10] are, some structural properties of min- ABC trees were observed and proved by Gutman et al. in [11].

Lemma 2.1. [12] Let \(T\) be an \(n\)-vertex min-ABC tree. Then
(1) \(T\) has no internal paths of length \(\geq 2\);
(2) \(T\) has no pendent paths of length \(\geq 4\);
(3) \(T\) has at most one pendent path of length 3.

It was also conjectured [12] that, such a tree has no pendent paths of length 1. Soon this was confirmed by Lin et al. [13].

Lemma 2.2. [13] Let \(T\) be an \(n\)-vertex min-ABC tree. Then each pendent path of \(T\) is of length 2 or 3.

Lemma 2.2 reveals that, each vertex of degree 1 or 2 of an \(n\)-vertex min- ABC tree \(T\) is contained in a so-called \(B_{k}\)- or \(B_{k}^{*}\)-branch (shown in Figure 1). From Lemma 2.1 (3) \(T\) has a unique \(B_{k}^{*}\)-branch if \(T\) has a pendent path of length 3. Based on these facts Gutman and Furtula [14] implicitly made the following conjecture.

Conjecture 2.3 Let \(T\) be an \(n\)-vertex min-ABC tree. Then
(1) \(T\) has a single high-degree vertex \(v_{0}\);
(2) To \(v_0\) only \(B_{k}\)- or \(B_{k}^{*}\)-branches, \(1\leq k \leq 5\), are attached.

Actually, Conjecture 2.3 is somehow natural. Let \(T\) be an \(n\)-vertex min- ABC tree, and \(T[\delta]\) the subgraph of \(T\) induced by the vertices of degree at least \(\delta\). From Lemma 2.1 (2), \(T[3]\) is connected and thus is a tree. Moreover, based on the known search results at that time, \(T[3]\) is conjectured to be a star (see [13]). With the priori assumptions in Conjecture 2.3, Gutman and Furtula [14] conducted a heuristic incomplete computer search for \(n\)-vertex min- ABC tree(s) up to \(n=700\). This is an easy task, because the key is to find the solution set of the Diophantine equation \(n=1+2x_{1}+5x_{2}+7x_{3}+9x_{4}+11x_{5}+x_{6}\), where \(x_{i} \geq 0\) denotes the number of \(B_{k}\)-branches, \(1 \leq i \leq 5\), and \(x_{6} \in \{0,1\}\) is the number of pendent paths of length 3.

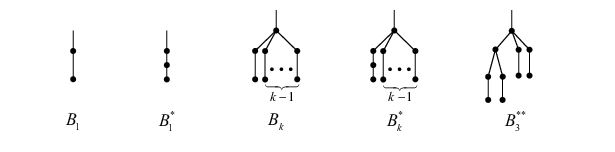
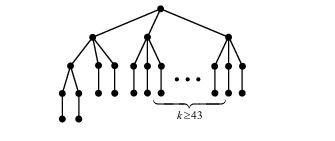
The output of this heuristic search shows that, when \(n\) is sufficiently large (e.g., \(n \geq 175\)) the structure of \(n\)-vertex min- ABC trees present a peculiar modulo 7 regularity. Therefore, the so-called “modulo 7 conjecture” was proposed [14]. Unfortunately, soon later this plausible conjecture was disproved by Ahmad et al. [15, 16]. In particular, the counterexample (shown in Figure 2) provided in [15] violates Conjecture 2.3, and indicates the existence of the so-called \(B_{3}^{**}\)-branches (see Figure 1) in a min- ABC tree.

On the other hand, since the trees considered in [14] as candidates with minimal ABC index, have an interesting structure, they were named Kragujevac trees in [16]. The modulo 7 conjecture with slight corrections, was shown to be valid for Kragujevac trees.

3. Greedy trees and search based on tree degree sequence

Gan et al. [18] and Xing et al. [19] independently proved that, the so-called “greedy tree” minimizes the ABC index in \(T(\pi)\). Soon later, Lin et al. [21] generalized this result to connected graphs. One can refer to [20] for the definitions of greedy trees and BFS-graphs.

Lemma 3.1. [20] Let \(\pi\) be a degree sequence. Then there exists a BFS-graph \(G^{*}\) with minimal ABC index in \(\mathcal{C} (\pi)\).

Note that, given the degree sequence of a greedy tree (or equivalently, BFS-tree) \(T\), \(ABC(T)\) can be easily computed. With Lemma 3.1 computer search for min- ABC trees can be done by enumerating degree sequences of trees. Dimitrov [21] presented the first such algorithm, which consists of three successive steps.
1. Generate all tree degree sequences (recursively);
2. Find corresponding greedy trees for each generated degree sequence;
3. Calculate the ABC index of each greedy tree and select the tree with minimal value.

Comparing with the brute-force algorithm presented in [10], Dimitrov’s is much more superior. It avoids generating and storing all \(n\)-vertex trees, and just needs to generate degree sequences of \(n\)-vertex trees. The search space is far less. For example, for \(n=31\), there are 40,330,829,030 trees, but only 4565 tree degree sequences. Hence Dimitrov’s algorithm is able to find all \(n\)-vertex min- ABC trees for \(n \leq 300\) on a single processor platform in about 15 days.

Later Dimitrov’s algorithm was improved by Lin et al. [1, 23]. For convenience, we say a non-increasing positive integer sequence \(\pi =(d_{0}, d_{1}, \cdots, d_{n-1})\) is optimal, if it is the degree sequence of a min- ABC tree. [22] and [23] obtained some features of an optimal tree degree sequence, which can be used to significantly narrow the search space. As reported in [22], for \(n=31\) only 49 (about \(1\%\)) tree degree sequences have to be generated. The MPI+OpenMP implement in [23] founds all \(n\)-vertex min- ABC tree(s) up to \(n=400\) in 23 hours on a workstation group with 36 CPU cores. It is worth to remark that, the search results in [22] for the first time disprove Conjecture 2.3, and confirm the existence of \(B_{3}^{**}\)-branches in a min- ABC tree.

Based on his search result, Dimitrov modified the modulo 7 conjecture initially proposed in [14]. The modified conjecture is valid for \(n \leq 400\). However, this plausible conjecture was shown to be completely false for sufficiently large \(n\) by Ahmadi et al. [24]. Hence a much more efficient search algorithm or implementation is still desired to identify large min- ABC trees.

4. On branches and search up to order 1100

Let \(\pi = ( \Delta = d_{0}, d_{1}, \cdots, d_{t}, d_{t+1}, \cdots, d_{n-1})\) \((d_{t} \geq 3\) and \(d_{t+1} \leq 2)\) be the (non-increasing) degree sequence of a min- ABC tree \(T\), \(n_{k}\) denotes the number of \(k\)’s among \(\{d_{1}, d_{2}, \cdots, d_{n-1}\}\), and \(d=\sum_{i=1}^{t} d_{i}/t\). \(\#P_{3}=(n-t-1)\) mod 2 indicates the number of paths of length 3 in \(T\). Since \(B_{k}^{(*)}\)-branches \((B_{k}\)- or \(B_{k}^{*}\)-branches) are the main structure of a min- ABC tree \(T\), it is meaningful to pay attentions to the number \(b_{k}\) of \(B_{k}^{(*)}\)-branches in \(T\). Note please, here a \(B_{3}^{**}\)-branch is regarded as one \(B_{2}\)-branch and two \(B_{1}\)-branches. In fact, in 2014 Hosseini et al. [17] have considered this task for Kragujevac trees. For general trees, most works were done by Dimitrov et al. and Du et al. in [25, 26, 27, 28, 29, 30]. We summarize the main results in Theorem 4.1.

Theorem 4.1. [25, 26, 27, 28, 29, 30]
(1) \(b_{1}\leq 2\), \(b_{2}\leq 11\), \(b_{4}\leq 4\), and \(b_{k}=0\) for \(k\geq 5\);
(2) \(b_{1}b_{4}= b_{2}b_{4}=0\);
(3) If \(n>18\) and \(\#P_{3}=1\), then \(b_{1}=0\), \(b_{2}\leq 2\), and \(b_{k}=0\) for \(k\geq 4\);
(4) If \(n>415\), then \(\#P_{3}=0\).

From Theorem 4.1 the features of an optimal tree degree sequence obtained in [22] and [23] were significantly refined in [11] as following.

Theorem 4.2. [11]
(1) \(n_{1}=\lfloor (n-t-1)/2 \rfloor\), \(n_{2}=\lceil (n-t-1)/2 \rceil\), \(n_{3}=b_{2} \leq 11\), and \(n_{4} \geq b_{3} \geq (2t-31)/3\);
(2) \(\# P_{3}=0\) if \(n\geq 416\), and so \(n_{1}=n_{2}=(n-t-1)/2\);
(3) \((n-9)/7 \leq t \leq(n+13)/5\);
(4) \(4\leq \Delta \leq t\) and \(\Delta \leq n/7 +3\) if \(n\geq 40\);
(5) \(2\Delta +5t \leq n+21\);
(6) \(4-77/(n-9) \leq d< 5\);

By applying Theorem 4.1 Dimitrov [31] conducted a computer search for \(n\)-vertex min- ABC tree(s) up to \(n=800\). Soon later by Theorem 4.2 Lin et al. [11] presented the fastest algorithm so far. The test was performed up to \(n=1100\) within 9 days on a single PC. Table 1 shows the performance of the main computer search algorithms.

Table 1. The performance of some search algorithms.

Algorithm	Range of \(n\)	Time	Test platform
Brute-force search [10]	\(n ≤ 31\)		PC grid, 400 CPUs
Dimitrov’s algorithm [21]	\(30 ≤ n ≤ 300\)	15 days	PC, 2 cores, 2.3 GHz
Algorithm in [22]	\(30 ≤ n ≤ 350\)	107.8 hours	PC, 8 cores, 1.8 GHz
Algorithm in [23]	\( 30 ≤ n ≤ 400\)	23 hours	PC Group, 36 cores
Dimitrov’s algorithm [31]	\(30 ≤ n ≤ 800\)		PC, 2 cores, 2.3 GHz
Algorithm in [11]	\(30 ≤ n ≤ 1100\)	207.1 hours	PC, 4 cores, 2.2 GHz

First row is a table header Preview How to use it?

5. Further discussions

As pointed out in [11] that, the fastest algorithm is not yet polynomial time one, and still too powerless for large \(n\) (e.g., \(n=5000\)), even a large workstation group is involved. Hence towards the complete solution of the min- ABC tree problem, at this point the main task is to find more properties of (sufficiently large) min- ABC trees. The following are some possible directions in further investigation.

1. Refine the upper bounds of \(b_{1}\), \(b_{2}\), and \(b_{4}\). We guess \(b_{1}=b_{2}=0\) and \(b_{4} \leq 2\).
2. Obtain a non-trivial lower bound of \(\Delta\) on \(n\) and/or \(t\).
3. Investigate the behavior of \(d=\sum _{i=1}^{t} d_{i}/t\) with \(n\) increases, so as to get better bounds of \(d\) for large \(n\). Better bounds of \(d\) can help us refine Theorem 4.2. On the other hand, \(d< 5\) implies that, the number of high-degree vertices should be small. In fact, we guess the high-degree vertices induce a star.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 11771362 ).

Competing Interests

The authors declare that they have no competing interests.