The exact solutions of most nonlinear difference equations cannot be obtained theoretically sometimes. Therefore, a massive number of researchers predict the long behaviour of most difference equations by investigating some qualitative behaviours of these equations from the governing equations. In this article, we aim to analyze the asymptotic stability, global stability, periodicity of the solution of an eighth-order difference equation. Moreover, a theoretical solution of a special case equation will be presented in this paper.
Theorem 1. Let \(\left\vert c_{1}c_{3}-c_{4}\right\vert +c_{4}\left\vert 1-c_{1}\right\vert < \left\vert c_{3}-c_{4}\right\vert .\) Then, the fixed point of Equation (1) is locally asymptotically stable.
Proof. It can be simply observed from Theorem A of [16] that the equilibrium point of Equation (1) is locally asymptotically stable if \begin{equation*} \left\vert p_{1}\right\vert +\left\vert p_{2}\right\vert < 1. \end{equation*} This gives us \begin{equation*} \left\vert -\Bigg(c_{1}-\frac{c_{4}(1-c_{1})}{c_{3}-c_{4}}\Bigg)\right\vert +\left\vert -\frac{c_{4}(1-c_{1})}{c_{3}-c_{4}}\right\vert < 1, \end{equation*} which can be written on the following form \begin{equation*} \left\vert c_{1}(c_{3}-c_{4})-c_{4}(1-c_{1})\right\vert +c_{4}\left\vert 1-c_{1}\right\vert < \left\vert (c_{3}-c_{4})\right\vert . \end{equation*} Hence, \begin{equation*} \left\vert c_{1}c_{3}-c_{4}\right\vert +c_{4}\left\vert 1-c_{1}\right\vert < \left\vert c_{3}-c_{4}\right\vert . \end{equation*} This complete the proof.
Theorem 2. Let \(c_{1}c_{4}.\)
Proof. Let \(a,\ b \in \mathbb{R}\) and suppose that \(h:\left[ a,b\right] ^{2}\longrightarrow \left[ a,b\right] \) is a function defined by Equation (2). We assume that \(c_{1}< \frac{c_{2}c_{4}s}{(c_{3}r-c_{4}s)^{2}},\) then the function \(h\) is decreasing in \(r\) and increasing in \(s.\) Now, we suppose that \((\phi, \psi)\) is a solution to the system given by $$\phi=h(\psi,\phi),\ \psi=h(\phi,\psi).$$ Therefore, \begin{align*} \phi &= h(\psi,\phi)=c_{1} \psi +\frac{c_{2} \psi}{c_{3}\psi-c_{4}\phi}, \\ \psi&=h(\phi,\psi)=c_{1}\phi+\frac{c_{2}\phi}{c_{3}\phi-c_{4}\psi}. \end{align*} Clearing the denominators gives
Theorem 3. Let \(c_{1}>\frac{c_{2}c_{4}s}{(c_{3}r-c_{4}s)^{2}},\) then the equilibrium point of Equation (1) is a global attractor if \(c_{3}< c_{4}\) and \(c_{1}< 1.\)
Proof. The proof can be accomplished in a similar way to the previous one. Thus, it is omitted.
Theorem 4. The Equation (1) has no prime period two solutions.
Proof. Assume that the Equation (1) has a prime period two solution given as follows \begin{equation*} \ldots,\ t,\ \tau,\ t,\ \tau,\ \ldots, \end{equation*} with \(t \neq \tau.\) From Equation (1), one can observe that \begin{eqnarray*} t&=&c_{1}t+\frac{c_{2}t}{c_{3}t-c_{4}t},\\ \tau &=& c_{1}\tau+\frac{c_{2}\tau}{c_{3}\tau-c_{4}\tau}. \end{eqnarray*} Hence, \begin{eqnarray*} (1-c_{1})t&=&\frac{c_{2}}{c_{3}-c_{4}},\\ (1-c_{1})\tau &=& \frac{c_{2}}{c_{3}-c_{4}}. \end{eqnarray*} This implies that \(t=\tau,\) which contradicts our assumption.
Theorem 5. Let \(\left \{x_{n}\right\}_{n=-7}^{\infty}\) be a solution of Equation (7) and assume that \(x_{-7}=\alpha,\ x_{-6}=\beta,\ x_{-5}=\gamma,\ x_{-4}=\delta,\ x_{-3}=\epsilon,\ x_{-2}=\zeta,\ x_{-1}=\kappa,\ x_{0}=\omega.\) Then, for \(n=0,1,2,…,\) the solution of Equation (7) is given by the following relations \begin{eqnarray*} x_{8n-7} &=&-\frac{\left[ \left( n-1\right) \alpha -n\epsilon \right] \left[ \alpha -\epsilon -n\right] }{\alpha -\epsilon },\ \ \ x_{8n-6}=-\frac{\left[ \left( n-1\right) \beta -n\zeta \right] \left[ \beta -\zeta -n\right] }{% \beta -\zeta }, \\ x_{8n-5} &=&-\frac{\left[ \left( n-1\right) \gamma -n\kappa \right] \left[ \gamma -\kappa -n\right] }{\gamma -\kappa },\ \ \ x_{8n-4}=-\frac{\left[ \left( n-1\right) \delta -n\omega \right] \left[ \delta -\omega -n\right] }{% \delta -\omega }, \\ x_{8n-3} &=&-\frac{\left[ n\alpha -\left( n+1\right) \epsilon \right] \left[ \alpha -\epsilon -n\right] }{\alpha -\epsilon },\ \ \ x_{8n-2}=-\frac{\left[ n\beta -\left( n+1\right) \zeta \right] \left[ \beta -\zeta -n\right] }{% \beta -\zeta }, \\ x_{8n-1} &=&-\frac{\left[ n\gamma -\left( n+1\right) \kappa \right] \left[ \gamma -\kappa -n\right] }{\gamma -\kappa },\ \ \ x_{8n}=-\frac{\left[ n\delta -\left( n+1\right) \omega \right] \left[ \delta -\omega -n\right] }{% \delta -\omega }. \end{eqnarray*}
Proof. It can be easily seen that the formulae are true at \(n=0.\) Next, we assume that \(n>0\) and suppose that our solution is correct at \(n-1\) as follows \begin{eqnarray*} x_{8n-15} &=&-\frac{\left[ \left( n-2\right) \alpha -\left( n-1\right) \epsilon \right] \left[ \alpha -\epsilon -n+1\right] }{\alpha -\epsilon },\ \ \ x_{8n-14}=-\frac{\left[ \left( n-2\right) \beta -\left( n-1\right) \zeta % \right] \left[ \beta -\zeta -n+1\right] }{\beta -\zeta }, \\ x_{8n-13} &=&-\frac{\left[ \left( n-2\right) \gamma -\left( n-1\right) \kappa \right] \left[ \gamma -\kappa -n+1\right] }{\gamma -\kappa },\ \ \ x_{8n-12}=-\frac{\left[ \left( n-2\right) \delta -\left( n-1\right) \omega % \right] \left[ \delta -\omega -n+1\right] }{\delta -\omega }, \\ x_{8n-11} &=&-\frac{\left[ \left( n-1\right) \alpha -n\epsilon \right] \left[ \alpha -\epsilon -n+1\right] }{\alpha -\epsilon },\ \ \ x_{8n-10}=-\frac{% \left[ \left( n-1\right) \beta -n\zeta \right] \left[ \beta -\zeta -n+1% \right] }{\beta -\zeta }, \\ x_{8n-9} &=&-\frac{\left[ \left( n-1\right) \gamma -n\kappa \right] \left[ \gamma -\kappa -n+1\right] }{\gamma -\kappa },\ \ \ x_{8n-8}=-\frac{\left[ \left( n-1\right) \delta -n\omega \right] \left[ \delta -\omega -n+1\right] }{\delta -\omega }. \end{eqnarray*} Now, we prove the first relation. Equation (7) gives \begin{eqnarray*} x_{8n-7} &=&x_{8n-11}+\frac{x_{8n-11}}{x_{8n-11}-x_{8n-15}} \end{eqnarray*} \begin{eqnarray*} &=&-\frac{\left[ \left( n-1\right) \alpha -n\epsilon \right] \left[ \alpha -\epsilon -n+1\right] }{\alpha -\epsilon }+\frac{-\frac{\left[ \left( n-1\right) \alpha -n\epsilon \right] \left[ \alpha -\epsilon -n+1\right] }{% \alpha -\epsilon }}{-\frac{\left[ \left( n-1\right) \alpha -n\epsilon \right] \left[ \alpha -\epsilon -n+1\right] }{\alpha -\epsilon }+\frac{\left[ \left( n-2\right) \alpha -\left( n-1\right) \epsilon \right] \left[ \alpha -\epsilon -n+1\right] }{\alpha -\epsilon }} \\ &=&-\frac{\left[ \left( n-1\right) \alpha -n\epsilon \right] \left[ \alpha -\epsilon -n+1\right] }{\alpha -\epsilon }-\frac{\left[ \left( n-1\right) \alpha -n\epsilon \right] }{\epsilon -\alpha } \\ &=&-\left[ \frac{\left[ \left( n-1\right) \alpha -n\epsilon \right] \left[ \alpha -\epsilon -n+1\right] }{\alpha -\epsilon }-\frac{\left[ \left( n-1\right) \alpha -n\epsilon \right] }{\alpha -\epsilon }\right] \\ &=&-\frac{\left[ \left( n-1\right) \alpha -n\epsilon \right] \left[ \alpha -\epsilon -n\right] }{\alpha -\epsilon }. \end{eqnarray*} We now prove the second formula. Again, Equation (7) gives \begin{eqnarray*} x_{8n-6} &=&x_{8n-10}+\frac{x_{8n-10}}{x_{8n-10}-x_{8n-14}} \\ &=&-\frac{\left[ \left( n-1\right) \beta -n\zeta \right] \left[ \beta -\zeta -n+1\right] }{\beta -\zeta }+\frac{-\frac{\left[ \left( n-1\right) \beta -n\zeta \right] \left[ \beta -\zeta -n+1\right] }{\beta -\zeta }}{-\frac{% \left[ \left( n-1\right) \beta -n\zeta \right] \left[ \beta -\zeta -n+1% \right] }{\beta -\zeta }+\frac{\left[ \left( n-2\right) \beta -\left( n-1\right) \zeta \right] \left[ \beta -\zeta -n+1\right] }{\beta -\zeta }} \\ &=&-\left[ \frac{\left[ \left( n-1\right) \beta -n\zeta \right] \left[ \beta -\zeta -n+1\right] }{\beta -\zeta }-\frac{\left[ \left( n-1\right) \beta -n\zeta \right] }{\beta -\zeta }\right] \\ &=&-\frac{\left[ \left( n-1\right) \beta -n\zeta \right] \left[ \beta -\zeta -n\right] }{\beta -\zeta }. \end{eqnarray*} The proofs of the remaining relations can be achieved in a similar way. Thus, the remaining proofs are omitted.
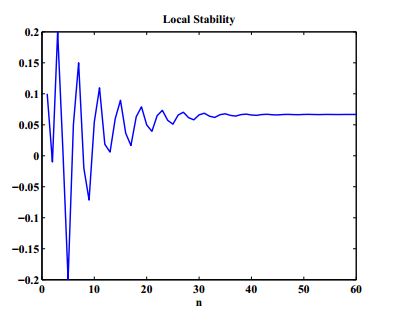
Example 1. In this example, we confirm the local stability of the equilibrium point under the values \(c_{1}=0.5,\ c_{2}=0.3,\ c_{3}=10,\ c_{4}=1,\ x_{-7}=-0.02,\ x_{-6}=0.15,\ x_{-5}=0.05,\ x_{-4}=-0.2,\ x_{-3}=0.01,\ x_{-2}=0.2,\ x_{-1}=-0.01,\ x_{0}=0.1. \) See Figure 1.
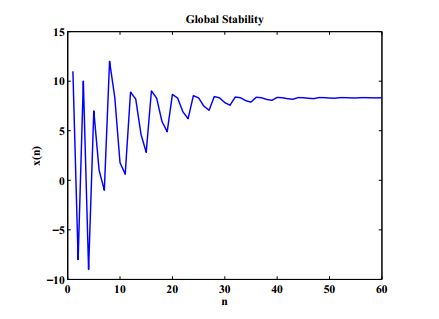
Example 2. Figure 2 shows the global stability of the fixed point when we let \(c_{1}=0.5,\ c_{2}=10,\ c_{3}=3,\ c_{4}=0.6,\ x_{-7}=12,\ x_{-6}=-1,\ x_{-5}=1,\ x_{-4}=7,\ x_{-3}=-9,\ x_{-2}=10,\ x_{-1}=-8,\ x_{0}=11. \)
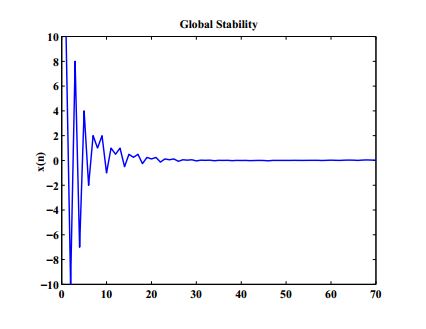
Example 3. In Figure 3, we plot the global stability under the conditions given in Theorem 3. Here, we consider the values \(c_{1}=0.5,\ c_{2}=0.025,\ c_{3}=5,\ c_{4}=6,\ x_{-7}=1,\ x_{-6}=2,\ x_{-5}=-2,\ x_{-4}=4,\ x_{-3}=-7,\ x_{-2}=8,\ x_{-1}=-10,\ x_{0}=10. \)
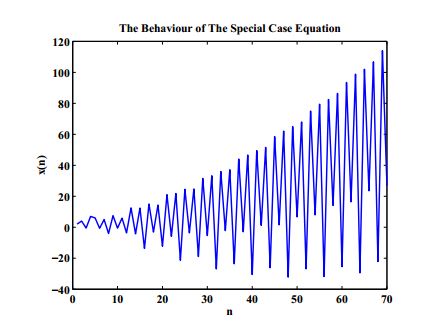
Example 4. The behaviour of the solution of Equation (7) is plotted in Figure 4 according to the following values: \(c_{1}=0.5,\ c_{2}=0.025,\ c_{3}=5,\ c_{4}=6,\ x_{-7}=1,\ x_{-6}=2,\ x_{-5}=-2,\ x_{-4}=4,\ x_{-3}=-7,\ x_{-2}=8,\ x_{-1}=-10,\ x_{0}=10.\)