For every \(n\ge 3\), we determine the minimum number of edges of graph with \(n\) vertices such that for any non edge \(xy\) there exits a hamiltonian cycle containing \(xy\).
For all graph theoretical terms and notations not defined here the reader is referred to [1]. We only consider simple finite loopless undirected graphs. For a graph \(G=(V,E)\) with \(\vert V\vert=n\) vertices, an edge is a pair of two connected vertices \(x,y\), we denote it by \(xy,xy\in E\); when two vertices \(x,y\) are not connected this pair form the non-edge \(xy,xy\not\in E\). In \(G\) a \(2\)-factor is a subset of edges \(F\subset E\) such that every vertex is incident to exactly two edges of \(F\). Since \(G\) is finite a \(2\)-factor consists of a collection of vertex disjoint cycles spanning the vertex set \(V \). When the collection consists of an unique cycle the \(2\)-factor is connected, so it is a hamiltonian cycle.
We intend to determine, for any integer \(n\ge 3\), a graph \(G=(V,E),n=\vert V\vert\) with a minimum number of edges such that for every non-edge \(xy\) it is always possible to include the non-edge \(xy\) into a connected \(2\)-factor, i.e., the graph \(G_{xy}=(V,E\cup \{xy\})\) has a hamiltonian cycle \(H,xy\in H\). In other words for any non-edge \(xy\) of \(G\) there exits a hamiltonian path between \(x\) and \(y\).
This problem is related to the minimal \(2\)-factor extension studied in [2] in which the \(2\)-factors are not necessary connected. It is also related to the problem of finding minimal graphs for non-edge extensions in the case of perfect matchings (\(1\)-factors) studied in [3]. Another problem of hamiltonian extension can be found in [4].
Definition 1. Let \(G=(V,E)\) be a graph and \(xy\not\in E\) an non-edge. If \(G_{xy}=(V,E\cup \{xy\})\) has a hamitonian cycle that contains \(xy\) we shall say that \(xy\) has been extended (to a connected \(2\)-factor, to an hamiltonian cycle).
Definition 2. A graph \(G=(V,E)\) is connected 2-factor expandable or hamiltonian expandable (shortly expandable) if every non-edge \(xy\not\in E\) can be extended.
Definition 3. An expandable graph \(G=(V,E)\) with \(\vert V \vert=n\) and a minimum number of edges is a minimum expandable graph. The size \(\vert E\vert\) of its edge set is denoted by \(Exp_h(n)\).
The case where the \(2\)-factor is not constrained to be hamiltonian is studied in [2]. In this context \(Exp_2(n)\) denotes the size of a minimum expandable graph with \(n\) vertices. It follows that \(Exp_h(n)\ge Exp_2(n)\). We use the following notations. For \(G=(V,E)\), \(N(v)\) is the set of neighbors of a vertex \(v\), \(\delta(G)\) is the minimum degree of a vertex. A vertex with exactly \(k\) neighbors is a \(k\)-vertex. When \(P=v_i,\ldots,v_j\) is a sequence of vertices that corresponds to a path in \(G\), we denote by \({\bar P}=v_j,\ldots,v_i\) its mirror sequence (both sequences correspond to the same path). We state our result.Theorem 1. The minimum size of a connected \(2\)-factor expandable graph is: $$Exp_h(3)=2,Exp_h(4)=4,Exp_h(5)=6; Exp_h(n)= \lceil {3\over 2}n\rceil,n\ge 6$$
Proof.
For \(n\ge 3\) we have \(Exp_h(n)\ge Exp_2(n)\).
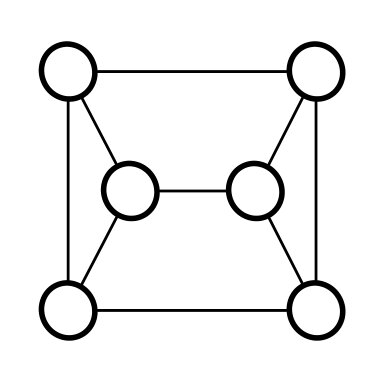
In [2] it is proved that the three graphs given by Figure 1 are minimum for \(2\)-factor extension. They are also minimum expandable for connected \(2\)-factor extension.
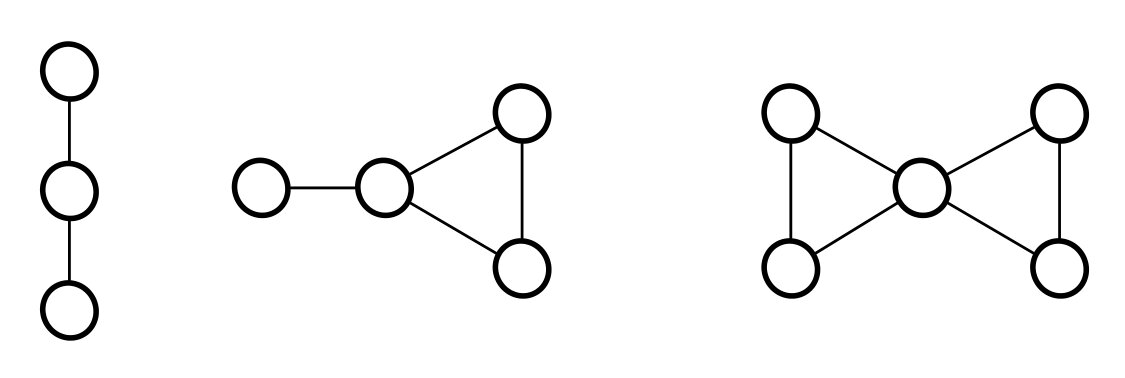
Suppose that \(G\) is a minimum expandable graph with \(n\ge 7\) and \(\delta(G)=2\). Let \(v\in V\) with \(d(v)=2\), \(N(v)=\{u_1,u_2\}\). If \(u_1u_2\not\in E\) then \(u_1u_2\) cannot be expanded into a hamiltonian cycle. So \(u_1u_2\in E\). If \(d(u_1)=2\) then \(u_2\in N(u_1)\cap N(v)\) and \(Exp_h(n)\ge {3\over 2}n\). So from now one we may assume \(d(u_1),d(u_2)\ge 3\). Suppose that \(d(u_1)=d(u_2)=3\). Let \(N(u_1)=\{v,u_2,v_1\}, N(u_2)=\{v,u_1,v_2\}\). If \(v_1\ne v_2\) then \(u_1v_2\) is not expandable. If \(v_1= v_2\) then \(vv_1\) is not expandable. From now we can suppose that \(d(u_1)\ge 3,d(u_2)\ge 4\). Moreover \(v\) is the unique \(2\)-vertex in \(N(u_2)\). It follows that every \(2\)-vertex \(u\in V\) can be matched with a distinct vertex \(u_2\) with \(d(u_2)\ge 4\). Then \(\Sigma_{v\in V}d(v)\ge 3n\) and thus \(m\ge {3\over 2}n\).
When \(\delta(G)\ge3\) we have \(\Sigma_{v\in V}d(v)\ge 3n\). Thus for any expandable graph we have \(\vert E\vert=m\ge {3\over 2}n,n\ge 7\).
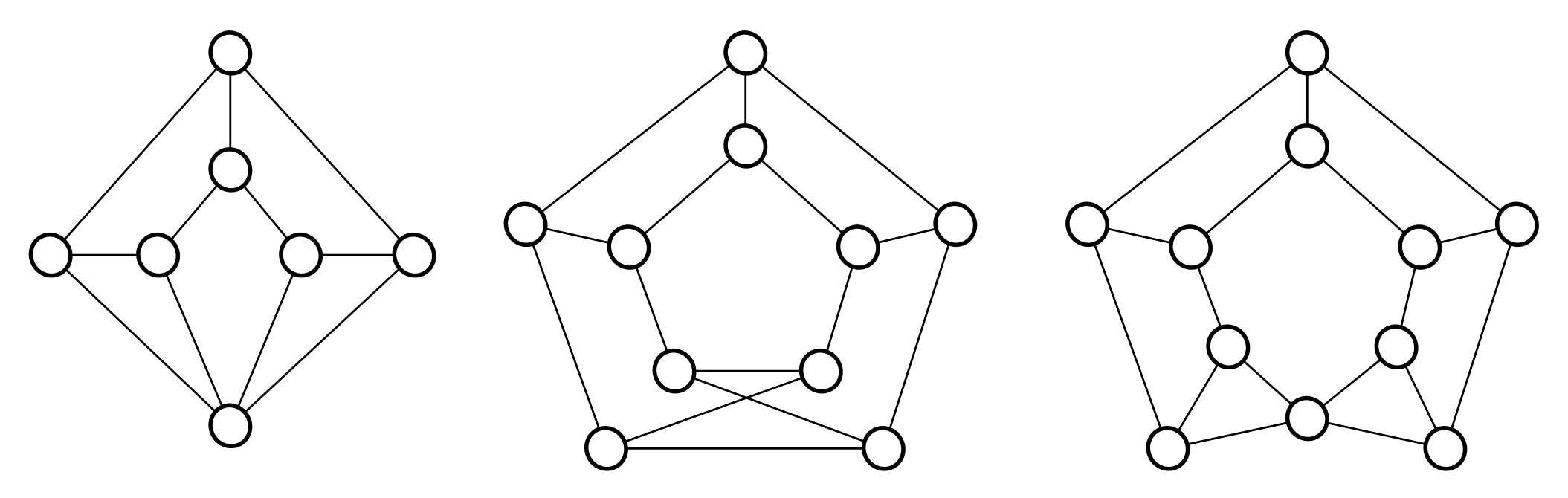
For any even integer \(n\ge 8\) we define the graph \(G_n=(V,E)\) as follows. Let \(n=2p\), \(V=A\cup B\) where \(A=\{a_1,\ldots,a_p\}\) and \(B= \{b_1,\ldots,b_p\}\). \(A\) (resp. \(B\)) induces the cycle \(C_A=(A,E_A)\) with \(E_A=\{a_1a_2,a_2a_3,\ldots,a_pa_1\}\) (resp. \(C_B=(B,E_B)\) with \(E_B=\{b_1b_2,b_2b_3,\ldots,b_pb_1\}\). Now \(E=E_A\cup E_B\cup E_C\) with \(E_C=\{a_2b_2,a_3b_3,\ldots,a_{p-1}b_{p-1},a_1b_p,a_pb_1\}\). Note that \(G_n\) is cubic so \(m= {3\over 2}n\). (see \(G_{10}\) in Fig. 3)
We show that \(G_n\) is expandable. First we consider a non-edge \(a_ia_j,p\ge j>i\ge 1\). Note that the case of a non-edge \(b_ib_j\) is analogous. We have \(j\ge i+2\) and since \(a_1a_p\in E\) from symmetry we can suppose that \(j< p\). Let \(P=a_j,a_{j-1},\ldots,a_{i+1},b_{i+1},b_{i+2},\ldots,b_{j+1},a_{j+1},a_{j+2},b_{j+2},\ldots,c_j\) where \(c_j\) is either \(a_p\) or \(b_p\) and let \(Q=a_i,b_i,b_{i-1},a_{i-1},\ldots,c_i\) where \(c_i\) is either \(a_1\) or \(b_1\). From \(P\) and \(Q\) one can obtain an hamiltonian cycle containing \(a_ib_j\) whatever \(c_i\) and \(c_j\) are.
Now we consider a non-edge \(a_ib_j\). Without loss of generality we assume \(j\ge i\). Suppose first that \(j=i\), so either \(i=1\) or \(i=p\). Without loss of generality we assume \(i=j=1\): \(a_1,b_p,b_{p-1},\ldots, b_2,a_2,a_3,\ldots, a_p,b_1,a_1\) is an hamiltonian cycle. Now assume that \(j>i\): Let \(P_j=b_j,b_{j-1},\ldots,b_{i+1},a_{i+1},a_{i+2},\ldots,a_{j_+1},b_{j+1},b_{j+2}, a_{j+2},\ldots, c_p\) where either \(c_p=a_p\) or \(c_p=b_p\), \(P_i=a_i,b_i,b_{i-1},a_{i-1},a_{i-2},\ldots,c_1\) where either \(c_1=a_1\) or \(c_1=b_1\). If \(c_p=a_p\) and \(c_1=a_1\) then \(P_j,b_1,b_p,P_i,a_j\) is an hamiltonian cycle. If \(c_p=a_p\) and \(c_1=b_1\) then \(P_j,a_1,b_p,P_i,a_j\) is an hamiltonian cycle. The two other cases are symmetric.
For any odd integer \(n=2p+1\ge 7\) we define the graph \(G_n=(V,E)\) as follows. We set \(V=A\cup B\cup\{v_{n}\}\) where \(A=\{a_1,\ldots,a_p\}\) and \(B= \{b_1,\ldots,b_p\}\). \(A\cup\{v_n\}\) (resp. \(B\cup\{v_n\}\)) induces the cycle \(C_A=(A\cup\{v_n\},E_A)\) with \(E_A=\{a_1a_2,a_2a_3,\ldots,a_pv_n,v_na_1\}\) (resp. \(C_B=(B\cup\{v_n\},E_B)\) with \(E_B=\{b_1b_2,b_2b_3,\ldots,b_pv_n,v_nb_1\}\). Now \(E=E_A\cup E_B\cup E_C\) with \(E_C=\{a_ib_i\vert 1\le i\le p\}\cup\{a_1v_n,b_1v_n,a_pv_n,b_pv_n\}\). Note that \(m= \lceil{3\over 2}n\rceil\). (see \(G_{7}\) and \(G_{11}\) in Figure 3)
We show that \(G_n\) is expandable. First, we consider a non-edge \(a_ia_j,p\ge j>i\ge 1\) (the case of a non-edge \(b_ib_j\) is analogous). \(a_i,a_{i+1},\ldots,a_{j-1},b_{j-1},b_{j-2},b_{j-3},\ldots,b_i,b_{i-1}, a_{i-1},a_{i-2},b_{i-2},\ldots,v_n,c_p,d_p,d_{p-1},c_{p-1},\ldots, c_j,d_j\), where \(d_j=a_j\) and for any \(k,j\le k\le p,\) the ordered pairs \(c_k,d_k\) correspond to either \(a_k,b_k\) or \(b_k,a_k\), is an hamiltonian cycle. Second, let a non-edge \(a_ib_j,p\ge j>i\ge 1\). We use the same construction as above taking \(d_j=b_j\).