The paper is concerned with the KG-Sombor index (\(KG\)), a recently introduced vertex-and-edge-degree-based version of the Sombor index, applied to Kragujevac trees (\(Kg\)). A general combinatorial expression for \(KG(Kg)\) is established. The species with minimum and maximum \(KG(Kg)\)-values are determined.
Let \(G\) be a simple graph, with vertex set \(\mathbf V(G)\) and edge set \(\mathbf E(G)\). Then \(|\mathbf V(G)|\) and \(|\mathbf E(G)|\) are the number of vertices and edges of \(G\). By \(e=uv \in \mathbf E(G)\) we denote the edge of \(G\), connecting the vertices \(u\) and \(v\). The degree of a vertex \(u \in \mathbf V(G)\) (= number of vertices that are adjacent to \(u\)) is denoted by \(d(u)\). The degree of an edge \(e \in \mathbf E(G)\) (= number of edges that are incident to \(e\)) is denoted by \(d(e)\). Recall that if \(e=uv\), then \(d(e)=d(u)+d(v)-2\).
For other graph-theoretical notions, the readers are referred to textbooks [1,2,3].
In the mathematical and chemical literature, some fifty or more different vertex-degree-based graph invariants (topological indices) have been defined and examined, all of the form
The oldest such invariant, conceived as early as in the 1970s, is the first Zagreb index, \(Zg\) [4]. One of the newest such invariant is the Sombor index, \(SO\) [5,6]. These are defined as
Recently a vertex-edge variant of the Sombor index was introduced [16,17], defined as
By continuing the considerations from Ref. [27], we now focus our attention to the KG-Sombor index. In order that the present article be self-contained, we repeat the definition of Kragujevac trees (as slightly modified in [27]).
Let \(n\) be a positive integer. For \(k=0,1,\ldots,n\), we denote by \(B_k\) the rooted tree with \(2k+1\) vertices, constructed by attaching \(k\) two-vertex branches to the root, see Figure 1.
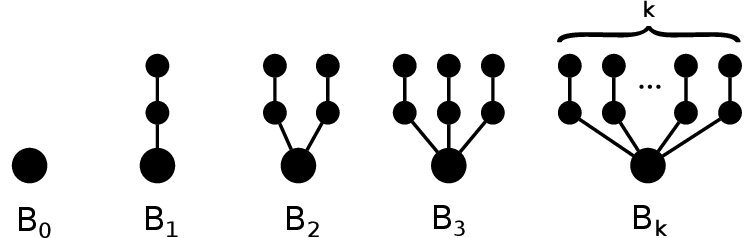
Let \(k_i\,,\,i=1,2,\ldots,n\), be non-negative integers, such that
Definition 1. Let the parameters \(k_1,k_2,…,k_n\) satisfy the condition (6). Then the Kragujevac tree \(Kg(k_1,k_2,\ldots,k_n)\) is the tree obtained from \(B_{k_1}\), \(B_{k_2}\), \(\ldots\) \(B_{k_n}\), by connecting their roots to a new vertex.
In Figure 2 an example is depicted, illustrating Definition 1.
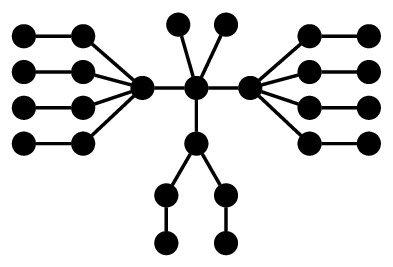
According to Definition 1, the Kragujevac tree with parameters \(k_1,k_2,\ldots,k_n\) has
\[ 1 + \sum_{i=1}^n (2\,k_i + 1) = 2K + n + 1 \] vertices.An edge connecting a vertex of degree \(i\) and a vertex of degree \(j\) will be referred to as an \((i,j)\)-edge. Directly from Definition 1 we obtain:
Proposition 2. Let \(Kg(k_1,k_2,\ldots,k_n)\) be a Kragujevac tree. Then it has \(K\) \((1,2)\)-edges, \(k_i\) \((k_i+1,2)\)-edges for each \(i=1,2,\ldots,n\), and a \((k_i+1,n)\)-edge for each \(i=1,2,\ldots,n\).
Applying Proposition 2 to Eq. (5) we arrive at:Lemma 3. The KG-Sombor index of the Kragujevac tree \(Kg(k_1,k_2,\ldots,k_n)\) depends on its structural parameters as
Lemma 4. Let \(Kg = Kg(k_1,k_2,\ldots,k_n)\) be the Kragujevac tree whose parameters satisfy Eqs. (6) and (7). Then \(Zg(Kg)\) is minimal if and only if \[ k_i \in \left\{ \left\lfloor \frac{K}{n} \right\rfloor, \left\lceil \frac{K}{n} \right\rceil \right\} \ \ \mbox{for} \ \ i=1,2,\ldots, n, \hspace{10mm} \mbox{i.e.,} \hspace{10mm} k_n – k_1 \leq 1\,. \] and \(Zg(Kg)\) is maximal if and only if \[ k_1=k_2= \cdots = k_{n-1}=0 \hspace{10mm} \mbox{and} \hspace{10mm} k_n=K\,. \]
In order to use the results of Lemma 4, we need to establish a relation between the first Zagreb and the KG-Sombor indices. This is achieved using the following simple argument. Note that bounds analogous to (10) were previously obtained for the ordinary Sombor index, Eq. (3) [6].For any positive numbers \(a\) and \(b\),
Lemma 5. For any graph \(G\) with \(m\) edges,
Inequalities (10) indicate that the KG-Sombor and first Zagreb indices should be linearly correlated. Indeed, in the case of trees (with a fixed number of vertices) this correlation was found to be remarkably good, see Figures 3 and 4, and Table 1.
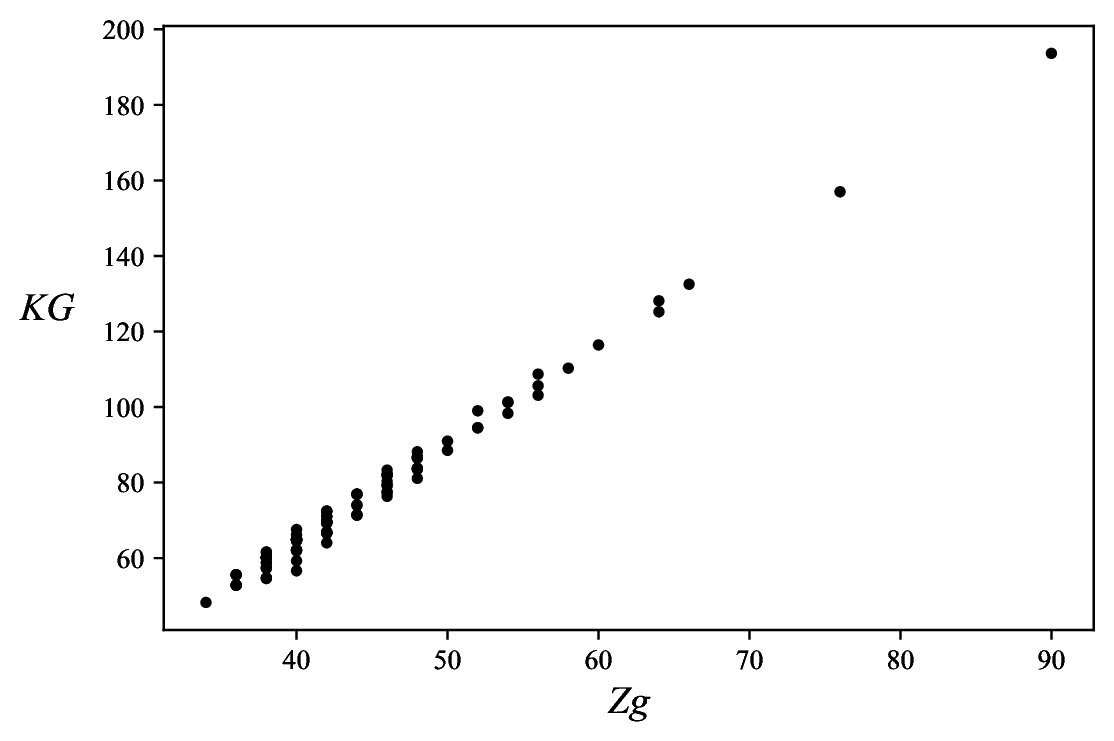
| \(N\) | \(a\) | \(b\) | \(R\) |
|---|---|---|---|
| 10 | \(2.61 \pm 0.03\) | \(-40.27 \pm 1.15\) | 0.9952 |
| 11 | \(2.60 \pm 0.02\) | \(-44.94 \pm 0.89\) | 0.9947 |
| 12 | \(2.58 \pm 0.01\) | \(-49.13 \pm 0.64\) | 0.9946 |
| 13 | \(2.58 \pm 0.01\) | \(-53.71 \pm 0.47\) | 0.9942 |
| 14 | \(2.57 \pm 0.01\) | \(-58.13 \pm 0.34\) | 0.9940 |
| 15 | \(2.57 \pm 0.03\) | \(-62.69 \pm 0.24\) | 0.9937 |
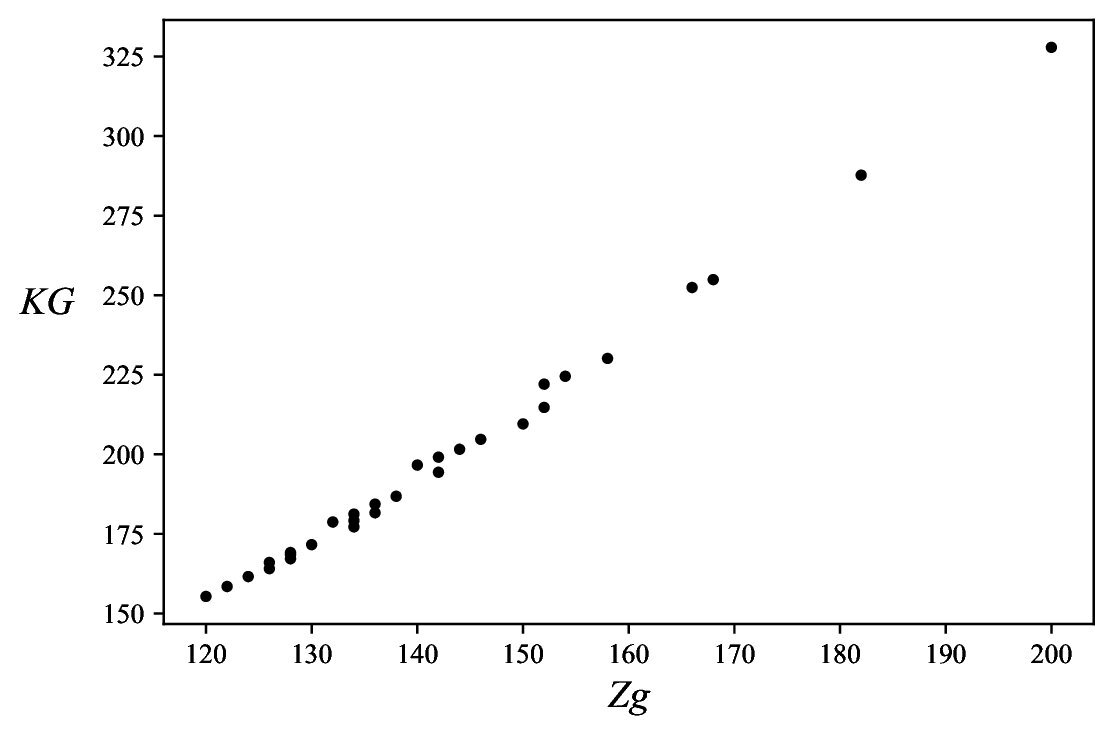
Bearing these numerical results in mind, we maintain to be justified to state the following analogue of Lemma 4:
Proposition 6. Let \(Kg = Kg(k_1,k_2,\ldots,k_n)\) be the Kragujevac tree whose parameters satisfy Eqs. (6) and (7). Then \(KG(Kg)\) is minimal if and only if \[ k_i \in \left\{ \left\lfloor \frac{K}{n} \right\rfloor, \left\lceil \frac{K}{n} \right\rceil \right\} \ \ \mbox{for} \ \ i=1,2,\ldots, n, \hspace{10mm} \mbox{i.e.,} \hspace{10mm} k_n – k_1 \leq 1\,. \] and \(KG(Kg)\) is maximal if and only if \[ k_1=k_2= \cdots = k_{n-1}=0 \hspace{10mm} \mbox{and} \hspace{10mm} k_n=K\,. \]
A somewhat stronger claim, based on the numerical results presented in Figure 4, would be:Proposition 7. Let \(Kg_a\) and \(Kg_b\) be two Kragujevac trees with equal \(n\) and \(K\) values. Then \[ Zg(Kg_a) > Zg(Kg_b) \ \Leftrightarrow \ KG(Kg_a) > KG(Kg_b)\,. \]
Assuming that Proposition 6 is valid, we have the following results:If \(Kg\) is a Kragujevac tree with parameters \(n\) and \(K\), then the maximum value of \(KG(Kg)\) is
\begin{eqnarray*} && (\sqrt{8}+\sqrt{5})K + \sqrt{2}\,K^2 + K\,\sqrt{K^2+2K+5} + \sqrt{2K^2+n^2+2nK-2n+2} +\, \sqrt{K^2+2Kn-2K+2n^2-2n+1}\,. \end{eqnarray*} The minimum value of \(KG(Kg)\) depends on the parameter \(p\), defined via \(K \equiv p\,(\hspace{-3mm} \mod n)\). For instance, for \(p=0\), this minimum value is \begin{eqnarray*} && (\sqrt{8}+\sqrt{5})K + \sqrt{2}\,K\,x + K\,\sqrt{x^2+2x+5} + n\,\sqrt{2x^2+n^2+2nx-2n+2} + \, n\,\sqrt{x^2+2nx-2x+2n^2-2n+1}\,, \end{eqnarray*} where \(x=K/n\).In this paper, a combinatorial expression, Eq. (5), is established for the KG-Sombor index of Kragujevac trees. Because of the perplexing form of formula (5), our approach towards finding the extremal values of \(KG(Kg)\), Proposition 6, used the analogous results earlier established for the first Zagreb index (Lemma 4), combined with Lemma 5, and the fact that there exists an excellent linear correlation between KG-Sombor and first Zagreb indices. This latter fact was empirically verified for both general and Kragujevac trees, see Figs. 3 and 4. Finding a rigorous analytical proof of our Propositions 6 and 7 remains a challenge for the future but appears to be a prohibitively tricky task.
Comparing Eqs. (3) Furthermore, (4), it is obvious why ”Sombor” is used in the name of the KG-index. At this point, we reveal that ”KG” indicates the names of the inventors of this index – V. R. K & I. G.