Coronoids are nice chemical structures that may be represented mathematically in the planar hexagonal lattice. They have been well-studied both for their chemical properties and also their enumerative aspects. Typical approaches to the latter type of questions often include classification and algorithmic techniques. Here we study one simple class of coronoids called hollow hexagons. Notably, hollow hexagons may be represented with a collection of partitions on the set \(\{2,3,4,6\}\). The hollow hexagons are used to classify another family of primitive coronoids, which we introduce here, called lattice path coronoids. Techniques from lattice path enumeration are used to count these newly-defined structures within equivalence classes indexed by enclosing hollow hexagons.
Chemical structures can provide interesting opportunities for mathematicians to study geometric, topological, or enumerative properties outside of the structures’ chemical significance. Here, we will consider hydrocarbon molecules, specifically, coronoid hydrocarbons. As planar objects, these are particularly nice to study mathematically. By deleting the carbon-hydrogen bonds, the molecules can be represented by chains of hexagons on the planar hexagonal lattice with an internal corona hole. In particular, we want to look at a class of coronoid systems called primitive coronoids. Primitive coronoids are single cyclic chains of hexagons connected along edges. These have been studied prominently in various papers by Bergan, Brendsdal, Brunvoll, Cyvin, Cyvin, Gutman, Kovačević, and Tošić [1-4], for example. Throughout this paper, we examine enumerative aspects of a class of coronoids associated with another kind of well-studied combinatorial objects – lattice paths.
Section 2 will make precise the definitions of the chemical structures of interest and provide some vocabulary. Section 3 provides a bijection between the class of primitive coronoids known as hollow hexagons and a set of partitions with restricted part size. In Section 4, we introduce lattice path coronoids: these are considered in two cases and enumerative results are given in the next two sections. In Section 5, we look at the first case where there is no overlap of lattice paths in the structure, and Section 6 considers the more involved case with overlap. We conclude with some questions.
The hexagonal lattice is a planar lattice of identical regular hexagons where each hexagon is simply connected to six other hexagons. Many chemical structures can be represented on the hexagonal lattice including a benzenoid, which is a planar set of simply connected regular hexagons that is defined by a cycle of edges called the perimeter. Algorithmic and enumerative results on benzenoids are due to Vöge, Guttmann, and Jensen [5] for example, or also see Gutman and Cyvin’s more comprehensive text [6]. Single coronoids or simply coronoids are similar to benzenoids in that they are composed of simply connected hexagons on the hexagonal lattice, but a coronoid must have an interior hole of at least two hexagons. (Single refers to the single corona hole in the interior of the coronoid. All structures in this paper will have a single corona hole, but generalizations to molecules with multiple holes exist.) Thus coronoids are defined by two cycles on the lattice, that is, the inner perimeter and the outer perimeter, where the inner perimeter is completely contained within the outer. Here we want to further consider a subset of coronoids called primitive coronoids. Coronoids (and benzenoids) have an interior vertex when the vertex is a vertex for three hexagons in the molecule. From the dual perspective, interior vertices exist when there is a triangle in the dual graph. Coronoids and benzenoids that do not have any interior vertices are called catacondensed. (Those with interior vertices are called pericondensed.) See Brunvoll, Cyvin, and Cyvin [7] for a historical discussion on the classification and study of these objects. We define primitive coronoids to be the coronoids consisting of a single cyclic chain of hexagons without any interior vertices; also described as unbranched catacondensed coronoids. See Figure 1 for examples of each of these structures, and note, there is no expectation of convexity. Further, benzenoids and coronoids are not usually considered fixed objects, so rotations and reflections of a benzenoid are not distinct. When counting, each coronoid we count represents the equivalence class of its fixed rotations and reflections.
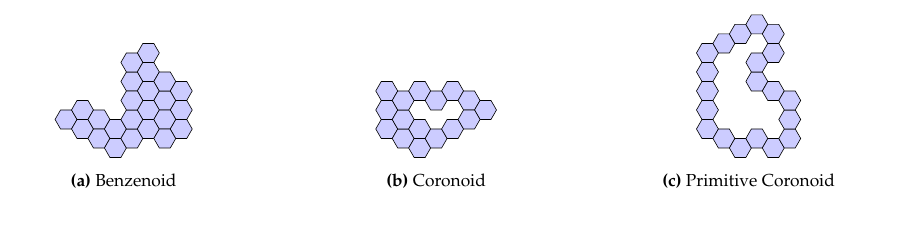
Finally, because primitive coronoids are catacondensed chains, each hexagon is connected to exactly two other hexagons. If three hexagons appear in a line, the middle hexagon is said to be linearly annulated, otherwise the middle hexagon is angularly annulated. More simply, we will refer to angularly annulated hexagons as corners. A corner may be protruding or intruding, respectively, if it has three edges on the outer perimeter or inner perimeter, respectively. We note, all primitive coronoids must have at least six protruding corners. In fact, hollow hexagons are defined to be the primitive coronoids that that contain only six corners (all of which must be protruding). These are aptly named because exactly six protruding corners implies exactly six edges. Figure 2 displays some examples of hollow hexagons.
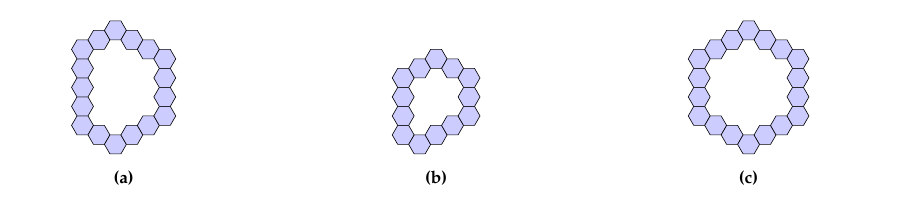
Before introducing the main object of this paper, another subset of primitive coronoids, we first look at the class of hollow hexagons.
Hollow hexagons are the simplest class of primitive coronoids, and enumerative results are known. Cyvin et al. [4] and Cyvin, Brunvoll, and Cyvin [3], provide computer generated counts of hollow hexagons and exact numerical results in terms of formulas and a generating function.
For our purposes, we wish to utilize the relationship of hollow hexagons with certain kind of integer partition which was observed in entry A029136 of the Online Encyclopedia of Integer Sequences [8] by Arndt. In order to define a correspondence between a hollow hexagon and a partition, we provide a bijective proof of this known result.
Theorem 1. Given an integer \(n> 6\), the set of hollow hexagons with area \(n\) hexagons is in bijection with the set of integer partitions of \(n\) into parts of size 2, 3, 4, or 6 with at least one 6.
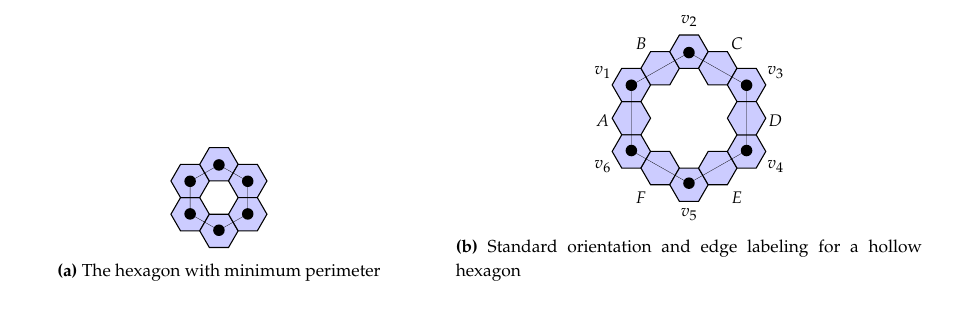
Proof. First, let us identify each hollow hexagon \(h\) with \((a,b,c,d,e,f)\) where this ordered 6-tuple is the cycle of lengths of the edges of the dual graph of \(h\), thus the edge lengths are determined by the number of hexagons along that side minus one. We may construct a hexagon with area equal to \(6\) hexagons (see Figure 3), but technically because the corona hole must consist of at least two interior hexagons, this is not a primitive coronoid. We use this hexagon \(h_{6} = (1,1,1,1,1,1)\) as the foundational object in the proof. For any integer partition, we grow the edges of this minimal hexagon based on the integers in the partition.
Given an integer partition \(\lambda\) of \(n>6\) composed of parts from the set \(\{2,3,4,6\}\) with at least one 6, let \(k_i\) be the number of \(i\)’s in the partition for \(i\in \{2,3,4,6\}\). Define a map from the set of partitions \(\{\lambda\}\) to the set of hollow hexagons \(\{h\}\) as follows: \[\lambda \mapsto h_{\lambda} =(a,b,c,d,e,f),%(1+k_2+k_3+k_4+k_6, 1+k_4+k_6, 1+k_3+k_6, 1+k_2+k_4+k_6, 1+k_3+k_4+k_6, 1+k_6),\] where \[\begin{aligned} a& = k_2+k_3+k_4+k_6, \\ b&=k_4+k_6, \\ c&=k_3+k_6, \\ d&=k_2+k_4+k_6,\\ e&=k_3+k_4+k_6, \\ f&=k_6. \end{aligned}\]
We claim that every such integer partition creates a unique hexagon. Given any two partitions \(\lambda_1\) and \(\lambda_2\), suppose \(h_{\lambda_1} = h_{\lambda_2}\), that is, \((a_1,b_1,c_1,d_1,e_1,f_1)=(a_2,b_2,c_2, d_2, e_2,f_2)\). Because \(f_1=f_2\), using the equations above, it must be the case that \(k_{6_1} = k_{6_2}\), so we know \(\lambda_1\) and \(\lambda_2\) have the same number of \(6\)’s. Because \(b_1=b_2\) and \(c_1=c_2\), we have that \(k_{4_1}=k_{4_2}\) and \(k_{3_1}=k_{3_2}\). But now this implies \(k_{2_1} =k_{2_2}\) and consequently \(\lambda_1=\lambda_2\). Therefore the map is injective.
The process may be reversed. We utilize the identities that pairs of adjacent opposite sides must be equal, that is, \(a+b = d+e\), \(b+c = e+f\), and \(c+d=a+f\). Then starting with a hexagon \(h=(a,b,c,d,e,f)\) oriented so that \(a\) is a maximum length edge, the identity \(a+b=d+e\) implies \(b\leq d\) and \(b\leq e\). Similarly, the identity \(a+f=c+d\) implies \(f\leq c\) and \(f\leq d\). Therefore either \(b\) or \(f\) is minimum. Thus we may orient the cycle so the edge with maximum length is \(a\) and the edge with minimum length is \(f\). We will shrink the edges of the hexagon in steps, first observing that the edges must have lengths \(a,b,c,d,e,f\geq 1\).
Start with an empty partition \(\lambda = 0\).
Shrink all sides of the hexagon by the distance \(f-1\) and add \(f-1\) 6’s into \(\lambda\). Because \(f\) is the minimum length edge, the remaining sides all have length at least 1.
Our new hexagon has the form \((a-f+1, b-f+1, c-f+1, d-f+1, e-f+1, 1)\). Shrink sides with lengths originally labeled by \(a\), \(c\), and \(e\) by \(c-f\) thus reducing the side originally labeled with \(c\) to length \(1\). We have \((b-f+1)+(c-f+1)=(e-f+1)+1\), so \(b-f+1=(e-f+1)-(c-f)\). Similarly, \((d-f+1)+(c-f+1)=(a-f+1)+1\), that is \(d-f+1=(a-f+1)-(c-f)\). Therefore because sides \(b,d\geq 1\), we may subtract \(c-f\) from \(a-f+1\) and \(e-f+1\) while still preserving positive side lengths. We add \(c-f\) 3’s to the partition \(\lambda\).
Now we have a hexagon with side lengths \((a-c+1, b-f+1, 1, d-f+1, e-c+1,1)\). Next, shrink sides originally labeled with lengths \(a\), \(b\), \(d\), and \(e\) by \(b-f\). Applying the identities, we know \(b-f=e-c\) and \(d-f=a-c\). Therefore we may subtract \(b-f\) from edges originally labeled with \(b\) and \(e\) to get edge lengths of \(1\) and because \(a\geq e\), we also preserve positive edge lengths along edges originally labelled with \(a\) and \(d\). Add \(b-f\) 4’s into \(\lambda\).
Finally, we are left with the hexagon with sides \((a-e+1,1,1,d-b+1,1,1)\). Our identities imply that \(a-e+1=d-b\), thus we may shrink both sides in positions originally labelled with \(a\) and \(d\) by \(d-b\), leaving the hexagon \((1,1,1,1,1,1)\). We add \(d-b\) 2’s to the partition as well as one 6 for the remaining minimal hexagon.
It is not difficult to see that this process is the inverse of the first, and it is also injective. Suppose we have two hexagons \(h_{\lambda_1}\) and \(h_{\lambda_2}\) where \(\lambda_1 = \lambda_2\). Namely, starting with the edge of minimum length, if \(f_1 \not= f_2\), then the partitions will have a different number of \(6's\) which contradicts are assumption so \(f_1=f_2\). Next if \(c_1 \not= c_2\), the partitions would have a different number of \(3\)’s and could not be equal. Similarly, if we assume \(b_1 \not= b_2\), we get a contradiction in the number of \(4\)’s in the partition. Assuming \(f_1=f_2\), \(c_1=c_2\), and \(b_1=b_2\), we may also conclude that \(e_1=e_2\) because of the identity in Step 3 of the function. Last, if \(d_1 \not=d_2\) we would have a different number of \(2\)’s in our partitions. Thus we have arrived at a contradiction and the map must be injective. ◻
Throughout this paper when we refer to the correspondence between \(\lambda\) and \(h_\lambda\), it will always be via the map described in Theorem 1. Next, we formalize our discussion of lattice path coronoids.
We begin by describing the lattice path steps on a hexagonal lattice. From any hexagon, one may step over an edge to another hexagon through a choice of six steps. We call these steps north (N), northeast (NE), southeast (SE), south (S), southwest (SW), and northwest (NW). Now we define the primary object of interest.
Definition 2. A lattice path coronoid is a primitive coronoid whose cycle always has a protruding corner between any pair of intruding corners.
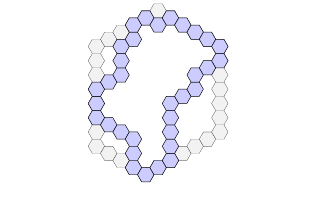
Lattice path coronoids are so named because they can be described as an ordered \(6\)-tuple of lattice paths \((L_1, L_2, L_3, L_4, L_5, L_6)\) where the lattice paths are in bijection with traditional lattice paths on a rectangular lattice, that is, each lattice path consists of only two types of steps. In particular, \(L_1\) will consist of only N and NE steps, \(L_2\) consists of only NE and SE sets, \(L_3\) consists of only SE and S steps, \(L_4\) consists only S and SW steps, \(L_5\) consists of only SW and NW steps, and \(L_6\) consists of only NW and N steps. Because intruding corners must be followed by protruding corner, we may never have more than two directions in each lattice path. See Figure 4 for an example and Figure 1c for a non-example. The idea is that locally we are bending each corner of a hollow hexagon into a lattice path in such a way that none of the lattice paths overlap and a single corona hole remains in the middle of the coronoid. Brunvoll, Cyvin, and Cyvin [1] utilize a somewhat similar process of bending corners with multiple steps where protruding corners are moved to intruding corners.
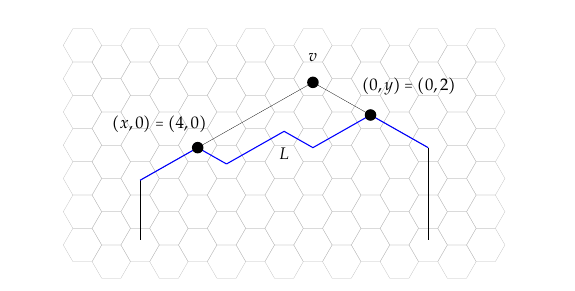
Before moving on to the results, we need a few standard conventions. Throughout we will use the same labeling and orientation for the hexagons. The hexagons will have edges labeled \(A,B,C,D,E\) and \(F\) whose lengths are \(a,b,c,d,e,\) and \(f\), respectively, where \(a\) is maximum and \(f\) is minimum. The vertices in the cycle are \((v_1, v_2, v_3, v_4, v_5, v_6)\) with \(v_1\) between edges \(A\) and \(B\), \(v_2\) between edges \(B\) and \(C\), and so on. The edges will always be ordered by the cycle \((a,b,c,d,e,f)\) with side \(A\) of length \(a\) fixed as the left vertical edge as is the case in Figure 3b. Note that the length of an edge will be given by the length of the corresponding dual edge, that is, the length of the line segment from the center of the first hexagon to the center of the last hexagon along that edge. This means the length is not equal to the number of hexagons, but rather the number of hexagons minus one. With this metric, the perimeter is equal to the number of hexagons in the chain and so both perimeter and area are given by \(h=a+b+c+d+e+f\). Further, lattice path \(L_i\) around vertex \(v_i\) is oriented so \(v_i=(0,0)\) with the lattice paths typically starting at \((x_i,0)\) and ending at \((0,y_i)\) under this orientation. For convenience, we often denote the start as \(x_i\) and the finish as \(y_i\) with the assumed coordinates.
Next, we describe the relationship between lattice path coronoids and hollow hexagons.
Lemma 3. The set of lattice path coronoids can be partitioned into area-preserving equivalence classes indexed by hollow hexagons.
Proof. Given any lattice path coronoid, we can identify the unique minimal size hollow hexagon which contains the primitive coronoid. This is done by enclosing the coronoid in any larger hexagon and shrinking by rows in each of the six dimensions until the hexagon cannot be any smaller without uncovering part of the coronoid. Any rotation or reflection of this coronoid will result in rotation or reflection of the enclosing minimal hollow hexagon, so equivalent coronoids remain in the same equivalence class of hollow hexagons. Because a lattice path on the rectangular lattice has the same length as two adjacent sides of the enclosing rectangle, it may always be extended out to this rectangle. Similarly, the lattice paths placed on each vertex \(v\) of the enclosing hollow hexagon, more precisely the lattice path placed from one adjacent vertex of \(v\) to the other, are restricted to the directions of the of the edges meeting at \(v\), so these may also be extended out to the minimal enclosing hexagon with the same perimeter as the lattice path coronoid. ◻
Our aim is to count lattice path coronoids using these partition-indexed equivalence classes of hollow hexagons. To that end we define some simple piece-wise functions.
Definition 4. Let \(s: \mathbb{N} \times \mathbb{N} \longrightarrow \mathbb{N}\) be an integer-valued piecewise function where \[s(x,y) = \left\{\begin{array}{ll} \binom{x+y-2}{y-1} & \hbox{ if } x,y>0\\ &\\ 1 & \hbox{ if } x=y=0\\ &\\ 0 & \hbox{ otherwise}\\ \end{array} \right.\]
We will to use \(s(x,y)\) to count the number of lattice paths that may be placed on a particular corner of a hollow hexagon.
Proposition 5. The function \(s\) enumerates the number of lattice paths \(L\) that may be placed on a corner \(v\) starting at \(x\) and ending at \(y\).
Proof. Let the \(x\) and \(y\) variables correspond to distances away from a vertex \(v\) in each of its two directions (either N and NE, NE and SE, SE and S, S and SW, SW and NW, and NW and N). In particular, if we place a two-coordinate axis along these two directions with \(v\) at \((0,0)\), then \((x,0)\) and \((0,y)\) are the two positions where the lattice path from one of the vertices adjacent to \(v\) to the other vertex adjacent to \(v\) changes directions for the first and last time, respectively. (See Figure 5.) These points are the starting and ending points of the lattice path. It is well known that the number of lattice paths on a rectangular lattice with \(k\) E steps and \(n\) N steps is \(\binom{n+k}{k}\), so applying a transformation of the plane, the number of lattice paths from \((x,0)\) to \((0,y)\) on the hexagonal lattice starting with a step in the first direction and ending with a step in the second direction is \(s(x,y)\) for \(x,y > 0\), that is, after discounting the fixed first and last steps we have \(x-1\) steps in the first direction and \(y-1\) steps in the second direction. When the distances \(x\) and \(y\) are zero, we are not altering the edges of the hexagon around vertex \(v\). Further, we cannot have exactly one of \(x\) and \(y\) equal to zero, because if the lattice path takes a step in the first direction it must also take a step in the second direction. ◻
(Note, throughout the binomial coefficient \(\binom{n}{k}\) represents the ordinary combinatorial binomial coefficient and thus is zero when \(k>n\) or when \(n\) or \(k\) is negative.)
We will also need to consider a specific type of lattice path.
Definition 6. Given lattice path \(L\) with steps \(s_1 s_2 \cdots s_k\) in direction \(d_1\) or direction \(d_2\), the reverse of \(L\) is \[rev(L) =\bar{s}_k \cdots \bar{s}_2 \bar{s}_1\] where \(\bar{s}\) is a step in direction \(d_1\) if and only if \(s\) is a step in direction \(d_2\). We say a lattice path \(L\) is symmetric, if \(L=rev(L)\).
The count for symmetric lattice paths from \((x,0)\) to \((0,x)\) is also well-known.
Lemma 7. For \(x>0\), the number of symmetric lattice paths on the rectangular lattice from \((x,0)\) to \((0,x)\) is \(2^x\).
Proof. We know \(s_i = \bar{s}_{2x-i+1}\), so the lattice path is totally determined by the first \(x\) steps. Summing over all lattice paths from \((x,0)\) to \((i,i)\), a point on the line \(y=x\), that is, we sum \(\binom{(x-i) +i}{i}\) over \(0\leq i \leq x\) concludes the proof. ◻
Thus we define another piecewise function to take into consideration for the fact that if \(x,y>0\) paths from \((x,0)\) and \((0,x)\) begin and end with a fixed step in different directions as well as to deal with the case where \(x=0\) or \(y=0\).
Definition 8. Let \(t: \mathbb{N} \longrightarrow \mathbb{N}\) be an integer-valued piecewise function where \[t(x) = \left\{ \begin{array}{ll} 2^{x-1} &\hbox{ if } x > 0\\ 1 &\hbox{ if } x=0\\ 0 &\hbox{ otherwise }\\ \end{array} \right.\]
Thus we have the following corollary:
Corollary 9. The function \(t\) enumerates the number of symmetric lattice paths \(L\) that may be placed on a corner \(v\) starting at \(x\) and ending at \(x\).
Now we wish to use these piecewise functions in general formulas to count lattice path coronoids.
We begin by stating a result with much historical attribution; see Neumann [9]. Sometimes known as Cauchy-Frobenius Lemma, it was cited and proved in Burnside’s book Theory of Groups of Finite Order [10] and became mistakenly known as Burnside’s Lemma. The result is also the basis for the Pólya Enumeration Theorem. We state the lemma using modern notation.
Lemma 10 (Cauchy-Frobenius). Given a finite group \(G\) acting on a finite set \(X\), let \(X^g\) be the elements in the set that are fixed by the group element \(g\) and let \(X/G\) be the set of orbits of \(X\) under \(G\). Then \[|X/G|= \frac{1}{|G|} \sum_{g \in G} |X^g|.\]
It is not unusual to apply versions of this lemma in counting questions on chemical molecules; see for instance Rosenfeld, Klein, and Oliva [11] who apply a version of Pólya’s result to enumerate molecules whose structure is represented by bridged pairs of icosahedra.
We will use the group actions of the dihedral group \[D_{12} =\langle 1, r, r^2, r^3, r^4, r^5, q, qr, qr^2, qr^3, qr^4, qr^5 \rangle\] where \(r\) is a \(60^{\circ}\) rotation and \(q\) is the reflection across the line bisecting \(A\) and \(D\). The aim is to define functions for enumerating the number of lattice path coronoids in the equivalence class of a hexagon fixed by each of the groups actions, that is, for each action \(g\in D_{12}\) define \(f_g(a,b,c,d,e,f)\) such that \(f\) is the number of lattice path coronoids whose enclosing hollow hexagon is fixed by the action of \(g\).
We observe the following about hollow hexagons whose corresponding partitions do not contain a four.
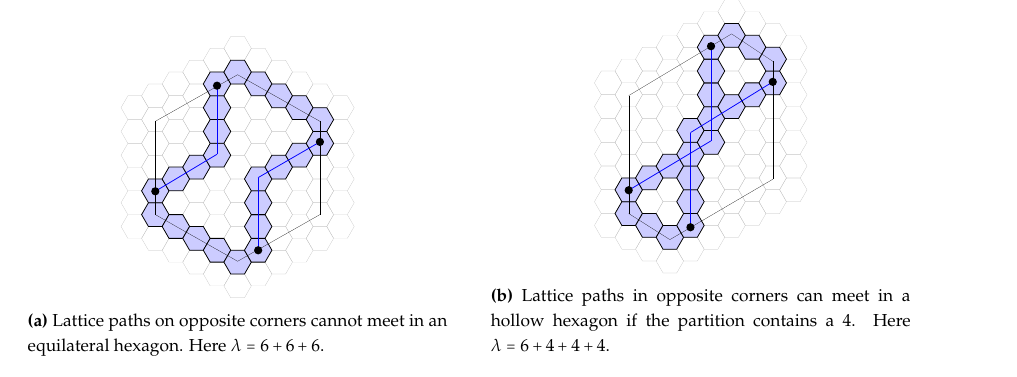
Remark 1. If the corresponding partition to a hollow hexagon does not contain a four, any pair of lattice paths placed on opposite corners are always non-adjacent. This is not necessarily true if the partition does contain a four.
Because lattice path coronoids are catacondensed, that is, intruding adjacent corners are forbidden, the farthest towards the center that a corner vertex of a hollow hexagon could go is by using the L-shaped lattice path that bends where \(x\) and \(y\) are equal to their respective side lengths minus one. In the case of an equilateral hollow hexagon, this is at \(x=a-1\) and \(y=a-1\). Therefore lattice paths on opposite corners are always at least one hexagon apart as illustrated in Figure 6a. Furthermore, if the hollow hexagon corresponds to a partition of only 2’s, 3’s, and 6’s, then the lattice paths on opposite corners are also always separated. This is because when you add a 2 into the partition sides \(A\) and \(D\) increase by one, so either the maximum bend on opposite corners doesn’t increase or the size of the L-shaped lattice path on each opposite increases by one, but in parallel directions, so the lattice paths remain horizontally the same distance apart (although they are pulled farther apart along the vertical direction). If a 3 is added into the partition, sides \(A\), \(C\), and \(E\) increase by one. But at each corner, the maximum bend in the lattice path is limited by the sides that do not increase and so cannot move closer together and cause an intersection. However, this is not true when a 4 is added to the partition. In this case, the opposing corners at \(v_1\) and \(v_4\) can now have lattice paths that move further to the center in both of its two directions. See Figure 6b for an example of this.
For the whole of Section 4, we assume the structure of the hollow hexagon is such that no opposite lattice paths may be adjacent and consequently the corresponding partition does not contain a 4. We now separate our discussion into rotations and reflections where we will set up functions to count the number of distinct lattice path coronoids fixed under each action. With these functions we may then apply Cauchy-Frobenius to count all such coronoids.
Define \(f_{r_1}\) to be the enumeration function of lattice path coronoids that are fixed by \(r_1\), the rotation by \(60^{\circ}\). Given a lattice path coronoid with lattice paths \((L_1, L_2, L_3, L_4, L_5,L_6)\) that is in the equivalence class indexed by \(h_{\lambda}\) for some partition \(\lambda\), we see that \(h_\lambda\) is fixed by \(r_1\) if and only if each lattice path is equal to the path to the left of it, in other words, we have \(L_1=L_2=L_3=L_4=L_5=L_6\). Therefore we only need to find one lattice path to determine the entire coronoid. Lattice path \(L_1\) starts on edge \(A\) and ends on edge \(B\). We choose the ending point along edge \(B\) as \(0\leq y_1 \leq b-1\). However, the beginning \(x_1\) of \(L_1\) on \(A\) must not conflict with the end of \(L_6\), but because \(L_1=L_6\), we have \(0\leq x_1 \leq a-1-y_1\). \[\sum_{y_1=0}^{b-1} \sum_{x_1=0}^{a-1-y_1} s(x_1,y_1) = 1 + \sum_{y_1=1}^{b-1} \sum_{x_1=1}^{a-1-y_1} \binom{x_1+y_1-2}{x_1-1} = 1+\sum_{y=1}^{a-1} \left( \binom{y-1}{0} + \binom{y}{1} + \cdots + \binom{b-3}{b-2-y}\right).\] Of course the only way that an element can be fixed in this case is if \(a=b\) and applying a change of variables where \(s\) is the sum \(x_1+y_1\) where \(x_1\) ranges from \(1\) to \(s-1\), we have \[f_{r_1} (a) = 1+\sum_{y_1=1}^{a-1} \sum_{x_1=1}^{a-1y_2} s(x_1,y_1) =1+ \sum_{s=2}^{a-1} \sum_{x_1=1}^{s-1} \binom{s-2}{x_1-1} = 1+\sum_{s=2}^{a-1} 2^{s-2}= \left\{ \begin{array}{ll} 2^{a-2} & \hbox{ if } a>1\\ 1 & \hbox{ if } a=1 \end{array} \right.\tag{1}\] We note that the set of lattice path coronoids fixed by \(r_1\) is the same as the set of lattice path coronoids fixed by the rotation \(r_5=r_1^5\), because a rotation of \(60^{\circ}\) to the right has the same effect as a rotation of \(60^{\circ}\) to the left and also implies \(L_1=L_2=L_3=L_4=L_5=L_6\). Thus we have \[f_{r_5} (a) = f_{r_1}(a).\tag{2}\]
Next, we will look at lattice path coronoids fixed by the rotation \(r_2 = r_1^2\), that is, a clockwise rotation of \(120^{\circ}\). In this case, we have \(L_1=L_3=L_5\) and \(L_2=L_4=L_6\), so we need to choose the two lattice paths, \(L_1\) and \(L_2\) to determine the coronoid. As before, we choose \(0 \leq y_1 \leq b-1\) as the ending point of \(L_1\) along edge \(B\) and we also choose \(0 \leq y_2 \leq c-1\) as the ending point of \(L_2\) along the edge \(C\). If the lattice path coronoid is fixed by \(r_2\), we must have that \(a=c=e\) and \(b=d=f\), consequently \(0 \leq y_2\leq a-1\). Then, because the starting point of \(L_1\) along edge \(A\) must not overlap the ending of \(L_6\) which is equal to \(L_2\), so we choose this point as \(0\leq x_1 \leq a-1 -y_2\). Further, the starting point for \(L_2\) must be \(0\leq x_2 \leq b-1-y_1\). We have the equation \[f_{r_2}(a,b)=\sum_{y_1=0}^{b-1} \sum_{y_2=0}^{a-1} \sum_{x_1=0}^{a-1-y_2} \sum_{x_2=0}^{b-1-y_1} s(x_1,y_1) s(x_2,y_2).\tag{3}\] In this case, we also have another rotation whose set of fixed points is equivalent, namely rotating \(240^{\circ}\) is the same as rotating \(-120^{\circ}\), so \[f_{r_4}(a,b)=f_{r_2} (a,b)\tag{4}\] where \(r_4=r_1^4\).
The final rotation \(r_3=r_1^3\) is the rotation by \(180^{\circ}\). Here \(L_1=L_3\), \(L_2=L_4\), and \(L_3=L_6\). Now we need to select lattice paths \(L_1\), \(L_2\), and \(L_3\). Following a similar strategy to the case above, we see \[f_{r_3}(a,b,c)=\sum_{y_1=0}^{b-1} \sum_{y_2=0}^{c-1} \sum_{y_3=0}^{a-1} \sum_{x_1=0}^{a-1-y_3} \sum_{x_2=0}^{b-1-y_1} \sum_{x_3=0}^{c-1-y_2} s(x_1,y_1) s(x_2,y_2) s(x_3,y_3).\tag{5}\]
Before looking at actions by reflections, we also need to count the entire class of lattice path coronoids, that is, those fixed by the identity element 1. We will need to choose each of the six lattice paths \((L_1, L_2, L_3, L_4, L_5, L_6)\), all of which could be distinct, along with starting and ending points. We have the function \(f_{\hbox{{1}}}(a,b,c,d,e,f)=\)
\[\sum_{y_1=0}^{b-1} \sum_{y_2=0}^{c-1} \sum_{y_3=0}^{d-1} \sum_{y_4=0}^{e-1} \sum_{y_5=0}^{f-1} \sum_{y_6=0}^{a-1} \sum_{x_1=0}^{a-1-y_6} \sum_{x_2=0}^{b-1-y_1} \sum_{x_3=0}^{c-1-y_2} \sum_{x_4=0}^{d-1-y_3} \sum_{x_5=0}^{e-1-y_4} \sum_{x_6=0}^{f-1-y_5} s(x_1,y_1) s(x_2,y_2) s(x_3,y_3) s(x_4,y_4) s(x_5,y_5) s(x_6,y_6)\tag{6}\]
Now we consider reflections in the actions of \(D_{12}\).
The six reflections in a hexagon are of two types: reflections over lines through vertices and reflections over lines bisecting edges. Because \(q\) is the horizontal reflection across the line bisecting edges \(A\) and \(D\), \(qr_2\) is the reflection across the line bisecting edges \(B\) and \(E\), and \(q r_4\) is the reflection across the line bisecting \(C\) and \(F\). Further \(q r_1\), \(q r_3\), and \(qr_5\), respectively, are reflections across the lines through vertices \(v_1\) and \(v_4\), \(v_2\) and \(v_5\), and \(v_3\) and \(v_6\), respectively. We will enumerate the former cases first.
Without loss of generality, we consider the reflection over the line bisecting \(A\) and \(D\). (The other two cases are easily generated by substitutions in the formula of \(a\) and \(d\) with either \(b\) and \(e\) or \(c\) and \(f\).) To find lattice-path coronoids that are fixed by a reflection across the line bisecting \(A\) and \(D\), we know \(L_1=rev(L_6)\), \(L_2=rev(L_5)\) and \(L_3=rev(L_4)\). Thus the lattice path coronoid is determined by the choice of \(L_1\), \(L_2\), and \(L_3\).
As we have done in the case of reflections, we first choose the ending point of each of the lattice paths. The ending point of \(L_1\) is \(0\leq y_1 \leq b-1\), and the ending point of \(L_2\) is \(0\leq y_2 \leq c-1\). Because \(L_3=rev(L_4)\), the ending point of \(L_3\) must be strictly less than half the length of \(D\), so we have \(0 \leq y_3 \leq \lfloor \frac{d-1}{2} \rfloor\). We may then choose the three starting points with the restrictions of the choices of ending points, so \(0\leq x_2 \leq b-1-y_1\) and \(0 \leq x_3 \leq c-1-y_2\). Because \(y_6=x_1\), we also have that \(x_1\) must be less than half of \(a\), and thus \(0\leq x_1 \leq \lfloor \frac{a-1}{2} \rfloor\). Putting this together, we have \[f_{q}(a,b,c,d)=\sum_{y_1=0}^{b-1} \sum_{y_2=0}^{c-1} \sum_{y_3=0}^{\lfloor \frac{d-1}{2} \rfloor} \sum_{x_1=0}^{\lfloor \frac{a-1}{2} \rfloor} \sum_{x_2=0}^{b-1-y_1} \sum_{x_3=0}^{c-1-y_2} s(x_1,y_1) s(x_2,y_2) s(x_3,y_3),\tag{7}\] and \[f_{qr_2} (b,c,d,e) = f_q (b,c,d,e) \hbox{ and } f_{qr_4}(c,d,e,f) =f_q(c,d,e,f).\tag{8}\]
Finally, we need to enumerate lattice path coronoids fixed by reflections across lines through opposing pairs of points. Without loss of generality, we consider the reflection across the line through the vertices \(v_1\) and \(v_4\). In this case lattice paths \(L_1\) and \(L_4\) must be symmetric, that is \(L_1 = rev(L_1)\) with \(x_1=y_1\) and \(L_4=rev(L_4)\) with \(x_4=y_4\). Further \(L_2 = rev(L_6)\) and \(L_3=rev(L_5)\). We choose the ending points for \(L_2\) and \(L_3\) as \(0\leq y_2 \leq c-1\) and \(0 \leq y_3 \leq d-1\). Because \(L_1\) is symmetric, we choose \(L_1\) in \(t(y_1)\) ways for \(0 \leq y_1 \leq b-1\). Similarly, we choose \(L_4\) in \(t(x_4)\) ways for \(0 \leq x_4 \leq d-1 – y_3\). We choose the other two starting points for \(L_2\) and \(L_3\) as before with \(0\leq x_2 \leq b-1-y_1\) and \(0\leq x_3 \leq c-1-y_2\). Thus, the function is \[f_{qr_1}(b,c,d)= \sum_{y_1=0}^{b-1} \sum_{y_2=0}^{c-1} \sum_{y_3=0}^{d-1} \sum_{x_2=0}^{b-1-y_1} \sum_{x_3=0}^{c-1-y_2} \sum_{x_4=0}^{d-1-y_3} t(y_1) s(x_2,y_2) s(x_3,y_3) t(x_4).\tag{9}\] We also have \[f_{qr_3}(c,d,e)=f_{qr_1}(c,d,e) \hbox{ and } f_{qr_5}(a,b,c)=f_{qr_1}(a,b,c).\tag{10}\]
Collectively Equations 1-10, impart the following result:
Proposition 11. Given a hollow hexagon \(h_\lambda = (a,b,c,d,e,f)\) where \(\lambda\) does not contain a 4, the number of lattice path coronoids in the equivalence class indexed by \(h_\lambda\) and fixed under the action of the \(g\in D_{12}\) is \(f_g(h_\lambda)\).
We create counting functions indexed by the parts of a partition.
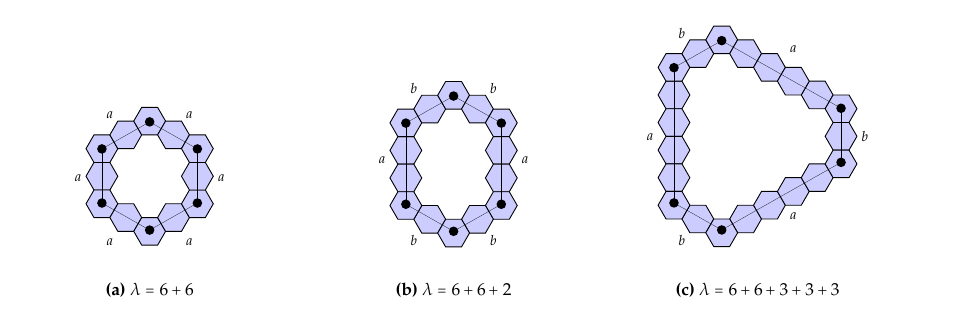
There are four cases for the edge lengths of hollow hexagons whose partitions, \(\lambda\), contain 2’s, 3’s, and 6’s. (Some examples of such hollow hexagons are shown in Figure 7.) Each has a different set of symmetric group actions, so we consider them individually starting with the case that the partition only contains 6’s.
Proposition 12. Given a partition \(\lambda\) of \(n\).
If \(\lambda\) contains 6’s, the corresponding hollow hexagon is equilateral and so has the form \(h_{\lambda}=(a,a,a,a,a,a)\). The number of distinct lattice path coronoids, up to rotation and reflection, in the equivalence class indexed by \(h_\lambda\) is \[g_6(a) =\frac{1}{12} \bigr(f_{\hbox{{1}}}(a,a,a,a,a,a) + 2f_{r_1}(a) + 2f_{r_2}(a,a) + f_{r_3}(a,a,a) + 3f_{q}(a,a,a,a)+3f_{qr_1}(a,a,a) \bigr)\]
If \(\lambda\) contains only 2’s and 6’s with at least one of each, the corresponding hollow hexagon has the form \(h_\lambda= (a,b,b,a,b,b)\), and the number of distinct lattice path coronoids, up to rotation and reflection, in the equivalence class indexed by \(h_\lambda\) is \[g_{6,2}(a,b)=\frac{1}{4} \bigr(f_{\hbox{{1}}}(a,b,b,a,b,b) + f_{r_3}(a,b,b) + f_q(a,b,b,a) +f_{qr_1}(b,a,b)\bigr)\]
If \(\lambda\) contains only 3’s and 6’s with at least one of each, the corresponding hollow hexagon has the form \(h_\lambda = (a,b,a,b,a,b)\), and the number of distinct lattice path coronoids, up to rotation and reflection, in the equivalence class indexed by \(h_\lambda\) is \[g_{6,3}(a,b)=\frac{1}{6} \bigr(f_{\hbox{{1}}}(a,b,a,b,a,b) + 2f_{r_2}(a,b) + 3f_q(a,b,a,b) \bigr)\]
If \(\lambda\) contains only 2’s, 3’s, and 6’s with at least one of each, the corresponding hollow hexagon has the form \(h_\lambda = (a,b,c,d,c,b)\), and the number of distinct lattice path coronoids, up to rotation and reflection, in the equivalence class indexed by \(h_\lambda\) is \[g_{6,3,2}(a,b,c,d) =\frac{1}{2} \bigr(f_{\hbox{{1}}}(a,b,c,d,c,b) + f_q (a,b,c,d) \bigr)\]
Proof. The first result follows directly from the application of Lemma 10 and Proposition 11. For the next, a 2 in the partition implies the relationships \(a=d > b=c=e=f\). There are four group elements acting on this figure: the identity \(1\), \(r_3\), a rotation by \(180^{\circ}\), \(q\), the reflection across the horizontal line bisecting the hexagon, and \(qr_3\), the reflection across a vertical line bisecting the hexagon. The result follows from Lemma 10. Then, when the partition contains only 3’s and 6’s, we have that \(a=c=e>b=d=f\). In this case our group consists of the identity \(1\), a rotation by \(120^{\circ}\), a rotation by \(240^{\circ}\), the reflection over the horizontal line bisecting edges \(A\) and \(D\), as well as compositions of these which give the reflections across the lines bisecting edges \(B\) and \(E\) and \(C\) and \(F\). Note, \(f_q(a,b,a,b)=f_q(b,a,b,a)\), so the two rotations and three reflections are counted by the same functions respectively, and the third result follows. Last, when there is a 2 and a 3 in the partition, we know \(a>c=e\) and \(d>b=f\), so we need possibly four distinct variables to define the function. Here the reflection group has only one line of symmetry, that is, through the edges \(A\) and \(D\). We again apply Lemma 10. ◻
In the next section, we will allow partitions with parts of size four. In this case we will have to adjust the counting functions to avoid placing adjacent lattice paths on opposite corners of a hexagon as these adjacent paths will damage the single corona hole.
Partitions containing a four can be more involved that those that do not contain a four because it is possible for lattice paths on opposing vertices of the hexagon to meet in the center and create more than one corona hole or interior vertices. To prevent this, we modify the function \(s(x,y)\) to avoid not only intersections between the opposing lattice paths but also pairs of lattice paths that are adjacent with no hexagon between them.
Definition 13. Given a hollow hexagon \(h=(a,b,c,d,e,f)\), let \(u: \mathbb{N} \times \mathbb{N} \times \mathbb{N} \times \mathbb{N} \longrightarrow \mathbb{N}\) be an integer-valued piecewise function where \[u(x_1, y_1, x_4, y_4) = \left\{ \begin{array}{ll} \binom{x_1+y_1-2}{ y_1-1} \binom{x_4+y_4-2}{y_4-1}- \binom{x_1+x_4+b-d-2}{b+c-3}\binom{y_1+y_4-b+d-2}{c+d-3}& \hbox{ if }x_1,y_1,x_4,y_4>0\\ \\ \binom{x_1+y_1-2}{y_1-1} & \hbox{ if }x_1,y_1> 0 \hbox{ and } x_4=y_4=0\\ \\ \binom{x_4+y_4-2}{y_4-1} & \hbox{ if } x_4, y_4>0 \hbox{ and } x_1=y_1=0\\ \\ 1 & \hbox{ if } x_1=y_1=x_4=y_4=0\\ \\ 0 & \hbox{ otherwise} \end{array} \right.\]
Note, the function \(u\) is also dependent on the edge lengths of the enclosing hollow hexagon.
Proposition 14. The function \(u\) enumerates the number of pairs of non-adjacent lattice paths, \(L_1\) and \(L_4\), that can be placed on the opposite corners, \(v_1\) and \(v_4\), of a hollow hexagon \(h_\lambda=(a,b,c,d,e,f)\) where \(L_1\) and \(L_4\), respectively, start at \(x_1\) and \(x_4\) respectively, and end at \(y_1\) and \(y_4\), respectively.
Before proving Proposition 14, we state a result due to Lindström [12]. This result appears in various forms in the literature of physics, chemistry, and mathematics. See Krattenthaler [13] for an interesting discussion of this history. Here we only give the simplified version of the theorem needed for this paper.
Proposition 15 (Lindström). Let \(P(A,B)\) count the number of lattice path from \(A\) to \(B\), and let \(Q\big( (A,B), (C,D) \big)\) count the number of pairs of lattice paths \((A,B)\) and \((C,D)\) that do not intersect. Then \[\left| det \begin{bmatrix} P(A,B) & P(A,D)\\ P(C,B) & P(C,D)\\ \end{bmatrix} \right| = Q\big((A,B), (C,D)\big) – Q\big( (A,D) , (C,B)\big).\]
We are now ready to prove Proposition 14.
Proof of Proposition 14. Given a hexagon \(h_{\lambda}=(a,b,c,d,e,f)\), we want to choose lattice paths \(L_1\) and \(L_4\) to be non-adjacent, that is, there is at least one hexagon between every pair of points with one point in the pair on each path. If there is no change to the hollow hexagon at either one or both of the corners with lattice path \(L_1\) and \(L_4\), then there can be no overlap between the two paths and thus \(s(x,y)\) can be applied in this case. Now suppose \(x_1, y_1, x_4, y_4 > 0\). In order to enumerate these paths we utilize a coordinate system on the hexagonal lattice. Orient the coordinate system so that the point \((0,0)\) lies on the corner of the hexagon at vertex \(v_1\) between edge \(A\) and edge \(B\). Lattice path \(L_1\) consists of Northeast steps (NE) at an angle of \(60^\circ\) from side \(A\) of the hexagon and North steps (N) at an angle of \(120^{\circ}\) from the NE steps. Further, \(L_1\) is a lattice path from \(S_1=(x_1,0)\) to \(E_1=(0,y_1)\) which begins with an NE step and ends with a N step. Lattice path \(L_4\) consists of similarly defined Southwest and South steps under this orientation. In order to use a consistent set of sets, we reverse the standard direction of \(L_4\) and assume the lattice path begins along edge \(E\) and ends along edge \(D\). So the lattice path \(L_4\) is from \(S_4=(c+d, b+c-y_4)\) to \(E_4=(c+d-x_4, b+c)\) beginning with a N step and ending with a NE step. See Figure 8. Because \(L_1\) must begin with an NE step and end with a N step in order to have the coronoid start and finish at \(x_1\) and \(y_1\) respectively, all possible paths \(L_1\) are in bijection with all lattice paths from \((x_1,1)\) to \((1,y_1)\). Similarly for \(L_4\), we can count lattice paths from \(\hat{S}_4=(c+d-1, b+c-y_4)\) to \(\hat{E}_4=(c+d-x_4,b+c-1)\).
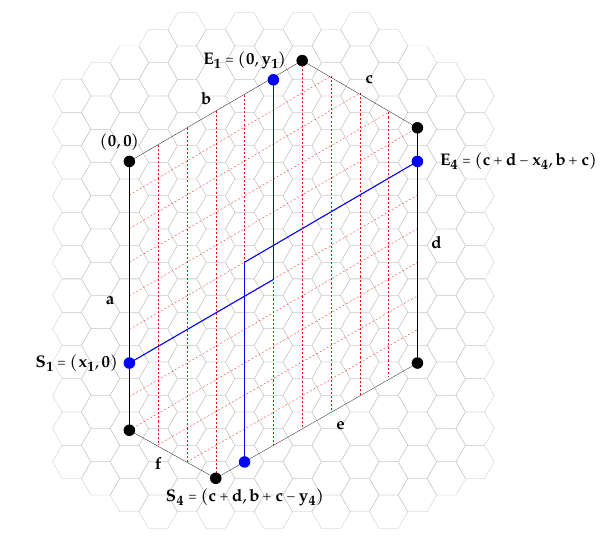
Further, we need pairs of lattice paths that not only do not intersect, but also are such that at least one point in the lattice (that is one hexagon) is between any pair of points with one point from each path. This is important to preserve a single corona hole and to prevent the creation of an interior vertex. We apply a simple transformation to a lattice path from \((x_1,1)\) to \((1,y_1)\) where all points are shifted south one step and to the northeast one step, creating a path from \(\hat{S}_1=(x_1+1,2)\) to \(\hat{E}_1=(2,y_1+1)\). Now, any pair of non-intersecting lattice paths \(\hat{L}_1\) and \(\hat{L}_4\) where the first path is from \(\hat{S}_1\) to \(\hat{E}_1\) and the second is from \(\hat{S}_4\) to \(\hat{E}_4\) can be transformed by reversing the map and by adding the appropriate \(N\) and \(NE\) steps to the beginning and end of the maps into the desired non-adjacent paths \(L_1\) and \(L_4\) which are separated for every pair of points by at least one hexagon. (This transformation is illustrated in Figure 9.)
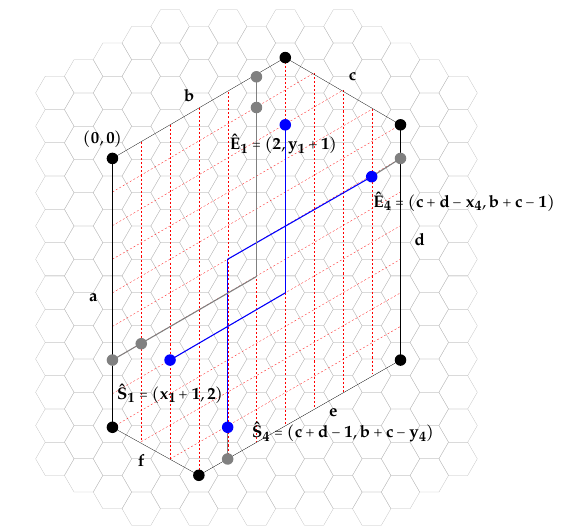
Finally, we claim if we consider the other pair of paths, \((\hat{S}_1, \hat{E}_4)\) and \((\hat{S}_4, \hat{E}_1)\), these paths always intersect and thus \(Q\bigr( (\hat{S}_1, \hat{E}_4), (\hat{S}_4, \hat{E}_1) \bigr) =0\). We look at the relative positions of pairs of starting and ending points. First, we note that each of the points \(\hat{S}_1\) and \(\hat{S}_4\) must have \(x\)-coordinates greater and \(y\)-coordinates less that those of the ending points \(\hat{E}_1\) and \(\hat{E}_4\), because otherwise there is no path using the allowable N and NE steps. Using the orientation where a larger \(x\)-coordinate implies a point is to the right and a larger \(y\)-coordinate implies a point is above, we see that starting points are always to the right and below ending points. Next, consider the relative positions of \(\hat{S}_1\) and \(\hat{S}_4\). Because \(x_1 \leq a-1\) and \(y_4 \leq e-1\) we have for the \(x\)-coordinates \(x_1+1 \leq a \leq a+f-1=c+d-1\) and for the \(y\)-coordinates \(2 \leq f+1 \leq e+f-y_4 = b+c-y_4\). Therefore \(\hat{S}_1\) is always to the left and below \(\hat{S}_4\). Similarly, because \(x_4\leq d-1\) and \(y_1 \leq b-1\), we know the \(x\)-coordinates are \(2\leq c+1 \leq c+d-x_4\) and the \(y\)-coordinates are \(y_1+1 \leq b\leq b+c-1\), so \(\hat{E}_1\) is to the left and below \(\hat{E}_4\). Because the \(y\)-coordinate of \(\hat{E}_4\) is above all other starting or ending points, and the \(y\)-coordinate of \(\hat{S}_1\) is below all other points, the \(x\)-coordinate of \(\hat{E}_1\) is to the left and the \(x\)-coordinate of \(\hat{S_4}\) is to the right of all other points, there is no way for a path from \(\hat{S}_4\) to \(\hat{E}_1\) to fail to intersect a path from \(\hat{S}_1\) to \(\hat{E}_4\).
We can now count the number of lattice paths between these pairs of vertices. \[\begin{aligned} &\hbox{Lattice paths } \hat{S}_1 \hbox{ to } \hat{E}_1: \binom{(x_1+1-2)+(y_1+1-2)}{y_1+1-2} = \binom{x_1+y_1-2}{ y_1-1}\\ &\hbox{Lattice paths } \hat{S}_1 \hbox{ to } \hat{E}_4: \binom{((x_1+1)-(c+d-x_4))+(b+c-1-2)}{b+c-1-2} =\binom{x_1+x_4+b-d-2}{b+c-3}\\ &\hbox{Lattice paths } \hat{S}_4 \hbox{ to } \hat{E}_1: \binom{(c+d-1-2)+(y_1+1-(b+c-y_4))}{c+d-1-2} = \binom{y_1+y_4-b+d-2}{c+d-3}\\ &\hbox{Lattice paths } \hat{S}_4 \hbox{ to } \hat{E}_4: \binom{(c+d-1-(c+d-x_4))+(b+c-1-(b+c-y_4))}{b+c-1-(b+c-y_4)} =\binom{x_4+y_4-2}{y_4-1}\\ \end{aligned}\]
(We stated before that the starting points must always have greater \(x\)-coordinates and smaller \(y\)-coordinates than the ending points in order for a path to exist. This is also indicated by the binomial coefficients being zero if this is not the case.)
Applying Proposition 15, the determinant is \[\begin{aligned} \det &\begin{bmatrix} \binom{x_1+y_1-2}{ y_1-1} & \binom{x_1+x_4+b-d-2}{b+c-3}\\ &\\ \binom{y_1+y_4-b+d-2}{c+d-3} & \binom{x_4+y_4-2}{y_4-1}\\ \end{bmatrix} = \\ &\\ &\binom{x_1+y_1-2}{ y_1-1} \binom{x_4+y_4-2}{y_4-1}- \binom{x_1+x_4+b-d-2}{b+c-3}\binom{y_1+y_4-b+d-2}{c+d-3}, \end{aligned}\] as desired. We note, because \(a+f=c+d\) and \(b+c=e+f\), we may equivalently write this expression in terms of \(a\), \(e\), and \(f\) as follows: \[\binom{x_1+y_1-2}{ y_1-1}\binom{x_4+y_4-2}{y_4-1}- \binom{x_1+x_4-a+e-2}{e+f-3}\binom{y_1+y_4+a-e-2}{a+f-3}\] ◻
The possible group actions on a hexagon whose corresponding partition contains at least one \(4\) are the identity \(1\), the rotation of \(180^{\circ}\), the reflection across the line through edges \(C\) and \(F\), and the reflection over the line through vertices \(a\) and \(d\). Because there is a 4 in the partition, it is not possible for edges \(A\), \(B\), \(D\), or \(E\) to equal edge \(F\). Thus we cannot have rotations by \(60^{\circ}\), \(120^{\circ}\), \(240^{\circ}\), or \(300^{\circ}\). Nor can there be reflection across the lines through vertices \(v_4\) and \(v_5\) or \(v_3\) and \(v_6\) or reflections across lines bisection edges \(A\) and \(D\) or \(B\) and \(E\).
We begin with the identify function. Using our new function \(u\), it is straight-forward to replace our counting function \(f_{\hbox{{1}}}\) with \(\bar{f}_{\hbox{{1}}}\) to enumerate the total number of coronoids fixed by the identity \({1}\). We have \(\bar{f}_{\hbox{{1}}}(a,b,c,d,e,f)=\) \[\begin{aligned} &\sum_{y_1=0}^{b-1} \sum_{y_2=0}^{c-1} \sum_{y_3=0}^{d-1} \sum_{y_4=0}^{e-1} \sum_{y_5=0}^{f-1} \sum_{y_6=0}^{a-1} \sum_{x_1=0}^{a-1-y_6} \sum_{x_2=0}^{b-1-y_1} \sum_{x_3=0}^{c-1-y_2} \sum_{x_4=0}^{d-1-y_3} \sum_{x_5=0}^{e-1-y_4} \sum_{x_6=0}^{f-1-y_5} u(x_1, y_1, x_4, y_4)s(x_2,y_2) s(x_3,y_3) s(x_5,y_5) s(x_6,y_6) \end{aligned}\]
Remark 2. Note the function \(u(x_1, y_1, x_4, y_4)\) on the opposite corners with vertices \(v_1\) and \(v_4\) is the same as \(s(x_1,y_1) \cdot s_(x_4, y_4)\) in the case that any pair of lattice paths could not be adjacent, because in that case either \(x_1+1< c+d-x_4\) or \(y_1+1<b+c-y_4\) and the subtrahend in \(u\) is zero.
Next we look at coronoids fixed by the rotation of \(180^{\circ}\), that is, \(r_3\). As before, we see that \(L_1=L_4\), \(L_2=L_5\), and \(L_3=L_6\). We introduce another function.
Definition 16. Given a hollow hexagon \(h=(a,b,c,d,e,f)\), let \(v:\mathbb{N} \times \mathbb{N} \longrightarrow \mathbb{N}\) be an integer-valued piecewise function where \[v(x,y) = \left \{ \begin{array}{ll} \binom{x+y-2}{x-1} & \hbox{ if } x\leq \lfloor \frac{c+d}{2} \rfloor, y>0\\ &\\ \sum_{z=1}^{\lfloor \frac{b+c}{2}\rfloor-1}\binom{x+z-\lfloor \frac{a+c}{2} \rfloor -1}{z-1 } \binom{y-z+\lfloor \frac{a+c}{2} \rfloor-1}{y-z} – & \hbox{ if } x>\lfloor \frac{a+c}{2} \rfloor, y>0, \\ &\\ \binom{x-z+b+c-\lceil \frac{a+c}{2} \rceil-1}{b+c-z-2} \binom{y+z-b-c+\lceil \frac{a+c}{2} \rceil-1}{y+z-b-c+1} &\hbox{ and } a+c \hbox{ odd}\\ &\\ \sum_{z=1}^{\lfloor \frac{b+c}{2}\rfloor-1} \binom{x+z-\lfloor \frac{a+c}{2} \rfloor -1}{z-1 } \Bigr( \binom{y-z+\lfloor \frac{a+c}{2} \rfloor-1}{y-z} – \binom{y+z-\lceil \frac{a+c}{2} \rceil -b+d-1}{y+z-b-c} \Bigr)& \hbox{ if } x>\lfloor \frac{a+c}{2} \rfloor, y>0, \\ &\\ -\Bigr( \binom{x-z+b+c+\lceil \frac{a+c}{2} \rceil-1}{b+c-z-2}- \binom{x+z-\lfloor\frac{a+c}{2} \rfloor -1}{z-2} \Bigr) \binom{y+z-b-c-\lceil \frac{a+c}{2} \rceil-1}{y+z-b-c+1} +&\hbox{ and } a+c \hbox{ even}\\ &\\ 1 & \hbox{ if } x=y=0\\ &\\ 0 &\hbox{ otherwise } \end{array} \right.\]
Proposition 17. The function \(v\) counts the number of pairs of non-adjacent lattice paths \(L_1\) and \(L_4\) placed on opposite corners \(v_1\) and \(v_4\) of a hollow hexagon \(h_\lambda= (a,b,c,d,e,f)\) that is fixed under the rotation \(r_3\) where \(L_1\) and \(L_4\) both start at \(x\) and end at \(y\).
Proof. In order to enumerate lattice path coronoids that are fixed under \(r_3\), we know that path \(L_4\) is equal to \(L_1\), so \(x_1=x_4\) and \(y_1=y_4\). We also have equality among some edge lengths with \(a=d\), \(b=e\), and \(c=f\). We apply the same orientation as in the proof of Proposition 14 where \(v_1=(0,0)\) and we reverse the direction of \(L_4\) so it starts along edge \(E\) and ends along edge \(D\). There are two cases to consider. In the first case, assume the parameter \(x_1 \leq \lfloor \frac{c+d}{2} \rfloor-1\). This means lattice path \(L_1\) does not cross the NE line \(x=\lfloor \frac{c+d}{2} \rfloor-1\) and similarly lattice path \(L_4\) does not cross the line \(x=c+d – \lfloor \frac{c+d}{2} \rfloor+1=\lceil \frac{c+d}{2} \rceil +1\). So for any choice of \(x_1=x_4\), the lattice paths are non-adjacent. For \(1\leq y_1 \leq b-1\), there are \(\binom{x_1+y_1-2}{x_1-1}\) pairs of paths.
In the second case, assume \(x > \lfloor \frac{c+d}{2} \rfloor-1\). We introduce a parameter \(z\) where we let \(z\) be the \(y\)-coordinate of the path \(L_1\) where it intersects the line \(x=\lfloor \frac{c+d}{2} \rfloor\). Because of the symmetry \(z\) is also the \(y\)-coordinate of the lattice path \(L_4\) where \(L_4\) intersects the line \(x= \lceil \frac{c+d}{2} \rceil\). (See Figure 10.) These two intersection points lie either on the same line or on adjacent lines. Because the lattice paths \(L_1\) and \(L_4\) cannot intersect, and in fact must have at least one hexagon between them to preserve the corona hole, \(z\) must be strictly less than \(\lfloor \frac{b+c}{2}\rfloor\). Further, observe the part of path \(L_1\) from \((x_1,0)\) to \((\lfloor \frac{c+d}{2} \rfloor,z)\) is equal to the reverse of the part of the path \(L_4\) from \((\lceil \frac{c+d}{2} \rceil,b+c-z)\) to \((c+d-x_4,b+c)\), and there is a similar relationship for the remaining parts of the two paths. Thus we need only check that the partial paths \((x_1,0)\) to \((\lfloor \frac{c+d}{2} \rfloor,z)\) and \((c+d, b+c-y_4)\) to \((\lceil \frac{c+d}{2} \rceil,b+c-z)\) are non-adjacent for all \(z\). As in the previous proof, we note that each path must start with a proscribed N or NE step (although it could end with either kind of step), and we must apply a shift to the lower path to ensure that the paths are not just non-intersecting but also non-adjacent. We have a path from \(\hat{S}_1= (x_1+1,2)\) to \(\hat{E}_1=(\lfloor \frac{c+d}{2} \rfloor +1,z+1)\) and path from \(\hat{S}_4=(c+d-1,b+c-y_4)\) to \(\hat{E}_4 = (\lceil \frac{c+d}{2} \rceil, b+c-z)\).
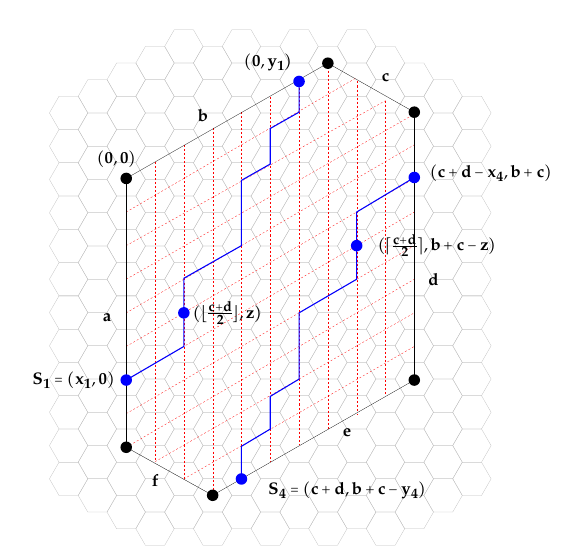
First count the number of pairs of intersecting lattice paths \((\hat{S}_1, \hat{E}_4)\) and \((\hat{S}_4, \hat{E}_1)\). The argument follows similarly to that in the proof of Proposition 14. Because \(x_1 > \lfloor \frac{c+d}{2} \rfloor\) and because \(z\geq 1\) we can show the \(x\)-coordinate of \(\hat{S}_1\) is greater and the \(y\)-coordinate of \(\hat{S}_1\) is less than those of \(\hat{E}_1\). The same relationships hold for \(\hat{S}_4\) and \(\hat{E}_4\) because \(z \leq y_1=y_4\) and \(c,d\geq 1\). We know the \(x\)-coordinate and the \(y\)-coordinate of \(\hat{S}_1\) are less than the corresponding coordinates of \(\hat{S}_4\) by the same argument in Proposition 14. Finally, when \(c+d\) is odd, the \(x\)– and \(y\)-coordinates of \(\hat{E}_1\) are also both less than those of \(\hat{E}_4\) because \(z\leq \lfloor \frac{b+c}{2} \rfloor -1\). Therefore, those two paths will always intersect. However, when \(c+d\) is even, the \(x\)– and \(y\)-coordinates of \(\hat{E}_1\) are each one unit greater than those of \(\hat{E}_4\). In this case, there are non-intersecting pairs of paths.
To count these paths, first we note a non-intersecting path \(\hat{S}_1\) to \(\hat{E}_4\) must pass through the point \(P'=(\lfloor \frac{c+d}{2} \rfloor, z)\) that is the point one unit to the right and below \(\hat{E}_1\). From there the path must travel straight up to \(\hat{E}_4\). We have \[\begin{aligned} &\hbox{Lattice paths } \hat{S}_1 \hbox{ to } P': \binom{ (x_1+1 – \lfloor \frac{c+d}{2} \rfloor)+(z-2)}{z-2} = \binom{x_1+z-\lfloor\frac{c+d}{2} \rfloor -1}{z-2}\\ &\hbox{Lattice paths } \hat{S}_4 \hbox{ to } P': \binom{(c+d-1 – \lfloor \frac{c+d}{2} \rfloor)+(z-(b+c-y_4)) }{z-(b+c-y_4)}=\binom{y_4+z-\lceil \frac{c+d}{2} \rceil -b+d-1}{y_4+z-b-c}\\ \end{aligned}\]
Before we can apply Proposition 15, we also need the paths to \(\hat{E}_1\). These are:
\[\begin{aligned} &\hbox{Lattice paths } \hat{S}_1 \hbox{ to } \hat{E}_1: \binom{(x_1+1-(\lfloor \frac{c+d}{2} \rfloor+1))+((z+1)-2)}{(z+1)-2} = \binom{x_1+z-\lfloor \frac{c+d}{2} \rfloor -1}{z-1 }\\ &\hbox{Lattice paths } \hat{S}_4 \hbox{ to } \hat{E}_1: \binom{(c+d-1-(\lfloor \frac{c+d}{2} \rfloor +1))+(z+1-(b+c-y_4))}{z+1-(b+c-y_4)}= \binom{y_4+z-b-c+\lceil \frac{c+d}{2} \rceil-1}{y_4+z-b-c+1}\\ \end{aligned}\]
Now, we have \[Q\bigr( (\hat{S}_1, \hat{E}_4), (\hat{S}_4, \hat{E}_1) \bigr) = Q\bigr( (\hat{S}_1, P'), (\hat{S}_4, \hat{E}_1) \bigr) = \det \begin{bmatrix} P(\hat{S}_1, P') &P(\hat{S}_1, \hat{E}_1)\\ &\\ P(\hat{S}_4, P') & P(\hat{S}_4, \hat{E}_1)\\ \end{bmatrix}+ Q\bigr( (\hat{S}_1, \hat{E}_1), (\hat{S}_4, P') \bigr).\] Note, the final term in the sum is zero because of the relative positions of \(\hat{S}_1\) and \(\hat{S}_4\) and because \(P'\) has a smaller \(x\) and \(y\)-coordinates than \(\hat{E}_1\), so the number of non-intersection pairs of paths \((\hat{S}_1, \hat{E}_4)\) and \((\hat{S}_4, \hat{E}_1)\) is
\[\binom{x+z-\lfloor\frac{c+d}{2} \rfloor -1}{z-2} \binom{y_4+z-b-c+\lceil \frac{c+d}{2} \rceil-1}{y_4+z-b-c+1} – \binom{x_1+z-\lfloor \frac{c+d}{2} \rfloor -1}{z-1 }\binom{y_4+z-\lceil \frac{c+d}{2} \rceil -b+d-1}{y_4+z-b-c}.\]
We will need to apply Proposition 15 a second time. \[\begin{aligned} &\hbox{Lattice paths } \hat{S}_1 \hbox{ to } \hat{E}_4: \binom{(x_1+1-\lceil \frac{c+d}{2} \rceil)+(b+c-z-2)}{b+c-z-2} =\binom{x_1+b+c-\lceil \frac{c+d}{2} \rceil-z-1}{b+c-z-2}\\ &\hbox{Lattice paths } \hat{S}_4 \hbox{ to } \hat{E}_4: \binom{(c+d-1-\lceil \frac{c+d}{2} \rceil)+(b+c-z-(b+c-y_4))}{b+c-z-(b+c-y_4)} =\binom{y_4-z+\lfloor \frac{c+d}{2} \rfloor-1}{y_4-z}\\ \end{aligned}\] Applying the change of variable where \(d=a\), the result then follows from the determinant and the calculations above.
To complete the proof, we note clearly if \(x=0\) or \(y=0\), then symmetries implies the other must also be zero, and there is only one way to leave the hexagon unchanged at those corners. ◻
Now, we may modify \(f_{r_3}\). \[\bar{f}_{r_3}(a,b,c)=\sum_{y_1=0}^{b-1} \sum_{y_2=0}^{c-1} \sum_{y_3=0}^{a-1} \sum_{x_1=0}^{a-1-y_3} \sum_{x_2=0}^{b-1-y_1} \sum_{x_3=0}^{c-1-y_2} v(x_1,y_1) s(x_2,y_2) s(x_3,y_3).\]
Now considering the action of the reflection \(qr_4\) over the line bisecting edges \(C\) and \(F\), we see \(L_1=rev(L_4)\), \(L_2=rev(L_3)\), and \(L_5=rev(L_6)\), so we need a modified version of \(f_{qr_4}\).
Definition 18. Given a hollow hexagon \(h=(a,b,c,d,e,f)\), let \(w:\mathbb{N} \times \mathbb{N} \longrightarrow \mathbb{N}\) be the integer-valued piece-wise function where \[w(x,y) = \left \{ \begin{array}{ll} \binom{x+y-2}{x-1} – \binom{x+y-2}{x+y-a-f+1} & \hbox{ if } x,y>0\\ 1 & \hbox{ if } x=y=0\\ 0 & \hbox{ otherwise } \end{array} \right.\]
Proposition 19. The function \(w\) counts the number of pairs of non-adjacent lattice paths \(L_1\) and \(L_4\) placed on opposite corners \(v_1\) and \(v_4\) of a hollow hexagon \(h_\lambda = (a,b,c,d,e,f)\) that is fixed under the action of \(qr_4\) where \(L_1\) and \(L_4\) respectively start at \(x\) and \(y\) and end at \(y\) and \(x\), respectively.
Proof. Under the action of \(qr_4\), lattice paths \(L_1\) and \(L_4\) are fixed under the reflection over the line bisecting edges \(C\) and \(F\). We will apply a different orientation than in previous proofs and orient the hexagon so \((0,0)\) is the start of the path \(L_1\) at \((x_1,1)\); see Figure 11. Under this orientation the path starts at \((0,0)\) and ends at \((x_1-1,y_1-1)\) and must stay strictly below the line \(y=x +(a+f-x_1-1)\).
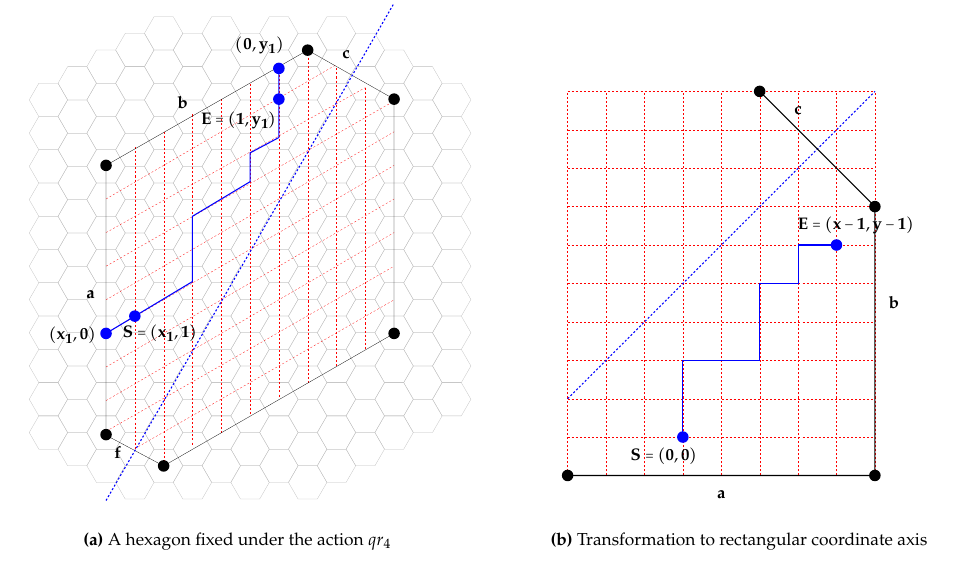
The reflection principle can be used to solve Ballot Theorem questions which ask how many ways can votes be counted so Candidate A is always at least \(t\) votes ahead of Candidate B. This is equivalent to counting the number of lattice paths that do not cross the line \(x=t\). (The problem was studied by Bertrand [14] and André [15] among others, although they did not use the reflection principle.) Here we need to count the number of N and E lattice paths from \((p_1,p_2)\) to \((s_1,s_2)\) that are weakly below a line \(x=t\). The desired count is given by \[\binom{s_1-p_1+s_2-p_1}{s_1-p_1} – \binom{s_1-p_1+s_2-p_2}{s_2-p_1-t},\] so since we need the lattice paths to be strictly below \(y=x+a+f-x_1-1\) we set \(t=a+f-x_1-2\) and thus the desired amount is \[\binom{x_1+y_1-2}{y_1-1} – \binom{x_1+y_1-2}{y_1-1 -(a+f-x_1-2)}.\] ◻
Therefore we have the a new counting function: \[\bar{f}_{qr_4} (a,b,c,f)=\sum_{y_1=0}^{b-1} \sum_{y_2=0}^{\lfloor \frac{c-1}{2} \rfloor} \sum_{y_6=0}^{a-1} \sum_{x_1=0}^{a-1-y_6} \sum_{x_2=0}^{b-1-y_1} \sum_{x_6=0}^{\lfloor \frac{f-1}{2} \rfloor} w(x_1,y_1) s(x_2,y_2) s(x_6,y_6).\]
Finally, the reflection across the line through the opposite vertices \(v_1\) and \(v_4\) creates symmetric lattice paths \(L_1\) and \(L_4\). Further, we also must have that these two paths do not intersect, and specifically \(L_1 = rev(L_1)\), \(L_2=rev(L_6)\), \(L_3=rev(L_5)\), and \(L_4=rev(L_4)\).
Definition 20. Given a hollow hexagon \(h=(a,b,c,d,e,f)\), let \(p:\mathbb{N} \times \mathbb{N} \longrightarrow \mathbb{N}\) be the integer-valued function where \[p(x,y) = \left \{ \begin{array}{ll} \sum_{z_1=1}^{b+c-2} \sum_{z_4=1}^{b+c-2-z_1}\binom{y-1}{z_4-1}\binom{x-1}{z_1-1}-\binom{y-1}{b+c-z_1-2}\binom{x-1}{b+c-z_4-2} & \hbox{ if } x, y>0\\ \\ \sum_{z_1=1}^{b+c-2} \binom{x-1}{z_1-1} & \hbox{ if } x>0 \hbox{ and } y=0\\ %Upper bound a-1 \\ \sum_{z_4=1}^{b+c-2} \binom{y-1}{z_4-1} & \hbox{ if } x=0 \hbox{ and } y>0\\ %Upper bound a-1 \\ 1 & \hbox{ if } x=y=0\\ \\ 0 &\hbox{ otherwise } \end{array} \right.\]
Proposition 21. The function \(p\) counts the number of pairs of non-adjacent lattice paths \(L_1\) and \(L_4\) placed on opposite corners \(v_1\) and \(v_4\) of a hollow hexagon \(h_\lambda=(a,b,c,d,e,f)\) that is fixed under the action of \(qr_1\) where \(L_1\) starts and ends at \(x\) while \(L_4\) starts and ends at \(y\).
Proof. In this case we need two parameters, \(z_1\) and \(z_4\) that will denote the intersection of lattice paths \(L_1\) and \(L_4\) with the line between vertices \(v_1\) and \(v_4\); See Figure 12. Because the lattice paths are equal to their reverse, the paths from \((x_1,0)\) to the line of reflection and from \((0,y_4)\) to the line of reflection completely determine \(L_1\) and \(L_4\).
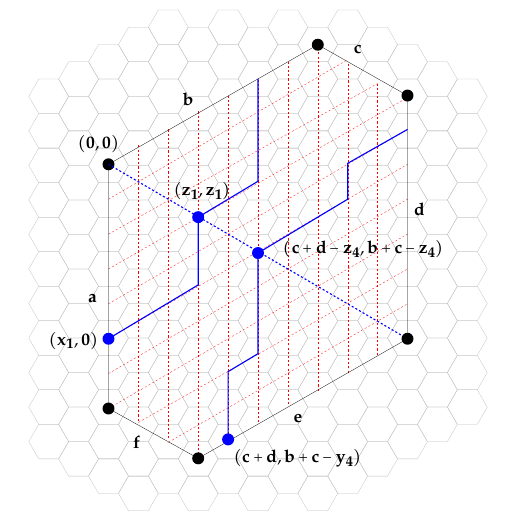
To find the bounds on \(z_1\) and \(z_4\), we have \(z_1 \leq x_1 \leq b-1\), so \(z_1 \leq b+c-2\) because \(c\geq 1\), and similarly for \(z_2\). Further, if \(z_1, z_4 \geq 1\), their sum must be less than the distance across the hexagon, that is, \(b+c\), so if \(1\leq z_1 \leq b+c-2\) then \(1\leq z_4 \leq b+c-2-z_1\). As in previous proof, we will need to shift the lattice path from \((x_1, 0)\) to \((z_1,z_1)\) south and northeast, because we want the two paths to be not just non-crossing, but also non-intersecting. Thus we need to enumerate the number of pairs of non-crossing paths with start \(\hat{S}_1 = (x_1+1,2)\) and end \(\hat{E}_1=(z_1+1, z_1+1)\) and start \(\hat{S}_4 =(c+d-1,b+c-y_4)\) and end \(\hat{E}_4=(c+d-z_4, b+c-z_4)\).
Again we apply Proposition 15, first checking that all paths \((\hat{S}_1, \hat{E}_4)\) and \((\hat{S}_4, \hat{E}_1)\) intersect. These arguments follow similarly to that cases in the proofs of Propositions 14 and 17, where we check the locations of these points relative to each other using their \(x\)– and \(y\)-coordinates and applying the relationship between \(z_1\) and \(z_4\), so we omit the details here.
With these bounds on \(z_1\) and \(z_4\), we may enumerate the lattice paths similarly to the proof of Proposition 17, only with two parameters. \[\begin{aligned} &\hbox{Lattice paths } \hat{S}_1 \hbox{ to } \hat{E}_1: \binom{(x_1+1-(z_1+1))+(z_1+1)-2}{z_1+1-2} = \binom{x_1-1}{ z_1-1}\\ &\hbox{Lattice paths } \hat{S}_1 \hbox{ to } \hat{E}_4: \binom{(x_1+1-(c+d-z_4))+(b+c-z_4-2)}{b+c-z_4-2} =\binom{x_1+b-d-1}{b+c-z_4-2}\\ &\hbox{Lattice paths } \hat{S}_4 \hbox{ to } \hat{E}_1: \binom{(c+d-1-(z_1+1))+(z_1+1-(b+c-y_4)}{c+d-1-(z_1+1)} = \binom{y_4-b+d-1}{c+d-z_1-2}\\ &\hbox{Lattice paths } \hat{S}_4 \hbox{ to } \hat{E}_4: \binom{(c+d-1-(c+d-z_4))+(b+c-z_4-(b+c-y_4))}{c+d-1-(c+d-z_4)} =\binom{y_4-1}{z_4-1}\\ \end{aligned}\]
Note, if the \(x\)-coordinate of \(\hat{S}_1\) is not greater and the \(y\)-coordinate of \(\hat{S}_1\) is not less than those of \(\hat{E}_4\) or if similarly \(\hat{S}_4\) is not to the right and below \(\hat{E}_1\), there is no lattice path and the binomial coefficient is also zero. Thus the desired result follows, noting that if \(x_1>0\) and \(y_4 =0\), we need only count the number of lattice paths from \((x_1,1)\) to \((z_1,z_1)\) where \(z_1\) is only limited by the side length \(a\), and similarly if \(x_1=0\) and \(y_4 >0\). ◻
Now we may modify our previous function \(f_{qr_1}\). \[\bar{f}_{qr_1}(b,c,d)= \sum_{y_1=0}^{b-1} \sum_{y_2=0}^{c-1} \sum_{y_3=0}^{d-1} \sum_{x_2=0}^{b-1-y_1} \sum_{x_3=0}^{c-1-y_2} \sum_{x_4=0}^{d-1-y_3} p(x_4,y_1) s(x_2,y_2) s(x_3,y_3).\]
Now, we can complete the enumeration.
With the reflection and rotation functions established we can count lattice path coronoids corresponding to hollow hexagons whose partitions have at least one \(4\) and at least one \(6\).
Proposition 22. Given a partition \(\lambda\) of \(n\).
If \(\lambda\) contains only 4’s, and 6’s with at least one of each, the corresponding hollow hexagon has the form \(h_\lambda = (a,a,c,a,a,c)\), and the number of distinct lattice path coronoids, up to rotation and reflection, in the equivalence class indexed by \(h_\lambda\) is \[g_{6,4} (a,c) =\frac{1}{4} \bigr(\bar{f}_{\hbox{{1}}}(a,a,c,a,a,c) + \bar{f}_{r_3}(a,a,c) + \bar{f}_{qr_4}(a,a,c,a) +\bar{f}_{qr_1}(a,a,c) \bigr)\]
If \(\lambda\) contains only 2’s, 4’s, and 6’s with at least one of each, the corresponding hollow hexagon has the form \(h_\lambda = (a,b,c,a,b,c)\), and the number of distinct lattice path coronoids, up to rotation and reflection, in the equivalence class indexed by \(h_\lambda\) is \[g_{6,4,2} (a,b,c) = \frac{1}{2} \bigr(\bar{f}_{\hbox{{1}}}(a,b,c,a,b,c) + \bar{f}_{r_3}(a,b,c)\bigr)\]
If \(\lambda\) contains only 3’s, 4’s, and 6’s with at least one of each, the corresponding hollow hexagon has the form \(h_\lambda = (a,b,c,b,a,f)\), and the number of distinct lattice path coronoids, up to rotation and reflection, in the equivalence class indexed by \(h_\lambda\) is \[g_{6,4,3}(a,b,c,b,a,f)= \frac{1}{2}\bigr(\bar{f}_{\hbox{{1}}}(a,b,c,b,a,f) + \bar{f}_{qr_4} (a,b,c,f)\bigr)\]
If \(\lambda\) contains 2’s, 3’s, 4’s, and 6’s with at least one of each, the corresponding hollow hexagon has the form \(h_\lambda = (a,b,c,d,e,f)\), and the number of distinct lattice path coronoids, up to rotation and reflection, in the equivalence class indexed by \(h_\lambda\) is \[g_{6,4,3,2}(a,b,c,d,e,f)=\bar{f}_{\hbox{{1}}}(a,b,c,d,e,f)\]
The proof is straightforward.
Proof. A partition having parts of size 4 and 6 implies that the corresponding hexagon has edge lengths where \(a=b=d=e>c=f\). The symmetric group that acts on this hexagon has the identity, the rotation by \(180^{\circ}\), the reflection through the vertices \(a\) and \(d\), and the reflection over the line that bisects edges \(C\) and \(F\) and the first result follows. Adding at least one 2 into a partition that already contains 4’s and 6’s modifies the edge lengths, so \(a=d>b=e>c=f\). The group acting on this shape has only two actions: the identity \({1}\) and the rotation by \(180^{\circ}\). Apply Lemma 10 to obtain the second result. When the partition has parts of size 4 and 3 , but none of size 2, the edge lengths satisfy the following: \(a=e>b=d>f\) and \(a=e>c>f\). The group acting on this shape has only two members: the identity \(1\), and the reflection over the line bisecting edges \(C\) and \(F\). The third result follows. Finally, in the fourth result, all side lengths are distinct, so the symmetric group action is only by the identity. ◻
Given a partition \(\lambda\) using parts from \(S_{\lambda} \subseteq \{2,3,4,6\}\) with corresponding hexagon \(h_{\lambda}=(a,b,c,d,e,f)\), let \(g_{S_{\lambda}} (h_{\lambda})\) denote the appropriate counting function from Propositions 12 and 22. We have the following culminating theorem:
Theorem 23. The number of lattice path coronoids composed of \(n\) hexagons is \(\displaystyle{\sum_{\lambda \mapsto n} g_{S_{\lambda}} (h_{\lambda})}.\)
For mathematicians or computational chemists interested in these types of problems, there are other characteristics of coronoids to study.
Kekulé structures or bonds correspond to perfect matchings on the hexagonal graph of the lattice path coronoid. Can we enumerate or find bounds for the number of Kekulé structures for classes of lattice path coronoids?
What if we consider lattice path coronoid systems, that is, lattice path coronoids with more than one corona hole such as lattice path double-coronoids or triple-coronoids? Can these be enumerated by modifying the counting function in Section 5 to allow opposite lattice paths to meet?
We could also try to count the analogously defined lattice path benzenoids whose structure will have an inner and outer perimeters defined by lattice paths.