For an arborescence \(A_r\), a directed pathos total digraph \(Q=DPT(A_r)\) has vertex set \(V(Q)=V(A_r)\cup A(A_r)\cup P(A_r)\), = where \(V(A_r)\) is the vertex set, \(A(A_r)\) is the arc set, and \(P(A_r)\) is a directed pathos set of \(A_r\). The arc set \(A(Q)\) consists of the following arcs: \(ab\) such that \(a,b \in A(A_r)\) and the head of \(a\) coincides with the tail of \(b\); \(uv\) such that \(u,v \in V(A_r)\) and \(u\) is adjacent to \(v\); \(au\) \((ua)\) such that \(a\in A(A_r)\) and \(u \in V(A_r)\) and the head (tail) of \(a\) is \(u\); \(Pa\) such that \(a \in A(A_r)\) and \(P \in P(A_r)\) and the arc \(a\) lies on the directed path \(P\); \(P_iP_j\) such that \(P_i, P_j \in P(A_r)\) and it is possible to reach the head of \(P_j\) from the tail of \(P_i\) through a common vertex, but it is possible to reach the head of \(P_i\) from the tail of \(P_j\). For this class of digraphs we discuss the planarity; outerplanarity; maximal outerplanarity; minimally nonouterplanarity; and crossing number one properties of these digraphs. The problem of reconstructing an arborescence from its directed pathos total digraph is also presented.
Notations and definitions not introduced here can be found in [1]. There are many graph valued functions (or graph operators) with which one can construct a new graph from a given graph, such as the line graphs, the total graphs, and their generalizations. The line graph of a graph \(G\), written \(L(G)\), is the graph whose vertices are the edges of \(G\), with two vertices of \(L(G)\) adjacent whenever the corresponding edges of \(G\) have a common vertex. This concept was originated with Whitney [2]. Harary and Norman [3] extended the concept of line graph of a graph and introduced the concept of line digraph of a directed graph. The line digraph \(L(D)\) of a digraph \(D\) has the arcs of \(D\) as vertices. There is an arc from \(D\)-arc \(pq\) towards \(D\)-arc \(uv\) if and only if \(q=u\).
Behzad [4] introduced the concept of total graph of a graph. The total graph of a graph \(G\), written \(T(G)\), is the graph whose vertices can be put in one-to-one correspondence with the vertices and edges of \(G\) in such a way that two vertices of \(T(G)\) are adjacent if and only if the corresponding elements of \(G\) are adjacent, where the vertices and edges of \(G\) are called its \(members\). Gary Chatrand and James Stewart [5] extended the concept of total graph of a graph to the directed case there by introducing the total digraph.
The total digraph of a directed graph \(D\), written \(T(D)\), is the digraph whose vertices are in one-to-one correspondence with the vertices and arcs of \(D\) and such that the vertex \(u\) is adjacent to the vertex \(v\) in \(T(D)\) if and only if the element corresponding to \(u\) is adjacent to the element corresponding to \(v\) in \(D\).
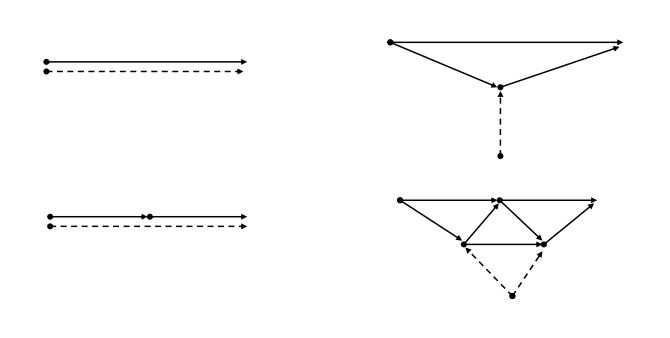
The concept of pathos of a graph \(G\) was introduced by Harary [6] as a collection of minimum number of edge disjoint open paths whose union is \(G\). The path number of a graph \(G\) is the number of paths in any pathos. The path number of a tree \(T\) equals \(k\), where \(2k\) is the number of odd degree vertices of \(T\). Stanton and Cowan [7] calculated the path number of certain classes of graphs like trees and complete graphs. Gudagudi [8] extended the concept of pathos of graphs to trees there by introducing the concept called pathos line graph of a tree. A pathos line graph of a tree \(T\), written \(PL(T)\), is a graph whose vertices are the edges and paths of a pathos of \(T\), with two vertices of \(PL(T)\) adjacent whenever the corresponding edges of \(T\) are adjacent or the edge lies on the corresponding path of the pathos.
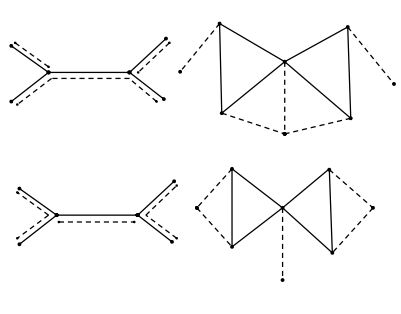
Since the pattern of pathos for a tree is not unique, the corresponding pathos line graph is also not unique. See Figure 1 for an example of a tree and its pathos line graph
It is the object of this paper to extend the concept of pathos of a tree to the directed case by introducing the concept called directed pathos total digraph of an arborescence and to develop some of its properties.
A graph \(G\) is planar if it has a drawing without crossings. For a planar graph \(G\), the inner vertex number \(i(G)\) is the minimum number of vertices not belonging to the boundary of the exterior region in any embedding of \(G\) in the plane. If a planar graph \(G\) is embeddable in the plane so that all the vertices are on the boundary of the exterior region, then \(G\) is said to be outerplanar, i.e., \(i(G)=0\). An outerplanar graph \(G\) is maximal outerplanar if no edge can be added without losing outerplanarity. A graph \(G\) is said to be minimally nonouterplanar if \(i(G)=1\). The least number of edge crossings of a graph \(G\), among all planar embeddings of \(G\), is called the crossing number of \(G\) and is denoted by cr\((G)\).
A directed graph (or just digraph) \(D\) consists of a finite non-empty set \(V(D)\) of elements called vertices and a finite set \(A(D)\) of ordered pairs of distinct vertices called arcs. Here \(V(D)\) is the vertex set and \(A(D)\) is the arc set of \(D\). For an arc \((u,v)\) or \(uv\) in \(D\), the first vertex \(u\) is its tail and the second vertex \(v\) is its head. The head and tail of an arc are its end-vertices. For an arc \(e=(u,v)\), we say that \(u\) is a neighbor of \(v\); and \(u\) is adjacent to \(e\) and \(e\) is adjacent to \(v\). A vertex \(u\) is adjacent to \(v\) if the arc \(uv\) is in \(D\); \(u\) is adjacent from \(v\) if \(vu\) is in \(D\). A digraph without any arcs is said to be totally disconnected. For a digraph \(D=(V,A)\), the out-neighbourhood \(N^{+}(v)\) of a vertex \(v\) is the set of all vertices \(w\) with \(vw \in A\). The in-neighbourhood \(N^{-}(v)\) of a vertex \(v\) is the set of all vertices \(w\) with \(wv \in A\).
The out-degree \(d^{+}(v)\) or in-degree \(d^{-}(v)\) of a vertex \(v\) is the cardinality of the out-neighbourhood or in-neighbourhood of \(v\), respectively. The total degree \(td(v)\) of a vertex \(v\) is the number of arcs incident with \(v\), that is, \(td(v)=d^{-}(v)+d^{+}(v)\). A source is any vertex of in-degree zero and a sink is a vertex of out-degree zero. A vertex is isolated if both out-degree and in-degree are zero.
A semi-directed path joining \(v_1\) and \(v_n\) is a collection of distinct vertices \(v_1,v_2,\ldots,v_n\) together with \(n-1\) vertices, one from each pair of arcs, \(v_1v_2\) or \(v_2v_1\); \(v_2v_3\) or \(v_3v_2\), \ldots, \(v_{n-1}v_n\) or \(v_nv_{n-1}\). A semi-directed cycle is obtained from a semi directed path on adding an arc joining the terminal vertex and the initial vertex of the semi-directed path.
A digraph is strongly connected (or just strong) if every two vertices are mutually reachable. A digraph is unilaterally connected or unilateral if for any two vertices, at least one is reachable from the other; it is strictly unilateral if it is unilateral but not strong.
A digraph is weakly connected or weak if every two vertices are joined by a semi-directed path; it is strictly weak if it is weak but notunilateral. A block \(B\) of a digraph \(D\) is a maximal weak subgraph of \(D\), which has no cut-vertex \(v\) such that \(B-v\) is disconnected. An entire digraph is a block if it has only one block. There are exactly three categories of blocks: strong, strictly unilateral, and strictly weak.
Digraphs that can be drawn without crossings between arcs (except at end vertices) are called planar digraphs. Clearly this property does not depend on the orientation of the arcs and hence we ignore the orientation while defining the planarity; outerplanarity; maximal outerplanarity; and minimally nonouterplanarity of a digraph. Furthermore, since most of the results and definitions of undirected graphs are valid for planar digraphs as far as their underlying graphs are concerned, the following definitions hold good for planar digraphs. A digraph \(D\) is said to be outerplanar if \(i(D)=0\) and minimally nonouterplanar if \(i(D)=1\).
The following result characterizes maximal outerplanar graphs, and the same can be used to check the maximal outerplanar property of a digraph.
Theorem 2.1. Every maximal outerplanar graph \(G\) with \(n\) vertices has \(2n-3\) edges.
Definition 3.1. An arborescence is a directed graph in which, for a vertex \(u\) called the root and any other vertex \(v\), there is exactly one directed path from \(u\) to \(v\).
We shall use \(A_r\) to denote an arborescence.Definition 3.2. A root arc of an arborescence \(A_r\) is an arc which is directed out of the root of \(A_r\), i.e., a root arc of \(A_r\) an arc whose tail is the root of \(A_r\).
Definition 3.3. If a directed path \(\vec{P}_n\) of order \(n\) \((n \geq 2)\) starts at one vertex and ends at a different vertex, then \(\vec{P}_n\) is called an open directed path.
Definition 3.4. The directed pathos of an arborescence \(A_r\) is defined as a collection of minimum number of arc disjoint open directed paths whose union is \(A_r\).
Definition 3.5. The directed path number \(k^{‘}\) of an arborescence \(A_r\) is the number of directed paths in any directed pathos of \(A_r\), and is equal to the number of sinks in \(A_r\), i.e., \(k^{‘}\) = number of sinks in \(A_r\).
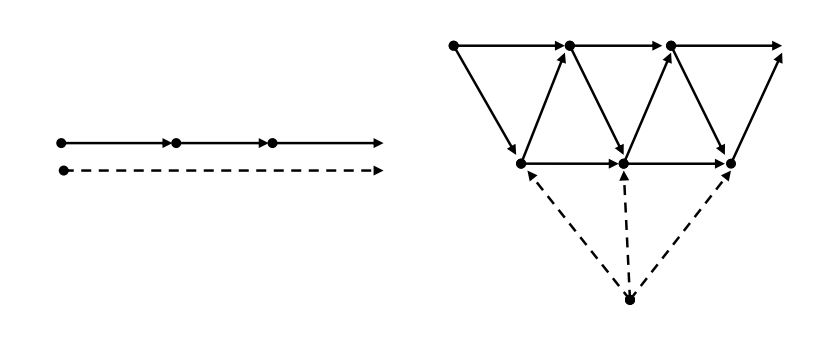
Note that the directed path number \(k^{‘}\) of an arborescence \(A_r\) is minimum only when the out-degree of the root of \(A_r\) is exactly one. Therefore, unless otherwise specified, the out-degree of the root of every arborescence is exactly one. Finally, we assume that the direction of the directed pathos is along the direction of the arcs in \(A_r\).Definition 3.6. For an arborescence \(A_r\), a directed pathos total digraph \(Q=DPT(A_r)\) has vertex set \(V(Q)=V(A_r)\cup A(A_r)\cup P(A_r)\), where \(V(A_r)\) is the vertex set, \(A(A_r)\) is the arc set, and \(P(A_r)\) is a directed pathos set of \(A_r\). The arc set \(A(Q)\) consists of the following arcs: \(ab\) such that \(a,b \in A(A_r)\) and the head of \(a\) coincides with the tail of \(b\); \(uv\) such that \(u,v \in V(A_r)\) and \(u\) is adjacent to \(v\); \(au\) \((ua)\) such that \(a\in A(A_r)\) and \(u \in V(A_r)\) and the head (tail) of \(a\) is \(u\); \(Pa\) such that \(a \in A(A_r)\) and \(P \in P(A_r)\) and the arc \(a\) lies on the directed path \(P\); \(P_iP_j\) such that \(P_i, P_j \in P(A_r)\) and it is possible to reach the head of \(P_j\) from the tail of \(P_i\) through a common vertex, but it is possible to reach the head of \(P_i\) from the tail of \(P_j\).
Since the pattern of directed pathos for an arborescence is not unique, the corresponding directed pathos total digraph is also not unique. But it is cleared from the definition of the directed path number \(k^{‘}\) and \(DPT(A_r)\) that, for a directed path \(\vec{P_{n}}\) of order \(n\) \((n \geq 2)\), the corresponding directed pathos total digraph is unique. Furthermore, one can observe easily that, for different pattern of directed pathos of an arborescence whose underlying graph is a star graph \(K_{1,n}\) on \(n \geq 3\) vertices, the corresponding directed pathos total digraphs are isomorphic.
A digraph \(A_r^{‘}\) is a directed pathos total digraph if there exists an arborescence \(A_r\) such that \(A_r^{‘}=DPT(A_r)\). See Figure 2 for an example of an arborescence and its directed pathos total digraph.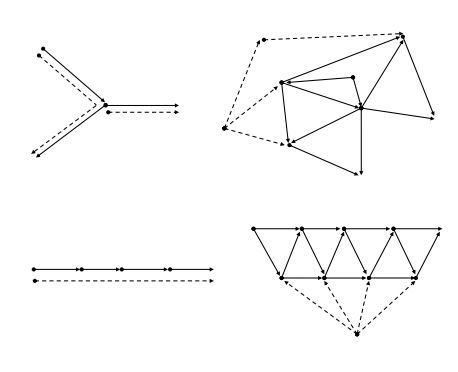
The main objective is to determine a necessary and sufficient condition that a digraph be a directed pathos total digraph.
A complete bipartite digraph is a directed graph \(D\) whose vertices can be partitioned into non-empty disjoint sets \(A\) and \(B\) such that each vertex of \(A\) has exactly one arc directed towards each vertex of \(B\) and such that \(D\) contains no other arc.
Let \(A_r\) be an arborescence with vertex set \(V(A_r)=\{v_1,v_2,\ldots,v_n\}\) and a directed pathos set \(P(A_r)=\{P_1,P_2,\ldots,P_t\}\). We consider the following cases.
Case 1. Let \(v\) be a vertex of \(A_r\) with \(d^{-}(v)=\alpha\) and \(d^{+}(v)=\beta\). Then \(\alpha\) arcs coming into \(v\) and the \(\beta\) arcs going out of \(v\) give rise to a complete bipartite subdigraph with \(\alpha\) tails and \(\beta\) heads and \(\alpha\cdot \beta\) arcs joining each tail with each head. This is the decomposition of \(L(A_r)\) (i.e., the line digraph of \(A_r\)) into mutually arc disjoint complete bipartite subdigraphs.
Case 2. An arc \(e=(u,v)\) with \(d^{+}(u)=d^{-}(v)=1\) give rise to a complete bipartite subdigraph with \(u\) as the tail and \(v\) head. This contributes \(n-1\) arcs to \(DPT(A_r)\).
Case 3. An arc \(e=(u,v)\) with \(d^{+}(u)=d^{-}(v)=1\) give rise to a complete bipartite subdigraph with \(u\) as the tail and \(e\) head. This contributes \(n-1\) arcs to \(DPT(A_r)\).
Case 4. An arc \(e=(u,v)\) with \(d^{+}(u)=d^{-}(v)=1\) give rise to a complete bipartite subdigraph with \(e\) as the tail and \(v\) head. This also contributes \(n-1\) arcs to \(DPT(A_r)\).
Case 5. Let \(P_j\) be a directed path which lies on \(\alpha^{‘}\) arcs in \(A_r\). Then \(\alpha^{‘}\) arcs give rise to a complete bipartite subdigraph with a single tail \(P_j\) and \(\alpha^{‘}\) heads and \(\alpha^{‘}\) arcs joining \(P_j\) with each head. This again contributes \(n-1\) arcs to \(DPT(A_r)\).
Case 6. Let \(P_j\) be a directed path and let \(\beta^{‘}\) be the number of directed paths whose head is reachable from the tail of \(P_j\) through a common vertex in \(A_r\). Then \(\beta^{‘}\) arcs give rise to a complete bipartite subdigraph with a single tail \(P_j\) and \(\beta^{‘}\) heads and \(\beta^{‘}\) arcs joining \(P_j\) with each head. This contributes \(k^{‘}-1\) arcs to \(DPT(A_r)\).
Hence by all the cases above, \(Q=DPT(A_r)\) is decomposed into mutually arc-disjoint complete bipartite subdigraphs with \(V(Q)=V(A_r) \cup A(A_r) \cup P(A_r)\) and arc sets, (i) \(\cup_{i=1}^{n} X_i \times Y_i\), where \(X_i\) and \(Y_i\) are the sets of in-coming and out-going arcs at \(v_i\) of \(A_r\), respectively; (ii) four times the size of \(A_r\), i.e., \(4(n-1)\); and (iii) \(k^{‘}-1\).
Conversely, let \(A_r^{‘}\) be a digraph of the type described above. Let \(t_1,t_2,\ldots,t_l\) be the vertices corresponding to complete bipartite subdigraphs \(T_1,T_2,\ldots,T_l\) of Case 1, respectively; and let \(w^{1},w^{2},\dots,w^{t}\) be the vertices corresponding to complete bipartite subdigraphs \(P_1^{‘},P_2^{‘},\ldots,P_t^{‘}\) of Case 5, respectively. Finally, let \(t_0\) be a vertex chosen arbitrarily.For each vertex \(v\) of the complete bipartite subdigraphs \(T_1,T_2,\ldots,T_l\), we draw an arc \(a_v\) as follows:
Note that, in \((t_j,w^{n})\) no matter what the value of \(j\) is, \(n\) varies from \(1\) to \(t\) such that the number of arcs of the form \((t_j,w^{n})\) is exactly \(t\).
We now mark the directed pathos as follows. It is easy to observe that the directed path number \(k^{‘}\) equals the number of subdigraphs of Case 5. Let \(\psi_1,\psi_2,\ldots,\psi_t\) be the number of heads of subdigraphs \(P_1^{‘},P_2^{‘},\ldots,P_t^{‘}\), respectively. Suppose we mark the directed path \(P_1\). For this we choose any \(\psi_1\) number of arcs and mark \(P_1\) on \(\psi_1\) arcs. Similarly, we choose \(\psi_2\) number of arcs and mark \(P_2\) on \(\psi_2\) arcs. This process is repeated until all the directed paths of a directed pathos are marked. The digraph \(A_r\) with directed pathos thus constructed apparently has \(A_r^{‘}\) as directed pathos total digraph. Thus we have,Theorem 4.1. A digraph \(A_r^{‘}\) is a directed pathos total digraph of an arborescence \(A_r\) if and only if \(V(A_r^{‘})=V(A_r) \cup A(A_r) \cup P(A_r)\) and arc sets, (i) \(\cup_{i=1}^{n} X_i \times Y_i\), where \(X_i\) and \(Y_i\) are the sets of in-coming and out-going arcs at \(v_i\) of \(A_r\), respectively; (ii) four times the size of \(A_r\), i.e., \(4(n-1)\); and (iii) \(k^{‘}-1\).
Given a directed pathos total digraph \(Q\), the proof of the sufficiency of Theorem above shows how to find an arborescence \(A_r\) such that \(DPT(A_r)=Q\). This obviously raises the question of whether \(Q\) determines \(A_r\) uniquely. Although the answer to this in general is no, the extent to which \(A_r\) is determined is given as follows.
One can check easily that using reconstruction procedure of the sufficiency of Theorem above, any arborescence (without directed pathos) is uniquely reconstructed from its directed pathos total digraph. Since the pattern of directed pathos for an arborescence is not unique, there is freedom in marking directed pathos for an arborescence in different ways. This clearly shows that if the directed path number is one, any arborescence with directed pathos is uniquely reconstructed from its directed pathos total digraph. It is known that a directed path is a special case of an arborescence. Since the directed path number \(k^{‘}\) of a directed path \(\vec{P_{n}}\) of order \(n\) \((n \geq 2)\) is exactly one, a directed path with directed pathos is uniquely reconstructed from its directed pathos total digraph.Property 5.1. For an arborescence \(A_r\), \(L(A_r) \subseteq T(A_r) \subseteq DPT(A_r)\), where \(\subseteq\) is the subdigraph notation.
Property 5.2. If the in-degree (out-degree) of a vertex \(v\) in \(A_r\) is \(n\), then the in-degree (out-degree) of the corresponding vertex \(v\) in \(DPT(A_r)\) is \(2n\).
Property 5.3. The in-degree of the vertex \(v\) in \(DPT(A_r)\) corresponding to the root arc of \(A_r\) is two.
Property 5.4. The in-degree of the vertex \(v\) in \(DPT(A_r)\) corresponding to a pendant arc of \(A_r\) is two.
Property 5.5. A directed pathos total digraph \(DPT(A_r)\) of an arborescence \(A_r\) does not contain any vertex \(v\) such that \(DPT(A_r)\) is disconnected. Hence \(DPT(A_r)\) is a block.
Property 5.6. Every pair of vertices and arcs of \(DPT(A_r)\) lie on a semi-directed cycle.
Property 5.7. For any three distinct vertices \(u,v\), and \(w\), there is a semi-directed path joining \(u\) and \(w\) which contains \(v\).
Property 5.8. For any three distinct vertices \(u,v\), and \(w\), there is a semi-directed path joining \(u\) and \(w\) which does not contains \(v\).
Property 5.9. Every \(DPT(A_r)\) is either strictly unilateral or strictly weak.
In order to prove the next property, we need the following Theorem and definitions.Theorem 5.10 [10] Let \(D\) be an acyclic digraph with precisely one source \(x\) in \(D\). Then for every \(v \in V(D)\), there is an \((x,v)\)-directed path in \(D\).
Definition 5.11. A transmitter is a vertex \(v\) whose out-degree is positive and whose in-degree is zero, i.e., \(d^{+}(v) >0\) and \(d^{-}(v)=0\).
Definition 5.12. A carrier is a vertex \(v\) whose out-degree and in-degree are both one, i.e., \(d^{+}(v)=d^{-}(v)=1\).
Definition 5.13. A receiver is a vertex \(v\) whose out-degree is zero and whose in-degree is positive, i.e., \(d^{+}(v)=0\) and \(d^{-}(v)>0\).
Definition 5.14. A vertex \(v\) is said to be ordinary if \(d^{+}(v) >0\) and \(d^{-}(v) >0\).
Definition 5.15. A directed pathos vertex is a vertex corresponding to the directed path of a directed pathos of \(A_r\).
Proposition 5.16. Let \(A_r\) be an arborescence of order \(n\) \((n \geq 2)\) with \(v_1\) and \(e_1=(v_1,v_2)\) as the root and root arc of \(A_r\), respectively. Then there exists exactly one vertex \(v\) with \(d^{+}(v) >0\) and \(d^{-}(v)=0\) (i.e., transmitter), and for every vertex \(w \in DPT(A_r)\) (except for the vertex \(v_1\)), there is an \((v,w)\)-directed path in \(DPT(A_r)\).
Proof. Let \(A_r\) be an arborescence with vertex set \(V(A_r)=\{v_1,v_1,\ldots,v_n\}\) and arc set \(A(A_r)=\{e_1,e_2,\ldots,e_{n-1}\}\) such that \(v_1\) and \(e_1=(v_1,v_2)\) are the root and root arc of \(A_r\), respectively. Then the vertices \(e_2,e_3,\ldots,e_{n-1}\) are reachable from \(e_1\) by a unique directed path in \(L(A_r)\). Let \(P(A_r)=\{P_1,P_2,\ldots,P_{k^{‘}}\}\) be a directed pathos set of \(A_r\) such that \(P_1\) lies on the arc \(e_1\). Since the direction of the directed pathos is along the direction of the arcs in \(A_r\), \(d^{+}(v_1)=2,d^{-}(v_1)=0\); \(d^{+}(P_1)> 0\), \(d^{-}(P_1)=0\); and the remaining vertices are either receiver or carrier or ordinary, in \(DPT(A_r)\). Clearly, \(DPT(A_r)\) is acyclic. By Theorem 5.10, for every (except \(v_1\)) vertex \(w \in DPT(A_r)\), there is an \((P_1,w)\)- directed path in \(DPT(A_r)\). This completes the proof.
When defining any class of digraphs, it is desirable to know the order and size of each; it is easy to determine for \(DPT(A_r)\).Proposition 5.17. Let \(A_r\) be an arborescence with \(n\) vertices \(v_1,v_2,\ldots,v_n\) and \(k^{‘}\) sinks. Then the order and size of \(DPT(A_r)\) are \(2n+k^{‘}-1\) and \(4n+\displaystyle\sum_{i=1}^{n} d^{-}(v_i)\cdot d^{+}(v_i)+k^{‘}-5\), respectively.
Proof. If \(A_r\) has \(n\) vertices and \(k^{‘}\) sinks, then it follows immediately that \(DPT(A_r)\) contains \(n+n-1+k^{‘}=2n+k^{‘}-1\) vertices. Furthermore, every arc of \(DPT(A_r)\) corresponds to an arc in \(A_r\) (there are \(n-1\) arcs); adjacent arcs in \(A_r\) (this is given by \(\displaystyle\sum_{i=1}^{n} d^{-}(v_i)\cdot d^{+}(v_i)\)); an arc adjacent to a vertex in \(A_r\) (there are \(n-1\) of these); a vertex adjacent to an arc in \(A_r\) (there are \(n-1\) of these); the arcs lie on the directed paths of a directed pathos of \(A_r\) (there are also \(n-1\) of these); and the arcs whose end-vertices are the directed pathos vertices (this is given by \(k^{‘}-1\)). Therefore, \(DPT(A_r)\) has \((n-1)+\displaystyle\sum_{i=1}^{n} d^{-}(v_i)\cdot d^{+}(v_i)+3(n-1)+k^{‘}-1=4n+\displaystyle\sum_{i=1}^{n} d^{-}(v_i)\cdot d^{+}(v_i)+k^{‘}-5\) arcs.
Theorem 6.1. A directed pathos total digraph \(DPT(A_r)\) of an arborescence \(A_r\) is planar if and only if the underlying graph of \(A_r\) is a star graph \(K_{1,n}\) on \(n \leq 3\) vertices.
Proof.
Suppose \(DPT(A_r)\) is planar. Assume that the underlying graph of \(A_r\) is a star graph \(K_{1,n}\) on \(n \geq 4\) vertices. Suppose that
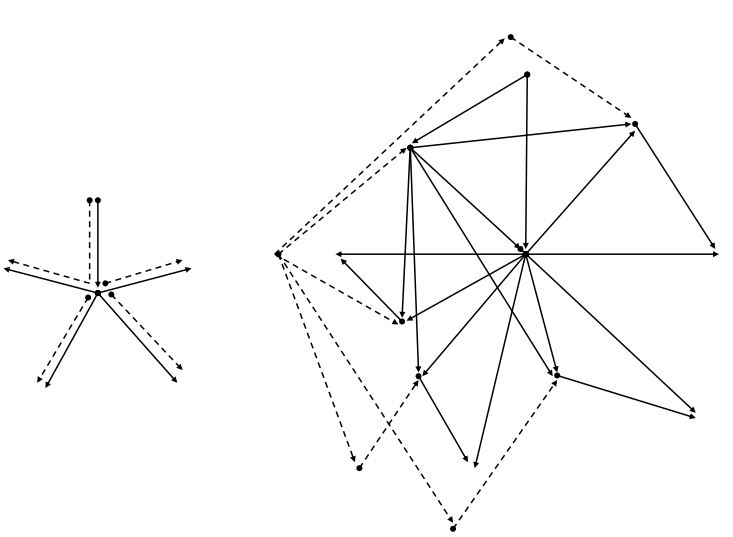
\(A_r = K_{1,4}\). Let \(V(A_r)=\{v_1,v_2,v_3,v_4,v_5\}\) be the vertex set and \(A(A_r)=\{e_1,e_2,e_3,e_4\}\) be the arc set of \(A_r\) such that \(v_1\) and \(e_1=(v_1,v_2)\) are the root and root arc of \(A_r\), respectively; and \(e_i=(v_2,v_{i+1})\) for \(2 \leq i \leq 4\). Then \((e_1,e_{i+1})\) for \(1 \leq i \leq 3\); \((v_1,v_2)\); \((v_2,v_{i+1})\) for \(2 \leq i \leq 4\); \((e_i,v_{i+1})\) for \(1 \leq i \leq 4\); \((v_1,e_1)\); and \((v_2,e_i)\) for \(2 \leq i \leq 4\) are the arcs of \(T(A_r)\). Let \(P(A_r)=\{P_1,P_2,P_3\}\) be a directed pathos set of \(A_r\) such that \(P_1\) lies on the arcs \((v_1,v_2),(v_2,v_3)\); \(P_2\) lies on \((v_2,v_4)\); and \(P_3\) lies on \((v_2,v_5)\). Then the directed pathos vertex \(P_1\) is a neighbor of the vertices \(v_1v_2,v_2v_3,P_2,P_3\); \(P_2\) is a neighbor of \(v_2v_4\); and \(P_3\) is a neighbor of \(v_2v_5\). This shows that the crossing number of \(DPT(A_r)\) is one, i.e., cr\((DPT(A_r))=1\), a contradiction (see Figure 3).
Conversely, suppose that the underlying graph of \(A_r\) is a star graph \(K_{1,n}\) on \(n \leq 3\) vertices. We consider the following three cases.
Case 1. Suppose that the underlying graph of \(A_r\) is \(K_{1,1}\), i.e., \(\vec{P_2}\). Then the underlying graph of \(DPT(A_r)\) is \(K_{1,3}+e\), i.e., the kite graph. Clearly \(DPT(A_r)\) is planar.
Case 2. Suppose that the underlying graph of \(A_r\) is \(K_{1,2}\), i.e., \(\vec{P_3}\). Let \(V(\vec{P_3})=\{v_1,v_2,v_3\}\) and the arcs of \(\vec{P_3}\) be \(e_i=(v_i,v_{i+1})\) for \(1 \leq i \leq 2\). Then \((e_1,e_2)\); \((v_i,v_{i+1})\) for \(1 \leq i \leq 2\); \((e_i,v_{i+1})\) for \( 1 \leq i \leq 2\); and \((v_i,e_i)\) for \(1 \leq i \leq 2\) are the arcs of \(T(A_r)\). The directed path number of \(\vec{P_3}\) is one, say \(P\). Then the directed pathos vertex \(P\) is a neighbor of the vertices \(e_1\) and \(e_2\). This shows that the crossing number of \(DPT(A_r)\) is zero, i.e., cr\((DPT(A_r))=0\) (see Figure 4). Hence \(DPT(A_r)\) is planar.
Case 3. Suppose that the underlying graph of \(A_r\) is \(K_{1,3}\). Let \(V(A_r)=\{v_1,v_2,v_3,v_4\}\) and \(A(A_r)=\{e_1,e_2,e_3\}\) such that \(v_1\) and \(e_1=(v_1,v_2)\) are the root and root arc of \(A_r\), respectively, and \(e_i=(v_2,v_{i+1})\) for \(2 \leq i \leq 3\). Then \((e_1,e_2)\); \((e_1,e_3)\); \((v_1,v_2)\); \((v_2,v_{i+1})\) for \(2 \leq i \leq 3\); \((e_i,v_{i+1})\) for \(1 \leq i \leq 3\); \((v_2,e_2)\); and \((v_2,e_3)\) are the arcs of \(T(A_r)\). Let \(P(A_r)=\{P_1,P_2\}\) be a directed pathos set of \(A_r\) such that \(P_1\) lies on the arcs \((v_1,v_2),(v_2,v_3)\) and \(P_2\) lies on \((v_2,v_4)\). Then the directed pathos vertex \(P_1\) is a neighbor of the vertices \(v_1v_2,v_2v_3,P_2\) and \(P_2\) is a neighbor of \(v_2v_4\). This shows that the crossing number of \(DPT(A_r)\) is zero (see Figure 3). Thus \(DPT(A_r)\) is planar. This completes the proof.
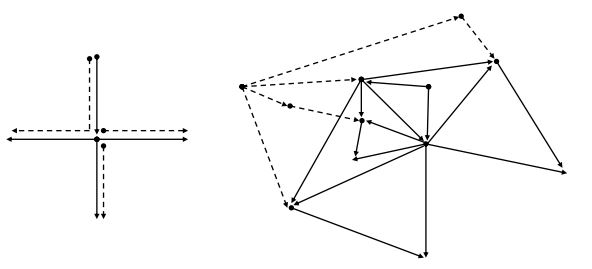
Theorem 6.2. A directed pathos total digraph \(DPT(A_r)\) of an arborescence \(A_r\) is outerplanar if and only if \(A_r\) is either \(\vec{P_2}\) or \(\vec{P_3}\).
Proof.
Suppose that \(DPT(A_r)\) is outerplanar. Assume that \(A_r=\vec{P_4}\). Let \(V(\vec{P_4})=\{v_1,v_2,v_3,v_4\}\) and the arcs of \(\vec{P_4}\) be \(e_i=(v_i,v_{i+1})\) for \(1 \leq i \leq 3\). Then \((e_1,e_2)\); \((e_2,e_3)\); \((v_i,v_{i+1})\) for \( 1 \leq i \leq 3\); \((e_i,v_{i+1})\) for \(1 \leq i \leq 3\); and \((v_i,e_i)\) for \(1 \leq i \leq 3\) are the arcs of \(T(A_r)\). The directed path number of \(\vec{P_4}\) is one, say \(P\). Then the directed pathos vertex \(P\) is a neighbor of the vertices \(e_1,e_2\), and \(e_3\). This shows that the inner vertex number of \(DPT(A_r)\) is one, i.e., \(i(DPT(A_r))=1\) (see Figure 5), a contradiction.
Conversely, suppose that \(A_r\) is either \(\vec{P_2}\) or \(\vec{P_3}\). If \(A_r\) is \(\vec{P_2}\), then the underlying graph of \(DPT(A_r)\) is \(K_{1,3}+e\). Clearly \(i(DPT(A_r))=0\). Thus \(DPT(A_r)\) is outerplanar. On the other hand, if \(A_r\) is \(\vec{P_3}\), then Case 2 of sufficiency of Theorem 6.1 implies that the crossing number of \(DPT(A_r)\) is zero. This also shows that the inner vertex number of \(DPT(A_r)\) is zero, i.e., \(i(DPT(A_r))=0\) (see Figure 4). Hence \(DPT(A_r)\) is outerplanar. This completes the proof.
Theorem 6.3. A directed pathos total digraph \(DPT(A_r)\) of an arborescence \(A_r\) is maximal outerplanar if and only if \(A_r\) is \(\vec{P_3}\).
Proof.
Suppose that \(DPT(A_r)\) is maximal outerplanar. We consider the following cases.
Case 1. Assume that the total degree of each vertex of \(A_r\) is at least four, i.e., \(td(v) \geq 4\), for every vertex \(v \in A_r\). By Theorem 6.1, \(DPT(A_r)\) is nonplanar, a contradiction.
Case 2. If there exists a vertex of total degree three in \(A_r\). By Theorem 6.2, \(DPT(A_r)\) is nonouterplanar, a contradiction.
Case 3. If \(A_r=\vec{P_2}\), then the underlying graph of \(DPT(A_r)\) is \(K_{1,3}+e\). Clearly \(i(DPT(A_r))=0\). Thus \(DPT(A_r)\) is outerplanar. Furthermore, since the addition of an arc does not alter the outerplanarity of \(DPT(A_r)\), it follows that \(DPT(A_r)\) is not maximal outerplanar, a contradiction.
Case 4. If \(A_r=\displaystyle \vec{P}_{n+3}\) \((n \geq 1)\), then the inner vertex number of the corresponding \(DPT(A_r)\) equals \(n\). Clearly, \(DPT(A_r)\) is nonouterplanar, again a contradiction.
Conversely, suppose that \(A_r=\vec{P_3}\). By Proposition 5.12, the order and size of \(DPT(A_r)\) are \(n=6\) and \(m=9\), respectively. But \(m=9=2n-3\). Since the size of \(DPT(A_r)\) is nine, Theorem 2.1 implies that \(DPT(A_r)\) is maximal outerplanar. This completes the proof.Theorem 6.4. A directed pathos total digraph \(DPT(A_r)\) of an arborescence \(A_r\) is minimally nonouterplanar if and only if \(A_r\) is \(\vec{P_4}\).
Proof.
Suppose that \(DPT(A_r)\) is minimally nonouterplanar. Assume that \(A_r=\vec{P_5}\). By Case 4 of necessity of Theorem 6.3, \(i(DPT(A_r))=2\) (see Figure.2), a contradiction.
Conversely, suppose that \(A_r=\vec{P_4}\). By Case 4 of necessity of Theorem 6.3, \(i(DPT(A_r))=1\) (see Figure 5). Hence \(DPT(A_r)\) is minimally nonouterplanar. This completes the proof.
Theorem 6.5. A directed pathos total digraph \(DPT(A_r)\) of an arborescence \(A_r\) has crossing number one if and only if the underlying graph of \(A_r\) is \(K_{1,4}\).
Proof.
Suppose \(DPT(A_r)\) has crossing number one. Assume that the underlying graph of \(A_r\) is \(K_{1,n}\) \((n \geq 5)\).
Suppose \(A_r = K_{1,5}\). Let \(V(A_r)=\{v_1,v_2,v_3,v_4,v_5,\) \(v_6\}\) and \(A(A_r)=\{e_1,e_2,e_3,e_4,e_5\}\) such that \(v_1\) and \(e_1=(v_1,v_2)\) are the root and root arc of \(A_r\), respectively; and \(e_i=(v_2,v_{i+1})\) for \(2 \leq i \leq 5\). Then \((e_1,e_i)\) for \(2 \leq i \leq 5\); \((v_1,v_2)\); \((v_2,v_i)\) for
\(3 \leq i \leq 6\); \((e_i,v_{i+1})\) for \(1 \leq i \leq 5\); \((v_1,e_1)\); and \((v_2,e_i)\) for \(2 \leq i \leq 5\) are the arcs of \(T(A_r)\).
Let \(P(A_r)=\{P_1,P_2,P_3,P_4\}\) be a directed pathos set of \(A_r\) such that \(P_1\) lies on the arcs \((v_1,v_2),(v_2,v_3)\); \(P_2\) lies on \((v_2,v_4)\); \(P_3\) lies on \((v_2,v_5)\); and \(P_4\) lies on \((v_2,v_6)\). Then the directed pathos vertex \(P_1\) is a neighbor of the vertices \(v_1v_2,v_2v_3,P_2,P_3,P_4\); \(P_2\) is a neighbor of \(v_2v_4\); \(P_3\) is a neighbor of \(v_2v_5\); and \(P_4\) is a neighbor of \(v_2v_6\). This shows that the crossing number of \(DPT(A_r)\) is more than one, i.e., cr\((DPT(A_r))>1\) (see Figure 6), a contradiction.
Conversely, suppose that the underlying graph of \(A_r\) is \(K_{1,4}\). By necessity of Theorem 6.1, the crossing number of \(DPT(A_r)\) is one. This completes the proof.