In the fields of chemical graph theory (CGT), mathematical chemistry and molecular topology, a~topological index (TI) also known as a connectivity~index~is a type of a molecular descriptor that is calculated based on the molecular graph of a chemical compound. \(BiI_{3}\) is an excellent inorganic compound and is very useful in qualitative inorganic analysis and topological indices of \(BiI_{3} \) help to predict many properties like boiling point, heat of formation, strain energy, rigidity and fracture toughness and correlate the structure with various physical properties, chemical reactivity and biological activities. This paper computes several degree-based topological indices like multiplicative first Zagreb index, multiplicative second Zagreb index, multiplicative atomic bond connectivity index, multiplicative first and second hyper Zagreb index and multiplicative geometric arithmetic index for Bismuth Tri-Iodide chains and sheets.
The \(BiI_{3}\) is an inorganic compound which is the result of the reaction of iodine and bismuth, which inspired the enthusiasm for subjective inorganic investigations [1]. \(BiI_{3}\) is an excellent inorganic compound and is very useful in “qualitative inorganic analysis” [1, 2].
It was proved that $Bi$-doped glass optical strands are one of the most promising dynamic laser media. Different kinds of Bi-doped fiber strands have been created and have been used to construct Bi-doped fiber lasers and optical loudspeakers [3].
Layered \(BiI_{3}\) gemstones are considered to be a three-layered stack structure in which a plane of bismuth atoms is sandwiched between iodide particle planes to form a continuous \(I-Bi-I\) plane [4].
The periodic superposition of the diamond-shaped three layers forms \(BiI_{3}\) crystals with \(R\)-3 symmetry [5, 6]. A progressive stack of \(I-Bi-I\) layers forms a symmetric hexagonal structure [7] and jewel of \(BiI_{3}\) was integrated in [8].
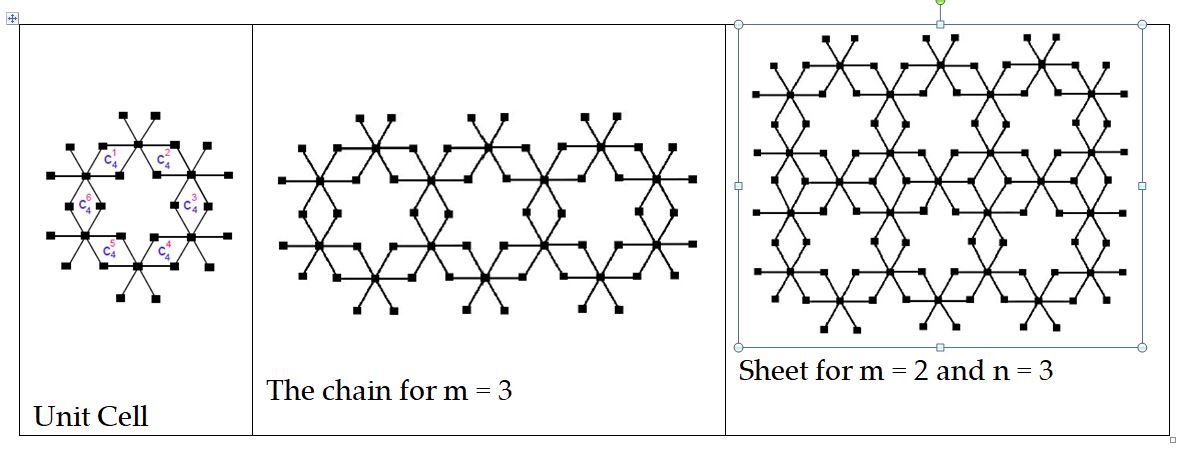
Mathematical chemistry is an area of research in chemistry in which mathematical tools are used to solve problems of chemistry. Chemical graph theory is an important area of research in mathematically chemistry which deals with topology of molecular structure such as the mathematical study of isomerism and the development of topological descriptors or indices. Infect, TIs are real numbers attached with graph networks and graph of chemical compounds and has applications in quantitative structure-property relationships. TIs remain invariant upto graph isomorphism and help to predict many properties of chemical compounds, networks and nanomaterials, for example, viscosity, boiling points, radius of gyrations, etc without going to lab [9, 10, 11, 12].
Other emerging field is Cheminformatics, in which we use QSAR and QSPR relationship to guess biological activity and chemical properties of nanomaterial and networks. In these investigations, some Physico-chemical properties and TIs are utilized to guess the behavior of chemical networks [13, 14, 15, 16, 17]. Like TIs, polynomials also fund considerable applications in network theory and chemistry, for example, Hosoya polynomial, which is also known as Wiener polynomial, introduced in [18] plays an important role in computation of distance-based TIs. M-polynomial [19] was defined in 2015 and plays a similar role in computation of numerous degree-based TIs [20, 21, 22, 23, 24]. The M-polynomial contains precious information about degree-based TIs and many TIs can be computed from this simple algebraic polynomial. The first TI was defined in 1947 by Weiner during studying boiling point of alkanes [25]. This index is now known as Weiner index. Thus Weiner established the framework of TIs and the Wiener index is initially the first and most concentrated TI [26, 27].
The other oldest TI is Randić index (RI), given by Milan Randić [28] in 1975. After the success of Randić index, in the year 1988, the generalized version of Randić index was introduced [29, 30]. This version attracts both the mathematicians and chemists [31]. Numerous numerical properties of this simple TI are studied in [32]. For comprehensive study about this index, the book [33] can be of great help.
The RI is a most mainstream regularly connected and most concentrated among all other TIs. Numerous research papers and text books, for example, [34, 35, 36] are published in different academic journals on this TI. Two surveys on RI was written by Milan Randi\'{c} [37, 38] and three more surveys are written on this TI by different scientists [39, 40 41]. The reason behind the success of such a simple TI is as yet a puzzle, although some conceivable clarifications were given.
After Randi\'{c} index, the most studied TIs are 1st Zagreb index (ZI) and 2nd ZI [42, 43, 44, 45, 46]. The modified 2nd ZI was defined in [47]. Another TI is symmetric division (SDI) [48], Harmonic index (HI) [49, 50], augmented ZI [51].
In this article, we compute general form of several degree-based topological indices for Bismuth Tri-Iodide chains and Bismuth Tri-Iodide sheets. For example we compute first and second multiplicative Zagreb indices, multiplicative atomic bond connectivity index, sum connectivity index, modify Randi\’c index, etc.\[ II_{1}(G) = \prod_{u \in V(G)} (d_u)^2 \]
\[ II_{2}(G) = \prod_{uv \in E(G)} d_u \cdot d_v \]
and the Narumi-Katayama index [52]: \[ NK(G) = \prod_{u \in V(G)} d_u \]
Like the Wiener index, these types of indices are the focus of considerable research in computational chemistry [54, 55, 56]. For example, in the year 2011, Gutman in [54] characterized the multiplicative Zagreb indices for trees and determined the unique trees that obtained maximum and minimum values for \(M_{1}(G)\) and \(M_{2}(G)\), respectively. Wang et al. in [57] extended the results of Gutman to the following index for k-trees:
\[ W_{1}^{s}(G) = \prod_{u \in V(G)} (d_u)^s \],
where \( s = 1, 2 \) is the Narumi-Katayama and Zagreb index, respectively. Based on the successful consideration of multiplicative Zagreb indices, Eliasi et al. [58] continued to define a new multiplicative version of the first Zagreb index as:
\[ II_{1}^{*}(G) = \prod_{uv \in E(G)} (d_u + d_v) \].
Furthering the concept of indexing with the edge set, the first author introduced the first and second hyper-Zagreb indices of a graph [59]:
\[HII_{1}(G) = \prod_{uv \in E(G)} (d_u + d_v)^2 \],
\[ HII_{2}(G) = \prod_{uv \in E(G)} (d_u \cdot d_v)^2 \].
In [60], Kulli et al. defined the first and second generalized Zagreb indices:
\[ MZ_{1}^{a}(G) = \prod_{uv \in E(G)} (d_u + d_v)^{\alpha} \],
\[ MZ_{2}^{a}(G) = \prod_{uv \in E(G)} (d_u \cdot d_v)^{\alpha} \].
Multiplicative sum connectivity and multiplicative product connectivity indices [61] are defined as:
\[ SCII(G) = \prod_{uv \in E(G)} \frac{1}{\sqrt{d_u + d_v}} \],
\[ PCII(G) = \prod_{uv \in E(G)} \frac{1}{\sqrt{d_u \cdot d_v}} \].
Multiplicative atomic bond connectivity index and multiplicative Geometric arithmetic index are defined as:
\[ ABCII(G) = \prod_{uv \in E(G)} \sqrt{\frac{d_u + d_v – 2}{d_u \cdot d_v}} \],
\[ GAII(G) = \prod_{uv \in E(G)} \frac{2 \sqrt{d_u \cdot d_v}}{d_u + d_v} \],
\[ GA^{a} II(G) = \prod_{uv \in E(G)} \left( \frac{2 \sqrt{d_u \cdot d_v}}{d_u + d_v} \right)^{\alpha} \].
Shigehalli and Kanabur [62] introduced the following new degree-based topological indices:
Arithmetic-Geometric (AG1) index: \[ AG_{1}(G) = \sum_{uv \in E(G)} \frac{d_u + d_v}{2\sqrt{d_u d_v}} \], \[ SK(G) = \sum_{uv \in E(G)} \frac{d_u + d_v}{2} \], \[ SK_{2}(G) = \sum_{uv \in E(G)} \left( \frac{d_u + d_v}{2} \right)^2 \].
Theorem 1. Let \(G\) be the molecular graph of \(m-BiI_{3}\). Then
Proof.
Let \(G\) be the molecular graph of \(p-BiI_{3}\) bismuth tri-iodide chain. The edge set of \(p-BiI_{3}\) has following two partitions [1],
\(E_{1} =E_{\left\{1,6\right\}} =\left\{e=uv\in E\left(G\right) |d_{u} =1,\; d_{v} =6\right\},\)
\(E_{\left\{2,6\right\}} =\left\{e=uv\in E\left(G\right) |d_{u} =2,\; d_{v} =6\right\},\)
Such that
\(\left|E_{1} \left(G\right)\right|=4p+8,\)
\(\left|E_{2} \left(G\right)\right|=20p+4.\)
Now by definitions, we have
Corollary 2. Let \(G\) be the molecular graph of \(p-BiI_{3}\). Then
Proof. These results can be obtained immediately proved by taking \(\alpha =1\) in Theorem 1.
Corollary 3. Let \(G\) be the molecular graph of \(p-BiI_{3}\). Then
Proof. These results can be obtained immediately proved by taking \(\alpha =2\) in Theorem 1.
Corollary 4. Let \(G\) be the molecular graph of \(p-BiI_{3}\). Then
Proof. These results can be obtained immediately proved by taking \(\alpha =-\frac{1}{2}\) in Theorem 1.
Theorem 5. Let \(G\) be the molecular graph of \(p-BiI_{3}\). Then \[ABCII\left(G\right)=\left(\sqrt{\frac{5}{6} } \right)^{4p+8} \times \left(\sqrt{\frac{1}{2} } \right)^{20p+4} .\]
Proof. Using the edge partition given in Theorem 1 and definition of multiplicative Atomic bond Connectivity index, we have \begin{eqnarray*}ABCII\left(G\right)&=&\prod _{uv\in E\left(G\right)}\sqrt{\frac{d_{u} +d_{v} -2}{d_{u} \cdot d_{v} } } \\ &=&\left(\sqrt{\frac{1+6-2}{1\cdot 6} } \right)^{4p+8} \times \left(\sqrt{\frac{2+6-2}{2\cdot 6} } \right)^{20p+4} \\\ &=&\left(\sqrt{\frac{5}{6} } \right)^{4p+8} \times \left(\sqrt{\frac{1}{2} } \right)^{20p+4} . \end{eqnarray*}
Theorem 6. Let \(G\) be the graph of \(p-BiI_{3}.\) Then
Proof. Using edge partition given in Theorem 1 and definitions, we have 1. \begin{eqnarray*} SC\left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{1}{\sqrt{d_{u} +d_{v} } } \\ &=&\frac{1}{\sqrt{7} } \left(4p+8\right)+\frac{1}{2\sqrt{2} } \left(20p+4\right) \\ &=&\left(\frac{4}{\sqrt{7} } +\frac{10}{\sqrt{2} } \right)p+\left(\frac{8}{\sqrt{7} } +\sqrt{2} \right). \end{eqnarray*} 2. \begin{eqnarray*} AG_{1} \left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{d_{u} +d_{v} }{2\sqrt{d_{u} \times d_{v} } } \\ &=&\frac{7}{2\sqrt{6} } \left(4p+8\right)+\left(20p+4\right)\frac{2}{\sqrt{3} } \\ &=&\left(\frac{14}{\sqrt{6} } +\frac{40}{\sqrt{3} } \right)p+\left(\frac{28}{\sqrt{6} } +\frac{8}{\sqrt{3} } \right). \end{eqnarray*} 3. \begin{eqnarray*} SK\left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{d_{u} +d_{v} }{2} \\ &=&\frac{7}{2} \left(4p+8\right)+4\left(20p+4\right) \\ &=&94p+44. \end{eqnarray*} 4. \begin{eqnarray*} SK_{1} \left(G\right)&=&\sum _{uv\in E\left(G\right)}\frac{d_{u} \times d_{v} }{2} \\ &=&3\left(4p+8\right)+6\left(20p+4\right)\\ &=&132p+48.\end{eqnarray*} 5. \begin{eqnarray*}SK_{2} \left(G\right)&=&\sum _{uv\in E\left(G\right)}\left(\frac{d_{u} +d_{v} }{2} \right) ^{2} \\ &=&\frac{49}{4} \left(4p+8\right)+16\left(20p+4\right) \\ &=&369p+162.\end{eqnarray*} 6. \begin{eqnarray*}R’\left(G\right)&=&\sum _{uv\in E\left(G\right)}\left(\frac{1}{\max \left\{d_{u} ,d_{v} \right\}} \right) \\ &=&\frac{1}{6} \left(4p+8\right)+\frac{1}{6} \left(20p+4\right) \\ &=&4p+2.\end{eqnarray*}
Theorem 7. Let \(G\) be the molecular graph of \(BiI_{3} \left(p\times q\right)\). Then
Proof.
Let \(G\) be the graph of \(BiI_{3} \left(p\times q\right)\) bismuth tri-iodide sheet. The edge set of \(BiI_{3} \left(p\times q\right)\) has following three partitions [1],
\(E_{1} =E_{\left\{1,6\right\}} =\left\{e=uv\in E\left(G\right){ |}d_{u} =1,\; d_{v} =6\right\},\)
\(E_{2} =E_{\left\{2,6\right\}} =\left\{e=uv\in E\left(G\right){ |}d_{u} =2,\; d_{v} =6\right\},\)
\(E_{3} =E_{\left\{3,6\right\}} =\left\{e=uv\in E\left(G\right){ |}d_{u} =3,\; d_{v} =6\right\},\)
such that
\(\left|E_{1} \left(G\right)\right|=4p+4q+4,\)
\(\left|E_{2} \left(G\right)\right|=12pq+8p+8q-4,\)
\(\left|E_{3} \left(G\right)\right|=6pq-6q.\)
Now by definition
Corollary 8. Let \(G\) be the molecular graph of \(BiI_{3} \left(p\times q\right)\). Then
Proof. These result can be obtained immediately proved by taking \(\alpha =1\) in Theorem 7.
Corollary 9. Let \(G\) be the molecular graph of \(BiI_{3} \left(p\times q\right)\). Then
Proof. These result can be obtained immediately proved by taking \(\alpha =2\) in Theorem 7.
Corollary 10. Let \(G\) be the molecular graph of \(BiI_{3} \left(p\times q\right)\). Then
Proof. These result can be obtained immediately proved by taking \(\alpha =-\frac{1}{2}\) in Theorem 7.
Theroem 11. Let \(G\) be the molecular graph of \(BiI_{3} \left(p\times q\right)\). Then \[ABCII\left(G\right)=\left(\sqrt{\frac{5}{6} } \right)^{4p+4q+4} \times \left(\sqrt{\frac{1}{2} } \right)^{12pq+8p+8q-4} \times \left(\sqrt{\frac{7}{18} } \right)^{6pq-6q} .\]
Proof. \begin{eqnarray*} ABCII\left(G\right)&=&\prod _{uv\in E\left(G\right)}\sqrt{\frac{d_{u} +d_{v} -2}{d_{u} \cdot d_{v} } } \\ &=&\left(\sqrt{\frac{1+6-2}{1\cdot 6} } \right)^{4p+4q+4} \times \left(\sqrt{\frac{2+6-2}{2\cdot 6} } \right)^{12pq+8p+8q-4} \times \left(\sqrt{\frac{3+6-2}{3\cdot 6} } \right)^{6pq-6q} \\ &=&\left(\sqrt{\frac{5}{6} } \right)^{4p+4q+4} \times \left(\sqrt{\frac{1}{2} } \right)^{12pq+8p+8q-4} \times \left(\sqrt{\frac{7}{18} } \right)^{6pq-6q} . \end{eqnarray*}
Theroem 12. Let \(G\) be the graph of \(BiI_{3} \left(p\times q\right)\). Then
Proof. Using the edge partition given in Theorem 7, we have