Entropy patterns typically transfer actions of two-state relations in nonlinear systems. Here, multivalent logic is applied from autowave fields to selected Quantum Neurophysical systems.
Quantum Neurophysics is defined as the mechanics of a neural computational system at quantum-scale. Computational Neurophysics occur in an entropic continuum in mathematical constants and terms, which can advance development of neurology in quantum complexity and decision, as noted by Lowden [1]. As the Computational Neural System [CNS] manages Neurophysical computational states, neuromorphic computational machinery includes distributed transduction of electromagnetic phase states.
Cognition is defined as a computational modality that includes continuous wave decoherences to activate central nervous systems utilizing the Schrodinger wave function for a time-dependent equation
\[i\hslash \frac{d}{dt}|\Psi(t)\rangle =\mathop{H}|\Psi(t)\rangle . \tag{1}\]
These computational advances can be defined in terms of a total complexity of the Computational Neural System [CNS].
The piezoelectric propagation and relay of electromagnetic infrared range emissions has been demonstrated by Bigu del Blanco and Romero-Sierra [2] and additionally these authors demonstrated for spectrum conductance at approximately 8.95 Ghz. Infrared mechanics for quantum neurophysics are studied in this research work by Callahan [sensilla and antennae], and Penrose and Hameroff [microtubulin and microtubules of pyramidal neurons]. These physical mechanisms for the estimation formula probably include the quantum potential in the total mass of the unit and the complexity and efficiency of the connecting mechanisms, such as circuits, cells, synapses and tubulins. These work to break down perception into the most efficient bits of information for the complete Computational Neural System [CNS] to process in the fastest and most energy-efficient method possible over space and time criteria.
In the Materialist definition Computation is distinguished from the physical observer Universe, being comprised of Neurophysical, such as quantumizable, electrophysical events and probability series in the Computational Neural System [CNS]. Demonstrations of this hypothesis include functions such as photonic relay across microtubulin, neurotubules, glia, axons, actin and synapses resulting in complex computational sequences of amino acids and cellular neurophysics [3-5].
In this computational physical definition, Tiger Moths [Lepidoptera][6], Aviary insects, Lybia crabs, Aviates [Corvus moneduloides], Chiroptera, Reptilia [Pit vipers], and Cetaceans [7] have evolved two-state, quantum tunneling Computational Neural System [CNS] utilizing infrared-range computational mechanics for the purpose of increasing physical ability to complete evolutionary algorithms of problem-solving challenges in their environments. Advancing Pribram, Bohm and Gabor’s research in Holonomic Brain Theory [HBT], thematically-sequential holographic associative memory, later hypotheses demonstrated by Hawkins and George’s Hierarchical Temporal Memory [HTM] illustrate for a theoretical structure for autowaves affecting analogous neurophysical clique topologies [8].
Regarding problem-solving and charting and Computational Neural System [CNS] development, sensory algorithmic methods are therefore demonstrated as an applied basis for the proposed Dynamic Global Workspace Theory-Intelligent Computational System Organization [DGWT-ICSO]. This hypothesis advances in computable einselection and decoherence, orthogonal pointer states [9] where \[H\boldsymbol{\Psi} (t)=Tr (p\boldsymbol{\Psi}(t) logp \boldsymbol{\Psi}(t)), \tag{2}\]
from bifringement patterns in evolving state/phase vectors. [10,11]. Zurek has advanced the mathematical physics for quantum stochasticity [12] where
\[|\boldsymbol{\Psi}(t) \rangle = \exp\left(-iH \frac{t}{\hbar}\right) \boldsymbol{\Psi}(0) \rangle\;\; for\;\; \boldsymbol{\Psi}(0) \rangle = \boldsymbol{\psi} \rangle |A0 \rangle = a_i |s_i \rangle |A0 \rangle \boldsymbol{\rightarrow} a_i |s_i \rangle |Ai \rangle = \boldsymbol{\Psi}(t) \rangle ,\tag{3}\]
essentially \[|\mathbf{\Psi}t\rangle = a_i | s_i\rangle|A_i\rangle= b_i|r_i\rangle|B_i\rangle .\tag{4}\]
The propagation path of the wavicle is demonstrated by boolean operations on the real physical worldvolume until
\[\mathbf{\Delta}x \sim \left( \frac{h\bar{}}{\mathbf{\Delta}p_0} \right) e^{\Lambda t} \quad \text{or} \quad t\bar{h} \simeq \Lambda^{-1} \ln \left( \mathbf{\Delta}p_0 \chi \right) .\tag{5}\]
These can be read at Wigner-space where
\[\textbf{a} = d \times d \, p = \frac{\hbar}{\bar{\mathrm{\times}}} \, \frac{\bar{h}}{L} \, P = \frac{\hbar^2}{I} , \tag{6}\]
where I \(\mathrm{\simeq}\) LP is the classical action. The quantum conditional mechanics are
\[\begin{aligned} \overline{\boldsymbol{\Psi}_0}\rangle =& \overline{\boldsymbol{\psi}^\uparrow}\rangle\overline{A_0}\rangle \\ =& a_i \overline{s_i}\rangle \overline{A_0} \rangle \\ &\xrightarrow{i} a_i \overline{s_i}\rangle \overline{A_i}\rangle \\ =& \overline{\boldsymbol{\Psi}_t}\rangle. \end{aligned}\]
The reduction of the state vector is
\[\begin{aligned} \Delta H &= H(\boldsymbol{\rho}_\mathrm{up}) – H(\boldsymbol{\rho}_\mathrm{c}) = – (\bar{\alpha}^2 \lg |\alpha|^2 + \bar{\beta}^2 \lg |\beta|^2) \ [\text{units}] \end{aligned},\]
and environmentally correlated where \[|\boldsymbol{\Phi c}\rangle| E \rangle=(\alpha|\uparrow\rangle|d \rangle+\beta|\downarrow\rangle|d \rangle)| E \rangle\Rightarrow\alpha|\uparrow\rangle|d \rangle| E \rangle+\beta|\downarrow\rangle|d \rangle| E \rangle=|\Psi\rangle. \tag{7}\]
Hiley advances q-monadic sheaves are described in Topological Quantum Field Theory [TQFT] as quasi-paradoxical Duron time, essentially \[\Delta T = t_2 – t_1 \text{ for } [T_1,T_2] \rightarrow T_1 \, T_2 \rightarrow \psi_L(t_1)E_a\psi_R(t_2), \tag{8}\]
on a generic tesselation spacetime of the Wpw or relativistic quantum and monadic wavicle of
\[\lim_{\Delta x, \Delta t \to 0} \Delta t .\tag{9}\]
Connes advances this notion from Heisenberg where
\[\mathbf{X}_{mn}(t) = R_{mn} \exp[i(\nu_m – \nu_n)t]. \tag{10}\]
In the Computational Neural System [CNS] the evolutionary or pragmatical purpose for directed hippocampal complexifying clique topologies [ibid] is for maximal granular information processing. This can be studied in the optogenetic approach in the pyramidal neurons to test Graph automorphisms, and for the purpose of advancing new algorithms against various evolutionary development fitness landscapes and adaptive systems. Ultrametrics in automata algorithms have been advanced in complex adaptive systems [14].
Autowave reverberations in memristors and spintronics, have been hypothesized and advanced. Initially operating as a Cellular Neural Network studied by Albrecht-Buehler, [15,16] Autowaves can also be studied in the multivalent logic of complex nonlinear systems and generic Computational Neural Systems [CNS], topological mapping in Radio Memory Cellular Neural Networks [RMCNN], and theoretically as algorithmic continuous spatial automata. [17] M.T. Greshova indicated that:
Autowaves (AW) are distributed analogues of the self-oscillation observed in pointwise systems. [18]
Regarding Computational Neural System [CNS] quantum information transfer regimes of autowaves via Extremely Low Frequency [ELF]-amplitude in infrared range, P.S. Callahan has demonstrated the photonic field-disturbance in infrared communication dynamics of Lepidoptera and Formicidae:
This work on Cabannes and Rayeligh scattering of coherent radiation reinforces other work on photon storage in biological systems.[19]
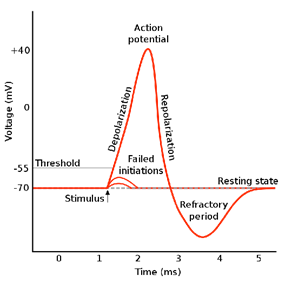
In a classical dissipative system autowave nonlinear systems utilize a general formula \[dx/dt=R(x,P),\] and where \[P(t)=t0/M,\] is therefore mapped
\[\mathbf{\Phi}: R\boldsymbol{\mathrm{\wedge}}u \boldsymbol{\mathrm{>}}\boldsymbol{\mathrm{>}}S\boldsymbol{\mathrm{\wedge}}1. \tag{11}\]
However, in the mathematical physics of a non-classical quantum dissipative system, fractional wave equations on the two-state quantum system on a complex Hilbert space can be demonstrated where
\[\textbf{x eH } \lim_{n \rightarrow \infty}\liminf_{(x-x_n,x-x_n)}=0. \tag{12}\]
Furthermore, in box-counting for dimensions on the iterative function space of fractional drums, a general formula can be built where for \(\boldsymbol{\Delta}\) u+\(\boldsymbol{\Lambda}\) u=0 u \(\boldsymbol{\delta}\) D=0 and from
\[\textbf{P(A)} = \pi + p_j + \dots + p_k. \tag{13}\]
This formula can be computed as two-state or multi-state variable automata series on a probability density function generally for
\[\mathbf{\phi}(\textit{x}) = (2\pi)^{-\frac{1}{2}}\mathrm{e}^{-\frac{x^2}{2}}. \tag{14}\]
Weyl demonstrated
\[\textbf{N}(R)-(2\boldsymbol{\pi})-d\boldsymbol{\Omega}VRd/2\_1/4(2\boldsymbol{\pi})-d+l\boldsymbol{\Omega}d – 1\textbf{AR}(d-1)/2\_0(R(d-1)/2). \tag{15}\]
The Peter-Weyl function density, and nonlinear thermodynamic radiation entrainment, turbulence and harmonic oscillation, sympathetic resonance, topological entanglement entropy in quantum mechanics is formulated
\[\textbf{SL} \gg \gg \alpha\text{L-}\gamma + o(\text{L-v}), v \gg 0. \tag{16}\]
Multivalent logic, after Łukasiewicz, is by definition and practice, composed of three, or ternary operations of logic in the element and set tables, allowing for more complexity in determination of value [True, False, Unknown]. In Quantum Physical terms, this Ternary quantum probability field can be formulated as infrared-driven Quantum Cellular Automata [QCA] where k = 2\(\boldsymbol{\alpha}\)/\(\boldsymbol{\pi}\)fN [Handel] and where S (f) \(\mathrm{\propto}\) 1/f \(\alpha\).
In Information Physics terms of the Quantum Neurophysical system, the multivalent set variable values can be projected as eigenvalues from isofractal and isospectral value. These can be derived from the multifractional Ultrametric field of primes [20] where the inequality holds for Multivalent logic for Gassmann triples, such that
\[\textbf{d}(x,z) \leq \max { \textbf{d}(y,z), \textbf{d}(y,z) } \text{ in } G = \text{SL}_3(\mathbb{F}_2). \tag{17}\] In isospectral Riemannians and special cases, such as Ramanujan graphs for Zeta infinites on eigenvalues limits these inequalities can be demonstrated from
\[\lim_{n \rightarrow \infty} G \in G_{dn} \Lambda(G) \geq 2 \sqrt{d-1}, \tag{18}\]
given \[\mathbf{\Lambda}1 \geq 2 \sqrt{d-1} – 2 \sqrt{2-1} – \frac{1}{\lfloor m/2 \rfloor}. \tag{19}\]
The Z-transform can be applied generally where the Topological Quantum Field Theory [TQFT] from the unilateral
\[\mathbf{X(z)} = \boldsymbol{\mathrm{Z}}\{x[n]\} = \infty \sum_{n=0} x[n] z^{-n}. \tag{20}\]
This bridged topology has been demonstrated by McPherson and Schweinhart. [21] Additional Topological Quantum Field Theory [TQFT] state entropy dynamics, hypergeometric functions, and Gaussian processes are studied as multifractional systems, where s (x\(\boldsymbol{\mathrm{>}}\) + a\(\boldsymbol{\mathrm{>}}\)) – s(x\(\boldsymbol{\mathrm{>}}\)) \(\boldsymbol{\mathrm{\sim}}\) ah(x\(\boldsymbol{\mathrm{>}}\)), for given fractional integration and differentiation regimes. These can be demonstrated as autoregressive fractionally-integrated moving averages [AFIMA] where symplectically
\[(1 – p\mathbf{\mathrm{\sum}}_{i=1} \Phi_i B_i) (1-B)d Xt = (1+q \mathbf{\mathrm{\sum}}_{i=1} \theta_i B_i) \mathbf{\mathrm{E}}_t. \tag{21}\]
Therefore noise-radiation and thermoentropic-radiation in dissipative systems [Heszler] can be demonstrated where in general formula
\[\frac{dV(x(t))}{dt} \leq u(t) \cdot y(t), \tag{22}\]
for ferroelectronic circuit fluctuations and extended values of wandering sets. Hiley and Callaghan [22] demonstrate the quantum phase space event in the Clifford algebra, where if Cli,j and \(\boldsymbol{\Phi}\) L (r,t) and \(\boldsymbol{\Phi}\) R(r,t) = \(\boldsymbol{\mathrm{\sim}}\) \(\boldsymbol{\Phi}\) L(r,t) then
\[\mathbf{\mathrm{P}} c(r,t) = \Phi L(r,t) \sim \Phi L(r,t) \quad \text{for} \quad i\gamma \partial_{\mu} \Phi L – m \Phi L = 0 \quad \text{and} \quad i\Phi R \partial_{\mu} \gamma + m\Phi R = 0 \quad. \tag{23}\]
This system can be compared in Pauli particle-wavefunctions and exclusionary zones [23] to a quantization of phase where
\[|\mathbf{\Psi}_n(t)\rangle = e^{i\gamma_n(t)e^{-i/\hbar \mathrm{H}}\int_{0}^{t} dt'\, \mathrm{E}_n(R(t'))} |n(R(t))\rangle, \tag{24}\]
in the nonlinear system
\[\mathbf{\Gamma}n(t) = i \int_{t_0}^{t} dt' \langle n(R(t')) | \frac{d}{dt'} | n(R(t')) \rangle = i \int_{R(t_0)}^{R(t)} dR \langle n(R) | \nabla R | n(R) \rangle ,\tag{25}\]
and therefore
\[\Omega_{n,\mu v(R)} = i\sum_{n' \neq n < n} \left|\frac{\Delta H}{\Delta R}\right|_{n' > n} \left|\frac{\Delta H}{\Delta R}v\right|_{n > n} – \frac{(v_{< n} v_{> n} \mu)}{(E-E_{n'})^2}. \tag{26}\]
Dirac particle-wavefunctions are demonstrated to have additional respective spin phase space event
\[\mathbf{H} = -\frac{1}{2}J \sum_{i,j} \mathbf{S}_i \cdot \mathbf{S}_j – g\mu B \sum_i \mathbf{H} \cdot \mathbf{S}_i .\tag{27}\]
These interior spin and Cartan-Weyl group particle-wave events can be therefore applied to torsional photonic streams for the given nonlinear system.
Given a binary unit interval [0,1], the Gassmann Triples as component variances are demonstrated where d(x,z) \(\boldsymbol{\mathrm{\le}}\) max \(\boldsymbol{\mathrm{\{}}\)d(x,y),d(y,z)\(\boldsymbol{\mathrm{\}}}\). Łukasiewicz triplets are defined using an undefined and irrational variable in the formula or atom of category monadic value, on the quantum first order logic. Therefore given quantumizable entropy in the nonlinear system the topological quantum field Clifford Lie Algebra \[\textbf{Cli, } j \text{ and } \boldsymbol{\Phi} \text{ L} (r, t) \text{ and } \boldsymbol{\Phi} \text{ R}(r, t) = \boldsymbol{\mathrm{\sim}}\Phi\text{L}(r, t) \text{ then } \boldsymbol{\rho}\text{c}(r, t) = \boldsymbol{\Phi}\text{L}(r, t)\boldsymbol{\mathrm{\sim}}\Phi\text{L}(r, t), \tag{28}\]
in n-valued Multivalent Logic, the Time variable is introduced T where \(T_{1}, T_{2}, \ldots, T_{p}\) , for all L and R wave function distributions in the Multivalent triplet logic [T,F,U], that \(0 \leq T + U + F \leq 3. \)
These multivalent sets can also be represented as Cantor sets where
\[\mathbf{\sum_{i=1}^{\infty}} \frac{\epsilon_i}{3^i} \text{for 0 or 2 on the real interval} [0,1] ,\tag{29}\]
and can be further expanded to 3D or 4D continuum and quantum geometric entropies-in-system.
Hensellian data sets as mutually-unbiased naive operator formula ZhatXhat = \(\boldsymbol{\omega}\) Xhat Zhat are hypothesized in toposdynamics from topos-sheaves, site-categories, and quantum phase-spaces, such as n\({}^{3}\) = n \(\boldsymbol{\mathrm{\times}}\) n\({}^{2}\). When the potential for probability in computational aggregation is present in the computational algorithm, these states are inherent in pyramidal neurons at the nm-scale microtubulin and neurotubulin computation ranges as demonstrated by Hameroff and Penrose [24]. Therefore, inversely, it can be stated for a computation space outside the ultrametric, (\(\boldsymbol{\mathrm{-}}\)n)\({}^{3}\) = \(\boldsymbol{\mathrm{-}}\)(n\({}^{3}\)) and on the extended topos-sheaf. These seeming paradoxes can be invoked when referring to problems of quantum-entangled quantum phase regimes to properly measure and predict eigenstates of quantum tunneling, and subsequent solutions in Dynamic Global Workspace Theory-Intelligent Computational System Organization (DGWT-ICSO).
These apparent paradoxes can be addressed in the mathematical formalism when utilizing atomic grammar and quantum probability phase projection-space. Here, the computational algebra is presented as related in computational ancestry to Hilber’t syzygy problem, and exactness of sequences for phase projection and probability spaces of monoidal functions of Qp sheaves. The sheaves are posited as inherent in H-spaces and CW complexes for quantum computational challenges of infinitesimal generators where generally f : R\({}^{n}\) \(\mathrm{\to}\) R.
Similarly, various interacting particle systems can be demonstrated for Hensellian lemmas or p-Adic number fields [25] from
\[\mathbf{f'(x)} = \frac{f(x_{\Delta}) – f(x)}{\Delta x}, \tag{30}\]
on some Spernerian Hypergraph. These algorithmic functions can be represented by Hilbert’s theorem where in a p-Adically-closed field
\[\textbf{f}_1, \dots, \textbf{f}_m, \textbf{g} \in \textbf{K}[X_1, \dots, X_n] \quad \text{then} \quad \textbf{g}N = \lambda_1 \textbf{f}_1 + \dots + \lambda_m \textbf{f}_m \quad \text{with} \quad R, \textbf{K}[X_1, \dots, X_n], \tag{31}\] with \[\mathbf{\Lambda}i \in \mathbb{R}[K[X_1, \dots, X_n]] \text{ and } R = \frac{\Phi}{1+p \Psi} \text{ and } R \text{ such that } \Phi, \Psi \in \mathcal{O}K[\Gamma(K(X_1, \dots, X_n))]. [\textit{ibid}]. \tag{32}\]
Dragovich has demonstrated q-Adic, p-Adic, or n-Adic discrete maths variants on the path integrals at approximately Planckscale which can be applied to quantum topological phenomena. [26] A 5-adic Cantor set and fractional algorithm have been demonstrated. [27] It is hypothesized from testing of high energy hadronic showers [28], and Huygens and Ampere waves on Gaussian and Fourier analysis. From Hameroff-Penrose, and Pribram-Bohm, Holonomic Brain Theory [HBT] can extend the quantum neurology from ordinal Computational Neural System [CNS] phase spaces in the p-adic and ultrametric, whence a Homogeneous coordinate ring where
\[\textbf{R} = \textit{K}[\textit{X}_0, \textit{X}_1, \textit{X}_2, \ldots, \textit{X}_N]/\textit{I} .\tag{33}\]
These physical wavefunctions are utilized through Neurophysical sensory operations to to generate allomatic and automatic [Gestalt-Inverse-Gestalt] modules of computational problem-solving. The neurophysical modules are existent from whence ideation, praexology and mechanistics present in Cognitive cycling [0-390 ms] [29] advance, essentially as real-time, nm+ scale, orders of magnitudes in Modular sheaf operations in computational information physical dynamics from nm-to-cm scale. Decoding Computational Neural System [CNS] phase spaces as neurophysical processes explains a function or functions of thermodynamic state horizon events, in which the [perceived] future is experientiated via time inversion and local entropy as present Object-interactive-time from quantum locality elements, such as Schrodinger’s two-state vector formalism, and quantum entanglement regimes via Bell’s Theorems [30,31].
Additionally, Gestalt critera of Emergence; Reification; Multiobject Stasis; Invariance; Multiobject Group Dynamics; and Fuzzy Trace Theory advance for a Two-state theoretical system. This system utilizes the computational ability of symbol-value calculation and representation comprehension. Here isomorphism is utilized as a Mathematical Structural function topos of quantum probability phenomena, meaning syntactical proper and accurate computation and operation of given symbol values in global or concurrent sets operate. These can be studied in number theory in Lyapunov fractional mechanics and dynamics. [32] These challenges also appear in Quantum phase estimation algorithms and quantum chemical criticality of the phase transition, in quantum Fourier and is demonstrated in repeated squaring [33].
Dynamic Global Workspace Theory-Intelligent Computational System Organization [DGWT-ICSO] as a quantum cognitive programming statement can be applied to Quantum Zeno, as an answer to a given algorithmic statement. Engineered computational complexity utilizes neuromorphic [34,35], and quantum multiplexing [36]. These technologies can be engineered from Computational Neural System [CNS] scalar and quantum values of given quantum entanglement and decoherence regimes [37].