Dominator and total dominator colorings in vague graphs

1. Introduction

Fuzzy set generalize classical sets by use of a membership function such that each element is assigned a number in the real unit interval [0,1], which measures its grade of membership in the set. The theory of fuzzy sets was proposed by Zadeh in 1965 [1]. Since then, the theory was used in a wide range of domains in which information is incomplete or imprecise, such as such as management science, medical science, social science, financial science, environment science and bioinformatics [2]. In 1993, Gau et al. [3] presented the concept of vague set theory as a generalization of fuzzy set theory, which allow a separation of evidence for membership (grade of membership) and evidence against membership (negation of membership). They used a subinterval of [0,1] to replace the value of an element in a set. That is, a vague set is characterized by two functions. Namely, a truth-membership function \(t_{v}(x)\) and false-membership function \(f_{v}(x)\) are used to describe the boundaries of the membership degree.

Graph theory is a very useful and well developed branch of discrete mathematics, and it also is an important tool for modeling many types of relations and processes in biological, physical, social and information systems. Realizing the importance of graph theory and inspiring of Zadeh’s fuzzy relations [4], Kauffman [5] proposed the definition of fuzzy graph in 1973. Then Rosenfeld [6] proposed another elaborated definition of fuzzy graph in 1975. Since then, there was a vast research on fuzzy graph [7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 19]. Inspired by fuzzy graph, in 2009, Ramakrishna [20] introduced the concept of vague graphs and studied some important properties. After that, Samata et al. [21] analysed the concepts of vague graphs and its strength. Rashmanlou et al. [22] introduced the notion of vague h-morphism on vague graphs and regular vague graphs, and they investigated some properties of an edge regular vague graph [23]. At the same time, they introduced some connectivity concepts in the vague graphs [24].

The Dominator coloring of a graph was proposed by Gera et al [25] in 2006. In the same paper, they showed that dominator chromatic number is NP-complete. After that, they studied the bounds and realization of the dominator chromatic number in terms of chromatic number and domination number [26] and the dominator colorings in bipartite graphs [27]. Recently, several researchers have theoretically investigated the dominator coloring number of Claw-free graph [28], Certain Cartesian Products [29], trees [30] and more [31, 32]. Motivated by dominator chromatic number, Kazemi [33] studied the new concept of a total dominator chromatic number of a graph. And they showed that total dominator chromatic number is NP-complete. A survey of total dominator chromatic number in graphs can also be found in [34, 35].

Borzooei et al. [36] in their work introduced the concepts of special kinds of dominating sets in vague graph. Kumar et al. [37] discuss the new concepts of coloring in vague graphs with application. In this paper, we introduce the concept of the dominator coloring and total dominator coloring of a vague graph and establish mathematical modelling for these problems.

2. Preliminaries

A vague set \(A\) in an ordinary finite non-empty set \(X\) is a pair \((t_{A}, f_{A})\), where \(t_{A} : X \rightarrowtail [0, 1]\), \(f_{A} : X \rightarrowtail [0, 1]\), and \(0 \leq t_{A}(x) + f_{A}(x) \leq 1\) for each element \(x \in X\). Note that the truth-membership \(t_{A}(x)\) is considered as the lower bound on grade of membership of \(x\) derived from the evidence for \(x \in X\) and the false-membership \(f_{A}(x)\) is the lower bound on negation of membership of \(x\) derived from the evidence against \(x \in X\). The grade of membership for \(x\) is characterized by the interval \([t_{A}(x), 1 – f_{A}(x)]\) not a crisp value. And if \(t_{A}(x) = 1 – f_{A}(x)\) for all \(x \in X\), the vague set degrades to a fuzzy set. In this paper, we denote by \(P_{n}, \ C_{n}, \ K_{n}\) the path, cycle and complete graph on \(n\) vertices, respectively. The complete bipartite graph with part size \(m,\ n\) is denoted by \(K_{m,n}\) and the ladder graph is the Cartesion product of \(P_{2}\) and \(C_{n}\), denoted by \(P_{2} \Box C_{n}\).

Definition 1. Let \(G = (V,E)\) be a graph. A pair \(G’ = (A,B)\) is called a vague graph on \(G\) where \(A = (t_{A}, f_{A})\) is a vague set on \(V\) and \(B = (t_{B}, f_{B})\) is a vague set on \(E\) such that \(t_{B}(uv) \leq min\{ t_{A}(u), t_{A}(v) \}\), \(f_{B}(uv) \geq max \{f_{A}(u), f_{A}(v) \}\) for each \(uv \in E\).

Definition 2. For a vague graph \(G = (A, B)\), an edge \(uv\) is called a strong edge if \(t_{B}(uv) = min \{ t_{A}(u), t_{A}(v) \}\), \(f_{B}(uv) = max \{ f_{A}(u), f_{A}(v) \}\). Let \(N(u) = \{v|uv \ is \ a \ strong \ edge \ in \ G \}\) and \(N[u] = N(u) \cup \{u\}\). We say \(u\) dominates all vertices in \(N(u)\) and totally dominates all vertices in \(N[u]\).

Definition 3. Dominator coloring of a vague graph \(G\) is a coloring of the vertices of \(G\) such that every vertex dominates all vertices of at least one other class. The dominator chromatic number \(\chi^d(G)\) of \(G\) is the minimum number of colors among all dominator colorings of \(G\).

Definition 4. Total dominator coloring of a vague graph \(G\) is a coloring of the vertices of \(G\) such that every vertex totally dominates all vertices of at least one other class. The total dominator chromatic number \(\chi^d_{t}(G)\) of \(G\) is the minimum number of colors among all total dominator colorings of \(G\).

3. Dominator coloring problems

Let \([k] = \{1, 2, \dots , k \}\). Let \(V_{c} \subseteq V\) denotes set of vertices with assigned color \(c\). Further, let decision variables \(x_{i,c}\) be defined as \[ x_{i,c} = \begin{cases} 1, & i \in V_{c} \\ 0, & i \in V_{c} \end{cases} \] For a vague graph \(G\) and an integer \(k\), let \(E^s\) be the set of all strong edges of \(G\). We propose integer linear programming \((ILP)\) formulations (called Dominator Coloring ILP and Total Dominator Coloring ILP, respectively), for the dominator coloring problem and total dominator coloring problem as follows:

Dominator coloring ILP

Theorem 5. Conditions \((1)-(7)\) defined for the graph \(G\) are satisfied if and only if \(G\) admits a dominator coloring with \(k\) colors.

Proof. \(\Rightarrow\) Condition \((1)\) ensures that each vertex is assigned with exactly one color. Condition \((2)\) ensures that each color should be used. Conditions \((3)\) and \((4)\) ensure that every vertex dominates all vertices of at least one other class. Condition \((5)\) ensures that the assignment is a proper coloring. Conditions \((6)\) and \((7)\) ensure that each variable is boolean. Therefore, if each condition is satisfied, then \(G\) admits a dominator coloring with \(k\) colors. \(\Leftarrow\) By the definition of the dominator coloring, it is clear that Conditions \((1)-(7)\) defined for the graph \(G\) are satisfied.

Total dominator coloring ILP

Theorem 6. Conditions \((8)-(14)\) defined for the graph \(G\) are satisfied if and only if \(G\) admits a total dominator coloring with \(k\) colors.

Proof. Condition \((8)\) ensures that each vertex is assigned with exactly one color. Condition \((9)\) ensures that each color should be used. Conditions \((10)\) and \((11)\) ensure that every vertex totally dominates all vertices of at least one other class. Condition \((12)\) ensures that the assignment is a proper coloring. Conditions \((13)\) and \((14)\) ensure that each variable is boolean. Therefore, if each condition is satisfied, then \(G\) admits a total dominator coloring with \(k\) colors. \(\Leftarrow\) By the definition of the total dominator coloring, it is clear that Conditions \((1)-(7)\) defined for the graph \(G\) are satisfied.

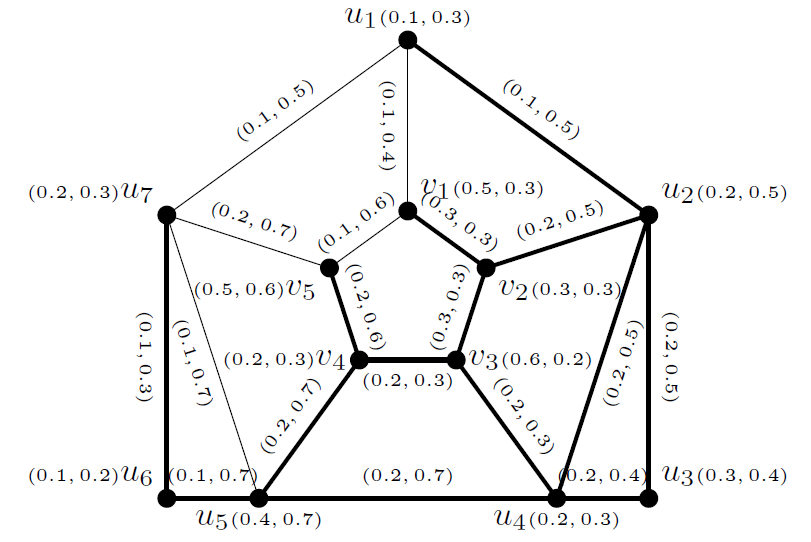
Example 1. Let \(G\) be a vague graph depicted in Figure 1. Then the set of strong edges is \(\{(u_{1}u_{2}), (u_{2}v_{2}), (u_{2}u_{4}),(u_{2}u_{3}), (u_{3}u_{4}), (u_{4}v_{3}), (u_{4}u_{5}), (u_{5}v_{4}), (u_{5}u_{6}), (u_{6}u_{7}),(v_{1}v_{2}), (v_{2}v_{3}), (v_{3}v_{4}), (v_{4}v_{5})\}\).

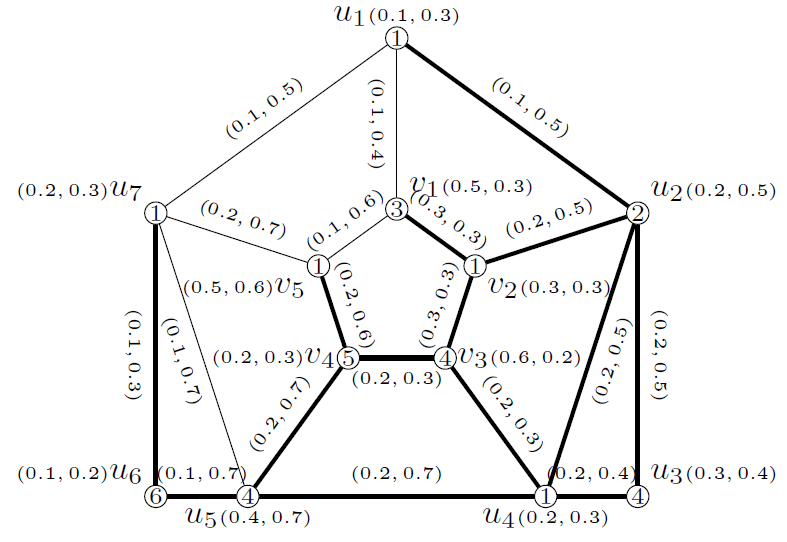
Example 2. Let \(G\) be a vague graph depicted in Figure 2. Then by solving the instance from Dominator Coloring ILP, we obtain \(\gamma^d(G) = 6\). A dominator coloring \(f\) with \(6\) colors is \(f(u_{1}) = 1, \ f(u_{2}) = 2, \ f(u_{3}) = 4, \ f(u_{4}) = 1, f(u_{5}) = 4, f(u_{6}) = 6, \ f(u_{7}) = 1, f(v_{1}) = 3, \ f(v_{2}) = 1, \ f(v_{3}) = 4, \ f(v_{4}) = 5, \ f(v_{5}) = 1\) which is presented in Figure 2.

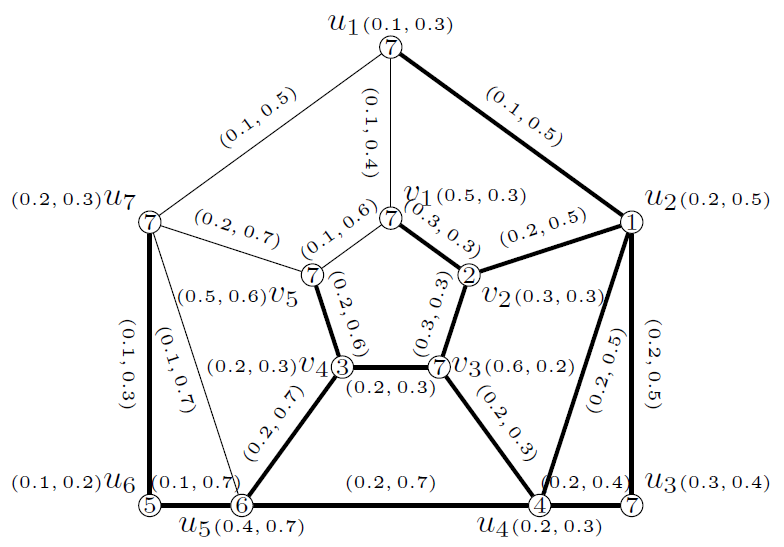
Example 3. Let \(G\) be a vague graph depicted in Figure 3. Then by solving the instance from Total Dominator Coloring ILP, we obtain \(\gamma^d_{t}(G) = 7\). A dominator coloring \(f\) with \(7\) colors is \(f(u_{1}) =7, \ f(u_{2}) = 1, f(u_{3}) = 7, f(u_{4}) = 4, \ f(u_{5}) = 6, f(u_{6}) = 5, f(u_{7}) = 7, \ f(v_{1}) = 7, \ f(v_{2}) = 2, f(v_{3}) = 7, \ f(v_{4}) = 3, f(v_{5}) = 7\) which is presented in Figure 3.

4. Dominator coloring number of some classes of vague graphs

Definition 7. For a vague graph \(G\), we define an underlying graph of \(G\), denoted by \(\widetilde{G}\), with \(V(\widetilde{G}) = V (G)\), and \(xy \in E(\widetilde{G})\) if and only if \(x \in N(y)\) in \(G\).

By the definition of Dominator coloring, we have

Proposition 8. For any vague graph \(G\), \(\chi^d(G) = \chi^d(\widetilde{G})\) and \(\chi^t_{d}(G) = \chi^t_{d}(\widetilde{G})\).

Proposition 9.(see [28]) For any vague graph \(G\) with \(\widetilde{G} \cong K_{n},\) we have \(\chi_{d}(G) = \chi^t_{d}(G) = n\).

Proof. By the definition, we have \(\chi^t_{d}(G) \geq \chi_{d}(G) \geq \chi(G) = n\). Let \(V(G) = \{v_{1}, v_{2}, \ldots, v_{n}\}\). We consider a function \(f : V(G) \rightarrowtail \{1, 2, \ldots , n\} \) with \(f(v_{i}) = i\) for any \(i\), then we have \(f\) is a total dominator coloring of \(G\) with \(n\) colors. Therefore, we have \(\chi^t_{d}(G) \leq n\) and so the desired result holds.

Proof. The following results are straightforward:

Proposition 10(see [28]) For any vague graph \(G\) with \(\widetilde{G} \cong K_{m,n}\), we have \(\chi^d(G) = \chi^t_{d}(G) = 2\).

Proposition 11.(see [28]) For any vague graph \(G\) with \(\widetilde{G} \cong C_{n} (n \geq 3)\), we have \(\chi^d(G) = 3\) for \(n \equiv 3\) (mod 6) and \(\chi_{d}(G) = 2\) otherwise.

Proposition 12.(see [35]) For any vague graph \(G\) with \(\widetilde{G} \cong P_{n} \ or \ C_{n} (n \geq 3)\), we have \(\chi^t_{d}(G) = \bigg[ \frac{n}{2}\bigg] + \bigg[ \frac{n}{4}\bigg] – \bigg[ \frac{n}{4}\bigg]\).

The Cartesian product \(G \Box H\) of two graphs \(G\) and \(H\) is a graph with \(V(G) \times V (H)\) and two vertices \((g_{1}, h_{1})\) and \((g_{2}, h_{2})\) are adjacent if and only if either \(g_{1} = g_{2}\) and \((h_{1}, h_{2}) \in E(H)\), or \(h_{1} = h_{2}\) and \((g_{1}, g_{2}) \in E(G)\). Let \(V(C_{n}) = \{1, 2, 3, \dots n\}\), \(E(C_{n}) = \{i(i + 1)\}, \ 1n|i = 1, 2, \ldots n – 1\}\) and \(V (P_{2}) = \{1, 2\}, \ E(P_{2}) = \{(12)\}\). Let \(u_{i,j}\) be a vertex of \(P_{2} \Box C_{n}\) where \(i = 1, 2, \ j = 1, 2, \ldots n\). We have the following result:

Proposition 12. For any vague graph \(G\) with \(\widetilde{G} \cong P_{2} \Box C_{n}\) with \(n \geq 6\), \[ \gamma^d_{t}(G) \leq \begin{cases} \frac{2n}{3} + 2, & n \equiv 0 \ \ \ \ (mod \ 6) \\ \frac{2n}{3} + 4, & n \equiv 1,2 \ (mod \ 6) \\ \frac{2n}{3} + 3, & n \equiv 3 \ \ \ \ (mod \ 6) \\ \frac{2n}{3} + 2, & n \equiv 4,5 \ (mod \ 6) \\ \end{cases} \]

Proof. We use two lines of numbers to denote a total dominator coloring of \(P_{2} \Box C_{n}\). The total dominator coloring can be represented as a \(2 \times n\) array as follows: \[ f(P_{2} \Box C_{n}) = \begin{cases} f(u_{1,1}) \ f(u_{1,2}) \ldots f(u_{1,n-1}) \ f(u_{1,n})
f(u_{2,1}) \ f(u_{2,2}) \ldots f(u_{2,n-1}) \ f(u_{2,n})
\end{cases} \] If \(i = 1\) and \(j \equiv 1, 3\) (mod 6), let \(f(u_{i,j}) = 1\).
If \(i = 1\) and \(j \equiv 2, 4\) (mod 6), let \(f(u_{i,j}) = 2\).
If \(i = 1\) and \(j \equiv 5\) (mod 6), let \(f(u_{i,j}) = 4 \frac{j}{6} + 5\).
If \(i = 1\) and \(j \equiv 0\) (mod 6), let \(f(u_{i,j}) = 4\frac{j}{6} + 6\).
If \(i = 2\) and \(j \equiv 4, 5\) (mod 6), let \(f(u_{i,j}) = 1\).
If \(i = 2\) and \(j \equiv 0, 5\) (mod 6), let \(f(u_{i,j}) = 2\).
If \(i = 2\) and \(j \equiv 2\) (mod 6), let \(f(u_{i,j}) = 4\frac{j}{6} + 3\).
If \(i = 2\) and \(j \equiv 3\) (mod 6), let \(f(u_{i,j}) = 4\frac{j}{6} + 4\).
We will consider the following cases:
Case 1. \(n \equiv 0\) (mod 6).
Obviously, \(f\) is total dominator coloring with desired number of colors. For example, let \(n = 12\), we have \[ f(P_{2} \Box C_{12}) = \begin{cases} 1 \ 2 \ 1 \ 2 \ 5 \ 6 \ 1 \ 2 \ 1 \ 2 \ 9 \ 10 \\ 2 \ 3 \ 4 \ 1 \ 2 \ 1 \ 2 \ 7 \ 8 \ 1 \ 2 \ 1 \end{cases} \] Case 2. \(n \equiv 1, 2, 4, 5\) (mod 6).
Let \(h(x) = f(x)\) for any \(x \in V (P_{2} \Box C_{n}) \backslash \{u_{1,n}, u_{2,n}\}\), \(h(u_{1,n}) = 2 \times \frac{n}{3}, \ h(u_{2,n}) = 2 \times \frac{n}{3} + 4\). Obviously, \(h\) is total dominator coloring with desired number of colors. For example, let \(n = 13\), we have \[ f(P_{2} \Box C_{13}) = \begin{cases} 1 \ 2 \ 1 \ 2 \ 5 \ 6 \ 1 \ 2 \ 1 \ 2 \ 9 \ 10 \ 11 \\ 2 \ 3 \ 4 \ 1 \ 2 \ 1 \ 2 \ 7 \ 8 \ 1 \ 2 \ 1 \ 12 \end{cases} \] Let \(n = 14\), we have \[ f(P_{2} \Box C_{14}) = \begin{cases} 1 \ 2 \ 1 \ 2 \ 5 \ 6 \ 1 \ 2 \ 1 \ 2 \ 9 \ 10 \ 1 \ 11 \\ 2 \ 3 \ 4 \ 1 \ 2 \ 1 \ 2 \ 7 \ 8 \ 1 \ 2 \ 1 \ 2 \ 12 \end{cases} \] Let \(n = 16\), we have \[ f(P_{2} \Box C_{16}) = \begin{cases} 1 \ 2 \ 1 \ 2 \ 5 \ 6 \ 1 \ 2 \ 1 \ 2 \ 9 \ 1 0 \ 1 \ 2 \ 1 \ 13 \\ 2 \ 3 \ 4 \ 1 \ 2 \ 1 \ 2 \ 7 \ 8 \ 1 \ 2 \ 1 \ 2 \ 11 \ 12 \ 14 \end{cases} \] Let \(n = 17\), we have \[ f(P_{2} \Box C_{17}) = \begin{cases} 1 \ 2 \ 1 \ 2 \ 5 \ 6 \ 1 \ 2 \ 1 \ \ 2 \ 9 \ 10 \ 1 \ 2 \ 1 \ 2 \ 13 \\ 2 \ 3 \ 4 \ 1 \ 2 \ 1 \ 2 \ 7 \ 8 \ 1 \ 2 \ 1 \ 2 \ 11 \ 12 \ 1 \ 14 \end{cases} \] Case 3. \(n \equiv 3\) (mod 6).
Let \(h(x) = f(x)\) for any \(x \in V (P_{2} \Box C_{n}) \backslash \{u_{1,n}\}, \ h(u_{1,n}) = \frac{2n}{3}+ 3\). Obviously, \(h\) is total dominator coloring with desired number of colors. As an example, let \(n = 15\), we have \[ f(P_{2} \Box C_{15}) = \begin{cases} 1 \ 2 \ 1 \ 2 \ 5 \ 6 \ 1 \ 2 \ 1 \ 2 \ 9 \ 10 \ 1 \ 2 \ 13 \\ 2 \ 3 \ 4 \ 1 \ 2 \ 1 \ 2 \ 7 \ 8 \ 1 \ 2 \ 1 \ 2 \ 11 \ 12 \end{cases} \] Now the proof is complete.

5. Conclusion

Fuzzy graph theory has substantial applications for real-world life in different domains, such as in the fields of biological science, neural networks, decision making, physics and chemistry. At present, the graph coloring problem can be applied in sequencing, timetabling, scheduling, electronic bandwidth allocation, computer register allocation and printed circuit board testing. Also the domination is also one of the fundamental concepts in graph theory and it has been wide used to distributed computing, biological networks, resource allocation and social networks. In this paper, motivated with the combination of fuzzy graph theory, graph coloring and graph domination, we introduce the concept of the dominator coloring and total dominator coloring of a vague graph and establish mathematical modelling for these problems.

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest:

The authors declare no conflict of interest.