The Wiener index is a topological index of a molecule, defined as the sum of distances between all pairs of vertices in the chemical graph. Hexagonal chains consist of hexagonal rings connected with each other by edges. This class of chains contains molecular graphs of unbranched catacondensed benzenoid hydrocarbons. A segment of length \(\ell\) of a chain is its maximal subchain with \(\ell\) linear annelated hexagons. We consider chains in which all segments have equal lengths. Such chains can be uniquely represented by binary vectors. The Wiener index of hexagonal chains under some operations on the corresponding binary vectors are investigated. The obtained results may be useful in studying of topological indices for sets of hexagonal chains induced by algebraic constructions.
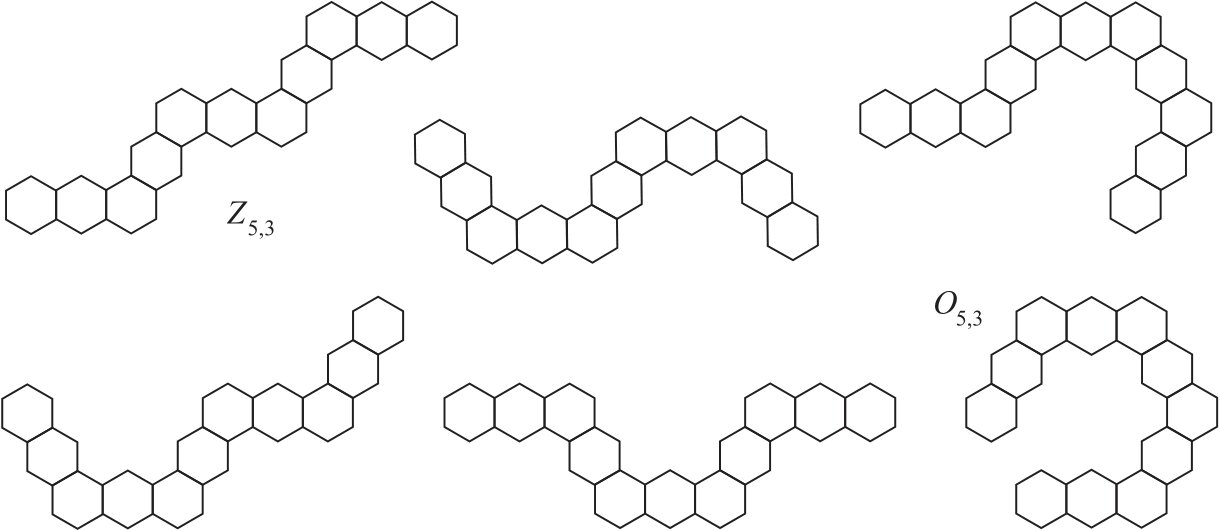
The structure of hexagonal chains is completely defined by a way of segment attachment. We consider a nonterminal segment \(S\) with two neighboring segments embedded into the regular hexagonal lattice on the plane and draw a line through the centers of the hexagons of \(S\). If the neighboring segments of \(S\) lie on different sides of the line, then \(S\) is called a zigzag segment. If these segments lie on the same side, then \(S\) is said to be a spiral segment. It is convenient to assume that the terminal segments are zigzag segments. For a hexagonal chain \(X\), denote by \(U(X)\) the set of its spiral segments, \(u_X=|U(X)|\).
Based on two types of segments, hexagonal chains of \({\cal G}_{n,\ell}\) can be represented by binary codes. We assume that all segments of a chain are sequentially numbered by \(0, 1,\dots, n-1\) beginning from a terminal segment. Since the terminal segments can be ignored when a chain is restored, codes of all hexagonal chains of \({\cal G}_{n,\ell}\) have a length of \(n-2\), \(n\ge 3\). Assume that every spiral segment of chain \(X\) corresponds to 1 in the code of \(X\) while every zigzag segment corresponds to 0. A binary code of hexagonal chain \(X\) and a hexagonal chain \(X\) induced by a binary word \(r\) will be denoted by \(r(X)\) and \(X(r)\), respectively. Note that molecular graphs of more general classes of benzenoid hydrocarbons can be also represented by binary codes [31, 38].
There are two extremal chains with respect to the type of segments. The zigzag hexagonal chain \(Z_{n,\ell} \in {\cal G}_{n,\ell}\) contains only zigzag segments, \(r(Z_{n,\ell})=(00..0)\). All segments of the spiral hexagonal chain \(O_{n,\ell} \in {\cal G}_{n,\ell}\) are spiral ones (with the exception of the terminal segments), \(r(O_{n,\ell})=(11..1)\). The zigzag and the spiral hexagonal chains of \({\cal G}_{5,3}\) are shown in Figure 1. Denote by \(e_i\) the binary vector \(e_i=(0…0\!\stackrel{i}{1}\!0…0)\) of length \(n-2\) for \(n \ge 3\), \(i=1,2,\dots,n-2\). These vectors form the standard basis for the vector space of dimension \(n-2\) over \(\mathbf{Z}_2\). Let \(C_i\) be the basis hexagonal chains corresponding to basis vectors \(e_i\), \(i=1,2,\dots,n-2\). Then code \(r(X)\) of \(X \in {\cal G}_{n,\ell}\) can be expressed as a linear combination of the basis vectors: \(r(X)= x_1 \, e_1 + x_2 \, e_2 + \dots + x_{n-2} \, e_{n-2}\). Since codes \(e_i\) and \(e_{n-i-1}\) are symmetrical, basis chains \(C_i\) and \(C_{n-i-1}\) are isomorphic and \(W(C_i) = W(C_{n-i-1})\).
Hexagonal chains \(O_{n,\ell}\) and \(Z_{n,\ell}\) are extremal graphs with respect to the Wiener index among all chains of \({\cal G}_{n,\ell}\) [13]: \(W(O_{n,\ell}) < W(G) < W(Z_{n,\ell})\) for all \(G \in {\cal G}_{n,\ell} \setminus \{O_{n,\ell}, Z_{n,\ell}\}\), where \begin{eqnarray*} W_{\min} & = & \big( 8 n^3 (\ell-1)^2 (2 \ell-3)+96 n^2 (\ell-1)^2-2 n (\ell-1)(2 \ell -75) + 81 \big) /3, \\ W_{\max} & = & \big( 16 n^3 (\ell-1)^3 + 72 n^2 (\ell-1)^2 + n(\ell-1)(12 \ell+134)+81 \big)/3. \end{eqnarray*}
The average of these extremal values is equal to \begin{eqnarray*} W_{\mathrm{avr}} & = & \left( W_{\min}+W_{\max} \right)/2 \\ & = & \left( 4 n^3 (\ell-1)^2 (4\ell-5) + 84 n^2 (\ell-1)^2 + 2 n(\ell-1) (2 \ell+71)+81 \right)/3. \end{eqnarray*}Proposition 1. For a hexagonal chain \(X \! \in {\cal G}_{n,\ell}\) with a code \((x_1,x_2, \dots, x_{n-2})\), \begin{eqnarray*} W(X) & = & W_{\max} – 16(\ell-1)^2 \sum_{i=1}^{n-2} i(n-i-1) x_i. \end{eqnarray*}
The sum of Wiener indices of a hexagonal chain and its complement is twice the average value \(W_{\mathrm{avr}}\).Proposition 2. If \(X \in {\cal G}_{n,\ell}\), then \(W(\overline{X})=W_{\min}+W_{\max} – W(X)\).
Proof. By Proposition 1, \begin{eqnarray*} W(X) + W(\overline{X}) & = & W_{\max} + W_{\max}-16(\ell-1)^2 \sum_{i=1}^{n-2} i(n-i-1)\cdot 1 \\ & = & W_{\max} + W_{\min}. \end{eqnarray*}
Proposition 2 allows to determine the structure of hexagonal chains with average value of the Wiener index. If \(r(X)=r(\overline{X})\), then chains \(X\) and \(\overline{X}\) are obviously isomorphic. This implies equality \(W(X)=W_{\mathrm{avr}}\). There are also non-isomorphic chains \(X\) and \(\overline{X}\) with property \(W(X)= W(\overline{X})= W_{\mathrm{avr}}\) [26]. Consider hexagonal chains without units in the same positions of their codes.Proposition 3. Let \(X, Y \in {\cal G}_{n,\ell}\) and \(XY=Z_{n,\ell}\). If \(G=X+Y\), then $$ W(G) = W(X) + W(Y) – W_{\max}. $$
Proof. Let \(x=r(X)\) and \(y=r(Y)\). By Proposition 1, we can write $$ W(X) + W(Y) – W_{\max} = W_{\max}-16(\ell-1)^2 \sum_{i} i(n-i-1) (x_i+y_i) = W(G). $$
As an illustration, consider chains \(X, Y \in {\cal G}_{7,3}\) and \(G=X+Y\) shown in Figure 2. These graphs have codes \(r(X)=(10010)\), \(r(Y)=(00101)\), and \(r(G)=(10111)\). By computer calculations, their Wiener indices are \(W(X)=19327\), \(W(Y)=19263\), \(W(G)=18431\), and \(W_{\max}=20159\). By Proposition 3, \(W(G)=19327 + 19263 – 20159=18431\).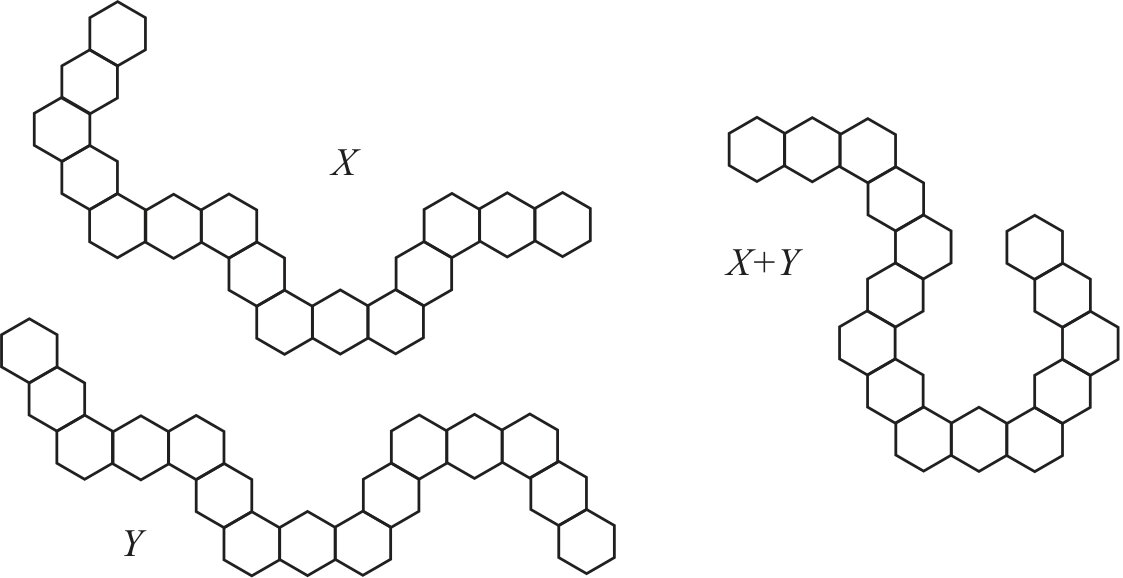
Proposition 4. Let \(X, Y \in {\cal G}_{n,\ell}\) and \(Y \le X\). If \(G=X-Y\), then $$ W(G) = W(X) – W(Y) + W_{\max}. $$
Proof. If \(x=r(X)\) and \(y=r(Y)\), then by Proposition 1 \begin{eqnarray*} W(Y) – W(X) – W_{\max} & = & \mbox{} -W_{\max} + 16(\ell-1)^2 \sum_{i} i(n-i-1) (x_i-y_i) \\ & = & \mbox{} -W(G). \end{eqnarray*} Since \(y_i \le x_i\), \((x_i-y_i) \ge 0\) for every \(i\).
Hexagonal chains \(X, Y \in {\cal G}_{7,3}\) and \(G=X-Y\) shown in Figure 3 illustrate Proposition 4. Codes of these graphs are \(r(X)=(11001)\), \(r(Y)=(01001)\), and \(r(G)=(10000)\). Computer calculations give the following Wiener indices: \(W(X)=19007\), \(W(Y)=19327\), and \(W(G)=19839\). By Proposition 4, \(W(G)=19007 – 19327 + 20159=19839\). The next result answers on the following question: how many times do we need to apply operation \(t_{i,j}\) to a hexagonal chain \(X\) such that \(W(X)=W(t_{i,j}(X))\)? For asymmetrical chains, it is sufficient to apply the operation once time.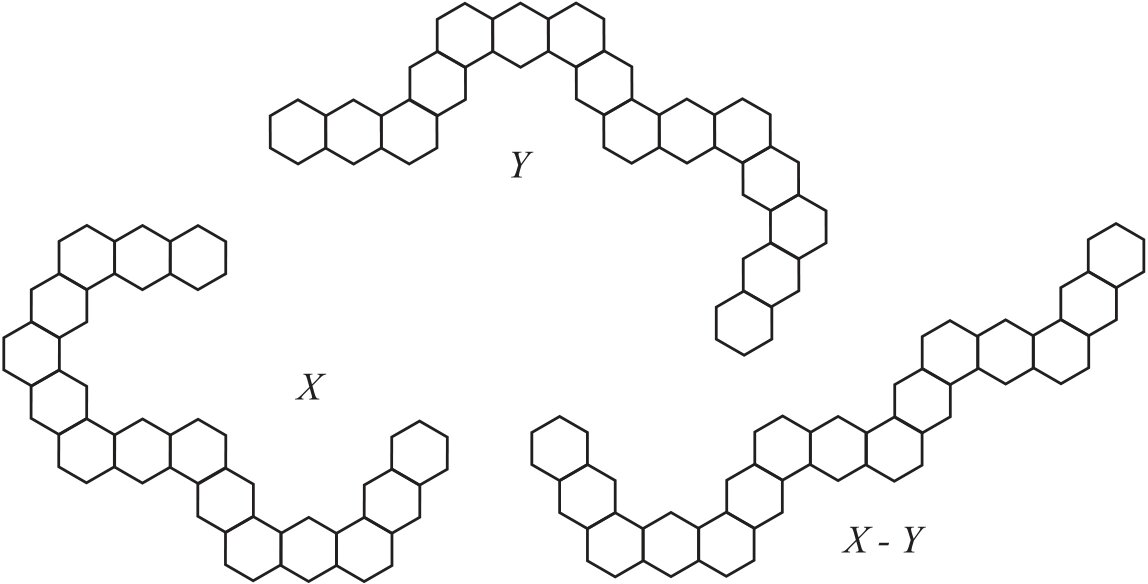
Corollary 2. Let \(X \in {\cal G}_{n,\ell}\) be an asymmetrical hexagonal chain with a code \((x_1, x_2,\dots,x_{n-2})\), i.e., \(x_i \not = x_{n-i-1}\) for some \(i \in \{1,2,\dots,\lceil(n-2)/2\rceil\}\). If \(Y=t_{i,n-i-1}(X)\), then \(W(Y)=W(X)\).
Proof. Assume that \(x_i=0\) and \(x_{n-i-1}=1\). Then \(Y=(X + C_i) – C_{n-i-1}\). By Propositions 4 and 3, we can write \(W(Y)= W(X + C_i) – W(C_{n-i-1}) + W_{\max} = W(X) + W(C_i) – W_{\max} – W(C_{n-i-1}) + W_{\max} = W(X)\).
Let \(\mu(X)\) be the number of pairs of non-equal \(i\)-th and \((n-i-1)\)-th components of chain’s code \(r(X)\), \(i=1,2,\dots,\lceil (n-2)/2 \rceil\). Repeating Corollary 1, one can construct a family of \(2^{\mu(X)}\) chains having the same Wiener index (some chains may be isomorphic).
Decomposition of the Wiener index of chains of \({\cal G}_{n,\ell}\) into the sum of Wiener indices of basis hexagonal chains was reported in [26]. It can be also derived using graph operations.Corollary 3. Let \(X \in {\cal G}_{n,\ell}\) and \(r(X)=(x_1,x_2,\dots,x_{n-2})\). Then $$ W(X) = x_1 W(C_1) + x_2 W(C_2) + \dots + x_{n-2} W(C_{n-2}) – (u-1)W_{\max}, $$ where \(u = x_1 + x_2 + \dots + x_{n-2}\) is the number of units of \(x\).
Proof. Let \(i_1, i_2,\dots,i_u\) be positions of units in \(x\). Then the corresponding hexagonal chain \(X\) can be represented as \(X=C_{i_1} + C_{i_2} + \dots + C_{i_u}\). Applying Proposition 3, we get \(W(X) = W(C_{i_1}) + W(C_{i_2}) + \dots+ W(C_{i_u}) – (u-1) W_{\max} = x_1 W(C_1) + x_2 W(C_2) + \dots + x_{n-2} W(C_{n-2}) – (u-1)W_{\max}\).
Let us consider operations of hexagonal chains with arbitrary codes.Proposition 5. Let \(X, Y \in {\cal G}_{n,\ell}\). If \(G=X+Y\), then $$ W(G) = W(X) + W(Y) – 2 W(XY) + W_{\max}. $$
Proof. It is easy to verify that the hexagonal chain \(G\) can be represented as \(G=X+Y=(X-XY) + (Y-XY)\), where \((X-XY)(Y-XY)=Z_{n,\ell}\) and \(X \ge XY\), \(Y \ge XY\). By Propositions 3 and 4, \begin{eqnarray*} W(G) & = & W(X-XY) + W(Y-XY) – W_{\max} \\ & = & W(X) – W(XY) + W_{\max} + W(Y) – W(XY) + W_{\max} – W_{\max} \\ & = & W(X) + W(Y) – 2 W(XY) + W_{\max}. \end{eqnarray*}
Hexagonal chains \(X, Y \in {\cal G}_{7,3}\) and \(G=X+Y\) shown in Figure 4 illustrate Proposition 5. These chains have codes \(r(X)=(11100)\), \(r(Y)=(00110)\), \(r(XY)=(00100)\), and \(r(G)=(11010)\). Their Wiener indices are \(W(X)=18751\), \(W(Y)=19071\), \(W(XY)=19583\), and \(W(G)=18815\). By applying Proposition 5, \(W(G)= 18751 + 19071 – 2\cdot 19583 + 20159=18815\).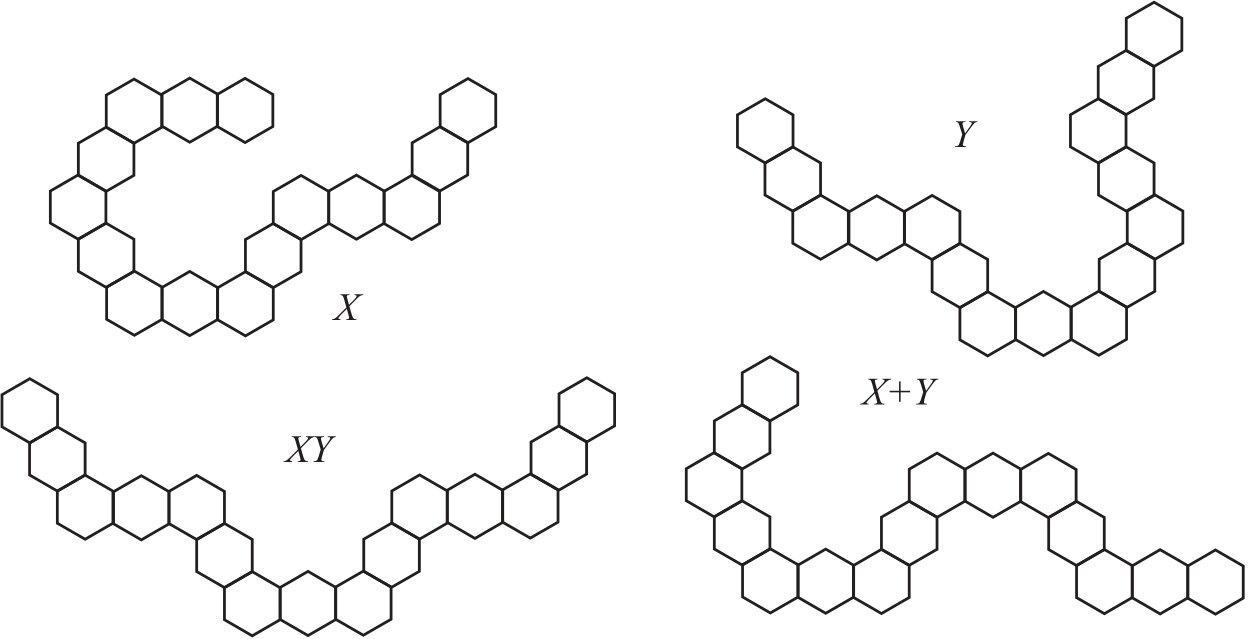
Proposition 6. Let \(X, Y \in {\cal G}_{n,\ell}\). If \(G=X-Y\), then $$ W(G) = W(X) – W(Y) + 2W(\overline{X}Y) – W_{\max}. $$
Proof. Hexagonal chain \(G\) can be decomposed as \(G=X-Y=(X+\overline{X}Y) – (Y-\overline{X}Y)\), where \((X+\overline{X}Y) \ge (Y-\overline{X}Y)\), \(X(\overline{X}Y)=Z_{n,\ell}\) and \(Y \ge \overline{X}Y\). By Propositions 3 and 4, \begin{eqnarray*} W(G) & = & W(X+\overline{X}Y) – W(Y-\overline{X}Y) + W_{\max} \\ & = & W(X) + W(\overline{X}Y) – W_{\max} – (W(Y) – W(\overline{X}Y) + W_{\max}) + W_{\max} \\ & = & W(X) – W(Y) + 2 W(\overline{X}Y) – W_{\max}. \end{eqnarray*}
Consider again hexagonal chains \(X\) and \(Y\) shown in Figure 4. Chains \(\overline{X}Y\) and \(X-Y\) have codes \(r(\overline{X}Y)=(00010)\), \(r(X-Y)=(00101)\), and Wiener indices \(W(\overline{X}Y)=19647\), \(W(X-Y)=18815\). By Proposition \ref{XYminusGen}, we obtain \(W(G)= 18751 – 19071 + 2 \cdot 19647 – 20159=18815\).Proposition 7. Let \(X, Y \in {\cal G}_{n,\ell}\). If \(G=X \vee Y\), then $$ W(G) = W(X) + W(Y) – W(XY). $$
Proof. Using Proposition 1, we get \begin{eqnarray*} W(X)\!+\!W(Y)\!-\!W(XY) & = & W_{\max}\!-\!16(\ell-1)^2 \sum_{i} i(n-i-1) (x_i+y_i-x_i y_i), \\ W(X \vee Y) &= & W_{\max}-16(\ell-1)^2 \sum_{i} i(n-i-1) (x_i \vee y_i). \end{eqnarray*} Comparison of these equalities completes the proof.
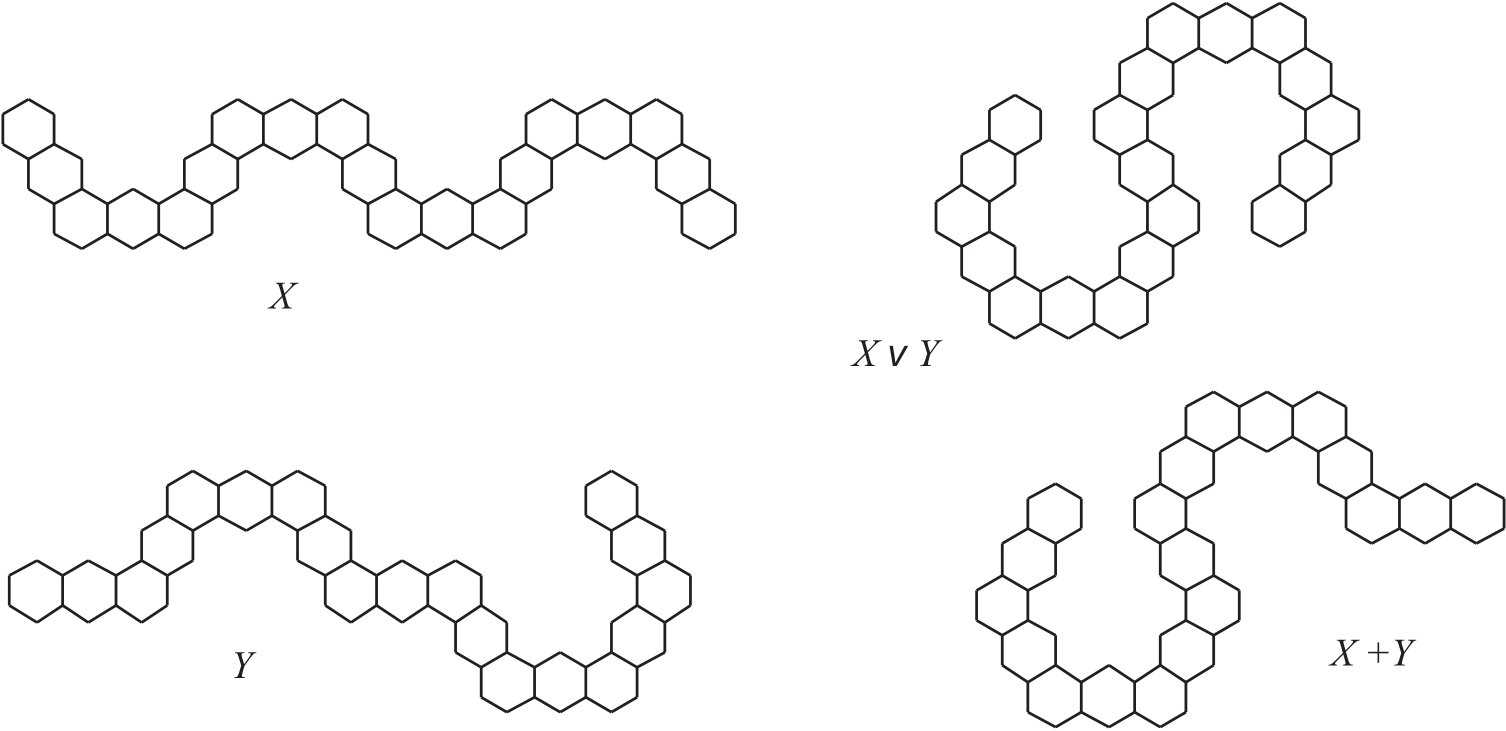
Hexagonal chains \(X, Y \in {\cal G}_{9,3}\) and \(G=X \vee Y\) of Figure 5 illustrate Proposition 7. The structure of graph \(X+Y\) is presented for comparison. These chains have codes \(r(X)=(1010101)\), \(r(Y)=(0100011)\), \(r(XY)=(0000001)\), and \(r(G)=(1110111)\), and their Wiener indices are equal to \(W(X)=37111\), \(W(Y)=37943\), \(W(XY)=39479\), and \(W(G)=35575\). By Proposition 7, \(W(G)=37111+37943-39479=35575\).
In conclusion, we note that the considered approach may be useful in studying of topological indices for sets of hexagonal chains induced by algebraic constructions.