The Sombor index (\(SO\)) and the modified Sombor index (\(^mSO\)) are two closely related vertex-degree-based graph invariants. Both were introduced in the 2020s, and have already found a variety of chemical, physicochemical, and network-theoretical applications. In this paper, we examine the product \(SO \cdot {^mSO}\) and determine its main properties. It is found that the structure-dependence of this product is fully different from that of either \(SO\) or \(^mSO\). Lower and upper bounds for \(SO \cdot {^mSO}\) are established and the extremal graphs are characterized. For connected graphs, the minimum value of the product \(SO \cdot {^mSO}\) is the square of the number of edges. In the case of trees, the maximum value pertains to a special type of eclipsed sun graph, trees with a single branching point.
I] n this paper, we are concerned with simple graphs. In order to avoid unnecessary complications, the graphs considered will be assumed to be connected. Let \(G\) be such a graph with vertex set \(\mathbf V(G)\) and edge set \(\mathbf E(G)\), with \(|\mathbf V(G)|=n\) vertices and \(|\mathbf E(G)|=m\) edges. By \(e=uv \in \mathbf E(G)\) we denote the edge of \(G\), connecting the vertices \(u\) and \(v\). The degree of the vertex \(u\) (= the number of first neighbors of \(u\)) will be denoted by \(d(u)\). For other graph-theoretical notions, the readers are referred to [1].
In contemporary discrete mathematics and mathematical chemistry, a class of graph invariants of the form \[TI = TI(G) = \sum_{uv \in \mathbf E(G)} F\big(d(u),d(v) \big)\] attracted much attention and is studied in detail [2-4]. Here \(F\) is a suitably chosen function with properties \(F(x,y)=F(y,x)\) and \(F(x,y)\geq 0\). These invariants are usually referred to as “vertex-degree-based topological indices”, or shorter: VDB indices. Nowadays, several dozens of VDB indices are being examined in the literature, and their number is increasing.
A few years ago, based on geometric considerations, a new vertex-degree-based graph invariant was introduced [5-7], named Sombor index, defined as \[SO = SO(G) = \sum_{uv \in \mathbf E(G)} \sqrt{d(u)^2+d(v)^2}\] where, of course, \(d(u)^2\) denotes the square of the degree of the vertex \(u\). In a short time, this index gained much popularity, and its applicability in chemistry and network science was soon recognized. The mathematical properties [6,8-18] and the various applications [19-25] of the Sombor index have been studied in detail.
A short time after the invention of the Sombor index, its modified version \[^mSO = {^mSO(G)} = \sum_{uv \in \mathbf E(G)} \frac{1}{\sqrt{d(u)^2+d(v)^2}}\] was put forward [26], and studied in a few consecutive papers [27-29].
The Sombor and modified Sombor indices have a number of analogous (opposite) properties. For instance, \[SO(G+e) > SO(G) \hspace{5mm} ; \hspace{5mm} {^mSO(G+e)} < {^mSO(G)}\] where \(G+e\) is the graph obtained by inserting a new edge to \(G\); \[SO(G) \leq SO(K_n) \hspace{5mm} ; \hspace{5mm} {^mSO(G)} \geq {^mSO(K_n)}\] where \(K_n\) is the complete graph and where the equalities hold if and only if \(G \cong K_n\); \[SO(P_n) < SO(T_n) < SO(S_n) \hspace{5mm} ; \hspace{5mm} {^mSO(P_n)} > {^mSO(T_n)} > {^mSO(S_n)}\] where \(P_n\) and \(S_n\) are the \(n\)-vertex path and star, respectively, and \(T_n\) is any \(n\)-vertex tree different from \(P_n\) and \(S_n\).
The close correlation between \(SO\) and \({^mSO}\) is seen in the example depicted in Figure 1.
Bearing in mind the close analogy between Sombor and modified Sombor indices, we got interested in their product, \[\pi SO = \pi SO(G) = SO(G) \cdot {^mSO(G)}\] i.e., \[\label{pi} \pi SO = \pi SO(G) = \left( \sum_{uv \in \mathbf E(G)} \sqrt{d(u)^2+d(v)^2} \right)\, \left( \sum_{uv \in \mathbf E(G)} \frac{1}{\sqrt{d(u)^2+d(v)^2}} \right) \tag{1}\] which we will refer to as the \(\pi\)-Sombor index.
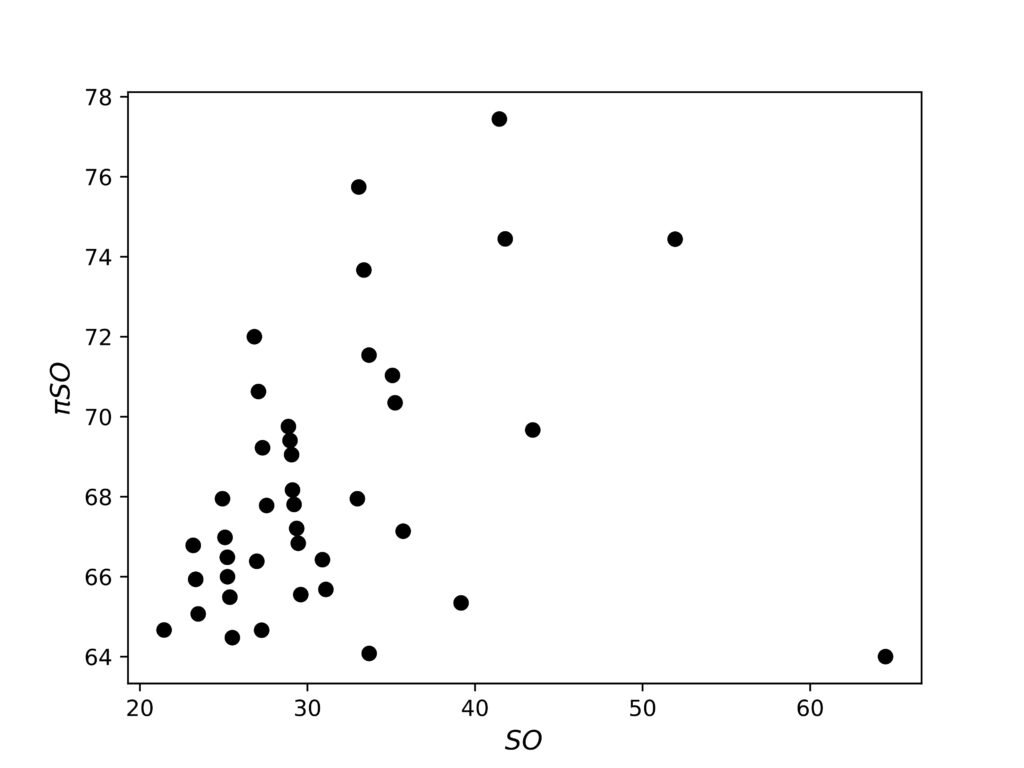
Interestingly, the \(\pi\)-Sombor and the Sombor indices are completely uncorrelated, as shown by the example depicted in Figure 2.
In what follows we establish a few basic properties of \(\pi SO\). First, however, we prove a pair of more general results.
As before, \(G\) is a connected simple graph possessing \(n\) vertices and \(m\) edges.
Theorem 1. Let \(f(u)\) be any quantity, defined for a vertex \(u \in \mathbf V(G)\), such that \(f(u)>0\) for all \(u \in \mathbf V(G)\). Then, \[\label{t1} \left( \sum_{u \in \mathbf V(G)} f(u) \right)\, \left( \sum_{u \in \mathbf V(G)} \frac{1}{f(u)} \right) \geq n^2\,. \tag{2}\] Equality holds if and only if \(f(u)\) are mutually equal for all \(u \in \mathbf V(G)\).
Theorem 2. Let \(g(e)\) be any quantity, defined for an edge \(e \in \mathbf E(G)\), such that \(g(e)>0\) for all \(e \in \mathbf E(G)\). Then, \[\label{t2} \left( \sum_{e \in \mathbf E(G)} g(e) \right)\, \left( \sum_{e \in \mathbf E(G)} \frac{1}{g(e)} \right) \geq m^2\,. \tag{3}\] Equality holds if and only if \(g(e)\) are mutually equal for all \(e \in \mathbf E(G)\).
Proof. According to the Cauchy–Schwarz inequality, \[\label{CS} \left( \sum_{i=1}^p a_i\,b_i \right)^2 \leq \sum_{i=1}^p a_i^2 \, \sum_{i=1}^p b_i^2 \tag{4}\] holds for any positive-valued \(a_i\) and \(b_i\), with equality if and only if \[a_1=a_2=\cdots=a_p \hspace{5mm} \mbox{and} \hspace{5mm} b_1=b_2=\cdots=b_p\,.\] Setting in (4), \(a_i=\sqrt{f(u)}\) and \(b_i=1/\sqrt{f(u)}\), after summation over all \(u \in \mathbf V(G)\), we arrive at inequality (2). For \(a_i=\sqrt{g(e)}\) and \(b_i=1/\sqrt{g(e)}\), after summation over all \(e \in \mathbf E(G)\), we arrive at inequality (3). ◻
Setting \(g(e)=\sqrt{d(u)^2+d(v)^2}\) into Theorem 2, we immediately arrive at:
Theorem 3. Let \(G\) be a connected graph with \(n \geq 2\) vertices and \(m\) edges, and let its \(\pi\)-Sombor index be defined via Eq. (1). Then, \[\label{t3} \pi SO(G) \geq m^2\,. \tag{5}\] Equality holds if \(G\) is either a regular graph or a complete bipartite graph \(K_{p,q}\).
Remark 1. Inequality (5) holds also for non-connected graphs. However, the equality case is somewhat more complicated. First of all, in a trivial manner, if equality holds for a graph \(G\), then equality holds also for the graph obtained by adding to \(G\) any number of isolated vertices.
Because of \(1^2+7^2=5^2+5^2\), equality in (3) will hold for a graph whose components are the 8-vertex star and any regular graph of degree 5. Examples of this kind can be constructed ad libitum.
Theorem 3 has a number of noteworthy consequences.
Corollary 4. For \(n=1,2,3\), there exists a single \(n\)-vertex tree. For all \(n \geq 4\), the unique n-vertex tree with minimum \(\pi\)-Sombor index is the star \(S_n\) (identical to the complete bipartite graph \(K_{1,n-1}\)).
Corollary 5. For \(n=3\), there exists a single \(n\)-vertex connected unicyclic graph. For all \(n \geq 4\), the unique n-vertex connected unicyclic graph with minimum \(\pi\)-Sombor index is the cycle \(C_n\) (the regular graph of degree 2).
Corollary 6. Among connected bicyclic graphs, equality in (5) holds only if \(n=5\) and \(G \cong K_{3,2}\).
Corollary 7. Among connected tricyclic graphs, equality in (5) holds only if either \(n=4\) and \(G \cong K_4\) or \(n=6\) and \(G \cong K_{4,2}\).
Corollary 8. Among connected tetracyclic graphs, equality in (5) holds only if either \(n=6\) and \(G\) is one of the two regular graphs of degree 3 (of which one is \(K_{3,3}\)) or \(n=7\) and \(G \cong K_{5,2}\).
Corollary 9. Among connected pentacyclic graphs, equality in (5) holds only if \(n=8\) and either \(G \cong K_{6,2}\) or \(G\) is a regular graph of degree 3.
Corollary 10. Among connected hexacyclic graphs, equality in (5) holds only if either \(n=5\) and \(G \cong K_5\) or \(n=9\) and \(G \cong K_{7,2}\) or \(n=10\) and \(G\) is a regular graph of degree 3.
Because of the absence of correlation between Sombor and \(\pi\)-Sombor indices (cf. Figure 2), characterizing the graphs with maximum \(\pi SO\)-value appears to be a much more difficult task. We tried to shed some light on this problem in the case of trees. For this end, we made a computer search of all trees up to \(n=17\) vertices.
In order to describe our findings, we need some preparation.
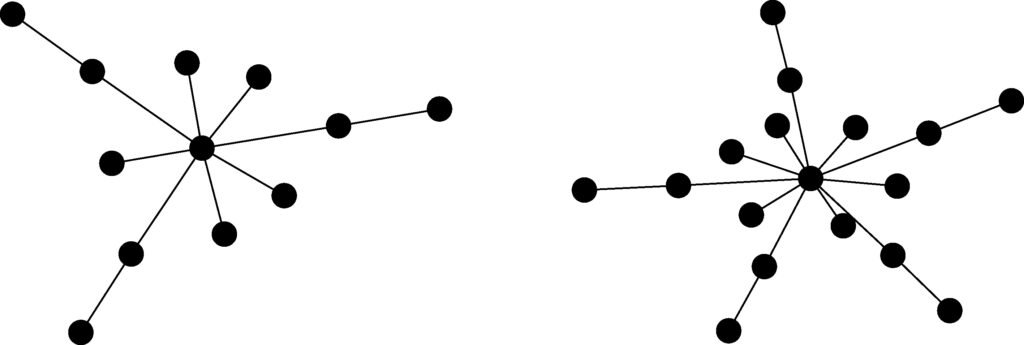
Definition 11. The sun graph is a tree having a central vertex to which 2-vertex branches are attached. The eclipsed sun graph is a tree having a central vertex to which 2-vertex branches and pendent vertices are attached. The eclipsed sun graph with \(n\) vertices and \(k\) 2-vertex branches will be denoted by \(ES(n,k)\), see Figure 3.
Recall that if \(k=0\), then \(ES(n,k)\) coincides with the star \(S_n\). If \(n\) is odd and \(k=(n-1)/2\), then \(ES(n,k)\) coincides with the ordinary sun graph.
All calculations (up to \(n=17\)) showed that the tree with maximum \(\pi SO\)-value is an eclipsed sun graph. Two characteristic examples are depicted in Figure 4.
Moreover, we found that the respective eclipsed sun graphs are:
\(ES(n,1)\) for \(n=5,6,7\)
\(ES(n,2)\) for \(n=8,9,10\)
\(ES(n,3)\) for \(n=11,12,13\)
\(ES(n,4)\) for \(n=14,15,16\)
\(ES(n,5)\) for \(n=17\) .
This encourage us to state the following:
Conjecture 12. For \(n \geq 5\), the \(n\)-vertex tree with maximum \(\pi\)-Sombor index is the eclipsed sun graph \(E(n,k)\) for \(k = \lfloor (n-2)/3 \rfloor\).
Bearing in mind that \[\begin{aligned} SO\big(ES(n,k)\big) & = & \sqrt{5}\,k + k\,\sqrt{4+d^2} + (n-2k-1)\sqrt{1+d^2} \\[3mm] ^mSO\big(ES(n,k)\big) & = & \frac{k}{\sqrt{5}} + \frac{k}{\sqrt{4+d^2}} + \frac{n-2k-1}{\sqrt{1+d^2}} \end{aligned}\] we can re-formulate Conjecture 12 as
Conjecture 13. Let \(T_n\) be an \(n\)-vertex tree, \(n \geq 5\). Then, \[\pi SO(T_n) \leq \Big[ \sqrt{5}\,k + k\,\sqrt{4+d^2} + (n-2k-1)\sqrt{1+d^2} \Big] \left[ \frac{k}{\sqrt{5}} + \frac{k}{\sqrt{4+d^2}} + \frac{n-2k-1}{\sqrt{1+d^2}} \right]\] for \(k = \lfloor (n-2)/3 \rfloor\). Equality holds if and only if \(T_n \cong ES(n,\lfloor (n-2)/3 \rfloor)\).
The result stated as Conjectures 12 and 13 were verified by direct calculation up to \(n=17\). Establishing if these are generally valid (or are violated for some larger value of \(n\)) remains a task for the future. Bearing in mind the structure of the eclipsed sun graph, this task appears to be difficult. It will stay as a challenge to mathematicians better than the present authors.
What also remains to be done is to study additional properties of the \(\pi\)-Sombor index, especially of its correlating properties with regard to physicochemical parameters of chemical substances, first of all of alkanes. Results along these lines are expected to be achieved in a reasonable future.
Bondy, J. A., & Murty, U. S. R. (1976). Graphs and subgraphs. Graph Theory With Applications, The Macmillan Press, New York.
Gutman, I. (2013). Degree-based topological indices. Croatica chemica acta, 86(4), 351-361.
Kulli, V. R. (2020). Graph indices, in: Pal, M., Samanta, S., & Pal, A. (Eds.), Handbook of Research of Advanced Applications of Graph Theory in Modern Society. Hershey: Global, pp. 66–91.
Todeschini, R., & Consonni, V. (2009). Molecular descriptors for chemoinformatics: volume I: alphabetical listing/volume II: appendices, references. John Wiley & Sons.
Gutman, I. (2021). Geometric approach to degree-based topological indices: Sombor indices. MATCH Communications in Mathematical and in Computer Chemistry, 86(1), 11-16.
Gutman, I. (2021). Some basic properties of Sombor indices. Open Journal of Discrete Applied Mathematics, 4(1), 1-3.
Gutman, I. (2022). Gutman, I. (2022). Sombor indices-back to geometry. Open Journal of Discrete Applied Mathematics, 5(2), 1-5.
Devaragudi, V., & Chaluvaraju, B. (2023). Block Sombor index of a graph and its matrix representation. Open Journal of Discrete Applied Mathematics, 6, 1-11.
Horoldagva, B., & Xu, C. (2021). On Sombor index of graphs. MATCH Communications in Mathematical and in Computer Chemistry, 86, 793–713.
Liu, H., Gutman, I., You, L., & Huang, Y. (2022). Sombor index: review of extremal results and bounds. Journal of Mathematical Chemistry, 60(5), 771-798.
Liu, H., You, L., & Huang, Y. (2023). Sombor index of c-cyclic chemical graphs. MATCH Communications in Mathematical and in Computer Chemistry, 90, 495-504.
Naz, K., Ahmad, S., & Bashier, E. (2022). On computing techniques for Sombor index of some graphs. Mathematical Problems in Engineering, 2022. Article, 1329653
Oboudi, M. R. (2023). Mean value of the Sombor index of graphs. MATCH Communications in Mathematical and in Computer Chemistry. 89, 733–740.
Oboudi, M. R. (2023). On graphs with integer Sombor index. Journal of Applied Mathematics and Computing, 69, (2023) 941–952.
Rada, J., Rodrı́guez, & J. M., Sigarreta, J. M. (2021). General properties on Sombor indices. Discrete Applied Mathematics, 299, 87–97.
Reja, S., & Nayeem, A. (2023). On Sombor index and graph energy. MATCH Communications in Mathematical and in Computer Chemistry. 89, 451–465.
Ünal, S. O. (2022). Sombor index over the tensor and Cartesian product of monogenic semigroup graphs. Symmetry, 14(5), Article, 1071.
Deng, H., Tang, Z., & Wu, R. (2021). Molecular trees with extremal values of Sombor indices. International Journal of Quantum Chemistry, 121(11), Article, e26622.
Fang, X., You, L., & Liu, H. (2021). The expected values of Sombor indices in random hexagonal chains, phenylene chains and Sombor indices of some chemical graphs. International Journal of Quantum Chemistry, 121(17), Article, e26740.
Alikhani, S., & Ghanbari, N. (2021). Sombor index of polymers. MATCH Communications in Mathematical and in Computer Chemistry, 86, 715–728.
Asif, F., Zahid, Z., Husin, M. N., Cancan, M., Tas, Z., Alaeiyan, M., & Farahani, M. R. (2022). On Sombor indices of line graph of silicate carbide \(Si_2C_3–I[p,q]\). Journal of Discrete Mathematical Sciences and Cryptography, 25, 301–310.
Divyashree, B. K., Jagadeesh, R., & Siddabasappa (2022). Sombor indices of \(TUAC_6\) and \(TUZC_6\) nanotubes. Journal of Applied Chemical Science International, 13(4), 70–79.
Liu, H., Chen, H., Xiao, Q., Fang, X., & Tang, Z. (2021). More on Sombor indices of chemical graphs and their applications to the boiling point of benzenoid hydrocarbons, International Journal of Quantum Chemistry, 121(17), Article, e26689.
Redžepović, I. (2021). Chemical applicability of Sombor indices. Journal of the Serbian Chemical Society, 86, 445–457.
Shashidhara, A. A., Ahmed, H., Nandappa, D. S., & Cancan, M. (2023). Domination version: Sombor index of graphs and its significance in predicting physicochemical properties of butane derivatives. Eurasian Chemical Communications, 5, 91–102.
Hunag, Y., & Liu, H. (2021). On the modified Sombor indices of some aromatic compounds. Journal of South China Normal University (Natural Science Edition, 53(4) 91–99 (in Chinese).
Huang, Y., & Liu, H. (2021). Bounds of modified Sombor index, spectral radius and energy. AIMS Mathematics, 6(10), 11263–11274.
Shooshtari, H., Sheikholeslami, S. M., & Amjadi, J. (2023). Modified Sombor index of unicyclic graphs with a given diameter, Asian-European Journal of Mathematics. https://doi.org/10.1142/S1793557123500985.
Zuo, X., Rather, B. A., Imran, M., & Ali, A. (2022). On some topological indices defined via the modified Sombor matrix. Molecules, 27, Article, 6776.