A bijective mapping \(\varsigma\) assigns each vertex of a graph \(G\) a unique positive integer from 1 to \(|V(G)|\), with edge weights defined as the sum of the values at its endpoints. The mapping ensures that no two adjacent edges at a common vertex have the same weight, and each \(k\)-color class is connected to every other \(k-1\) color class. A graph \(G\) possesses \(b\)-color local edge antimagic coloring if it satisfies the aforementioned criteria and it corresponds to a maximum graph coloring. This paper extensively studies the bounds, non-existence, and results of b-color local edge antimagic coloring in fundamental graph structures.
T his study analyzes a finite, connected, and undirected graph denoted by \(G\). Here, \(V(G)\) and \(E(G)\) are the set of vertices and edges. We denote the minimum and maximum degrees of \(G\) as \(\delta(G)\) and \(\Delta(G)\) respectively. An antimagic vertex labeling assigns a unique positive integer to each vertex of a graph. The sum of labels of edges incident to any two vertices is always different. The concept of \(b\)-coloring was introduced by Irving and Manlove [1], while the concept of \(b\)-chromatic index was introduced by Carlos Vinícius G.C. Lima et al. [2] in 2013. In a \(b\)-coloring problem, the goal is to assign \(k\) colors to the edges of the graph. We must ensure that every set of \(k\) colors has neighbors in every set of \(k – 1\) colors. Resolving the local edge antimagic coloring and \(b\)-chromatic index for a given graph is widely seen as an NP-complete problem [3], leading to the development of many algorithms to tackle this challenge. The local edge antimagic coloring \((\gamma_{lea}(G))\) was studied by I.H. Agustin [4], by which a bijective function labels the vertices of \(G\) based on the cardinality of vertices of \(G\). In 2018, Ika et al. [5] analysed the lower bounds of local edge antimagic coloring and exhibited the results of comb product of path and cycle with path, cycle and star graphs. Further Rajkumar et al. [6] extended the study of this coloring for some special graphs.
Arumugam et al. introduced the concept of local antimagic
vertex coloring []
that merges antimagic labeling and vertex coloring. Building upon this
idea, Dafik et al. [8] prposed a new notion called, Rainbow
Antimagic coloring, for which Septory et al. [9] provided a general lower
bound. Motivated by these developments, we have put forth a novel
coloring scheme termed as \(b\)-color
local edge antimagic coloring, which combines the principles of local
edge antimagic coloring and \(b\)-chromatic index. By combining these
ideas, our approach not only improves the existing techniques but also
lets us explore new problems in graph theory. The maximum number of
colors required to achieve \(b\)-edge
coloring through local edge antimagic labeling is denoted as the \(b\)-color local edge antimagic connetion
number, \(\varphi'_{ac}(G)\). The
\(b\)-color local edge antimagic
connection number of any given graph is bounded between maximum degree
and \(b\)-chromatic index of \(G\), that involves the local edge antimagic
coloring. Significant progress in \(b\)-coloring and \(b\)-chromatic index is evident in works
[10-14].
Though the \(b\)-chromatic index can be
determined for any graph \(G\), the
\(b\)-color local edge antimagic
connection number is not applicable universally across all the graphs.
Certain graphs have exceptions to the \(b\)-color local edge antimagic connection
number. These include even order cycle \(C_p\), except \(p=6\) and \(p=8\); wheel graph for \(p=3\); fan graph for \(p=3,4\); complete graph \(K_p\), unless \(p
\leq 3\) and complete bipartite graph \(K_{q,p}\), unless \(q=1\) and \(p
\geq 2\). These exceptions highlight the nuance of \(b\)-color local edge antimagic connection
numbers that they can be applied only to specific graph structures.
In this section, we provide definitions of the coloring under study and describe some graph structures. For a bijective function \(\varsigma:V(G) \rightarrow \{1,2,3,\ldots,|V(G)|\}\) whose corresponding edge weights are defined by, \(W^i_{\varsigma}(xy)=\varsigma(x)+\varsigma(y)\), \(G\) is said to have \(b\)-color local edge antimagic coloring if:
For every \(i \neq j\), \(W^i_{\varsigma}(e) \neq W^j_{\varsigma}(e')\) for edges \(e,e' \in E(G)\) incident on a common vertex \(x \in V(G)\), and
Each \(k\)-color class has neighbors in every other \(k-1\) color class.
A simple connected graph obtained by adding a hub vertex and connecting all the \(p\) vertices of a cycle to the hub vetex is called a wheel graph \((\mathsf{W}_{1,p})\) [15,16]. It has \(p+1\) vertices and \(2p\) edges with a maximum degree of \(p\). If the cycle in the wheel graph is replaced by a path and all the \(p\) vertices of a path are connected to a hub vertex, it forms a fan graph \(({F_{1,p}})\) [17] that has \(p+1\) vertices and \(2p-1\) edges with maximum degree \(p\). A friendship graph \((\mathscr{F}_p)\) [18] is a simple connected graph constructed by taking \(p\) copies of cycle \(C_3\) and joining one vertex from each copy of \(C_3\) to form a hub vertex. The resulting graph has \(2p+1\) vertices and \(3p\) edges with a maximum degree of \(2p\).
Vizing [19] proved that for any graph \({G}\), \(\chi'( {G})\) lies in the range \(\Delta({G})\) and \(\Delta( {G})+1\). Graphs whose edge coloring is \(\Delta( {G})\) are called class I graphs, and those whose edge coloring is \(\Delta( {G})+1\) are called class II graphs. Eventually, the \(b\)-chromatic index of the above graphs have close accordance with its maximum degree \(\Delta(G)\), except in the case of cycle \(C_p\) when \(p=odd\) and wheel graph when \(p=4\), whose \(b\)-chromatic index is \(\Delta(G)+1\).
Lemma 1. [4,6] The local edge antimagic chromatic number of certain graphs (path, cycle, wheel, fan, friendship, complete and star graphs) are:
For \(p \geq 3\), \(\gamma_{lea}(P_p) = 2\)
For \(p \geq 3\), \(\gamma_{lea}(C_p) = 3\)
For \(p \geq 3\), \(\gamma_{lea}(\mathsf{W}_{1,p}) = \begin{cases} 5, & \text{for~~} p = 3, 4\\ p, & \text{for~~} p \geq 5\\ \end{cases}\)
For \(p \geq 2\), \(\gamma_{lea}(F_{1,p}) = \begin{cases} p+1, & \text{for~~} p = 2,3\\ p, & \text{for~~} p \geq 4\\ \end{cases}\)
For \(p \geq 1\), \(\gamma_{lea}(\mathscr{F}_p) = \begin{cases} 3, & \text{for~~} p = 1\\ 2p, & \text{for~~} p \geq 2\\ \end{cases}\)
For \(p \geq 3\), \(\gamma_{lea}(K_p) = 2p-3\)
For \(p \geq 2\), \(\gamma_{lea}(K_{1,p}) = p\)
Lemma 2. [11] The \(b\)-chromatic index of certain graphs (path, cycle, wheel, fan, friendship, complete, star and complete bipartite graphs) are:
For \(p \geq 3\), \(\varphi'(P_p)= \begin{cases} 2, & \text{ for ~~} 3 \leq p \leq 5\\ 3, & \text{ for ~~} p \geq 6\\ \end{cases}\)
For \(p \geq 3\), \(\varphi'(C_p)= \begin{cases} 2, & \text{ for ~~} p = 4\\ 3, & \text{ for ~~} p \geq 3; p \neq 4\\ \end{cases}\)
For \(p \geq 3\), \(\varphi'(\mathsf{W}_{1,p})= \begin{cases} 5, & \text{ for ~~} p = 4\\ p, & \text{ for ~~} p \geq 3; p \neq 4\\ \end{cases}\)
For \(p \geq 3\), \(\varphi'(F_{1,p})=p\)
For \(p \geq 2\), \(\varphi'(\mathscr{F}_{p}) = 2p\)
For \(3 \leq p \leq 6\), \(\varphi'(K_3) = \varphi'(K_4) = 3\), \(\varphi'(K_5) = 5\) and \(\varphi'(K_6) = 6\)
For \(p \geq 2\), \(\varphi'(K_{1,p}) = p\)
For \(p \leq r \leq p(p-1)\), \(\varphi'(K_{p,r}) \leq min \{p(p-1),~ p+r-1\}\)
Lemma 3. For any connected graph \(G\), the bound of \(b\)-color local edge antimagic coloring is given by, \(\Delta(G) \leq \gamma_{lea}(G) \leq \varphi'_{ac}(G) \leq % \Delta(G) + 1 \leq \varphi'(G)\).
Proof. By the definition of \(b\)-chromatic index [11], \(\Delta(G) \leq \chi'(G) \leq \varphi'(G) \leq 2\Delta(G)-1\). Eventually, \(\Delta(G) \leq \varphi'(G)\). By [4], \(\gamma_{lea}(G) \geq \Delta(G)\). Since, \(b\)-coloring is a maximum coloring it constitues an upper bound of the \(b\)-color local edge antimagic coloring, as such we can write, \(\Delta(G) \leq \gamma_{lea}(G) \leq \varphi'_{ac}(G) \leq \varphi'(G)\). In case, \(\varphi'(G) = \Delta(G)\), then \(\varphi'_{ac}(G) \leq \Delta(G)\). ◻
Theorem 4. The \(b\)-color local edge antimagic connection number does not exist for:
An even order cycle \(C_p\), except \(p = 6, 8\).
A complete graph \(K_p\), unless \(p \leq 3\).
A wheel graph \(\mathsf{W}_{1,p}\), when \(p = 3\).
A fan graph \(F_{1,p}\), when \(p = 3\).
Complete bipartite graph \(K_{q,p}\), unless \(q = 1; p \geq 2\).
Proof. The \(b\)-color local edge antimagic connection number of the following graphs does not exist:
For an even order cycle \(C_p\), for \(p=4\) and \(p \geq 10\), assign an antimagic labeling as, \(\varsigma{(x_1, x_3, x_5, \ldots, x_{p-1})} = \{1,2,3,\ldots,\frac{p}{2}\}\) and \(\varsigma{(x_2, x_4, x_6, \ldots, x_p)} = \{p,~ p-1,~ p-2,\ldots,\frac{p}{2}+1\}\). The corresponding edge weights are \(\{p+1,~ p+2,~ \frac{p}{2}+2\}\), among which only \(p+1\) is adjacent with all the other color classes, whereas other colors fails to satisfy the adjacency.
For a complete graph \(K_p,\,\, p > 3\), assign an antimagic labeling as, \(\varsigma{(x_1, x_2, x_3, \ldots, x_p)} = \{1,2,3,\ldots,p\}\) whose corresponding edge weights are \(\{3,4,5,\ldots,2p-1\}\) in which \(p+1\) occuring at an edge \(\{x_px_1\} \in E(K_p)\) is the only color that is adjacent with all the other color classes, whereas other colors fails to satisfy the adjacency.
Since \(\mathsf{W}_{1,3} \cong K_4\), following (ii), it is clear that \(b\)-color local edge antimagic connection number of \(\mathsf{W}_{1,3}\) does not exist.
A fan graph \(F_{1,3}\) can be obtained either by joining or deleting an edge \(e_1e_3\) or \(e_2e_4\) in \(C_4\) or \(K_4\) respectively. Since \(b\)-color local edge antimagic connection number of both the cases does not exist, it is easy to show that \(b\)-color local edge antimagic connection number of \(F_{1,3}\) does not exist.
A complete bipartite graph \(K_{p,r}\) with \(p=1\) and \(r \geq 2\) is a star graph [20] whose \(\varphi'_{ac}(K_{1,r}) = r\) for \(r \geq 2\). For \(p,r \geq 2\), label the vertices antimagically as, \(A_{\{x_1,x_2,x_3,\ldots,x_p\}} = i\), for \(1 \leq i \leq p\) and \(B_{\{y_1,y_2,y_3,\ldots,y_r\}} = p + j\), for \(1 \leq j \leq r\). The corresponding edge weights are, \(\{p+2,p+3,p+4,\ldots,2p+r\}\) among which only few colors are adjacent with all the other color classes, whereas other colors fails to satisfy the adjacency.
◻
Theorem 5. For any positive integer \(p \geq 3\), the \(b\)-color local edge antimagic connection number of a path is \[\displaystyle\varphi'_{ac}(P_p) =\\ \begin{cases} 2, &\,\,\,\text{for $3 \leq p \leq 5$ and $p=even; p \neq 6,8$}\\ 3, &\,\,\,\text{for $p= 6, 8$ and $p=odd; p \neq 3,5$}\\ \end{cases}\]
Proof. Let \(P_p\) be a
path graph, whose vertex and edge cardinalities are, \(|V(P_p)| = p\) and \(|E(P_p)| = p-1\). The maximum and minimum
degrees are, \(\Delta(P_p)=2\) and
\(\delta(P_p)=1\).
Case 1: When \(3 \leq p \leq
5\), \(\varphi'(P_p) =
\Delta(P_p)\), so by Lemma 3, \(\varphi'(P_p) \leq 2\) is the upper
bound. Also, when p = even, except for \(p=6,8\), using Lemma 1, 2 and 3, the upper bound
is, \(\varphi'_{ac}(P_p) \leq 3\).
In order to prove the lower bound, label the vertices local
antimagically as, \(\varsigma{(x_1,x_2,x_3,\ldots,x_p)} = \{1,\,\,
p,\,\, 2,\,\, p-1,\,\, 3,\,\, p-2,\,\, \ldots\}\). The
corresponding edge weights are: \(p+1\)
and \(p+2\), i.e., \(\varphi'_{ac}(P_p) \geq 2\). Thus,
\(\varphi'_{ac}(P_p) = 2\), for
\(3 \leq p \leq 5\) and \(p=even; p \neq 6,8\). Figure 1 shows the difference
arising in the \(b\)-chromatic index
and \(b\)-color local edge antimagic
coloring of \(P_{10}\).
Case 2: When \(p=6,8\)
and when p = odd, except for \(p =
3,5\), through Lemma 1, 2 and 3, the upper bound
is, \(\varphi'_{ac}(P_p) \leq 3\).
In order to prove the lower bound for \(p=6,8\), label the vertices as follows:
\[\varsigma(x_t : 1 \leq t \leq 6) =
\{1,4,5,2,3,6\} \text{ and }\\
\varsigma(x_t : 1 \leq t \leq 8) = \{1,6,5,2,7,4,3,8\}\]
The corresponding edge weights are: \(p-1, p+1\) and \(p+3\) then, \(\varphi'_{ac}(P_p) \geq 3\). Thus, \(\varphi'_{ac}(P_p) = 3\), for \(p=6,8\). To prove the lower bound, when p = odd; \(p \neq 3,5\), label the vertices local antimagically as, \[\varsigma{(x_1,x_2,x_3,\ldots,x_p)} = \{1,\,\, p,\,\, 3,\,\, p-2,\,\, 5,\,\, p-4,\,\, \ldots,\,\, 4,\,\, p-1,\,\, 2 \}\]
whose corresponding edge weights are: \(p+1, p+2\) and \(p+3\) then, \(\varphi'_{ac}(P_p) \geq 3\). Thus, \(\varphi'_{ac}(P_p) = 3\), when p = odd; \(p \neq 3,5\).
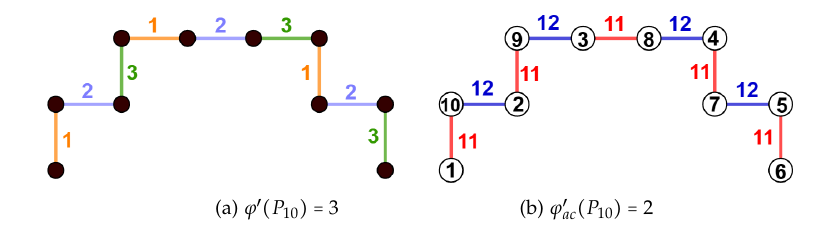
Theorem 6. For any odd positive integer \(p \geq 3\), the \(b\)-color local edge antimagic connection number of cycle is \(\varphi'_{ac}(C_p) = 3\).
Proof. Let \(C_p\) be a
cycle whose vertex set is \(V(C_p)=\{x_t : 1
\leq t \leq p\}\) and edge set is \(E(C_p)=\{\{x_tx_{t+1} : 1 \leq t \leq p-1\} \cup
\{x_px_1\}\}\). Through Lemma 1, 2 and 3, the upper bound
is, \(\varphi'_{ac}(C_p) \leq 3\).
In order to prove the lower bound, define an antimagic labeling \(\varsigma_1 : V(C_p) \rightarrow
\{1,2,3,\ldots,p\}\) by, \[\varsigma_1(x_t) =
\begin{cases}
\frac{t+1}{2}, &\,\,\,\text{for $t=1,3,5,\ldots,p$}\\
p-\frac{t}{2}+1, &\,\,\,\text{for $t=2,4,6,\ldots,p-1$}
\end{cases}\]
Based on the labeling, the corresponding edge weights are: \[\begin{aligned}
{4}
W^1_{\varsigma_1}(x_tx_{t+1}) &= p+1 & \,\,\,&
\text{for $t=1,3,5,\ldots,p-2$}\\
W^2_{\varsigma_1}(x_tx_{t+1}) &= p+2 & & \text{for
$t=2,4,6,\ldots,p-1$}\\
W^3_{\varsigma_1}(x_px_1) & = \frac{p+3}{2} & &
\text{$\forall p \in N$}
\end{aligned}\] The edge weight calculation shows that, \(\varphi'_{ac}(C_p) \geq 3\). On
combining the upper and lower bounds, \(\varphi'_{ac}(C_p) = 3\). Table 1
shows that each color class has at least one dominating b-edge which is
incident with all the other neighboring color classes.
| Color Class | b-Edges | |
| \(W^1_{\varsigma_1} = p+1\) | \(x_1x_2\) | |
| \(W^2_{\varsigma_1} = p+2\) | \(x_p-1x_p\) | |
| \(W^3_{\varsigma_1} = \frac{p+3}{2}\) | \(x_px_1\) | |
◻
Corollary 7. For any even positive integer \(p\), the \(b\)-color local edge antimagic connection number of cycle exists only for \(p=6,8\).
Proof. Using Lemma 1, 2 and 3, the upper bound
is, \(\varphi'_{ac}(C_p) \leq 3\).
To prove the lower bound, define a local edge antimagic labeling by,
\[\varsigma(x_t : 1 \leq t \leq 6) =
\{1,4,5,2,3,6\} \,\,\,\text{for $p=6$}\] \[\varsigma(x_t : 1 \leq t \leq 8) =
\{1,6,5,2,7,4,3,8\} \,\,\, \text{for $p=8$}\] The
corresponding edge weights are: \(p-1,
p+1\) and \(p+3\) and the
dominant \(b\)-edges are: \(x_1x_2\), \(x_px_1\) and \(x_{p-1}x_p\) respectively. The total number
of edge weights are \(\varphi'_{ac}(C_p)
\geq 3\). Thus, \(\varphi'_{ac}(C_p) = 3\). In all the
other cases of even \(p\), the coloring
exceeds and fails to satisfy \(b\)-edge
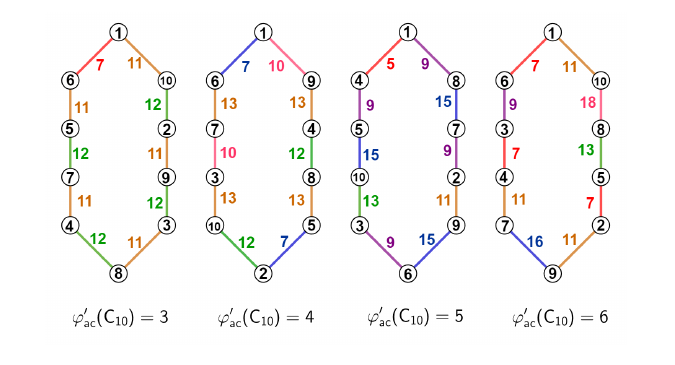
coloring. Figure 2 can be
used to check the optimal coloring patterns for even order cycles.
Moreover, all the coloring pattern fails to satisfy \(b\)-edge coloring property for even cycle
\(p\), when \(p \geq 10\).
Theorem 8. For any positive integer \(p \geq 4\), the \(b\)-color local edge antimagic connection number of wheel graph is \[p \leq \varphi'_{ac}(\mathsf{W}_{1,p}) \leq \begin{cases} 5 & \text{if $p = 4$}\\ p & \text{if $p \geq 5$}\\ \end{cases}\]
Proof. Let \(\mathsf{W}_{1,p}\) be a wheel graph with vertex set \(V(\mathsf{W}_{1,p})=\{\{h\} \cup \{x_t : 1 \leq t \leq p\}\}\) and edge set \(E(\mathsf{W}_{1,p})=\{\{x_tx_{t+1} : 1 \leq t \leq p-1\} \cup \{x_px_1\} \cup \{hx_t : 1 \leq t \leq p\}\}\). To prove the theorem, consider the following two cases.
Case 1: For \(p =
4\)
Using Lemma 1, 2 and 3, the
upper bound is, \(\varphi'_{ac}(\mathsf{W}_{1,4}) \leq p+1 =
5\). In order to prove the lower bound, label the vertices as
follows: \[\begin{aligned}
{4}
\,\,\,\varsigma_2(h) &= 3
\end{aligned}\] \[\varsigma_2(x_t) =
\begin{cases}
\frac{p+1}{2}, &\,\,\, t=1,3 \\
\frac{p}{2}+3, &\,\,\, t=2,4
\end{cases}\]
Based on the labeling, the corresponding edge weights are: \[\begin{aligned} {2} W^1_{\varsigma_2}(hx_1) & = 4\\ W^2_{\varsigma_2}(hx_3) & = W^2_{\varsigma_2}(x_1x_2) & = 5\\ W^3_{\varsigma_2}(x_2x_3) & = W^3_{\varsigma_2}(x_4x_1) & = 6\\ % \end{alignat*} % \begin{alignat*}{2} W^4_{\varsigma_2}(hx_2) & = W^4_{\varsigma_2}(x_3x_4) & = 7\\ W^5_{\varsigma_2}(hx_4) & = 8 \end{aligned}\] The edge weight calculation shows that, \(\varphi'_{ac}(\mathsf{W}_{1,p}) \geq 5\). On combining the upper and lower bounds, \(\varphi'_{ac}(\mathsf{W}_{1,4}) = 5\). Table 2 shows that each color class has at least one dominating b-edge which is incident with all the other neighboring color classes.
| Color Class | b-Edges | |
| \(W^1_{\varsigma_2} = 4\) | \(hx_1\) | |
| \(W^2_{\varsigma_2} = 5\) | \(hx_3\) | |
| \(W^3_{\varsigma_2} = 6\) | \(x_4x_1\) | |
| \(W^4_{\varsigma_2} = 7\) | \(hx_2\) | |
| \(W^5_{\varsigma_2} = 8\) | \(hx_4\) | |
Case 2: If \(p \geq
5\)
Since, \(\varphi'(\mathsf{W}_{1,p}) =
\Delta(\mathsf{W}_{1,p})\), by Lemma 3, \(\varphi'_{ac}(\mathsf{W}_{1,p}) \leq
p\) is the upper bound. In order to prove the lower bound,
consider the following subcases.
Subcase 1: When \(p \equiv
1(mod\, 2)\), define a local edge antimagic labeling \(\varsigma_3 : V(\mathsf{W}_{1,p}) \rightarrow
\{1,2,3,\ldots,p+1\}\) by,
\(\varsigma_3(h) = \frac{p+1}{2}\)
\[\varsigma_3(x_t) =
\begin{cases}
\frac{t+1}{2} & \text{for $t=1,3,5,\ldots,p-2$}\\
p-\frac{t}{2}+2 & \text{for $t=2,4,6,\ldots,p-1$}\\
\frac{p+3}{2} & \text{for $t = p$}
\end{cases}\] Based on the labeling, the corresponding edge
weights are: \[\begin{aligned}
{4}
W^1_{\varsigma_3}(hx_t) &= \frac{p+t+2}{2} &
\,\,\,& \text{for $t=1,3,5,\ldots,p-2$}\\
W^2_{\varsigma_3}(hx_t) &= \frac{3p-t+5}{2} & &
\text{for $t=2,4,6,\ldots,p-1$}\\
W^3_{\varsigma_3}(hx_t) &= p+2 & & \text{for $t =
p$}\\
W^4_{\varsigma_3}(x_tx_{t+1}) &= p+2 & & \text{for
$t=1,3,5,\ldots,p-2$}\\
% \end{alignat*}
% \begin{alignat*}{4}
W^5_{\varsigma_3}(x_tx_{t+1}) &= p+3 & \,\,\,&
\text{for $t=2,4,6,\ldots,p-3$}\\
W^6_{\varsigma_3}(x_tx_{t+1}) &= p+4 & & \text{for
$t=p-1$}\\
W^7_{\varsigma_3}(x_px_1) &= \frac{p+5}{2} & &
\text{$\forall p \in N$}
\end{aligned}\] As the edge weights \(W^4_{\varsigma_3}, W^5_{\varsigma_3},
W^6_{\varsigma_3}\) and \(W^7_{\varsigma_3}\) has already been
included in \(W^1_{\varsigma_3},
W^2_{\varsigma_3}\) and \(W^3_{\varsigma_3}\), they are deemed
superfluous and therefore, it is excluded. The total number of edge
weights are obtained using N-term formula: \[\begin{array}{c c c}
U^{W^1_{\varsigma_3}}_N = a + (N-1)d \longleftrightarrow &
\,\,\, p = \frac{p+3}{2} + (N-1)(1) \,\,\,
\longleftrightarrow & N = |W^1_{\varsigma_3}| = \frac{p-1}{2}\\
U^{W^2_{\varsigma_3}}_N = a + (N-1)d \longleftrightarrow &
\frac{2p+6}{2} = \frac{3p+3}{2} + (N-1)(-1) \longleftrightarrow & N
= |W^2_{\varsigma_3}| = \frac{p-1}{2}\\
\end{array}\] Notably, \(|W^3_{\varsigma_3}| = 1\). Hence, \(\sum_{i=1}^{3}|W^i_{\varsigma_3}| = \frac{p-1}{2}
+ \frac{p-1}{2} + 1 = p\), implies \(\varphi'_{ac}(\mathsf{W}_{1,p}) \geq
p\). Table 3 shows that each color class has at least
one dominating b-edge which is incident with all the other neighboring
color classes.
| Color Class | b-Edges | |
| \(W^1_{\varsigma_3} = \frac{p+t+2}{2}\) | \(hx_1,hx_3, hx_5,\ldots,hx_p-2\) | |
| \(W^2_{\varsigma_3} = \frac{3p-t+5}{2}\) | \(hx_2, hx_4, hx_6,\ldots,hx_p-1 \) | |
| \(W^3_{\varsigma_3} = p+2\) | \(hx_p\) | |
Subcase 2: When \(p \equiv
0(mod\, 2); p \neq 4\), define a local edge antimagic labeling
\(\varsigma_4 : V(\mathsf{W}_{1,p})
\rightarrow \{1,2,3,\ldots,p+1\}\) by,
\(\varsigma_4(h) = \frac{p+2}{2}\)
\[\varsigma_4(x_t) =
\begin{cases}
\frac{t+1}{2} & \text{for $t=1,3,5,\ldots,p-1$}\\
\frac{p+4}{2} & \text{for $t = 2$}\\
p-\frac{t}{2}+3 & \text{for $t=4,6,8,\ldots,p$}
\end{cases}\] Based on the labeling, the corresponding edge
weights are: \[\begin{aligned}
{4}
W^1_{\varsigma_4}(hx_t) &= \frac{p+t+3}{2} &
\,\,\,& \text{for $t=1,3,5,\ldots,p-1$}\\
W^2_{\varsigma_4}(hx_t) &= \frac{3p-t}{2}+4 & &
\text{for $t=4,6,8,\ldots,p$}\\
W^3_{\varsigma_4}(hx_t) &= p+3 & & \text{for $t =
2$}\\
% \end{alignat*}
% \begin{alignat*}{4}
W^4_{\varsigma_4}(x_tx_{t+1}) &= \frac{p}{2}+3 &
\,\,\,& \text{for $t=1$}\\
W^5_{\varsigma_4}(x_tx_{t+1}) = W^5_{\varsigma_4}(x_px_1) &=
\frac{p}{2}+4 & & \text{for $t=2$}\\
W^6_{\varsigma_4}(x_tx_{t+1}) &= p+3 & & \text{for
$t=3,5,7,\ldots,p-1$}\\
W^7_{\varsigma_4}(x_tx_{t+1}) &= p+4 & & \text{for
$t=4,6,8,\ldots,p-2$}
\end{aligned}\] As the edge weights \(W^4_{\varsigma_4}, W^5_{\varsigma_4},
W^6_{\varsigma_4}\) and \(W^7_{\varsigma_4}\) has already been
included in \(W^1_{\varsigma_4},
W^2_{\varsigma_4}\) and \(W^3_{\varsigma_4}\), they are deemed
superfluous and therefore, it is excluded. The total number of edge
weights are obtained using N-term formula: \[\begin{array}{c c c c c}
U^{W^1_{\varsigma_4}}_N = a + (N-1)d & \longleftrightarrow &
\frac{2p+2}{2} = \frac{p+4}{2} + (N-1)(1) & \longleftrightarrow
& N = |W^1_{\varsigma_4}| = \frac{p}{2}\\
U^{W^2_{\varsigma_4}}_N = a + (N-1)d & \longleftrightarrow &
p+4 = \frac{3p+4}{2} + (N-1)(-1) & \longleftrightarrow & N =
|W^2_{\varsigma_4}| = \frac{p}{2}-1\\
\end{array}\] Notably, \(|W^3_{\varsigma_4}| = 1\). Hence, \(\sum_{i=1}^{3}|W^i_{\varsigma_4}| = \frac{p}{2} +
\frac{p}{2}-1 + 1 = p\), implies \(\varphi'_{ac}(\mathsf{W}_{1,p}) \geq
p\). Figure 3 illustrates the local edge antimagic
labeling of \(\mathsf{W}_{1,p}\) that
satisfies the \(b\)-edge coloring and
Table 4 clearly shows that each color class has
at least one dominating b-edge which is incident with all the other
neighboring color classes.
| Color Class | b-Edges | |
| \(W^1_{\varsigma_4} = \frac{p+t+3}{2}\) | \(hx_1,hx_3, hx_5,\ldots,hx_p-1\) | |
| \(W^2_{\varsigma_4} = \frac{3p-t}{2}+4\) | \(hx_4, hx_6, hx_8,\ldots,hx_p \) | |
| \(W^3_{\varsigma_4} = p+3\) | \(hx_2\) | |
From Subcase 1 and Subcase 2, it is evident that, \(\varphi'_{ac}(\mathsf{W}_{1,p}) \geq p\). On combining both upper and lower bounds, we get, \(\varphi'_{ac}(\mathsf{W}_{1,p}) = p\), for \(p \geq 5\).
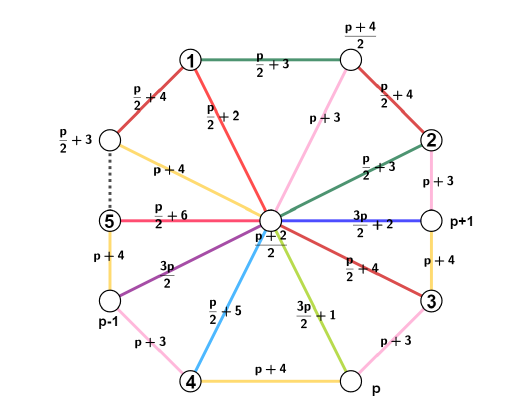
◻
Theorem 9. For any positive integer \(p \geq 4\), the \(b\)-color local edge antimagic connection number of fan graph is \(\varphi'_{ac}(F_{1,p}) = p\)
Proof. Let \(F_{1,p}\) be a
fan graph with vertex set \(V(F_{1,p})=\{\{h\}
\cup \{x_t : 1 \leq t \leq p\}\}\) and edge set \(E(F_{1,p})=\{\{x_tx_{t+1} : 1 \leq t \leq p-1\}
\cup \{hx_t : 1 \leq t \leq p\}\}\). Since, \(\varphi'(F_{1,p}) = \Delta(F_{1,p})\),
by Lemma 3, \(\varphi'_{ac}(F_{1,p}) \leq p\) is the
upper bound. In order to prove the lower bound, consider the following
two cases.
Case 1: When \(p \equiv
1(mod\,2)\), define a local edge antimagic labeling \(\varsigma_5 : V(F_{1,p})
\rightarrow \{1,2,3,\ldots,p+1\}\) by,
\(\varsigma_5(h) = \frac{p+1}{2}\)
\[\varsigma_5(x_t) =
\begin{cases}
\frac{t+1}{2} & \text{for $t=1,3,5,\ldots,p-2$}\\
p-\frac{t}{2}+2 & \text{for $t=2,4,6,\ldots,p-1$}\\
\frac{p+3}{2} & \text{for $t = p$}
\end{cases}\] Based on the labeling, the corresponding edge
weights are: \[\begin{aligned}
{4}
W^1_{\varsigma_5}(hx_t) &= \frac{p+t}{2}+1 &
\,\,\,& \text{for $t=1,3,5,\ldots,p-2$}\\
W^2_{\varsigma_5}(hx_t) &= \frac{3p-t+5}{2} & &
\text{for $t=2,4,6,\ldots,p-1$}\\
W^3_{\varsigma_5}(hx_t) &= p+2 & & \text{for $t =
p$}\\
W^4_{\varsigma_5}(x_tx_{t+1}) &= p+2 & \,\,\,&
\text{for $t=1,3,5,\ldots,p-2$}
\end{aligned}\] \[\begin{aligned}
{4}
W^5_{\varsigma_5}(x_tx_{t+1}) &= p+3 & \,\,\,&
\text{for $t=2,4,6,\ldots,p-1$}\\
W^6_{\varsigma_5}(x_{p-1}x_p) &= p+4 & & \text{for
$t=3,5,7,\ldots,p-1$}
\end{aligned}\] As the edge weights \(W^4_{\varsigma_5}, W^5_{\varsigma_5}\) and
\(W^6_{\varsigma_5}\) has already been
included in \(W^2_{\varsigma_5}\) and
\(W^3_{\varsigma_5}\), they are deemed
superfluous and therefore, it is excluded. The total number of edge
weights are obtained using N-term formula: \[\begin{array}{c c c c c}
U^{W^1_{\varsigma_5}}_N = a + (N-1)d &\longleftrightarrow
& p= \frac{p+3}{2} + (N-1)(1) &\longleftrightarrow & N =
|W^1_{\varsigma_5}| = \frac{p-1}{2}\\
U^{W^2_{\varsigma_5}}_N = a + (N-1)d &\longleftrightarrow &
\frac{2p+6}{2} = \frac{3p+3}{2} + (N-1)(-1) &\longleftrightarrow
& N = |W^2_{\varsigma_5}| = \frac{p-1}{2}\\
\end{array}\] Notably, \(|W^3_{\varsigma_5}| = 1\). Hence, \(\sum_{i=1}^{3}|W^i_{\varsigma_5}| = \frac{p-1}{2}
+ \frac{p-1}{2} + 1 = p\), implies \(\varphi'_{ac}(F_{1,p}) \geq p\). Table
5 shows that each color class has at least
one dominating b-edge which is incident with all the other neighboring
color classes.
| Color Class | b-Edges | |
| \(W^1_{\varsigma_4} = \frac{p+t+3}{2}\) | \(hx_1,hx_3, hx_5,\ldots,hx_p-1\) | |
| \(W^2_{\varsigma_4} = \frac{3p-t}{2}+4\) | \(hx_4, hx_6, hx_8,\ldots,hx_p \) | |
| \(W^3_{\varsigma_4} = p+3\) | \(hx_2\) | |
Case 2: When \(p=4\), the antimagic labeling of vertices
are, \(\varsigma(h) = \{4\}\) and \(\varsigma(x_1, x_2, x_3, x_4) =
\{1,5,2,3\}\), whose corresponding edge weights are, \(W_{\varsigma} = \{5,6,7,9\}\). Hence, \(|W_{\varsigma}| = 4\). Further, when \(p \equiv 0(mod\, 2) ; p \neq 4\), define a
local edge antimagic labeling \(\varsigma_6 :
V(F_{1,p}) \rightarrow \{1,2,3,\ldots,p+1\}\) by,
\(\varsigma_6(h) = \frac{p}{2}\) \[\varsigma_6(x_t) =
\begin{cases}
\frac{t+1}{2} & \text{for $t=1,3,5,\ldots,p-3$}\\
p-\frac{t}{2}+2 & \text{for $t=2,4,6,\ldots,p$}\\
\frac{p+2}{2} & \text{for $t = p-1$}
\end{cases}\] Based on the labeling, the corresponding edge
weights are: \[\begin{aligned}
{4}
W^1_{\varsigma_6}(hx_t) &= \frac{p+t+1}{2} &
\,\,\,& \text{for $t=1,3,5,\ldots,p-3$}\\
W^2_{\varsigma_6}(hx_t) &= \frac{3p-t}{2}+2 & &
\text{for $t=2,4,6,\ldots,p$}\\
W^3_{\varsigma_6}(hx_t) &= p+1 & & \text{for $t =
p-1$}\\
W^4_{\varsigma_6}(x_tx_{t+1}) &= p+2 & & \text{for
$t=1,3,5,\ldots,p-3$}\\
W^5_{\varsigma_6}(x_tx_{t+1}) &= p+3 & & \text{for
$t=2,4,6,\ldots,p$ and $t=p-1$}\\
W^6_{\varsigma_6}(x_tx_{t+1}) &= p+4 & & \text{for
$t=p-2$}
\end{aligned}\] As the edge weights \(W^4_{\varsigma_6},W^5_{\varsigma_6}\) and
\(W^6_{\varsigma_6}\) has already been
included in \(W^2_{\varsigma_6}\), they
are deemed superfluous and therefore, it is excluded. The total number
of edge weights are obtained using N-term formula: \[\begin{array}{c c c c c c}
U^{W^1_{\varsigma_6}}_N = a + (N-1)d &\longleftrightarrow &
\frac{2p-2}{2} = \frac{p+2}{2} + (N-1)(1) & \longleftrightarrow
& N = |W^1_{\varsigma_6}| = \frac{p}{2}-1\\
U^{W^2_{\varsigma_6}}_N = a + (N-1)d &\longleftrightarrow &
p+2 = \frac{3p+2}{2} + (N-1)(-1) & \longleftrightarrow & N =
|W^2_{\varsigma_6}| = \frac{p}{2}\\
\end{array}\] Notably, \(|W^3_{\varsigma_6}| = 1\). Hence, \(\sum_{i=1}^{3}|W^i_{\varsigma_6}| = \frac{p}{2} -1
+ \frac{p}{2} + 1 = p\), implies \(\varphi'_{ac}(F_{1,p}) \geq p\). Table
6 shows that each color class has at least
one dominating b-edge which is incident with all the other neighboring
color classes.
| Color Class | b-Edges | |
| \(W^1_{\varsigma_6} = \frac{p+t+1}{2}\) | \(hx_1,hx_3, hx_5,\ldots,hx_p-3\) | |
| \(W^2_{\varsigma_6} = \frac{3p-t}{2}+2\) | \(hx_2, hx_4, hx_6,\ldots,hx_p \) | |
| \(W^3_{\varsigma_6} = p+2\) | \(hx_p-1\) | |
From Case 1 and Case 2, it is evident that \(\varphi'_{ac}(\mathsf{F}_{1,p}) \geq p\). On combining both the upper and lower bounds, we get, \(\varphi'_{ac}(\mathsf{F}_{1,p}) = p\). ◻
Theorem 10. For any positive integer \(p \geq 2\), the \(b\)-color local edge antimagic connection number of friendship graph is \(\varphi'_{ac}(\mathscr{F}_p) = 2p\).
Proof. Let \(\mathscr{F}_p\) be a friendship graph whose
vertex set \(V(\mathscr{F}_p)=\{h\} \cup \{x_t
: 1 \leq t \leq p\}\) and edge set \(E(\mathscr{F}_p)=\{hx_t,hy_t,x_ty_t : 1 \leq t
\leq p\}\). Since, \(\varphi'(\mathscr{F}_p) =
\Delta(\mathscr{F}_p)\), by Lemma 3, \(\varphi'_{ac}(\mathscr{F}_p) \leq 2p\)
is the upper bound. In order to prove the lower bound, define a local
edge antimagic labeling \(\varsigma_7 :
V(\mathscr{F}_p) \rightarrow \{1,2,3,\ldots,2p+1\}\) by,
\(\varsigma_7(h) = p\) \[\varsigma_7(x_t) =
\begin{cases}
t & \text{for $1 \leq t \leq p-1$}\\
t+1 & \text{for $t=p$}
\end{cases}
\,\,\, \[\varsigma_7(y_t)
=
\begin{cases}
2p-t+2 & \text{for $1 \leq t \leq p-1$}\\
t+2 & \text{for $t=p$}
\end{cases}\] Based on the labeling, the corresponding edge
weights are: \[\begin{aligned}
{4}
W^1_{\varsigma_7}(hx_t) &= p+t & \,\,\,&
\text{for $1 \leq t \leq p-1$}\\
W^2_{\varsigma_7}(hx_t) &= 2(p+1) & \,\,\,&
\text{for $t=p$}\\
W^3_{\varsigma_7}(hy_t) &= 3p-t+2 & & \text{for $1
\leq t \leq p-1$}\\
W^4_{\varsigma_7}(hy_t) &= 2p+1 & & \text{for
$t=p$}\\
W^5_{\varsigma_7}(x_ty_t) &= 2(p+1) & & \text{for $1
\leq t \leq p-1$}\\
W^6_{\varsigma_7}(x_ty_t) &= 2p+3 & & \text{for
$t=p$}
\end{aligned}\] Since the edge weights \(W^5_{\varsigma_7}\) and \(W^6_{\varsigma_7}\) are already included in
\(W^2_{\varsigma_7}\) and \(W^3_{\varsigma_7}\), they are deemed
superfluous and therefore, it is excluded. The total number of edge
weights can be obtained using N-term formula: \[\begin{array}{c c c c}
U^{W^1_{\varsigma_7}}_N = a + (N-1)d \longleftrightarrow & 2p-1
= p+1 + (N-1)(1) & \longleftrightarrow & N = |W^1_{\varsigma_7}|
= p-1\\
U^{W^3_{\varsigma_7}}_N = a + (N-1)d \longleftrightarrow & 2p+3
= 3p+1 + (N-1)(-1) & \longleftrightarrow & N =
|W^3_{\varsigma_7}| = p-1\\
\end{array}\] Notably, \(|W^2_{\varsigma_7}| = |W^4_{\varsigma_7}| =
1\). Hence, \(\sum_{i=1}^{4}|W^i_{\varsigma_7}| = p-1 + 1 + p-1
+ 1 =2p\), implies \(\varphi'_{ac}(\mathscr{F}_p) \geq 2p\)
is the lower bound. On combining the upper and lower bounds, \(\varphi'_{ac}(\mathscr{F}_p) = 2p\).
Table 7 shows that each color class has at least
one dominating b-edge which is incident with all the other neighboring
color classes.
| Color Class | b-Edges | |
| \(W^1_{\varsigma_7} = p+t\) | \(hx_1, hx_2, hx_3, \ldots, hx_p-1\) | |
| \(W^2_{\varsigma_7} = 2(p+1)\) | \(hx_p\) | |
| \(W^3_{\varsigma_7} = 3p-t+2\) | \(hy_1, hy_2, hy_3, \ldots, hy_p-1\) | |
| \(W^4_{\varsigma_7} = 2p+1\) | \(hy_p\) | |
◻
Theorem 11. For any positive integer \(p \geq 2\), the \(b\)-color local edge antimagic connection number of star graph is \(\varphi'_{ac}(K_{1,p}) = p\).
Proof. Since, \(\varphi'(K_{1,p}) = \Delta(K_{1,p})\), by Lemma 3, \(\varphi'_{ac}(K_{1,p}) \leq p\) is the upper bound. Since all the edges of a star graph are incident to a single hub vertex \(h\), each edge has a unique edge weight and every color class has neighbors in every other classes. Hence the total number of edge weights are \(p\), i.e., \(\varphi'_{ac}(K_{1,p}) \geq p\). On combining both the upper and lower bounds, \(\varphi'_{ac}(K_{1,p}) = p\). ◻
The proposed \(b\)-color local edge antimagic coloring of graphs represents a new and innovative approach to this field of research, which is currently wide open for exploration. This innovative coloring technique takes inspiration from the successful implementation of rainbow antimagic coloring [8,9] and \(b\)-chromatic index in diverse graph structures. The paper offers meticulous proofs that establish the optimality of the proposed coloring approach for specific graphs, with future endeavors aimed at extending these findings to other captivating graph families.
Irving, R. W., & Manlove, D. F. (1999). The \(b\)-chromatic number of a graph. Discrete Applied Mathematics, 91, 127-141.
Lima, C. V. G. C., Martins, N. A., Sampaio, L., Santos, M. C., & Silva, A. (2013). b-chromatic index of graphs. Electronic Notes in Discrete Mathematics, 44, 9-14.
Campos, V. A., Lima, C. V., Martins, N. A., Sampaio, L., Santos, M. C., & Silva, A. (2015). The \(b\)-chromatic index of graphs. Discrete Mathematics, 338(11), 2072-2079.
Agustin, I. H., Dafik, D., Hasan, M., Alfarisi, R., & Prihandini, R. M. (2017). Local edge antimagic coloring of graphs. Far East Journal of Mathematical Sciences, 102(9), 1925-1941.
Agustin, I. H., Hasan, M., Dafik, D., Alfarisi, R., Kristiana, A. I., & Prihandini, R. M. (2018). Local edge antimagic coloring of comb product of graphs. Journal of Physics: Conference Series, 1008.
Rajkumar, S., & Nalliah, M. (2022). On local edge antimagic chromatic number of graphs. Proyecciones Journal of Mathematics, 41(6), 1397-1412.
Arumugam, S., Premalatha, K., Bača, M., & Semaničová-Feňovčíková, A. (2017). Local antimagic vertex coloring of a graph. Graphs and Combinatorics, 33, 275-285.
Dafik, D., Susanto, F., Alfarisi, R., Septory, B. J., Agustin, I. H., & Venkatachalam, M. (2021). On rainbow antimagic coloring of graphs. Advanced Mathematical Models & Applications, 6(3), 278-291.
Septory, B. J., Utoyo, M. I., Dafik, D., Sulistiyono, B., & Agustin, I. H. (2021). On rainbow antimagic coloring of special graphs. Journal of Physics: Conference Series, 1836.
Koch, I., & Peterin, I. (2015). The \(b\)-chromatic index of direct product of graphs. Discrete Applied Mathematics, 190, 109-117.
Jakovac, M., & Peterin, I. (2015). The \(b\)-chromatic index of a graph. Bulletin of the Malaysian Mathematical Sciences Society, 38, 1375-1392.
Kouider, M., & Mahéo, M. (2002). Some bounds for the \(b\)-chromatic number of a graph. Discrete Mathematics, 256(1-2), 267-277.
Falcón, R. M., Venkatachalam, M., & Margaret, S. J. (2023). Solving the \(b\)-coloring problem for subdivision-edge neighborhood coronas. Discrete Mathematics, Algorithms and Applications, 16(2), 2350009.
Cabello, S., & Jakovac, M. (2011). On the \(b\)-chromatic number of regular graphs. Discrete Applied Mathematics, 159(13), 1303-1310.
Vivin, J. V., & Venkatachalam, M. (2015). On \(b\)-chromatic number of sunlet graph and wheel graph families. Journal of the Egyptian Mathematical Society, 23(2), 215-218.
Pratama, S. A., Setiawani, S., & Slamin, S. (2020). Local super antimagic total vertex coloring of some wheel related graphs. Journal of Physics: Conference Series, 1538.
Vivin, J. V., & Venkatachalam, M. (2014). A note on \(b\)-coloring of fan graphs. Journal of Discrete Mathematical Sciences and Cryptography, 17(5-6), 443-448.
Nalliah, M., Shankar, R., & Wang, T. M. (2022). Local antimagic vertex coloring for generalized friendship graphs. Journal of Discrete Mathematical Sciences and Cryptography, 1-16.
Vizing, V. G. (1968). Some unsolved problems in graph theory. Russian Math. Surveys, 23(6), 125.
Vivin, J. V., & Venkatachalam, M. (2010). The \(b\)-chromatic number of star graph families.Le Matematiche, 65(1), 119-125.