Let \( V(G) = \{v_1, v_2, \ldots, v_n\} \) be the vertex set and \( E(G) = \{e_1, e_2, \ldots, e_m\} \) be the edge set of a graph \( G \). The Seidel adjacency matrix of a graph \( G \) is defined as \( S(G) = [s_{ij}] \) of order \( n \times n \), in which \( s_{ij} = -1 \) if \( v_i \) is adjacent to \( v_j \), \( s_{ij} = 1 \) if \( v_i \) is not adjacent to \( v_j \) and \( s_{ii} = 0 \). We introduce here the \( (-1,1) \)-incidence matrix of \( G \) as \( B_S(G) = [c_{ij}] \) of order \( n \times m \), in which \( c_{ij} = -1 \) if \( v_i \) is incident to \( e_j \) and \( c_{ij} = 1 \) if \( v_i \) is not incident to \( e_j \). Further we explore properties of \( B_S(G) \) and of its transpose.
Graph theory is utilized to describe a variety of real world phenomena such as to study the properties of molecules [1– 3], social networks [4], nano-networks [5, 6], ladder networks [7] etc. The matrices of graphs are used to study the spectral and structural properties of graphs [8, 9]. There are several matrices of graphs exists, such as adjacency matrix, incidence matrix, Seidel matrix, Laplacian matrix, distance matrix etc. The Seidel adjacency matrix of a graph has been studied in the literature [10]. The elements of the Seidel adjacency matrix are either \(-1\) or \(1\) or zero. In this paper we introduce a new matrix, which we call \((-1, 1)\)-incidence matrix of a graph, whose elements are either \(-1\) or \(1\) and explore some of its properties.
Let \(G\) be a finite, simple graph with \(n \geq 2\) vertices and \(m \geq 1\) edges. Let \(V(G) = \{v_1, v_2, \ldots, v_n \}\) be the vertex set of \(G\) and \(E(G) = \{e_1, e_2, \ldots, e_m\}\) be the edge set of \(G\). The degree of a vertex \(v_i\) is the number of edges incident to it and is denoted by \(d(v_i)\). The degree of an edge \(e_i\) whose end points are \(u\) and \(v\) is \(d(e_i) = d(u) + d(v) -2\). The line graph of \(G\) is a graph \(L(G)\), whose vertex set has one-to-one correspondence with the edge set of \(G\) and two vertices in \(L(G)\) are adjacent if and only if the corresponding edges are adjacent in \(G\) [11]. Let \(I_n\) denotes the identity matrix of order \(n\), \(J_{p\times q}\) be the matrix of order \(p \times q\), whose all elements are equal to \(1\) and \(M^T\) be the transpose of the matrix \(M\).
The adjacency matrix [12] of a graph \(G\) is a matrix \(A(G) = [a_{ij}]\) of order \(n \times n\), where \[a_{ij} = \left\{ \begin{array}{ll} 1 & \;\;\text{if $v_i$ is adjacent to $v_j$},\\ 0 & \;\; \text{otherwise.} \end{array} \right.\]
The incidence matrix [12] of a graph \(G\) is a matrix \(B(G) = [b_{ij}]\) of order \(n \times m\), where \[b_{ij} = \left\{ \begin{array}{ll} 1 & \;\;\text{if vertex $v_i$ is incident to an edge $e_j$},\\ 0 & \;\; \text{otherwise.} \end{array} \right.\]
The degree matrix of a graph \(G\) is a diagonal matrix \(D(G) = \text{diag}[d(v_1), d(v_2), \ldots, d(v_n)]\).
Lemma 1. [12] For any graph \(G\) with \(n\) vertices and \(m\) edges,
(i) \(B(G)B(G)^T = A(G) + D(G)\) and
(ii) \(B(G)^TB(G) = A(L(G)) + 2I_m\).
The Seidel adjacency matrix of a graph \(G\), introduced by van Lint and Seidel [13], is a matrix \(S(G) = [s_{ij}]\) of order \(n \times n\), where \[s_{ij} = \left\{ \begin{array}{rl} -1 & \;\;\text{if $v_i$ is adjacent to $v_j$},\\ 1 & \;\;\text{if $v_i$ is not adjacent to $v_j$},\\ 0 & \;\; \text{if $i = j$.} \end{array} \right.\]
Properties of Seidel adjacency matrix and its eigenvalues can be found in [14– 17].
Recent studies on graph, including the fault-tolerant mixed metric dimension [18], Cycle-super magic labeling of polyomino linear and zig-zag chains [19], and mixed partition dimension [20], provide valuable insights into the structural properties of the structures.
Analogous to the Seidel adjacency matrix of a graph, we define here the \((-1, 1)\)-incidence matrix of \(G\) as \(n \times m\) matrix \(B_S(G) = [c_{ij}]\), where \[c_{ij} = \left\{ \begin{array}{rl} -1 & \;\;\text{if the vertex $v_i$ is incident to the edge $e_j$},\\ 1 & \;\;\text{if the vertex $v_i$ is not incident to the edge $e_j$.} \end{array} \right.\]
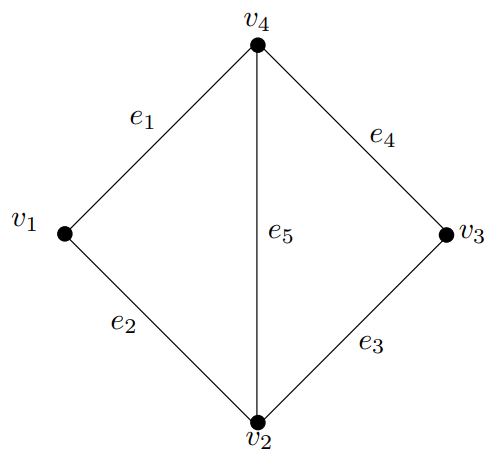
The \((-1, 1)\)-incidence matrix of a graph given in Figure 1 is \[B_S(G) = \left[\begin{array}{rrrrr} -1 & -1 & 1 & 1 & 1 \\ 1 & -1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 & 1 \\ -1 & 1 & 1 & -1 & -1 \end{array} \right].\]
Let graph \(G\) has two components \(G_1\) and \(G_2\). If \(G_i\) has \(n_i\) vertices and \(m_i \geq 1\) edges, \(i = 1,2\). Then the vertices and edges of \(G\) can be labeled in such a way that its \((-1, 1)\)-incidence matrix is of the form \[\left[ \begin{array}{cc} B_S(G_1) & J_{n_1 \times m_2} \\ J_{n_2 \times m_1} & B_S(G_2) \end{array} \right].\]
Proposition 2. If \(G\) is a graph with \(n\) vertices \(v_1, v_2, \ldots, v_n\) and \(m\) edges, then
(i) \(-1\) appeares \(d(v_i)\) times and \(1\) appeares \(m-d(v_i)\) times in the \(i\)-th row of \(B_S(G)\).
(ii) \(-1\) appeares \(2\) times and \(1\) appeares \(n-2\) times in each column of \(B_S(G)\).
Proof. (i) Vertex \(v_i\) is incident to \(d(v_i)\) edges. Hence \(-1\) appeares \(d(v_i)\) times and \(1\) appeares \(m-d(v_i)\) times in the \(i\)-th row of \(B_S(G)\).
(ii) Each edge is incident to its two end points. Hence \(-1\) appeares \(2\) times and \(1\) appeares \(n-2\) times in each column of \(B_S(G)\). ◻
Proposition 3. If \(G\) is a graph with \(n\) vertices \(v_1, v_2, \ldots, v_n\) and \(m\) edges, then
(i) \(B_S(G) = J_{n \times m} – 2B(G)\).
(ii) \(B_S(G)^T = J_{m \times n} – 2B(G)^T\).
(iii) sum of the elements of \(i\)-th row in \(B_S(G)\) is \(m – 2d(v_i)\).
(iv) sum of the elements of each column in \(B_S(G)\) is \(n-4\).
Proof. (i) By the definition of \((-1,1)\)-incidence matrix, we have \(B_S(G) = -B(G) + J_{n \times m} – B(G) = J_{n \times m} – 2B(G)\).
(ii) By above (i), \(B_S(G)^T = (J_{n \times m} – 2B(G))^T = J_{m \times n} – 2B(G)^T\).
(iii) By the first result of Proposition 2, the sum of the elements of the \(i\)-th row in \(B_S(G)\) is \(-d(v_i) + m – d(v_i) = m – 2d(v_i)\).
(iv) By the second result of Proposition 2, the sum of the elements of each column in \(B_S(G)\) is \(-2+n-2 = n-4\). ◻
Corollary 4. If \(G\) is a graph with \(n\) vertices \(v_1, v_2, \ldots, v_n\) and \(m\) edges, then
(i) sum of the elements of \(i\)-th row in \(B_S(G)\) is zero if \(d(v_i) = m/2\).
(ii) sum of the elements of \(i\)-th row in \(B_S(G)\) is positive if \(d(v_i) < m/2\).
(iii) sum of the elements of \(i\)-th row in \(B_S(G)\) is negative if \(d(v_i) > m/2\).
Corollary 5. For a graph \(G\) with \(n\) vertices and \(m\) edges,
(i) the sum of the elements of any column in \(B_S(G)\) is zero if \(n = 4\).
(ii) the sum of the elements of any column in \(B_S(G)\) is positive if \(n > 4\).
(iii) the sum of the elements of any column in \(B_S(G)\) is negative if \(n < 4\).
Since \(d(v_i)\) is a non-negative integer, by Corollary 4(i), we note that there is no graph with odd number of edges so that the sum of the elements of at least one row in \(B_S(G)\) is zero. Also by Corollary 5(i), there is no graph with \(n\) vertices (\(n \neq 4\)) so that the sum of the elements of any column in \(B_S(G)\) is zero.
Analogous to Lemma 1, we give Proposition 6.
For this we define the matrix \(D_S(G) = [d_{ij}]\) of order \(n \times n\), where \[d_{ij} = \left\{ \begin{array}{cl} d(v_i) + d(v_j) & \;\;\text{if $i \neq j$},\\ 0 & \;\;\text{if $i = j$.} \end{array} \right.\]
Proposition 6. For a graph \(G\) with \(n\) vertices and \(m\) edges,
(i) \(B_S(G)B_S(G)^T = mJ_{n \times n} + 4A(G) – 2D_S(G)\).
(ii) \(B_S(G)^TB_S(G) = (n-8)J_{m \times m} + 4A(L(G)) + 8I_m\).
Proof. Let \(v_1, v_2, \ldots, v_n\) be the vertices of \(G\). By Proposition 3 we have, \[B_S(G) = J_{n \times m} – 2B(G) \;\;\;\;\; \text{and} \;\;\;\;\; B_S(G)^T = J_{m \times n} – 2B(G)^T.\]
(i)\[\begin{aligned} B_S(G)B_S(G)^T & = (J_{n \times m} – 2B(G))(J_{m \times n} – 2B(G)^T) \\ & = J_{n \times m}J_{m \times n} – 2B(G)J_{m \times n} – 2J_{n \times m}B(G)^T + 4 B(G)B(G)^T \\ & = mJ_{n \times n} – 2 \left[ \begin{array}{cccc} d(v_1) & d(v_1) & \cdots & d(v_1)\\ d(v_2) & d(v_2) & \cdots & d(v_2)\\ \vdots & \vdots & \\ d(v_n) & d(v_n) & \cdots & d(v_n) \end{array} \right] \\ & – 2 \left[ \begin{array}{cccc} d(v_1) & d(v_2) & \cdots & d(v_n)\\ d(v_1) & d(v_2) & \cdots & d(v_n)\\ \vdots & \vdots & \\ d(v_1) & d(v_2) & \cdots & d(v_n) \end{array} \right] +4(A(G) + D(G)) \\ & = mJ_{n \times n} + 4A(G) – 2 \left[ \begin{array}{cccc} 0 & d(v_1) + d(v_2) & \cdots & d(v_1) + d(v_n)\\ d(v_2) + d(v_1) & 0 & \cdots & d(v_2) + d(v_n) \\ \vdots & \vdots & \\ d(v_n) + d(v_1) & d(v_n) + d(v_2) & \cdots & 0 \end{array} \right] \\ & = m J_{n \times n} + 4A(G) – 2D_S(G). \end{aligned}\]
(ii)\[\begin{aligned} \;\;\;\;\;\;\; B_S(G)^TB_S(G) & = (J_{m \times n} – 2B(G)^T)(J_{n \times m} – 2B(G)) \\ & = J_{m \times n}J_{n \times m} – 2B(G)^TJ_{n \times m} – 2J_{m \times n}B(G) + 4B(G)^TB(G) \\ & = nJ_{m \times m} – 4J_{m \times m} – 4J_{m \times m} + 4(A(L(G)) + 2I_m)\\ & = (n-8)J_{m \times m} + 4A(L(G)) + 8I_m. \end{aligned}\] ◻
Proposition 7. If \(G\) is a graph with \(n\) vertices \(v_1, v_2, \ldots, v_n\) and \(m\) edges, then
(i) \((ij)\)-th element of \(B_S(G)B_S(G)^T\) is \(m+4-2(d(v_i)+d(v_j))\) if \(v_i\) is adjacent to \(v_j\).
(ii) \((ij)\)-th element of \(B_S(G)B_S(G)^T\) is \(m-2(d(v_i)+d(v_j))\) if \(v_i\) is not adjacent to \(v_j\).
(iii) \((ii)\)-th element of \(B_S(G)B_S(G)^T\) is \(m\).
Proof. (i) Let \(v_i\) be adjacent to \(v_j\). Then the \((ij)\)-th element of \(A(G)\) is \(1\) and \((ij)\)-th element of \(D_S(G)\) is \(d(v_i)+d(v_j)\). Therefore by the first result of Proposition 6, the \((ij)\)-th element of \(B_S(G)B_S(G)^T\) is \(m+4-2(d(v_i)+d(v_j))\).
(ii) Let \(v_i\) be not adjacent to \(v_j\). Then the \((ij)\)-th element of \(A(G)\) is \(0\) and \((ij)\)-th element of \(D_S(G)\) is \(d(v_i)+d(v_j)\). Therefore by the first result of Proposition 6, the \((ij)\)-th element of \(B_S(G)B_S(G)^T\) is \(m+0-2(d(v_i)+d(v_j)) = m-2(d(v_i)+d(v_j))\).
(iii) Diagonal elements of \(A(G)\) and \(D_S(G)\) are zeros. Therefore by the first result of Proposition 6, the \((ii)\)-th element of \(B_S(G)B_S(G)^T\) is \(m\). ◻
Proposition 8. If \(G\) is a graph with \(n\) vertices and \(m\) edges \(e_1, e_2, \ldots, e_m\), then
(i) \((ij)\)-th element of \(B_S(G)^TB_S(G)\) is \(n-4\) if \(e_i\) is adjacent to \(e_j\).
(ii) \((ij)\)-th element of \(B_S(G)^TB_S(G)\) is \(n-8\) if \(e_i\) is not adjacent to \(e_j\).
(iii) \((ii)\)-th element of \(B_S(G)^TB_S(G)\) is \(n\).
Proof. (i) Let \(e_i\) be adjacent to \(e_j\). Then the \((ij)\)-th element of \(A(L(G))\) is \(1\) and \((ij)\)-th element of \(I_m\) is zero (\(i \neq j\)). Therefore by the second result of Proposition 6, the \((ij)\)-th element of \(B_S(G)^TB_S(G)\) is \(n-8+4+0 = n-4\).
(ii) Let \(e_i\) be not adjacent to \(e_j\). Then the \((ij)\)-th element of \(A(L(G))\) and of \(I_m\) is zero (\(i \neq j\)). Therefore by the second result of Proposition 6, the \((ij)\)-th element of \(B_S(G)^TB_S(G)\) is \(n-8+0+0 = n-8\).
(iii) Diagonal elements of \(A(L(G))\) are zeros. Therefore by the second result of Proposition 6, the \((ii)\)-th element of \(B_S(G)^TB_S(G)\) is \(n-8+0+8 = n\). ◻
Proposition 9. For any graph \(G\), the matrices \(B_S(G)B_S(G)^T\) and \(B_S(G)^TB_S(G)\) are symmetric.
Proof. Let \(v_1, v_2, \ldots, v_n\) be the vertices of \(G\) and \(e_1, e_2, \ldots, e_m\) be the edges of \(G\).
By Proposition 7, if \(v_i\) is adjacent to \(v_j\), then the \((ij)\)-th element and \((ji)\)-th element of \(B_S(G)B_S(G)^T\) is \(m + 4 -2(d(v_i) + d(v_j))\). Also if \(v_i\) is not adjacent to \(v_j\), then the \((ij)\)-th element and \((ji)\)-th element of \(B_S(G)B_S(G)^T\) is \(m -2(d(v_i) + d(v_j))\). Further \((ii)\)-th element of \(B_S(G)B_S(G)^T\) is \(m\). Hence \(B_S(G)B_S(G)^T\) is a symmetric matrix.
Similarly by Proposition 8 we can show that \(B_S(G)^TB_S(G)\) is also symmetric matrix. ◻
Proposition 10. If \(G\) is a graph with \(n\) vertices \(v_1, v_2, \ldots, v_n\) and \(m\) edges \(e_1, e_2, \ldots, e_m\), then
(i) the sum of the elements of \(i\)-th row (or \(i\)-th column) in \(B_S(G)B_S(G)^T\) is \((n-4)(m-2d(v_i))\).
(ii) the sum of the elements of \(i\)-th row (or \(i\)-th column) in \(B_S(G)^TB_S(G)\) is \((n-8)m + 4d(e_i) + 8\).
Proof. (i) By Proposition 6, \(B_S(G)B_S(G)^T = mJ_{n \times n} + 4A(G) – 2D_S(G)\) and it is symmetric by the Proposition 9. Therefore sum of the elements of \(i\)-th row (or \(i\)-th column) in \(B_S(G)B_S(G)^T\) is \[\begin{aligned} mn + 4d(v_i) – 2\sum_{j=1;\; i \neq j}^{n}[d(v_i) + d(v_j)] &=& mn + 4d(v_i) -2[(n-1)d(v_i) + 2m – d(v_i)] \;\;\;\; \left(\text{since} \;\;\; \sum_{j=1}^{n} d(v_j) = 2m \right) \\ & = (n-4)(m – 2d(v_i)). \end{aligned}\]
(ii) By Proposition 6, \(B_S(G)^TB_S(G) = (n-8)J_{m \times m} + 4A(L(G)) + 8I_m\) and it is symmetric by the Proposition 9. Therefore sum of the elements of \(i\)-th row (or \(i\)-th column) in \(B_S(G)^TB_S(G)\) is \((n-8)m + 4d(e_i) + 8\). ◻
Corollary 11. If \(G\) is a graph with \(n\) vertices \(v_1, v_2, \ldots, v_n\) and \(m\) edges, then
(i) the sum of the elements of \(i\)-th row (or \(i\)-th column) in \(B_S(G)B_S(G)^T\) is zero if \(n=4\) or \(d(v_i) = m/2\).
(ii) the sum of the elements of \(i\)-th row (or \(i\)-th column) in \(B_S(G)B_S(G)^T\) is positive if \(n > 4\) and \(d(v_i) < m/2\).
(iii) the sum of the elements of \(i\)-th row (or \(i\)-th column) in \(B_S(G)B_S(G)^T\) is negative if \(n < 4\) and \(d(v_i) > m/2\).
Corollary 12. If \(G\) is a graph with \(n\) vertices and \(m\) edges \(e_1, e_2, \ldots, e_m\), then
(i) the sum of the elements of \(i\)-th row (or \(i\)-th column) in \(B_S(G)^TB_S(G)\) is zero if \(d(e_i) = (8m – mn -8)/4\).
(ii) the sum of the elements of \(i\)-th row (or \(i\)-th column) in \(B_S(G)^TB_S(G)\) is positive if \(d(e_i) > (8m – mn -8)/4\).
(iii) the sum of the elements of \(i\)-th row (or \(i\)-th column) in \(B_S(G)^TB_S(G)\) is negative if \(d(e_i) < (8m – mn -8)/4\).
Example 1. For a graph given in Figure 1, \[\begin{aligned} B_S(G)B_S(G)^T = \left[\begin{array}{rrrrr} -1 & -1 & 1 & 1 & 1 \\ 1 & -1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 & 1 \\ -1 & 1 & 1 & -1 & -1 \end{array} \right] \left[\begin{array}{rrrr} -1 & 1 & 1 & -1 \\ -1 & -1 & 1 & 1 \\ 1 & -1 & -1 & 1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & 1 & -1 \end{array} \right] = \left[\begin{array}{rrrr} 5 & -1 & -3 & -1 \\ -1 & 5 & -1 & -3 \\ -3 & -1 & 5 & -1 \\ -1 & -3 & -1 & 5 \end{array} \right], \end{aligned}\] and \[\begin{aligned} 5J + 4A(G) – 2D_S(G) = 5\left[\begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{array} \right] + 4\left[\begin{array}{rrrr} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{array} \right] – 2\left[\begin{array}{rrrr} 0 & 5 & 4 & 5 \\ 5 & 0 & 5 & 6 \\ 4 & 5 & 0 & 5 \\ 5 & 6 & 5 & 0 \end{array} \right]= \left[\begin{array}{rrrr} 5 & -1 & -3 & -1 \\ -1 & 5 & -1 & -3 \\ -3 & -1 & 5 & -1 \\ -1 & -3 & -1 & 5 \end{array} \right]. \end{aligned}\]
Therefore \(B_S(G)B_S(G)^T = 5J + 4A(G) – 2D_S(G)\).
Also
\[\begin{aligned} B_S(G)^T B_S(G) = \left[\begin{array}{rrrr} -1 & 1 & 1 & -1 \\ -1 & -1 & 1 & 1 \\ 1 & -1 & -1 & 1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & 1 & -1 \end{array} \right] \left[\begin{array}{rrrrr} -1 & -1 & 1 & 1 & 1 \\ 1 & -1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 & 1 \\ -1 & 1 & 1 & -1 & -1 \end{array} \right] = \left[\begin{array}{rrrrr} 4 & 0 & -4 & 0 & 0 \\ 0 & 4 & 0 & -4 & 0 \\ -4 & 0 & 4 & 0 & 0 \\ 0 & -4 & 0 & 4 & 0 \\ 0 & 0 & 0 & 0 & 4 \end{array} \right], \end{aligned}\] and \[\begin{aligned} (4 – 8)J + 4A(L(G)) + 8I & = -4\left[\begin{array}{rrrrr} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \end{array} \right] + 4\left[\begin{array}{rrrrr} 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \end{array} \right] + 8\left[\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array} \right] \\ & = \left[\begin{array}{rrrrr} 4 & 0 & -4 & 0 & 0 \\ 0 & 4 & 0 & -4 & 0 \\ -4 & 0 & 4 & 0 & 0 \\ 0 & -4 & 0 & 4 & 0 \\ 0 & 0 & 0 & 0 & 4 \end{array} \right]. \end{aligned}\]
Therefore \(B_S(G)^TB_S(G) = -4J + 4A(G) + 8I\).
Corollary 13. For all graphs \(G\) with \(n \geq 8\) vertices, the sum of the elements of any row (or column) in \(B_S(G)^TB_S(G)\) is positive.
In this article we have introduced the \((-1, 1)\)-incidence matrix \(B_S(G)\) of a graph \(G\) and explored some properties of it and its transpose. This matrix further may be studied to explore the spectral and structural properties of a graph. Particularly, the study of singular values of \(B_S(G)\).
Abu-Saleem, M. (2025). The folded map on an identification graph and its application. Afrika Matematika, 36, Article 23.
Ali, H., Ifthikar, B., Naqvi, S. A., & Fatima, U. (2024). Calculation of degree-based entropy measures for benzenoid planar octahedron networks. Open Journal of Discrete Applied Mathematics, 7, 1–16.
Ramane, H. S. & Yalnaik, A. S. (2017). Status connectivity indices of graphs and its applications to the boiling point of benzenoid hydrocarbons. Journal of Applied Mathematics and Computing, 55, 609–627.
Agrawal, R., Arquam, M., & Singh, A. (2020). Community detection in networks using graph embedding. Procedia Computer Science, 173, 372–381.
Liu, P., Ali, S., Azeem, M., Jamil, M. K., Zahid, M. A., Ali, W., & Almohsen, B. (2024). Mixed metric dimension and exchange property of hexagonal nano-network. Scientific Reports, 14, Article 26536.
Ali, S., Ahmad, F., & Jamil, M. K. (2024). The novel resolvability parameter, local edge partition dimension of graphs. Open Journal of Discrete Applied Mathematics, 3, 69–71.
Khan, A., Ali, S., Hayat, S., Azeem, M., Zhong, Y., Zahid, M. A., & Alenazi, M. J. F. (2025). Fault-tolerance and unique identification of vertices and edges in a graph: The fault-tolerant mixed metric dimension. Journal of Parallel and Distributed Computing, 197, Article 105024.
Bapat, R. B. (2014). Graphs and Matrices. Springer. New York.
Cvetković, D., Rowlinson, P., & Simić, S. (2010). An Introduction to the Theory of Graph Spectra. Cambridge University Press, Cambridge.
Brouwer, A. E., & Haemers, W. H. (2012). Spectra of Graphs. Springer, New York.
Harary, F. (1969). Graph Theory. Addison–Wesley, Reading.
Cvetković, D. M., Doob, M., & Sachs, H. (1980). Spectra of Graphs – Theory and Application. Academic Press, New York.
Van Lint, J. H., & Seidel, J. J. (1966). Equilateral point sets in elliptic geometry. Nederlandse Akademie van Wetenschappen, Proceedings Series A, 69 & Indagationes Mathematicae, 28, 335–348.
Haemers, W. H. (2012). Seidel switching and graph energy. MATCH Communication in Mathematical and in Computer Chemistry, 68, 653–659.
Ramane, H. S., Gutman, I., & Gundloor, M. M. (2015). Seidel energy of iterated line graphs of regular graphs. Kragujevac Journal of Mathematics, 39, 7–12.
Oboudi, M. R. (2016). Energy and Seidel energy of graphs. MATCH Communication in Mathematical and in Computer Chemistry, 75, 291–303.
Akbari, S., Askari, J., & Das, K. C. (2020). Some properties of eigenvalues of the Seidel matrix. Linear and Multilinear Algebra, 70, 1–12.
Ali, S., Azeem, M., Zahid, A.M., Usman, M., & Pal, M. (2024). Novel resolvability parameter of some well-known graphs and exchange properties with applications. Journal of Applied Mathematics and Computing 70, 4373–4394.
Azeem, M., Cycle-super magic labeling of polyomino linear and zig-zag chains (2023). Journal of Operations Intelligence, 1(1), 67-81.
Zamri, S. N. A., Ali, S., Azeem, M., Neamah, H. A., & Almohsen, B. (2025). The mixed partition dimension: A new resolvability parameter in graph theory. IEEE Access, 13, 60122-60130.
