Zaslavsky (1991) characterized all single-element coextensions of graphic matroids in terms of a graphical structure called a biased graph. In this paper we characterize all orientations of a single-element coextension of a graphic matroid in terms of graphically defined orientations of its associated biased graph.
We assume that the reader has some familiarity with matroids and oriented matroids as in [1, 2]. Every orientation of a graphic matroid \(M(G)\) is realized by an orientation \(\tau\) of \(G\). Thus, up to reorientation \(M(G)\) has only one orientation (see, for example, [1, Propositions 7.9.3 and 7.9.4]).
Zaslavsky [3, 4] characterized single-element coextensions of graphic matroids in graphical terms using a struture called a biased graph. (Biased graphs will be reviewed in §2.) When \((G,\mathcal L)\) is a biased graph, the associated single-element coextension of \(M(G)\) is denoted by \(L_0(G,\mathcal L)\). In this paper we will define an orientation of a biased graph \((G,\mathcal L)\) in terms of graphical structures. The orientation will be a pair \((o,\tau)\) in which: \(\tau\) is an orientation of the graph \(G\) and a \(o\) is a function which we will call a pre-orientation that chooses a direction along each cycle which is not in \(\mathcal L\). Our three main results are as follows. One, every orientation of \((G,\mathcal L)\) produces an orientation of its matroid \(L_0(G,\mathcal L)\) (Theorem 4). Two, if \((o_1,\tau_1)\) and \((o_2,\tau_2)\) are orientations of \((G,\mathcal L)\) and \(G\) is 2-connected and loopless (equivalently, if \(M(G)\) is connected with rank at least 2), then the associated orientations of \(L_0(G,\mathcal L)\) are equal under reorientation if and only if \(o_1=\pm o_2\) (Theorem 5). Three, any orientation of \(L_0(G,\mathcal L)\) is given by some orientation \((o,\tau)\) of \((G,\mathcal L)\) (Theorem 7). These results are part of the PhD thesis of the author [5].
The dual concept of single-element extensions of graphic matroids as well as their orientations were both characterized in graphic terms by Slilaty and Zaslavsky [6] and Slilaty [7] respectively.
A theta graph consists of two degree-3 vertices connected by three internally disjoint paths. A theta graph contains exactly three cycles. A collection of cycles in a graph \(G\) is called a linear class when each theta subgraph contains zero, one, or three cycles from \(\mathcal L\); equivalently, no theta subgraph contains exactly two cycles from \(\mathcal L\). We say that \(\mathcal L\) is trivial when it contains all of the cycles of \(G\). A biased graph is a pair \((G,\mathcal L)\) in which \(G\) is a graph and \(\mathcal L\) is a linear class of cycles of \(G\). Cycles of \(G\) which are in \(\mathcal L\) are called balanced. A subgraph \(H\) of \(G\) is called balanced when every cycle in it is balanced. If \(B\subset E(G)\) and \(G\backslash B\) is balanced, then \(B\) is called a balancing set of \((G,\mathcal L)\). If \(B\) is a minimal balancing set, then \(G\backslash B\) has the same number of connected components as \(G\) because a forest is always balanced.
In a graph \(G\), an oriented edge is an edge \(e\) along with a chosen direction along that edge. In this paper we will always denote the reverse orientation of \(e\) by \(-e\). The set of all possible oriented edges of \(G\) is denote by \(\vec E(G)\).
Let \(C\) be a cycle with \(E(C)=\{e_1,\ldots,e_n\}\). An orientation of \(C\) is \(o(C)=\{e_1',\ldots,e_n'\}\) in which \(e_i'\) is an orientation of \(e_i\) such that \(e_1',\ldots,e_n'\) are all in the same direction around \(C\). If \(o(C)\) is an orientation of \(C\), then the reverse orientation is denoted \(-o(C)\).
Oriented edges are depicted in the usual fashion as a segment with an arrow in the middle. An orientation of a cycle \(C\) will be depicted as a circular arc near \(C\) with an arrow at one end, see Figure 1.
Now let \(\Gamma\) be an additive group. A \(\Gamma\)–gain function is a function \(\varphi\colon\vec E(G)\to\Gamma\) satisfying \(\varphi(-e)=-\varphi(e)\).1 If \(o(C)\) is an orientation of cycle \(C\), then define \(\varphi(o(C))=\sum_{e\in o(C)}\varphi(e)\). Say that \(C\) is balanced when \[0=\varphi(o(C))=-\varphi(o(C))=\varphi(-o(C))\] and denote the collection of balanced cycles in \(G\) by \(\mathcal L_\varphi\).
Proposition 1(Zaslavsky [3]) If \(\Gamma\) is an additive group and \(\varphi\) a \(\Gamma\)-gain function of \(G\), then \((G,\mathcal L_\varphi)\) is a biased graph.
We remark that for any graph \(G\), there is an \(\mathbb R\)-gain function \(\varphi\) such that \(\mathcal L_\varphi=\emptyset\). Consider some set of \(|E(G)|\) distinct prime numbers \(\{p_e:e\in E(G)\}\). Now arbitrarily choose some orientation for each \(e\in E(G)\) and set \(\varphi(e)=\log(p_e)\). Now for any oriented cycle \(o(C)\) in \(G\) we have that \(\varphi(o(C))\neq\log(1)=0\).
A pair of cycles \(C_1,C_2\) in a graph \(G\) form a modular pair when \(C_1\cap C_2\) is either: empty, a single vertex, or a path; that is, when \(C_1\cup C_2\) has two edges whose removal leaves a forest (see Figure 2).
The matroid of Theorem 1 is denoted by \(L_0(G,\mathcal L)\) and is called the complete lift matroid of \((G,\mathcal L)\). We will only be using the circuits and cocircuits of this matroid. If \(\mathcal L\) is trivial, then the single-element coextension associated with \(\mathcal L\) is just \(M(G)\) along with a new element that is either a loop or coloop.
Theorem 1(Zaslavsky [4]). If \(\mathcal L\) is a non-trivial linear class of cycles of \(G\), then there is a matroid with element set \(E(G)\cup e_0\) in which \(e_0\) is neither a loop nor a coloop and whose cocircuits consist of the edge sets of the following subgraphs:
(1) cycles in \(\mathcal L\),
(2) \(C\cup e_0\) in which \(C\) is a cycle which is not \(\mathcal L\), and
(3) \(C_1\cup C_2\) in which \(C_1,C_2\) is a modular pair of cycles such that no cycle \(C\subset C_1\cup C_2\) is in \(\mathcal L\).
Conversely, if \(N\) is a single-element coextension of the graphic matroid \(M(G)\) with new element \(e_0\) which is neither a loop nor a coloop of \(N\), then there is a unique and non-trivial linear class of cycles \(\mathcal L\) of \(G\) such that the circuits of \(N\) consist of the sets above.
Theorem 2 (Zaslavsky [4]). If \(\mathcal L\) is a non-trivial linear class of cycles of \(G\), then the cocircuits of \(L_0(G,\mathcal L)\) consist of the following:
(1) bonds of \(G\) and
(2) sets of the form \(B\cup e_0\) in which \(B\) is a minimal balancing set of \((G,\mathcal L)\).
Let \(M\) be a matroid. A pair of circuits \(C_1,C_2\) in \(M\) is a modular pair if and only if \(r(C_1\cup C_2)=|C_1\cup C_2|-2\). Circuits \(C_1\) and \(C_2\) are adjacent when the pair is modular and \(M|(C_1\cup C_2)\) is a connected matroid. The reader can verify that if \(C_1,C_2\) is a modular pair of circuits, then \(M|(C_1\cup C_2)\) is connected if and only if \(C_1\cap C_2\neq\emptyset\). More generally, if \(C_1,C_2\) is any pair of circuits for which \(C_1\cap C_2\neq\emptyset\), then \(M|(C_1\cup C_2)\) will be connected. The converse, however, need not be true when \(C_1,C_2\) is not modular.
A subset \(\mathcal L\) of the set of circuits of a matroid \(M\) is called a linear class when every modular pair of circuits \(C_1,C_2\) satisfies the property that if \(C_1,C_2\in\mathcal L\) then every circuit of \(M|(C_1\cup C_2)\) is in \(\mathcal L\). Equivalently, either zero, one, or all circuits of \(M|(C_1\cup C_2)\) are in \(\mathcal L\) for every modular pair of circuits \(C_1,C_2\). A simple example of a linear class is the following. Let \(e\in E(M)\) and let \(\mathcal L_e\) denote the set of circuits of \(M\) which do not contain \(e\). Clearly \(\mathcal L_e\) is a linear class.
It is important to note that a modular pair of cycles in a graph \(G\) as we have defined it is exactly a modular pair of circuits in \(M(G)\). Now if \(C_1,C_2\) are a modular pair of cycles in \(G\), then \(M(G)|(C_1\cup C_2)\) is connected if and only if \(E(C_1)\cap E(C_2)\neq\emptyset\) if and only if \(C_1\cup C_2\) is a theta graph.
A circuit path in a matroid \(M\) is a sequence of circuits \(C_1,\ldots, C_n\) such that \(C_i\) and \(C_{i+1}\) are adjacent. If \(\mathcal L\) is a linear class of circuits in \(M\), then a circuit path is off \(\mathcal L\) if each \(C_i\notin\mathcal L\).
Theorem 3(Tutte [8, (4.34)]).If \(M\) is a connected matroid and \(\mathcal L\) a linear class of circuits in \(M\), then for each pair of circuits \(C,C'\notin\mathcal L\), there is a circuit path off \(\mathcal L\) from \(C\) to \(C'\).
Given a biased graph \((G,\mathcal L)\), consider a function \(o\) on the unbalanced cycles of \(C\) where \(o(C)\) is a choice of orientation of \(C\). We call \(o\) a pre-orientation of \((G,\mathcal L)\) when it satisfies the following properties for any theta subgraph \(H\) of \(G\).
If \(H\) has exactly two unbalanced cycles \(C_1\) and \(C_2\), then \(o(C_1)\) and \(o(C_2)\) agree on the path \(C_1\cap C_2\).
If \(H\) has three unbalanced cycles, then the cycles may be labeled \(C_1,C_2,C_3\) such that \(o(C_1)\) and \(o(C_2)\) disagree on \(C_1\cap C_2\), \(o(C_1)\) and \(o(C_3)\) agree on \(C_1\cap C_3\), and \(o(C_2)\) and \(o(C_3)\) agree on \(C_2\cap C_3\).
Required cycle orientations in \(\theta\)-subgraphs corresponding to the given pre-orientation are illustrated in Figure 3.
Let \(\varphi\) be an \(\mathbb R\)-gain function on \(G\) and let \(o(C)\) be an oriented cycle in \(G\). If \(\varphi(o(C))=0\), then \(C\) is balanced. If \(C\) is unbalanced, then define \(o_\varphi(C)=o(C)\) when \(\varphi(o(C))>0\) and \(o_\varphi(C)=-o(C)\) when \(\varphi(o(C))<0\).
Proposition 2.If \(\varphi\) is an \(\mathbb R\)-gain function on \(G\), then \(o_\varphi\) is a pre-orientation of \((G,\mathcal L_\varphi)\).
Proof. Let \(o(C_1),o(C_2),o(C_3)\) be orientations of the three cycles of theta subgraph \(H\) of \(G\) as shown in Figure 4. Therefore \(\varphi(o(C_1))+\varphi(o(C_2))+\varphi(o(C_3))=0\). If exactly one \(\varphi(o(C_i))=0\), say \(i=3\), then without loss of generality \(o_\varphi(C_1)=o(C_1)\) and \(o_\varphi(C_2)=-o(C_2)\) which means \(o_\varphi\) satisfies Property (1) for pre-orientations. If all \(\varphi(C_i)\neq0\), then two of these \(\varphi\)-values have the same sign (say without loss of generality that \(\varphi(o(C_1))\) and \(\varphi(o(C_1))\) are both positive) and \(\varphi(o(C_3))\) is negative. Thus \(o_\varphi(C_1)=o(C_1)\), \(o_\varphi(C_2)=o(C_2)\), and \(o_\varphi(C_3)=-o(C_3)\). Thus \(o_\varphi\) satisfies Property (2) for pre-orientations. ◻
An orientation of a biased graph \((G,\mathcal L)\) is a pair \((o,\tau)\) in which \(o\) is a pre-orientation of \((G,\mathcal L)\) and \(\tau\) is an orientation of \(G\). We will use \((o,\tau)\) to define a circuit signature and cocircuit signature of \(L_0(G,\mathcal L)\). In Theorem 4 we will prove that these signatures define an orientation and dual orientation of \(L_0(G,\mathcal L)\). The resulting oriented matroid with underlying matroid \(L_0(G,\mathcal L)\) will be denoted by \(\mathfrak O(\tau,e)\).
For each circuit \(C\) of \(L_0(G,\mathcal L)\), an orientation \((o,\tau)\) of \((G,\mathcal L)\) will produce two signed circuits \([o,\tau,C]\) and \(-[o,\tau,C]\) which are defined as follows. The notation \([o,\tau,C]\) is used because the underlying circuit of this signed circuit is \(C\) and the signing depends on \((o,\tau)\).
If \(C\) is a balanced cycle, then arbitrarily choose one orientation of the cycle. Now \(e\in[o,\tau,C]_+\) when \(e\) under \(\tau\) is in the chosen orientation; otherwise, \(e\in[o,\tau,C]_-\).
If \(C=C_0\cup e_0\) in which \(C_0\) is an unbalanced cycle, then \(e\in[o,\tau,C]_+\) when \(e=e_0\) or the orientation of \(e\) under \(\tau\) is in \(o(C)\); otherwise, \(e\in[o,\tau,C]_-\).
If \(C=C_1\cup C_2\) where \(C_1,C_2\) is a modular pair of cycles with the additional condition that \(o(C_1)\) and \(o(C_2)\) disagree on \(C_1\cap C_2\) when \(C\) is a theta graph, then \(e\in[o,\tau,C]_+\) when the orientation of \(e\) under \(\tau\) is in \(o(C_1)\) or \(-o(C_2)\); otherwise, \(e\in[o,\tau,C]_-\).
Cyclic orientations of circuits formed by the union of modular pairs of cycles are illustrated in Figure 5.
For each cocircuit \(C\) of \(L_0(G,\mathcal L)\), an orientation \((o,\tau)\) will produce two signed cocircuits \([o,\tau,C]\) and \(-[o,\tau,C]\); however, before we can define \([o,\tau,C]\), we need to establish a property of minimal balancing sets.
Let \(o\) be a pre-orientation of \((G,\mathcal L)\), \(B\) a minimal balancing set of \((G,\mathcal L)\), and \(e\in B\). Because \(G\backslash B\) is balanced and \(B\) is minimal, a cycle in \((G\backslash B)\cup e\) is unbalanced if and only if it contains \(e\); furthermore, such an unbalanced cycle must exist. So let \(C\) be an unbalanced cycle in \((G\backslash B)\cup e\). Let \((C,o,B,e)\) denote the orientation of \(e\) which is in \(o(C)\). In Proposition 3 we show that \((C,o,B,e)\) is independent of \(C\) and so we denote this orientation of \(e\) with respect to \(B\) and \(o\) by \((o,B,e)\).
Proposition 3. For any two unbalanced cycles \(C_1\) and \(C_2\) in \((G\backslash B)\cup e\), \((C_1,o,B,e)=(C_2,o,B,e)\).
Proof. First, assume that \(C_1,C_2\) is a modular pair of cycles in \(G\). Since \(e\in C_1\cap C_2\) it must be that \(C_1\cup C_2\) is a theta graph whose third cycle is balanced. By the property of pre-orientations on \((G,\mathcal L)\) \((C_1,o,B,e)=(C_2,o,B,e)\), as required.
Now suppose that \(C_1,C_2\) is not a modular pair of cycles. Since \(e\in C_1\cap C_2\), \(M(G)|(C_1\cup C_2)\) is a connected matroid. Let \(\mathcal L_e\) be the linear class of cycles in \(M(G)|(C_1\cup C_2)\) that do not contain \(e\). By Theorem 3 there is a path of adjacent cycles \(A_1,\ldots,A_t\) with \(A_1=C_1\), \(A_t=C_2\), and \(A_i\notin\mathcal L_e\) for each \(i\). Now \((A_i,o,B,e)=(A_{i+1},o,B,e)\) as in the previous paragraph because the third cycle of the theta graph \(A_i\cup A_{i+1}\) is balanced. Our result follows. ◻
Now for a cocircuit \(C\) of \(L_0(G,\mathcal L)\) we define the signed cocircuit \([o,\tau,C]\) as follows.
If \(C\) is a bond in \(G\), then arbitrarily choose one direction across \(C\). Now \(e\in [o,\tau,C]_+\) when the orientation of \(e\) given by \(\tau\) is in the chosen direction across \(C\); otherwise, \(e\in[o,\tau,C]_-\).
If \(C=B\cup e_0\) in which \(B\) is a minimal balancing set of \((G,\mathcal L)\), then \(e\in[o,\tau,C]_+\) when \(e=e_0\) or when the orientation of \(e\) given by \(\tau\) is \(-(o,B,e)\); otherwise, \(e\in[o,\tau,C]_-\).
Theorem 4 (Main Result 1). If \((o,\tau)\) is an orientation of biased graph \((G,\mathcal L)\), then the circuit signature given by \((o,\tau)\) is an orientation of \(L_0(G,\mathcal L)\) and the cocircuit signature given by \((o,\tau)\) is the corresponding dual orientation of \(L_0(G,\mathcal L)\).
Proof. Let \(C\) be a circuit and \(D\) a cocircuit of \(L_0(G,\mathcal L)\). The signed circuit \([o,\tau,C]\) and signed cocircuit \([o,\tau,D]\) are orthogonal when \[\big([o,\tau,C]_+\cap [o,\tau,D]_-\big)\cup\big([o,\tau,C]_-\cap [o,\tau,D]_+\big)\neq\emptyset,\]and\[\big([o,\tau,C]_+\cap [o,\tau,D]_+\big)\cup\big([o,\tau,C]_-\cap [o,\tau,D]_-\big)\neq\emptyset.\]
In order to prove our theorem, we need to show that for each circuit \(C\) and cocircuit \(D\) with \(2\leq|C\cap D|\leq3\) that \([o,\tau,C]\) and \([o,\tau,D]\) are orthogonal. (See, for example, [1, Theorem 3.4.3].) In Case 1 say that \(D\) is a bond and in Case 2 that \(D=B\cup e_0\) in which \(B\) is a minimal balancing set.
Case 1. Either \(C\backslash e_0\) is a cycle (either balanced or unbalanced) or \(C=C_1\cup C_2\) in which \(C_1,C_2\) is a modular pair of cycles. If \(C_1\cup C_2\) is a theta graph, then assume that \(C_1\) and \(C_2\) are the cycles for which \(o(C_1)\) and \(o(C_2)\) disagree on \(C_1\cap C_2\). In the former case \(C\cap D=\{e_1,e_2\}\) and in the latter case \(C_i\cap D=\{e_1,e_2\}\) for some \(i\). Now \(e_1\) and \(e_2\) have the same sign in \([o,\tau,D]\) if and only if these edges are oriented by \(\tau\) in the same direction across the bond \(D\) and \(e_1\) and \(e_2\) have the same sign in \([o,\tau,C]\) if and only if they are oriented in opposite directions across the bond \(D\). Thus \([o,\tau,C]\) and \([o,\tau,D]\) are orthogonal.
Case 2. By its definition and the definition of our circuit and cocircuit signatures, orthogonality is not affected by reorientation of \(\tau\). So we may assume throughout Case 2 that \([o,\tau,C]\) is all positive. In Case 2.1 assume that \(C\backslash e_0\) is a cycle and in Case 2.2 that \(C\) is a union of a modular pair of cycles.
Subcase 2.1. Let \(C_0=C\backslash e_0\). Thus \(1\leq|C_0\cap B|\leq3\). Split this case into three subcases based on \(|C_0\cap B|\).
Subsubcase 2.1.1. Write \(C_0\cap B=\{e\}\). Thus \(C=C_0\cup e_0\). By assumption in this case \(e_0,e\in[o,\tau,C]_+\) which implies that \(e\) is in the direction of \((o,B,e)\) under \(\tau\). Thus \(e\in[o,\tau,D]_-\) while \(e_0\in[o,\tau,D]_+\) and so \([o,\tau,C]\) and \([o,\tau,D]\) are orthogonal.
Subsubcase 2.1.2. Write \(C_0\cap B=\{e_1,e_2\}\). Now write \(C_0=P_1\cup e_1\cup P_2\cup e_2\) where \(P_1\) and \(P_2\) are the two vertex-disjoint paths between \(e_1\) and \(e_2\) on \(C_0\). Since \(G\backslash B\) has the same number of connected components as \(G\), there is a path \(P_0\subseteq G\backslash B\) connecting \(P_1\) to \(P_2\) such that \(P_0\cup C_0\) is a theta graph. The cycle \(C_0\) may be balanced or unbalanced but the other two cycles of the theta graph, call them \(C_1\) and \(C_2\), are unbalanced.
Suppose that \(C_0\) is balanced. Then \(o(C_1)\) and \(o(C_2)\) agree on \(C_1\cap C_2=P_0\). This implies that \((o,B,e_1)\) and \((o,B,e_2)\) are in opposite directions along \(C_0\). Thus \(e_1\) and \(e_2\) have different signs in \([o,\tau,D]\) and so \([o,\tau,C]\) and \([o,\tau,D]\) are orthogonal.
Suppose \(C_0\) is unbalanced. If \(o(C_1)\) and \(o(C_2)\) agree on \(C_1\cap C_2=P_0\), then \([o,\tau,C]\) and \([o,\tau,D]\) are orthogonal as in the previous paragraph because, again, \((o,B,e_1)\) and \((o,B,e_2)\) are in opposite directions along \(C_0\). If, however, \(o(C_1)\) and \(o(C_2)\) disagree on \(C_1\cap C_2=P_0\), then \((o,B,e_1)\) and \((o,B,e_2)\) are in the same direction along \(C_0\); in fact, it must be that \((o,B,e_1),(o,B,e_2)\in o(C_0)\) because \(o(C_0)\) must agree with both \(o(C_1)\) and \(o(C_2)\) on their paths of intersection by the properties of a pre-orientation. Thus \(e_1,e_2\in[o,\tau,D]_-\) while \(e_0\in[o,\tau,D]_+\). Thus \([o,\tau,C]\) and \([o,\tau,D]\) are orthogonal.
Subsubcase 2.1.3. Write \(C_0\cap B=\{e_1,e_2,e_3\}\). Because \(|C\cap B|\leq3\), \(e_0\notin C\) which makes \(C\) a balanced cycle. Now write \(C=e_1\cup P_1\cup e_2\cup P_2\cup e_3\cup P_3\) in which \(P_1,P_2,P_3\) are mutually vertex-disjoint paths with \(P_i\) connecting \(e_i\) to \(e_{i+1}\). Since \([o,\tau,C]\) is all positive, we need to show that there are \(i,j\in\{1,2,3\}\) such that \((o,B,e_i)\) and \((o,B,e_j)\) are not in the same direction around \(C\). By way of contradiction, assume that \((o,B,e_1),(o,B,e_2),(o,B,e_3)\) are all in the same direction around \(C\). Again, there is a path \(P\subseteq G\backslash B\) connecting \(P_i\) and \(P_j\) such that \(C\cup P\) is a theta graph. Let \(C_1,C_1'\) denote the two cycles of \(C\cup P\) whose intersection is \(P\). Without loss of generality \(e_1\in C_1\) and \(e_2,e_3\in C_1'\). Since \(C_1\cap B=\{e_1\}\), we must have that \((o,B,e_1)\in o(C_1)\). Since \(C\) is balanced, \(o(C_1')\) agrees with \(o(C_1)\) on \(P\). Thus \((o,B,e_2),(o,B,e_3)\notin o(C_1')\) (see the left configuration in Figure 6.)
Now, there is a path \(P'\subseteq G\backslash B\) for which \(C_1'\cup P'\) is a theta graph. Let \(C_2,C_3\) denote the two cycles of \(C_1'\cup P'\) whose intersection is \(P'\). Say \(e_2\in C_2\) and \(e_3\in C_3\). For \(i\in\{2,3\}\), \(C_i\cap B=\{e_i\}\) and so \((o,B,e_i)\in o(C_i)\). Now, however, \(o(C_1'),o(C_2),o(C_3)\) pairwise disagree on their paths of intersection. This contradicts the fact that \(o\) is a pre-orientation of \((G,\mathcal L)\) (See the right configuration in Figure 6.)
Subcase 2.2. Say that \(C=C_1\cup C_2\) in which \(C_1,C_2\) is a modular pair of unbalanced cycles. In the case that \(C\) is a theta graph, choose \(C_1,C_2\) so that \(o(C_1)\) and \(o(C_2)\) disagree on \(C_1\cap C_2\). Now \([o,\tau,C_1\cup e_0]\) is all positive and \([o,\tau,C_2\cup e_0]\) is all negative aside from \(e_0\in[o,\tau,C_2\cup e_0]_+\). By Case 2.1 both \([o,\tau,C_1\cup e_0]\) and \([o,\tau,C_2\cup e_0]\) are orthogonal to \([o,\tau,D]\) and so there is \(e_1\in C_1\) for which \(e_1\in[o,\tau,D]_-\) and \(e_2\in C_2\) for which \(e_2\in[o,\tau,D]_+\). Thus \([o,\tau,C]\) and \([o,\tau,D]\) are orthogonal. ◻
Example 1. Let \(3K_2\) be the theta graph consisting of three parallel links \(a,b,c\). The matroid \(L_0(3K_2,\emptyset)\) is the uniform matroid \(U_{2,4}\). Up to reorientation, there are three orientations of a labeled copy of \(U_{2,4}\). The three orientations of \((3K_2,\emptyset)\) shown in Figure 7 produce the circuit signatures given below which are pairwise unequal up to reorientation.
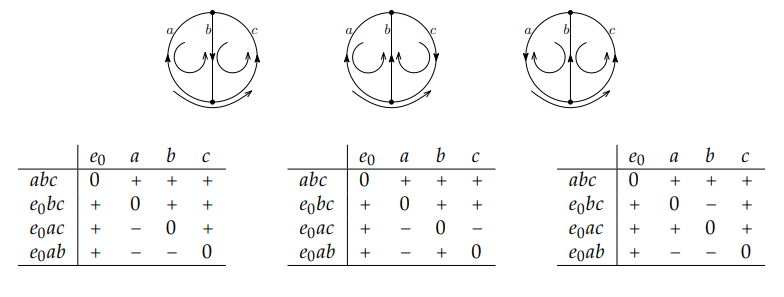
| \(e_0\) | \(a\) | \(b\) | \(c\) | |
|---|---|---|---|---|
| \(abc\) | 0 | \(+\) | \(+\) | \(+\) |
| \(e_0bc\) | \(+\) | 0 | \(+\) | \(+\) |
| \(e_0ac\) | \(+\) | \(-\) | 0 | \(+\) |
| \(e_0ab\) | \(+\) | \(-\) | \(-\) | 0 |
| \(e_0\) | \(a\) | \(b\) | \(c\) | |
|---|---|---|---|---|
| \(abc\) | 0 | \(+\) | \(+\) | \(+\) |
| \(e_0bc\) | \(+\) | 0 | \(+\) | \(+\) |
| \(e_0ac\) | \(+\) | \(-\) | 0 | \(-\) |
| \(e_0ab\) | \(+\) | \(-\) | \(+\) | 0 |
| \(e_0\) | \(a\) | \(b\) | \(c\) | |
|---|---|---|---|---|
| \(abc\) | 0 | \(+\) | \(+\) | \(+\) |
| \(e_0bc\) | \(+\) | 0 | \(-\) | \(+\) |
| \(e_0ac\) | \(+\) | \(+\) | 0 | \(+\) |
| \(e_0ab\) | \(+\) | \(-\) | \(-\) | 0 |
If \(\tau\) is an orientation of a graph \(G\), then denote the reorientation of \(\tau\) on \(X\subseteq E(G)\) by \(\tau_X\). Now let \((o,\tau)\) be an orientation of \((G,\mathcal L)\) and \(\mathfrak O(o,\tau)\) denote the orientation of \(L_0(G,\mathcal L)\) given by \((o,\tau)\). The reorientation of \(\mathfrak O(o,\tau)\) on \(X\subseteq E(G)\) is clearly given by \(\mathfrak O(o,\tau_X)\) according to our definition of circuit signatures. Furthermore, as with any general oriented matroid, the reorientation of \(\mathfrak O(o,\tau)\) on \(X\cup e_0\) is the same as the reorientation of \(\mathfrak O(o,\tau)\) on the complement of \(X\cup e_0\); that is, \(E(G)\backslash X\). Thus reorientations of \(\tau\) on subsets of \(E(G)\) are enough to describe all reorientations \(\mathfrak O(o,\tau)\).
Proposition 4. If \(o\) is a pre-orientation of \((G,\mathcal L)\), then any two orientations of \(L_0(G,\mathcal L)\) given by \(o\) and \(-o\) are equal up to reorientation.
Proof. The reorientation of \(\mathfrak O(o,\tau)\) on \(e_0\) is \(\mathfrak O(o,\tau_{E(G)})\) which according to our definition of circuit signatures is \(\mathfrak O(-o,\tau)\). This implies our result. ◻
Theorem 5(Main Result 2). Let \(G\) be a 2-connected graph without loops. If \(o_1\) and \(o_2\) are pre-orientations of \((G,\mathcal L)\), then any two orientations of \(L_0(G,\mathcal L)\) given by \(o_1\) and \(o_2\) are equal up to reorientation if and only if \(o_1=\pm o_2\).
Proof. The easier direction is given by Proposition 4. So now assume that \(o_1\neq\pm o_2\). This means that there are unbalanced cycles \(C\) and \(C'\) for which \(o_1(C)=o_2(C)\) and \(o_1(C')\neq o_2(C')\). Since \(G\) is 2-connected and without loops \(M(G)\) is connected. Theorem 3 implies that there is a path of unbalanced cycles \(A_1,\ldots,A_t\) for which \(C=A_1\), \(C'=A_t\), and \(A_i\cup A_{i+1}\) is a theta graph. Thus there is \(i\) for which \(o_1\) and \(o_2\) agree on \(A_i\) and disagree on \(A_{i+1}\). Since \(o_1\) and \(o_2\) are pre-orientations, this implies that the theta graph \(A_i\cup A_{i+1}\) does not contain any balanced cycles. The cosimplification of \(L_0(G,\mathcal L)|(A_i\cup A_{i+1})\) is \(U_{2,4}\) and so the circuit signatures on the coparallel classes of elements of \(L_0(G,\mathcal L)|(A_i\cup A_{i+1})\) are among those shown in Figure 7. Thus any two orientations given by \(o_1\) and \(o_2\) are unequal up to reorientation on \(L_0(G,\mathcal L)|(A_i\cup A_{i+1})\) and hence on the whole of \(L_0(G,\mathcal L)\). ◻
There are examples of biased graphs for which there are only two pre-orientations \(o\) and \(-o\). The canonical example is an additively biased graph. A biased graph \((G,\mathcal L)\) is additively biased when every theta subgraph contains either one or three balanced cycles (i.e., never contains zero balanced cycles).
Theorem 6. Let \(G\) be a 2-connected graph without loops. If \((G,\mathcal L)\) is additively biased and has a pre-orientation \(o\), then \(o\) and \(-o\) are the only pre-orientations of \((G,\mathcal L)\).
Proof. Let \(o_1\) and \(o_2\) be pre-orientations on \((G,\mathcal L)\) and \(C\) be an unbalanced cycle. Using negation, assume that \(o_1(C)=o_2(C)\). Now for any other unbalanced cycle \(C'\) in \((G,\mathcal L)\) we may use Theorem 3 as in the proof of Theorem 5 to show that \(o_1\) and \(o_2\) are equal on \(C'\). ◻
Our final result is Theorem 7. This result combined with Theorems 4 and 5 tell us that every orientation of any single-element coextension of a connected graphic matroid is uniquely represented by an orientation \((o,\tau)\) of the associated biased graph \((G,\mathcal L)\) up to negation of \(o\).
Theorem 7 (Main Result 3). Every orientation of \(L_0(G,\mathcal L)\) is given by an orientation \((o,\tau)\) of \((G,\mathcal L)\).
Proof. Let \(\mathfrak O\) be an oriented matroid whose underlying matroid is \(L_0(G,\mathcal L)\). Thus \(\mathfrak O/e_0\) is an orientation of \(M(G)\) and there are exactly two orientations of \(G\), say \(\tau\) along with its reversal \(\tau_{E(G)}\), which represent \(\mathfrak O/e_0\). Now let \(C\) be an unbalanced cycle of \((G,\mathcal L)\) and let \(\hat C\) be the signing of circuit \(C\cup e_0\) in \(\mathfrak O\) in which \(e_0\) is positive. Since the signing of \(C\) in \(\mathfrak O/e_0\) is inherited by \(\mathfrak O\), the edges of \(C\) which are positive in \(\hat C\) are all oriented under \(\tau\) in the same direction around \(C\). Let \(o(C)\) be the orientation of \(C\) which contains these oriented edges. We have now defined \(o\) on all unbalanced cycles. We claim that \(o\) is a pre-orientation and that \((o,\tau)\) determines \(\mathfrak O\). The latter will be done by checking that the circuit signatures of \(\mathfrak O\) are given by \((o,\tau)\) which we have just established is the case for both the balanced and unbalanced cycles.
Consider a circuit of \(C_1\cup C_2\) in which \(C_1\) and \(C_2\) are edge-disjoint unbalanced cycles. Reorient \(\mathfrak O\) on the edges of \(C_1\) so that we have an all-positive signing, call it \(\hat C_1\), of \(C_1\cup e_0\). Reorient the edges of \(C_2\) (which is edge disjoint from \(C_1\)) so that we have a signing, call it \(\hat C_2\), of circuit \(C_2\cup e_0\) that is all positive except for \(e_0\). We have already established that the signatures on \(\hat C_1\) and \(\hat C_2\) are given by \((o,\tau)\). Thus the orientation of the edges of \(C_1\) given by \(\tau\) are all in \(o(C_1)\) and the orientation of the edges of \(C_2\) given by \(\tau\) are all in \(-o(C_2)\). Thus according to our definition, this signature (which is all positive) on \(C_1\cup C_2\) is given by \((o,\tau)\), (confer Figure 5).
Now, consider a circuit of \(C_1\cup C_2\) which is a theta graph. Let \(C_3\) denote the third cycle of \(C_1\cup C_2\). For some pair of cycles \(C_i,C_j\in\{C_1,C_2,C_3\}\) it must be true that \(o(C_i)\) and \(o(C_j)\) disagree on the path \(C_i\cap C_j\). Assume without loss of generality that it is true for \(C_1,C_2\). Because \(o(C_1)\) and \(o(C_2)\) disagree on the path \(C_1\cap C_2\) we may obtain \(\hat C_1\) and \(\hat C_2\) as in the previous paragraph. After we show that \(o\) is a pre-orientation (which we do in the last two paragraphs of this proof) our definition of circuit signatures will yield that the all-positive signature on \(C_1\cup C_2\) is given by \((o,\tau)\).
It remains only to show that \(o\) is a pre-orientation. Let \(C_1\cup C_2\) be a theta graph with third cycle \(C_3\). First, assume that \(C_1,C_2,C_3\) are all unbalanced and let \(\hat C_1\) and \(\hat C_2\) be as in the last paragraph. If we perform signed circuit exchange on \(\hat C_1\) and \(\hat C_2\) using some arbitrary \(e\in C_1\cap C_2\), then we obtain the signing for \(C_3\cup e_0\) in which the elements of \(E(C_3\cap C_1)\cup e_0\) are positive and \(E(C_3\cap C_2)\) are negative. Thus \(o(C_3)\) must agree with both \(o(C_1)\) and \(o(C_2)\) on their paths of intersection. Thus \(o\) satisfies Property (2) for pre-orientations.
Finally, assume that \(C_1\) and \(C_2\) are unbalanced and \(C_3\) is balanced. Reorient \(\mathfrak O\) on the edges of \(C_1\) so that we have an all-positive signing, call it \(\hat C_1\), of \(C_1\cup e_0\). Now reorient \(\mathfrak O\) on \(E(C_3)\backslash E(C_1)\) so that signed circuit \(\hat C_3\) on the edges of \(C_3\) is also all positive. Performing signed circuit exchange on \(e\in E(C_1)\cap E(C_3)\) using \(\hat C_1\) and \(-\hat C_3\) gives that the signing on \(C_2\cup e_0\) is positive on \(E(C_1\cap C_2)\cup e_0\). Thus \(o(C_1)\) and \(o(C_2)\) must agree on \(C_1\cap C_2\). Thus \(o\) satisfies Property (1) for pre-orientations. ◻
In some contexts a \(\Gamma\)-gain function is called a \(\Gamma\)–voltage function and general groups are often used rather than just additive ones. The use of general groups, however, requires some additional considerations which are not necessary in this work.↩︎
Björner, A., Las Vergnas, M., Sturmfels, B., White, N., & Ziegler, G. M. (1999). Oriented Matroids (2nd ed., Vol. 46). Cambridge University Press.
Oxley, J. G. (2006). Matroid Theory (Vol. 3). Oxford University Press, USA.
Zaslavsky, T. (1989). Biased graphs. I. Bias, balance, and gains. Journal of Combinatorial Theory, Series B, 47(1), 32-52.
Zaslavsky, T. (1991). Biased graphs. II. The three matroids. Journal of Combinatorial Theory, Series B, 51(1), 46-72.
Slilaty, D. C. (2000). Orientations of biased graphs and their matroids. State University of New York at Binghamton.
Slilaty, D., & Zaslavsky, T. (2024). Cobiased Graphs: Single-Element Extensions and Elementary Quotients of Graphic Matroids. The Electronic Journal of Combinatorics, 31, P1-54.
Slilaty, D. (n.d.). Orientations of single-element extensions of graphic matroids. Manuscript submitted for publication.
Tutte, W. T. (1965). Lectures on matroids. Journal of Research of the National Bureau of Standards Section B Mathematics and Mathematical Physics, 69(1 and 2), 1-47.