Let \(E(G)\) and \(d_x\) denote the edge set and degree of a vertex \(x\) in \(G\), respectively. Recently, the elliptic Sombor index has been defined as \[ESO(G) = \sum_{xy \in E(G)} (d_x + d_y) \sqrt{d_x^2 + d_y^2}\,.\] A molecular tree is a tree in which the maximum degree does not exceed \(4\). In this paper, we establish sharp upper and lower bounds for the \(ESO\) index in the class of molecular trees with order \(n\) and exactly \(k\) vertices of maximum degree \(\Delta \geq 2\). Moreover, we completely characterize the extremal trees attaining these bounds. Our findings contribute to the structural analysis of molecular trees and further the understanding of the elliptic Sombor index in chemical graph theory.
Article introduction. Throughout this paper, we consider only simple connected undirected graphs. Let \(G\) be such a graph, with vertex set \(V(G)\) and edge set \(E(G)\). Let \(d_x=d_x(G)\), \(N_x=N_x(G)\) and \(\Delta=\Delta(G)\) denote, respectively, the degree of the vertex \(x \in V (G)\), the neighbor set of the vertex \(x\), and the maximum degree of a vertex in \(G\). The number of vertices of maximum degree \(\Delta\) will be denoted by \(k\).
An \(r\)-vertex is a vertex of degree \(r\). If \(r=1\) and \(r \geq 3\), then an \(r\)-vertex is said to be pendent and branching, respectively.
If there is an edge between vertices \(x\) and \(y\), we denote it by \(xy\) (or \(yx\)). Let \(G \setminus \{xy\}\) and \(G \cup \{xy\}\) represent the subgraphs of \(G\) obtained by deleting the edge \(xy\) and adding the edge \(xy \notin E(G)\), respectively. In what follows, the sequence \(\pi = (d_1, d_2, \ldots, d_n)\) is said to be the degree sequence of the graph \(G\) if \(d_i=d_{x_i}\) holds for \(1 \leq i \leq n\), where \(V(G) = \{x_1, x_2, \ldots x_n \}\). Hereafter, we use the symbol \(p^q\) to define \(q\) copies of the real number \(p\).
As usual, let \(P_n\) and \(S_n\) denote the path graph and the star graph over \(n\) vertices. The double star graph \(DS_{i,j}\) with \(n\) vertices is formed by connecting the centers of two stars \(S_{i+1}\) and \(S_{j+1}\), where \(i + j + 2 = n\). The broom tree \(B_{n,\Delta}\) with \(n\) vertices is constructed by attaching \(\Delta-1\) pendent vertices to one end-vertex of the path \(P_{n-\Delta+1}\). A pendent segment of a tree \(T\) is a path-subtree \(S\) with one end as a pendent vertex and the other of degree different from \(2\) in \(T\), while an internal segment has both ends of degrees greater than \(2\). All intermediate vertices (if any) of \(S\) have degree \(2\) in \(T\).
We denote by \(n_i=n_i(G)\) the number of vertices of degree \(i\), and by \(x_{ij}=x_{ij}(G)\) the number of edges between adjacent vertices of degrees \(i\) and \(j\) in \(G\). When the graph under consideration is evident, we omit \(G\) from the notations. A connected acyclic graph whose maximum degree does not exceed \(4\) is referred to as a molecular tree (or chemical tree).
The undefined notations used, can be found in [1].
For an \(n\)-vertex molecular graph, we have the well-known relation: \[\begin{aligned}\label{5} \sum_{\substack{j=1\\ j \neq i}}^{\Delta=4}x_{ji}+2\,x_{ii}=i\cdot n_{i}\,\,\,\,\, \forall\,\,i=\{1,\ldots,\Delta=4\}. \end{aligned} \tag{1}\]
Topological indices numerically characterize molecular structures and help estimating physicochemical properties [2]. Many degree-based indices have been introduced in the literature [3]. One such index, the Sombor index, is based on a geometric interpretation of edge degree radius, and is defined in [4]. This index has attracted significant attention, leading to extensive studies on its mathematical and physicochemical properties [5– 14]. Quite recently, the elliptic Sombor index [15] was introduced as a variant of the Sombor index, also formulated using geometric arguments. It is defined as: \[\begin{aligned} ESO(G)=\sum_{{xy}\in E(G)} (d_x+d_y)\sqrt{d_{x}^2+d_{y}^2}. \end{aligned}\]
Extremal graph problems for topological indices play an important role in Chemical Graph Theory. Here we present a concise review of these studies, pertaining to the \(ESO\) index. In [15], the authors introduced the \(ESO\) index, investigating its mathematical and chemical properties, and characterizing extremal graphs among \((i)\) trees and \((ii)\) connected graphs. Tang et al. [16] determined the maximal \(ESO\) values for trees with a given \((i)\) diameter, \((ii)\) matching number, and \((iii)\) number of pendent vertices, and characterized the the corresponding extremal graphs. The chemical applicability of the \(ESO\) index in modeling physicochemical properties of benzenoid hydrocarbons was studied through regression models in [17], while its ordering in benzenoid systems was explored in [18, 19]. Qi et al. [20] established maximal bicyclic graphs for the \(ESO\) index and characterized the corresponding extremal graph. In [21], the authors demonstrated that the \(ESO\) outperforms the \(SO\) index in predicting physicochemical properties such as entropy, acentric factor, and enthalpy of vaporization. They also established the following bounds for trees with complete characterization: \((i)\) lower bounds for trees with given branching vertices or maximum degree, \((ii)\) lower and upper bounds for trees with given segments or degree-\(2\) vertices. In [22], the authors solve some optimization problems for the generalized \(ESO\), in particular on the set of graphs (respectively, trees) with \(n\) vertices. Alternative formulations, including multiplicative and modified versions, were considered in [23, 24]. Espinal et al. [25] solved the extremal problems for the \(ESO\) index over chemical graphs and chemical trees of fixed order. Additional contributions can be found in [26].
Building on the earlier works on bounds of trees with fixed order and maximum degree (see [27– 34]), we aim to establish sharp bounds on the \(ESO\) index for molecular trees. By fixing not only the maximum degree \(\Delta\) but also the number of vertices of maximum degree, \(n_{\Delta} = k \geq 1\), we introduce an additional constraint that makes the problem more suited to chemical applications.
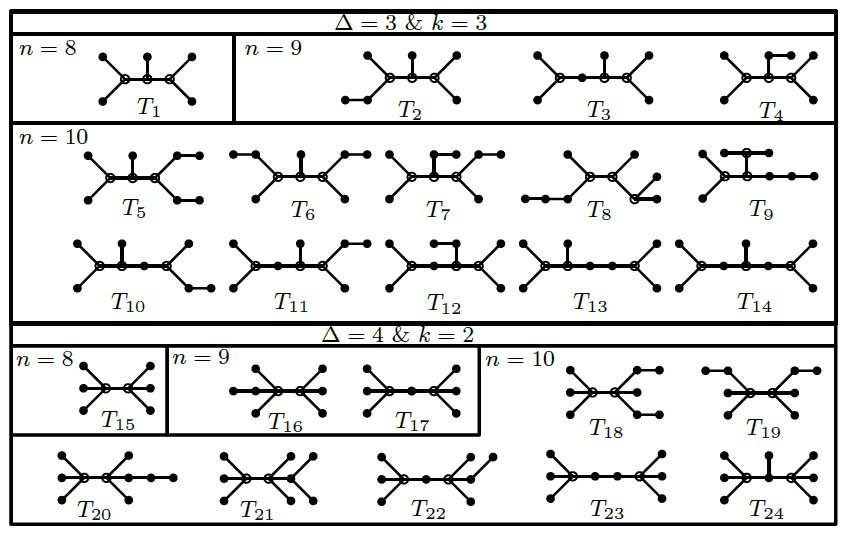
As an illustrative example, in Figure 1 are displayed the (molecular) trees for selected values of \(8 \leq n \leq 9\), \(3 \leq \Delta \leq 4\), and \(2 \leq k \leq 3\).
Since \(n_{\Delta}=k\), we have the following well-known relations: \[ \begin{cases} n_1+n_2+\sum\limits_{i=3}^{\Delta-1}n_i+k=n,\\ n_1+2 n_2+\sum\limits_{i=3}^{\Delta-1}i\,n_i+\Delta \, k=2\,(n-1). \end{cases} \tag{2}\]
From the above, we obtain \(n_1=2+n_3+2n_4+ \cdots +k(\Delta-2)\geq 2+ k(\Delta-2)\). Combining this with \(n\geq n_1+k\), we obtain \(n\geq (\Delta-1)k+2\).
Define the class \(\Gamma_{n,\Delta}^k\) as the set of molecular trees of order \(n \geq (\Delta-1)k+2\), maximum degree \(\Delta \geq 2\), and \(k \geq 1\). For recent studies on this class, we refer the reader to [35, 36]. If \(\Delta = 2\), then obviously the path is the unique element of \(\Gamma_{n,2}^{n-2}\). Therefore, in what follows, it will be assumed that \(\Delta \geq 3\).
We start with an auxiliary result that will have frequent applications in the subsequent section.
Lemma 1. Let \[\begin{aligned} f(y)=(s+y)\sqrt{s^2+y^2}-(t+y)\sqrt{t^2+y^2}, \end{aligned}\] for \(y \geq 1\) and \(s, t>0\). Then:
(i) \(f(y)\) is an increasing function for \(s\geq t\) and strictly increasing for \(s>t\).
(ii) \(f(y)\) is a decreasing function for \(s\leq t\) and strictly decreasing for \(s<t\).
Proof. Since \(y \geq 1\) and \(s, t>0\), it follows that \[\begin{aligned} & (s-t)\left((st)^2(s+t)+2y(st)^2+2y^3(s-t)^2 + y^2(s+t)(s^2+t^2)+y^4(s+t)+2y^3(st+2y^2)\right) \\ & \qquad= (s^2+2y^2+sy)^2(t^2+y^2)-(t^2+2y^2+ty)^2(s^2+y^2). \end{aligned}\]
This means \[\begin{aligned} \label{e0} (s^2+2y^2+sy)^2(t^2+y^2) \geq (\mbox{or}~ \leq)(t^2+2y^2+ty)^2(s^2+y^2)~~\mbox{for}~s \geq t~ (\mbox{or}~s \leq t). \end{aligned} \tag{3}\]
The relation in (3) is strict if \(s>t\) or \(s<t\).
The derivative of \(f(y)\) is \[\begin{aligned} f'(y)= \dfrac{1}{{\sqrt{(s^2+y^2)(t^2+y^2)}}} \left[{(s^2+2y^2+sy)\sqrt{t^2+y^2}-(t^2+2y^2+ty)\sqrt{s^2+y^2}}\right]. \end{aligned}\]
(i) If \(s\geq t\), then from (3), it follows immediately that \(f'(y)\geq 0\), \(i.e.\), \(f(x)\) is an increasing function. Moreover, one can see that \(f(y)\) is strictly increasing for \(s>t\).
(ii) If \(s \leq t\), then the desired result follows directly from (3). In addition, the function \(f(y)\) strictly decreases when \(s<t\). ◻
The remainder of the paper is organized as follows. In §2, we establish best possible bounds on the elliptic Sombor index for trees within \(\Gamma_{n,\Delta}^k\). In §3, we conclude with final insights and remarks.
This section establishes sharp upper and lower bounds for the elliptic Sombor index within \(\Gamma_{n,\Delta}^k\) and characterizes the corresponding extremal trees. Throughout this paper, denote by \(\Theta(i,j)=(i+j)\,\sqrt{i^2+j^2}\), where \(\Theta(i,j)=\Theta(j,i)\) and \(\min \{i,j\}>0\).
This subsection reports an upper bound for the \(ESO\) index in \(\Gamma_{n,\Delta}^k\), along with a complete characterization of the molecular trees that achieve this bound. For \(\Delta = 3\) and \(n \geq 2k+2\), the vertices of degree \(2\) must be placed either on internal or pendent segments (for an example, see trees \(T_1,\,T_2,\, \ldots, T_{14}\) in Figure 1). This case is addressed in Theorem 1. Next we examine structural properties of trees attaining the highest \(ESO\) index in \(\Gamma_{n,\Delta}^k\) for \(\Delta = 4\), \(k \geq 1\) and \(n \geq 3k+2\), leading to the following key observations:
Lemma 2. For a tree \(T\in \Gamma_{n,4}^k\) with the highest \(ESO\) index, \(n_2\leq 1\) holds.
Proof. By contradiction, suppose that \(T\) contains at least two vertices \(x\) and \(y\) of degree \(2\). Let \(N_x=\{x_1,x_2\}\) and \(N_y=\{y_{1'},y_{2'}\}\). Without loss of generality, assume that \(x_1\) and \(y_{1'}\) lie on the \(x-y\) path. Thus \(d_{1}\geq 2\) and \(d_{1'}\geq 2\). Let \(T_1 \in \Gamma_{n,4}^k\) be a tree obtained from \(T\) by deleting the edge \(yy_{2'}\) and adding the edge \(xy_{2'}\). This modification results in \(d_x(T_1)=3\), \(d_y(T_1)=1\), while maintaining \(d_v(T_1)=d_v(T)\) \(\forall\) \(v\in V(T)\backslash \{x,y\}\). We now proceed by considering the following two cases:
Case 1. \(xy \notin E(T)\). Then \[\begin{aligned} ESO({ T}')-ESO ({ T})&=\Theta(3,d_{2})-\Theta(2,d_{2})+\Theta(3,d_{1})-\Theta(2,d_{1})+\Theta(3,d_{2'})-\Theta(2,d_{2'})+\Theta(1,d_{1'})-\Theta(2,d_{1'})\\ &>\Theta(3,d_{1})-\Theta(2,d_{1})+\Theta(1,d_{1'})-\Theta(2,d_{1'}). \end{aligned}\]
Since \(d_{1}\geq 2\) and \(d_{1'}\geq 2\), then from Lemma 1 \((i)\) and \((ii)\), it follows that \[\begin{aligned} ESO({ T}')-ESO ({ T})&>\Theta(3,2)-\Theta(2,2)+\Theta(1,4)-\Theta(2,4)\approx0.46>0,~~\mbox{a contradiction}. \end{aligned}\]
Case 2. \(xy \in E(T)\). Then \[\begin{aligned} ESO({ T}')-ESO ({ T})&= \Theta(3,d_{2})-\Theta(2,d_{2})+\Theta(3,d_{2'})-\Theta(2,d_{2'})+\Theta(1,3)-\Theta(2,2)>0. \end{aligned}\]
In each case, we arrive at a contradiction to our assumption. Hence, for the tree \(T\), \(n_2 \leq 1\) holds. ◻
From Lemma 2, we conclude that \(T\in \Gamma_{n,4}^k\) with highest \(ESO\) index contains at most one vertex of degree \(2\). In the following lemma, we establish the conditions under which \(T\) either has no vertex of degree \(2\) or exactly one vertex of degree \(2\).
Lemma 3. The tree \(T\in \Gamma_{n,4}^k\) satisfies the following:
(a) \(n_2=0\) if and only if \(n-k\equiv 0\pmod2\). Moreover, \(T\) has the degree sequence \(\left(4^{(k)},3^{(\frac{n-3k-2}{2})}, 1^{({\frac{n+k+2}{2})}}\right)\).
(b) \(n_2=1\) if and only if \(n-k\equiv 1\pmod2\). Moreover, \(T\) has the degree sequence \(\left(4^{(k)},3^{(\frac{n-3k-3}{2})},2^{(1)}, 1^{({\frac{n+k+1}{2})}}\right)\).
Proof. For a chemical tree, from (2) we have \[\begin{aligned} \label{eq4.1} \begin{cases} n= n_1+n_2+n_3+k, \\ 2n-2= n_1+2n_2+3n_3+4k. \end{cases} \end{aligned} \tag{4}\]
By combining both relations in (4), we obtain \[\label{eq4.3} n_1=2+n_3+2k. \tag{5}\]
Combining the first relation of (4) with (5), yields \[\label{eq4.5} n-k=2(n_3+k+1)+n_2, ~\mbox{that is},~ n-k\equiv n_2\,(\bmod\,\, 2). \tag{6}\]
From (6), we get \[\label{eq4.4} n_3=\frac{n-3k-n_2-2}{2}. \tag{7}\]
From (5) and (7), we get \[\label{eq4.6} n_1=\frac{n+k-n_2+2}{2}. \tag{8}\]
From (6)–(8), the desired results follow. ◻
Lemma 4. If the tree \(T\in \Gamma_{n,4}^k\) with the highest \(ESO\) index contains a vertex of degree \(2\), then that vertex does not have more than one branching neighbor.
Proof. By Lemma 2, we have \(n_2 \leq 1\). Suppose in contrast that a \(2\) degree vertex \(x\) is adjacent to two branching vertices \(x_1\) and \(x_2\) in \(T\). Therefore \(d_1 \geq 3\) and \(d_2 \geq 3\). We now suppose that a pendent vertex \(y\) is adjacent to a branching vertex \(y_{1'}\) in \(T\) (as \(n_2 \leq 1)\). Without loss of generality, let \(x_1\) lies on the \(x-y\) path. Let \(T_1 \in \Gamma_{n,4}^k\) can be constructed from \(T\) as follows \(T_1=(T \backslash \{x_2x,xx_1\}) \cup \{x_2x_1,yx\}\). This results in \(d_y(T_1)=2\), \(d_x(T_1)=1\), while preserving \(d_v(T)=d_v(T_1)\) \(\forall~ v\in V(T) \backslash\{x,y\}\). Then \[\begin{aligned} ESO(T_1)-ESO (T)&=\Theta(1,2)+\Theta(2,d_{1'})-\Theta(1,d_{1'})+\Theta(d_1,d_2)-\Theta(d_1,2)-\Theta(2,d_2). \end{aligned}\]
Since \(d_{1'} \geq 3\), by Lemma 1 \((i)\), it follows that \[\begin{aligned} ESO(T_1)-ESO (T)&\geq \Theta(1,2)+\Theta(2,3)-\Theta(1,3)+\Theta(d_1,d_2)-\Theta(d_1,2)-\Theta(2,d_2). \end{aligned}\]
By setting \(y=d_1\geq 3\), \(s=d_2 \geq 3\) and \(t=2\) in Lemma 1 \((i)\), we obtain \(f(d_1)=\Theta(d_1,d_2)-\Theta(d_1,2) > \Theta(3,d_2)-\Theta(3,2)=f(3)\). Then by again setting \(y=d_2 \geq 3\), \(s=3\) and \(t=2\) in Lemma 1 \((i)\), we obtain \(f(d_2)=\Theta(3,d_2)-\Theta(2,d_2) > \Theta(3,3)-\Theta(2,3)=f(3)\). By combining these results with the preceding relation, we obtain \[\begin{aligned} ESO(T_1)-ESO (T) > \Theta(1,2)+\Theta(2,3)-\Theta(1,3)+\Theta(3,3)-\Theta(3,2)-\Theta(2,3) \approx 1.46>0. \end{aligned}\]
We arrive at a contradiction to our assumption. Thus we conclude that a \(2\) degree vertex in \(T\) does not have more than one branching neighbor. ◻
Lemma 5. If \(k\geq 2\), then for the tree \(T\in \Gamma_{n,4}^k\) with the highest \(ESO\) index it holds \(x_{44}=k-1\).
Proof. We prove this result by contradiction. Since \(n_4=k \geq 2\), thus for otherwise, we suppose that \(x_{44}<k-1\) in \(T\). By Lemma 4, note that if \(T\) contains a vertex of degree \(2\), then it lies on pendent segment. Thus we suppose that \(T\) contains a path \(x_0-x_{\ell}:x_0x_1\cdots x_{\ell-1}x_{\ell}\) of length \(\ell \geq 2\), where \(d_0=4=d_{\ell}\) and \(d_{1}\cdots =d_{\ell-1}=3\). Since \(n_4=k \geq 2\) and \(n_2 \leq 1\) (by Lemma 2), it follows that \(T\) has a pendent vertex \(y\) adjacent to a branching vertex \(y_{1'}\). Therefore \(d_{1'}\geq 3\). The vertex \(y_{1'}\) may or may not be coincident with either of the vertices \(x_0\) and \(x_{\ell}\). Let \(T_1 \in \Gamma_{n,4}^k\) can be obtained from \(T\) as follows: \[T_1=(T\backslash\{x_0x_1,x_{\ell-1}x_{\ell},y_{1'}y\})\cup\{x_0x_{\ell},y_{1'}x_1,x_{\ell-1}y\}.\]
This implies that the degree of all vertices remains unchanged in \(T\) and \(T_1\). We now continue by distinguishing two cases:
Case 1. The vertex \(y_{1'}\) is distinct from both \(x_0\) and \(x_{\ell}\). Then \[\begin{aligned} ESO(T_1)-ESO (T)&=\Theta(4,4)-\Theta(4,3)+\Theta(1,3)-\Theta(4,3)+\Theta(3,d_{1'})-\Theta(1,d_{1'}). \end{aligned}\]
Since \(d_{1'}\geq 3\), then from Lemma 1 \((i)\), it follows that \[\begin{aligned} ESO(T_1)-ESO (T)>\Theta(4,4)-\Theta(4,3)+\Theta(1,3)-\Theta(4,3)+\Theta(3,3)-\Theta(1,3)\approx0.71>0, \end{aligned}\] which is a contradiction.
Case 2. The vertex \(y_{1'}\) coincides with either \(x_0\) or \(x_{\ell}\). In this case, \[\begin{aligned} ESO({ T}')-ESO (T)= \Theta(4,4)-\Theta(4,3)+\Theta(1,3)-\Theta(4,3)+\Theta(3,4)-\Theta(1,4)\approx 2.26>0. \end{aligned}\]
In each case, one arrives at a contradiction. Thus we conclude that \(x_{44}=k-1\). ◻
Lemma 6. For tree \(T \in \Gamma_{n,4}^k\) with highest \(ESO\) index, \(x_{33}\) and \(x_{14}\) cannot be simultaneously positive.
Proof. Suppose to the contrary that \(x_{33},x_{14}>0\) holds. Then \(T\) contains \(xy, wz\in E(T)\) such that \(d_x=3=d_{y}\), \(d_w=4\) and \(d_z=1\). Let \(N_x \backslash \{y\}=\{x_1, x_2\}\). Without loss of generality, assume that \(y\) lies on the \(x-z\) path. Let \(T_1=(T \backslash \{xx_1,xx_{2}\}) \cup\{zx_1,zx_{2}\}\) be a tree in \(\Gamma_{n,4}^k\) such that \(d_x(T_1)=1\), \(d_z(T_1)=3\) and \(d_v(T_1)=d_v(T)\) \(\forall ~v\in V(T) \backslash \{x,z\}\). Then \[\begin{aligned} ESO(T_1)-ESO (T)=\Theta(1,3)+\Theta(4,3)-\Theta(3,3)-\Theta(1,4)\approx 1.56>0, \end{aligned}\] which is a contradiction. Hence \(x_{33}\) and \(x_{14}\) cannot be simultaneously positive. ◻
Base on Lemma 3 \((b)\), which states that \(T\) contains exactly one vertex of degree \(2\) when \(n-k\equiv 1\pmod2\), we now discuss the adjacency of this degree \(2\) vertex in the following lemma.
Lemma 7. For \(n-k\equiv 1\pmod2\), for a tree \(T\in \Gamma_{n,4}^k\) with highest \(ESO\) index the following holds:
(a) If \(n\leq 7k+5\), then \(x_{23}=0\).
(b) If \(n\geq 7k+7\), then \(x_{24}=0\).
Proof. By Lemmas 2 and 3 \((b)\), we obtain \(n_2=1\) and \(n_3=\frac{n-3k-3}{2}\) for \(n-k\equiv 1\pmod2\). This (namely, \(n_2=1\)) by Lemma 4 implies that \(x_{12}=1\). Therefore we suppose that a \(2\) degree vertex \(x\) is adjacent to a pendent vertex \(x_2\). By Lemma 5, we have \(x_{44}=k-1\).
(a) By contradiction, suppose that \(x_{23}=1\) (as \(n_2=1\) and \(x_{12}=1\)). Then \(T\) contains a \(3\) degree vertex that is adjacent to \(x\). Since \(n_2=1\) and \(x_{12}=1=x_{23}\), then it is evident that \(x_{22}=x_{24}=0\). By setting \(i=\Delta=4\) in (1), then this with \(x_{24}=0\) and \(x_{44}=k-1\) implies that \(x_{14}+x_{34}=2k+2\). Since \(n_3=\frac{n-3k-3}{2}\leq 2k+1\), then this with \(x_{14}+x_{34}=2k+2\) implies that \(x_{14}+x_{34} \geq n_3+1\). This means \(x_{14}\geq1\). Thus \(T\) contains a pendent vertex \(y\) adjacent to a \(4\) degree vertex in \(T\). Let \(T_1\) be a tree in \(\Gamma_{n,4}^k\) such that \(T_1=(T\backslash\{xx_2\}) \cup \{yx_2\}\). Then \(d_x(T_1)=1\), \(d_y(T_1)=2\) and \(d_v(T_1)=d_v(T)\) \(\forall ~v \in V(T) \backslash \{x,y\}\). We obtain \[\begin{aligned} ESO(T_1)-ESO (T)=\Theta(2,4)+\Theta(1,3)-\Theta(1,4)-\Theta(2,3)\approx 0.82>0, \end{aligned}\] which is a contradiction.
(b) We prove that \(x_{24}=0\). Otherwise, suppose that \(x_{24}=1\) (as \(n_2=1\) and \(x_{12}=1\)). Then \(T\) contains a \(4\)-vertex (say, \(x_1\)) adjacent to \(x\). Since \(n_2=1\) and \(x_{12}=1=x_{24}\), then it is obvious that \(x_{22}=x_{23}=0\). By setting \(i=\Delta=4\) in (1), then this with \(x_{24}=1\) and \(x_{44}=k-1\) implies that \(x_{14}+x_{34}=2k+1\). Since \(n_3=\frac{n-3k-3}{2}\geq 2k+2\), then this with \(x_{14}+x_{34}=2k+1\) implies that \(n_3 \geq x_{14}+x_{34}+1\). This means \(x_{33}\geq1\) as \(x_{23}=0\). Hence \(T\) contains an edge \(yz \in E(T)\) such that \(d_y=3=d_z\). Without loss of generality, let \(x\) and \(y\) be located on the \(x_1-z\) path. Let \(T_2 \in \Gamma_{n,4}^k\) can be obtained from \(T\) such that \(T_2=(T \backslash \{xx_1,yz\}) \cup \{x_1z,yx\}\). This results in \(d_v(T_2)=d_v(T)\) \(\forall ~ v\in V(T)\). Then \[\begin{aligned} ESO(T_2)-ESO (T)&=\Theta(4,3)+\Theta(3,2)-\Theta(4,2)-\Theta(3,3)\approx 0.72>0, \end{aligned}\] which is a contradiction. ◻
We define the degree sequences \(\pi_0(T)\), \(\pi_1(T)\) and \(\pi_2(T)\) as follows: \[\begin{aligned} \pi_0(T)=(3^{(k)}, &2^{(n-2k-2)}, 1^{(k+2)}),~~ \pi_1(T)=\left(4^{(k)},3^{(\frac{n-3k-2}{2})}, 1^{({\frac{n+k+2}{2})}}\right)~~\mbox{and}\\[2mm] &\pi_2(T)=\left(4^{(k)},3^{(\frac{n-3k-3}{2})},2^{(1)}, 1^{({\frac{n+k+1}{2})}}\right),~~\mbox{respectively}. \end{aligned}\]
Denote by \(\Gamma_0\subseteq \Gamma_{n,3}^k\) the subset of \(n\)-vertex molecular trees characterized by the degree sequence \(\pi_0(T)\) and the structural properties of those trees outlined in Table 1.
| \(n\) | \(x_{33}\) | \(x_{23}\) | \(x_{13}\) | \(x_{22}\) | \(x_{12}\) | |
|---|---|---|---|---|---|---|
| \(\Gamma_0 \subseteq \Gamma_{n, 3}^k\) | \(n \leq 3k+4\) | \(k-1\) | \(n-2k-2\) | \(3k+4-n\) | \(0\) | \(n-2k-2\) |
| \(n > 3k +4\) | \(k-1\) | \(2k+2\) | \(0\) | \(n-3k+4\) | \(2k+2\) | |
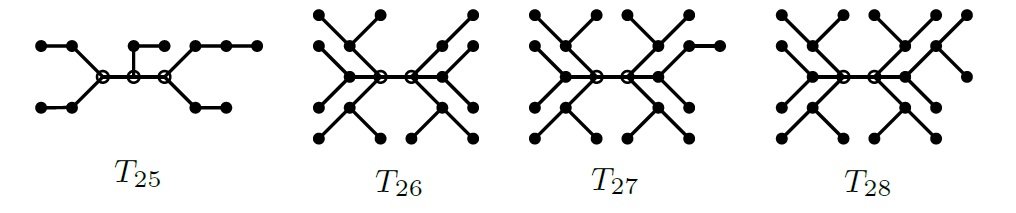
For a pictorial representation of trees in \(\Gamma_0 \subseteq \Gamma_{n,3}^3\), refer to \(T_2\) and \(T_3\) for \(n=9\), and \(T_5, T_6,\) and \(T_7\) for \(n=10\) in Figure 1. Additionally, see \(T_{25} \in \Gamma_0 \subseteq \Gamma_{14,3}^3\) in Figure 2.
Let \(\Gamma_1\) and \(\Gamma_2\) be the subclasses of \(\Gamma_{n,4}^k\) consisting of trees containing no vertex of degree \(2\) and exactly one vertex of degree \(2\), respectively. According to Lemmas 2 and 3, trees in \(\Gamma_1\) or \(\Gamma_2\) satisfy \(n-k\equiv 0 (\bmod\,\, 2)\) or \(n-k\equiv 1 (\bmod\,\, 2)\) with degree sequence \(\pi_1(T)\) or \(\pi_2(T)\), respectively. Taking these properties into account, we define the structural properties \((i.e.,\) the values of \(x_{ij})\) for the trees in \(\Gamma_1 \subseteq \Gamma_{n, 4}^k\) and \(\Gamma_2 \subseteq \Gamma_{n, 4}^k\), as presented in Table 2.
| \(\Gamma_1 ~ \& ~\Gamma_2\) | \(n\) | \(x_{44}\) | \(x_{34}\) | \(x_{1 4}\) | \(x_{33}\) | \(x_{13}\) | \(x_{24}\) | \(x_{23}\) | \(x_{12}\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\Gamma_1 \subseteq \Gamma_{n, 4}^k\) | \(n \leq 7k-6\) | \(k-1\) | \(\frac{n-3k-2}{2}\) | \(\frac{7k+6-n}{2}\) | \(0\) | \(n-3k-2\) | \(0\) | \(0\) | \(0\) |
| \(n > 7k -6\) | \(k-1\) | \(2k+2\) | \(0\) | \(\frac{n-7k-6}{2}\) | \(\frac{n+2+k}{2}\) | \(0\) | \(0\) | \(0\) | |
| \(\Gamma_2 \subseteq \Gamma_{n, 4}^k\) | \(n \leq 7k+5\) | \(k-1\) | \(\frac{n-3k-3}{2}\) | \(\frac{7k+5-n}{2}\) | \(0\) | \(n-3k-3\) | \(1\) | \(0\) | \(1\) |
| \(n > 7k+5\) | \(k-1\) | \(2k+2\) | \(0\) | \(\frac{n-7k-7}{2}\) | \(\frac{n+k-1}{2}\) | \(0\) | \(1\) | \(1\) |
For instance, see \(T_{21} \in \Gamma_1 \subseteq \Gamma_{10,4}^2\) and \(T_{16} \in \Gamma_2 \subseteq \Gamma_{9,4}^2\) in Figure 1. Additionally, \(T_{26} \in \Gamma_2 \subseteq \Gamma_{19,4}^2\), \(T_{27} \in \Gamma_2 \subseteq \Gamma_{21,4}^2\), and \(T_{28} \in \Gamma_1 \subseteq \Gamma_{22,4}^2\) in Figure 2.
We are now in the state of providing the main theorem.
Theorem 1. Let \(T\) be a molecular tree in \(\Gamma_{n,\Delta}^k\). Then \[\begin{aligned} ESO(T)&\leq (k-1) \begin{cases} \Theta(3,3)+ \begin{cases} (3k+4-n)\Theta(1,3)+(n-2k-2)[\Theta(1,2)+\Theta(2,3)],~~~ \text{if $\Delta=3$ and $n< 3k+4$}; \\[1mm] (n-3k+4)\Theta(2,2)+(2k+2)[\Theta(1,2)+\Theta(2,3)],~~~~~~~~~~\text{if $\Delta=3$ and $n\geq 3k+4$};\\ \end{cases}\\[12mm] \Theta(4,4)+ \begin{cases} (n-3k-2)\Theta(1,3)+\Theta(3,4)\frac{n-3k-2}{2}+\frac{7k+6-n}{2}\Theta(1,4),\\[0.5mm] ~~~~~~~~~~~~~~\qquad\qquad\qquad\text{if $\Delta=4$, $n\leq7k+6$ and $n-k\equiv 0(\bmod 2)$}; \\[2mm] \frac{n+k+2}{2}\Theta(1,3)+\Theta(3,4)(2k+2)+\frac{n-7k-6}{2}\Theta(3,3),\\[0.5mm] ~~~~~~~~~~~~~~\qquad\qquad\qquad\text{if $\Delta=4$, $n>7k+6$ and $n-k\equiv 0(\bmod 2)$};\\[2mm] (n-3k-3)\Theta(1,3)+\Theta(3,4)\frac{n-3k-3}{2}+\frac{7k+5-n}{2}\Theta(1,4)+\Theta(1,2)+\Theta(2,4),\\[0.5mm] ~~~~~~~~~~~~~~\qquad\qquad\qquad\text{if $\Delta=4$, $n\leq 7k+5$ and $n-k\equiv 1(\bmod 2)$};\\[2mm] \frac{n+k-1}{2}\Theta(1,3)+\Theta(3,4)(2k+2)+\frac{n-7k-7}{2}\Theta(3,3)+\Theta(1,2)+\Theta(2,3),\\[0.5mm] ~~~~~~~~~~~~~~\qquad\qquad\qquad\text{if $\Delta=4$, $n>7k+5$ and $n-k\equiv 1(\bmod 2)$}. \end{cases} \end{cases} \end{aligned}\]
The equality holds if and only if \(T \in \Gamma_0\) for \(\Delta=3\); \(T \in \Gamma_1\) for \(\Delta=4\) and \(n-k\equiv 0(\bmod 2)\), and \(T \in \Gamma_2\) for \(\Delta=4\) and \(n-k\equiv 1(\bmod 2)\).
Proof. Let \(T^{\star}\) be a molecular tree with the highest \(ESO\) index among all trees in \(\Gamma_{n,\Delta}^k\), where \(3 \leq \Delta \leq 4\), \(n\geq (\Delta-1)k+2\) and \(k\geq 1\). It follows that \(ESO(T) \leq ESO(T^{\star})\) with equality if and only if \(T \cong T^{\star}\). We now proceed to discuss the problem in two cases: \(\Delta=3\) and \(\Delta=4\).
Case 1. \(\Delta=3\). This with \(n_3=k\) and (3) implies that \[\pi_0(T^{\star})=\left(3^{(k)},2^{(n-2k-2)},1^{(k+2)}\right).\]
We now establish the following claims:
Claim 1. If \(k\geq 2\), then for the tree \(T^{\star}\), \(x_{33}=k-1\) holds.
Proof of Claim 1. By contradiction, suppose that \(T^{\star}\) contains an internal segment of length \(\ell\geq 2\) with both terminal vertices of degree \(3\). Since \(T\) is a tree, it is evident that \(T^{\star}\) contains a pendent segment of length \(\ell' \geq 1\). We obtain \(T_1\) from \(T^{\star}\) by replacing the path of length \(\ell\) with a path of length \(1\) and the path of length \(\ell'\) with a path of length \(\ell+\ell'-1\). We now discuss the possible cases that may arise:
Case 1.1. \(\ell'=1\). In this case, we obtain \[\begin{aligned} ESO(T_1)-ESO ({ T^{\star}})=\Theta(3,3)+\Theta(2,1)-\Theta(3,1)-\Theta(3,2)\approx1.487>0. \end{aligned}\]
Case 1.2. \(\ell'\geq 2\). Then \[\begin{aligned} ESO({ T}')-ESO ({ T^{\star}})=\Theta(3,3)+\Theta(2,2)-2\Theta(3,2)\approx 0.714>0. \end{aligned}\]
In each case, we arrive at a contradiction. Thus we conclude that \(x_{33}=k-1\). This completes the Claim 1. ◻
Combining \(\pi_0(T^{\star})\) and Claim 1 with (2), we derive \[\begin{cases} \begin{aligned}\label{sv22} x_{12}+x_{13}&=k+2,\\ x_{12}+2\,x_{22}+x_{23}&=2\,(n-2k-2),\\ x_{13}+x_{23}&=k+2. \end{aligned} \end{cases} \tag{9}\]
Claim 2. \(x_{13}\) and \(x_{22}\) cannot be simultaneously positive.
Proof of Claim 2. We prove this result by contradiction. Otherwise, assume that \(x_{13},x_{22}>0\). This together with Claim 1 implies that \(T^{\star}\) contains pendent segments of length \(1\) and at least \(3\). We construct a tree \(T_2 \in \Gamma_{n,3}^k\) from \(T^{\star}\) by replacing a pendent segment of length \(1\) with one of length \(2\) and a pendent segment of length at least \(3\) with one of at least \(2\), ensuring that \(d_v(T_2)=d_v(T^{\star})\) \(\forall\) \(v\in V(T^{\star})\). Then we have \[\begin{aligned} ESO(T_2)-ESO(T^{\star})&=\Theta(2,3)+\Theta(1,2)-\Theta(1,3)-\Theta(2,2)\approx 0.76>0, \end{aligned}\] a contradiction. Thus we conclude that \(x_{13}\) and \(x_{22}\) cannot be simultaneously positive, which completes the proof of Claim 2. ◻
According to Claims 1 and 2, we need to place vertices of degree \(2\) between the vertices of degree \(3\) and \(1\) in \(T^{\star}\), ensuring that each pendent segment has a length of at most \(2\). The remaining vertices of degree \(2\) can then be placed arbitrarily on any pendent segment of length at least \(2\). Thus the following possible cases arise:
Case 1.1. \(n\leq 3k+4\). Since \(n_2=n-2k-2\) and \(n_1=k+1\), in this case, \[\begin{aligned} n_2= n-2k-2 \leq k+1=n_1. \end{aligned}\]
We now prove that \(x_{22}=0\). Otherwise, suppose that \(x_{22}>0\). This with above relation and Claim 1 implies that \(x_{13}>0\). However, Claim 2 then yields a contradiction. Hence \(x_{22}=0\). Combining this with Claim 1 and (9), we obtain \(x_{12}=n-2k-2=x_{23}\), \(x_{13}=3k+4-n\) and \(x_{33}=k-1\). Thus \(T^{\star} \in \Gamma_0\). As a result \[\begin{aligned} ESO(T^{\star})=(k-1)\Theta(3,3)+(3k+4-n)\Theta(1,3)+(n-2k-2)[\Theta(1,2)+\Theta(2,3)]. \end{aligned}\]
Case 1.2. \(n > 3k+4\). This implies \(n_2= n-2k-2 > k+1=n_1\). In this case, we prove that \(x_{13}=0\). Otherwise, assume that \(x_{13}>0\). This together with \(n_2 > n_1\) and Claim 1 ensures that \(x_{22}>0\). However, by Claim 2, we obtain a contradiction. Thus we conclude that \(x_{13}=0\). Combining this with Claim 1 and incorporating it into (9), we get \(x_{12}=k+2=x_{23}\), \(x_{22}=n-3k-4\) and \(x_{33}=k-1\). So \(T^{\star} \in \Gamma_0\). Consequently \[\begin{aligned} ESO(T^{\star})=(k-1)\Theta(3,3)+(n-3k-4)\Theta(2,2)+(k+2)\left[\Theta(1,2)+\Theta(2,3)\right]. \end{aligned}\]
Case 2. \(\Delta=4\).
By Lemma 2, we have \(n_2\leq 1\). If \(n_2=0\), then by Lemma 3 \((a)\), \(n-k\equiv 0(\bmod\,\, 2)\) and we conclude that \(T^{\star}\) has the degree sequence \(\pi_1(T^{\star})\). If \(n_2=1\), then by Lemma 3 \((b)\), \(n-k\equiv 1(\bmod\,\, 2)\) and hence \(T^{\star}\) has the degree sequence \(\pi_2(T^{\star})\). Based on these observations, we discuss the proof into the following two cases:
Case 2.1. \(n-k\equiv 0\,(\bmod\,\, 2)\). In this case, by Lemma 3 \((b)\), \(T^{\star}\) has the degree sequence \[\begin{aligned} \pi_1(T^{\star})=\left(4^{(k)},3^{\left(\frac{n-3k-2}{2}\right)}, 1^{\left(\frac{n+k+2}{2}\right)}\right). \end{aligned}\]
By Lemma 5, it holds that \(x_{44}=k-1\). Taking this and the above degree sequence into consideration along with (1), we derive \[\label{eq4.7} \begin{cases} \begin{aligned} x_{13}+x_{14}&=\frac{n+k+2}{2},\\ x_{13}+2x_{33}+x_{34}&=3\bigg(\frac{n-3k-2}{2}\bigg),\\ x_{14}+x_{34}+2(k-1)&=4k. \end{aligned} \end{cases} \tag{10}\]
From the above, we obtain \[\begin{aligned} \label{es10} x_{33}-x_{14}=\frac{1}{2}\,(n-7k-6) . \end{aligned} \tag{11}\]
We now consider the following two cases that arise:
Case 2.1.1. \(n\leq 7 k-6\). In this case, we prove that \(x_{33}=0\). Otherwise, assume that \(x_{33}>0\). Since \(n\leq 7k-6\), by (11), we obtain \(x_{14} \geq x_{33} \geq 1\) (as \(x_{33} \geq 1\)). Therefore \(x_{33}, x_{14}>0\). Then by Lemma 6, we can obtain a contradiction. Hence \(x_{33}=0\). Combining this with (10), we obtain \(x_{13} = n-3k-2\), \(x_{34} =\frac{n-3k-2}{2}\), \(x_{14} =\frac{7k+6-n}{2}\) and \(x_{44}=k-1\). Thus \(T^{\star}\in \Gamma_1\). Consequently \[\begin{aligned} ESO(T^{\star})=(k-1)\,\Theta(4,4)+ (n-3k-2)\,\Theta(1,3)+\frac{n-3k-2}{2}\,\Theta(3,4)+\frac{7k+6-n}{2}\,\Theta(1,4). \end{aligned}\]
Case 2.1.2. \(n>7k-6\). For this case, we prove that \(x_{14} = 0\). Otherwise, assume that \(x_{14}>0\). Since \(n > 7k-6\), by (11), we obtain \(x_{33} > x_{14} \geq 1\) (as \(x_{14} \geq 1\)). Thus \(x_{33}, x_{14}>0\), this contradicts the Lemma 6. Hence we conclude that \(x_{14} = 0\). This combining along with (13) implies that \(x_{13} = \frac{n+k+2}{2}\), \(x_{34} =2k+2\), \(x_{33} =\frac{n-7k-6}{2}\) and \(x_{44}=k-1\). Thus \(T^{\star}\in \Gamma_1\). As a result \[\begin{aligned} ESO(T^{\star})= (k-1)\,\Theta(4,4)+ \left(\frac{n+k+2}{2}\right)\,\Theta(1,3)+(2k+2)\,\Theta(3,4)+\left(\frac{n-7k-6}{2}\right)\,\Theta(3,3). \end{aligned}\]
Case 2.2. \(n-k\equiv 1(\bmod\,\, 2)\). In this case, by Lemmas 2 and 3 \((b)\), \(T^{\star}\) has the degree sequence \[\begin{aligned} \pi_2(T^{\star})=\left(4^{(k)},3^{(\frac{n-3k-3}{2})},2^{(1)}, 1^{({\frac{n+k+1}{2})}}\right). \end{aligned}\]
By Lemmas 4 and 5, it holds that \[\begin{aligned} x_{12}=1~~\mbox{and}~~ x_{44}=k-1, \end{aligned}\] respectively. By combining above relations and the degree sequence \(\pi_2(T^{\star})\) along with (1), we obtain \[\label{eq4.8} \begin{cases} \begin{aligned} 1+x_{13}+x_{14}&=\frac{n+k+1}{2},\\ x_{23}+x_{24}&=1,\\ x_{13}+x_{23}+2x_{33}+x_{34}&=3\bigg(\frac{n-3k-3}{2}\bigg),\\ x_{14}+x_{24}+x_{34}+2(k-1)&=4k. \end{aligned} \end{cases} \tag{12}\]
Case 2.2.1. \(n\leq 7k+5\). By Lemma 7 \((a)\), we have \(x_{23}=0\). This with (12) implies that \(x_{33}-x_{14}=\frac{1}{2} (n-7k-5)\). In this case, we prove \(x_{33}=0\). Otherwise, suppose that \(x_{33}>0\). Since \(n\leq 7k+5\) and \(x_{33}-x_{14}=\frac{1}{2} (n-7k-5)\), then by combining these, we obtain \(x_{14} \geq x_{33} \geq 1\) (as \(x_{33} \geq 1\)). Thus we have \(x_{33}, x_{14}>0\). Then by Lemma 6, we can obtain a contradiction. Hence \(x_{33}=0\). Bearing this and \(x_{23}=0\) into consideration with (12) and solving them simultaneously, we obtain \(x_{13} = n-3k-3\), \(x_{34} =\frac{n-3k-3}{2}\), \(x_{14} = \frac{7k-n+5}{2}\) and \(x_{24}=1\). So \(T^{\star} \in \Gamma_{3}\). Consequently \[\begin{aligned} ESO(T^{\star})&=(k-1)\Theta(4,4)+(n-3k-3)\Theta(1,3)+\left(\frac{n-3k-3}{2}\right)\Theta(3,4)\\[2mm] &\qquad+\left(\frac{7k+5-n}{2}\right)\Theta(1,4)+\Theta(1,2)+\Theta(2,4). \end{aligned}\]
Case 2.2.2. \(n \geq 7k+7\). By Lemma 7 \((b)\), we have \(x_{24}=0\). This with (12) implies that \(x_{33}-x_{14}=\frac{1}{2} (n-7k-7)\). In this case, we prove \(x_{14}=0\). Otherwise, suppose that \(x_{14}>0\). Since \(n \geq 7k+7\) and \(x_{33}-x_{14}=\frac{1}{2} (n-7k-7)\), then by combining these, we obtain \(x_{33} \geq x_{14} \geq 1\) (as \(x_{14} \geq 1\)). Thus \(x_{33}, x_{14}>0\). Then by applying the Lemma 6, we obtain a contradiction. Hence \(x_{14}=0\). Taking this and \(x_{24}=0\) into account along with (12) and by some computation, we obtain \(x_{13} = \frac{n+k-1}{2}\), \(x_{34} =2k+2\), \(x_{33} = \frac{n-7k-7}{2}\) and \(x_{23}=1\). Thus \(T^{\star} \in \Gamma_3\). Hence \[\begin{aligned} ESO(T^{\star})&=(k-1)\Theta(4,4)+\left(\frac{n+k-1}{2}\right)\Theta(1,3)+(2k+2)\,\Theta(3,4)+\left(\frac{n-7k-7}{2}\right)\Theta(3,3)\\[1mm] &\qquad+\Theta(1,2)+\Theta(2,3). \end{aligned}\]
This concludes the proof of this theorem. ◻
In this subsection, we establish the sharp lower bound for the \(ESO\) index in \(\Gamma_{n,\Delta}^k\) and characterize the corresponding molecular trees. For \(k=1\) and \(\Delta+1 \leq n \leq \Delta+2\), we have \(\Gamma_{4,3}^1=\{S_4\}\) and \(\Gamma_{5,3}^1=\{DS_{2,1}\}\) for \(\Delta=3\), while \(\Gamma_{5,4}^1=\{S_5\}\) and \(\Gamma_{6,4}^1=\{DS_{3,1}\}\) for \(\Delta=4\). We analyze the problem by considering two cases: \((i)\) \(k=1\) with \(n\geq \Delta+3\) and \((ii)\) \(k\geq 2\) with \(n\geq (\Delta-1)k+2\). We first establish the following result for \(k=1\).
Theorem 2. Let \(T\in \Gamma_{n,\Delta}^1\) be a molecular tree with \(n\geq\Delta+3\). Then \[\begin{aligned} ESO(T)\geq (\Delta-1)\,\Theta(\Delta,1)+ \Theta(\Delta,2)+(n-\Delta-2)\,\Theta(2,2)+\Theta(2,1). \end{aligned}\]
The inequality becomes equality if and only if \(T\cong B_{n,\Delta}\).
Proof. Let \(T^{\ast}\in \Gamma_{n,\Delta}^1\) be a tree with the lowest \(ESO\) index. We prove that \(T^{\ast} \cong B_{n, \Delta}\). Suppose to the contrary that \(T\) is not isomorphic to \(B_{n, \Delta}\). Then \(T^{\ast}\) with \(n_{\Delta}=k=1\) contains at least two pendent segments of lengths \(\ell \geq 2\) and \(\ell' \geq 2\), respectively. We replace two pendent segments by pendent segments of lengths \(1\) and \(\ell+\ell'-1\) to obtain a new tree \(T_1\) from \(T^{\ast}\). Then \[\begin{aligned} ESO(T_1)-ESO(T^{\ast}) = \Theta(\Delta, 1)-\Theta(\Delta, 2)+\Theta(2, 2)-\Theta(1, 2). \end{aligned}\]
By selecting \(y=\Delta \geq 3\), \(s=2\) and \(t=1\) in Lemma 1 \((i)\), it follows that \(f(2)=\Theta(2, 2)-\Theta(2, 1)< \Theta(\Delta, 2)-\Theta(\Delta, 1)=f(\Delta)\). This means \(ESO(T_1)-ESO(T^{\ast})<0\), which is a contradiction. Hence we conclude that \(T^{\ast} \cong B_{n, \Delta}\). As a result \[\begin{aligned} ESO(B_{n,\Delta})= (\Delta-1)\,\Theta(\Delta,1)+ \Theta(\Delta,2)+(n-\Delta-2)\,\Theta(2,2)+\Theta(2,1). \end{aligned}\]
Thus we complete the proof. ◻
Let us define a degree sequence \(\pi_3(T)\) as follows: \[\begin{aligned} \pi_3(T)=\left(\Delta^{(k)}, 2^{(n-k(\Delta-1)-2)},1^{(k(\Delta-2)+2)}\right)~~\mbox{for}~~\Delta\in \{3,4\}. \end{aligned}\]
Denote by \(\Gamma_3 \subseteq \Gamma_{n,\Delta}^k\) the family of molecular trees with \(n \geq (\Delta-1)k+2\), \(k \geq 2\), and degree sequence \(\pi_3(T)\). Moreover, trees in \(\Gamma_3\) possess the structural properties given in the following table.
| \(n\) | \(x_{\Delta \Delta}\) | \(x_{2\Delta}\) | \(x_{1\Delta}\) | \(x_{22}\) | |
|---|---|---|---|---|---|
| \(\Gamma_3 \subseteq \Gamma_{n, \Delta}^k\) | \(n \leq \Delta k\) | \(\Delta k-n+1\) | \(2n-2k(\Delta-1)-4\) | \(k(\Delta-2)+2\) | \(0\) |
| \(n \geq \Delta k +1\) | \(0\) | \(2(k-1)\) | \(k(\Delta-2)+2\) | \(n-\Delta k-1\) | |
To illustrate the trees in \(\Gamma_3\), refer to Figure 1, where \(T_3 \in \Gamma_3 \subseteq \Gamma_{9,3}^3\), \(T_{14} \in \Gamma_3 \subseteq \Gamma_{10,3}^3\), \(T_{17} \in \Gamma_3 \subseteq \Gamma_{9,4}^2\), and \(T_{23} \in \Gamma_3 \subseteq \Gamma_{10,4}^2\).
We now proceed to establish our main result for \(k\geq2\).
Theorem 3. Let \(T\in \Gamma_{n,\Delta}^k\,\,(k\geq 2)\) be a molecular tree, then we have \[\begin{aligned} ESO(T)&\geq (k(\Delta-2)+2)\,\Theta(1,\Delta)+ \begin{cases} 2(n-k(\Delta-1)-2)\,\Theta(2,\Delta)+(\Delta k-n+1)\,\Theta(\Delta,\Delta), \quad \text{if ~$n\leq \Delta k$}; \\[2mm] 2(k-1)\,\Theta(2,\Delta)+(n-\Delta k-1)\,\Theta(2,2),\quad~~~~~~~~~~~~~~~~~~~~~~ \text{if ~$n\geq \Delta k+1$}. \end{cases} \end{aligned}\]
The equality holds if and only if \(T\in \Gamma_4\) for \(n\leq \Delta k\), and \(T\in\Gamma_5\) for \(n\geq \Delta k+1\).
Proof. Among the family of molecular trees in \(\Gamma_{n,\Delta}^k\), let \(T^{\ast}\) be the tree with the lowest \(ESO\) index. We now proceed to establish certain claims:
Claim 3. If \(\Delta=4\), then for the tree \(T^{\ast}\), \(n_3=0\) holds.
Proof of Claim 3. We prove this claim by contradiction method. Suppose that \(T^{\ast}\) contains a vertex \(x\) of degree \(3\) and \(N_x=\{x_1,x_2,x_3\}\). Let \(y\) be a pendent vertex adjacent to \(y_{1'}\) such that \(d_{1'}\geq 2\). Without loss of generality, assume that \(x_3\) lies on \(x-y\) path (possibly \(x_3=y_{1'}\)). This means \(d_3\geq 2\). We consider a tree \(T_1=(T^{\ast} \backslash \{xx_1\})\cup \{yx_1\}\) in \(\Gamma_{n,\Delta}^k\) such that \(d_{x}(T_1)=2\), \(d_{y}(T_1)=2\) and \(d_v(T_1)=d_v(T^{\ast})\) \(\forall\) \(v\in V(T^{\ast})\backslash \{x,y\}\). We now consider the following possible two cases:
Case 1. \(xy \notin E(T^{\ast})\). Then \[\begin{aligned} ESO(T_1)-ESO ({T^{\ast}})&=\Theta(2,d_3)-\Theta(3,d_3)+\Theta(2,d_2)-\Theta(3,d_2)+\Theta(2,d_1)-\Theta(3,d_1)\\&~~~~+\Theta(2,d_{1'})-\Theta(1,d_{1'})\\&<\Theta(2,d_3)-\Theta(3,d_3)+\Theta(2,d_{1'})-\Theta(1,d_{1'}).\nonumber \end{aligned}\]
Since \(d_3\geq 2\) and \(d_{1'}\leq 4\), it follows from Lemma 1 \((i)\) and \((ii)\) that \[\begin{aligned} ESO(T_1)-ESO (T^{\ast})<\Theta(2,2)-\Theta(3,2)+\Theta(2,4)-\Theta(1,4)\approx -0.48<0.\nonumber \end{aligned}\]
Case 2. \(xy \in E(T^{\ast})\). Then we have \[\begin{aligned} ESO(T_1)-ESO(T^{\ast})=\Theta(2,d_2)-\Theta(3,d_{2})+\Theta(2,d_1)-\Theta(3,d_1)+\Theta(2,2)-\Theta(3,1)<0. \end{aligned}\]
From the above cases, we derive a contradiction. Thus \(T^{\ast}\) does not contain any vertex of degree \(3\). This proves the Claim 3. ◻
By taking into consideration the Claim 3 (namely, \(n_3=0\) when \(\Delta=4\)) or \(\Delta=3\) with (2), we conclude that \(T^{\ast}\) has the degree sequence: \[\begin{aligned} \pi_3(T^{\ast})=\left(\Delta^{(k)}, 2^{(n-k(\Delta-1)-2)},1^{(k(\Delta-2)+2)}\right),~\mbox{where}~ \Delta\in \{3,4\}. \end{aligned}\]
Claim 4. For the tree \(T^{\ast}\), \(x_{12}=0\) holds.
Proof of Claim 4. By contradiction, assume that \(T^{\ast}\) contains a pendent vertex \(x\) adjacent to a \(2\) degree vertex (say \(x_1\)). Since \(k\geq 2\), it follows that \(T^{\ast}\) contains an internal segment \(y_{\ell}\ldots y_0\) of length \(\ell\geq 1\) such that \(d_0, d_{\ell} \geq 3\). Without loss of generality, we can assume that \(y_0\) is not located on \(x-y_{\ell}\) path. Let \(T_2=(T^{\ast} \backslash \{xx_1, y_{\ell}y_{\ell-1}\}) \cup \{x_1 y_{\ell-1}, y_{\ell}x\}\) be a tree in \(\Gamma_{n,\Delta}^k\) such that \(d_v(T_2)=d_v(T^{\ast})\) \(\forall\) \(v\in V(T^{\ast})\). We now distinguish the following two cases:
Case 1. \(\ell \geq 2\). Then \[\begin{aligned} ESO(T_2)-ESO ({T^{\ast}})&=\Theta(1,d_{\ell})-\Theta(2,d_{\ell})+\Theta(2,2)-\Theta(1,2). \end{aligned}\]
By choosing \(y=d_{\ell}\geq 3\), \(s=1\) and \(t=2\) in Lemma 1 \((ii)\), it is evident that \(f(d_{\ell})=\Theta(1,d_{\ell})-\Theta(2,d_{\ell})<\Theta(1,2)-\Theta(2,2)=f(2)\). In conjunction with the above, this leads to \[\begin{aligned} ESO(T_2)-ESO (T^{\ast})<0, \end{aligned}\] a contradiction.
Case 2. \(\ell=1\). Then we have \[\begin{aligned} ESO(T_2)-ESO(T^{\ast})&=\Theta(1,d_0)-\Theta(d_{\ell},d_0)+\Theta(d_{\ell},2)-\Theta(1,2). \end{aligned}\]
By setting \(y=d_{\ell}\geq 3\), \(s=1\) and \(t=d_{0}\geq 3\) in Lemma 1 \((ii)\), we obtain \(f(d_{\ell})=\Theta(1,d_{\ell})-\Theta(d_{0},d_{\ell}) < \Theta(1,2)-\Theta(d_{0},2)=f(2)\). By combining this result with the preceding relation, we conclude that \[\begin{aligned} ESO(T_2)-ESO(T^{\ast})<0, \end{aligned}\] which is a contradiction.
From the above cases, we obtain a contradiction. Hence \(x_{12}=0\), which establishes Claim 4. ◻
By taking into account the degree sequence \(\pi_3(T^{\ast})\) and Claim 4 with (1), we obtain \[\begin{cases} \begin{aligned}\label{sv2} &x_{1\Delta}=k(\Delta-2)+2,\\ &2\,x_{22}+x_{2\Delta}=2\,(n-2-k(\Delta-1)),\\ &x_{1\Delta}+x_{2\Delta}+2\,x_{\Delta\Delta}=\Delta \times k. \end{aligned} \end{cases} \tag{13}\]
From the above relation, we obtain \[\begin{aligned} \label{e1} x_{22}-x_{\Delta\Delta}=n-(\Delta k-1). \end{aligned} \tag{14}\]
Claim 5. \(x_{\Delta\Delta}\) and \(x_{22}\) cannot be simultaneously positive.
Proof of Claim 5 . We prove this result by contradiction. For this we assume that \(x_{\Delta \Delta},x_{22}>0\). This with Claim 4 yields that \(T^{\ast}\) contains an internal segments of length \(1\) and of length at least \(3\). We transform a tree \(T_3 \in \Gamma_{n,\Delta}^k\) from \(T^{\ast}\) by modifying its internal paths: replacing an internal path of length \(1\) with one of length \(2\) and an internal path of length at least \(3\) with one of at least \(2\), while preserving the degree of each vertex, that is, \(d_v(T_3)=d_v(T^{\ast})\) \(\forall\) \(v\in V(T^{\ast})\). Then we have \[\begin{aligned} ESO(T_3)-ESO(T^{\ast})&=\Theta(2,\Delta)+\Theta(2,\Delta)-\Theta(\Delta,\Delta)-\Theta(2,2). \end{aligned}\]
Since \(\Delta\geq 3\), we start with an evident relation \(\Delta^2\left((\Delta-2)^2-1\right)+(2\Delta-4)^2+\Delta^2>0\). Using this, we have \(2(\Delta^2+4)^2>(2+\Delta)^2(\Delta^2+4)\), which implies that \[\begin{aligned} 2(2+\Delta)\sqrt{4+\Delta^2}<2\Delta^2\sqrt{2}+4\sqrt{8},~~\mbox{that is}, ~\Theta(2,\Delta)+\Theta(2,\Delta)<\Theta(\Delta,\Delta)+\Theta(2,2), \end{aligned}\] from which it immediately follows that \(ESO(T_3)-ESO(T^{\ast})<0\). Hence either \(x_{\Delta\Delta}=0\) or \(x_{22}=0\). This completes the Claim 5. ◻
We now discuss the following cases:
Case 1. \(n\leq \Delta k\). In this case, we prove that \(x_{22}=0\). For the sake of contradiction, we suppose that \(x_{22}>0\). Since \(x_{12}=0\) (by Claim 4), it follows that \(T^{\ast}\) contains an internal segment of length at least \(3\). Since \(n\leq \Delta k\), by (14), we obtain \(x_{\Delta \Delta} \geq x_{22} \geq 1\). Therefore there exists an internal segment of length \(1\). So \(T^{\ast}\) obeys the conditions \(x_{\Delta \Delta}, x_{22}>0\). Then by Claim 5, we obtain a contradiction. Consequently \(x_{22}=0\).
Taking into account \(x_{22}=0\) along with (13) and solving the equations simultaneously, we obtain \(x_{1\Delta} = k(\Delta-2)+2\), \(x_{2\Delta} =2(n-k(\Delta-1)-2)\) and \(x_{\Delta \Delta} = \Delta k-n+1\). Thus \(T^{\ast}\in \Gamma_4\). Consequently \[\begin{aligned} ESO(T^{\ast})= (k(\Delta-2)+2)\,\Theta(1,\Delta)+ 2(n-k(\Delta-1)-2)\,\Theta(2,\Delta)+(\Delta k-n+1)\,\Theta(\Delta,\Delta). \end{aligned}\]
Case 2. \(n\geq \Delta k+1\). For this case, we prove that \(x_{\Delta \Delta} = 0\). Suppose, for the sake of contradiction, that \(x_{\Delta \Delta} \geq 1\). Since \(n \geq \Delta k + 1\), it follows from (14) that \(x_{22} \geq x_{\Delta \Delta} \geq 1\) (as \(x_{\Delta \Delta} \geq 1\)). Together with \(x_{12} = 0\) (by Claim 4), this implies that \(T^{\ast}\) must contain an internal segment of length at least \(3\). Thus \(T^{\ast}\) satisfies the conditions \(x_{\Delta \Delta}, x_{22}>0\). However, this contradicts Claim 5. Hence we conclude that \(x_{22} = 0\).
By incorporating \(x_{22}=0\) along with (13) and evaluating the respective system of equations, we deduce \(x_{1\Delta} = k(\Delta-2)+2\), \(x_{2\Delta} =2(k-1)\) and \(x_{22} = n-\Delta k-1\). Hence \(T^{\ast}\in \Gamma_5\). As a result \[\begin{aligned} ESO(T^{\ast})= (k(\Delta-2)+2)\,\Theta(1,\Delta)+ 2(k-1)\,\Theta(2,\Delta)+(n-\Delta k-1)\,\Theta(2,2). \end{aligned}\]
This completes the proof. ◻
In this paper, we established sharp upper and lower bounds on the elliptic Sombor index for molecular trees within the class \(\Gamma_{n, \Delta}^k\), along with a complete characterization of the trees attaining these bounds. Our analysis reveals that the extremal molecular trees are not unique. Specifically, molecular trees achieving the upper bound are classified into three families based on their degree sequences: \(\pi_0(T)\), \(\pi_1(T)\), and \(\pi_2(T)\). Likewise, those attaining the lower bound form a single set determined by the degree sequence \(\pi_3(T)\). An interesting direction for future research is to derive sharp bounds on the \(ESO\) index for trees in \(\Gamma_{n, \Delta}^k\) when \(\Delta \geq 5\).
Bondy J. A., & Murty U. S. R. (1976). Graph Theory with Applications. Macmillan Press, New York.
Gozalbes R., Doucet J., & Derouin F. (2002). Application of topological descriptors in QSAR and drug design: History and new trends. Current Drug Targets – Infectious Disorders, 2, 93–102.
Gutman I. (2013). Degree–based topological indices. Croatica Chemica Acta, 86, 351–361.
Gutman I. (2021). Geometric approach to degree–based topological indices: Sombor indices. MATCH Communications in Mathematical and in Computer Chemistry, 86, 11–16.
Chen H., Li W., & Wang J. (2022). Extremal values on the Sombor index of trees. MATCH Communications in Mathematical and in Computer Chemistry, 87, 23–49.
Das K. C., & Gutman I. (2022). On Sombor index of trees. Applied Mathematics and Computation, 412, #126575.
Deng H., Tang Z., & Wu R. (2021). Molecular trees with extremal values of Sombor indices. International Journal of Quantum Chemistry, 121, #e26622.
Liu H., Gutman I., You L., & Huang Y. (2022). Sombor index: review of extremal results and bounds. Journal of Mathematical Chemistry, 60, 771–798.
Liu H., You L., Huang Y., & Tang Z. (2023). On extremal Sombor indices of chemical graphs, and beyond. MATCH Communications in Mathematical and in Computer Chemistry, 89, 415–436.
Rada J., Rodrı́guez J. M., & Sigarreta J. M. (2023). On integral Sombor indices. Applied Mathematics and Computation, 452, #128036.
Ravindran B. A. (2025). Sombor index on trees–A review. MATCH Communications in Mathematical and in Computer Chemistry, 94, 291–305.
Redžepović I. (2021). Chemical applicability of Sombor indices. Journal of the Serbian Chemical Society, 86, 445–457.
Shetty S., & Bhat K. (2024). Sombor index of hypergraphs. MATCH Communications in Mathematical and in Computer Chemistry, 91, 235–254.
Wang Z., Mao Y., Li Y., & Furtula B. (2022). On relations between Sombor and other degree based indices. Journal of Applied Mathematics and Computing, 2022, 1–17.
Gutman I., Furtula B., & Oz M. S. (2024). Geometric approach to vertex-degree-based topological indices–Elliptic Sombor index, theory and application. International Journal of Quantum Chemistry, 124, #e27346.
Tang Z., Li Y., & Deng H. (2024). Elliptic Sombor index of trees and unicyclic graphs. Electronic Journal of Mathematics, 7, 19–34.
Shanmukha M., Usha A., Kulli V., & Shilpa K. (2024). Chemical applicability and curvilinear regression models of vertex-degree-based topological index: Elliptic Sombor index. International Journal of Quantum Chemistry, 124, #e27376.
Chen X., Wu B., & Li Z. (2025). Sombor index and elliptic Sombor index of benzenoid systems. MATCH Communications in Mathematical and in Computer Chemistry, 94, 263–285.
Rada J., Rodrı́guez J. M., & Sigarreta J. M. (2024). Sombor index and elliptic Sombor index of benzenoid systems. Applied Mathematics and Computation, 475, #128756.
Qi F., & Lin Z. (2024). Maximal elliptic Sombor index of bicyclic graphs. Contributions to Mathematics, 10, 25–29.
Ahmad S., Das K. C., & Farooq R. (2025). On elliptic Sombor index with applications. Bulletin of the Malaysian Mathematical Sciences Society, 48, #108.
Rada J., Rodrı́guez J. M., & Sigarreta J. M. (2025). Optimization problems for general elliptic Sombor index. MATCH Communications in Mathematical and in Computer Chemistry, 93, 819–838.
Kulli V. (2024). Modified elliptic Sombor index and its exponential of a graph. International Journal of Computer Mathematics, 12, 3949–3954.
Kulli V. (2024), Multiplicative elliptic Sombor and multiplicative modified elliptic Sombor indices. Annals of Pure and Applied Mathematics, 29 19–23.
Espinal C., Gutman I., & Rada J. (2025). Elliptic Sombor index of chemical graphs. Communications in Combinatorics and Optimization, 10, 989–999.
Ali A., Sekar S., Balachandran S., Elumalai S., Alanazi A. M., Hassan T. S., & Shang Y. (2024). Graphical edge-weight-function indices of trees. AIMS Mathematics, 9, 32552–32570.
Ahmad S., Farooq R., & Das K. C. (2025). The general Sombor index of extremal trees with a given maximum degree. MATCH Communications in Mathematical and in Computer Chemistry, 94, 825–853.
Borovićanin B., & Lampert T. A. (2015). On the maximum and minimum Zagreb indices of trees with a given number of vertices of maximum degree. MATCH Communications in Mathematical and in Computer Chemistry, 4, 81–96.
Lin H. (2014). A note on the maximal Wiener index of trees with given number of vertices of maximum degree. MATCH Communications in Mathematical and in Computer Chemistry, 72, 783–790.
Liu H., Yan X., & Yan Z. (2007). Bounds on the general Randić index of trees with a given maximum degree. MATCH Communications in Mathematical and in Computer Chemistry, 58, 155–166.
Raza Z., Balachandran S., Elumalai S., & Ali A. (2022). On general sum-connectivity index of trees of fixed maximum degree and order. MATCH Communications in Mathematical and in Computer Chemistry, 88, 643–658.
Swartz E., & Vetrík T. (2025). General sum-connectivity index of unicyclic graphs with given maximum degree. Discrete Applied Mathematics, 366, 238–249.
Wang S., Wang C., Chen L., & Liu J.-B. (2017). On extremal multiplicative Zagreb indices of trees with given number of vertices of maximum degree. Discrete Applied Mathematics, 227, 166–173.
Zhou T., Lin Z., & Miao L. (2021). The Sombor index of trees and unicyclic graphs with given maximum degree. Discrete Mathematics Letters, 7, 24–29.
Faheem H., Ahmad S., & Farooq R. (in press), Maximal and minimal Zagreb indices of trees with fixed number of vertices of maximum degree. MATCH Communications in Mathematical and in Computer Chemistry.
Jahangir I., Ahmad M., Ahmad S., & Farooq R. (in press). The Sombor index and harmonic index of chemical trees with a given number of vertices of maximum degree. Journal of Discrete Mathematical Sciences and Cryptography.