Let \(G\) be a simple and finite graph. A graph is said to be decomposed into subgraphs \(H_1\) and \(H_2\) which is denoted by \(G= H_1 \oplus H_2\), if \(G\) is the edge disjoint union of \(H_1\) and \(H_2\). If \(G= H_1 \oplus H_2 \oplus \cdots \oplus H_k\), where \(H_1\), \(H_2\), …, \(H_k\) are all isomorphic to \(H\), then \(G\) is said to be \(H\)-decomposable. Furthermore, if \(H\) is a cycle of length \(m\) then we say that \(G\) is \(C_m\)-decomposable and this can be written as \(C_m|G\). Where \(G\times H\) denotes the tensor product of graphs \(G\) and \(H\), in this paper, we prove that the necessary conditions for the existence of \(C_6\)-decomposition of \(K_m \times K_n\) are sufficient. Using these conditions it can be shown that every even regular complete multipartite graph \(G\) is \(C_6\)-decomposable if the number of edges of \(G\) is divisible by \(6\).
Let \(C_m\), \(K_m\) and \(K_m -I\) denote cycle of length \(m\), complete graph on \(m\) vertices and complete graph on \(m\) vertices minus a \(1\)-factor respectively. By an \(m\)-cycle we mean a cycle of length \(m\). All graphs considered in this paper are simple and finite. A graph is said to be decomposed into subgraphs \(H_1\) and \(H_2\) which is denoted by \(G= H_1 \oplus H_2\), if \(G\) is the edge disjoint union of \(H_1\) and \(H_2\). If \(G= H_1 \oplus H_2 \oplus \cdots \oplus H_k\), where \(H_1\), \(H_2\), …, \(H_k\) are all isomorphic to \(H\), then \(G\) is said to be \(H\)-decomposable. Furthermore, if \(H\) is a cycle of length \(m\) then we say that \(G\) is \(C_m\)-decomposable and this can be written as \(C_m|G\). A \(k\)-factor of \(G\) is a \(k\)-regular spanning subgraph. A \(k\)-factorization of a graph \(G\) is a partition of the edge set of \(G\) into \(k\)-factors. A \(C_k\)-factor of a graph is a \(2\)-factor in which each component is a cycle of length \(k\). A resolvable \(k\)-cycle decomposition (for short \(k\)-RCD) of \(G\) denoted by \(C_k ||G\), is a \(2\)-factorization of \(G\) in which each \(2\)-factor is a \(C_k\)-factor.
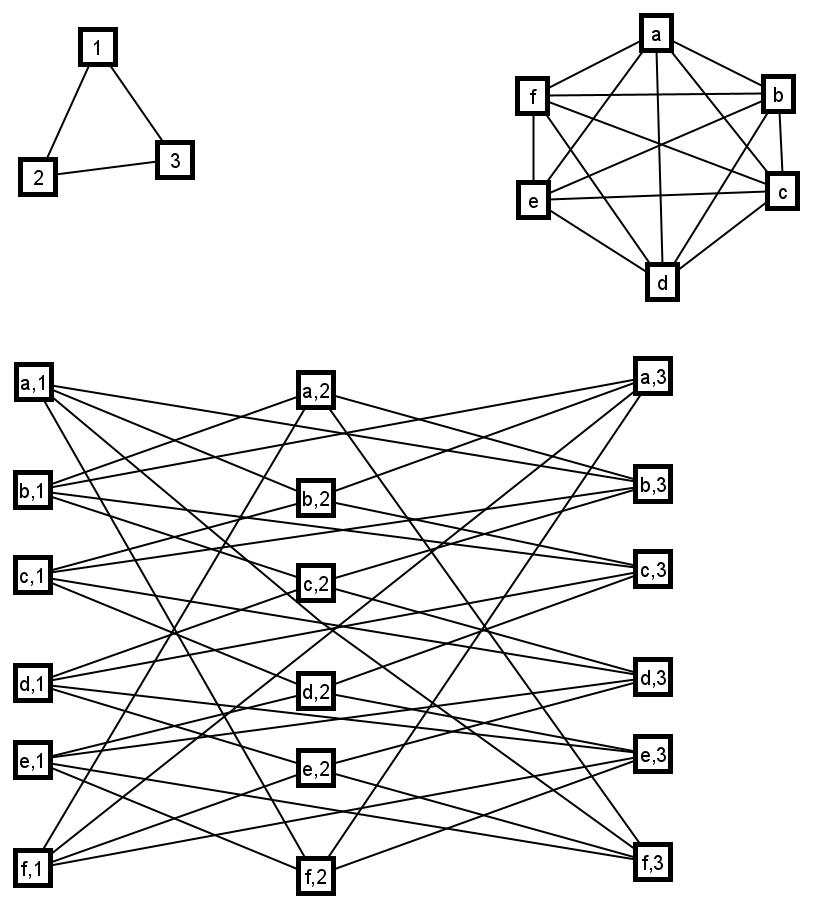
For two graphs \(G\) and \(H\) their tensor product \(G \times H\) has vertex set \(V(G) \times V(H)\) in which two vertices \((g_1,h_1)\) and \((g_2,h_2)\) are adjacent whenever \(g_1g_2 \in E(G)\) and \(h_1h_2 \in E(H)\). From this, note that the tensor product of graphs is distributive over edge disjoint union of graphs, that is if \(G= H_1 \oplus H_2 \oplus \cdots \oplus H_k\), then \(G \times H = (H_1 \times H)\oplus (H_2 \times H) \oplus \cdots \oplus(H_k \times H)\). Now, for \(h \in V(H)\), \(V(G) \times h = \{(v,h)|v \in V(G)\}\) is called a column of vertices of \(G \times H\) corresponding to \(h\). Further, for \(y \in V(G)\), \(y \times V(H) = \{(y,v)|v \in V(H)\}\) is called a layer of vertices of \(G \times H\) corresponding to \(y\).
In [1], Oyewumi et al., obtained an interesting result on the decompositions of certain graphs. The problem of finding \(C_k\)-decomposition of \(K_{2n+1}\) or \(K_{2n}-I\) where \(I\) is a \(1\)-factor of \(K_{2n}\), is completely settled by Alspach, Gavlas and Sajna in two different papers (see [2,3]). A generalization to the above complete graph decomposition problem is to find a \(C_k\)-decomposition of \(K_m \ast \overline K_n\), which is the complete \(m\)-partite graph in which each partite set has \(n\) vertices. The study of cycle decompositions of \(K_m \ast \overline K_n\) was initiated by Hoffman et al., [4]. In the case when \(p\) is a prime, the necessary and sufficient conditions for the existence of \(C_p\)-decomposition of \(K_m \ast \overline K_n\), \(p\geq 5\) is obtained by Manikandan and Paulraja in [5,6,7]. Billington [8] studied the decomposition of complete tripartite graphs into cycles of length 3 and 4. Furthermore, Cavenagh and Billington [9] studied \(4\)-cycle, \(6\)-cycle and \(8\)-cycle decomposition of complete multipartite graphs.
Billington et al., [10] solved the problem of decomposing \((K_m \ast \overline K_n)\) into \(5\)-cycles. Similarly, when \(p \geq 3\) is a prime, the necessary and sufficient conditions for the existence of \(C_{2p}\)-decomposition of \(K_m \ast \overline K_n\) was obtained by Smith (see [11]). For a prime \(p \geq 3\), it was proved in [12] that \(C_{3p}\)-decomposition of \(K_m \ast \overline K_n\) exists if the obvious necessary conditions are satisfied. As the graph \(K_m \times K_n \cong K_m \ast \overline K_n – E(nK_m)\) is a proper regular spanning subgraph of \(K_m \ast \overline K_n\). It is natural to think about the cycle decomposition of \(K_m \times K_n\).
The results in [5,6,7] also give necessary and sufficient conditions for the existence of a \(p\)-cycle decomposition, (where \(p \geq 5\) is a prime number) of the graph \(K_m \times K_n\). In [13] it was shown that the tensor product of two regular complete multipartite graph is Hamilton cycle decomposable. Muthusamy and Paulraja in [14] proved the existence of \(C_{kn}\)-factorization of the graph \(C_k \times K_{mn}\), where \(mn \neq 2 (\textrm{mod}\ 4)\) and \(k\) is odd. While Paulraja and Kumar [15] showed that the necessary conditions for the existence of a resolvable \(k\)-cycle decomposition of tensor product of complete graphs are sufficient when \(k\) is even. Oyewumi and Akwu [16] proved that \(C_4\) decomposes the product \(K_m \times K_n\), if and only if either (1) \(n \equiv 0 \ (\textrm{mod}\ 4)\) and \(m\) is odd, (2) \(m \equiv 0 \ (\textrm{mod}\ 4)\) and \(n\) is odd or (3) \(m \ or \ n \equiv 1 \ (\textrm{mod}\ 4)\).
As a companion to the work in [16], i.e., to consider the decomposition of the tensor product of complete graphs into cycles of even length. This paper proves that the obvious necessary conditions for \(K_m \times K_n\), \(2 \leq m,n\), to have a \(C_6\)-decomposition are also sufficient. Among other results, here we prove the following main results.
It is not surprising that the conditions in Theorem 1 are “symmetric” with respect to \(m\) and \(n\) since \(K_m \times K_n \cong K_n \times K_m\).
Theorem 1. Let \(2 \leq m,n, \) then \(C_6| K_m \times K_n\) if and only if \(m \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\) or \(n \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\).
Theorem 2. Let \(m\) be an even integer and \(m \geq 6\), then \(C_6| K_m – I \times K_n\) if and only if \(m \equiv 0 \ \text{or} \ 2\ (\textrm{mod}\ 6)\).
Theorem 3. Let \(n \in N\), then \(C_6|C_3 \times K_n\).
Proof. Following from the definition of tensor product of graphs, let \(U^1= \{u_1,v_1,w_1\}\), \(U^2= \{u_2,v_2,w_2\} \),\(…\), \(U^n=\{u_n,v_n,w_n\}\) form the partite set of vertices in \(C_3 \times K_n\). Also, \(U^i\) and \(U^j\) has an edge in \(C_3 \times K_n\) for \(1\leq i,j\leq n\) and \(i\neq j\) if the subgraph induce \(K_{3,3}-I\), where \(I\) is a \(1\)-factor of \(K_{3,3}\). Now, each subgraph \(U^i \cup U^j\) is isomorphic to \(K_{3,3}-I\). But \(K_{3,3}-I\) is a cycle of length six. Hence the proof.
Example 1. The graph \(C_3 \times K_7\) can be decomposed into cycles of length \(6\).
Proof. Let the partite sets (layers) of the tripartite graph \(C_3 \times K_7\) be \(U=\{u_1, u_2, . . . , u_7\}\), \(V=\{v_1, v_2, . . . , v_7\}\) and \(W=\{w_1,w_2, . . . ,w_7\}\). We assume that the vertices of \(U,V\) and \(W\) having same subscripts are the corresponding vertices of the partite sets. A \(6\)-cycle decomposition of \(C_3 \times K_7\) is given below:
\(\{u_1,v_2,w_1,u_2,v_1,w_2\}\),\(\{u_1,v_3,w_1,u_3,v_1,w_3\}\),\(\{u_2,v_3,w_2,u_3,v_2,w_3\}\),
\(\{u_1,v_4,w_1,u_4,v_1,w_4\}\),\(\{u_2,v_4,w_2,u_4,v_2,w_4\}\),\(\{u_3,v_4,w_3,u_4,v_3,w_4\}\),
\(\{u_1,v_5,w_1,u_5,v_1,w_5\}\),\(\{u_2,v_5,w_2,u_5,v_2,w_5\}\),\(\{u_3,v_5,w_3,u_5,v_3,w_5\}\),
\(\{u_4,v_5,w_4,u_5,v_4,w_5\}\),\(\{u_1,v_6,w_1,u_6,v_1,w_6\}\),\(\{u_2,v_6,w_2,u_6,v_2,w_6\}\),
\(\{u_3,v_6,w_3,u_6,v_3,w_6\}\),\(\{u_4,v_6,w_4,u_6,v_4,w_6\}\),\(\{u_5,v_6,w_5,u_6,v_5,w_6\}\),
\(\{u_1,v_7,w_1,u_7,v_1,w_7\}\),\(\{u_2,v_7,w_2,u_7,v_2,w_7\}\),\(\{u_3,v_7,w_3,u_7,v_3,w_7\}\),
\(\{u_4,v_7,w_4,u_7,v_4,w_7\}\),\(\{u_5,v_7,w_5,u_7,v_5,w_7\}\),\(\{u_6,v_7,w_6,u_7,v_6,w_7\}\).
Theorem 4. [17] Let \(m\) be an odd integer and \(m \geq 3\). If \(m \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\) then \(C_3|K_m\).
Theorem 5. [3] Let \(n\) be an even integer and \(m\) be an odd integer with \(3 \leq m \leq n\). The graph \(K_n- I\) can be decomposed into cycles of length \(m\) whenever \(m\) divides the number of edges in \(K_n – I\).
Theorem 6. [3] Let \(n\) be an odd integer and \(m\) be an even integer with \(3 \leq m \leq n\). The graph \(K_n\) can be decomposed into cycles of length \(m\) whenever \(m\) divides the number of edges in \(K_n\).
Lemma 1. \(C_6|C_6 \times K_2\).
Proof. Let the partite set of the bipartite graph \(C_6 \times K_2\) be \(\{u_1,u_2,…,u_6\}\), \(\{v_1,v_2,…,\) \(v_6\}\). We assume that the vertices having the same subscripts are the corresponding vertices of the partite sets. Now \(C_6 \times K_2\) can be decomposed into \(6\)-cycles which are \(\{u_1,v_2,u_3,v_4,u_5,v_6\}\) and \(\{v_1,u_2,v_3,u_4,v_5,u_6\}\).
Theorem 7. For all \(n\), \(C_6|C_6 \times K_n\).
Proof. Let the partite set of the \(6\)-partite graph \(C_6 \times K_n\) be \(U=\{u_1,u_2,…,u_n\}\), \(V=\{v_1,v_2,…,v_n\}\), \(W=\{w_1,w_2,…,w_n\}\), \(X=\{x_1,x_2,…,x_n\}\), \(Y=\{y_1,y_2,…,y_n\}\) and \(Z=\{z_1,z_2,…,z_n\}\), we assume that the vertices of \(U,V,W,X,Y\) and \(Z\) having the same subscripts are the corresponding vertices of the partite sets. Let \(U^1=\{u_1,v_1,w_1,x_1,y_1,z_1\}\), \(U^2=\{u_2,v_2,w_2,x_2,y_2,z_2\}\), …, \(U^n=\{u_n,v_n,w_n,x_n,y_n,z_n\}\) be the sets of these vertices having the same subscripts. By the definition of the tensor product, each \(U^i\), \(1 \leq i \leq n\) is an independent set and the subgraph induced by each \(U^i \cup U^j\), \(1\leq i,j\leq n\) and \(i\neq j\) is isomorphic to \(C_6 \times K_2\). Now by Lemma 1 the graph \(C_6 \times K_2\) admits a \(6\)-cycle decomposition. This completes the proof.
Proof of Theorem 1. Assume that \(C_6|K_m \times K_n\) for some \(m\) and \(n\) with \(2 \leq m,n\). Then every vertex of \(K_m \times K_n\) has even degree and \(6\) divides in the number of edges of \(K_m \times K_n\). These two conditions translate to \((m-1)(n-1)\) being even and \(6|m(m-1)n(n-1)\) respectively. Hence, by the first fact \(m\) or \(n\) has to be odd, i.e., has to be congruent to \(1 \ or \ 3 \ or \ 5\ (\textrm{mod}\ 6)\). The second fact can now be used to show that they cannot both be congruent to \(5\ (\textrm{mod}\ 6)\). It now follows that \(m \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\) or \(n \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\).
Conversely, let \(m \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\). By Theorem 4, \(C_3|K_m\) and hence \(K_m \times K_n =((C_3 \times K_n)\oplus \cdots \oplus(C_3 \times K_n))\). Since \(C_6|C_3 \times K_n\) by Theorem 3.
Finally, if \(n \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\), the above argument can be repeated with the roles of \(m\) and \(n\) interchanged to show again that \(C_6|K_m \times K_n\). This completes the proof.Proof of Theorem 2. Assume that \(C_6|K_m-I \times K_n, m\geq 6\). Certainly, \(6|mn(m-2)(n-1)\). But we know that if \(6|m(m-2)\) then \(6|mn(m-2)(n-1)\). But \(m\) is even therefore \(m \equiv 0 \ or \ 2\ (\textrm{mod}\ 6)\).
Conversely, let \(m \equiv 0 \ or \ 2 \ (\textrm{mod}\ 6)\). Notice that for each \(m\), \(\frac{m(m-2)}{2}\) is a multiple of \(3\). Thus by Theorem 5 \(C_3|K_m -I\) and hence \(K_m – I \times K_n =((C_3 \times K_n)\oplus \cdots \oplus(C_3 \times K_n))\). From Theorem 3, \(C_6|C_3 \times K_n\). The proof is complete.
Corollary 1. For any simple graph \(G\). If
Proof. We only need to show that \(C_3|G\). Applying Theorem 3 gives the result.
