KG-Sombor index of Kragujevac trees

1. Introduction

Let \(G\) be a simple graph, with vertex set \(\mathbf V(G)\) and edge set \(\mathbf E(G)\). Then \(|\mathbf V(G)|\) and \(|\mathbf E(G)|\) are the number of vertices and edges of \(G\). By \(e=uv \in \mathbf E(G)\) we denote the edge of \(G\), connecting the vertices \(u\) and \(v\). The degree of a vertex \(u \in \mathbf V(G)\) (= number of vertices that are adjacent to \(u\)) is denoted by \(d(u)\). The degree of an edge \(e \in \mathbf E(G)\) (= number of edges that are incident to \(e\)) is denoted by \(d(e)\). Recall that if \(e=uv\), then \(d(e)=d(u)+d(v)-2\).

For other graph-theoretical notions, the readers are referred to textbooks [1,2,3].

In the mathematical and chemical literature, some fifty or more different vertex-degree-based graph invariants (topological indices) have been defined and examined, all of the form

where \(F(x,y)\) is some function with property \(F(x,y)=F(y,x)\).

The oldest such invariant, conceived as early as in the 1970s, is the first Zagreb index, \(Zg\) [4]. One of the newest such invariant is the Sombor index, \(SO\) [5,6]. These are defined as

Recently the Sombor index attracted much attention and numerous of its mathematical properties have been established (see, for instance, [7,8,9,10,11,12]). For chemical applications of \(SO\) see [13,14,15].

Recently a vertex-edge variant of the Sombor index was introduced [16,17], defined as

where the summation goes over pairs of vertices (\(u\)) and edges (\(e\)), such that \(u\) is an endpoint of the edge \(e\). It could be easily shown [16] that \(KG\) is a topological index of the form (1), namely: In this paper we are concerned with a class of trees, called Kragujevac trees, defined below. Kragujevac trees emerged within the study of the atom-bond-connectivity (\(ABC\)) index. It was conjectured that the graph with minimal \(ABC\)-index is a Kragujevac tree [18]. Later it was found that the conjecture is violated for graphs with larger number of vertices; see [19] and the references cited therein. Nevertheless, Kragujevac trees were eventually extensively investigated [20,21,22,23,24,25,26]). In particular, the Sombor index of Kragujevac trees was studied in [27].

By continuing the considerations from Ref. [27], we now focus our attention to the KG-Sombor index. In order that the present article be self-contained, we repeat the definition of Kragujevac trees (as slightly modified in [27]).

2. Preparations

Let \(n\) be a positive integer. For \(k=0,1,\ldots,n\), we denote by \(B_k\) the rooted tree with \(2k+1\) vertices, constructed by attaching \(k\) two-vertex branches to the root, see Figure 1.

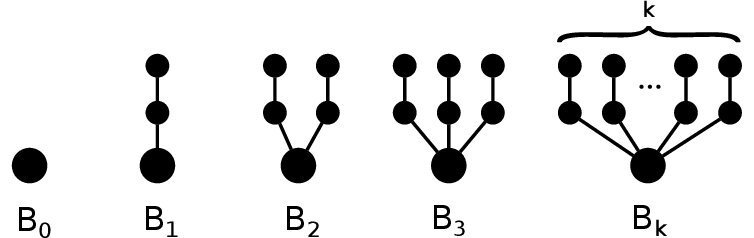
Let \(k_i\,,\,i=1,2,\ldots,n\), be non-negative integers, such that

and let Throughout this paper, both parameters \(n\) and \(K\) are assumed to have fixed values.

Definition 1. Let the parameters \(k_1,k_2,…,k_n\) satisfy the condition (6). Then the Kragujevac tree \(Kg(k_1,k_2,\ldots,k_n)\) is the tree obtained from \(B_{k_1}\), \(B_{k_2}\), \(\ldots\) \(B_{k_n}\), by connecting their roots to a new vertex.

In Figure 2 an example is depicted, illustrating Definition 1.

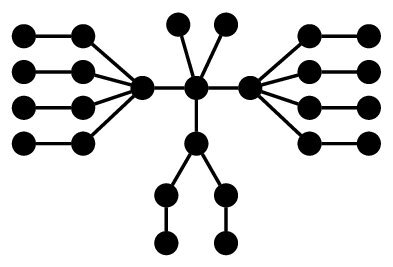
According to Definition 1, the Kragujevac tree with parameters \(k_1,k_2,\ldots,k_n\) has

\[ 1 + \sum_{i=1}^n (2\,k_i + 1) = 2K + n + 1 \] vertices.

An edge connecting a vertex of degree \(i\) and a vertex of degree \(j\) will be referred to as an \((i,j)\)-edge. Directly from Definition 1 we obtain:

Proposition 2. Let \(Kg(k_1,k_2,\ldots,k_n)\) be a Kragujevac tree. Then it has \(K\) \((1,2)\)-edges, \(k_i\) \((k_i+1,2)\)-edges for each \(i=1,2,\ldots,n\), and a \((k_i+1,n)\)-edge for each \(i=1,2,\ldots,n\).

Applying Proposition 2 to Eq. (5) we arrive at:

Lemma 3. The KG-Sombor index of the Kragujevac tree \(Kg(k_1,k_2,\ldots,k_n)\) depends on its structural parameters as

3. Main results

In this section, we determine the extremal Kragujevac trees (minimal and maximal) concerning the KG-Sombor index. In order to achieve this goal, we first recall a similar result established for the first Zagreb index, [27].

Lemma 4. Let \(Kg = Kg(k_1,k_2,\ldots,k_n)\) be the Kragujevac tree whose parameters satisfy Eqs. (6) and (7). Then \(Zg(Kg)\) is minimal if and only if \[ k_i \in \left\{ \left\lfloor \frac{K}{n} \right\rfloor, \left\lceil \frac{K}{n} \right\rceil \right\} \ \ \mbox{for} \ \ i=1,2,\ldots, n, \hspace{10mm} \mbox{i.e.,} \hspace{10mm} k_n – k_1 \leq 1\,. \] and \(Zg(Kg)\) is maximal if and only if \[ k_1=k_2= \cdots = k_{n-1}=0 \hspace{10mm} \mbox{and} \hspace{10mm} k_n=K\,. \]

In order to use the results of Lemma 4, we need to establish a relation between the first Zagreb and the KG-Sombor indices. This is achieved using the following simple argument. Note that bounds analogous to (10) were previously obtained for the ordinary Sombor index, Eq. (3) [6].

For any positive numbers \(a\) and \(b\),

Equality on the left-hand side holds if and only if \(a = b\). Applying the right-hand side inequality to Eq. (5), and taking into account the definition of the first Zagreb index, Eq. (2), we get \begin{eqnarray*} KG(G) & < & \sum_{uv \in \mathbf E(G)} \Big[ \big( d(u)+ [d(u)+d(v)-2] \Big) + \Big( d(v)+ [d(u)+d(v)-2] \Big) \,\Big] \\[3mm] & = & \sum_{uv \in \mathbf E(G)} \Big[ 3\,d(u)+3\,d(v)-4\,\Big] = 3 \sum_{uv \in \mathbf E(G)} \big[d(u)+d(v)]-4m \\[3mm] & = & 3\,Zg(G) – 4m\,, \end{eqnarray*} where \(m\) is the number of edges of the graph \(G\). Thus, in view of the inequalities (9), we arrive at:

Lemma 5. For any graph \(G\) with \(m\) edges,

Lemma 5 corrects Theorem 4.2 in Ref. [27].

Inequalities (10) indicate that the KG-Sombor and first Zagreb indices should be linearly correlated. Indeed, in the case of trees (with a fixed number of vertices) this correlation was found to be remarkably good, see Figures 3 and 4, and Table 1.

Table 1. The parameters of the regression line \(KG=a\,Zg + b\) for \(N\)-vertex trees; \(R\) = correlation coefficient.

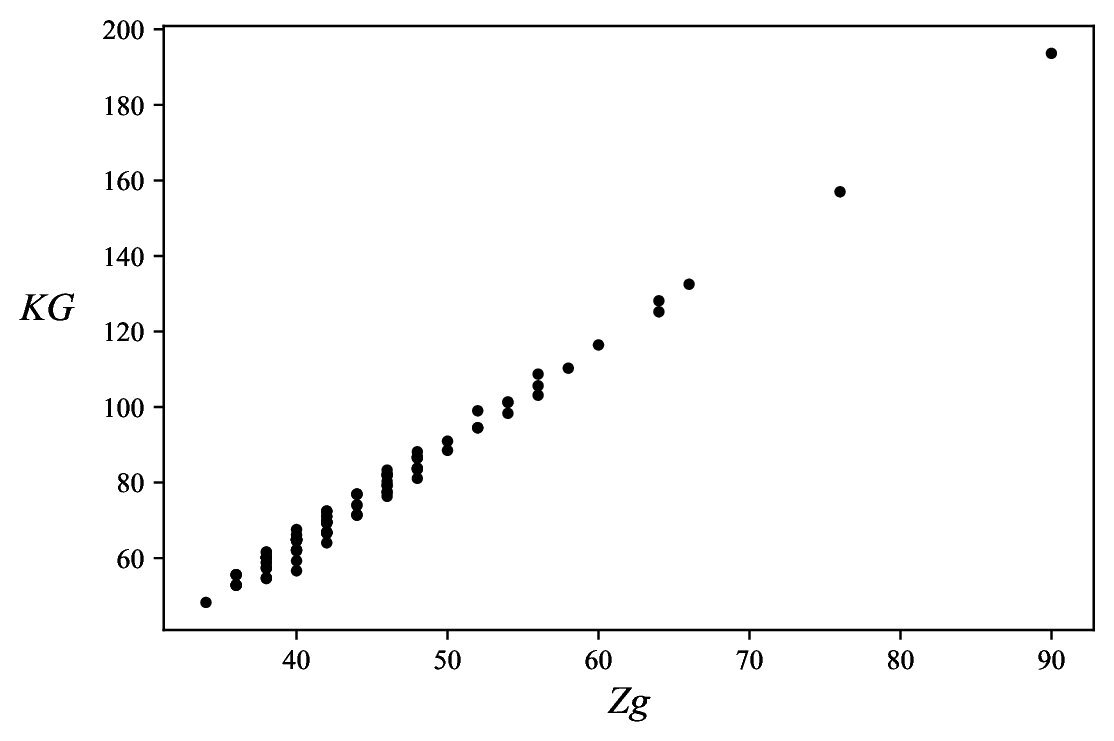
\(N\)	\(a\)	\(b\)	\(R\)
10	\(2.61 \pm 0.03\)	\(-40.27 \pm 1.15\)	0.9952
11	\(2.60 \pm 0.02\)	\(-44.94 \pm 0.89\)	0.9947
12	\(2.58 \pm 0.01\)	\(-49.13 \pm 0.64\)	0.9946
13	\(2.58 \pm 0.01\)	\(-53.71 \pm 0.47\)	0.9942
14	\(2.57 \pm 0.01\)	\(-58.13 \pm 0.34\)	0.9940
15	\(2.57 \pm 0.03\)	\(-62.69 \pm 0.24\)	0.9937

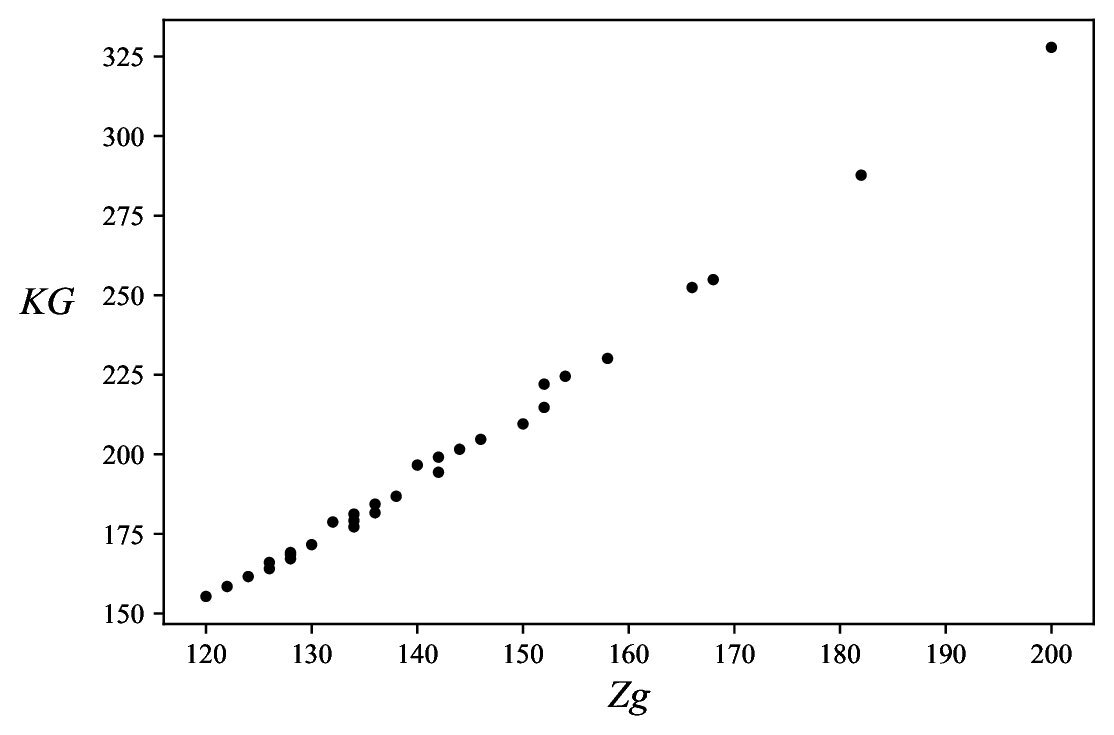
Bearing these numerical results in mind, we maintain to be justified to state the following analogue of Lemma 4:

Proposition 6. Let \(Kg = Kg(k_1,k_2,\ldots,k_n)\) be the Kragujevac tree whose parameters satisfy Eqs. (6) and (7). Then \(KG(Kg)\) is minimal if and only if \[ k_i \in \left\{ \left\lfloor \frac{K}{n} \right\rfloor, \left\lceil \frac{K}{n} \right\rceil \right\} \ \ \mbox{for} \ \ i=1,2,\ldots, n, \hspace{10mm} \mbox{i.e.,} \hspace{10mm} k_n – k_1 \leq 1\,. \] and \(KG(Kg)\) is maximal if and only if \[ k_1=k_2= \cdots = k_{n-1}=0 \hspace{10mm} \mbox{and} \hspace{10mm} k_n=K\,. \]

A somewhat stronger claim, based on the numerical results presented in Figure 4, would be:

Proposition 7. Let \(Kg_a\) and \(Kg_b\) be two Kragujevac trees with equal \(n\) and \(K\) values. Then \[ Zg(Kg_a) > Zg(Kg_b) \ \Leftrightarrow \ KG(Kg_a) > KG(Kg_b)\,. \]

Assuming that Proposition 6 is valid, we have the following results:

If \(Kg\) is a Kragujevac tree with parameters \(n\) and \(K\), then the maximum value of \(KG(Kg)\) is

\begin{eqnarray*} && (\sqrt{8}+\sqrt{5})K + \sqrt{2}\,K^2 + K\,\sqrt{K^2+2K+5} + \sqrt{2K^2+n^2+2nK-2n+2} +\, \sqrt{K^2+2Kn-2K+2n^2-2n+1}\,. \end{eqnarray*} The minimum value of \(KG(Kg)\) depends on the parameter \(p\), defined via \(K \equiv p\,(\hspace{-3mm} \mod n)\). For instance, for \(p=0\), this minimum value is \begin{eqnarray*} && (\sqrt{8}+\sqrt{5})K + \sqrt{2}\,K\,x + K\,\sqrt{x^2+2x+5} + n\,\sqrt{2x^2+n^2+2nx-2n+2} + \, n\,\sqrt{x^2+2nx-2x+2n^2-2n+1}\,, \end{eqnarray*} where \(x=K/n\).

4. Concluding remarks

Recently, the first Banhatti (a,b)-KA index of a graph was defined as [17] \[ BKA^1_{a,b}(G) = \sum_{ue} \Big[ d(u)^a + d(e)^a \Big]^b\,. \] We quickly see that \(BKA^1_{1,1}\) is the ordinary first Bahnatti index [28], whereas \(BKA^1_{2,1/2}\) is the KG-Sombor index. Thus, studying the \(BKA^1_{a,b}\)-index and its extremal values will be challenging.

In this paper, a combinatorial expression, Eq. (5), is established for the KG-Sombor index of Kragujevac trees. Because of the perplexing form of formula (5), our approach towards finding the extremal values of \(KG(Kg)\), Proposition 6, used the analogous results earlier established for the first Zagreb index (Lemma 4), combined with Lemma 5, and the fact that there exists an excellent linear correlation between KG-Sombor and first Zagreb indices. This latter fact was empirically verified for both general and Kragujevac trees, see Figs. 3 and 4. Finding a rigorous analytical proof of our Propositions 6 and 7 remains a challenge for the future but appears to be a prohibitively tricky task.

Comparing Eqs. (3) Furthermore, (4), it is obvious why ”Sombor” is used in the name of the KG-index. At this point, we reveal that ”KG” indicates the names of the inventors of this index – V. R. K & I. G.

Author Contributions:

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest:

”The authors declare no conflict of interest.”

Acknowledgments :

Izudin Redžepovic was supported by the Serbian Ministry of Education, Science and Technological Development (Grant No. 451-03-68/2022-14/200122).