Topological indices are real numbers associated with molecular graphs of compounds that help to guess properties of compounds. Hex-Derived networks has an assortment of valuable applications in drug store, hardware, and systems administration. Imran et al. [1] computed the general Randić, first Zagreb, ABC, GA, ABC\(_{4}\), and GA\(_{5}\) indices for these hex-derived networks. In this article, we extend the work of [1] and compute some new topological indices of these networks.
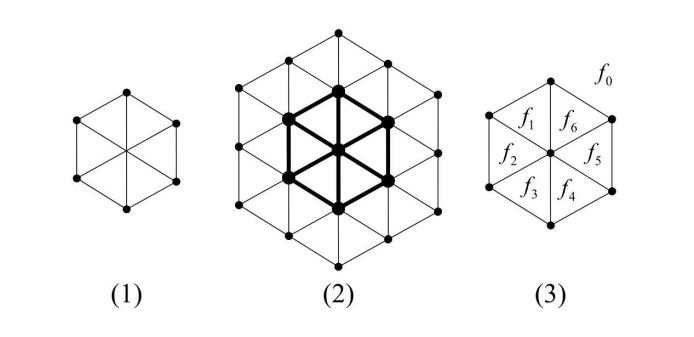
Among these types, degree based indices are of incredible significance and assume an indispensable part in chemistry. The idea of chemical indices originated from Wiener [2]. The hexagonal mesh was put forward by Chen et al. [3]. A hexagonal work is made up with an arrangement of triangles as depicted in Figure 1. A 2-dimensional hexagonal mesh \(HX(2)\) is made out of six triangles (see Figure 1(1). By adding a layer of triangles around the boundary of \(HX(2)\), a 3-dimensional hexagonal mesh \(HX(3)\) is obtained (see Figure 1(2)).
In this article, \(\mathcal{G}\) and \(\mathcal{H}\) are considered to be Hex-Derived networks of type 1 and type 2, with vertex set \(V\) and edge set \(\mathrm{E}\). The notations used in this article are mainly taken from books [4, 5].
Let \(\mathfrak{T}\) be a graph. Then the Wiener index of \(\mathfrak{T}\) is defined as \begin{equation*} W(\mathfrak{T})=\frac{1}{2}\sum\limits_{(r,s)}d_{\mathfrak{T}}(r,s) \end{equation*} where \((r,s)\) is any ordered pair of vertices in \(\mathfrak{T}\) and \(d(r,s)\) is \(r-s\) geodesic.
The Zagreb indices discovered many applications in QSAR and QSPR reviews. In the books by Todeschini and Consonni [6, 7], the details on the chemical applications of the two Zagreb indices can be found.
If \(d_{\mathfrak{T}}(r)\) be the degree of a vertex \(r\) of a molecular simple connected graph \(\mathfrak{T}\), the first and second Zagreb indices are defined as
\begin{equation*}
M_{1}(\mathfrak{T})= \sum\limits_{rs \in E(\mathfrak{T})}(d_{\mathfrak{T}}(r)+d_{\mathfrak{T}}(s)),
\end{equation*}
\begin{equation*}
M_{2}(\mathfrak{T})= \sum\limits_{rs \in E(\mathfrak{T})}(d_{\mathfrak{T}}(r)\cdot d_{\mathfrak{T}}(s)).
\end{equation*}
Hamzeh and R\(\acute{e}\)ti [8] concentrated on the Zagreb index disparity acquired from graph irregularity measures. For the essential delineation of a related graphs \(\mathfrak{T}\) with \(|V(\mathfrak{T})|\) vertices and \(|E(\mathfrak{T})|\) edges, two novel graph irregularity indices are presented, which are depicted as follows.
Let \(\mathfrak{T}\) be a graph with size \(`m’\) and order \(`n’,\) then the first and second Zagreb irregularity indices are defined as
\begin{equation*}
IRM_{1}(\mathfrak{T})=M_{1}(\mathfrak{T})-\frac{4|E(\mathfrak{T})|^2}{|V(\mathfrak{T})|},
\end{equation*}
\begin{equation*}
IRM_{2}(\mathfrak{T})=M_{2}(\mathfrak{T})-\frac{4|E(\mathfrak{T})|^3}{|V(\mathfrak{T})|^2}.
\end{equation*}
Another topological index in view of the level of the vertex is the Balaban index [9,10]. This index for a graph \(\mathfrak{T}\) of order \(`n’\), size \(`m’\) is characterized as
\begin{equation*}
J(\mathfrak{T})=\bigg(\frac{m}{m-n+2}\bigg)\sum\limits_{rs \in E(\mathfrak{T})}\frac{1}{\sqrt{d_{\mathfrak{T}}(r)\cdot d_{\mathfrak{T}}(s)}}.
\end{equation*}
Ghorbani and Azimi [11] defined the multiple Zagreb topological indices of a graph \(\mathfrak{T}\) based on degree of vertices of \(\mathfrak{T}\).
The first and second multiple Zagreb indices are defined as
\begin{equation*}
PM_1(\mathfrak{T})=\prod\limits_{rs \in E(\mathfrak{T})}(d_{\mathfrak{T}}(r)+d_{\mathfrak{T}}(s)),
\end{equation*}
\begin{equation*}
PM_2(\mathfrak{T})=\prod\limits_{rs \in E(\mathfrak{T})}(d_{\mathfrak{T}}(r)\cdot d_{\mathfrak{T}}(s)).
\end{equation*}
Properties of the first and second multiple Zagreb indices may be found in the work by Eliasi et al. [12] and Gutman [13].
Ranjini et al. [14] reclassified the Zagreb index and redefined Zagreb index as
\begin{equation*}
ReZG(\mathfrak{T})=\sum\limits_{rs \in E(\mathfrak{T})}\bigg(\frac{d_{\mathfrak{T}}(r)+d_{\mathfrak{T}}(s)}{d_{\mathfrak{T}}(r)\cdot d_{\mathfrak{T}}(s)}\bigg).
\end{equation*}
Nowadays there is an extensive research activity on several important chemical indices and their variants. For further study of topological indices of various graph families see, [15, 16, 17, 18, 19]. In this paper, we aim to study the add.
| \((d_{u},d_{v})\) where \(uv\in E(\mathcal{H})\) | \(\text{Number of edges}\) |
|---|---|
| \(\mathrm{E_1}=(3,5)\) | \(12\) |
| \(\mathrm{E_2}=(3,7)\) | \(18n-36\) |
| \(\mathrm{E_3}=(3,12)\) | \(18n^2-54n+42\) |
| \(\mathrm{E_4}=(5,7)\) | \(12\) |
| \(\mathrm{E_5}=(5,12)\) | \(6\) |
| \(\mathrm{E_6}=(7,7)\) | \(6n-18\) |
| \(\mathrm{E_7}=(7,12)\) | \(12n-24\) |
| \(\mathrm{E_8}=(12,12)\) | \(9n^2-33n+30\) |
Theorem 1. Let \((\mathcal{G})=HDN_{1}(n)\) be the hex derived network of type 1. Then
Proof.
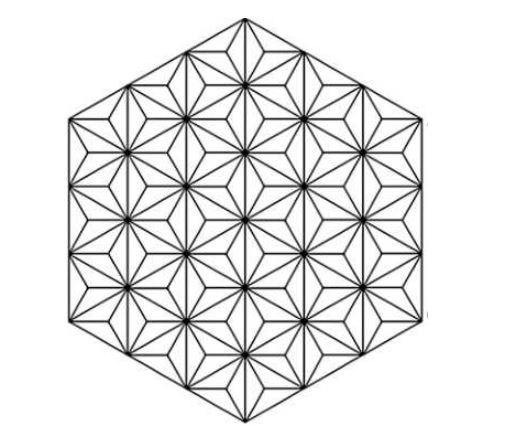
Let \(\mathcal{G}=HDN_{1}(n)\) be the hex derived network of type 1, where \(n\geq4\). T \(\mathcal{G}(n)\) has \(6n^2-12n+6\) vertices of degree 3, \(6\) vertices of degree 5, \(6n-12\) vertices of degree 7 and \(3n^2-9n+7\) vertices of degree 12. Table 1 shows the different edge partitions of \(\mathcal{G}(n)\).
(1) Now, from the definition of first Zagreb irregularity index, we have
\begin{eqnarray*}
IRM_{1}(\mathcal{G})&=&M_{1}(\mathcal{G})-\frac{4|E(\mathcal{G})|^2}{|V(\mathcal{G})|}\\
&=& \sum\limits_{rs \in \mathrm{E(\mathcal{G})}}(degree_{\mathcal{G}}(r)+degree_{\mathcal{G}}(s))-\frac{4((3(-1+n)(-8+9n))^2)}{1+3n(-5+3n)}\\
&=&\mathrm{E_{1}}(8)+\mathrm{E_{2}}(10)+\mathrm{E_{3}}(15)+\mathrm{E_{4}}(12)+
\mathrm{E_{5}}(17)+\mathrm{E_{6}}(14)+\mathrm{E_{7}}(19)\\&&+\mathrm{E_{8}}(24)-\frac{4((3(-1+n)(-8+9n))^2)}{1+3n(-5+3n))}\\
&=&(12)(8)+(18n-36)(10)+(18n^{2}-54n+42)(15)+(12)(12)\\&&+(6)(17)+(6n-18)(14)+(12n-24)(19)+(9n^{2}-33n+30)(24)\\&&-
\frac{4((3(-1+n)(-8+9n))^2)}{1+3n(-5+3n))}\\
&=&536-510n+162n^2+\frac{76-96n}{7+3n(-5+3n)}.
\end{eqnarray*}
(2) Now, from the definition of second Zagreb irregularity index, we have
\begin{eqnarray*}
IRM_{2}(\mathcal{G})&=&M_{2}(\mathcal{G})-\frac{4|E(\mathcal{G})|^3}{|V(\mathcal{G})|^2}\\
&=& \sum\limits_{rs \in \mathrm{E(\mathcal{G})}}(d_{\mathcal{G}}(r)+d_{\mathcal{G}}(r))-\frac{4((3(-1+n)(-8+9n))^3)}{(1+3n(-5+3n))^2}\end{eqnarray*}\begin{eqnarray*}
&=&\mathrm{E_{1}}(15)+\mathrm{E_{2}}(21)+\mathrm{E_{3}}(36)+\mathrm{E_{4}}(35)+\mathrm{E_{5}}(60)+
\mathrm{E_{6}}(49)+\mathrm{E_{7}}(84)\\&&+\mathrm{E_{8}}(144)-\frac{4((3(-1+n)(-8+9n))^3)}{(1+3n(-5+3n))^2}\\
&=&(12)(15)+(18n-36)(21)+(18n^{2}-54n+42)(36)+(12)(35)+\\&&(6)(60)+(6n-18)(49)+(12n-24)(84)+(9n^{2}-33n+30)(144)\\&&-
\frac{4((3(-1+n)(-8+9n))^3)}{(1+3n(-5+3n))^2}\\
&=&6\bigg(146-199n+81n^2-\frac{18(-1+n)^{3}(-8+9n)^3}{(7+3n(-5+3n))^2}\bigg).
\end{eqnarray*}
Theorem 2. Let \((\mathcal{G})=HDN_{1}(n)\) be the hex derived network of type 1. Then $$J(\mathcal{G})=\frac{3(-1+n)(-8+9n)(970-280\sqrt{2}+140\sqrt{15}-240\sqrt{21}+48\sqrt{35}}{140(7+3n(-5+3n))}+ \frac{5n(-305+28\sqrt{2}+24\sqrt{21}+105n))}{140(7+3n(-5+3n))}.$$
Proof. From the edge partition of \((\mathcal{G})=HDN_{1}(n)\) given in Table 1, we have \begin{eqnarray*} J(\mathcal{G})&=&\bigg(\frac{m}{m-n+2}\bigg)\sum\limits_{rs \in \mathrm{E}(\mathcal{G})}\frac{1}{\sqrt{d_{\mathcal{G}}(r)\cdot d_{\mathcal{G}}(s)}}\\ &=&\bigg(\frac{3(-1+n)(-8+9n)}{7+3n(-5+3n)}\bigg)\bigg(\mathrm{E_1}\bigg(\frac{1}{\sqrt{3\times5}}\bigg)+ \mathrm{E_2}\bigg(\frac{1}{\sqrt{3\times7}}\bigg)+\mathrm{E_3}\bigg(\frac{1}{\sqrt{3\times12}}\bigg)\\&&+ \mathrm{E_4}\bigg(\frac{1}{\sqrt{5\times7}}\bigg)+\mathrm{E_5}\bigg(\frac{1}{\sqrt{5\times12}}\bigg) +\mathrm{E_6}\bigg(\frac{1}{\sqrt{7\times7}}\bigg)+\mathrm{E_7}\bigg(\frac{1}{\sqrt{7\times12}}\bigg) +\mathrm{E_8}\bigg(\frac{1}{\sqrt{12\times12}}\bigg)\bigg)\\ &=&\bigg(\frac{3(-1+n)(-8+9n)}{7+3n(-5+3n)}\bigg)\bigg((12)\bigg(\frac{1}{15}\bigg)+ (18n-36)\bigg(\frac{1}{21}\bigg)\\&&+(18n^{2}-54n+42)\bigg(\frac{1}{36}\bigg)+ (12)\bigg(\frac{1}{\sqrt{35}}\bigg)+(6)\bigg(\frac{1}{\sqrt{60}}\bigg) +(6n-18)\bigg(\frac{1}{\sqrt{49}}\bigg)\\&&+(12n-24)\bigg(\frac{1}{\sqrt{84}}\bigg) +(9n^{2}-33n+30)\bigg(\frac{1}{\sqrt{144}}\bigg)\bigg)\\ &=&\frac{3(-1+n)(-8+9n)(970-280\sqrt{2}+140\sqrt{15}-240\sqrt{21}+48\sqrt{35}}{140(7+3n(-5+3n))}\\&&+ \frac{5n(-305+28\sqrt{2}+24\sqrt{21}+105n))}{140(7+3n(-5+3n))}. \end{eqnarray*}
Theorem 3. Let \((\mathcal{G})=HDN_{1}(n)\) be the hex derived network of type 1. Then
Proof. (1) From the edge partition of \((\mathcal{G})=HDN_{1}(n)\) given in Table 1 and definition of multiple first Zagreb index, we have \begin{eqnarray*} PM_1(\mathcal{G})&=&\prod\limits_{rs \in \mathrm{E(\mathcal{G})}}(d_{\mathcal{G}}(r)+d_{\mathcal{G}}(s))\\ &=&8^{\mathrm{E_{1}}(\mathcal{G})}\times10^{\mathrm{E_{2}}(\mathcal{G})}\times15^{\mathrm{E_{3}}(\mathcal{G})}\times 12^{\mathrm{E_{4}}(\mathcal{G})}\times17^{\mathrm{E_{5}}(\mathcal{G})}\times 14^{\mathrm{E_{6}}(\mathcal{G})}\times19^{\mathrm{E_{7}}(\mathcal{G})}\times24^{\mathrm{E_{8}}(\mathcal{G})}\\ &=&8^{(12)}+10^{(18n-36)}+15^{(18n^{2}-54n+42)}+12^{(12)}+17^{(6)}+14^{(6n-18)}+19^{(12n-24)}+24^{(9n^{2}-33n+30)}\\ &=&12827693806929\times5^{18(-2+n)}7^{6(-3+n)}19^{12(-2+n)}64^{1+4n}36^{18n^{2}-54n+42}\\&&24^{9n^{2}-33n+30}. \end{eqnarray*} (2) Now, the definition of multiple second Zagreb index, we have \begin{eqnarray*} PM_2(\mathcal{G})&=&\prod\limits_{rs \in \mathrm{E(\mathcal{G})}}(d_{\mathcal{G}}(r)\cdot d_{\mathcal{G}}(s))\\ &=&15^{\mathrm{E_{1}}(\mathcal{G})}\times 21^{\mathrm{E_{2}}(\mathcal{G})}\times 36^{\mathrm{E_{3}}(\mathcal{G})} \times35^{\mathrm{E_{4}}(\mathcal{G})}\times60^{\mathrm{E_{5}}(\mathcal{G})}\times49^{\mathrm{E_{6}}(\mathcal{G})}\times84^{\mathrm{E_{7}}(\mathcal{G})} \times144^{\mathrm{E_{8}}(\mathcal{G})}\\ &=&15^{(12)}\times21^{(18n-36)}\times36^{(18n^{2}-54n+42)}\times35^{(12)}\times60^{(6)}\times49^{(6n-18)}\times 84^{(12n-24)}\times144^{(9n^{2}-33n+30)}\\ &=&931322574615478515625\times4^{6(-3+2n)}7^{42(-2+n)}729^{-7+5n}36^{18n^{2}-54n+42}144^{9n^{2}-33n+30}. \end{eqnarray*}
Theorem 4. Let \((\mathcal{G})=HDN_{1}(n)\) be the hex derived network of type 1. Then \begin{eqnarray*} ReZG(\mathcal{G})&=&7+3n(-5+3n). \end{eqnarray*}
Proof. From the edge partition of \((\mathcal{G})=HDN_{1}(n)\) given in Table 1, we have \begin{eqnarray*} ReZG(\mathcal{G})&=&\sum\limits_{rs \in E(\mathcal{G})}\bigg(\frac{d_{\mathcal{G}}(r)+d_{\mathcal{G}}(s)}{d_{\mathcal{G}}(r)\cdot d_{\mathcal{G}}(s)}\bigg)\\ &=&\mathrm{E_{1}}\bigg(\frac{3+5}{3\times5}\bigg)+\mathrm{E_{2}}\bigg(\frac{3+7}{3\times7}\bigg)+ \mathrm{E_{3}}\bigg(\frac{3+12}{3\times12}\bigg) +\mathrm{E_{4}}\bigg(\frac{5+7}{5\times7}\bigg)+\mathrm{E_{5}}\bigg(\frac{5+12}{5\times12}\bigg)\\&&+\mathrm{E_{6}}\bigg(\frac{7+7}{7\times7}\bigg) +\mathrm{E_{7}}\bigg(\frac{7+12}{7\times12}\bigg)+\mathrm{E_{8}}\bigg(\frac{12+12}{12\times12}\bigg)\\ &=&(12)\bigg(\frac{8}{15}\bigg)+(18n-36)\bigg(\frac{10}{21}\bigg)+(18n^{2}-54n+42)\bigg(\frac{5}{12}\bigg)+ (12)\bigg(\frac{12}{35}\bigg)\\&&+(6)\bigg(\frac{17}{60}\bigg)+(6n-18)\bigg(\frac{2}{7}\bigg)+(12n-24)\bigg(\frac{19}{84}\bigg)+ (9n^{2}-33n+30)\bigg(\frac{1}{6}\bigg)\\ &=&7+3n(-5+3n). \end{eqnarray*}
Theorem 5. Let \(\mathcal{H}=HDN_2(n)\) be Hex Derived network of type 2. Then
Proof.
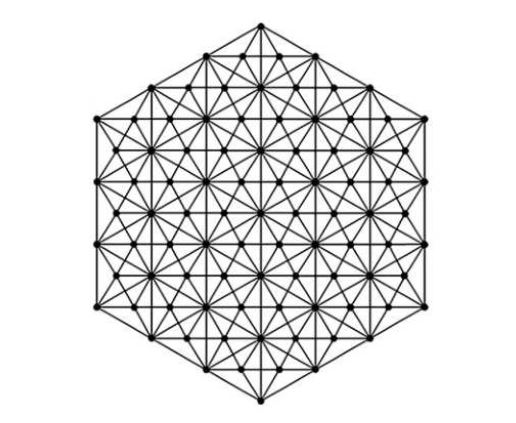
Suppose \(\mathcal{H}=HDN_2(n)\) be the Hex Derived network of type 2, where \(n\geq4\). \(\mathcal{H}\) has \(6n\) vertices of degree 5, \(6n^2-18n+12\) vertices of degree 6, \(6n-12\) vertices of degree 7 and \(3n^2-9n+7\) vertices of degree 12. The edge set of \(\mathcal{H}\) is divided into ten partitions based on the degree of end vertices. Table 2 shows the different edge partitions of \(\mathcal{H}\).
| \((d_{u},d_{v})\) where \(uv\in E(\mathcal{H})\) | \(\text{Number of edges}\) |
|---|---|
| \(\mathrm{E_1}=(3,5)\) | \(12\) |
| \(\mathrm{E_2}=(3,7)\) | \(18n-36\) |
| \(\mathrm{E_3}=(3,12)\) | \(18n^2-54n+42\) |
| \(\mathrm{E_4}=(5,7)\) | \(12\) |
| \(\mathrm{E_5}=(5,12)\) | \(6\) |
| \(\mathrm{E_6}=(7,7)\) | \(6n-18\) |
| \(\mathrm{E_7}=(7,12)\) | \(12n-24\) |
| \(\mathrm{E_8}=(12,12)\) | \(9n^2-33n+30\) |
Theorem 6.
Let \(\mathcal{H}=HDN_2(n)\) be Hex Derived network of type 2. Then
\(J(\mathcal{H})=36(1+n)^2\left[\frac{\bigg(\frac{18}{5}+\frac{6}{7}(-3+n)+2\sqrt{\frac{3}{7}}(-2+n)+2\sqrt{\frac{6}{5}}(-2+n)\bigg)}{7+3n(-5+3n)}+
\frac{\bigg(12(-1+n){\sqrt{35}}+\sqrt{\frac{3}{15}}n+\frac{3}{4}(-2+n)(-5+3n)+\frac{(-2+n)(-4+3n)}{\sqrt{2}}\bigg)}{7+3n(-5+3n)}\right]\)
Proof. From the edge partition given in Table 2 and definition of Balaban index, we have \begin{eqnarray*} J(\mathcal{H})&=&\sum\limits_{rs \in E(\mathcal{H})}\bigg(\frac{d_{\mathcal{\mathcal{H}}}(r)\cdot d_{\mathcal{H}}(s)}{d_{\mathcal{H}}(r)+ d_{\mathcal{H}}(s)-2}\bigg)^3\\ &=&E_{1}\bigg(\frac{5\times5}{5+5-2}\bigg)^3+E_{2}\bigg(\frac{5\times6}{5+6-2}\bigg)^3+E_{3}\bigg(\frac{5\times7}{5+7-2}\bigg)^3 +E_{4}\bigg(\frac{5\times12}{5+12-2}\bigg)^3\\&&+E_{5}\bigg(\frac{6\times6}{6+6-2}\bigg)^3+E_{6}\bigg(\frac{6\times7}{6+7-2}\bigg)^3 +E_{7}\bigg(\frac{6\times12}{6+12-2}\bigg)^3+E_{8}\bigg(\frac{7\times7}{7+7-2}\bigg)^3\\&&+E_{9}\bigg(\frac{7\times12}{7+12-2}\bigg)^3+ E_{10}\bigg(\frac{12\times12}{12+12-2}\bigg)^3\\ &=&(18)\bigg(\frac{15625}{512}\bigg)+(12n-24)\bigg(\frac{1000}{27}\bigg)+(12n-12)\bigg(\frac{343}{8}\bigg)+ (6n)(64)+\\&&(9n^{2}-33n+30)\bigg(\frac{5832}{125}\bigg)+(6n-12)\bigg(\frac{74088}{1331}\bigg)+(18n^{2}-60n+48)\bigg(\frac{729}{8}\bigg)\\&&+ (6n-18)\bigg(\frac{117649}{1728}\bigg)+(12n-24)\bigg(\frac{592704}{4913}\bigg)+(9n^{2}-33n+30)\bigg(\frac{373248}{1331}\bigg)\\ &=&36(1+n)^2\bigg[\frac{\bigg(\frac{18}{5}+\frac{6}{7}(-3+n)+2\sqrt{\frac{3}{7}}(-2+n)+2\sqrt{\frac{6}{5}}(-2+n)\bigg)}{7+3n(-5+3n)}+\\&& \frac{\bigg(12(-1+n){\sqrt{35}}+\sqrt{\frac{3}{15}}n+\frac{3}{4}(-2+n)(-5+3n)+\frac{(-2+n)(-4+3n)}{\sqrt{2}}\bigg)}{7+3n(-5+3n)}\bigg]. \end{eqnarray*}
Theorem 7. Let \(\mathcal{H}=HDN_2(n)\) be Hex Derived network of type 2. Then
Proof. (1) From the edge partition given in Table 2 and definition of multiple first Zagreb index, we have \begin{eqnarray*} PM_1(\mathcal{H})&=&\prod\limits_{rs \in E(\mathcal{H})}(d_{\mathcal{H}}(r)+d_{\mathcal{H}}(s))\\ &=&10^{E_{1}(\mathcal{H})}\times11^{E_{2}(\mathcal{H})}\times12^{E_{3}(\mathcal{H})}\times17^{E_{4}(\mathcal{H})}\times 12^{E_{5}(\mathcal{H})}\times13^{E_{6}(\mathcal{H})}\times18^{E_{7}(\mathcal{H})}\\&&\times 14^{E_{8}(\mathcal{H})}\times19^{E_{9}(\mathcal{H})} \times24^{E_{10}(\mathcal{H})}\\ &=&10^{(18)}\times11^{(12n-24)}\times12^{(12n-12)}\times17^{(6n)}\times12^{(9n^{2}-33n+30)}\times13^{(6n-12)} \\&&\times 18^{(18n^{2}-60n+48)}\times14^{(6n-18)}\times19^{(12n-24)}\times24^{(9n^{2}-33n+30)}\\ &=&38146972656252^{174+3n(-65+21n)}3^{144+6n(-29+9n)}7^{6(-3+n)}13^{6(-2+n)}\\&&17^{6n}209^{12(-2+n)}. \end{eqnarray*} (2) Now from the definition of multiple second Zagreb index, we have \begin{eqnarray*} PM_2(\mathcal{H})&=&\prod\limits_{rs \in E(\mathcal{H})}(d_{\mathcal{H}}(r)\cdot d_{\mathcal{H}}(s))\\ &=&25^{E_{1}(\mathcal{H})}\times 30^{E_{2}(\mathcal{H})}\times 35^{E_{3}(\mathcal{H})} \times60^{E_{4}(\mathcal{H})}\times36^{E_{5}(\mathcal{H})}\times42^{E_{6}(\mathcal{H})}\times72^{E_{7}(\mathcal{H})}\\&&\times 49^{E_{8}(\mathcal{H})}\times84^{E_{9}(\mathcal{H})}\times144^{E_{10}(\mathcal{H})}\\&=&25^{(18)}\times30^{(12n-24)}\times35^{(12n-12)} \times60^{(6n)}\times36^{(9n^{2}-33n+30)}\times42^{(6n-12)} \\&&\times 72^{(18n^{2}-60n+48)}\times 49^{(6n-18)}\times84^{(12n-24)}\times144^{(9n^{2}-33n+30)}\\ &=&2^{12(-5+3n)(-4+3n)}3^{156+72(-3+n)n}5^{30n}7^{42(-2+n)}. \end{eqnarray*}
Theorem 8. Let \(\mathcal{H}=HDN_2(n)\) be Hex Derived network of type 2. Then \begin{eqnarray*} ReZG(\mathcal{H})&=&7+3n(-5+3n). \end{eqnarray*}
Proof. From the edge partition given in Table 2, we have \begin{eqnarray*} ReZG(\mathcal{H})&=&\sum\limits_{rs \in E(\mathcal{H})}\bigg(\frac{d_{\mathcal{H}}(r)+d_{\mathcal{H}}(s)}{d_{\mathcal{H}}(r)\cdot d_{\mathcal{H}}(s)}\bigg)\\ &=&\mathrm{E_{1}}\bigg(\frac{5+5}{5\times5}\bigg)+\mathrm{E_{2}}\bigg(\frac{5+6}{5\times6}\bigg)+ \mathrm{E_{3}}\bigg(\frac{5+7}{5\times7}\bigg) +\mathrm{E_{4}}\bigg(\frac{5+12}{5\times12}\bigg)+\mathrm{E_{5}}\bigg(\frac{6+6}{6\times6}\bigg)\\&&+\mathrm{E_{6}}\bigg(\frac{6+7}{6\times7}\bigg) +\mathrm{E_{7}}\bigg(\frac{6+12}{6\times12}\bigg)+\mathrm{E_{8}}\bigg(\frac{7+7}{7\times7}\bigg)+\mathrm{E_{9}}\bigg(\frac{7+12}{7\times12}\bigg) +\mathrm{E_{10}}\bigg(\frac{12+12}{12\times12}\bigg)\\ &=&(18)\bigg(\frac{2}{5}\bigg)+(12n-24)\bigg(\frac{11}{30}\bigg)+(12n-12)\bigg(\frac{12}{35}\bigg)+ (6n)\bigg(\frac{17}{60}\bigg)\\&&+(9n^{2}-33n+30)\bigg(\frac{1}{3}\bigg)+(6n-12)\bigg(\frac{13}{42}\bigg)+ (18n^{2}-60n+48)\bigg(\frac{1}{4}\bigg)\\&&+ (6n-18)\bigg(\frac{2}{7}\bigg)+ (12n-24)\bigg(\frac{19}{84}\bigg)+ (9n^{2}-33n+30)\bigg(\frac{1}{6}\bigg)\\ &=&7+3n(-5+3n). \end{eqnarray*}
