TEMO = topological effect on molecular orbitals was discovered by Polansky and Zander in 1982, in connection with the eigenvalues of molecular graphs. Eventually, analogous regularities were established for a variety of other topological indices. We now show that a TEMO-type regularity also holds for the Sombor index (\(SO\)): For the graphs \(S\) and \(T\), constructed by connecting a pair of vertex-disjoint graphs by two edges, \(SO(S) < SO(T)\) holds. Analogous relations are verified for several other degree-based graph invariants.
In this paper, we consider a pair of graphs that traditionally are denoted by \(S\) and \(T\). These are constructed by starting with any two vertex-disjoint graphs \(G_1\) and \(G_2\). Let \(a\) and \(b\) be two distinct vertices of \(G_1\), and let \(c\) and \(d\) be two distinct vertices of \(G_2\). Then \(S\) is the graph obtained from \(G_1\) and \(G_2\) by connecting \(a\) with \(c\) and \(b\) with \(d\). The graph \(T\) is obtained analogously, by connecting \(a\) with \(d\) and \(b\) with \(c\), see Figure 1.
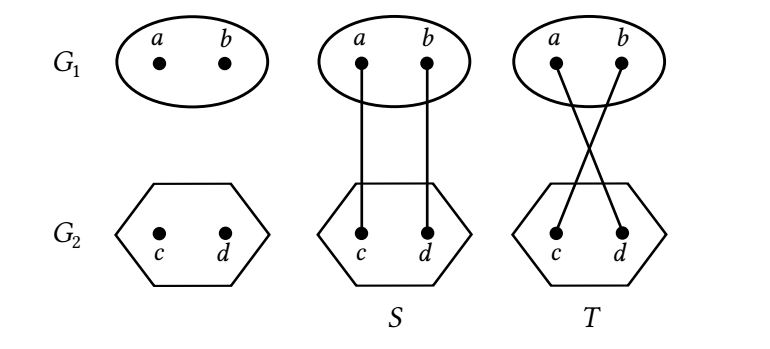
The inequality (1) implies certain regularities for the distribution of the eigenvalues of \(S\) and \(T\) [2,3,4] and have appropriate (experimentally verifiable) consequences on the distribution of the molecular orbital energy levels [5]. The authors of [1] called this a ” topological effect on molecular orbitals” and used the acronym TEMO. Eventually, TEMO was extensively investigated; a detailed bibliography of this research can be found in the books [6,7].
After the discovery of the regularities between the eigenvalues of \(S\) and \(T\), a number of other TEMO-like relations for these pairs of graphs was discovered [8,9,10,11,12,13,14,15,16].
In what follows, we establish a TEMO-like property of the Sombor index, i.e., investigate the relation between \(SO(S)\) and \(SO(T)\).
Denote by \(\delta_a,\delta_b,\delta_c,\delta_d\) the degrees of the vertices \(a,b,c,d\) of the graphs \(S\) and \(T\) (see Fig. 1). It is obvious that if either \(\delta_a=\delta_b\) or \(\delta_c=\delta_d\) or both, then \(SO(S)=SO(T)\). Therefore, we consider the case \(\delta_a \neq \delta_b\) and \(\delta_c \neq \delta_d\). Without loss of generality, we may assume that \(\delta_a > \delta_b\) and \(\delta_c > \delta_d\).
Theorem 1. Let \(G_1\) and \(G_2\) be arbitrary vertex-disjoint graphs and \(a,b,c,d\) their vertices as indicated in Figure 1. If \(\delta_a > \delta_b\) and \(\delta_c > \delta_d\), then \(SO(S) < SO(T)\).
Note that the degree of the vertex \(a\) in the graph \(G_1\) is \(\delta_a-1\), etc.
Proof. Observe first that \begin{eqnarray*} SO(S) & = & \sqrt{\delta_a^2+\delta_c^2} + \sqrt{\delta_b^2+\delta_d^2} + SO^\ast\,, \\ SO(T) & = & \sqrt{\delta_a^2+\delta_d^2} + \sqrt{\delta_b^2+\delta_c^2} + SO^\ast\,, \end{eqnarray*} where \(SO^\ast\) is the sum of the terms \(\sqrt{\delta_u^2 + \delta_v^2}\) over other edges of \(S\) or \(T\). Thus, \[ SO(S)-SO(T) = \sqrt{\delta_a^2+\delta_c^2} + \sqrt{\delta_b^2+\delta_d^2} – \sqrt{\delta_a^2+\delta_d^2} – \sqrt{\delta_b^2+\delta_c^2}\,. \] It needs to be demonstrated that
Using the notation of Eq. (2), the second Zagreb index \(M_2\), the Randic index \(R\), the reciprocal Randic index \(RR\), and the nirmala index \(N\) are, respectively, defined as [23,24,25,26]
\begin{eqnarray*} M_2 = M_2(G) & = & \sum_{uv \in \mathbf E(G)} \delta_u\,\delta_v \,,\\ R = R(G) & = & \sum_{uv \in \mathbf E(G)} \frac{1}{\sqrt{\delta_u\,\delta_v}}\,, \\ RR = RR(G) & = & \sum_{uv \in \mathbf E(G)} \sqrt{\delta_u\,\delta_v} \,,\\ N = N(G) & = & \sum_{uv \in \mathbf E(G)} \sqrt{\delta_u+\delta_v}\,. \end{eqnarray*}Theorem 2. Let \(G_1\) and \(G_2\) be arbitrary vertex-disjoint graphs and \(a,b,c,d\) their vertices as indicated in Figure 1. If \(\delta_a > \delta_b\) and \(\delta_c > \delta_d\), then
