Wiener index of hexagonal chains under some transformations

1. Introduction

Distance-based graph invariants, called topological indices, are widely used in studying of structure of molecular graphs in organic chemistry. The Wiener index is a well-known topological index introduced as structural descriptor for acyclic organic molecules [1]. It is defined as the sum of distances between all unordered pairs of vertices of an undirected connected graph \(G\) with vertex set \(V(G)\): $$ W(G) \ = \sum_{\{u,v\} \subseteq V(G)} d(u,v), $$ where distance \(d(u,v)\) is the number of edges in the shortest path connecting vertices \(u\) and \(v\) in \(G\). The Wiener index is intensively studied in mathematical and theoretical chemistry and has found numerous applications in the modeling of physico-chemical, pharmacological and biological properties of organic molecules (see books [2,3,4,5,6,7,8,9,10] and reviews [11, 12, 13, 14, 15, 16, 17, 18, 19]). We will consider the Wiener index of hexagonal chains that include molecular graphs of catacondensed unbranched benzenoid hydrocarbons. Since this class of chemical compounds is attracting the great attention of theoretical chemists, the theory of the Wiener index of the respective molecular graphs has been developed for many years [20, 21]. Changes of the Wiener index of polycyclic structures under transformations of various kinds were investigated in [22, 23, 24, 25, 26, 27, 28, 29]. The structure of hexagonal chains of certain classes can be encoded by binary vectors. Operations on chains’ binary codes generate new hexagonal chains. In this paper, relations between Wiener indices of chains for some operations on chains’ codes are studied and illustrative numeric examples are presented.

2. Hexagonal chains and their segments

The classification of molecular graphs of benzenoid hydrocarbons is based on the kind of connection of hexagonal rings with one another [30]. A hexagonal chain is a connected plane graph in which every inner face is bounded by a hexagon. An inner face with its hexagonal bound is called a hexagonal ring (or simply ring ). Two hexagonal rings of a chain are either disjoint or have exactly one common edge (adjacent rings), and no three rings share a common vertex. A ring having exactly one adjacent ring is called terminal . A hexagonal chain has exactly two terminal rings. A ring adjacent to exactly two other rings has two vertices of degree 2. If these two vertices are adjacent, then the ring is angularly connected; if these two vertices are not adjacent, then it is linearly connected. A segment is a maximal subchain in which all rings are linearly connected. A segment including a terminal hexagon is a terminal segment . The number of hexagons in a segment is called its length . Denote by \({\cal G}_{n,{\ell}}\) the set of all hexagonal chains having \(n\) segments of length \(\ell\). All hexagonal chains of \({\cal G}_{5,3}\) are shown in Figure 1. Some properties of graphs of this class were studied in [31, 32, 33, 34, 35]. Hexagonal chains of \({\cal G}_{n,2}\) with minimal length of segments are known as fibonacenes [36, 37]. The number of hexagonal rings of \(G \in {\cal G}_{n,{\ell}}\) is equal to \(h=n(\ell-1)+1\) and the number of segments is \(n=(h-1)/(\ell-1)\). Since \(|\,{\cal G}_{n,2} | = |\,{\cal G}_{n,\ell}\,|\) for all \(\ell \ge 3\), the cardinality of \({\cal G}_{n,{\ell}}\) is equal to \(|\,{\cal G}_{n,{\ell}}\,| = 2^{n-3} + 2^{\lfloor {\frac{n-3}{2}} \rfloor}\), \(n\ge 2\) [37].

3. Representation of hexagonal chains

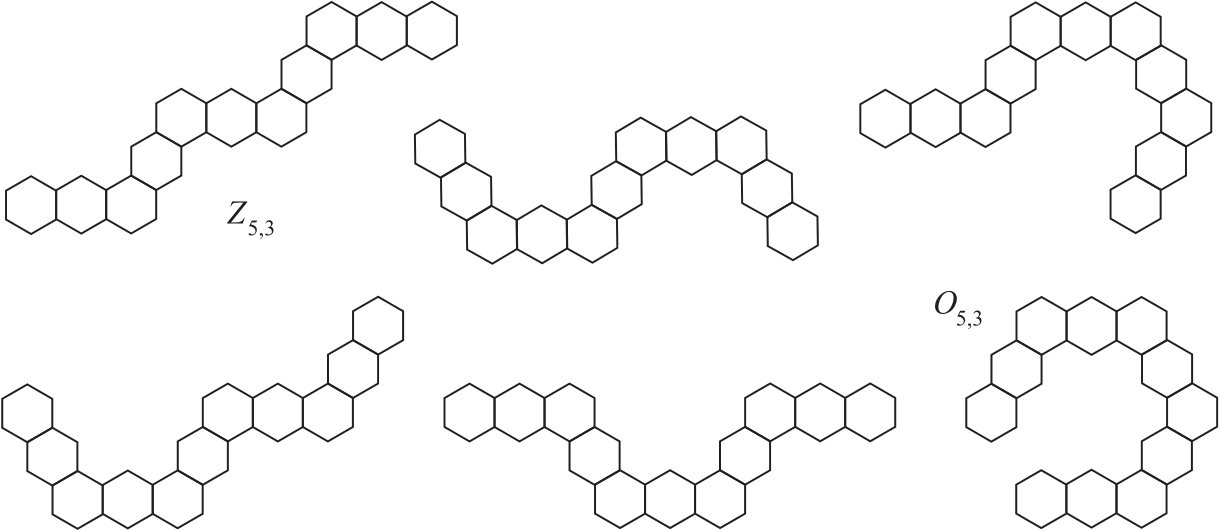
The structure of hexagonal chains is completely defined by a way of segment attachment. We consider a nonterminal segment \(S\) with two neighboring segments embedded into the regular hexagonal lattice on the plane and draw a line through the centers of the hexagons of \(S\). If the neighboring segments of \(S\) lie on different sides of the line, then \(S\) is called a zigzag segment. If these segments lie on the same side, then \(S\) is said to be a spiral segment. It is convenient to assume that the terminal segments are zigzag segments. For a hexagonal chain \(X\), denote by \(U(X)\) the set of its spiral segments, \(u_X=|U(X)|\).

Based on two types of segments, hexagonal chains of \({\cal G}_{n,\ell}\) can be represented by binary codes. We assume that all segments of a chain are sequentially numbered by \(0, 1,\dots, n-1\) beginning from a terminal segment. Since the terminal segments can be ignored when a chain is restored, codes of all hexagonal chains of \({\cal G}_{n,\ell}\) have a length of \(n-2\), \(n\ge 3\). Assume that every spiral segment of chain \(X\) corresponds to 1 in the code of \(X\) while every zigzag segment corresponds to 0. A binary code of hexagonal chain \(X\) and a hexagonal chain \(X\) induced by a binary word \(r\) will be denoted by \(r(X)\) and \(X(r)\), respectively. Note that molecular graphs of more general classes of benzenoid hydrocarbons can be also represented by binary codes [31, 38].

There are two extremal chains with respect to the type of segments. The zigzag hexagonal chain \(Z_{n,\ell} \in {\cal G}_{n,\ell}\) contains only zigzag segments, \(r(Z_{n,\ell})=(00..0)\). All segments of the spiral hexagonal chain \(O_{n,\ell} \in {\cal G}_{n,\ell}\) are spiral ones (with the exception of the terminal segments), \(r(O_{n,\ell})=(11..1)\). The zigzag and the spiral hexagonal chains of \({\cal G}_{5,3}\) are shown in Figure 1. Denote by \(e_i\) the binary vector \(e_i=(0…0\!\stackrel{i}{1}\!0…0)\) of length \(n-2\) for \(n \ge 3\), \(i=1,2,\dots,n-2\). These vectors form the standard basis for the vector space of dimension \(n-2\) over \(\mathbf{Z}_2\). Let \(C_i\) be the basis hexagonal chains corresponding to basis vectors \(e_i\), \(i=1,2,\dots,n-2\). Then code \(r(X)\) of \(X \in {\cal G}_{n,\ell}\) can be expressed as a linear combination of the basis vectors: \(r(X)= x_1 \, e_1 + x_2 \, e_2 + \dots + x_{n-2} \, e_{n-2}\). Since codes \(e_i\) and \(e_{n-i-1}\) are symmetrical, basis chains \(C_i\) and \(C_{n-i-1}\) are isomorphic and \(W(C_i) = W(C_{n-i-1})\).

Hexagonal chains \(O_{n,\ell}\) and \(Z_{n,\ell}\) are extremal graphs with respect to the Wiener index among all chains of \({\cal G}_{n,\ell}\) [13]: \(W(O_{n,\ell}) < W(G) < W(Z_{n,\ell})\) for all \(G \in {\cal G}_{n,\ell} \setminus \{O_{n,\ell}, Z_{n,\ell}\}\), where \begin{eqnarray*} W_{\min} & = & \big( 8 n^3 (\ell-1)^2 (2 \ell-3)+96 n^2 (\ell-1)^2-2 n (\ell-1)(2 \ell -75) + 81 \big) /3, \\ W_{\max} & = & \big( 16 n^3 (\ell-1)^3 + 72 n^2 (\ell-1)^2 + n(\ell-1)(12 \ell+134)+81 \big)/3. \end{eqnarray*}

The average of these extremal values is equal to \begin{eqnarray*} W_{\mathrm{avr}} & = & \left( W_{\min}+W_{\max} \right)/2 \\ & = & \left( 4 n^3 (\ell-1)^2 (4\ell-5) + 84 n^2 (\ell-1)^2 + 2 n(\ell-1) (2 \ell+71)+81 \right)/3. \end{eqnarray*}

4. Graph operations

Let \(X, Y \in {\cal G}_{n,\ell}\) with codes \(r(X)=x=(x_1,x_2,\dots,x_{n-2})\) and \(r(Y)=y=(y_1,y_2,\dots,y_{n-2})\). Define the following operations of these hexagonal chains:

• the complement of a hexagonal chain \(X\) is a new chain \(Y\) with code \(r(Y)=r(\overline{X}) =(\overline{x}_1,\overline{x}_2,\dots,\overline{x}_{n-2})\), that is, \(r(Y)\) is a bitwise complement of \(r(X)\). This operation changes the type of all segments of \(X\). Example: \((\overline{10011})=(01100)\);
• the unary operation \(t_{i,j}(X)\) changes the type of \(i\)-th and \(j\)-th segments to opposite. For example, if \(r(X)=(1000111)\), then hexagonal chain \(Y=t_{2,6}(X)\) has code \(r(Y)= (1100101)\);
• the sum modulo 2 of hexagonal chains \(X\) and \(Y\) is a new chain \(G=X+Y\) with code \(r(G)= x + y =(x_1+y_1,x_2+y_2,\dots,x_{n-2}+y_{n-2})\). The resulting chain inherits spiral segments of the initial chains except spiral segments in the same positions. Example: \((10011) + (10101) = (00110)\);
• the difference modulo 2 of hexagonal chains \(X\) and \(Y\) is a new chain \(G=X-Y\) with code \(r(G)= x – y =(x_1-y_1,x_2-y_2,\dots,x_{n-2}-y_{n-2})\). Despite of \(G=X-Y =X+Y\), we will distinguish between these operations. Example: \((10011) – (10101) = (00110)\);
• a hexagonal chain \(G=XY\) is called the product of chains \(X\) and \(Y\) with code \(r(G)= xy=(x_1y_1,x_2y_2,\dots,x_{n-2}\,y_{n-2})\). This operation is an analogue of bitwise logical operation “AND”. The resulting chain has spiral segments if they are in the same positions of the initial chains. Example: \((10011) (10101) = (10001)\);
• operation “\(\vee\)” of hexagonal chains \(X\) and \(Y\) gives a new chain \(G=X \vee Y\) with code \(r(G)= x \vee y =(x_1 \vee y_1, x_2 \vee y_2,\dots,x_{n-2} \vee y_{n-2})\), where \(x_i \vee y_i\) is an analogue of bitwise logical operation “OR”. All spiral segments of the initial chains are served in \(G\). Example: \((10011) \vee (10101) = (10111)\).

The binary relation \(X \le Y\) between chains \(X, Y \in {\cal G}_{n,\ell}\) is defined by conditions \(x_i \le y_i\), \(i=1,2,\dots,n-2\). This relation induces a partial order on \({\cal G}_{n,\ell}\). In the next section, changes of the Wiener index under introduced operations over chains’ codes are examined.

5. Changes of the Wiener index

The following useful formula allows the calculation Wiener index of hexagonal chains through their binary codes [26].

Proposition 1. For a hexagonal chain \(X \! \in {\cal G}_{n,\ell}\) with a code \((x_1,x_2, \dots, x_{n-2})\), \begin{eqnarray*} W(X) & = & W_{\max} – 16(\ell-1)^2 \sum_{i=1}^{n-2} i(n-i-1) x_i. \end{eqnarray*}

The sum of Wiener indices of a hexagonal chain and its complement is twice the average value \(W_{\mathrm{avr}}\).

Proposition 2. If \(X \in {\cal G}_{n,\ell}\), then \(W(\overline{X})=W_{\min}+W_{\max} – W(X)\).

Proof. By Proposition 1, \begin{eqnarray*} W(X) + W(\overline{X}) & = & W_{\max} + W_{\max}-16(\ell-1)^2 \sum_{i=1}^{n-2} i(n-i-1)\cdot 1 \\ & = & W_{\max} + W_{\min}. \end{eqnarray*}

Proposition 2 allows to determine the structure of hexagonal chains with average value of the Wiener index. If \(r(X)=r(\overline{X})\), then chains \(X\) and \(\overline{X}\) are obviously isomorphic. This implies equality \(W(X)=W_{\mathrm{avr}}\). There are also non-isomorphic chains \(X\) and \(\overline{X}\) with property \(W(X)= W(\overline{X})= W_{\mathrm{avr}}\) [26]. Consider hexagonal chains without units in the same positions of their codes.

Proposition 3. Let \(X, Y \in {\cal G}_{n,\ell}\) and \(XY=Z_{n,\ell}\). If \(G=X+Y\), then $$ W(G) = W(X) + W(Y) – W_{\max}. $$

Proof. Let \(x=r(X)\) and \(y=r(Y)\). By Proposition 1, we can write $$ W(X) + W(Y) – W_{\max} = W_{\max}-16(\ell-1)^2 \sum_{i} i(n-i-1) (x_i+y_i) = W(G). $$

As an illustration, consider chains \(X, Y \in {\cal G}_{7,3}\) and \(G=X+Y\) shown in Figure 2. These graphs have codes \(r(X)=(10010)\), \(r(Y)=(00101)\), and \(r(G)=(10111)\). By computer calculations, their Wiener indices are \(W(X)=19327\), \(W(Y)=19263\), \(W(G)=18431\), and \(W_{\max}=20159\). By Proposition 3, \(W(G)=19327 + 19263 – 20159=18431\).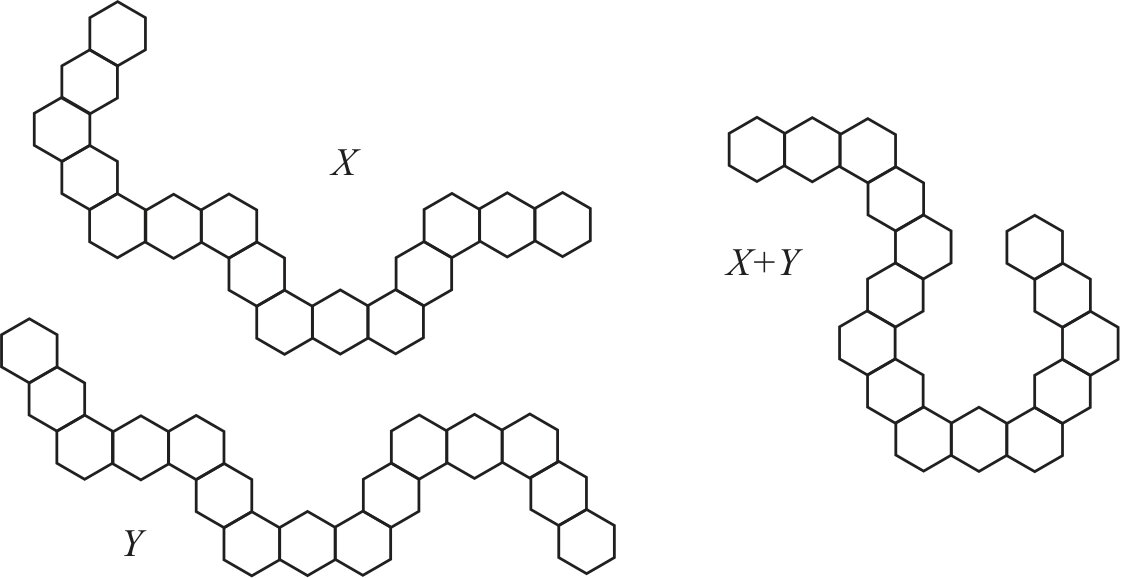

Proposition 4. Let \(X, Y \in {\cal G}_{n,\ell}\) and \(Y \le X\). If \(G=X-Y\), then $$ W(G) = W(X) – W(Y) + W_{\max}. $$

Proof. If \(x=r(X)\) and \(y=r(Y)\), then by Proposition 1 \begin{eqnarray*} W(Y) – W(X) – W_{\max} & = & \mbox{} -W_{\max} + 16(\ell-1)^2 \sum_{i} i(n-i-1) (x_i-y_i) \\ & = & \mbox{} -W(G). \end{eqnarray*} Since \(y_i \le x_i\), \((x_i-y_i) \ge 0\) for every \(i\).

Hexagonal chains \(X, Y \in {\cal G}_{7,3}\) and \(G=X-Y\) shown in Figure 3 illustrate Proposition 4. Codes of these graphs are \(r(X)=(11001)\), \(r(Y)=(01001)\), and \(r(G)=(10000)\). Computer calculations give the following Wiener indices: \(W(X)=19007\), \(W(Y)=19327\), and \(W(G)=19839\). By Proposition 4, \(W(G)=19007 – 19327 + 20159=19839\). The next result answers on the following question: how many times do we need to apply operation \(t_{i,j}\) to a hexagonal chain \(X\) such that \(W(X)=W(t_{i,j}(X))\)? For asymmetrical chains, it is sufficient to apply the operation once time.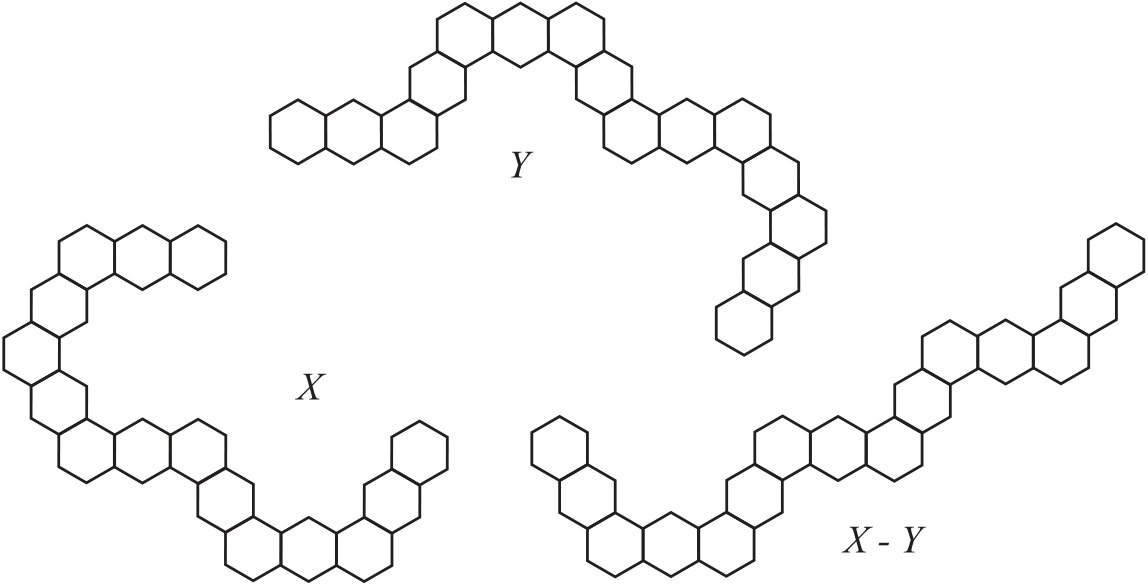

Corollary 2. Let \(X \in {\cal G}_{n,\ell}\) be an asymmetrical hexagonal chain with a code \((x_1, x_2,\dots,x_{n-2})\), i.e., \(x_i \not = x_{n-i-1}\) for some \(i \in \{1,2,\dots,\lceil(n-2)/2\rceil\}\). If \(Y=t_{i,n-i-1}(X)\), then \(W(Y)=W(X)\).

Proof. Assume that \(x_i=0\) and \(x_{n-i-1}=1\). Then \(Y=(X + C_i) – C_{n-i-1}\). By Propositions 4 and 3, we can write \(W(Y)= W(X + C_i) – W(C_{n-i-1}) + W_{\max} = W(X) + W(C_i) – W_{\max} – W(C_{n-i-1}) + W_{\max} = W(X)\).

Let \(\mu(X)\) be the number of pairs of non-equal \(i\)-th and \((n-i-1)\)-th components of chain’s code \(r(X)\), \(i=1,2,\dots,\lceil (n-2)/2 \rceil\). Repeating Corollary 1, one can construct a family of \(2^{\mu(X)}\) chains having the same Wiener index (some chains may be isomorphic).

Decomposition of the Wiener index of chains of \({\cal G}_{n,\ell}\) into the sum of Wiener indices of basis hexagonal chains was reported in [26]. It can be also derived using graph operations.

Corollary 3. Let \(X \in {\cal G}_{n,\ell}\) and \(r(X)=(x_1,x_2,\dots,x_{n-2})\). Then $$ W(X) = x_1 W(C_1) + x_2 W(C_2) + \dots + x_{n-2} W(C_{n-2}) – (u-1)W_{\max}, $$ where \(u = x_1 + x_2 + \dots + x_{n-2}\) is the number of units of \(x\).

Proof. Let \(i_1, i_2,\dots,i_u\) be positions of units in \(x\). Then the corresponding hexagonal chain \(X\) can be represented as \(X=C_{i_1} + C_{i_2} + \dots + C_{i_u}\). Applying Proposition 3, we get \(W(X) = W(C_{i_1}) + W(C_{i_2}) + \dots+ W(C_{i_u}) – (u-1) W_{\max} = x_1 W(C_1) + x_2 W(C_2) + \dots + x_{n-2} W(C_{n-2}) – (u-1)W_{\max}\).

Let us consider operations of hexagonal chains with arbitrary codes.

Proposition 5. Let \(X, Y \in {\cal G}_{n,\ell}\). If \(G=X+Y\), then $$ W(G) = W(X) + W(Y) – 2 W(XY) + W_{\max}. $$

Proof. It is easy to verify that the hexagonal chain \(G\) can be represented as \(G=X+Y=(X-XY) + (Y-XY)\), where \((X-XY)(Y-XY)=Z_{n,\ell}\) and \(X \ge XY\), \(Y \ge XY\). By Propositions 3 and 4, \begin{eqnarray*} W(G) & = & W(X-XY) + W(Y-XY) – W_{\max} \\ & = & W(X) – W(XY) + W_{\max} + W(Y) – W(XY) + W_{\max} – W_{\max} \\ & = & W(X) + W(Y) – 2 W(XY) + W_{\max}. \end{eqnarray*}

Hexagonal chains \(X, Y \in {\cal G}_{7,3}\) and \(G=X+Y\) shown in Figure 4 illustrate Proposition 5. These chains have codes \(r(X)=(11100)\), \(r(Y)=(00110)\), \(r(XY)=(00100)\), and \(r(G)=(11010)\). Their Wiener indices are \(W(X)=18751\), \(W(Y)=19071\), \(W(XY)=19583\), and \(W(G)=18815\). By applying Proposition 5, \(W(G)= 18751 + 19071 – 2\cdot 19583 + 20159=18815\).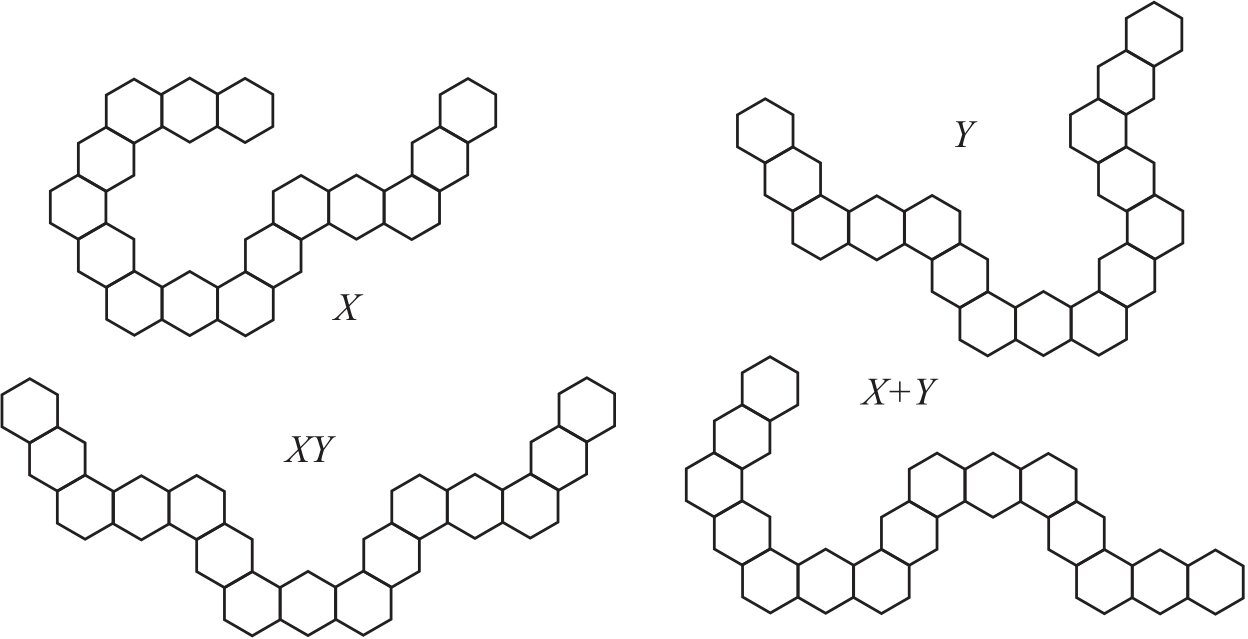

Proposition 6. Let \(X, Y \in {\cal G}_{n,\ell}\). If \(G=X-Y\), then $$ W(G) = W(X) – W(Y) + 2W(\overline{X}Y) – W_{\max}. $$

Proof. Hexagonal chain \(G\) can be decomposed as \(G=X-Y=(X+\overline{X}Y) – (Y-\overline{X}Y)\), where \((X+\overline{X}Y) \ge (Y-\overline{X}Y)\), \(X(\overline{X}Y)=Z_{n,\ell}\) and \(Y \ge \overline{X}Y\). By Propositions 3 and 4, \begin{eqnarray*} W(G) & = & W(X+\overline{X}Y) – W(Y-\overline{X}Y) + W_{\max} \\ & = & W(X) + W(\overline{X}Y) – W_{\max} – (W(Y) – W(\overline{X}Y) + W_{\max}) + W_{\max} \\ & = & W(X) – W(Y) + 2 W(\overline{X}Y) – W_{\max}. \end{eqnarray*}

Consider again hexagonal chains \(X\) and \(Y\) shown in Figure 4. Chains \(\overline{X}Y\) and \(X-Y\) have codes \(r(\overline{X}Y)=(00010)\), \(r(X-Y)=(00101)\), and Wiener indices \(W(\overline{X}Y)=19647\), \(W(X-Y)=18815\). By Proposition \ref{XYminusGen}, we obtain \(W(G)= 18751 – 19071 + 2 \cdot 19647 – 20159=18815\).

Proposition 7. Let \(X, Y \in {\cal G}_{n,\ell}\). If \(G=X \vee Y\), then $$ W(G) = W(X) + W(Y) – W(XY). $$

Proof. Using Proposition 1, we get \begin{eqnarray*} W(X)\!+\!W(Y)\!-\!W(XY) & = & W_{\max}\!-\!16(\ell-1)^2 \sum_{i} i(n-i-1) (x_i+y_i-x_i y_i), \\ W(X \vee Y) &= & W_{\max}-16(\ell-1)^2 \sum_{i} i(n-i-1) (x_i \vee y_i). \end{eqnarray*} Comparison of these equalities completes the proof.

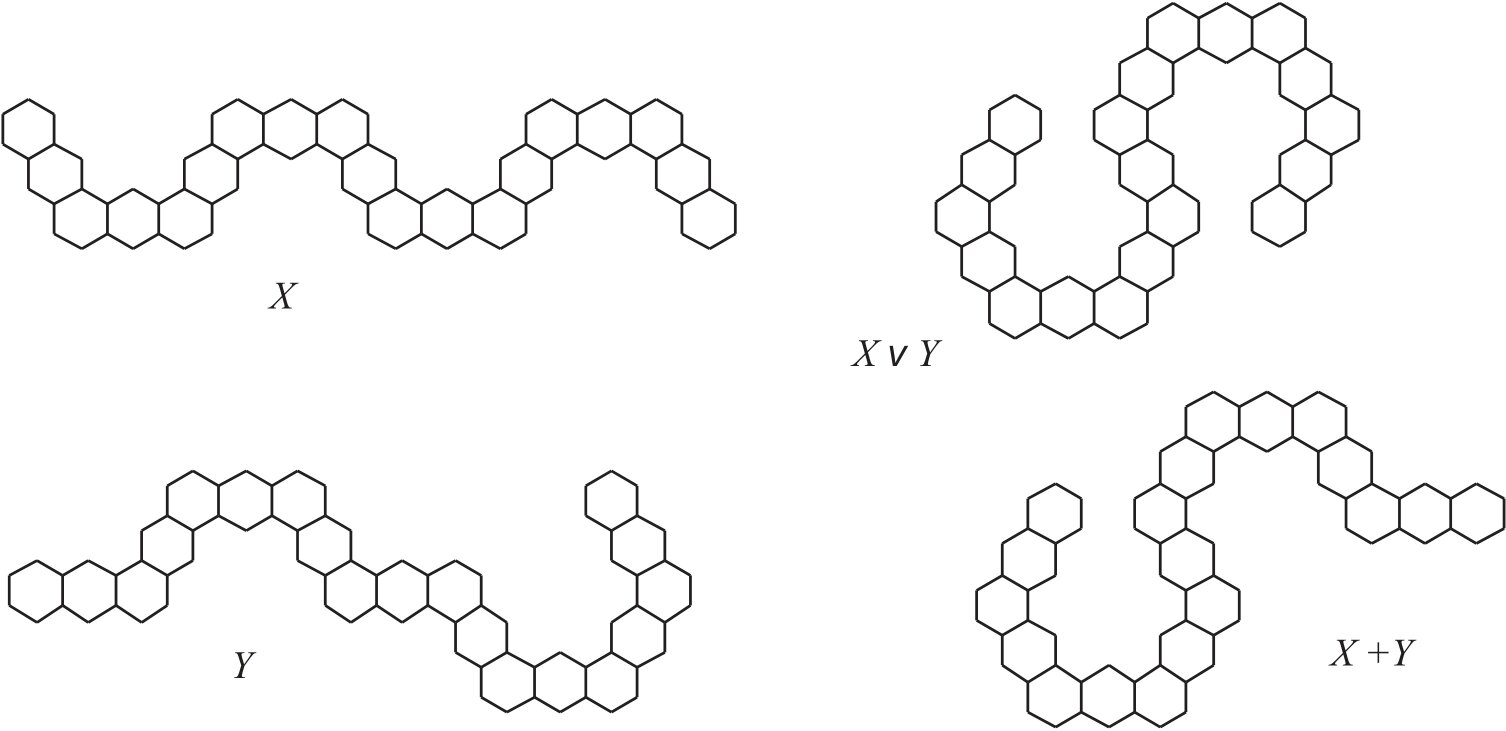
Hexagonal chains \(X, Y \in {\cal G}_{9,3}\) and \(G=X \vee Y\) of Figure 5 illustrate Proposition 7. The structure of graph \(X+Y\) is presented for comparison. These chains have codes \(r(X)=(1010101)\), \(r(Y)=(0100011)\), \(r(XY)=(0000001)\), and \(r(G)=(1110111)\), and their Wiener indices are equal to \(W(X)=37111\), \(W(Y)=37943\), \(W(XY)=39479\), and \(W(G)=35575\). By Proposition 7, \(W(G)=37111+37943-39479=35575\).

In conclusion, we note that the considered approach may be useful in studying of topological indices for sets of hexagonal chains induced by algebraic constructions.

Acknowledgments

This work is supported by the Russian Foundation for Basic Research (project numbers 19–01–00682 and 17–51–560008) and the Iranian National Science Foundation (INSF) under the contract No. 96004167.

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest:

The authors declare no conflict of interest.