The application of graph theory in chemical and molecular structure research far exceeds people’s expectations, and it has recently grown exponentially. In the molecular graph, atoms are represented by vertices and bonded by edges. In this report, we study the M-polynomial of line graph of \(HAC_{5}C_{6}C_{7}[p,q]\) and recover many degree-based topological indices from it.

Dfinition 2.1.[27] The M-polynomial of \(G\) is defined as: $$M(G, x,y)= \sum\limits_{\delta\leq i\leq j\leq \triangle}m_{ij}(G)x^{i}y^{j}$$ where \(\delta= \min\{d_{v}: v\in V(G)\}\), \(\triangle= \max\{d_{v}: v\in V(G)\}\) and \(m_{ij}(G)\) is the edge \(uv\in E(G)\) such that \(d_{u}=i\) and \(d_{v}=j\).
Wiener index and its various applications are discussed in [28, 29, 30]. Randić index, \(R_{-\frac{1}{2}}(G)\), is introduced by Milan Randić in 1975 defined as: \(R_{-\frac{1}{2}}(G)=\sum\limits_{uv\in E(G)}\frac{1}{\sqrt{d_{u}d_{v}}}\). For general details about \(R_{-\frac{1}{2}}(G)\), and its generalized Randic index, \(R_{\alpha}(G)=\sum\limits_{uv\in E(G)}\frac{1}{(d_{u}d_{v})^{\alpha}}\) please see [31, 32, 33, 34, 35]. The inverse Randić index is defined as \(RR_{\alpha}(G)=\sum\limits_{uv\in E(G)}(d_{u}d_{v})^{\alpha}\) Clearly \(R_{-\frac{1}{2}}(G)\) is a special case of \(R_{\alpha}(G)\) when \(\alpha=\frac{1}{2}\). This index has many applications in diverse areas. Many papers and books such as [36, 37, 38] are written on this topological index as well. Gutman and Trinajstić introduced two indices defined as: \(M_{1}(G)=\sum\limits_{u\in V(G)}(d_{u}+d_{v})\) and \(M_{2}(G)=\sum\limits_{uv\in E(G)}d_{u}\times d_{u}\). The second modified Zagreb index is defined as: \(^{m}M_{2}(G)=\sum\limits_{uv\in E(G)}\frac{1}{d_{u}\times d_{u}}\). We refer [39, 40, 41, 42, 43] to the readers for comprehensive details of these indices. Other famous indices are Symmetric division index: \(SDD(G) = \sum\limits_{uv\in E(G)}\left\{\frac{\min(d_{u},d_{v})}{\max(d_{u},d_{v})},\frac{\max(d_{u},d_{v})}{\min(d_{u},d_{v})}\right\}\) harmonic index: \(H(G)=\sum\limits_{uv\in E(G)}\frac{2}{d_{u}+d_{v}}\) inverse sum index: \(I(G)=\sum\limits_{uv\in E(G)}\frac{d_{u}d_{v}}{d_{u}+d_{v}}\) and augmented Zagreb index: \(A(G) = \sum\limits_{uv\in E(G)}\left\{\frac{\max(d_{u},d_{v})}{\max(d_{u},d_{v})}\right\}^{3}\) [39, 40, 41]. Tables presented in [44, 45, 46, 47, 48] relates some of these well-known degree-based topological indices with M-polynomial with following reserved notations Where \(D_xf= x\frac{\partial(f(x,y))}{\partial x}, D_yf = y\frac{\partial(f(x,y))}{\partial y}, S_x = \int_0^x\frac{f(y,t)}{t}dt,\) \(S_y = \int_0^y\frac{f(x,t)}{t}dt, j(f(x,y))=f(x,x), Q_{\alpha} (f(x,y))= x^{\alpha} f(x,y),\) for non zero \({\alpha},\) \(j(f(x,y))= f(x,x)\)Theorem 3.1. Let \(G\) be the line graph of \(HAC_{5}C_{6}C_{7}[p,q]\) nanotube. Then the M-Polynomial of \(G\) is \begin{equation} M(G,x,y)=2x^{2}y^{2}+12x^{2}y^{3}+(16p+1)x^{3}y^{3}+(12p+10)x^{3}y^{4}+(70p-37)x^{4}y^{4} \end{equation}
Proof.
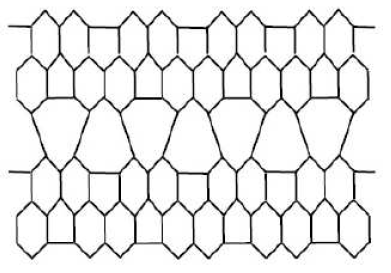
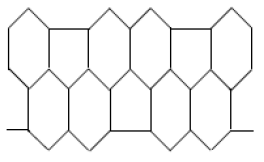
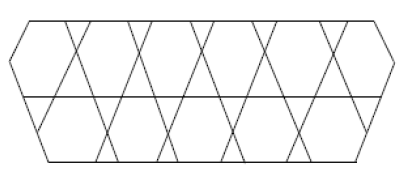
Let \(G\) be the line graph of \(HAC_{5}C_{6}C_{7}[p,q]\) nanotubes where \(p\) denotes the number of pentagons in one row and \(q\) denotes the number of periods in whole lattice .
The edge set of line graph of \(HAC_{5}C_{6}C_{7}[p,q]\) with \(p\geq 1\) and \(q=2\) has following five partitions,
\(E_{2,2}= \{e=vu\in E(HAC_{5}C_{6}C_{7}[p,q])| d_u=2,d_v=2\}\)
\(E_{2,3}= \{e=vu\in E(HAC_{5}C_{6}C_{7}[p,q])| d_u=2,d_v=3\}\)
\(E_{3,3}= \{e=vu\in E(HAC_{5}C_{6}C_{7}[p,q])| d_u=3,d_v=3\}\)
\(E_{3,4}= \{e=vu\in E(HAC_{5}C_{6}C_{7}[p,q])| d_u=3,d_v=4\}\)
and
\(E_{4,4}= \{e=vu\in E(HAC_{5}C_{6}C_{7}[p,q])| d_u=4,d_v=4\}\).
Now,
$$|E_{2,2}|=2$$
$$|E_{2,2}|=12$$
$$|E_{2,2}|=6p+1$$
$$|E_{2,2}|=12p+10$$
and
$$|E_{2,2}|=70p-37$$
So, The M-polynomial of \((HAC_{5}C_{6}C_{7}[p,q])\) is equal to:
\begin{eqnarray*}
M(G,x,y)&=& \sum_{i \leq j} m_{ij}(G)x^i y^j\\
&=& \sum_{2\leq 2}m_{2,2}(G)x^2 y^2+ \sum_{2\leq 3}m_{2,3}(G)x^2 y^{3}\\
&&+\sum_{3\leq 3}m_{3,3}(G)x^3 y^3+ \sum_{3\leq 4}m_{3,4}(G)x^3 y^{4}\\
&&+\sum_{4\leq 4}m_{4,4}(G)x^4 y^4\\
&=& \sum_{E_{2,2}}m_{2,2}(G)x^2 y^2+ \sum_{E_{2,3}}m_{2,3}(G)x^2 y^{3}\\
&&+\sum_{E_{3,3}}m_{3,3}(G)x^3 y^3+ \sum_{E_{3,4}}m_{3,4}(G)x^3 y^{4}\\
&&+\sum_{E_{4,4}}m_{4,4}(G)x^4 y^4\\
&=& |E_{2,2}|x^2 y^2+ |E_{2,3}|x^2 y^{3}+|E_{3,3}|x^3 y^3+ |E_{3,4}|x^3 y^{4}\\
&&+|E_{4,4}|x^4 y^4\\
&=& 2x^{2}y^{2}+12x^{2}y^{3}+(16p+1)x^{3}y^{3}+(12p+10)x^{3}y^{4}\\
&&+(70p-37)x^{4}y^{4}.
\end{eqnarray*}
Proposition 3.2. Let \(G\) be the line graph of \((HAC_{5}C_{6}C_{7}[p,q])\) nanotube, then
Proof. Let $$M(G,x,y)=2x^{2}y^{2}+12x^{2}y^{3}+(16p+1)x^{3}y^{3}+(12p+10)x^{3}y^{4}+(70p-37)x^{4}y^{4}$$ Then, $$D_{x}f(x,y)=4x^{2}y^{2}+24x^{2}y^{3}+3(16p+1)x^{3}y^{3}+3(12p+10)x^{3}y^{4}+4(70p-37)x^{4}y^{4}.$$ $$D_{y}f(x,y)=4x^{2}y^{2}+36x^{2}y^{3}+3(16p+1)x^{3}y^{3}+4(12p+10)x^{3}y^{4}+4(70p-37)x^{4}y^{4}.$$ $$D_{y}D_{x}f(x,y)=8x^{2}y^{2}+72x^{2}y^{3}+9(6p+1)x^{3}y^{3}+12(12p+10)x^{3}y^{4}+16(70p-37)x^{4}y^{4}.$$ $$S_{x}S_{y}f(x,y)=\frac{1}{2}x^{2}y^{2}+2x^{2}y^{3}+\frac{1}{9}(16p+1)x^{3}y^{3}+\frac{1}{12}(12p+10)x^{3}y^{4}+\frac{1}{16}(70p-37)x^{4}y^{4}.$$ $$D_{x}^{\alpha}D_{y}^{\alpha}f(x,y)=2^{2\alpha+1}x^{2}y^{2}+2^{\alpha+2}3^{\alpha+1}x^{2}y^{3}+3^{2\alpha}(16p+1)x^{3}y^{3}+3^{\alpha}4^{\alpha}(12p+10)x^{3}y^{3}+4^{2\alpha}(70p-37)x^{3}y^{3}.$$ $$S_{x}^{\alpha}S_{y}^{\alpha}f(x,y)=\frac{1}{2^{2\alpha-1}}x^{2}y^{2}+\frac{1}{2^{\alpha-2}3^{\alpha-1}}x^{2}y^{3}+\frac{1}{3^{2\alpha}}(16p+1)x^{3}y^{3}+\frac{1}{3^{\alpha}4^{\alpha}}(12p+10)x^{3}y^{4}+\frac{1}{4^{2\alpha}}(70p-37)x^{4}y^{4}.$$ $$S_{y}D_{x}f(x,y)=2x^{2}y^{2}+8x^{2}y^{3}+(16p+1)x^{3}y^{3}+\frac{3}{4}(12p+10)x^{3}y^{3}+(70p-37)x^{4}y^{4}.$$ $$S_{x}D_{y}f(x,y)=2x^{2}y^{2}+18x^{2}y^{3}+(16p+1)x^{3}y^{3}+\frac{3}{4}(12p+10)x^{3}y^{3}+(70p-37)x^{4}y^{4}.$$ $$S_{x}Jf(x,y)=\frac{1}{2}x^{4}+\frac{12}{5}x^{5}+\frac{9}{6}(6p+1)x^{6}+\frac{12}{7}(12P+10)x^{7}+2(70p-37)x^{8}.$$ $$S_{x}JD_{y}D_{x}f(x,y)f(x,y)=16x^{4}+\frac{72}{5}x^{5}+\frac{9}{6}(6p+1)x^{6}+\frac{12}{7}(12P+10)x^{7}+2(70p-37)x^{8}.$$ $$S_{x}^{3}Q_{-2}JD_{x}^{3}D_{y}^{3}f(x,y)=16x^{2}+96x^{3}+\frac{729}{64}(6p+1)x^{4}+\frac{1728}{125}(12P+10)x^{5}+\frac{4096}{216}(70p-37)x^{6}.$$
1. First Zagreb Index $$M_{1}(G)=(Dx+Dy)[f(x,y)]_{y=x=1}= 2(85p-19)$$
2. Second Zagreb Index $$M_{2}(G)=(Dx\cdot Dy)[f(x,y)]_{y=x=1}=1318p-383$$
3. Second Modified Zagreb Index $$^{m}M_{2}(G)=(SxSy)[f(x,y)]_{x=y=1}=^{m}M_{2}(G)=\frac{145}{24}p+\frac{163}{144}$$
4. Randic Index \begin{eqnarray*} R_{\alpha}(G)=(D_x^{\alpha}D_y^{\alpha})[f(x,y)]_{y=x=1}&=&(2.3^{2\alpha+1}+2^{2(\alpha+1)}.3^{\alpha+1}+35.2^{4\alpha+1})p\\ &&+(2^{2\alpha+1}+2^{\alpha+2}3^{\alpha+1}(3^{2\alpha}\\ &&+2^{2\alpha+1}.3^{\alpha}.5-37.2^{4\alpha}) \end{eqnarray*}
5. General Randic Index \begin{eqnarray*} RR_{\alpha}(G)=(S_x^{\alpha} S_y^{\alpha})[f(x,y)]_{x=y=1}&=&\left(\frac{2}{3^{2\alpha-1}}+\frac{1}{2^{2(\alpha-1)}.3^{\alpha-1}}+\frac{35}{2^{4\alpha+1}}\right)p\\ &&+(\frac{1}{2^{2\alpha-1}}+\frac{1}{2^{\alpha-2}3^{\alpha-1}}\frac{1}{3^{2\alpha}}\\ &&+\frac{5}{2^{2\alpha-1}.3^{\alpha}}-\frac{37}{2^{4\alpha}}) \end{eqnarray*}
6. Symmetric Division Index $$SSD(G)=(D_x S_y+ D_y S_x)[f(x,y)]=177p-\frac{127}{6}$$
7. Harmonic Index $$H(G)=2S_x J[f(x,y)]_{y=x=1}=\frac{321}{14}p+\frac{109}{420}$$
8. Inverse Sum Index $$I(G)=S_x [J(D_x D_y)][f(x,y)]_{y=x=1}=\frac{1187}{7}p+\frac{2727}{70}$$
9. Augmented Zagreb Index $$A(G)=S_x^3 Q_{-2} J D_x^3 D_y^3[f(x,y)]_{x=y=1}=\frac{168657029}{108000}p-\frac{19007957}{43200}$$