3-total edge mean cordial labeling of some standard graphs

1. Introduction

We begin with finite, undirected, simple and connected graph \(\mathcal{G}=(V_{\mathcal{G}},E_{\mathcal{G}})\). The set \(V_{\mathcal{G}}\) is called vertex set and the set \(E_{\mathcal{G}}\) is called edge set of graph \(\mathcal{G}\). Order of a graph is the number of vertices in \(\mathcal{G}\) and size of a graph is the number of edges in \(\mathcal{G}\). We follow the standard notations and terminology of graph theory as in [1]. Graph labeling were first introduced in the late \(1960's\). A graph labeling is an assignment of integers to the vertices or edges or both subject to certain condition(s). If the domain of mapping is the set of vertices (or edges) then the labeling is called a vertex labeling (or an edge labeling). We have the following notations, in order to know cordial labeling \(\alpha\) and its sorts .

1. The number of vertices labeled by \(x\) is \(v_{\alpha} (x)\);
2. The number of edges labeled by \(x\) is \(e_{\alpha} (x)\);
3. \(v_{\alpha}(x,y)=v_{\alpha}(x)-v_{\alpha}(y)\);
4. \(e_{\alpha}(x,y)=e_{\alpha}(x)-e_{\alpha}(y)\);
5. \(s(x)\)=\(v_{\alpha}(x) + e_{\alpha}(x)\);
6. \(\mathbb{Z}_k\) denotes the first \(k\) non negative integers, i.e \(\mathbb{Z}_k=\{0,1,\ldots,k-1\}.\)

Cordial labeling was introduced by Cahit in [2]. Now we will define cordial labeling and its different types.

Definition 1. Let \({\alpha}: V_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) be a mapping that induces \({\alpha}^*: E_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) as \({\alpha}^*(uv)=|{\alpha}(u)-{\alpha}(v)|\) where \(uv \in E_{\mathcal{G}}\). Then \({\alpha}\) is called cordial labeling if \(|v_{\alpha}(1,0)|\leq1\) and \(|e_{\alpha}(1,0)|\leq1\).

Definition 2. Let \({\alpha}: V_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) be a mapping that induces \({\alpha}^*: E_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) as \({\alpha}^*(uv)={\alpha}(u){\alpha}(v)\) where \(uv \in E_{\mathcal{G}}\). Then \({\alpha}\) is called product cordial labeling if \(|v_{\alpha}(1,0)|\leq1\) and \(|e_{\alpha}(1,0)|\leq1\). For details see [3].

Definition 3. Let \({\alpha}: V_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) be a mapping that induces \({\alpha}^*: E_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) as \({\alpha}^*(uv)={\alpha}(u){\alpha}(v)\) where \(uv \in E_{\mathcal{G}}\). Then \({\alpha}\) is called total product cordial labeling if \(|s(0)-s(1)|\leq1\). For details see [4, 5.

Definition 4. Let \( {\alpha}:V_{\mathcal{G}} \rightarrow\mathbb{Z}_k\), \(2\leq k\leq|E_{\mathcal{G}}|\) be a mapping that induces \({\alpha}^*: E_{\mathcal{G}}\rightarrow\mathbb{Z}_k\) as \({\alpha}^*(uv)={\alpha}(u){\alpha}(v)\) \((\text{mod}k)\) where \(uv \in E_{\mathcal{G}}\). Then \({\alpha}\) is called a k-total product cordial labeling if \(|s(a)-s(b)|\leq1\) for all \(a,b\in\mathbb{Z}_k\). For details see [6].

Definition 5. Let \( {\alpha}:E_{\mathcal{G}} \rightarrow\mathbb{Z}_2\) be a mapping that induces \({\alpha}^*: V_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) such that \({\alpha}^*(u)={\alpha}(e_1){\alpha}(e_2) \ldots {\alpha}(e_n)\) for edges \(e_1,e_2,\ldots,e_n \) incident to \(u\), then \({\alpha}\) is called edge product cordial labeling if \(|v_{\alpha}(0,1)|\leq1\) and \(|e_{\alpha}(0,1)|\leq1\). For details see [7, 8]VB4,VB1}.

Definition 6. Let \({\alpha} : E_{\mathcal{G}} \rightarrow \mathbb{Z}_2\) be a mapping that induces \({\alpha}^* : V_{\mathcal{G}} \rightarrow \mathbb{Z}_2\) such that \({\alpha}^*(u)={\alpha}(e_1){\alpha}(e_2) \ldots {\alpha}(e_n)\) for edges \(e_1,e_2,\ldots,e_n \) that are incident to \(u\), then \({\alpha}\) is called a total edge product cordial labeling if \(|s(0)-s(1)|\leq1\). For details see [9, 10].

Definition 7. Let \({\alpha}:E_{\mathcal{G}} \longrightarrow\mathbb{Z}_k\), \( 2\leq k\leq|E_{\mathcal{G}}|\) be a mapping that induces \({\alpha}^*:V_{\mathcal{G}} \longrightarrow\mathbb{Z}_k\) such that \({\alpha}^*(u)={\alpha}(e_1){\alpha}(e_2) \ldots {\alpha}(e_n)\)(mod \(k\)) for edges \(e_1,e_2,\ldots,e_n \) incident to \(u\), then \({\alpha}\) is called \(k\)-total edge product cordial labeling if it satisfy \(|s(a)-s(b)|\leq1\) for all \(a,b\in\mathbb{Z}_k\). For details see [11, 12, 13, 14, 15, 16, 17, 18, 19].

Motivated by the above definitions, we introduce new labeling named k-total edge mean cordial labeling which is defined as:

Definition 8. Let \({\alpha}: E_G\longrightarrow\mathbb{Z}_k\) be a mapping that induces \({\alpha}^*:V_G\longrightarrow\mathbb{Z}_k\) such that for each vertex \(u\), \({\alpha}^*(u)\) =\(\lceil\ {\alpha}(e_1)+{\alpha}(e_2)\ldots+{\alpha}(e_n) /n\rceil\),\ where \(e_1\), \(e_2\),\ldots, \(e_n\) are incident with \(u\) then \({\alpha}\) is called k-total edge mean cordial labeling (k-TEMC) if \(|s(i)-s(j)|\leq 1\) where \(i,j\in\mathbb{Z}_k\). A graph with a \(k\)-total edge mean cordial labeling is called \(k\)-total edge mean cordial graph.

The rest of the paper is structured as follows: In Section 2, 3-TEMC labeling of path is discussed. Section 3 devoted to the study 3-TEMC labeling of double comb graph. In Section 4, we study ladder graph and its 3-TEMC labeling. In Section 5, 3-TEMC labeling of fan graph is discussed.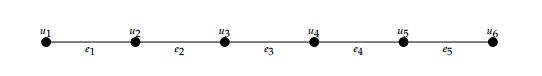

2. 3-TEMC labeling of path graph

A path graph \(P_n\) is a graph whose vertices can be listed in the order \(u_1,u_2,u_3,\ldots, u_n\) such that the edges are \(u_1u_2,u_2u_3,\ldots,u_{n-1}u_n\). Here \(V_{P_n}= \{u_i : 1\leq i \leq n\}\) and \( E_{P_n}= \{e_i=u_i u_{i+1} : 1\leq i \leq n-1\}\). (see Figure 1).

Next theorem tells us the 3-TEMC labeling of path graph.

Theorem 9. Any path \(P_n\) for \(n\geq3\) admits 3-TEMC labeling.

Proof. The following cases should be considered in order to prove that \(P_n\) is 3-TEMC.
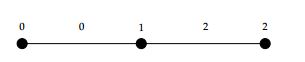
Case 1. If \(n\equiv0 \text{ (mod }3)\) then \(n= 3q\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(P_3\) (see Figure 2).

If \(q\geq2,\) then we define the function \( \alpha:E(P_n)\rightarrow\mathbb{Z}_3\) as
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q-1. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 2q, & \text{ if \(i=0,1\)}\\ 2q-1, & \text{if \(i=2.\)} \end{cases}\).Case 2. Let \(n\equiv1 \text{ (mod }3)\) then \(n= 3q+1\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(P_4\) (see Figure 3).

If \(q\geq2,\) then we define the function \( \alpha:E(P_n)\rightarrow\mathbb{Z}_3\) as
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 2q, & \text{ if \(i=0,1\)}\\ 2q+1, & \text{if \(i=2.\)} \end{cases}\).Case 3. If \(n\equiv2 \text{ (mod }3)\) then \(n= 3q+2\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(P_5\) (see Figure 4).

If \(q\geq2,\) then we define the function \( \alpha:E(P_n)\rightarrow\mathbb{Z}_3\) as
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+3\leq i \leq 2q+1; \)}\\ 2, & \text{if \( 2q+2\leq i \leq 3q+1. \)} \end{cases}\) and \(\alpha(e_{q+2})=0\), \(\alpha(e_{q+1})=1\).
Hence \(\alpha\) is 3-TEMC labeling because \(s(i)= 2q+1,\) for all \(i=0,1,2.\) Hence \(P_n\) have 3-TEMC labeling for \(n\geq2\).

3. 3-TEMC labeling of ladder graph

The ladder graph \(L_n\) is defined as the cartesian product of \(P_n\) by \(K_2\) where \(P_n\) is a path with \(n\) vertices and \(K_2\) is a complete graph with two vertices. Here \(V_{L_n}= \{{u_i,v_i : 1\leq i \leq n}\)\} and \( E_{L_n}= \{e_i=u_iu_{i+1}: 1\leq i \leq n-1\}\cup\{f_i=u_iv_i, 1\leq i \leq n\}\cup\{g_i=v_iv_{i+1}: 1\leq i \leq n-1\}\)(see Figure 5).

Next theorem tells us the 3-TEMC labeling of ladder graph.

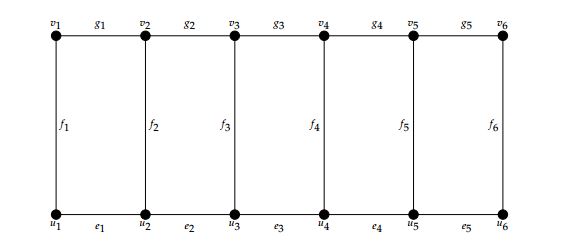
Theorem 10. Let \(L_n\) be a ladder graph, then \(L_n\) admits 3-TEMC labeling.

Proof. The following cases should be considered in order to prove that \(L_n\) is 3-TEMC.
Case 1. If \(n\equiv0 \text{ (mod }3)\) then \(n= 3q\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(L_3\) (see Figure 6).

If \(q\geq2,\) then we define the function \( \alpha:E(L_n)\rightarrow\mathbb{Z}_3\) as
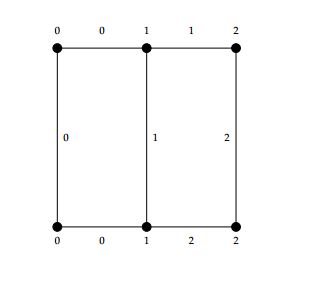
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q-1; \)}\\ 2, & \text{if \( 2q\leq i \leq 3q-1. \)} \end{cases}\) \(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) \(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q+1; \)}\\ 2, & \text{if \( 2q+2\leq i \leq 3q-1. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 5q, & \text{ if \(i=0\)}\\ 5q-1, & \text{if \(i=1,2.\)} \end{cases}\)Case 2. If \(n\equiv1 \text{ (mod }3)\) then \(n= 3q+1\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(L_4\) (see Figure 7).

If \(q\geq2,\) then we define the function \( \alpha:E(L_n)\rightarrow\mathbb{Z}_3\) as
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) \(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+2; \)}\\ 2, & \text{if \( 2q+3\leq i \leq 3q+1. \)} \end{cases}\) \(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=5q+1\), for all \(i=0,1,2.\) For \(q=1\), we have the following labeling of \(L_5\) (see Figure 8).

If \(q\geq2,\) then we define the function \( \alpha:E(L_n)\rightarrow\mathbb{Z}_3\) as
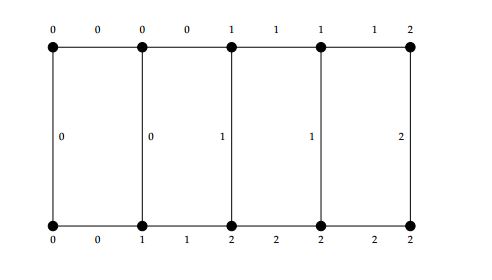
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q+1. \)} \end{cases}\) \(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+2; \)}\\ 2, & \text{if \( 2q+3\leq i \leq 3q+2. \)} \end{cases}\) \(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+2; \)}\\ 2, & \text{if \( 2q+3\leq i \leq 3q+1. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 5q+3, & \text{ if \(i=0,1\)}\\ 5q+2, & \text{if \(i=2.\)} \end{cases}\) Hence the ladder graph \(L_n\) have 3-TEMC labeling.

4. 3-TEMC labeling of double comb graph

Double comb graph \(DCO_n\) is a graph achieved by unification of two pendant edges \(u_iv_i\) and \(u_iw_i\) to every vertex \(u_i\) of a path graph. Here \(V_{DCO_n}= V_{P_n}\cup\{{v_i,w_i : 1\leq i \leq n}\)\} and \(E_{DCO_n}= E_{P_n}\cup\{{f_i=u_iv_i, g_i=u_iw_i : 1\leq i \leq n}\}\) (see Figure 9).

Next theorem tells us the 3-TEMC labeling of double comb graph.

Theorem 11. Let \(DCO_n\) be a double comb graph, then \(DCO_n\) admits 3-TEMC labeling.

Proof. The following cases should be considered in order to prove that \(DCO_n\) is 3-TEMC. \begin{description}Case 1. If \(n\equiv0 \text{ (mod }3)\) then \(n= 3q\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(DCO_3\) (see Figure 10).

If \(q\geq2,\) then we define the function \( \alpha:E(DCO_n)\rightarrow\mathbb{Z}_3\) as
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q-1. \)} \end{cases}\) \(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\)\(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 6q, & \text{ if \(i=0,1\)}\\ 6q-1, & \text{if \(i=2.\)} \end{cases}\)Case 2. If \(n\equiv1 \text{ (mod }3)\) then \(n= 3q+1\), where \(q\in \mathbb{Z}^+\). For \(q=1,\) we have the following labeling of \(DCO_4\) (see Figure 11).

If \(q\geq2,\) then we define the function \( \alpha:E(DCO_n)\rightarrow\mathbb{Z}_3\) as
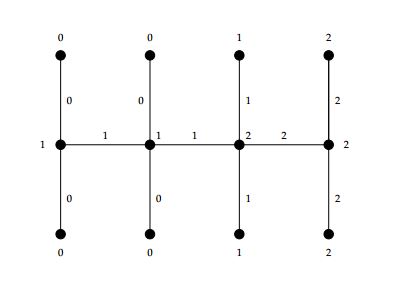
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q-1; \)}\\ 1, & \text{if \( q\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\)\(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+1; \)}\\ 2, & \text{if \( 2q+2\leq i \leq 3q+1. \)} \end{cases}\) \(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+1; \)}\\ 2, & \text{if \( 2q+2\leq i \leq 3q+1. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 6q+2, & \text{ if \(i=0,1\)}\\ 6q+1, & \text{if \(i=2.\)} \end{cases}\)Case 3. If \(n\equiv2 \text{ (mod }3)\) then \(n= 3q+2\), where \(q\in \mathbb{Z}^+\). For \(q=1,\) we have the following labeling of \(DCO_5\) (see Figure 12).

If \(q\geq2,\) then we define the function \( \alpha:E(DCO_n)\rightarrow\mathbb{Z}_3\) as
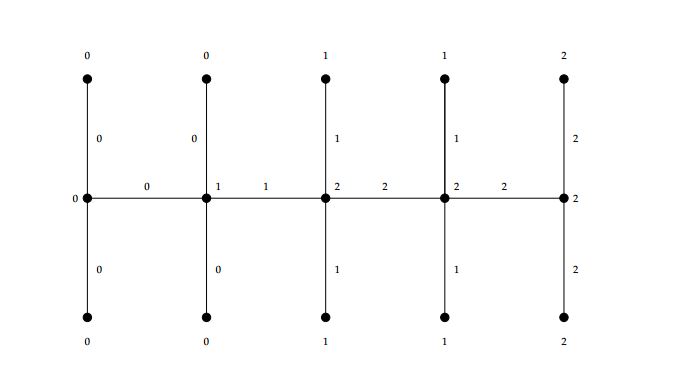
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q+1. \)} \end{cases}\)\(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+2; \)}\\ 2, & \text{if \( 2q+3\leq i \leq 3q+2. \)} \end{cases}\) \(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+2; \)}\\ 2, & \text{if \( 2q+3\leq i \leq 3q+2. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 6q+4, & \text{ if \(i=0,1\)}\\ 6q+3, & \text{if \(i=2.\)} \end{cases}\) Hence the double comb graph \(DCO_n\) have 3-TEMC labeling.

5. 3-TEMC labeling of fan graph

A Fan graph \(F_n\) is the graph obtained by taking \(n\) copies of the cycle graph \(C_3\) with a vertex \(u\) in common. Here \(V_{F_n} = \{{uu_i : 1\leq i \leq 2n}\)\} and \(E_{F_n} = {\{e_i=uu_i : 1\leq i \leq 2n}\}\cup\{{f_i = u_iu_{i+1} : 1\leq i \leq n-1} \text{ and } i \text{ is odd} \}\) (see Figure 13).

Next theorem tells us the 3-TEMC labeling of fan graph.

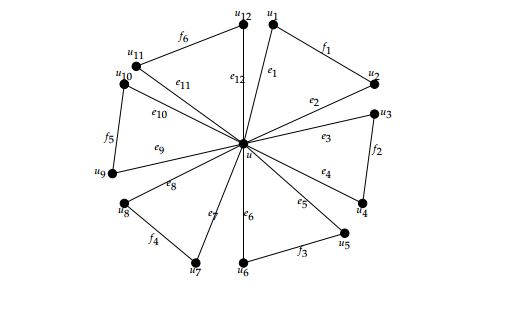
Theorem 12. Fan graph \(F_n\) for \(n\geq2\) admits 3-TEMC labeling.

Proof. The following cases should be considered in order to prove that \(F_n\) is 3-TEMC.
Case 1. Let \(n\equiv1 \text{(mod }3)\) then \(n= 3q\), where \(q\in \mathbb{Z}^+\). For \(q=1,\) we have the following labeling of \(F_3\) (see Figure 14).

If \(q\geq2,\) then we define the function \( \alpha:E(F_n)\rightarrow\mathbb{Z}_3\) as
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq 2q; \)}\\ 1, & \text{if \( 2q+1\leq i \leq 4q; \)}\\ 2, & \text{if \( 4q+1\leq i \leq 6q. \)} \end{cases}\)\(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 5q, & \text{ if \(i=0,2\)}\\ 5q+1, & \text{if \(i=1.\)} \end{cases}\)
Case 2. Let \(n\equiv1 \text{ (mod }3)\) then \(n= 3q+1\), where \(q\in \mathbb{Z}^+\). For \(q=1,\) we have the following labeling of \(F_4\) (see Figure 15).

If \(q\geq2,\) then we define the function \( \alpha:E(F_n)\rightarrow\mathbb{Z}_3\) as
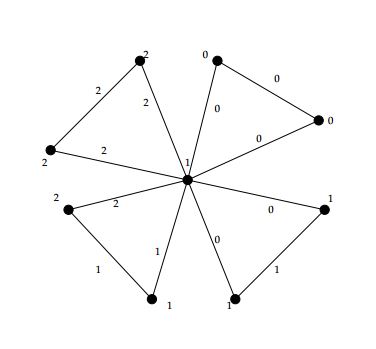
\(\alpha(e_i)=\begin{cases} 0 & \text{if \( 1\leq i \leq 2q+2; \)}\\ 1 & \text{if \( 2q+3\leq i \leq 4q+1; \)}\\ 2 & \text{if \( 4q+2\leq i \leq 6q+2. \)} \end{cases}\)\(\alpha(f_i)=\begin{cases} 0 & \text{if \( 1\leq i \leq q; \)}\\ 1 & \text{if \( q+1\leq i \leq 2q+1; \)}\\ 2 & \text{if \( 2q+2\leq i \leq 3q+1. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=5q+2,\) for all \(i=0,1,2.\)
Case 3. If \(n\equiv1 \text{ (mod }3)\) then \(n= 3q+2\), where \(q\in \mathbb{Z}^+\). we have the following labeling of \(F_2\) (see Figure 16).

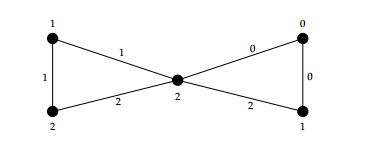
If \(q\geq1,\) then we define the function \( \alpha:E(F_n)\rightarrow\mathbb{Z}_3\) as
\(\alpha(e_i)=\begin{cases} 0 & \text{if \( 1\leq i \leq 2q+1; \)}\\ 1 & \text{if \( 2q+2\leq i \leq 4q+3; \)}\\ 2 & \text{if \( 4q+4\leq i \leq 6q+4. \)} \end{cases}\)\(\alpha(f_i)=\begin{cases} 0 & \text{if \( 1\leq i \leq q+1; \)}\\ 1 & \text{if \( q+2\leq i \leq 2q+1; \)}\\ 2 & \text{if \( 2q+2\leq i \leq 3q+2. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 5q+3, & \text{ if \(i=0\)}\\ 5q+4, & \text{if \(i=1,2.\)} \end{cases}\) Hence the fan graph \(F_n\) have 3-TEMC labeling for \(n\geq2\).

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Competing Interests

The author(s) do not have any competing interests in the manuscript.