There are many possible definitions of derivatives, here we present some and present one that we have called generalized that allows us to put some of the others as a particular case of this but, what interests us is to determine that there is an infinite number of possible definitions of fractional derivatives, all are correct as differential operators each of them must be properly defined its algebra. We introduce a generalized version of fractional derivative that extends the existing ones in the literature. To those extensions it is associated a differentiable operator and a differential ring and applications that shows the advantages of the generalization. We also review the different definitions of fractional derivatives and it is shown how the generalized version contains the previous ones as a particular cases.
Fractional derivative was defined for responding to a question ‘what does it mean \( \frac{d^{\alpha}f}{dt^{\alpha}} \) if \( \alpha=\frac{1}{2} \)’ in 1695. Following that, finding the right definition of fractional derivative has attracted significant attention of researcher and in the last few years it has seen significantly progress in mathematical and non-mathematical journals (see [1,2,3,4,5,6,7,8,9,10]). In fact, there are articles which in few months have gained hundreds of citations. In particular in past three years several definitions of fractional derivative have been proposed (see [3,4,10,11,12,13,14,15,16,17,18,19,20,21,22,23]). Since some of previous definitions do not satisfy the classical formulas of the usual derivative, it has been proposed an ad hoc algebra associated to each definition. To unify that diversity, we propose a version of fractional derivative that has the advantages that generalized the already existing in the literature and where the different algebras are unified under the notion of fractional differential ring.
The present paper is organized as follows: In the Section 2 we give the previous definitions of fractional derivative and our generalized fractional derivative (GFD) definition, in the Section 3 we introduce a fractional differential ring, in the Section 4 we give some result of GFD, in the Section 5 we give a definition of partial fractional differential derivative, in the Section 6 we give a definition of GFD when \( \alpha\in(n,n+1] \).
Let \( \alpha\in (0,1] \) be a fractional number, we want to give a definition of generalized fractional derivative of order \( \alpha\) for a differentiable function \( f \). We denote \( \alpha-\)th derivative of \( f\) by \( D^{\alpha}(f) \) and we denote the first derivative of \( f\) by \( D(f) \).
We begin the present section listing previous definition of fractional derivative; later we present our proposal of generalized one showing how it contains the once already described. We finish the section providing some examples.
Definition 1. Given a differentiable function \(f :[0,\infty) \rightarrow \mathbb{R}\), the generalized fractional derivative(GFD) for \( \alpha \in (0,1] \) at point \( t \) is defined by: \begin{array}{llll} D^{\alpha}f(t)= \lim_{\varepsilon\rightarrow 0}\frac{f(t+w_{t,\alpha} t^{1-\alpha}\varepsilon)-f(t)}{\varepsilon}, \end{array} where \(w_{t,\alpha}\) is a function that may depend on \( \alpha \) and \( t \).
Remark 1. As a consequence of Definition 1 we can see \[ D^{\alpha}f(t)=w_{t,\alpha} t^{1-\alpha}Df(t). \]
Definition 2. A differentiable function \( f: [0,\infty) \rightarrow \mathbb{R}\) is said to be \(\alpha-\)generalized fractional differentiable function over \( [0,\infty) \) if it exists \( D^{\alpha}(f)(t) \) for all \( t\in [0,\infty) \) for \( \alpha\in (0,1] \).
We denote \( C^{\alpha}[0,\infty) \) the set of \( \alpha- \)generalized differentiable functions with real values in the interval \([0,\infty)\) in variable \(t\). The set \( (C^{\alpha}[0,\infty),+,.)\) is a ring. In the following we want to see the relation between GFD and the others definitions:If the system is periodic with period \( T\), then we have \( \tau=T \). In the quantum systems \( \tau \) is the Bohr radius and in astronomy \( \tau \) is the light year. The characteristic of system \( \tau \) depends on the systems and the derivative. If \( t \) is time, \( \tau \) is time too. If \( t \) is space, \( \tau \) is space too. In fact the unit of \( t \) is \( \tau \), i.e., \( t=c\tau \) where \( c \) is a constant. In the general \( \tau =1\).
Example 1. Let \( \alpha,\beta \in (0,1] \). Let \( f,h \) be two functions in \(C^{\alpha}[0,\infty) \). We suppose \(w_{t,\alpha}= g(t,\alpha)\tau^{\alpha-1} \) with \( \tau=1\).
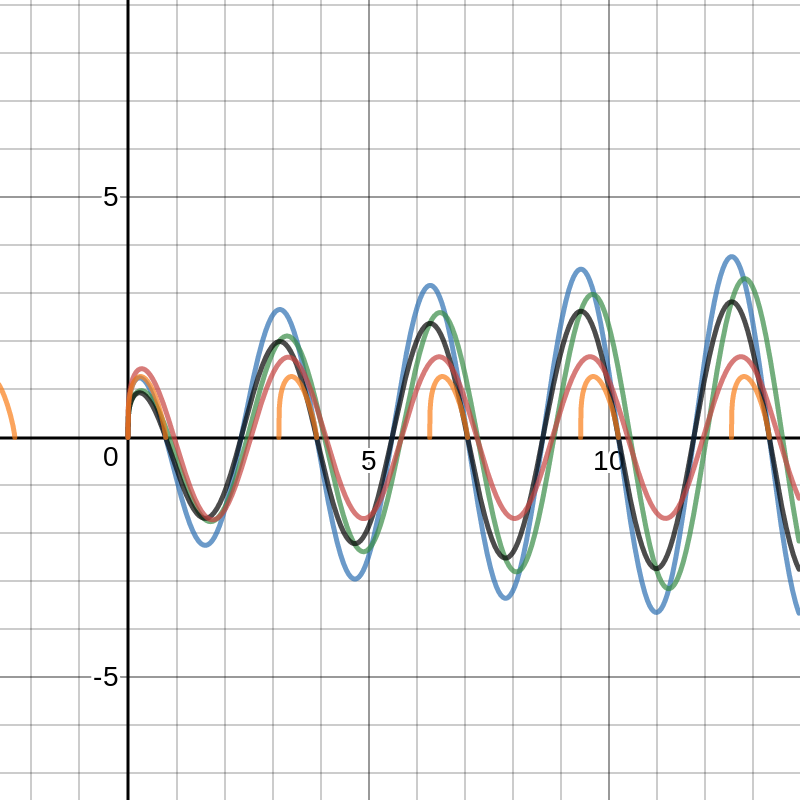
Example 2. We want to present the corresponding figure to the generalized fractional derivatives for \( \alpha=\frac{3}{4}\) for a trigonometric, using all the fractional derivative definitions that we have already mentioned in this article. It can be seen from all the figures that in principle these definitions do not find a reason to discard them. That is, they have a fairly reasonable behavior. We consider \( f(t)=\sin(2t) \), the graph of \(f\) can be seen in Figure 1.
Definition 3. Let \(R\) be a commutative ring with unity. A derivation on \(R\) is a map \(d : R \rightarrow R\) that satisfies \(d(a + b) = d(a) + d(b)\) and \(d(ab) = d(a)b + ad(b),\forall a, b \in R\). The pair \((R, d)\) is called a differential ring (see [26]).
Theorem 1. Let \( \alpha\in (0,1] \), then the ring \( C^{\alpha}[0,\infty)\) with operator \(D^{\alpha}: C^{\alpha}[0,\infty)\rightarrow C^{\alpha}[0,\infty)\) is a differential ring.
Proof. Since \( C^{\alpha}[0,\infty)\) is a commutative ring with unity \( f(t)=1 \) and the derivation \(D^{\alpha}\) for \( \alpha\in (0,1] \) satisfies following properties from Remark 1
By considering previous properties of GFD we called \( C^{\alpha}[0,\infty)\) a \(w_{t,\alpha} -\)generalized fractional differential ring of functions and we denote it by \((C^{\alpha}[0,\infty) ,D^{\alpha},w_{t,\alpha}) \). Let \( I \subset C^{\alpha}[0,\infty)\) be an ideal. If \( D^{\alpha}(I)\subset I \) then the ideal \( I \) is called a \(w_{t,\alpha} -\)generalized fractional differential ideal. By using the previous properties we can see the following result:
Theorem 2. Let \( \alpha\in(0,1] \), then, associated to any \( \alpha \) and any \( w_{t,\alpha} \) there exists a fractional differential ring.
Theorem 3. (Rolle’s Theorem for \( \alpha- \)Generalized Fractional Differentiable Functions)
Let \( a>0 \) and \( f:[a,b]\rightarrow \mathbb{R} \) be a function with the properties that
Proof. Since \(f \) is continuous on \( [a,b]\) and \( f(a)=f(b) \), then the function \( f \) has a local extreme in a point \( c\in (a,b) \) and \[ D^{\alpha} f(c)=\lim_{\varepsilon\rightarrow 0^{+}}\frac{f(c+w_{t,\alpha} c^{1-\alpha}\varepsilon)-f(c)}{\varepsilon}=\lim_{\varepsilon\rightarrow 0^{-}}\frac{f(c+w_{t,\alpha} c^{1-\alpha}\varepsilon)-f(c)}{\varepsilon}.\] But two limits have different signs, so \(D^{\alpha}f(c)=0 . \)
Theorem 4. (Mean Value Theorem for \( \alpha- \)Generalized Fractional Differentiable Functions) Let \( a>0 \) and \( f:[a,b]\rightarrow \mathbb{R} \) be a function with the properties that
Proof. Consider function \[ h(t)=f(t)-f(a)-\frac{\alpha w_{t,\alpha}(f(b)-f(a))}{b-a}\left(\frac{t^{\alpha}}{\alpha w_{t,\alpha}} -\frac{a^{\alpha}}{\alpha w_{t,\alpha}}\right). \] Then, the function \( h \) satisfies the conditions of the fractional Rolle’s Theorem. Hence, there exists \( c\in (a,b) \) such that \( D^{\alpha}h(c)=0. \) We have the result since \[ D^{\alpha}h(c)= D^{\alpha}f(c)-\frac{\alpha w_{t,\alpha}(f(b)-f(a))}{b-a}(1)=0. \]
Definition 4. Let \(f(t_{1},\cdots,t_{n}):[0,\infty)^n\rightarrow \mathbb{R}\) be a function with \( n \) variables such that \(\forall i\), then there exists the partial derivative of \( f \) respect to \(t_{i}\). Let \( \alpha\in (0,1]\) be a fractional number. We define \( \alpha-\)generalized partial fractional derivative(GPFD) of \( f \) with respect to \( t_{i} \) at point \( t=(t_{1},\ldots,t_{n}) \) \begin{array}{llll} \frac{\partial^{\alpha}f(t)}{\partial t_{i}^{\alpha}}= \lim_{\varepsilon\rightarrow 0}\frac{f(t_{1},\ldots,t_{i}+w_{t_{i},\alpha} t_{i}^{1-\alpha}\varepsilon,\ldots,t_{n})-f(t)}{\varepsilon}, \end{array} where \(w_{t_{i},\alpha}\) can be a function depend on \( \alpha\) and \( t_{i} \).
Remark 2. As a consequence of Definition 2 we can see for \( \alpha\in(0,1] \) and \( 1\leq i\leq n \): \[ \frac{\partial^{\alpha}f}{\partial t_{i}^{\alpha}}(t)=w_{t_{i},\alpha}( t_{i})^{1-\alpha} \frac{\partial f}{\partial t_{i}}(t). \]
Let \( \alpha\in (0,1] \) and \( 1\leq i\leq n \). A partial differentiable function \( f: [0,\infty)^n \rightarrow \mathbb{R}\) is said to be a \( \alpha- \)generalized partial fractional differentiable function respect to \( t_{i} \) over \( [0,\infty) \) if there exists \( \frac{\partial^{\alpha}f(t)}{\partial t_{i}^{\alpha}} \) for all \( t\in [0,\infty) \). We denote by \( C_{i}^{\alpha}[0,\infty)^n \) the set of \( \alpha-\)generalized partial fractional differentiable functions respect to \( t_{i} \) with real values in the interval \([0,\infty)^n\) in variable \(t=(t_{1},\ldots,t_{n})\). The set \( (C_{i}^{\alpha}[0,\infty)^n,+,.)\) is a ring.Theorem 5. Let \( \alpha\in(0,1] \) and \( 1\leq i\leq n \). The ring \( C_{i}^{\alpha}[0,\infty)^n\) with operator \[ \frac{\partial^{\alpha}}{\partial t_{i}^{\alpha}}: C_{i}^{\alpha}[0,\infty)^n\rightarrow C_{i}^{\alpha}[0,\infty)^n\] is a differential ring.
Proof. Since the ring \( C_{i}^{\alpha}[0,\infty)^n\) is a commutative ring with unity \( f(t_{1},\ldots,t_{n})=1 \) and the derivation \(\frac{\partial^{\alpha}}{\partial t_{i}^{\alpha}}\) for \(\alpha\in (0,1] \) satisfies the following properties from Remark 2;
We can see the following result by using the previous properties:
Theorem 6. Let \( \alpha\in(0,1] \) and \( 1\leq i \leq n \). Associated to any \( \alpha \) and any \( w_{t_{i},\alpha} \) there is a partial fractional differential ring.
Example 3. Let \( f(t_{1},t_{2}) =t_{1}^3\sin(t_{2})\) and \( \alpha\in [0,1)\) then we have \[ \frac{\partial^{\alpha}f}{\partial t_{1}^{\alpha}}= w_{t,\alpha}(t_{1})^{1-\alpha}(3t_{1}^2)\sin(t_{2}).\]
Definition 5. Let \( \alpha\in(0,1]\) be a fractional number. We define \( \alpha- \)generalized partial fractional derivative of second order with respect to \(t_{i}\) and \( t_{j} \) at point \( t=(t_{1},\cdots,t_{n}) \) is \begin{array}{llll} \frac{\partial^{\alpha^2}f(t)}{\partial t_{j}^{\alpha} \partial t_{i}^{\alpha}}=\frac{\partial^{\alpha}}{\partial t_{j}^{\alpha}}(\frac{\partial^{\alpha}f(t)}{\partial t_{i}^{\alpha}})= \lim_{\varepsilon\rightarrow 0}\frac{ \frac{\partial^{\alpha}f}{\partial t_{i}^{\alpha}}(t_{1},\ldots,t_{j}+w_{t_{j},\alpha} t_{j}^{1-\alpha}\varepsilon,\ldots,t_{n})-\frac{\partial^{\alpha}f(t)}{\partial t_{i}^{\alpha}}}{\varepsilon}. \end{array}
Remark 3. As a consequence of Definition 5 we can see for \( \alpha\in(0,1] \) and \( 1\leq i,j\leq n \); \[ \frac{\partial^{\alpha^2}f(t)}{\partial t_{j}^{\alpha} \partial t_{i}^{\alpha}}=w_{t_{j},\alpha}w_{t_{i},\alpha}(t_{j} t_{i})^{1-\alpha} \frac{\partial }{\partial t_{j}}( \frac{\partial f}{\partial t_{i}}(t)). \]
A partial differentiable function of second order \( f: [0,\infty)^n \rightarrow \mathbb{R}\) is said to be a \( \alpha- \)generalized fractional partial differentiable function of second order respect to \( t_{i}\) and \(t_{j} \) over \( [0,\infty) \) if there exists \( \frac{\partial^{\alpha^2}f(t)}{\partial t_{j}^{\alpha}\partial t_{i}^{\alpha}}\) for all \( t\in [0,\infty) \). We denote \( C_{i,j}^{\alpha^2}[0,\infty)^n \) the set of \( \alpha-\)generalized partial fractional differentiable functions of second order respect to \( t_{i}\) and \(t_{j} \) with real values in the interval \([0,\infty)^n\) in variable \(t=(t_{1},\ldots,t_{n})\). The set \( (C_{i,j}^{\alpha^2}[0,\infty)^n,+,.)\) is a ring.Definition 6. Let \( \alpha\in (n,n+1]\) be a fractional number for \( n\in \mathbb{N} \) and \( f:[0.\infty) \rightarrow \mathbb{R}\) be a \( n -\) differentiable. The generalized fractional derivative of order \( \alpha \) is defined by \begin{array}{llll} D^{\alpha}f(t)= \lim_{\varepsilon\rightarrow 0}\frac{f^{[\alpha]-1}(t+w_{t,\alpha} t^{[\alpha]-\alpha}\varepsilon)-f^{[\alpha]-1}(t)}{\varepsilon}, \end{array} where \([\alpha]\) is the smallest integer greater than or equal to \( \alpha. \)
As a consequence of Definition 6 we can see
\[ D^{\alpha}(f)=w_{t,\alpha}t^{[\alpha]-\alpha}D^{[\alpha]}(f), \] where \( \alpha\in (n,n+1] \).Let \( n< \alpha\leq n+1 \). A function \( f: [0,\infty) \rightarrow \mathbb{R}\) is said to be \(\alpha-\)generalized differentiable over \( [0,\infty)\) if there exists \( D^{\alpha}(f)(t) \) for all \( t\in [0,\infty). \) We denote \( C^{\alpha}[0,\infty) \) the set of \( \alpha- \)generalized fractional differentiable functions with real values in the interval \([0,\infty)\) in variable \(t\). The set \( (C^{\alpha}[0,\infty),+,.)\) is a ring.
Theorem 7. The ring \( (C^{\alpha}[0,\infty),+,.)\) with operator \( D^{\alpha} \) is not a differential ring for fractional number \( \alpha\in (n,n+1] \).
Proof. Since \( D^{\alpha}(fg)\neq fD^{\alpha}g+gD^{\alpha}(f) \) for every \( f,g\in C^{\alpha}[0,\infty) \).
Let \(0 < \alpha< 1 \), we define the \(\alpha\)-fractional taylor series of \( f \) at real number \( x_{0} \)
\[ f(x)=f(x_{0})+\sum_{i=1}^{\infty} \frac{D^{i}f(x_{0})}{w_{x,\alpha}\overline{(\alpha+i-1)!}} (x-x_{0})^{\alpha+i-1} , \] where \(\overline{(\alpha+i-1)!}= \alpha(\alpha+1)\cdots(\alpha+i-1) \).Let \( 1< \alpha\leq 2 \), we define the \(\alpha\)-fractional taylor series of \( f \) at real number \( x_{0}\)
\[ f(x)=f(x_{0})+Df(x_{0})(x-x_{0})+\sum_{i=2}^{\infty}\frac{D^{i}f(x_{0})(x-x_{0})^{\alpha+i-2}}{w_{x,\alpha}\overline{(\alpha+i-2)!}}, \] where \(\overline{(\alpha+i-2)!}= (\alpha-1)\alpha(\alpha+1)\cdots(\alpha+i-2) .\)Let \( n< \alpha\leq n+1 \) such that \( \alpha=n+A \) with \( 0< A< 1 \). We define the \(\alpha\)-fractional taylor series of \( f \) at real number \( x_{0}\),
\[ f(x)=f(x_{0})+\sum_{i=1}^{n}\frac{D^if(x_{0})(x-x_{0})^{i}}{i!}+\sum_{i=n+1}^{\infty}\frac{D^{i}f(x_{0})}{w_{x,\alpha}\overline{(A+i-1)!}}(x-x_{0})^{A+i-1}, \] where \( \alpha=n+A \), \(\overline{(A+i-1)!}= A(A+1)\cdots(A+i-1) \).By substituting GFD in the Equation (7) we have
\[ aw_{t,\alpha}t^{1-\alpha}Dy+by=c\Longrightarrow Dy+\frac{bt^{\alpha-1}}{aw_{t,\alpha}}y=\frac{t^{\alpha-1}c}{aw_{t,\alpha}}, \] the solutions of this equation have the form \(y(t)= \frac{c}{b}+c_{1}e^{(-\frac{bt^{\alpha}}{aw_{t,\alpha}\alpha})}. \)Example 4. We consider the partial fractional differential equation with boundary conditions
Example 5. We consider the partial fractional differential equation of second order;