Let \(G\) be a simple graph with vertex set \(V(G)\) and edge set \(E(G)\). A mapping \(g:V (G)\rightarrow\{1,2,…t\}\) is called \(t\)-coloring if for every edge \(e = (u, v)\), we have \(g(u) \neq g(v)\). The chromatic number of the graph \(G\) is the minimum number of colors that are required to properly color the graph. The chromatic polynomial of the graph \(G\), denoted by \(P(G, t)\) is the number of all possible proper coloring of \(G\). Dendrimers are hyper-branched macromolecules, with a rigorously tailored architecture. They can be synthesized in a controlled manner either by a divergent or a convergent procedure. Dendrimers have gained a wide range of applications in supra-molecular chemistry, particularly in host guest reactions and self-assembly processes. Their applications in chemistry, biology and nano-science are unlimited. In this paper, the chromatic polynomials for certain families of dendrimer nanostars have been computed.
A simple graph \(G=(V, E)\) is a finite nonempty set \(V(G)\) of objects known as vertices together with a set \(E(G)\) of unordered pairs of distinct vertices of \(G\) known as edges. The t-coloring of a graph \(G\) is a function \(g : V (G)\rightarrow\{1,2,…t\}\) which satisfies \(g(u)\neq\) \(g(v)\) for any edge \(e = (uv)\). In 1912, Birkhoff [1], presented the concept of chromatic polynomial to solve the four color problem. More precisely, a graph \(G\) is said to be t-colorable if such \(t\)-coloring exists and we say \(G\) is t- colorable. The chromatic number \(\chi (G)\) is the minimal \(t\) for which the graph is t-colorable, and we say that \(G\) is t-chromatic if \(\chi (G) = t\).
The chromatic polynomial is defined as the number of distinct \(t\)-colorings in a graph \(G\) and is denoted by the \(P(G,t)\). If the two graphs \(G\) and \(H\) have the same chromatic polynomial then the graphs defined as the chromatically equivalent graphs. In recent years, the fields of cheminformatics, physics, computer sciences and other social sciences have attracted their attention for research prospects in graph theory. A lot of research has been done by using concepts of graph theory in these fields. In molecular graphs, the vertices of the graph represent the atoms of the molecule, and the edges represent the chemical bonds.
Dendrimers are hyper-branched macromolecules, with a rigorously tailored architecture. They can be synthesized, in a controlled manner, either by a divergent or a convergent procedure. Dendrimers have gained a wide range of applications in supramolecular chemistry, particularly in host guest reactions and self-assembly processes. Their applications in chemistry, biology and nanoscience are unlimited. Currently, Alikhani et al. in [2] investigated the mathematical properties of the nanostructures and some of their chromatic polynomials. In this paper, we have investigated the chromatic polynomials of certain dendrimers nanostars.
Theorem 1. [3] Fundamental Reduction Theorem. $$P(G,t)=P(G-e,t)-P(G/e,t).$$
Suppose that \(G\) is a simple graph which has an edge \(e\). Then \(G-e\) is a graph obtained from the graph \(G\) by eliminating an edge \(e\) and \(G/e\) is a graph obtained from the graph \(G\) by contracting an edge \(e\) to one vertex. Let \(P_{m+1}\) be a path with vertices \(y_{o},y_{1},y_{2},…,y_{m}\) and \(G\) be any graph. The graph \(G_{v_{o}}(m)=G(m)\) is a graph obtained from \(G\) by identifying a vertex \(v_{o}\) of \(G\) with an end vertex \(y_{o}\) of \(P_{m+1}\), see Figure 1. For example, if \(G\) is a path \(P_{2}\), then \(G(m)=P_{2}(m)\) is the path \(P_{m+2}\).
Theorem 2. [4] If the graphs \(G\) and \(H\) have only one common vertex, such that \(V (G)\cup V (H) = { \nu }\), we have $$P(G \cup H,t) =\frac{P(G, t)P(H, t)}{t}.$$
Lemma 3. [5] Let \(G\) be a graph of order \(n\) and size \(m\) and \({P}(G,t)\) be the chromatic polynomial of \(G\), then

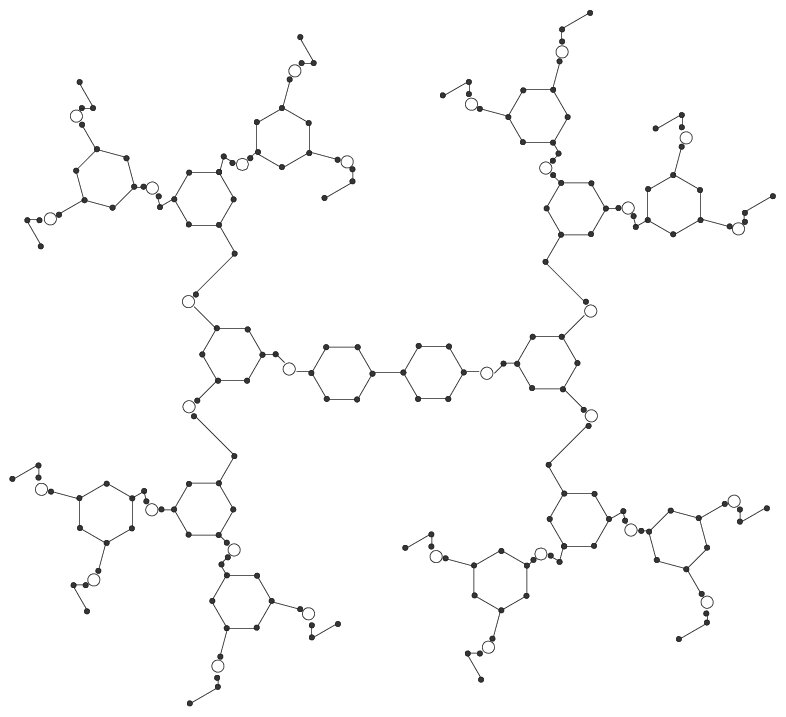
Theorem 4. The chromatic polynomial of the polyaryl ether dendrimer \(G_{1}(0)\) is $${P}(G_{1}(0),t)=t(t-1)^23(t^4-5t^3+10t^2-10t+5)^4.$$
Proof. By applying Theorem 2 and Equation (1), we get $${P}(G_{1}(0),t)=\frac{(t-1)^{19}({P}(C_{6},t))^4}{t^3}=t(t-1)^{23}(t^4-5t^3+10t^2-10t+5)^4.$$
Theorem 5. For \(n \geq 0 \), the chromatic polynomial of \(G_{1}(n)\) is as: $${P}(G_{1}(n),t)=t(t-1)^{28.2^n-5}(t^4-5t^3+10t^2-10t+5)2^{n+2}.$$
Proof. The proof is constructed by induction on \(n\). Since result is true for \(n=0\) by Theorem 4. Let us suppose that the result is true for any values less than \(n\) and we prove it for \(n\). The chromatic polynomial of core of polyaryl ether dendrimer graph is $${P}(G_{1}(0),t)=t(t-1)^{23}(t^4-5t^3+10t^2-10t+5)^4.$$ The chromatic polynomial of the graph \(H\) is computed by applying Theorem 2 and Equation (1). $${P}(H,t)=(t-1)^6{P}(C_{6},t)={P}(H,t)=t(t-1)^7(t^4-5t^3+10t^2-10t+5),$$ For \(n \geq 1\), the graph \(G_{1}(n)\) is obtained from \(G_{1}(n-1)\) by adding \(4(2)^{n-1}\) copies of the graph \(H\) such that each copy of the graph \(H\) has vertex in common with the graph \(G_{1}(n-1).\) Therefore by Theorem 2 we get, $${P}(G_{1}(m),t)=\frac{P(G_{1}(m-1),t)\times({P}(H,t))^{4(2^{m-1})}}{t^{4(2^{m-1})}},\,\,\,\,\,\,\,\,1\leq m\leq n.$$ Now by using the backward substitution, we get \begin{eqnarray*}{P}(G_{1}(n),t)&=&\frac{{P}(G_{1}(0),t)\times({P}(H,t))^{4(2^{n}-1))}}{t^{4(2^{n}-1)}}\\ &=&\frac{t(t-1)^{23}(t^4-5t^3+10t^2-10t+5)^4(t(t-1)^7(t^4-5t^3+10t^2-10t+5))^{4(2^n-1)}}{t^{4(2^n-1)}}.\end{eqnarray*} Hence we conclude that $${P}(G_{1}(n),t)=t(t-1)^{28(2^n)-5}(t^4-5t^3+10t^2-10t+5)^{2^{n+2}}.$$
The following result presents the formula for order and size of the Polyaryl ether dendrimer nanostar \(G_{1}(n)\).Corollary 6. Let \(G_{1}(n)\) be the polyaryl ether dendrimer nanostar. Then
Proof. a) Using Lemma 3(a), \(deg({P}(G,t))=|V(G)|\) which states that the degree of the chromatic polynomials is equal to the number of vertices in that graph. Since, \(deg({P}(G_{1}(n),t))=44(2^n)-4\) therefore by the Theorem \ref{1bcc}, we get $$|V(G_{1}(n)|=44(2^n)-4.$$ b) Using Lemma 3(c), the coefficient of \(-t^{|V(G)-1|}\) is equal with the number of edges of \(G\). So, Theorem \ref{1bcc} implies that $$|E(G_{1}(n)|=48(2^n)-5.$$
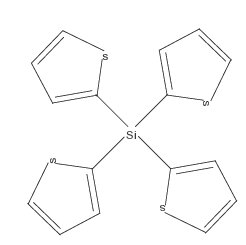

Theorem 7. The chromatic polynomial of Organosilicon dendrimer \(G[1]\) is $${P}(G[1],t)=t(t-1)^8(t^3-4t^2+6t-4)^4.$$ .
Proof. By applying Theorem 2, we get $${P}(H_{1},t)=\frac{{P}(C_5,t){P}(K_2,t)}{t}=(t-1)((t-1)^5-(t-1))=t(t-1)^2(t^3-4t^2+6t-4).$$ Since, the graph \(G[1]\) is composed of \(4\) copies of the graph \(H_{1}\) such that each copy of the \(H_{1}\) intersect at the common vertex \(t\), where \(t=Si\) from Figure 5. Therefore, from Theorem 2, we have $${P}(G[1],t)=\frac{{P}(H_1,t){P}(H_1,t){P}(H_1,t){P}(H_1,t)}{t.t.t}=\frac{t^4(t-1)^8(t^3-4t^2+6t-4)^4}{t^3},$$ This implies that, $${P}(G[1],t)=t(t-1)^8(t^3-4t^2+6t-4)^4.$$
Theorem 8. For \(n \geq 1\), the chromatic polynomial of \(G[n]\) is $${P}(G[n],t)=t(t-1)^{14(3^{n-1})-6}(t^3-4t^2+6t-4)^{6(3^{n-1})-2}.$$
Proof. The proof is constructed by induction on \(n\). Since the result is true for \(n=1\) by Theorem 7. Let us suppose that the result is true for any values less than \(n\) and we prove it for \(n\). The chromatic polynomial of organosilicon dendrimer for \(G[1]\) is, $${P}(G[1],t)=t(t-1)^8(t^3-4t^2+6t-4)^4.$$ The chromatic polynomial of Organosilicon dendrimer for the graph \(H\) can be computed by applying Theorem 2 and Equation (1), as follows $${P}(H,t)=\frac{(t-1)^4({P}(C_{5},t))^3}{t^2}=t(t-1)^7(t^3-4t^2+6t-4)^3.$$ For \(n \geq 2\), the graph \(G[n]\) is obtained from \(G[n-1]\) by adding \(4(3)^{n-2}\) copies of the graph H such that each copy of the graph \(H\) has vertex in common with the graph \(G[n-1].\) Therefore by Theorem 2, we get $${P}(G[m],t)=\frac{{P}(G[m-1],t)\times({P}(H,t))^{4(3^{m-2})}}{t^{4{(3^{m-2})}}},\,\,\,\,\,\,\,\,\, 2\leq m\leq n.$$ Now by using the backward substitution, we get \begin{eqnarray*}{P}(G[n],t)&=&\frac{{P}(G[1],t)\times({P}(H,t))^{2{(3^{n-1}-1))}}}{t^{2(3^{n-1}-1)}}\\ &=&t(t-1)^8(t^3-4t^2+6t-4)^4((t-1)^7(t^3-4t^2+6t-4))^{2(3^{n-1}-1)}\\ &=&t(t-1)^{14(3^{n-1})-6}(t^3-4t^2+6t-4)^{6\times3^{n-1}-2}.\end{eqnarray*}
The following result presents the formula for order and size of the Organosilicon dendrimer \(G[n]\).Corollary 9. For the Organosilicon dendrimer \(G[n]\), we have
Proof. a) Using Lemma 3(a), \(deg({P}(G,t))=|V(G)|\) which states that the degree of the chromatic polynomial is equal to the number of vertices in that graph. Since, \(deg({P}(G,t))=21+32[3^{n-1}-1]\), therefore Theorem 8 implies that $$|V(G[n])|=21+32[3^{n-1}-1].$$ b) Using Lemma 3(c), the coefficient of \(-t^{|V(G)-1|}\) is equal with the number of edges of \(G\). So Theorem 8 implies that $$|E(G[n])=24+38[3^{n-1}-1].$$
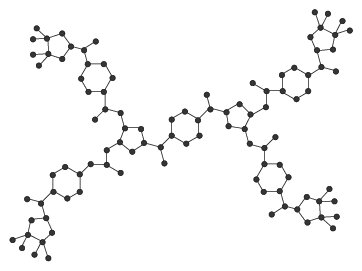
Theorem 10. The chromatic polynomial of Nanostar dendrimer \(NSC_{5}C_{6}\) denoted by \(G_{2}(1)\) is: $${P}(G_{2} (1),t)=t(t-1)^{17}(t^3-4t^2+6t-4)^2(t^4-5t^3+10t^2-10t+5).$$
Proof. By applying Theorem 2 and Equation (1), we get $${P}(G_{2}(1),t)=\frac{(t-1)^{14}{P}(C_6,t)({P}(C_5,t))^2}{t^2}=t(t-1)^{17}(t^3-4t^2+6t-4)^2(t^4-5t^3+10t^2-10t+5).$$
Theorem 11. For \(n \geq 0\), the chromatic polynomial of \(G_{2}(n)\) is: $${P}(G_{2}(n),t)=t(t-1)^{11(2^{n+1})-27}(t^3-4t^2+6t-4)^{2^{n+1}-2}(t^4-5t^3+10t^2-10t+5)^{2^{n+1}-3}.$$
Proof. The proof is constructed by induction on \(n\). Since the result is true for \(n=1\) by Theorem 10. Let us suppose that the result is true for any values less than \(n\) and we prove it for \(n\). The chromatic polynomial of \(G_{2}(1)\) is $${P}(G_{2}(1),t)=t(t-1)^{17}(t^3-4t^2+6t-4)^2(t^4-5t^3+10t^2-10t+5).$$ The chromatic polynomial for the graph \(H\) can be calculated by applying Theorem 2 and Equation (1), we get $${P}(H,t)=\frac{(t-1)^9{P}(C_{5},t){P}(C_{6},t)}{t}=t(t-1)^{11}(t^3-4t^2+6t-4)(t^4-5t^3+10t^2-10t+5).$$ For \(n \geq 2\), the graph \(G_{2}(n)\) is obtained from \(G_{2}(n-1)\) by adding \(4(2)^{n-2}\) copies of the added graph H such that each copy of the graph \(H\) has vertex in common with the graph \(G_{2}(n-1).\) Therefore by Theorem 2, we get $${P}(G_{2}(m),t)=\frac{{P}(G_{2}(m-1),t)\times({P}(H,t))^{4(2^{m-2})}}{t^{4(2^{m-2})}},\,\,\,\,\,\,2\leq m\leq n.$$ Now by using the backward substitution, we get \begin{eqnarray*}{P}(G_{2}(n),t)&=&\frac{{P}(G_{2}(1),t)\times({P}(H,t))^{4(2^{n-1}-1))}}{t^{4(2^{n-1}-1)}}\\ &=&t(t-1)^{17}(t^3-4t^2+6t-4)^2(t^4-5t^3+10t^2-10t+5)\\ &&\times[(t-1)^{11}(t^3-4t^2+6t-4)(t^4-5t^3+10t^2-10t+5)]^{4(2^{n-1}-1)}.\end{eqnarray*} Hence we conclude that $${P}(G_{2}(n),t)=t(t-1)^{11(2^{n+1})-27}(t^3-4t^2+6t-4)^{2^{n+1}-2}(t^4-5t^3+10t^2-10t+5)^{2^{n+1}-3}.$$
The following result presents the formula for order and size of the Nanostar dendrimer.Corollary 12, Let \(G_{2}(n)\) be the Nanostar dendrimer \(NSC_{5}C_{6}\). Then we have
Proof. a) Using Lemma 3(a), \(deg({P}(G,t))=|V(G)|\) which states that the degree of the chromatic polynomial is equal to the number of vertices in that graph. Since, \(deg({P}(G_{2}(n),t))=9\times2^{n+2}-44,\) therefore Theorem 11 implies that, $$|V(G_{2}(n),t)|=9\times2^{n+2}-44.$$ b) Using Lemma 3 (c), the coefficient of \(-t^{|V(G)-1|}\) is equal with the number of edges of \(G\). So Theorem 11 implies that $$|E(G_{2}(n),t)|=9\times2^{n+2}-45.$$
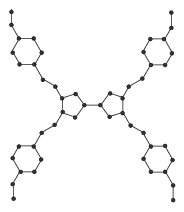

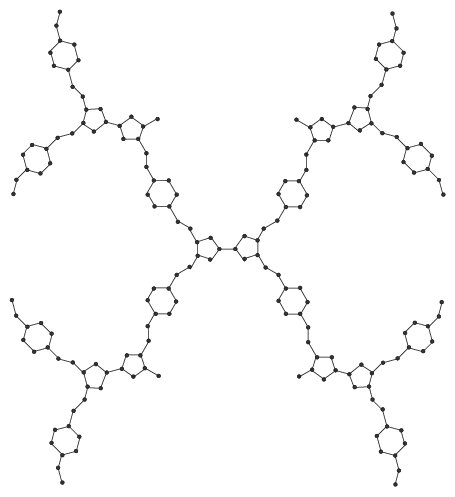
Theorem 13. The chromatic polynomial of tetrathiafulvalence dendrimer \(TD_{2}[0]\) is: $${P}(TD_{2}[0]),t )=t(t-1)^{27}(t^3-4t^2+6t-4)^2(t^4-5t^3+10t^2-10t+5)^4.$$
Proof. By applying Theorem 2 and Equation (1), we get $${P}(TD_{2}[0],t)=\frac{(t-1)^{21}({P}(C_6,t))^4({P}(C_5,t))^2}{t^5}.$$ This implies that $${P}(TD_{2}[0],t))=t(t-1)^{27}(t^3-4t^2+6t-4)^2(t^4-5t^3+10t^2-10t+5)^4.$$
Theorem 14. For \(n \geq 0\), the chromatic polynomial of \(TD_{2}[n]\) is: $${P}(TD_{2}[n],t)=t(t-1)^{17(2^{n+2})-41}(t^3-4t^2+6t-4)^{2^{n+3}-6}(t^4-5t^3+10t^2-10t+5)^{2^{n+3}-4}.$$
Proof. The proof is constructed by induction on \(n\). Since the result is true for \(n=0\) by Theorem 13. Let us suppose that the result is true for any values less than \(n\) and we prove it for \(n\). The chromatic polynomial of the graph \(TD_{2}[n]\) is $${P}(TD_{2}[0],t)=t(t-1)^{27}(t^3-4t^2+6t-4)^2(t^4-5t^3+10t^2-10t+5)^4.$$ The chromatic polynomial for graph \(H\) can be calculated by applying Theorem 2 and Equation (1), as follows: $${P}(H,t)=\frac{(t-1)^{13}({P}(C_6,t))^2({P}(C_5,t))^2}{t^3}=t(t-1)^{17}(t^3-4t^2+6t-4)^2(t^4-5t^3+10t^2-10t+5)^2.$$ For \(n \geq 1\), the graph \(TD_{2}[n]\) is obtained from \(TD_{2}[n-1]\) by adding \(4(2)^{n-1}\) copies of the graph \(H\) such that each copy of the graph \(H\) has vertex in common with the graph \(TD_{2}[n-1].\) Therefore by Theorem 2, we have $${P}(TD_{2}[m],t)=\frac{{P}(TD_{2}[m-1],t)\times({P}(H,t))^{4(2^{m-1})}}{t^{4(2^{m-1})}},\,\,\,\,\,1\leq m\leq n.$$ Now by using the backward substitution, we get \begin{eqnarray*}{P} (TD_{2}[n],t)&=&\frac{{P}(TD_{2}[0],t)\times({P}(H,t))^{4(2^{n}-1)}}{t^{4(2^{n}-1)}}\\ &=&\frac{t(t-1)^{27}(t^3-4t^2+6t-4)^2(t^4-5t^3+10t^2-10t+5)^4}{t^{4(2^{n-1})}}\\ &&\times\frac{[t(t-1)^{17}(t^3-4t^2+6t-4)^2(t^4-5t^3+10t^2-10t+5)^2]^{4(2^{n-1})}}{t^{4(2^{n-1})}}.\end{eqnarray*} Hence we conclude that $${P}(TD_{2}[n]),t)=t(t-1)^{17(2^{n+2})-41}(t^3-4t^2+6t-4)^{2^{n+3}-6}(t^4-5t^3+10t^2-10t+5)^{2^{n+3}-4}.$$
The following result presents the formula for size and order of Tetrathiafulvalence dendrimer.Corollary 15. For the Tetrathiafulvalence dendrimer \(TD_{2}[n]\), we have
Proof. a) Using Lemma 3(a), \(deg({P}(G,t))=|V(G)|\) which states that the degree of the chromatic polynomial is equal to the number of vertices in that graph. Since, \(deg({P}(TD_{2}[n],t))=50+124(2^{n}-1),\) therefore Theorem 14 implies that $$|V(TD_{2}[n],t)|=50+124(2^{n}-1).$$ b) Using Lemma 3(c), the coefficient of \(-t^{|V(G)-1|}\) is equal with the number of edges of \(G\). So Theorem 14 implies that $$|E(TD_{2}[n],t)|=5(28(2^n)-17).$$


Theorem 16. The chromatic polynomial of polyther dendrimer nanostar \(PD_{3}[0]\) is $${P}(PD_{3}[0],t)=t(t-1)^{10}(t^4-5t^3+10t^2-10t+5)^3.$$
Proof. By applying Theorem 2 and Equation (1), we get $${P}(PD_{3}[0],t)=\frac{(t-1)^7({P}(C_6,t))^{3}}{t^2}.$$ This implies that $${P}(PD_{3}[0],t)=t(t-1)^{10}(t^4-5t^3+10t^2-10t+5)^3.$$
Theorem 17. For \(n \geq 0\), the chromatic polynomial of \(PD_{3}[n]\) is: $${P}(PD_{3}[n],t)=t(t-1)^{33(2^n)-23}(t^4-5t^3+10t^2-10t+5)^{3(2^{n+1})-3}.$$
Proof. The proof is constructed by induction on \(n\). Since the result is true for \(n=0\) by Theorem 16. Let us suppose that the result is true for any values less than \(n\) and we prove it for \(n\). The chromatic polynomial of polyther dendrimer for \(PD_{3}[1]\) is $${P}(PD_{3}[0],t)=t(t-1)^{10}(t^4-5t^3+10t^2-10t+5)^3.$$ The chromatic polynomial for the graph \(H\) can be calculated by applying Theorem 2 and Equation (1), we get $${P}(H,t)=\frac{(t-1)^{9}({P}(C_6,t))^2}{t}=t(t-1)^{11}(t^4-5t^3+10t^2-10t+5)^{2}.$$ For \(n \geq 1\), the graph \(PD_{3}[n]\) is obtained from \(PD_{3}[n-1]\) by adding \(3(2)^{n-1}\) copies of the added graph H such that each copy of the graph \(H\) has vertex in common with the graph \(PD_{3}[n-1].\) Therefore by Theorem 2, we get $${P}(PD_{3}[m],t)=\frac{{P}(PD_{3}[m-1],t)\times({P}(H,t))^{3(2^{m-1})}}{t^{3(2^{m-1})}},\,\,\,\,\,1\leq m\leq n.$$ Now by using the backward substitution, we get $${P}(PD_{3}[n],t)=t(t-1)^{10}(t^4-5t^3+10t^2-10t+5)^3)[\frac{(t(t-1)^{11}(t^4-5t^3+10t^2-10t+5)^{2})^{3(2^n-1)}}{t^{3(2^n-1)}}].$$ Hence we conclude that $${P}(PD_{3}[n],t)=t(t-1)^{33(2^n)-23}(t^4-5t^3+10t^2-10t+5)^{3(2^{n+1})-3}.$$
The following result presents the formula for order and size of the polyther dendrimer \(PD_{3}[n]\).Corollary 18. For the Polyther dendrimer \(PD_{3}[n]\), we have
Proof. a) Using Lemma 3(a), \(deg({P}(G,t))=|V(G)|,\) which states that the degree of the chromatic polynomial is equal to the number of vertices in that graph. Since, \(deg({P}(PD_{3}[n],t))=57(2^n)-34,\) therefore Theorem 17 implies that $$|V(PD_{3}[n])|=57(2^n)-34.$$ b) Using Lemma 3(c), the coefficient of \(-t^{|V(G)-1|}\) is equal with the number of edges of \(G\). So Theorem 17 implies that $$|E(PD_{3}[n])=63(2^n)-38.$$