On smarandachely adjacent vertex total coloring of subcubic graphs

All graphs considered in this paper are simple and undirected. The terminology and notation used but undefined here can be found in [1]. Let \(G\) be a graph with vertex set \(V(G)\) and edge set \(E(G)\). We use \(d_G(v)\) to denote the degree of a vertex \(v\) in \(G\). A vertex \(v\) is called a \(t\)-vertex (\(t^-\)-vertex or \(t^+\)-vertex) of \(G\) if \(d_G(v)\)=\(t\) (\(d_G(v)\leq t\) or \(d_G(v)\geq t\)). We refer to \(t\)-vertices, \(t^-\)-vertices and \(t^+\)-vertices adjacent to \(v\) as \(t\)-neighbors, \(t^-\)-neighbors and \(t^+\)-neighbors of \(v\), respectively. Let \(\Delta(G)\) and \(\delta(G)\) denote the maximum degree and minimum degree of \(G\), respectively. The open neighborhood of \(v\), written as \(N_G(v)\), is defined as the set of vertices adjacent to \(v\) in \(G\), i.e. \(N_G(v) = \{u|uv \in E(G)\}\). For any \(V’\subset V(G)\) and \(E’\in E(G)\), we use \(G-V’\) (resp. \(G-E’\)) to denote the graph obtained from \(G\) by deleting vertices in \(V’\) and their incident edges (resp. by removing edges in \(E’\)). For any integers \(a, b\) with \(a< b\), let \([a, b]\)=\(\{a, a+1, \ldots, b\}\).

We, for convenience, denote by \(T(G)\) the set of vertices and edges of a graph \(G\), i.e. \(T(G)=V(G)\cup E(G)\). Let \(k\) be a positive integer, and \(f\) a mapping from \(T(G)\) to \([1, k]\). If \(f\) satisfies the following coloring conditions:

• (1) \(f(u)\neq f(v)\) for any \(uv\in E(G)\),
• (2) \(f(u)\neq f(e)\) for every vertex \(u\) and every edge \(e\) incident with \(u\),
• (3) \(f(e)\neq f(e’)\) for every pair \(e,e’\) of adjacent edges,

then we call \(f\) a proper total \(k\)-coloring of \(G\). For any \(v\in V(G)\), we call \(C_{f}(v)\) the color-set of \(v\) \((\)under \(f\) \()\), which denotes the set of colors of \(v\) and its incident edges under \(f\). Furthermore, let \(\overline{C}_f(x)=[1,k]\setminus C_{f}(x)\). To distinguish the color-sets of two adjacent vertices from the perspective of proper total coloring, Zhang et al.[2] introduced the concept of adjacent vertex distinguishing total coloring (or AVDTC simply), which is a proper total coloring \(f\) with the constraint (4) as follows:

• (4)] \(C_{f}(u)\neq C_{f}(v)\) for every \(uv\in E(G)\).

The minimum number \(k\) such that \(G\) has a \(k\)-AVDTC is the adjacent vertex distinguishing total chromatic number of \(G\), denoted by \(\chi_{at}(G)\). As for this parameter, a famous conjecture says that every graph \(G\) has an adjacent vertex distinguishing total coloring using at most \(\Delta(G)+3\) colors, i.e. \(\chi_{at}(G)\leq \Delta(G)+3\). This conjecture has been confirmed for special families of graphs, e.g. graphs with maximum degree 3 [3, 4, 5], graphs without \(K_4\)-minor [6], graphs with smaller maximum average degree and large maximum degree [7, 8], outerplane graphs [9], 2-degenerate graphs [10], graphs with maximum degree 4 [11], generalized Mycielski graphs [12], etc. In [13], a stronger version of AVDTC called smarandachely adjacent vertex total coloring (abbreviate to SAVTC) is studied. A \(k\)-SAVTC of a graph \(G\) is a proper total \(k\)-coloring that satisfies coloring condition (5) as below:

• (5)] \(C_{f}(u)\setminus C_{f}(v)\neq \emptyset\) and \(C_{f}(v)\setminus C_{f}(u)\neq \emptyset\) for every \(uv\in E(G)\).

We refer to the smallest number \(k\) such that \(G\) has a \(k\)-SAVTC as the smarandachely adjacent vertex total chromatic number of \(G\), denoted by \(\chi_{sat}(G)\). Clearly, condition (5) is a stronger version of condition (4). That is, if \(f\) is a \(k\)-SAVTC of \(G\), then \(f\) is a \(k\)-AVDTC of \(G\), whereas the converse is not necessarily true. For example, when a graph \(G\) contains no adjacent vertices with maximum degree, it is possible that \(\chi_{at}(G)=\Delta(G)+1\), e.g. the star graph \(S_n, n\geq 3\). However, by coloring condition (5), one can readily check that \(\chi_{sat}(G)\geq \Delta(G)+2\) for all graphs \(G\).

Therefore, such a parameter is independent, interesting and meaningful. In [13], Zhang proposed the following conjecture.

Conjecture 1.[13] For any graph \(G\), \(\chi_{sat}(G)\leq \Delta(G)+3\).

Observe that for two adjacent vertices \(u,v\in V(G)\) such that \(d_G(u)\leq d_G(v)\), to check that \(C_f(u)\) and \(C_f(v)\) satisfy the coloring condition (5) under a total coloring \(f\) of \(G\), it is sufficient to examine whether there is an element \(c\) such that \(c\in C_f(u)\) and \(c\notin C_f(v)\). Therefore, we have the following lemma, which demonstrates the relation between \(\chi_{at}(G)\) and \(\chi_{sat}(G)\) for regular graphs \(G\).

Lemma 2. Let \(G\) be a regular graph. Then, \(\chi_{at}(G)=\chi_{sat}(G)\).

To verify our results in this paper, we first introduce a simple but useful lemma as follows.

Lemma 3. Let \(A\), \(B\) be two sets containing \(p\) and \(q\) elements, respectively. If \(p\leq q-1\) and \(A\setminus B\neq \emptyset\), then for any element \(c\), \((A\cup \{c\})\setminus B\neq \emptyset\) and \(B\setminus (A\cup \{c\})\neq \emptyset\).

Proof. Since \(A\setminus B\neq \emptyset\), there exists an element \(a \in A\) and \(a\notin B\). In addition, \(q\geq p+1\) implies that \(B\) contains at least two distinct elements \(b_1,b_2\) such that \(b_1\notin A\) and \(b_2\notin A\). Therefore, \(|B\setminus(A\cup \{c\})|\geq 1\) and \(|(A\cup \{c\})\setminus B|\geq 1\).

If a graph contains a 1-vertex, then we have the following observation with regard to the SAVTC.

Lemma 4. Suppose that \(G\) is a graph with an 1-vertex \(u\) such that \(G-\{u\}\) has a \(k\)-SAVTC, \(k\geq \Delta(G)+2\). Let \(\{v\}=N_G(u)\), \(d_G(v)=\ell (\geq 2)\), and \(N\) the set of \((\ell-1)^-\)-neighbors of \(v\). If \(|N|\leq k-\ell\), then every \(k\)-SAVTC \(f\) of \(G-\{u\}\) can be extended to a \(k\)-SAVTC of \(G\).

Proof. Based on \(f\), edge \(uv\) has \(k-\ell\) available colors under the coloring conditions (1), (2) and (3). Because \(|N|\leq k-\ell\), there exists an available color \(\alpha\in [1,k]\) for \(uv\) such that \(C_{f}(v’)\not \subset (C_{f}(v)\cup \{\alpha\})\) for any \(v’\in N\setminus \{u\}\). By Lemma 3, we have that \((C_{f}(v)\cup \{\alpha\}) \not \subset C_{f}(v’)\) for any \(v’\in N_G(v)\setminus N\). Therefore, we obtain a \(k\)-SAVTC of \(G\) after coloring \(u\) with a color in \([1,k]\setminus (C_{f}(v)\cup \{\alpha\})\).

2. Subcubic graphs

A graph \(G\) is said to be cubic if \(\delta(G)=\Delta(G)=3\) and subcubic if \(\Delta(G)\leq 3\). Since \(\chi_{at}(G)\leq 6\) for every cubic graph \(G\) [3, 4, 5], it has that \(\chi_{sat}(G)\leq 6\) by Lemma 2. In this section, we aim to extend this result from cubic graphs to subcubic graphs. We prove the following theorem.

Theorem 5. If \(G\) is a subcubic graph, then \(\chi_{sat}(G)\leq 6\).

Proof. It is sufficient to deal with the case that \(G\) contains a \(2^-\)-vertex. Let \(G\) be a counterexample to Theorem 5 such that \(|E(G)|\) is minimum, and \(v\) a \(2^-\)-vertex. We will prove that \(G\) contains a 6-SAVTC, and get a contradiction. %Since \(G-\{v\}\) is subcubic, by the minimality \(G-\{v\}\) has a 6-SAVTC. If \(d_G(v)=1\), then by Lemma 4 we can get a 6-SAVTC of \(G\) from any 6-SAVTC of \(G-\{v\}\). Therefore, we assume \(d_{G}(v)=2\), and suppose that \(G\) does not contain any 1-vertex. Let \(\{u,w\}\) be the open neighborhood of \(v\).

Case 1. At least one of these two vertices, say \(u\), is a 2-vertex. Let \(u’=N_G(u)\setminus \{v\}\), and by the minimality \(f’\) a 6-SAVTC of \(G-\{vu\}\). We now extend \(f’\) by the following rule: if \((C_{f’}(u)\cup C_{f’}(w))\neq [1,6]\), let \(\alpha\in [1,6]\setminus (C_{f’}(u)\cup C_{f’}(w))\), and assign color \(\alpha\) to \(uv\) and recolor \(v\) with a color in \([1,6]\setminus (\{\alpha, f'(vw),f'(w)\}\cup C_{f’}(u))\) (observe that \(|C_{f’}(u)|=2\)). Denote by \(f\) the resulting coloring. Obviously, \(\alpha\notin C_f(w)\), \(f(v)\notin C_f(u)\), and by Lemma 3 \(C_f(u)\not \subset C_f(u’)\). This shows that \(f\) is a 6-SAVTC of \(G\); if \((C_{f’}(u)\cup C_{f’}(w))=[1,6]\), then \(C_{f’}(u)\cap C_{f’}(w)=\emptyset\). We therefore obtain a 6-SAVTC of \(G\) by coloring \(uv\) with \(f'(w)\) and recoloring \(v\) with \(f'(uu’)\).

Case 2. Both \(u\) and \(w\) are 3-vertices. When \(uw\in E(G)\), we will extend a 6-SAVTC \(f’\) of \(G-\{uv\}\) to a such coloring of \(G\). Let \(\{u’\}=N_G(u)\setminus \{v,w\}\). Observe that \(|C_{f’}(u)\cup \{f'(vw)\}|\leq 4\). We can choose a color \(\alpha\in [1,6]\setminus (C_{f’}(u)\cup \{f'(vw)\})\) such that \(C_{f’}(u’)\not\subset (C_{f’}(u)\cup \{\alpha\})\). By Lemma 3, \((C_{f’}(u)\cup \{\alpha\})\not \subset C_{f’}(w)\). If \(|C_{f’}(u)\cup C_{f’}(w)\cup \{\alpha\}|\neq 6\), then we can recolor \(v\) with a color in \([1,6]\setminus (C_{f’}(u)\cup C_{f’}(w)\cup \{\alpha\})\) to get a 6-SAVTC of \(G\). If \(|C_{f’}(u)\cup C_{f’}(w)\cup \{\alpha\}|=6\), then either \(\alpha\notin C_{f’}(w)\) and \(f'(vw)\notin C_{f’}(u)\), or \(\alpha\in C_{f’}(w)\) and \(f'(vw)\notin C_{f’}(u)\) (or \(\alpha\notin C_{f’}(w)\) and \(f'(vw)\in C_{f’}(u)\)). In the former case, we can recolor \(v\) with a color in \([1,6]\setminus \{\alpha, f'(u),f'(vw), f'(w)\}\) to get a 6-SAVTC of \(G\), while in the latter eventuality we can recolor \(v\) with a color in \([1,6]\setminus (C_{f’}(w)\cup \{f'(u)\})\) (or \([1,6]\setminus (C_{f’}(u)\cup \{\alpha, f'(w)\})\)) to gain a 6-SAVTC of \(G\). In the remainder of this proof, let \(uw\notin E(G)\).

Consider \(G’=(G-\{v\}) \cup \{uw\}\). We see that \(G’\) is a subcubic graph and \(|E(G’)|< |E(G)|\). By the minimality, \(G'\) has a 6-SAVTC \(f'\). Without loss of generality, we may suppose that \(C_{f'}(u)=\{1,2,3,4\}\), where \(f'(u)=4, f'(uw)=1\). Let \(N_{G}(u)=\{v,u_1,u_2\}\) and \(N_{G}(w)=\{v,w_1,w_2\}\). Suppose that \(\overline{C}_{f'}(w)=\{c_1,c_2\}\). We now extend \(f'\) to a 6-SAVTC of \(G\) by addressing the following two situations.

When \(1\notin \{f'(u_i), f'(w_i)|i=1,2\}\), we recolor \(u\) and \(w\) with 1, color \(uv\) with 4 and \(vw\) with \(f'(w)\). Denote by \(f\) the resulting coloring. Clearly, \(C_f(u)=C_{f’}(u)\) and \(C_f(w)=C_{f’}(w)\). If \(f'(w)\in \{5,6\}\), then \(f'(w)\notin C_f(u)\). Therefore, after coloring \(v\) with a color in \(\{c_1,c_2\}\setminus \{4\}\), we get a 6-SAVTC of \(G\). If \(f'(w)\notin \{5,6\}\), it has that \(f'(w)\in \{2,3\}\). Then, when \(4\in \{c_1,c_2\}\), we can color \(v\) with 5 or 6 to get a 6-SAVTC of \(G\); when \(4\notin \{c_1,c_2\}\), it follows that \(\{5,6\}\cap \{c_1,c_2\}\neq \emptyset\). Therefore, we obtain a 6-SAVTC of \(G\) by coloring \(v\) with a color in \(\{5,6\}\cap \{c_1,c_2\}\).

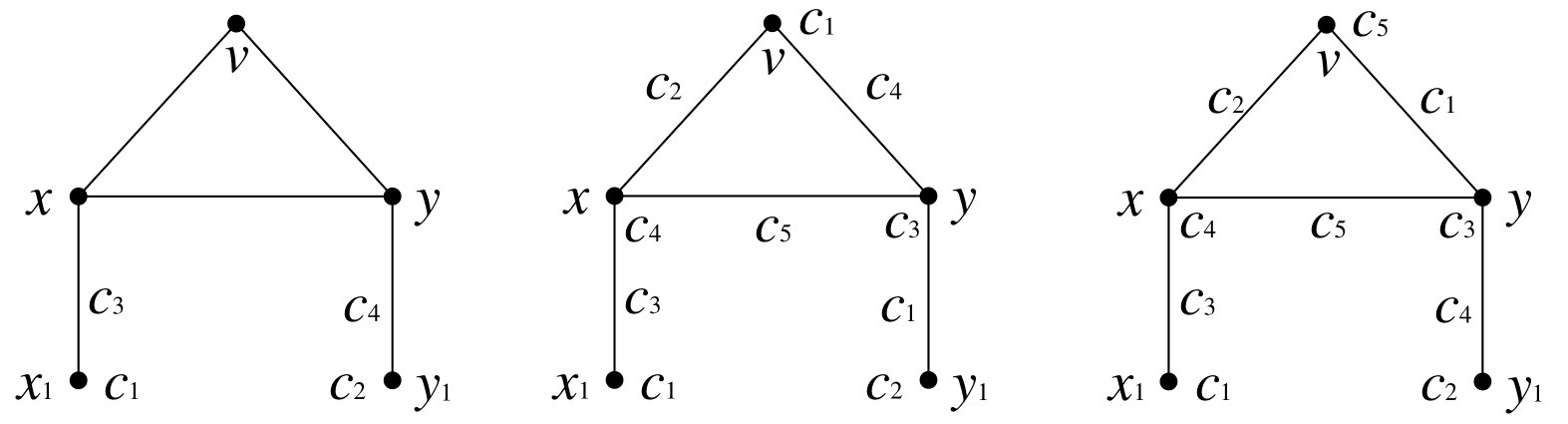
When \(1\in \{f'(u_i), f'(w_i)|i=1,2\}\), we, by symmetry, assume that \(f'(u_1)=1\). In this case, we first color \(vw\) with 1, and \(vu\) with a color \(c\in \{5,6\}\) such that \(C_{f’}(u_2)\not\subset \{2,3,4,c\}\). Then, color \(v\) with a color in \(\{c_1,c_2\}\setminus \{4,c\}\) if \(\{4,c\}\neq \{c_1,c_2\}\) (observe that \(f'(w)\notin \{c_1,c_2\}\)); otherwise, color \(v\) with a color in \(\{2,3\}\setminus \{f'(w)\}\). Denote by \(f\) the resulting coloring. It has that \(C_f(w)=C_{f’}(w)\), \(C_f(u)=\{2,3,4,c\}\), \(1\in C_f(v), 1\in C_f(u_1), 1\notin C_f(u)\), and \(f(v)\notin C_f(w)\) or \(c\notin C_f(w)\). Therefore, \(f\) is a 6-SAVTC of \(G\).

3. Graphs with smarandachely adjacent vertex total chromatic number 5

In this section, we aim to construct a 5-SAVTC for the given classes of subcubic graphs. For this, we will get a 5-SAVTC of a hypothetical smallest counterexample \(G\) to the theorem we need prove by extending a 5-SAVTC \(f’\) of a smaller graph derived from \(G\), and obtain a contradiction. In the process of extending \(f’\), we by default color elements shared by \(G\) and \(G’\) with the restriction of \(f’\) to them if there is no specified note.

3.1. Outerplanar graphs with maximum degree 3

A planar graph \(G\) is called outerplanar if there is an embedding of \(G\) into the Euclidean plane such that all vertices lie on the boundary of its unbounded face. An outerplanar graph equipped with such an embedding is called an outerplane graph. To show that outerplane graphs with maximum degree 3 have a 5-SAVTC, we need the following lemma.

Lemma 6. Suppose that \(f\) is a partial coloring of the graph \(G\) shown in Figure 1 (a), where \(V(G)=\{v,x,y,x_1,y_1\}\) and \(f(x_1)=c_1,f(y_1)=c_2,f(x_1x)=c_3,f(y_1y)=c_4\). If \(|\{c_i|i=1,2,3,4\}|\geq 3\), \(c_1\neq c_2, c_1\neq c_3, c_2\neq c_4\) and \(c_3\neq c_4\), then we can construct a 5-SAVTC of \(G\) on the restriction of \(f\).

Proof. In Figures 1 (b) and (c), we give the corresponding 5-SAVTCs of \(G\) for the cases \(|\{c_i|i=1,2,3,4\}|=3\) and \(|\{c_i|i=1,2,3,4\}|=4\), respectively. Observe that under each 5-SAVTC of \(G\), \(c_1\) and \(c_2\) is not in the color-set of \(x\) and \(y\), respectively, and \(c_1,c_2\) belong to the color-set of \(v\).

Theorem 7. Let \(G\) be an outerplane graph with maximum degree 3. Then, \(\chi_{sat}(G)=5\).

Proof. It is enough to show that \(G\) has a 5-SAVTC. Let \(G\) be a counterexample to Theorem 7 with minimum number of edges. We distinguish two cases. Case 1. \(G\) contains a cut-vertex \(v\). Then, there are two smaller outerplane graphs \(G_1\) and \(G_2\) such that \(\Delta(G_i)\leq 3, i=1,2\), \(G_1\cup G_2=G\) and \(G_1\cap G_2=\{v\}\). By the minimality, \(G_i\) has a 5-SAVTC, denoted by \(f_i,i=1,2\). Without loss of generality, suppose that \(d_{G_1}(v)\leq 2\), \(d_{G_2}(v)=1\) and \(N_{G_2}(v)=\{u\}\).

Case 1.1. \(|V(G_2)|=2\), i.e. \(G_2=vu\). If \(d_{G_1}(v)=1\), then by Lemma 4 any 5-SAVTC of \(G_1\) can be extended to a 5-SAVTC of \(G\). We therefore assume that \(d_{G_1}(v)=2\) and \(N_{G_1}(v)=\{v_1,v_2\}\). If \(\{v_1,v_2\}\) contains an 1-vertex or 3-vertex, say \(v_1\), we extend \(f_1\) to a 5-SAVTC \(f\) by coloring \(vu\) with a color \(\alpha\in [1,5]\setminus C_{f_1}(v)\) such that \(C_{f_1}(v_2)\not \subset C_{f_1}(v)\cup \{\alpha\}\) (since \(|[1,5]\setminus C_{f_1}(v)|=2\), such a color \(\alpha\) does exist), and color \(u\) (or recolor \(v_1\) when \(d_{G_1}(v_1)=1\)) with \(\beta\), where \(\{\beta\}=[1,5]\setminus (C_{f_1}(v)\cup \{\alpha\})\). Since \(\beta\notin C_f(v)\) and by Lemma 3 \(C_f(v)\neq C_f(v_1)\) when \(d_{G_1}(v_1)=3\), \(f\) is a 5-SAVTC of \(G\).

Now, suppose that \(d_{G_1}(v_1)=d_{G_1}(v_2)=2\) and \(N_{G_1}(v_i)=\{v,v’_i\}\), \(i=1,2\). We omit the trivial case \(v_1v_2\in E(G_1)\) and by Lemma 4 assume \(d_{G’}(v’_i)\geq 2\) for \(i=1,2\). By the minimality, let \(f’\) be a 5-SAVTC of \(G-\{v\}\). Based on \(f’\), if \(C_{f’}(v_1)\cap C_{f’}(v_2)\) contains an element \(\gamma\), then we color \(v, vu, vv_1,vv_2\) with \([1,5]\setminus \{\gamma\}\) properly and color \(u\) with \(\gamma\); if \(C_{f’}(v_1)\cap C_{f’}(v_2)=\emptyset\), we recolor \(v_1\) with a color \(\gamma \in (\{f'(v_2),f'(v_2v’_2)\}\setminus \{f'(v’_1)\})\) and color \(vv_1\) with \(f'(v_1)\), \(vv_2\) with \(f(v_1v’_1)\), \(v\) with the color in \([1,5]\setminus(C_{f’}(v_1)\cup C_{f’}(v_2))\), \(vu\) with \(\{f'(v_2),f'(v_2v’_2)\}\setminus \{\gamma\}\) and \(u\) with \(\gamma\). Denote by \(f\) the resulting coloring. Since \(\gamma\notin C_f(v)\) and by Lemma 3 \(C_f(v_i)\not\subset C_f(v’_i)\) for \(i=1,2\), \(f\) is a 5-SAVTC of \(G\).

Case 1.2. \(|V(G_2)|\geq 3\). Let \(G’_1=G_1\cup vu\), \(G’_2=G_2\). By the minimality, \(G’_1\) and \(G’_2\) have a 5-SAVTC \(f’_1\) and \(f’_2\), respectively. By the color permutation, we assume \(f’_1(v)=f’_2(v)=1, f’_1(vu)=f’_2(vu)=2\) and \(f’_1(u)=f’_2(u)=3\). Clearly, \(3\notin C_{f’_1}(v)\) and \(1\notin C_{f’_2}(u)\). Let \(f=f’_1\cup f’_2\). We see that \(C_f(v)=C_{f’_1}(v)\), \(C_f(u)=C_{f’_2}(u)\) and \(3\in C_f(u), 1\in C_f(v)\). Therefore, \(f\) is a 5-SAVTC of \(G\).

Case 2. \(G\) is 2-connected. We claim that \(G\) does contain two adjacent 2-vertices. If not, suppose that \(u,v\) are such 2-vertices, where \(N_{G}(u)=\{v,u_1\}\) and \(N_{G}(v)=\{u,v_1\}\). Since \(G\) is 2-connected, \(d_{G}(u_1)\geq 2\) and \(d_{G}(v_1)\geq 2\). We first consider the case of \(u_1v_1\in E(G)\). In this case, \(d_{G’}(u_1)=d_{G’}(u_2)=3\). Given a 5-SAVTC \(f’\) of \(G-\{u\}\), for which we suppose that \(\overline{C}_{f’}(v_1)=\{5\}\). Obviously, \(5\in C_{f’}(u_1)\) and \(f'(v)=5\). Based on \(f’\), color \(uu_1\) with a color \(\alpha \in [1,5]\setminus C_{f’}(u_1)\) such that \(C_{f’}(u_2)\not \subset (C_{f’}(u_1)\cup \{\alpha\})\) (since \(|C_{f’}(u_1)|=3\)), where \(\{u_2\}=N_{G}(u_1)\setminus \{v_1,u\}\). Let \(\{\beta\}=[1,5]\setminus (C_{f’}(u_1)\cup \{\alpha\})\), and color \(u\) with \(\beta\) and \(uv\) with a color in \([1,5]\setminus \{\alpha, \beta, f'(vv_1), 5\}\). Observe that \(5\notin \{\alpha, \beta\}\); we obtain a 5-SAVTC of \(G\). Now, we assume that \(u_1v_1\notin E(G)\). Let \(G’=(G-\{u,v\})\cup \{u_1v_1\}\), and, by the minimality, \(f’\) be one of its 5-SAVTCs. Since \(u_1v_1\in E(G’)\), there exist \(\alpha_1 \in \overline{C}_{f’}(u_1)\) and \(\alpha_2\in \overline{C}_{f’}(v_1)\) such that \(\alpha_1\neq \alpha_2\). Then, \(f’\) can be extended to a 5-SAVTC of \(G\) by assigning color \(f'(u_1v_1)\) to \(uu_1\) and \(vv_1\), color \(\alpha_1\) to \(u\), color \(\alpha_2\) to \(v\), and a color in \([1,5]\setminus \{f'(u_1v_1),\alpha_1, \alpha_2\}\). This contradicts the assumption of \(G\).

From the foregoing discussion, we deduce that \(G\) contains a triangle \(uvwu\) such that \(d_G(u)=2\) and \(d_G(v)=d_G(w)=3\). Let \(N_G(v)=\{u,w,v’\}\) and \(N_G(w)=\{u,v,w’\}\). Clearly, \(d_{G}(v’)\geq 2\) and \(d_{G}(w’)\geq 2\). Let \(G’=(G-\{v,w\})\cup \{uv’,uw’\}\). By the minimality, \(G’\) has a 5-SAVTC, say \(f’\). Suppose that \(f'(uv’)=c_1, f'(uw’)=c_2\), \(f'(v’)=c_3\) and \(f'(w’)=c_4\), where \(c_i \in [1,5]\) for \(i\in[1,4]\). We now define a partial coloring \(g\) of \(G\) such that \(g(x)=f'(x)\) for any \(x\in T(G)\setminus \{u,v,w,uv,uw,vw,vv’ ww’\}\), \(g(vv’)=f'(uv’)=c_1\) and \(g(ww’)=f'(uw’)=c_2\). We see that \(C_{g}(y)=C_{f’}(y)\) for any \(y\in V(G)\setminus \{u,v,w\}\), and only elements in \(\{u,v,w,uv,uw,vw\}\) are uncolored. Observe that \(c_1\neq c_2\), \(c_1\neq c_3\) and \(c_2\neq c_4\). It suffices to deal with the situation of \(c_3=c_4\) (if \(c_3\neq c_4\), then by Lemma 6 \(g\) can be extended to a 5-SAVTC of \(G\)). Since \(d_{G}(v’)\geq 2\), there exists a color \(\alpha \in C_{f’}(v’)\) such that \(\alpha \notin \{c_1,c_3\}\). We color \(uv\) with \(c_3\), \(w\) with \(c_1\), \(vw\) with a color \(\beta \in [1,5]\setminus \{c_1,c_2,c_3,\alpha\}\), \(v\) with a color \(\gamma \in [1,5]\setminus \{c_1,c_3,\alpha, \beta\}\), \(uw\) with a color \(\alpha’\in [1,5]\setminus \{c_1,c_3,c_2,\beta\}\), and color \(u\) with \(\alpha\) (when \(\alpha’\neq \alpha\)) or with \(\beta\) (when \(\alpha’=\alpha\)). It is clear from the resulting coloring, say \(f\), that \(c_3\notin C_f(w)\), \(\alpha\notin C_f(v)\) and \(\{\alpha, c_3\}\subset C_f(u)\). Therefore, \(f\) is a 5-SAVTC of \(G\). This completes the proof.

3.2. Claw-free subcubic graphs

A graph is called claw-free if it contains no induced subgraph isomorphic to the complete bipartite graph \(K_{1,3}\). %Therefore, in a a cubic graph, every vertex belongs to a triangle. In this section, We will show that every claw-free subcubic graph has a 5-SAVTC. To see this, we first investigate an interesting class of claw-free subcubic graphs as follows.

We use \(\mathcal{D}\) to denote the family of graphs, in which every one is obtained from a cubic graph such that every vertex is incident with exactly one triangle by subdividing all edges not incident with triangles, where to subdivide an edge \(e\) is to delete \(e\) and add a new vertex \(v\), and join \(v\) to the ends of \(e\). By this definition, we see that for every graph \(G\in \mathcal{D}\), \(\delta(G)=2\), 2-vertices are independent and not incident with any triangle, and the subgraph induced by 3-vertices are the union of vertex-disjoint triangles. We prove that every such graph has a 5-SAVTC.

Theorem 8. For any \(G\in \mathcal{D}\), \(\chi_{sat}(G)=5\).

Proof. \(\chi_{sat}(G)\geq 5\) is obvious. We will give a construction of a 5-SAVTC of \(G\) by applying the famous Hall’s theorem on bipartite graphs. Let \(V_2\) and \(V_3\) be the set of 2-vertices and 3-vertices of \(G\), respectively. Then, \(V_2\) is an independent set, and the subgraph induced by \(V_3\) is the union of vertex-disjoint triangles, say \(T_1, T_2, \ldots, T_m\). %Clearly, \(|V_2|\)=\(\frac{3}{2}m\). Now, we construct a bipartite graph \(G’\) with bipartition \((X,Y)\), where \(X=V_2, Y=\{T_1,T_2,\ldots, T_m\}\), and \(xT\in E(G’)\) for \(x\in X\), \(T\in Y\), if and only if \(x\) is adjacent to a vertices incident with \(T\) in \(G\). By the definition, we see that \(d_{G’}(x)=2\) for every \(x\in X\) and \(d_{G’}(T)=3\) for every \(T\in Y\). Therefore, by the Hall’s theorem, \(G’\) has a matching \(M_1\) which covers every vertex in \(Y\). Consider \(G’-M_1\); we have that \(d_{G’-M_1}(x)\leq 2\) for every \(x\in X\) and \(d_{G’-M_1}(T)=2\) for every \(T\in Y\). Again by the Hall’s theorem, \(G’-M_1\) has a matching \(M_2\) which covers every vertex in \(Y\).

We assert that \(G’-M_1\) contains such a \(M_2\) that covers every 2-vertex in \(X\). If not, select \(M_2\) to be the one that covers the most number of 2-vertices in \(X\). Let \(x\) be a 2-vertex in \(X\) not covered by \(M_2\). Then, there is an \(M_2\)-alternating path \(P\) starting with \(x\) and end with a 1-vertex in \(X\), and \(M_2\vartriangle E(P)\) (the symmetric difference of \(M_2\) and \(E(P)\)) is also a matching of \(G’-M_1\) which covers every vertex in \(Y\) and covers more number of 2-vertices than \(M_2\), a contradiction.

Let \(M_1\) and \(M_2\) be the two matchings selected as above. Then, in \(G’-(M_1\cup M_2)\), \(x\in X\) is a \(1^-\)-vertex and \(T\in Y\) is a \(1\)-vertex. Now, we present an algorithm to construct a 5-SAVTC \(f\) of \(G\) as follows:

• 1: For each \(T_i\), \(i\in [1,m]\), we use [1,3] to color its vertices and edges, for which the coloring conditions (1), (2) and (3) are satisfied. That is, let \(V(T_i)=\{u_i,v_i,w_i\}\), we color \(u_i,v_i,w_i\) with 1,2,3 respectively, and color \(u_iv_i, v_iw_i, w_iu_i\) with 3,1,2 respectively.
• 2: Color each edge in \(M_1\) with 4 and in \(M_2\) with 5.
• 3: Observe that each \(v\in V_2\) is an \(1^-\)-vertex in \(G-(M_1\cup M_2)\). For each edge \(xy\in E(G)\setminus (M_1\cup M_2)\) such that \(x\in V_2\) and \(y\in V_3\), let \(xy’\) be another edge incident with \(x\) in \(G\) and assume \(xy’\) is colored by \(\alpha\). Clearly, \(\alpha\in [4,5]\) since \(xy’\in M_1\cup M_2\). Suppose that \(y\) and \(y’\) are colored with \(\beta\) and \(\beta’\) respectively, \(\beta,\beta’\in [1,3]\). If \(\beta\neq \beta’\), we recolor \(y\) with \(\alpha\), and color \(xy\) with \([4,5]\setminus \{\alpha\}\) and color \(x\) with \(\beta\); if \(\beta=\beta’\), then we recolor the vertices and edges of the triangle \(T\in Y\) incident with \(y\) such that \(\beta\) is not assigned to \(y\) (observe that each triangle \(T_i\) has only one vertex incident with uncolored edges in this step. Therefore, each such triangle \(T\) is recolored at most once. This implies that the recoloring approach does not destroy the coloring before this action). Thus, we can likewise recolor \(y\) with \(\alpha\), and color \(xy\) with \([4,5]\setminus \{\alpha\}\) and \(x\) with the color appearing at \(y\).
• 4: After the above three steps, only some 2-vertices are not colored (if possible). Let \(x\) be a such uncolored 2-vertex. Suppose that \(N_G(x)=\{x_1,x_2\}\), and let \(\alpha_1\) and \(\alpha_2\) be the colors appearing at \(x_1\) and \(x_2\). We then use the color \([1,3]\setminus \{\alpha_1,\alpha_2\}\) to color \(x\).

According to the above coloring, we see that for each triangle \(T_i\), \(i\in [1,m]\), \(\{\overline{C}_f(u_i)\), \(\overline{C}_f(v_i)\), \(\overline{C}_f(w_i)\}\) = \(\{4,5, \beta\}\) where \(\beta\in [1,3]\); for each 2-vertex \(x\), \(C_f(x)=\{4,5,\beta\}\) and \(\{\overline{C}_f(x_1),\overline{C}_f(x_2)\}\) \(\subset\) \(\{\{4, \beta\}, \{5, \beta\}, \{4, 5\}\}\) where \(\{x_1,x_2\}=N_G(x)\). Therefore, \(f\) is a 5-SAVTC of \(G\).

Theorem 9. Let \(G\) be a claw-free subcubic graph. Then, \(\chi_{sat}(G)=5\).

Proof. Suppose to the contrary that \(G\) is a counterexample to Theorem 9 such that \(E(G)\) is the minimum. It is sufficient to prove that \(G\) has a 5-SAVTC. With a similar proof as that in Theorem 7, we have the following claims.
Claim A. \(G\) is 2-connected, and \(G\) contains no adjacent 2-vertices and triangles incident with a 2-vertex. To round off the proof, we have to deal with some reducible configurations.
Claim B. \(G\) does not contains configurations \(\mathcal{H}_1, \mathcal{H}_2, \mathcal{H}_3\), as shown in Figure 2 (a), (d) and (g).

Proof of the claim B. We will show that each of these configurations is reducible, i.e. \(G\) has a 5-SAVTC if \(G\) contains one of them. Observe that \(K_4\) has a 5-SAVTC. Therefore, we assume that \(G\neq K_4\) in what follows.

Case 1. For \(\mathcal{H}_1\), since \(G\neq K_4\) and \(G\) is claw-free, we, by Claim A, may assume that \(x\neq u_4\), \(y\neq u_1\), \(x\neq y\) and \(xy\neq E(G)\) (if \(x=y\) or \(xy\in E(G)\), then \(G\) is isomorphic to the graph shown in Figure 2 (b) or (c), which has a 5-SAVTC)). Let \(G’=(G-\{u_i|i\in [1,4]\})\cup \{xy\}\). Then, \(G’\) is claw-free and subcubic.

By the minimality, \(G’\) admits a 5-SAVTC, say \(g\). Without loss of generality, assume \(g(x)=1, g(y)=2\) and \(g(xy)=3\). We can extend \(g\) to a 5-SAVTC of \(G\) by coloring elements in \(T(G)\setminus T(G’)\) as follows: assign color \(3\) to \(xu_1\), \(u_2u_3\) and \(yu_4\), color \(4\) to \(u_1\) and \(u_2u_4\), color \(5\) to \(u_4\) and \(u_1u_3\), color \(2\) to \(u_3\) and \(u_1u_2\), and color \(1\) to \(u_2\) and \(u_3u_4\).

Case 2. As for \(\mathcal{H}_2\), if \(u_1u_6\in E(G)\), \(x=y\) or \(xy\in E(G)\), then by Claim A \(G\) is isomorphic to the graph shown in Figure 2 \((e)\), \((f)\) or \((g)\), which has a 5-SAVTC. Let \(G’=(G-\{u_i|i\in [1,6]\})\cup \{xy\}\). Then, \(G’\) is claw-free and subcubic. By the minimality \(G’\) has a 5-SAVTC \(g\). We, without loss of generality, assume that \(g(x)=1, g(y)=2\) and \(g(xy)=3\). Now, based on the restriction of \(g\) to \(T(G)\cap T(G’)\), we construct \(f\) by letting \(f(xu_1)=f(yu_6)=f(u_2u_3)=f(u_4u_5)=3\), \(f(u_1)=f(u_4)=f(u_3u_5)=2\), \(f(u_3)=f(u_6)=f(u_2u_4)=1\), \(f(u_1u_2)=f(u_5u_6)=4\) and \(f(u_2)=f(u_5)=f(u_1u_3)=f(u_4u_6)=5\). Then, \(C_f(x)=C_g(x)\), \(C_f(y)=C_g(y)\), \(\overline{C}_f(u_1)=\overline{C}_f(u_5)=\{1\}\), \(\overline{C}_f(u_2)=\overline{C}_f(u_6)=\{2\}\), \(\overline{C}_f(u_3)=\overline{C}_f(u_4)=\{4\}\). Hence \(f\) is a 5-SAVTC of \(G\).

Case 3. Consider \(\mathcal{H}_3\). By Claim A, Case 1 and Case 2, we suppose that \(x_1\neq x_2\), \(y_1\neq y_2\), \(x_i\notin \{u_4,u_5\}\), \(y_i\) \(\notin\) \(\{u_2,u_3\}\), \(x_1x_2\notin E(G)\) and \(y_1y_2\notin E(G)\). Let \(G’=(G-\{u_i|i\in [1,6]\})\cup \{x_1x_2,y_1y_2\}\). Obviously, \(G’\) is claw-free subcubic graphs with \(|E(G’)|< |E(G)|\). By the choice of \(G\), \(G'\) has a 5-SAVTC \(g\). Without loss of generality, we assume that \(g(x_1)=1, g(x_2)=2, g(x_1x_2)=3, g(y_1)=c_1, g(y_2)=c_2\), and \(g(y_1y_2)=c_3\), where \(c_i\in [1,5]\) for \(i=1,2,3\) and \(c_i\neq c_j\) for \(1\leq i< j\leq 3\). We now construct a 5-SAVTC \(f\) of \(G\) based on the restriction of \(g\) to \(T(G)\cap T(G')\). We first assign color \(c_3\) to \(y_1u_4\) and \(y_2u_5\), and color \(3\) to \(x_1u_2\) and \(x_2u_3\). Clearly, \(C_f(t)=C_{g}(t)\) for any \(t\in \{x_1,x_2,y_1,y_2\}\).

Case 3.1. \(\{c_1,c_2\}\cap \{1,2\}\neq \emptyset\). Then by symmetry we assume that \(c_1=1\). Let \([1,5]=\{c_1,c_2,c_3,c_4,c_5\}\), and set \(f(u_4)=f(u_5u_6)=c_5\), \(f(u_5)=f(u_6u_1)=c_1\), \(f(u_4u_5)=c_4\), \(f(u_4u_6)=c_2\), \(f(u_6)=c_3\), \(f(u_2)=f(u_3u_1)=5\), \(f(u_2u_3)=4\), \(f(u_2u_1)=2\), \(f(u_3)=1\), and finally color \(u_1\) with a color in \(\{3,4\}\setminus \{c_3\}\) when \(c_4\in \{2,5\}\) or with the color \(c_4\) when \(c_4\in \{3,4\}\). According to the definition of \(f\), we have that \(\overline{C}_f(u_2)=\{1\}, \overline{C}_f(u_3)=\{2\}, \overline{C}_f(u_4)=\{c_1\}\), \(\overline{C}_f(u_5)=\{c_2\}\), \(\overline{C}_f(u_6)=\{c_4\}\), \(\{1,2,c_4\}\subset C_f(u_1)\). Thus we obtain a 5-SAVTC of \(G\).

Case 3.2. \(\{c_1,c_2\}\cap \{1,2\}=\emptyset\). When \(c_3\notin \{1,2\}\), or \(c_3\in \{1,2\}\) and \((\{1,2\}\setminus \{c_3\})\in C_f(y_i)\) for some \(i\in \{1,2\}\), we by symmetry assume that \(c_3=1\) when \(c_3\in \{1,2\}\), and suppose that \(2\in C_f(y_1)\) (observe that if \(c_3\notin \{1,2\}\), then since \(d_G(y_i)\geq 2\) for \(i=1,2\), there exists a color, say 2 here, in \(\{1,2\}\cap C_f(y_i)\) for some \(i\in \{1,2\}\)). Let \(\{\alpha\}=\{1,5\}\setminus \{c_1,c_2,c_3,2\}\), and set \(f(u_4)=f(u_5u_6)=\alpha\), \(f(u_5)=f(u_6u_1)=2\), \(f(u_4u_5)=c_1\), \(f(u_4u_6)=c_2\), \(f(u_6)=c_1\), \(f(u_3)=f(u_1u_2)=5\), \(f(u_2u_3)=4\), \(f(u_3u_1)=1\), \(f(u_2)=2\) and color \(u_1\) with \(c_3\) (when \(c_3\notin \{1,5\}\)) or a color in \(\{3,4\}\setminus \{c_1\}\) (when \(c_3\in \{1,5\}\)). Under such coloring \(f\), it follows that \(\overline{C}_f(u_2)=\{1\}, \overline{C}_f(u_3)=\{2\}\), \(\overline{C}_f(u_4)=\{2\}\), \(\overline{C}_f(u_5)=\{c_2\}\), \(\overline{C}_f(u_6)=\{c_3\}\) and \(\{1,2,c_3\}\subset \overline{C}_f(u_1)\), and hence \(f\) is a 5-SAVTC of \(G\).

When \(c_3\in \{1,2\}\) and \((\{1,2\}\setminus \{c_3\})\notin C_f(y_i)\) for \(i=1,2\), it has that \(d_G(y_1)=d_G(y_2)=2\) (otherwise \(C_g(y_1)\subseteq C_g(y_2)\) or \(C_g(y_2)\subseteq C_g(y_1)\)).

Suppose that \(c_3=1\) and let \(N_G(y_1)=\{u_4,y’\}\). Then, \(d_G(y’)=3\) and \(y’\) is incident with a triangle. If \(g(y’)\neq 1\), we recolor \(y_1\) with 1 and color \(u_4y_1\) with \(c_1\). Let \(\{\alpha\}=\{1,5\}\setminus \{c_1,c_2,1,2\}\), and set \(f(u_4)=f(u_5u_6)=2\), \(f(u_5)=c_1\), \(f(u_4u_5)=f(u_6)=\alpha\), \(f(u_4u_6)=c_2\), \(f(u_2)=f(u_3u_1)=5\), \(f(u_2u_3)=4\), \(f(u_2u_1)=2\), \(f(u_3)=f(u_1u_6)=1\), and finally color \(u_1\) with \(c_1\) (when \(c_1\neq 5\)) or a color in \(\{3,4\}\setminus \{\alpha\}\) (when \(c_1=5\)). Since \(\overline{C}_f(u_2)=\{1\}, \overline{C}_f(u_3)=\{2\}\), \(\overline{C}_f(u_4)=\{1\}\), \(\overline{C}_f(u_5)=\{c_2\}\), \(\overline{C}_f(u_6)=\{c_1\}\) and \(\{1,2,c_1\}\subset \overline{C}_f(u_1)\), \(f\) is a 5-SAVTC of \(G\).

If \(g(y’)=1\), then \(c_1\notin C_f(y’)\). We recolor \(y_1\) with the color \(\beta\in ([1,5]\setminus \{1,c_2, c_1, g(y_1y’)\})\), and color \(u_4y_1\) with \(c_1\). Clearly, \(2\in \{\beta,g(y_1y’)\}\). Let \(\{\alpha’\}=\{\beta, g(y_1y’)\}\setminus \{2\}\), and set \(f(u_4)=1\), \(f(u_5u_6)=c_1\), \(f(u_5)=2\), \(f(u_4u_5)=f(u_6)=\alpha’\), \(f(u_4u_6)=c_2\), \(f(u_3)=f(u_2u_1)=5\), \(f(u_2u_3)=4\), \(f(u_3u_1)=1\), \(f(u_2)=f(u_1u_6)=2\), and color \(u_1\) with a color in \(\{3,4\}\setminus \{\alpha’\}\). It is easy to see that \(\overline{C}_f(u_2)=\{1\}, \overline{C}_f(u_3)=\{2\}\), \(\overline{C}_f(u_4)=\{2\}\), \(\overline{C}_f(u_5)=\{c_2\}\), \(\overline{C}_f(u_6)=\{1\}\) and \(\{1,2\}\subset \overline{C}_f(u_1)\). Therefore, \(f\) is a 5-SAVTC of \(G\).

By Claims A and B, we see that \(G\) is a 2-connected claw-free subcubic graph which does not contain adjacent 2-vertices, triangles incident with 2-vertices, two triangles sharing a common edge or connecting by an edge (i.e. an edge whose ends incident with two distinct triangles). This indicates that \(G\in \mathcal{D}\), and by Theorem 8 \(G\) has a 5-SAVTC. This completes the proof of the theorem.

4. Remarks

For two graphs \(G\) and \(H\), let \(\sigma: V(G)\rightarrow V(H)\) be a surjection. If for every \(v\in V(G)\), the restriction of \(\sigma\) to the open neighbourhood of \(v\) in \(G\) is a bijection onto the open neighbourhood of \(\sigma(v)\) in \(H\), i.e. \(\sigma(N_G(v))=N_H(\sigma(v))\), then we call \(\sigma\) a covering map from \(G\) to \(H\). If there exists a covering map from \(G\) to \(H\), then \(G\) is called a covering graph of \(H\). As for covering graphs, we have the following conclusion on SAVTC.

Theorem 10. Let \(H\) be a graph containing a \(k\)-SAVTC \(g\). Then, every covering graph \(G\) of \(H\) has a \(k\)-SAVTC.

Proof. Let \(\sigma\) be a covering map from \(G\) to \(H\). We now use \(\sigma\) to lift a proper total \(k\)-coloring, denoted by \(f\), of \(G\), i.e. let \(f(v)=g(\sigma(v))\) for every \(v\in V(G)\) and \(f(uw)=g(\sigma(u)\sigma(w))\) for every \(uw\in E(G)\). According to the definition of covering map, if \(uw\in E(G)\) then \(\sigma(u)\sigma(w)\in E(H)\). We have \(f(u)(=g(\sigma(u)))\neq f(w)(=g(\sigma(w)))\) for every \(uw\in E(G)\), \(f(vu)(=g(\sigma(v)\sigma(u)))\neq f(vw)(=g(\sigma(v)\sigma(w)))\) for any \(vu,vw\in E(G)\), and \(f(v)(=g(\sigma(v))) \neq f(vu)(=g(\sigma(v)\sigma(u)))\) for any \(v\in V(G)\) and \(vu\in E(G)\). This shows that \(f\) is a proper total \(k\)-coloring of \(G\). Moreover, it is easy to see that \(C_f(v)=C_g(\sigma(v))\) for every \(v\in V(G)\). Therefore, \(f\) is a \(k\)-SAVTC of \(G\).

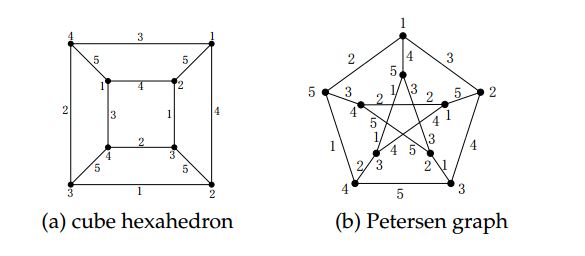
In this paper, we discuss an interesting graph parameter \(\chi_{sat}\), called the smarandachely adjacent vertex total chromatic number. We derive upper bound for subcubic graphs \(G\), i.e. \(\chi_{sat}(G)\leq 6\). We show, in particular, that if \(G\) is an outerplane graph with maximum degree 3 or a claw-free subcubic graph, then \(\chi_{sat}(G)=5\). There are also other classes of subcubic graphs with a 5-SAVTC, e.g., the subcubic bipartite graphs. Indeed, for any bipartite \(G\) with bipartition \((X,Y)\), we can easily give a \((\Delta(G)+2)\)-SAVTC by assigning color 1 to vertices in \(X\), color 2 to vertices in \(Y\), and coloring \(E(G)\) by \([3, \Delta(G)+2]\) (since the edge chromatic number of bipartite graphs is the maximum degree). Additionally, by Theorem 10, we can also address a series of subcubic graphs with a 5-SAVTC, which are non-outplanar and contain a claw, for example, the covering graphs of cube hexahedron or Petersen graph; see Figure 3.

In consideration of our conclusions, we propose the following problem:

Problem 11. Let \(G\) be a subcubic graph. Is it true that \(\chi_{sat}(G)\leq 5\)?

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Competing Interests

The author(s) do not have any competing interests in the manuscript.