In this study, we discussed the existence of golden ratio in Brihadeeshwarar temple, Tanjavur, Tamil Nadu, India, built in 1010 AD. It is listed on the UNESCO’s world heritage site of the Chola temples in southern India. This temple represents an outstanding creative achievement in the architectural idea of the pure form of the Dravida temples. Golden ratio has great influence in architecture, mathematics and art. We analyzed existence of the Golden ratio in structural design of Tanjavur Brihadeeshwarar temple prakaram. We used the Phi Grid and Phi Spiral software to measure the golden ratio and verified our result.
The Golden ratio, mathematics and aesthetics are intricately associated between each other. The Golden ratio is an irrational number that is approximately equal to 1.618, which is represented by the Greek symbol known as phi (\(\phi\)). This ratio is considered as the human optical sense and not limited to aesthetic beauty but also found its existence in natural world through the body proportions of living beings, the growth patterns of many plants, insects and also in the model of enigmatic universe. The properties of Golden section can be instituted in the pattern of mathematical series and geometrical patterns. Because of its unique and mystifying properties, many researchers and mathematicians have studied the Golden ratio. Akhtaruzzaman and Shafie [1] discussed the geometrical substantiation of \(\phi\), the Golden ratio and the Baroque of nature, architecture, design and engineering. Golden ratio is key to the secret of beauty Saraf et al., [2]. Thapa et al., [3] studied the relation of Golden ratio, mathematics and aesthetics. Craciunet et al., [4] analyzed the generalized Golden ratio as a fixed point of an operator defined by an arbitrary mean satisfying certain conditions. Iosa et al., [5] discussed Phi in physiology, psychology and biomechanics: The golden ratio between myth and science. Sen and Agarwal [6] investigated Golden ratio in science, as random sequence source. Proportions in architecture are discussed by Singh [7]. Fett [8] studied an in-depth investigation of the Divine ratio. Recently, many authors discussed golden ratio, see [9,10,11,12]
.Keeping this in mind, in present work we investigated existence of the Golden ratio in structural design of Tanjavur Brihadeeshwarar temple prakaram. We used the Phi Grid and Phi Spiral software to measure the golden ratio.
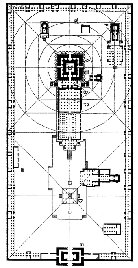
The Brihadeeshwarar temple is a Hindu temple dedicated to god Shiva located in Tanjavur. This temple plan and improvement make practical and effective use of the axial and symmetrical geometry rules. The temple wall consists of an entrance with a double row of pillars. The perimeter wall forms a rectangular monastery which could be divided into \(2\) squares. The centre of the first square contains the Nandhi pavilion and second contains the god Shiva statue. In this temple main tower (Gopuram) height is 60m. The tower of the main gateways is 30 m high. In this space there are five main sections: the sanctum with the towering superstructure (srivimana), the Nandhi pavilion in front (Nandi-mandapam) and in between these the main community hall (mukhamandapam), the great gathering hall (mahamandapam) and the pavilion that connects the great hall with the sanctum (ardhamandapam) (Geva and Mukherji [13] and Croker [14]). The Figure 1 points out the ideal places are represented by numerically. In Figure 1, A is the sanctuary, B is the Artha mandapam, C is the mahamandapam, D is the Nandi-mandapam, E is the Gopuram and F is the Shrine of subrahmanya.
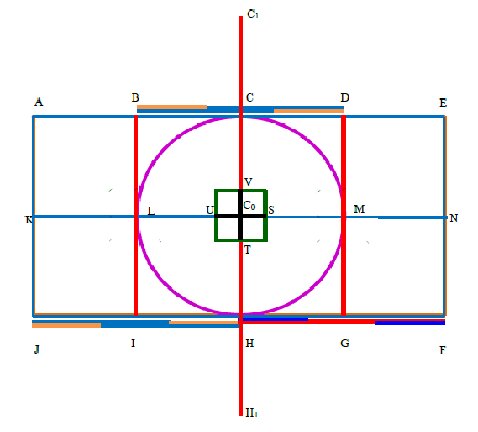
Draw a circle with radius is equal to distance between middle of karpagraham (or middle of Nandhi pavilion) to middle of the temple \([C_0L]\) (see Figure 2). Horizontally draw the straight line \(KN\) passing through center of the circle \(C_0\), which contains four equal line segments each segment equal to radius which pass along entrance of the temple \([N]\rightarrow\) middle of Nandhi pavilion \([M]\rightarrow\) middle of the temple \([C_0]\rightarrow\) middle of karpagraham \([L]\rightarrow\) back end of temple \([K]\).
\begin{equation*} NM=MC_0=C_0L=LK. \end{equation*}To measure the golden section for the line segment \(LM\) in \(LN\) and mark that point as \(U\) which divides the line \(LM\) into \(LU\) and \(UM\).
\begin{equation*} \frac{LM}{UM}=\frac{UM}{LU}=\phi. \end{equation*}Similarly, to measure the golden section for the line segment \(LM\) in \(KM\) and mark a point \(S\) which divides the line \(LM\) into \(LS\) and \(SM\), so that we get
\begin{equation*} \frac{LM}{LS}=\frac{LS}{SM}=\phi. \end{equation*}Repeat this process in vertical line segment \(CH\), we get the point \(T\) which divides the line \(CH\) into \(HT\) and \(CT\), we get \begin{equation*} \frac{CH}{CT}=\frac{CT}{HT}=\phi, \end{equation*} and point \(V\) which divides the line \(CH\) into \(HV\) and \(VC\). Hence we get \begin{equation*} \frac{CH}{HV}=\frac{HV}{VC}=\phi. \end{equation*}
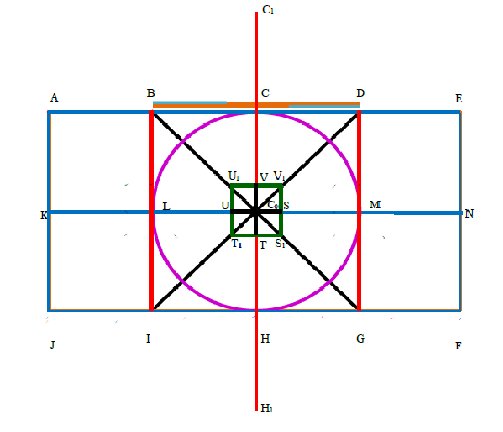
Now, we get four points \(S,T,U\) and \(V\) from that construction. Using that points draw square \(S_1T_1U_1V_1\) where \(S,T,U,V\) are midpoints of sides of that square. The square \(S_1T_1U_1V_1\) identify the golden section of \(BDGI\) (see Figure 3).
In that figure we consider the portion between middle of karpagraham to middle of nandhi pavilion and evaluate the Golden ratio between them from middle of temple prakaram.
From line segment \(LM\): \begin{equation*} \frac{LM}{UM}=\frac{LM}{LS}=\frac{LS}{SM}=\frac{LS}{UL}=\frac{UM}{UL}=\frac{UM}{SM}=\frac{LU}{US}=\frac{SM}{US}=\phi. \end{equation*}
From line segment \(CH\): \begin{equation*} \frac{CH}{HV}=\frac{CH}{CT}=\frac{CT}{CV}=\frac{CT}{TH}=\frac{CV}{VT}=\frac{HV}{CV}=\frac{HV}{TH}=\frac{HT}{TV}=\phi. \end{equation*}
From line segment \(BG\): \begin{equation*} \frac{BG}{BS_1}=\frac{BG}{GU_1}=\frac{BS_1}{GS_1}=\frac{BS_1}{BU_1}=\frac{GU_1}{GS_1}=\frac{GU_1}{BU_1}=\frac{BU_1}{U_1S_1}=\frac{GS_1}{U_1S_1}=\phi. \end{equation*}
From line segment \(ID\): \begin{equation*} \frac{DI}{DT_1}=\frac{DI}{IV_1}=\frac{DT_1 }{ IT_1}=\frac{DT_1}{DV_1 }=\frac{ IV_1}{ IT_1}=\frac{IV_1 }{DV_1}=\frac{DV_1 }{V_1T_1}=\frac{ IT_1}{V_1T_1}=\phi. \end{equation*}
Similarly repeat the same procedure for other two portion.
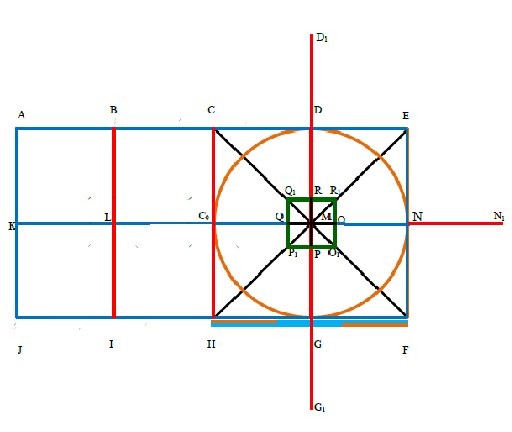
In Figure 4, we consider the portion between entrance of the temple to middle of the temple and evaluate the Golden ratio between them from nandhi pavilion.
From line segment \(C_0N \): \begin{equation*} \frac{C_0N}{QN}=\frac{ C_0N}{C_0O}=\frac{C_0O}{ON}=\frac{ C_0O}{ QC_0}=\frac{QN }{ QC_0}=\frac{QN}{ON}=\frac{C_0Q}{QO}=\frac{ON}{QO }=\phi. \end{equation*}
From line segment \(DG \): \begin{equation*} \frac{DG}{GR}=\frac{DG}{DP}=\frac{DP}{DR}=\frac{DP}{PG}=\frac{DR}{RP}=\frac{GR}{DR}=\frac{GR}{PG}=\frac{GP}{PR}=\phi. \end{equation*}
From line segment \(CF\): \begin{equation*} \frac{CF}{CO_1}=\frac{CF}{FQ_1}=\frac{CO_1}{FQ_1}=\frac{CO_1}{CQ_1}=\frac{FQ_1}{FO_1}=\frac{FQ_1}{CQ_1}=\frac{CQ_1}{Q_1O_1}= \frac{FO_1}{Q_1O_1}=\phi. \end{equation*}
From line segment \(HE\): \begin{equation*} \frac{EH}{EP_1}=\frac{EH}{HR_1}=\frac{EP_1}{HP_1}=\frac{EP_1}{ER_1}=\frac{HR_1}{HP_1}=\frac{HR_1}{ER_1}=\frac{ER_1}{R_1P_1}=\frac{HP_1}{R_1P_1}=\phi. \end{equation*}
From Figure 5, we consider the portion between back end of the temple to middle of the temple and evaluate the golden ratio between them from karpagraham.
From line segment \(KC_0\): \begin{equation*} \frac{KC_0}{YC_0}=\frac{KC_0}{KW}=\frac{KW}{WC_0}=\frac{KW}{YK}=\frac{YC_0}{YK}=\frac{YC_0}{WC_0}=\frac{KY}{YW}=\frac{WC_0}{YW}=\phi. \end{equation*}
From line segment \(BI\): \begin{equation*} \frac{IB}{BX}=\frac{IB}{IZ}=\frac{BX}{BZ}=\frac{BX}{IX}=\frac{IZ}{BZ}=\frac{IZ}{XI}=\frac{BZ}{XZ}=\frac{IX}{XZ}=\phi. \end{equation*}
From line segment \(AH\): \begin{equation*} \frac{AH}{AW_1}=\frac{AH}{HY_1}=\frac{AW_1}{HW_1}=\frac{AW_1}{AY_1}=\frac{HY_1}{HW_1}=\frac{HY_1}{AY_1}=\frac{AY_1}{Y_1W_1}=\frac{HW_1}{Y_1W_1}=\phi. \end{equation*}
From line segment \(CJ\): \begin{equation*} \frac{CJ}{CX_1}=\frac{CJ}{JZ_1}=\frac{CX_1}{JX_1}=\frac{CX_1}{CZ_1}=\frac{JZ_1}{JX_1}=\frac{JZ_1}{CZ_1}=\frac{CZ_1}{Z_1X_1}=\frac{JX_1}{Z_1X_1}=\phi. \end{equation*}

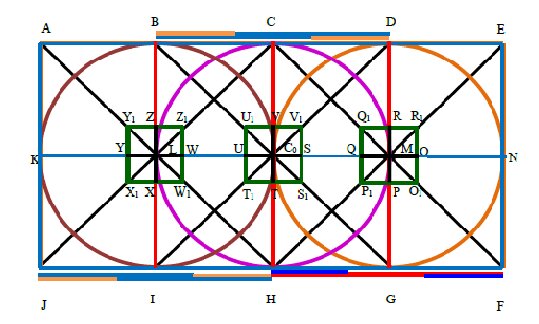


From Figures 6 and 7, we measure the ratio between the sides of each outer region (i.e. [EFHC], [BDGI] and [ACHJ]) of temple Prakaram to outer region of Karpagraham, Nadhi pavilion and middle of temple respectively.
Let the portion between entrance of the temple to middle of the temple.ie.[EFHC](see Figures 6 and 7), if we take \( CE=EF=FH=HC=\phi\) (say) then \(R_1Q_1=Q_1P_1=P_1O_1=O_1R_1=\frac{1}{\phi^2}\). Hence we get the ratio
\begin{equation*} \frac{CE=EF=FH=HC}{R_1Q_1=Q_1P_1=P_1O_1=O_1R_1}=\phi^3. \end{equation*}Same way in middle of Nandhi pavilion to middle of karpagraham, i.e., [BDGI] (see Figures 6 and 7), we get \begin{equation*} \frac{DB=BI=IG=GD}{S_1T_1=T_1U_1=U_1V_1=V_1S_1}=\phi^3. \end{equation*}
And middle of temple to back end of temple, i.e., [ACHJ] (see Figures 6 and 7), we get \begin{equation*} \frac{AC=CH=HJ=JA}{W_1X_1=X_1Y_1=Y_1Z_1=Z_1W_1}=\phi^3. \end{equation*}
Software are used to reduce the complexity of calculation and measurements. We used some available software to ensure our results. The following two software’s are used to measure the Golden ratio and we get the following outputs.
We concluded that this temple is one of mysterious gift of our ancient people which exposed architect, spirituality, tradition and science. An ancient Tamil architecture had more knowledge about the Golden ratio and they used to determine pleasing dimensional relationships between the length and width of Karpagragam, Nandhi pavilion and entire courtyard, so that Karpagragam (main place god statue) and Nandhi pavilion situated in inner courtyard of Brihadeeshwarar temple be acting on the major role to bring the Golden ratio for the entire courtyard. From this study, felt that one of the secret of beauty of the Brihadeeshwarar temple is Golden proportion influenced its plan of designs and constructions.