ISSN: 2523-0212 (Online) 2616-4906 (Print)

DOI: https://www.doi.org/10.30538/oms2020.0093

Research article

On 3-total edge product cordial labeling of tadpole, book and flower graphs

Author(s): ^¹, ^¹, ^¹

¹School of Mathematical Sciences, Anhui University, Hefei, Anhui, 230601, P.R. China.

Copyright © Umar Ali, Yasir Ahmad, Muhammad Shoaib Sardar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: 29/07/2019
Accepted: 13/02/2020
Published: 07/03/2020

Abstract

In this paper, we will determine the 3-total edge product cordial (3-TEPC) labeling. We study certain classes of graphs namely tadpole, book and flower graphs in the context of 3-TEPC labeling.

Keywords: 3-total edge product cordial labeling, book graphs, flower graphs.

1. Introduction

We define with simple, finite and undirected graph \(G=(E_G,V_G)\), where \(E_G\) and \(V_G\) is vertex set and edge set respectively. Cordinalities of there sets are called the size and order of \(G\). We follow the standard notations and terminology of graph theory as in[1] . A graph labeling is an assignment to vertices or edges or both subject to certain conditions. If the domain is \(V_G\cup E_G\) then we called the labeling is total labeling.

We have the following notations, in order to know cordial labeling \(h\) and its sorts.

\(v_h(j)\) is the number of vertices labeled by \(j\);
\(e_h(j)\) is the number of edges labeled by \(j\);
\(v_h(i, j)\) = \(v_h(i) – v_h(j)\);
\(e_h(i, j)\) = \(e_h(i) – e_h(j)\) and
the sum of all vertices and edges labeled by \(j\) is \(sum(j)\) i.e. \(sum(j)\) = \(v_h(j) + e_h(j)\)

Cahit [2] gave first concept of cordial labeling as a weaker version of graceful labeling. A vertex labeling \(h: V_G\rightarrow\{0, 1 \}\) that induce an edge labeling \(h^*: E_G\rightarrow\{0, 1\}\) defined by \(h^*(u v)=|h(u)-h(v)|,\) for all \(u,v\epsilon E_G\) if \(|v_{h}(1)- v_{h}(0)|\leq 1\) and \(|e_{h}(1)- e_{h}(0)|\leq 1\). The concept of product cordial labeling was introduced by Sundaram et al. in \(2014\). For details see [3]. In \(2006\) and \(2012\), Sundaram et al. develop the concept of total product cordial labeling and \(k\)-total product cordial labeling. For details see [4,5]. Vaidya and Barasara gave the concept of edge product cordial labeling and total edge product cordial labeling. For details see [6,7] Let \(k\) be an integer, \( 2\leq k\leq|E_G|\) an edge labeling \(h:E_G \longrightarrow\{0,1,\ldots,k-1\}\), with induced vertex labeling \(h^*:V_G \longrightarrow\{0,1,\ldots,k-1\}\) such that \(h^*(u)=h(e_1)h(e_2) \ldots h(e_n)\)(mod \(k\)), where edges \(e_1,e_2,\ldots,e_n \) are the edge incident to \(u\), then \(h\) is called \(k\)-total edge product cordial labeling if \(|sum(i)-sum(j)|\leq1\) for \(i,j\in\{0,1,\ldots,k-1\}\).

In 2015, Azaizeh et al. [8] was introduced the basic concept of k-total edge product cordial (\(k\)-TEPC) labeling. Recently Azaizeh et al. investigated the \(3\)-TEPC labeling for more families of graphs namely, path, circle, fan, double fan, triangular snake graph (see example [9,10]). Ahmad et al. [11] discussed \(3\)-TEPC labeling of gear, web and helm graph. Ali et al. [12] investigated the \(3\)-TEPC labeling for families of convex polytopes namely, double antiprism \(A_m\), \(S_m\) and \(T_m\). In 2018, Ahmad et al. [13] had discussed the \(3\)-TEPC labeling for hexagonal grid. Recently, Ali et al. [14] investigated the \(4\)-total edge product cordial labeling of some standard graphs. For more details see references [15,16,17,18].

Now we will define tadpole graph \((T_{p,q})\), book graph \((B_{q})\) and flower graph \((Fl_q)\) graph.

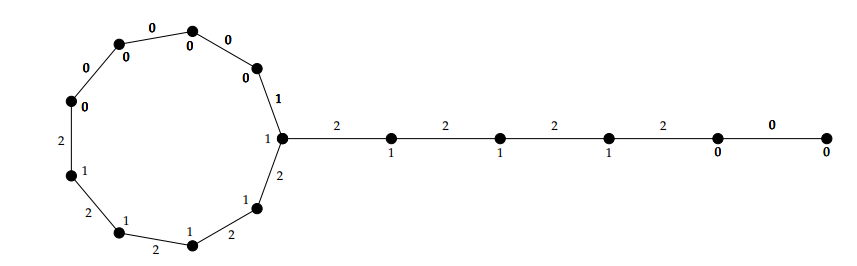
Definition 1. The tadpole graph is obtained by connecting a cycle graph \(C_p\) (of order \(p\)) to a path graph \(P_q\) (of order q) with a bridge and is denoted by \(T_{p,q}\) (see Figure 1).

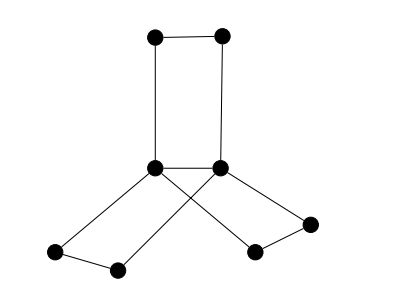
Definition 2. Book graph \(B_{q}\) is obtained by the cartesian product \(S_{q+1}\times P_2\), where \(S_{q+1}\) is the star graph of order \(q+1\) and \(P_2\) is the path graph of order \(2\) (see Figure 2).

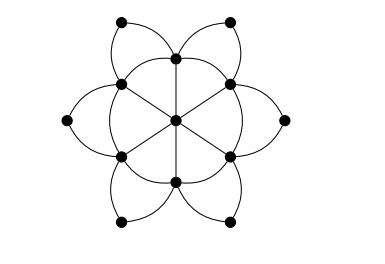
Definition 3. The flower graph \(Fl_q\) is the graph attain from a helm graph \(H_q\) of order \(q\) by joining each pendent vertex to the apex of the helm (see Figure 3).

2.Main results

In this section, we will discuss \(3\)-total edge product cordial (3-TEPC) labeling of tadpole, book and flower graphs.

Theorem 1. The tadpole graph \(T_{p,q}\) has \(3\)-TEPC labeling.

Proof. Let \(V_G= \{u_j, 1\leq j \leq p\}\cup \{v_j, 1\leq j \leq q\}\) and \( E_G= \{u_j u_{j+1}, 1\leq j\leq p-1 \}\cup \{v_j v_{j+1}, 1\leq j\leq q-1\}\cup \{u_p u_1 \}\cup \{v_q u_p\} \) as shown in Figure (1). Now we see the following three cases:

Case 1 Let \(p+q\equiv 0(\text{ mod }3)\) which implies \(p+q=3t,\) for \(t\geq 3.\) So for the given case, we need to discuss the following three subcases:

Case 1.1 If \(p=0 (\text { mod } 3)\) and \(q=0 (\text { mod } 3).\) We define \(h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \(1\leq j \leq \frac{p}{3}-1 \)};\\ 2, & \text{if \(\frac{p}{3} \leq j \leq p-1 \)}; \end{cases}\) and \(h(u_p u_1)=1.\)

\(h(v_j v_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{q}{3} \)};\\ 2, & \text{if \( \frac{q}{3}+1\leq j \leq q-1 \)}. \end{cases}\) , \(h(v_q u_p)=2\).

Case 1.2 If \(p > q\) but \(p\neq0 (\text { mod } 3)\) and \(q\neq0 (\text { mod } 3).\) We define \(h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq t-2 \)};\\ 2, & \text{if \( t-1\leq j \leq p-1 \)}; \end{cases}\) and \(h(u_p u_1)=1\).

\(h(v_j v_{j+1})=\begin{cases} 0, & \text{if \( j = 1 \)};\\ 2, & \text{if \( 2\leq j \leq q-1 \)}. \end{cases}\) , \(h(v_q u_p)=2.\)

Case 1.3 If \(p < q\) but \(p\neq0 (\text { mod } 3)\) and \(q\neq0 (\text { mod } 3).\) We define \(h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \( j = 1 \)};\\ 2, & \text{if \( 2\leq j \leq p-1 \)}; \end{cases}\) and \(h(u_p u_1)=1\).

\(h(v_j v_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq t-2 \)};\\ 2, & \text{if \( t-1\leq j \leq q-1 \)}. \end{cases}\) , \(h(v_q u_p)=2\).

So we obtain \(sum(0)=sum(1)=sum(2)=2t.\) Thus \(|sum(x_1) – sum(x_2)| \leq 1 \) for \(0 \leq x_1 < x_2 \leq 2.\) Hence \(h\) is \(3\)-TEPC labeling as discussed in Figure 4.

Figure 4. \(3\)-TEPC labeling of \(T_{6,6}\).

Case 2 Let \(p+q\equiv 1(\text{ mod }3)\) which implies \(p+q=3t+1,\) for \(t\geq 3.\) So for the given case, we need to discuss the following three subcases:

Case 2.1 If \(p=0 (\text { mod } 3)\) and \(q\neq0 (\text { mod } 3).\) We define \( h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{p}{3}-1 \)};\\ 2, & \text{if \( \frac{p}{3} \leq j \leq p-1 \)}; \end{cases}\) and \(h(u_p u_1)=1.\)

\(h(v_j v_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{q-1}{3} \)};\\ 2, & \text{if \( \frac{q-1}{3}+1\leq j \leq q-1 \)}. \end{cases}\) , \(h(v_q u_p)=2.\)

Case 2.2 If \(p\neq0 (\text { mod } 3)\) and \(q=0 (\text { mod } 3).\) We define \( h:E_G\rightarrow\{0,1,2\}\) as:

\(g(u_j u_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{p-1}{3}-1 \)};\\ 2, & \text{if \(\frac{p-1}{3} \leq j \leq p-1 \)}; \end{cases}\) and \(h(u_p u_1)=1.\)

\(h(v_j v_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{q}{3} \)};\\ 2, & \text{if \( \frac{q}{3}+1\leq j \leq q-1 \)}. \end{cases}\) , \(h(v_q u_p)=2.\)

Case 2.3 If \(p\neq0 (\text { mod } 3)\) and \(q\neq0 (\text { mod } 3).\) We define \( h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{p-2}{3} \)};\\ 2, & \text{if \(\frac{p-2}{3}+1 \leq j \leq p-1 \)}; \end{cases}\) and \(h(u_p u_1)=1.\)

\(h(v_j v_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{q-2}{3} \)};\\ 2, & \text{if \( \frac{q-2}{3}+1\leq j \leq q-1 \)}. \end{cases}\) , \(h(v_q u_p)=2.\)

So we obtain \(sum(0)=2t\), \(sum(1)=sum(2)=2t+1.\) Thus \(|sum(x_1) – sum(x_2)| \leq 1 \) for \(0 \leq x_1 < x_2 \leq 2.\) Hence \(h\) is \(3\)-TEPC labeling as discussed in Figure 5.

Figure 5. \(3\)-TEPC labeling of \(T_{8,5}\).

Case 3 Let \(p+q\equiv 2(\text{ mod }3)\) which implies \(p+q=3t+2,\) for \(t\geq 3\). So for the given case, we need to discuss the following three subcases:

Case 3.1 If \(p=0 (\text { mod } 3)\) and \(q\neq0 (\text { mod } 3).\) We define \( h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{p}{3} \)};\\ 2, & \text{if \( \frac{p}{3}+1 \leq j \leq p-1 \)}; \end{cases}\) and \(h(u_p u_1)=1.\)

\(h(v_j v_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{q-2}{3} \)};\\ 2, & \text{if \( \frac{q-2}{3}+1\leq j \leq q-1 \)}. \end{cases}\) , \(h(v_q u_p)=2. \)

Case 3.2 If \(p\neq0 (\text { mod } 3)\) and \(q=0 (\text { mod } 3).\) We define \( h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{p-2}{3} \)};\\ 2, & \text{if \( \frac{p-2}{3}+1 \leq j \leq p-1 \)}; \end{cases}\) and \(h(u_p u_1)=1.\)

\(h(v_j v_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{q}{3} \)};\\ 2, & \text{if \(\frac{q}{3}+1\leq j \leq q-1 \)}. \end{cases}\) , \(h( v_q u_p)=2. \)

Case 3.3 If \(p\neq0 (\text { mod } 3)\) and \(q\neq0 (\text { mod } 3).\) We define \( h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{p-1}{3} \)};\\ 2, & \text{if \( \frac{p-1}{3}+1 \leq j \leq p-1 \)}; \end{cases}\) and \(h(u_p u_1)=1.\)

\(h(v_j v_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq \frac{q-1}{3} \)};\\ 2, & \text{if \( \frac{q-1}{3}+1\leq j \leq q-1 \)}. \end{cases}\) , \(h(v_q u_p)=2. \)

So we obtain \(sum(0)=2t+2\), \(sum(1)=sum(2)=2t+1.\) Thus \(|sum(x_1) – sum(x_2)| \leq 1 \) for \(0 \leq x_1 < x_2 \leq 2.\) Hence \(h\) is \(3\)-TEPC labeling as discussed in Figure 6.

Figure 6. \(3\)-TEPC labeling of \(T_{9,5}\).

Theorem 2. The book graph \(B_q\) has \(3\)-TEPC labeling.

Proof. Let \(V_G= \{u,v,u_j,v_j, 1\leq j \leq q\}\) and \( E_G= \{u u_j, 1\leq j\leq q \} \cup \{v v_j, 1\leq j\leq q\}\cup \{u_j v_j, 1\leq j\leq q \}\cup \{u v\}\) as shown in Figure 2. Now we see the following three cases:

Case 1 Let \(q\equiv0 \text{ (mod }3)\) which implies \(q= 3t\), for \(t\geq1\). We define \( h:E_G\rightarrow\{0,1,2\}\) as:

Case 1.1 Now we define edge labeling if \(t\) is even:

\(h(u u_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq 3t. \)} \end{cases} \)

\(h(u_j v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t-1; \)}\\ 1, & \text{if \( t\leq j \leq 3t. \)} \end{cases} \)

\(h(v v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq \frac{3t}{2}; \)}\\ 1, & \text{if \( \frac{3t}{2}+1\leq j \leq 3t. \)} \end{cases} \) , \(h(uv)=2\)

1.2 Now we define edge labeling if \(t\) is odd:

\(h(u u_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq 3t. \)} \end{cases} \)

\(h(u_j v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t-1; \)}\\ 1, & \text{if \( t\leq j \leq 3t. \)} \end{cases} \)

\(h(v v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq \frac{3t+1}{2}; \)}\\ 1, & \text{if \( \frac{3t+1}{2}+1\leq j \leq 3t. \)} \end{cases} \) , \(h(uv)=1\)

So we obtain \(sum(0)=sum(1)=sum(2)=5t+1.\) Thus \(|sum(x_1) – sum(x_2)| \leq 1 \) for \(0 \leq x_1 < x_2 \leq 2.\) Hence \(h\) is \(3\)-TEPC labeling.

Case 2 Let \(q\equiv1 \text{ (mod }3)\) which implies \(q= 3t+1\), for \(t\geq1\). We define \( h:E_G\rightarrow\{0,1,2\}\) as:

Case 2.1 Now we define edge labeling if \(t\) is even:

\(h(v v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq 3t+1. \)} \end{cases} \)

\(h(u_j v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 1, & \text{if \( t+1\leq j \leq 3t+1. \)} \end{cases} \)

\(h(u u_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq \frac{3t}{2}; \)}\\ 1, & \text{if \( \frac{3t}{2}+1\leq j \leq 3t+1. \)} \end{cases} \) , \(h(uv)=2\).

Case 2.2 Now we define edge labeling if \(t\) is odd:

\(h(v v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq 3t+1. \)} \end{cases} \)

\(h(u_j v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 1, & \text{if \( t+1\leq j \leq 3t+1. \)} \end{cases} \)

\(h(uu_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq \frac{3t+1}{2}; \)}\\ 1, & \text{if \( \frac{3t+1}{2}+1\leq j \leq 3t+1. \)} \end{cases} \) , \(h(uv)=1\).

So we obtain \(sum(0)=5t+2\), \(sum(1)=sum(2)=5t+3.\) Thus \(|sum(x_1) – sum(x_2)| \leq 1 \) for \(0 \leq x_1 < x_2 \leq 2.\) Hence \(h\) is \(3\)-TEPC labeling.

Case 3Let \(q\equiv2 \text{ (mod }3)\) which implies \(q= 3t+2\), for \(t\geq1\). We define \( h:E_G\rightarrow\{0,1,2\}\) as:

Case 3.1 Now we define edge labeling if \(t\) is even:

\(h(v v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq 3t+2. \)} \end{cases} \)

\(h(u_j v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 1, & \text{if \( t+1\leq j \leq 3t+2. \)} \end{cases} \)

\(h(uu_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t+1; \)}\\ 2, & \text{if \( t+2\leq j \leq \frac{3t}{2}+1; \)}\\ 1, & \text{if \( \frac{3t}{2}+2\leq j \leq 3t+2. \)} \end{cases} \) , \(h(uv)=0\).

Case 3.2 Now we define edge labeling if \(t\) is odd:

\(h(vv_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq 3t+2. \)} \end{cases} \)

\(h(u_j v_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t+1; \)}\\ 1, & \text{if \( t+2\leq j \leq 3t+2. \)} \end{cases} \)

\(h(uu_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq \frac{3t+1}{2}; \)}\\ 1, & \text{if \( \frac{3t+1}{2}+1\leq j \leq 3t+2. \)} \end{cases} \) , \(h(uv)=2\).

So we obtain \(sum(0)=5t+5\), \(sum(1)=sum(2)=5t+4.\) Thus \(|sum(x_1) – sum(x_2)| \leq 1 \) for \(0 \leq x_1 < x_2 \leq 2.\) Hence \(h\) is \(3\)-TEPC labeling.

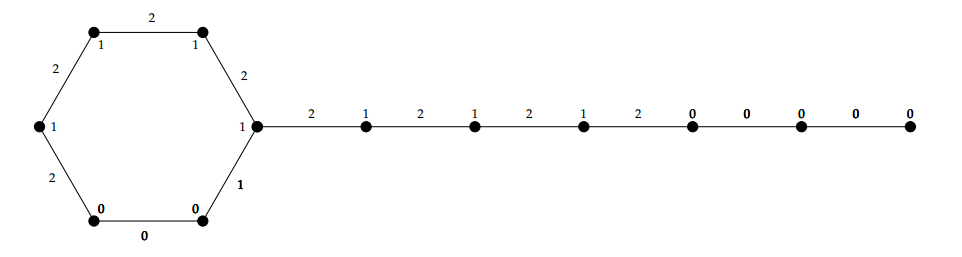
Example 1.The graph \(B_6\) and its given \(3\)-TEPC labeling as shown in Figure 7.

Figure 7. \(3\)-TEPC labeling of \(B_{6}\).

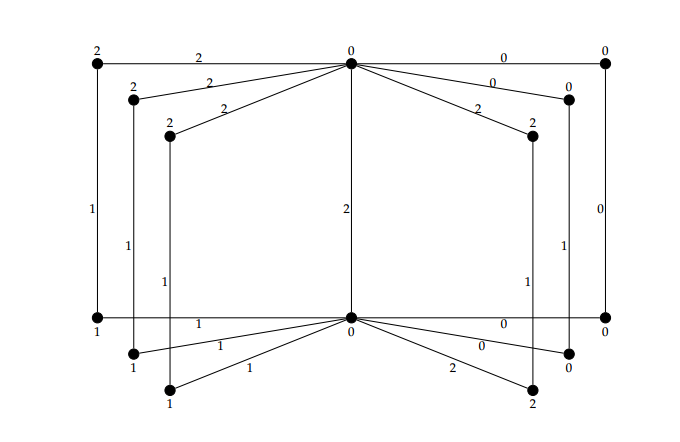
Theorem 3. The flower graph \(Fl_q\) has \(3\)-TEPC labeling.

Proof. Let \(V_G= \{u,u_j,v_j, 1\leq j \leq q\}\) and \( E_G= \{u u_j, 1\leq j\leq q \} \cup \{u_j u_{j+1}, 1\leq j\leq q-1\}\cup \{u_j v_j, 1\leq j\leq q \}\cup \{u_{j+1} v_j, 1\leq j\leq q-1 \}\cup \{u_q u_1\}\cup \{u_1 v_q\}\) as shown in Figure 3. Now we see the following three cases:

Case 1 Let \(q\equiv0 \text{ (mod }3)\) which implies \(q= 3t\), for \(t \geq1\). We define \( h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 1, & \text{if \( t+1\leq j \leq 3t-1; \)} \end{cases} \) and \(h(u_{3t } u_1)=1.\)

\(h(u_{j+1} v_j)=\begin{cases} 0, & \text{if \( 1 \leq j \leq t-1; \)}\\ 2, & \text{if \( t \leq j \leq 3t-1; \)} \end{cases} \) and \(h(u_1 v_{3t})=2.\)

\(h(u u_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t +1; \)}\\ 2, & \text{if \( t+2 \leq j \leq 2t; \)}\\ 1, & \text{if \( 2t+1\leq j \leq 3t . \)} \end{cases} \)

\(h(u_j v_j)=\begin{cases} 0, & \text{if \( 1 \leq j \leq t-1; \)}\\ 2, & \text{if \( t \leq j \leq 3t. \)} \end{cases} \)

So we obtain \(sum(1)=6t+1\), \(sum(0)=sum(2)=5t.\) Thus \(|sum(x_1) – sum(x_2)| \leq 1 \) for \(0 \leq x_1 < x_2 \leq 2.\) Hence \(h\) is \(3\)-TEPC labeling.

Case 2 Let \(q\equiv1 \text{ (mod }3)\) which implies \(q= 3t+1\), for \(t\geq1\). We define \( h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 1, & \text{if \( t+1\leq j \leq 3t; \)} \end{cases} \) and \(h(u_j u_{3t+1})=1.\)

\(h(u_{j+1} v_j)=\begin{cases} 0, & \text{if \( 1 \leq j \leq t; \)}\\ 2, & \text{if \( t+1 \leq j \leq 3t; \)} \end{cases} \) and \(h(u_1 v_{3t+1})=2.\)

\(h(u u_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t+1; \)}\\ 2, & \text{if \( t+2 \leq j \leq 2t+1; \)}\\ 1, & \text{if \( 2t+2\leq j \leq 3t+1. \)} \end{cases} \)

\(h(u_j v_j)=\begin{cases} 0, & \text{if \( 1 \leq j \leq t; \)}\\ 2, & \text{if \( t+1 \leq j \leq 3t+1. \)} \end{cases} \)

So we obtain \(sum(0)=6t+3\), \(sum(1)=sum(2)=5t+2.\) Thus \(|sum(x_1) – sum(x_2)| \leq 1 \) for \(0 \leq x_1 < x_2 \leq 2.\) Hence \(h\) is \(3\)-TEPC labeling.

Case 3 Let \(q\equiv2 \text{ (mod }3)\) which implies \(q= 3t+2\), for \(t\geq1\). We define \( h:E_G\rightarrow\{0,1,2\}\) as:

\(h(u_j u_{j+1})=\begin{cases} 0, & \text{if \( 1\leq j \leq t; \)}\\ 2, & \text{if \( t+1\leq j \leq 3t+1; \)} \end{cases} \) and \(h(u_{3t+2} u_1)=2.\)\\

\(h(u_{j+1} v_j)=\begin{cases} 0, & \text{if \( 1 \leq j \leq t; \)}\\ 1, & \text{if \( t+1 \leq j \leq 3t+1; \)} \end{cases} \) and \(h(u_1 v_{3t+2})=1.\)

\(h(u u_j)=\begin{cases} 0, & \text{if \( 1\leq j \leq t+1; \)}\\ 2, & \text{if \( t+2 \leq j \leq 3t+2. \)} \end{cases} \)

\(h(u_j v_j)=\begin{cases} 0, & \text{if \( 1 \leq j \leq t+1; \)}\\ 1, & \text{if \( t+2 \leq j \leq 3t+2. \)} \end{cases} \)

So we obtain \(sum(0)=6t+5\), \(sum(1)=sum(2)=5t+4.\) Thus \(|sum(x_1) – sum(x_2)| \leq 1 \) for \(0 \leq x_1 < x_2 \leq 2.\) Hence \(h\) is \(3\)-TEPC labeling.

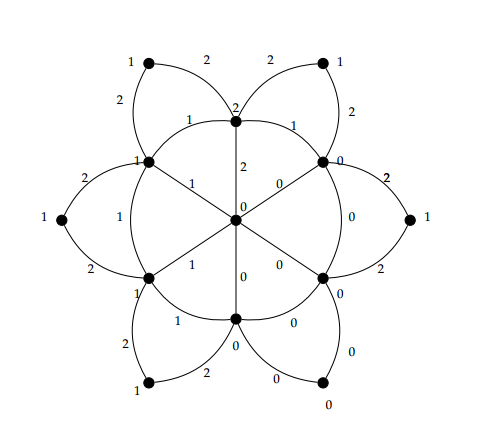
Example 2. The graph \(Fl_6\) and its given \(3\)-TEPC labeling as shown in Figure 8.

Figure 8. \(3\)-TEPC labeling of \(Fl_{6}\).

Acknowledgments

This article has benefited from constructive reviewing. Any remaining errors are my own

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflict of Interests

The authors declare no conflict of interest.

References:

West, D. B. (1996). Introduction to graph theory (Vol. 2). Upper Saddle River, NJ: Prentice hall. [Google Scholor]
Cahit, I. (1987). Cordial graphs-a weaker version of graceful and harmonious graphs. Ars Combinatoria,23, 201-207. [Google Scholor]
Sundaram, M., Ponraj, R., & Somasundaram, S. (2004). Product cordial labeling of graphs. Bull. Pure and Applied Sciences (Mathematics & Statistics), E, 23, 155-163.[Google Scholor]
Ponraj, R., Sundaram, M., & Sivakumar, M. (2012). K-total product cordial labelling of graphs. Applications and Applied Mathematics, 7, 708-716. [Google Scholor]
Sundaram, M., Ponraj, R., & Somasundram, S. (2006). Total product cordial labeling of graphs. Bulletin of Pure & Applied Sciences. Sec. E, Mathematics & Statistics, 25, 199-203. [Google Scholor]
Vaidya, S. K., & Barasara, C. M. (2012). Edge product cordial labeling of graphs. Journal of Mathematical and computational Science, 2(5), 1436-1450. [Google Scholor]
Vaidya, S. K., & Barasara, C. M. (2013). Total edge product cordial labeling of graphs. Malaya Journal of Matematik, 3(1), 55-63. [Google Scholor]
Azaizeh, A., Hasni, R., Ahmad, A., & Lau, G. C. (2015). 3-Totat edge product cordial labeling of graphs. Far East journal of Matheimatical sciences, 96(2), 193-209. [Google Scholor]
Ivanco, J. (2017). On 3-total edge product cordial connected graphs. Opuscula Mathematica, 37(5), 725-734. [Google Scholor]
Yan, L., Li, Y., Zhang, X., Saqlain, M., Zafar, S., & Farahani, M. R. (2018). 3-total edge product cordial labeling of some new classes of graphs. Journal of Information and Optimization Sciences, 39(3), 705-724. [Google Scholor]
Ahmad, Y., Ali, U., Zafar, S., & Zahid, Z. (2017). Some new standard graphs labeled by 3-total edge product cordial labeling. Applied Mathematics and Nonlinear Sciences, 2(1), 61-72. [Google Scholor]
Ali, U., Bilal, M., Zafar, S., & Zahid, Z. (2017). Some Families of Convex Polytopes Labeled by 3-Total Edge Product Cordial Labeling. Punjab University Journal of Mathematics, 49, 119-132. [Google Scholor]
Ahmad, A., Baca, M., Naseem, M., & Semanicová-Fenovcíková, A. (2017). On 3-total edge product cordial labeling of honeycomb. AKCE International Journal of Graphs and Combinatorics, 14(2), 149-157. [Google Scholor]
Ali, U., Iqbal, J., Zafar, S., & Zahid, Z. (2018). 4-total edge product cordial labeling of some standard graphs. Tamap Journal of Mathematics and Statistics, 16-31. [Google Scholor]
Ivanco, J. (2017). On k-total edge product cordial graphs. The Australasian Journal of Combinatorics, 67, 476-485. [Google Scholor]
Hasni, R., & Azaizeh, A. (2016). 3-total edge product cordial labeling of wheel related graphs. Matematika, 32(2),93-102. [Google Scholor]
Kuo, D., Chang, G. J., & Kwong, Y. H. (1997). Cordial labeling of \(mK_n.\) Discrete Mathematics, 169(1-3), 121-131. [Google Scholor]
Lai, Y. L., & Chen, Y. M., On the total product cordial labeling of \(P_n + mK_1\). National Chiayi University. http://people.chu.edu.tw/ algo2008/file/f55.pdf [Google Scholor]

Contents

Open Journal of Mathematical Science (OMS)