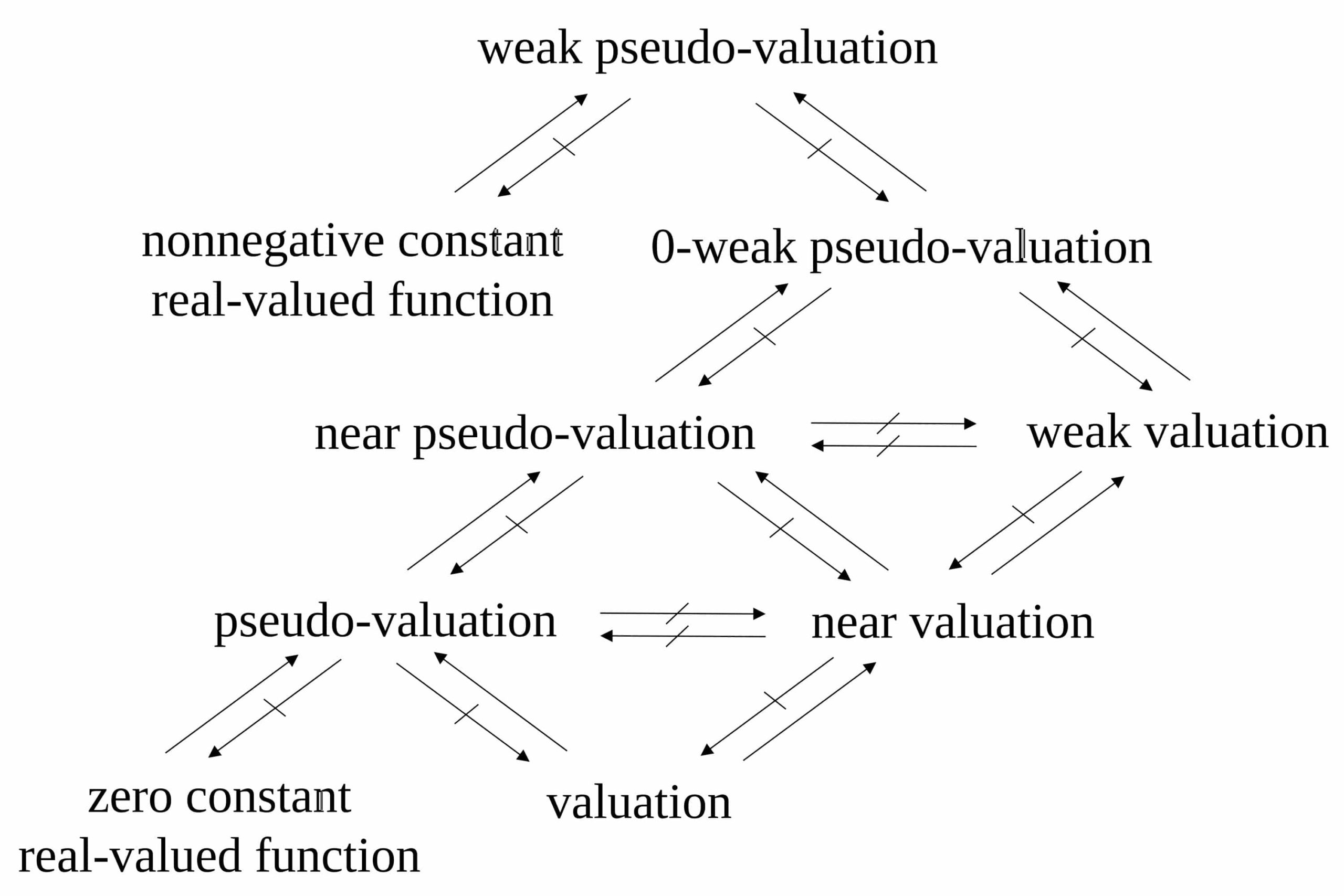
In this paper, we introduce the notions of a weak pseudo-valuation, a \(0\)-weak pseudo-valuation, a weak valuation, a near pseudo-valuation, a near valuation, a pseudo-valuation, and a valuation and induce a pseudo-metric without triangle inequality, a quasi pseudo-metric, a pseudo-metric, and a metric by some these mappings on a UP-algebra. We also prove that the binary operation defined on a UP-algebra is uniformly continuous under the induced metric by a valuation in some conditions.
The fundamental concept of pseudo-valuation was first introduced by Busne¸ag [1] in 1996. He defined a pseudo-valuation on a Hilbert algebra and proved that every pseudo-valuation induces a pseudo metric on a Hilbert algebra. In 2003, Buşneag [2] provided several theorems on extensions of pseudo-valuations. In 2007, Buşneag [3] introduced the notion of a pseudo-valuation (valuations) on a residuated lattice and proved some theorems of extension for these (using the model of a Hilbert algebra).
In 2010, Doh and Kang [4] introduced the notion of a pseudo-valuation on a BCK/BCI-algebra and studied results based on a pseudo-valuation. Ghorbani [5] defined a congruence relation and gave a quotient structure of a BCI-algebra based on a pseudo-valuation. In 2011, Doh and Kang [6] introduced the notion of a commutative pseudo valuation on a BCK-algebra. Jun et al., [7] introduced the notion of a positive implicative pseudo-valuation on a BCK-algebra and investigated its characterizations. In 2012, Jun et al., [8] introduced the notions of a pseudo-valuation and a valuation on a BCC-algebra. In 2013, Zhan and Jun [9] introduced the notions of a pseudo-valuation and an implicative pseudo-valuation on a \(R_{0}\)-algebra. Lee [10] introduced the notions of a pseudo-valuation and a valuation, and a pseudo-metric is induced by a pseudo-valuation on a BE-algebra. In 2015, Song et al., [11] introduced the notions of a quasi-valuation map based on a subalgebra and an ideal on a BCK/BCI-algebra. In 2017, Yang and Xin [12] introduced the notions of a pseudo pre-valuation, an implicative pseudo pre-valuation, a positive implicative pseudo pre-valuation, and a strong pseudo pre-valuation, and investigated some characterizations of an EQ-algebra. In 2018, Mehrshada and Kouhestanib [13] studied some properties of a pseudo-valuation and their induced metrics on a BCK-algebra and showed that there are many pseudo-valuations on a BCK-algebra.
In 2019, Koam et al., [14] introduced the notion of a pseudo-metric which induced from a pseudo-valuation on a KU-algebra. Ali et al., [15] introduced the notion of a pseudo-valuation and investigated the relationship between a pseudo-valuation and an ideal of a JU-algebra. Romano [16] introduced the notion of a pseudo-valuation on a UP-algebra and analyzed the relationship of these mappings with UP-substructures.
In this paper, we introduce the notions of a weak pseudo-valuation, a \(0\)-weak pseudo-valuation, a weak valuation, a near pseudo-valuation, a near valuation, a pseudo-valuation, and a valuation and induce a pseudo-metric without triangle inequality, a quasi pseudo-metric, a pseudo-metric, and a metric by some these mappings on a UP-algebra. We also prove that the binary operation defined on a UP-algebra is uniformly continuous under the induced metric by a valuation in some conditions.
Before we begin our study, we will give the definition of UP-algebras.
Definition 1. [17] An algebra \(A=(A,\cdot,0)\) of type \((2,0)\) is called a UP-algebra, where \(A\) is a nonempty set, \(\cdot\) is a binary operation on \(A\), and \(0\) is a fixed element of \(A\) (i.e., a nullary operation) if it satisfies the following axioms:
Example 1.[19] Let \(X\) be a universal set and let \(\Omega\in\mathcal{P}(X)\) where \(\mathcal{P}(X)\) means the power set of \(X\). Let \(\mathcal{P}_{\Omega}(X)=\{A\in\mathcal{P}(X)\mid\Omega\subseteq A\}\). Define a binary operation \(\cdot\) on \(\mathcal{P}_{\Omega}(X)\) by putting \(A\cdot B=B\cap (A^{C}\cup\Omega)\) for all \(A,B\in\mathcal{P}_{\Omega}(X)\) where \(A^{C}\) means the complement of a subset \(A\). Then \((\mathcal{P}_{\Omega}(X),\cdot,\Omega)\) is a UP-algebra and we shall call it the generalized power UP-algebra of type 1 with respect to \(\Omega\). Let \(\mathcal{P}^{\Omega}(X)=\{A\in\mathcal{P}(X)\mid A\subseteq\Omega\}\). Define a binary operation \(\ast\) on \(\mathcal{P}^{\Omega}(X)\) by putting \(A\ast B=B\cup (A^{C}\cap\Omega)\) for all \(A,B\in\mathcal{P}^{\Omega}(X)\). Then \((\mathcal{P}^{\Omega}(X),\ast,\Omega)\) is a UP-algebra and we shall call it the generalized power UP-algebra of type 2 with respect to \(\Omega\). In particular, \((\mathcal{P}(X),\cdot,\emptyset)\) is a UP-algebra and we shall call it the power UP-algebra of type 1, and \((\mathcal{P}(X),\ast,X)\) is a UP-algebra and we shall call it the power UP-algebra of type 2.
Example 2.[20] Let \(\mathbb {N}_{0}\) be the set of all natural numbers with zero. Define two binary operations \(\circ\) and \(\bullet\) on \(\mathbb{N}_{0}\) by \begin{align*} (\forall x,y\in\mathbb{N}_{0})\left(x\circ y = \left\{ \begin{array}{ll} y & \text{if}~xy~\text{or}~x=0, \\ 0 & \text{otherwise} \end{array} \right.\right). \end{align*} Then \((\mathbb{N}_{0},\circ,0)\) and \((\mathbb{N}_{0},\bullet,0)\) are UP-algebras.
Example 3.[21] Let \(A=\{0,1,2,3,4\}\) be a set with a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*}\label{eqMEX012} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 0 & 4 \\ 2 & 0 & 1 & 0 & 0 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 1 & 2 & 3 & 0 \\ \end{array} \end{equation*} Then \((A,\cdot,0)\) is a UP-algebra.
For more examples of UP-algebras, see [19,22,23,24,25].In a UP-algebra \(A=(A,\cdot,0)\), the following assertions are valid (see [17,24]).
\[\label{UP2_1} (\forall x\in A)(x\cdot x=0), \tag{1}\] \[\label{UP2_13} (\forall x,y,z\in A)(x\cdot y=0, y\cdot z=0 \Rightarrow x\cdot z=0), \tag{2}\] \[\label{UP2_6} (\forall x,y,z\in A)(x\cdot y=0 \Rightarrow (z\cdot x)\cdot (z\cdot y)=0), \tag{3}\] \[\label{UP2_7} (\forall x,y,z\in A)(x\cdot y=0 \Rightarrow (y\cdot z)\cdot (x\cdot z)=0), \tag{4}\] \[\label{UP2_14} (\forall x,y\in A)(x\cdot (y\cdot x)=0), \tag{5}\] \[\label{UP2_16} (\forall x,y\in A)((y\cdot x)\cdot x=0 \Leftrightarrow x=y\cdot x), \tag{6}\] \[\label{UP2_15} (\forall x,y\in A)(x\cdot (y\cdot y)=0), \tag{7}\] \[\label{UP2_add1} (\forall a,x,y,z\in A)((x\cdot(y\cdot z))\cdot(x\cdot((a\cdot y)\cdot (a\cdot z)))=0),\tag{8}\] \[\label{UP2_add2} (\forall a,x,y,z\in A)((((a\cdot x)\cdot (a\cdot y))\cdot z)\cdot((x\cdot y)\cdot z)=0), \tag{9}\] \[\label{UP2_add3} (\forall x,y,z\in A)(((x\cdot y)\cdot z)\cdot(y\cdot z)=0), \tag{10}\] \[\label{UP2_add4} (\forall x,y,z\in A)(x\cdot y=0 \Rightarrow x\cdot (z\cdot y)=0), \tag{11}\] \[\label{UP2_add5} (\forall x,y,z\in A)(((x\cdot y)\cdot z)\cdot(x\cdot(y\cdot z))=0),\, \tag{12}\]and
\[\label{UP2_add6} (\forall a,x,y,z\in A)(((x\cdot y)\cdot z)\cdot(y\cdot(a\cdot z))=0).\tag{13}\] From [17], the binary relation \(\leq\) on a UP-algebra \(A=(A,\cdot,0)\) is defined as follows: \[\begin{equation} (\forall x,y\in A)(x\leq y \Leftrightarrow x\cdot y=0). \end{equation}\tag{14}\] In UP-algebras, 5 types of special subsets are defined as follows:Definition 2. [17,26,27,28] A nonempty subset \(S\) of a UP-algebra \(A=(A,\cdot,0)\) is called
Iampan [26,27] proved that the notion of UP-subalgebras is a generalization of near UP-filters, near UP-filters is a generalization of UP-filters, UP-filters is a generalization of UP-ideals, and UP-ideals is a generalization of strong UP-ideals. Furthermore, they proved that the only strong UP-ideal of a UP-algebra \(A\) is \(A\).
In this section, we introduce the notions of a weak pseudo-valuation, a \(0\)-weak pseudo-valuation, a weak valuation, a near pseudo-valuation, a near valuation, a pseudo-valuation, and a valuation on a UP-algebra. From now on, unless another thing is stated, we take \(A=(A,\cdot,0)\) as a UP-algebra.
Definition 3. A real-valued function \(\varphi\) on \(A\) is called a pseudo-valuation on \(A\) if it satisfies the following conditions: \[\varphi(0)=0, \tag{15}\] \[(\forall x,y\in A)(\varphi(y)\leq\varphi(x\cdot y)+\varphi(x)). \tag{16}\] A pseudo-valuation \(\varphi\) on \(A\) is called a valuation on \(A\) if it satisfies the following condition:
Definition 4. A real-valued function \(\varphi\) on \(A\) is called a near pseudo-valuation on \(A\) if it satisfies the condition (15) and the following condition:
Definition 5. A real-valued function \(\varphi\) on \(A\) is called a weak pseudo-valuation on \(A\) if
Theorem 1. Every nonnegative constant real-valued function on \(A\) is a weak pseudo-valuation.
Proof. Let \(\varphi\) be a nonzero constant real-valued function on \(A\). Then there exists a nonnegative real number \(c\) such that \(\varphi(x)=c\) for all \(x \in A\). Let \(x,y\in A\). Then \begin{align*} \varphi(x\cdot y)=c \leq c+c=\varphi(x)+\varphi(y). \end{align*} Hence, \(\varphi\) is a weak pseudo-valuation on \(A\).
The following example shows that the converse of Theorem 1 is not true in general.Example 4. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 3 & 0 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 4 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0.2} \,\,\, {1\atop 0.6} \,\,\, {2\atop 0.7} \,\,\, {3\atop 0.5} \,\,\, {4\atop 0.2} \right). \end{equation*}
Then \(\varphi\) is a weak pseudo-valuation on \(A\). But \(\varphi\) is not a nonnegative constant real-valued function on \(A\) because \(\varphi(0)=0.2\neq0.6= \varphi(1)\).
Theorem 2. The zero constant real-valued function on \(A\) is a \(0\)-weak pseudo-valuation (resp., near pseudo-valuation, pseudo-valuation).
Proof. It is straightforward from the definitions of \(0\)-weak pseudo-valuations, near pseudo-valuations, and pseudo-valuations.
If \(A\) has more than one element, then the zero constant real-valued function on \(A\) is not a weak valuation, a near valuation, and a valuation.
The following example shows that the converse of Theorem 2 is not true in general.
Example 5. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 4 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 0 & 0 & 4 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.5} \,\,\, {2\atop 0.4} \,\,\, {3\atop 0.7} \,\,\, {4\atop 0.1} \right). \end{equation*}
Then \(\varphi\) is a pseudo-valuation on \(A\). But \(\varphi\) is not a zero constant real-valued function on \(A\) because \(\varphi(0)=0\neq0.5=\varphi(1)\).
Example 6. From Example 2, we have \((\mathbb{N}_{0},\circ,0)\) is a UP-algebra. Let \(\varphi\) be a real-valued function on \(\mathbb{N}_{0}\) defined by \(\varphi(0)=0\) and if \(x\leq y\) where \(\leq\) is the standard ordering among real numbers, then \(0< \varphi(x)\leq\varphi(y)\) for all positive numbers \(x, y\). Let \(x, y\in\mathbb{N}_{0}\).
Hence, \(\varphi\) is a valuation on \(\mathbb{N}_{0}\).
Example 7. From Example 2, we have \((\mathbb{N}_{0},\circ,0)\) is a UP-algebra. Let \(\varphi\) be a real-valued function on \(\mathbb{N}_{0}\) defined by \(\varphi(x)=x\) for all \(x\in\mathbb{N}_{0}\). By Example 6, we have \(\varphi\) is a valuation on \(\mathbb{N}_{0}\).
Example 8. From Example 2, we have \((\mathbb{N}_{0},\bullet,0)\) is a UP-algebra. Let \(\varphi\) be a real-valued function on \(\mathbb{N}_{0}\) defined by \(\varphi(0)=0\) and if \(x\leq y\) where \(\leq\) is the standard ordering among real numbers, then \(\varphi(x)\geq\varphi(y)>0\) for all positive numbers \(x, y\). Let \(x, y\in\mathbb{N}_{0}\).
Hence, \(\varphi\) is a valuation on \(\mathbb{N}_{0}\).
Example 9. From Example 2, we have \((\mathbb{N}_{0},\bullet,0)\) is a UP-algebra. Let \(c\) be a positive real number and \(\varphi\) be a real-valued function on \(\mathbb{N}_{0}\) defined by \(\varphi(0)=0\) and \(\varphi(x)=c\) for all positive number \(x\). By Example 8, we have \(\varphi\) is a valuation on \(\mathbb{N}_{0}\).
Example 10. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 4 \\ 2 & 0 & 1 & 0 & 0 & 0 \\ 3 & 0 & 1 & 2 & 0 & 0 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.5} \,\,\, {2\atop 0.7} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.2} \right). \end{equation*}
Then \(\varphi\) is a valuation on \(A\).
Example 11. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 4 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 0 & 0 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.5} \right). \end{equation*}
Then \(\varphi\) is a pseudo-valuation on \(A\).
Example 12. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 3 \\ 2 & 0 & 0 & 0 & 3 & 3 \\ 3 & 0 & 1 & 1 & 0 & 1 \\ 4 & 0 & 0 & 1 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.3} \,\,\, {2\atop 0.9} \,\,\, {3\atop 0.2} \,\,\, {4\atop 0.5} \right). \end{equation*}
Then \(\varphi\) is a near pseudo-valuation on \(A\).
Example 13. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 2 \\ 2 & 0 & 0 & 0 & 0 & 2 \\ 3 & 0 & 0 & 1 & 0 & 2 \\ 4 & 0 & 0 & 0 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.5} \,\,\, {2\atop 0.4} \,\,\, {3\atop 0.7} \,\,\, {4\atop 0.1} \right). \end{equation*}
Then \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\).
Example 14. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 0 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 0 & 0 & 4 \\ 4 & 0 & 4 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0.2} \,\,\, {1\atop 0.4} \,\,\, {2\atop 0.9} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.1} \right). \end{equation*}
Then \(\varphi\) is a weak pseudo-valuation on \(A\).
Example 15. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 1 & 0 & 4 & 0 \\ 3 & 0 & 1 & 0 & 0 & 0 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0.3} \,\,\, {3\atop 0.8} \,\,\, {4\atop 0.4} \right). \end{equation*}
Then \(\varphi\) is a near valuation on \(A\).
Example 16. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 2 \\ 2 & 0 & 0 & 0 & 3 & 2 \\ 3 & 0 & 1 & 1 & 0 & 2 \\ 4 & 0 & 0 & 0 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0.7} \,\,\, {3\atop 0.2} \,\,\, {4\atop 0.5} \right). \end{equation*}
Then \(\varphi\) is a weak valuation on \(A\).
Theorem 3. Every near pseudo-valuation \(\varphi\) on \(A\) satisfies the following condition:
Proof. Let \(x\in A\). Then \( 0 =\varphi(0) =\varphi(x\cdot x) \leq\varphi(x). \)
Theorem 4. Every valuation on \(A\) is a pseudo-valuation.
Proof. It is straightforward from the definitions of valuations and pseudo-valuations.
Theorem 5. Every pseudo-valuation on \(A\) is a near pseudo-valuation.
Proof. Let \(\varphi\) be a pseudo-valuation on \(A\). Let \(x,y\in A\). Then \( \varphi(x\cdot y) \leq\varphi(y\cdot(x\cdot y))+\varphi(y) =\varphi(0)+\varphi(y) =0+\varphi(y) =\varphi(y). \) Hence, \(\varphi\) is a near pseudo-valuation on \(A\).
Theorem 6. Every near pseudo-valuation on \(A\) is a \(0\)-weak pseudo-valuation.
Proof. Let \(\varphi\) be a near pseudo-valuation on \(A\). Clearly, \(\varphi(0)=0\). Let \(x,y\in A\). Then \(\varphi(x\cdot y) \leq\varphi(y)\leq\varphi(x)+\varphi(y). \) Hence, \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\).
Theorem 7. Every \(0\)-weak pseudo-valuation on \(A\) is a weak pseudo-valuation.
Proof. It is straightforward from the definitions of \(0\)-weak pseudo-valuations and weak pseudo-valuations.
Theorem 8. Every valuation on \(A\) is a near valuation.
Proof. It is straightforward from the definitions of valuations and near valuations and Theorem 5.
Theorem 9. Every near valuation on \(A\) is a weak valuation.
Proof. It is straightforward from the definitions of near valuations and weak valuations and Theorem 6.
Theorem 10. Every weak valuation on \(A\) is a \(0\)-weak pseudo-valuation.
Proof. It is straightforward from the definitions of weak valuations and \(0\)-weak pseudo-valuations.
Theorem 11. Every near valuation on \(A\) is a near pseudo-valuation.
Proof. It is straightforward from the definitions of near valuations and near pseudo-valuations.
The following example shows that the converse of Theorem 4 is not true in general.Example 17. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 0 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.5} \,\,\, {2\atop 0} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.2} \right). \end{equation*} Then \(\varphi\) is a pseudo-valuation on \(A\). But \(\varphi\) is not a valuation on \(A\) because there exists \(2\neq0\) and \(\varphi(2)=0\).
The following example shows that the converse of Theorem 5 is not true in general.Example 18. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 1 & 3 & 3 \\ 2 & 0 & 0 & 0 & 3 & 3 \\ 3 & 0 & 0 & 1 & 0 & 1 \\ 4 & 0 & 0 & 0 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0.5} \,\,\, {3\atop 0.1} \,\,\, {4\atop 0.4} \right). \end{equation*} Then \(\varphi\) is a near pseudo-valuation on \(A\). But \(\varphi\) is not a pseudo-valuation on \(A\) because \(\varphi(1)=0.2\nleq0.1=0+0.1=\varphi(0)+\varphi(3)=\varphi(3\cdot1)+\varphi(3)\).
The following example shows that the converse of Theorem 6 is not true in general.Example 19. From Example 13, let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.1} \,\,\, {2\atop 0.2} \,\,\, {3\atop 0.5} \,\,\, {4\atop 0.1} \right). \end{equation*} Then \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\). But \(\varphi\) is not a near pseudo-valuation on \(A\) as \(\varphi(1\cdot4)=\varphi(2)=0.2\nleq0.1=\varphi(4)\).
The following example shows that the converse of Theorem 7 is not true in general.Example 20. From Example 14, let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0.2} \,\,\, {1\atop 0.1} \,\,\, {2\atop 0.4} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.1} \right). \end{equation*} Then \(\varphi\) is a weak pseudo-valuation on \(A\). But \(\varphi\) is not a \(0\)-weak pseudo-valuation on \(A\) because \(\varphi(0)=0.2\).
The following example shows that the converse of Theorem 8 is not true in general.Example 21. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 1 & 0 & 4 & 0 \\ 3 & 0 & 1 & 2 & 0 & 0 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0.7} \,\,\, {3\atop 0.9} \,\,\, {4\atop 0.5} \right). \end{equation*} Then \(\varphi\) is a near valuation on \(A\). But \(\varphi\) is not a valuation on \(A\) because \(\varphi(4)=0.5\nleq0.2=0+0.2=\varphi(0)+\varphi(1)=\varphi(1\cdot4)+\varphi(1)\).
The following example shows that the converse of Theorem 9 is not true in general.Example 22. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 4 \\ 2 & 0 & 0 & 0 & 0 & 2 \\ 3 & 0 & 1 & 1 & 0 & 2 \\ 4 & 0 & 0 & 0 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0.5} \,\,\, {3\atop 0.2} \,\,\, {4\atop 0.3} \right). \end{equation*} Then \(\varphi\) is a weak valuation on \(A\). But \(\varphi\) is not a near valuation on \(A\) because \(\varphi(2\cdot4)=\varphi(2)=0.5\nleq0.3=\varphi(4)\).
The following example shows that the converse of Theorem 10 is not true in general.Example 23. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 4 \\ 2 & 0 & 0 & 0 & 0 & 1 \\ 3 & 0 & 1 & 1 & 0 & 1 \\ 4 & 0 & 0 & 0 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.10} \,\,\, {2\atop 0.45} \,\,\, {3\atop 0.75} \,\,\, {4\atop 0} \right). \end{equation*} Then \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\). But \(\varphi\) is not a weak valuation on \(A\) because \(\varphi(4)=0\).
The following example shows that the converse of Theorem 11 is not true in general.Example 24. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 1 & 0 & 0 & 0 \\ 3 & 0 & 1 & 2 & 0 & 0 \\ 4 & 0 & 1 & 2 & 4 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.7} \,\,\, {2\atop 0.9} \,\,\, {3\atop 0.1} \,\,\, {4\atop 0} \right). \end{equation*} Then \(\varphi\) is a near pseudo-valuation on \(A\). But \(\varphi\) is not a near valuation on \(A\) because there exists \(4\neq0\) and \(\varphi(4)=0\).
The following two examples show that a pseudo-valuation and a near valuation are not identical in general.Example 25. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 0 \\ 2 & 0 & 1 & 0 & 0 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.75} \,\,\, {2\atop 0.50} \,\,\, {3\atop 0} \,\,\, {4\atop 0.50} \right). \end{equation*} Then \(\varphi\) is a pseudo-valuation on \(A\). But \(\varphi\) is not a near valuation on \(A\) because there exists \(3\neq0\) and \(\varphi(3)=0\).
Example 26. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 1 & 3 & 3 \\ 2 & 0 & 0 & 0 & 3 & 3 \\ 3 & 0 & 0 & 1 & 0 & 1 \\ 4 & 0 & 0 & 1 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \ {1\atop 0.25} \ {2\atop 0.30} \ {3\atop 0.40} \ {4\atop 0.90} \right). \end{equation*} Then \(\varphi\) is a near valuation on \(A\). But \(\varphi\) is not a pseudo-valuation on \(A\) because \(\varphi(4)=0.9\nleq0.7=0.4+0.3=\varphi(3)+\varphi(2)=\varphi(2\cdot4)+\varphi(2)\).
The following two examples show that a near pseudo-valuation and a weak valuation are not identical in general.Example 27. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0} \,\,\, {2\atop 0.70} \,\,\, {3\atop 0.30} \,\,\, {4\atop 0.35} \right). \end{equation*} Then \(\varphi\) is a near pseudo-valuation on \(A\). But \(\varphi\) is not a weak valuation on \(A\) because there exists \(1\neq0\) and \(\varphi(1)=0\).
Example 28. Let \(A=\{0,1,2,3,4,5,6\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccccc} \cdot & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ 1 & 0 & 0 & 2 & 3 & 2 & 3 & 6 \\ 2 & 0 & 1 & 0 & 3 & 1 & 5 & 3 \\ 3 & 0 & 1 & 2 & 0 & 4 & 1 & 2 \\ 4 & 0 & 0 & 0 & 3 & 0 & 3 & 3 \\ 5 & 0 & 0 & 2 & 0 & 2 & 0 & 2 \\ 6 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.1} \,\,\, {2\atop 0.2} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.5} \,\,\, {5\atop 0.2} \,\,\, {6\atop 0.1} \right). \end{equation*} Then \(\varphi\) is a weak valuation on \(A\). But \(\varphi\) is not a near pseudo-valuation as \(\varphi(3\cdot6)=\varphi(2)=0.2\nleq0.1=\varphi(6)\).
Theorem 12. Every weak pseudo-valuation \(\varphi\) on \(A\) satisfies the condition (20).
Proof. For all \(x\in A\), \( \varphi(0) =\varphi(x\cdot x) \leq \varphi(x)+\varphi(x).\) In particular, \(\varphi(0)\leq \varphi(0)+\varphi(0)\), so \(0\leq \varphi(0)\). Hence, \(0\leq\varphi(0)\leq \varphi(x)+\varphi(x)=2\varphi(x)\) for all \(x\in A\), that is, \(0\leq\varphi(x)\) for all \(x\in A\).
Corollary 13. Every \(0\)-weak pseudo-valuation (resp., near pseudo-valuation, pseudo-valuation, valuation, weak valuation, near valuation) \(\varphi\) on \(A\) satisfies the condition (20).
Lemma 1. If \(\varphi\) is a real-valued function on \(A\) satisfying the condition (18) and the following condition:
Proof. For all \(x\in A\), \( \varphi(0) =\varphi(x\cdot x)\leq\varphi(x).\) By (21), we have \(\varphi(0)=0\), that is, \(\varphi\) satisfies the condition (15). Thus \(\varphi\) is a near pseudo-valuation on \(A\). By Corollary 13, we have \(\varphi\) satisfies the condition (20).
Theorem 14. If \(\varphi\) is a real-valued function on \(A\) satisfying the conditions (18) and (21) and the following condition:
Proof. Assume that \(\varphi\) is a real-valued function on \(A\) satisfying the conditions (18), (21), and (22). By Lemma 1, we have \(\varphi(x)\geq0\) for all \(x\in A\) and \(\varphi(0)=0\). Let \(x,y \in A\). Then \begin{align*} \varphi(y) &=\varphi(0\cdot y)\\ &\leq\varphi(0\cdot x)+\varphi(x\cdot y) \\ &=\varphi(x)+\varphi(x\cdot y)\\ &=\varphi(x\cdot y)+\varphi(x). \end{align*} Hence, \(\varphi\) is a pseudo-valuation on \(A\).
Definition 6. Let \(\varphi\) be a real-valued function on \(A\). Define the subset \(\mathrm{Ker}\,\varphi\) of \(A\) by \begin{equation*} \mathrm{Ker}\,\varphi:=\{x\in A\mid\varphi(x)=0\}. \end{equation*}
Theorem 15. If \(\varphi\) is a pseudo-valuation on \(A\), then \(\mathrm{Ker}\,\varphi\) is a UP-filter of \(A\).
Proof. Assume that \(\varphi\) is a pseudo-valuation on \(A\). By (15), we have \(0\in \mathrm{Ker}\,\varphi\). Let \(x,y\in A\) be such that \(x\cdot y\in \mathrm{Ker}\,\varphi\) and \(x\in \mathrm{Ker}\,\varphi\). Then \(\varphi(x\cdot y)=0\) and \(\varphi(x)=0\). By (16), we have \begin{align*} \varphi(y)\leq\varphi(x\cdot y)+\varphi(x)=0+0=0. \end{align*} It follows from Corollary 13 that \(\varphi(y)=0\), so \(y\in \mathrm{Ker}\,\varphi\). Hence, \(\mathrm{Ker}\,\varphi\) is a UP-filter of \(A\).
Theorem 16. If \(\varphi\) is a near pseudo-valuation on \(A\), then \(\mathrm{Ker}\,\varphi\) is a near UP-filter of \(A\).
Proof. Assume that \(\varphi\) is a near pseudo-valuation on \(A\). By (15), we have \(0\in \mathrm{Ker}\,\varphi\). Let \(x\in A\) and \(y\in \mathrm{Ker}\,\varphi\). Then \(\varphi(y)=0\). By (18), we have \begin{align*} \varphi(x\cdot y)\leq\varphi(y)=0. \end{align*} It follows from Corollary 13 that \(\varphi(x\cdot y)=0\), so \(x\cdot y\in \mathrm{Ker}\,\varphi\). Hence, \(\mathrm{Ker}\,\varphi\) is a near UP-filter of \(A\).
Theorem 17. If \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\), then \(\mathrm{Ker}\,\varphi\) is a UP-subalgebra of \(A\).
Proof. Assume that \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\). By (15), we have \(0\in \mathrm{Ker}\,\varphi\). Let \(x, y\in A\) be such that \(x\in \mathrm{Ker}\,\varphi\) and \(y\in \mathrm{Ker}\,\varphi\). Then \(\varphi(x)=0\) and \(\varphi(y)=0\). By (19), we have \begin{align*} \varphi(x\cdot y)\leq\varphi(x)+\varphi(y)=0+0=0, \end{align*} It follows from Corollary 13 that \(\varphi(x\cdot y)=0\), so \(x\cdot y\in \mathrm{Ker}\,\varphi\). Hence, \(\mathrm{Ker}\,\varphi\) is a UP-subalgebra of \(A\).
Theorem 18. If \(\varphi\) is a weak pseudo-valuation on \(A\), then a nonempty subset \(\mathrm{Ker}\,\varphi\) is a UP-subalgebra of \(A\).
Proof. Assume that \(\varphi\) is a weak pseudo-valuation on \(A\). Let \(\mathrm{Ker}\,\varphi\neq\emptyset\). Let \(x, y\in \mathrm{Ker}\,\varphi\). Then \(\varphi(x)=0\) and \(\varphi(y)=0\). By (19), we have \begin{align*} \varphi(x\cdot y)\leq\varphi(x)+\varphi(y)=0+0=0. \end{align*} It follows from Corollary 13 that \(\varphi(x\cdot y)=0\), so \(x\cdot y\in \mathrm{Ker}\,\varphi\). Hence, \(\mathrm{Ker}\,\varphi\) is a UP-subalgebra of \(A\).
Proposition 1. Let \(\varphi\) be a pseudo-valuation on \(A\). Then
Proof. (1) Let \(a, b, x \in A\) be such that \(a\leq b\cdot x\). Then \(a\cdot(b\cdot x)=0\). Thus \begin{align*} \varphi(x) &\leq\varphi(b\cdot x)+\varphi(b)\\ &\leq\varphi(a\cdot(b\cdot x))+\varphi(a)+\varphi(b)\\ &=\varphi(0)+\varphi(a)+\varphi(b)\\ &=0+\varphi(a)+\varphi(b)\\ &=\varphi(a)+\varphi(b). \end{align*}
Theorem 19. If \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\) satisfying the following condition:
Proof. Assume that \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\) satisfying the condition (23). Clearly, \(\varphi(0)=0\). Let \(x,y\in A\). If \(x\cdot y=0\), it follows from Corollary 13 that \begin{align*} \varphi(x\cdot y)=\varphi(0)=0\leq\varphi(y). \end{align*} If \(x\cdot y\neq0\), it follows from (23) that \(\varphi(x)=0\). By (19), we have \begin{align*} \varphi(x\cdot y)\leq\varphi(x)+\varphi(y)=0+\varphi(y)=\varphi(y). \end{align*} Hence, \(\varphi\) is a near pseudo-valuation on \(A\).
Theorem 20. If \(\varphi\) is a real-valued function on \(A\) satisfying the following condition:
Proof. Assume that \(\varphi\) is a real-valued function on \(A\) satisfying the condition (24). Let \(x,y\in A\). By (1), we have \(x\cdot y\leq x\cdot y\). By (24), we have \(\varphi(x\cdot y)\leq\varphi(x)+\varphi(y)\). Hence, \(\varphi\) is a weak pseudo-valuation on \(A\).
Theorem 21. If \(\varphi\) is a real-valued function on \(A\) satisfying the condition (15) and the following condition:
Proof. Assume that \(\varphi\) is a real-valued function on \(A\) satisfying the conditions (15) and (25). Let \(x\in A\). By (UP-3), we have \(x\leq 0\cdot 0\). By (25) and (15), we have \(\varphi(x)\leq\varphi(0)=0\). By (UP-3) and (1), we have \(0\leq0= x\cdot x\). By (15) and (25), we have \(0=\varphi(0)\leq \varphi(x)\). Thus \(\varphi(x)=0\) for all \(x\in A\), that is, \(\varphi\) is a zero constant real-valued function on \(A\). By Theorem 2, we have \(\varphi\) is a \(0\)-weak pseudo-valuation, a near pseudo-valuation, and a pseudo-valuation on \(A\).
Theorem 22. If \(\varphi\) is a real-valued function on \(A\) satisfying the condition (24) and the following condition:
Proof. Assume that \(\varphi\) is a real-valued function on \(A\) satisfying the conditions (24) and (26). By (UP-3), we have \(0\leq 0\cdot 0\). By (24), we have \(\varphi(0)\leq\varphi(0)+\varphi(0)\) and so \(0\leq\varphi(0)\). By (26), we have \(\varphi(0)=0\), that is, \(\varphi\) satisfies the condition (15). Let \(x\in A\). By (UP-3), we have \(x\leq 0\cdot 0\). By (24) and (15), we have \(\varphi(x)\leq\varphi(0)+\varphi(0)=0+0=0\). By (UP-3), we have \(0\leq x\cdot 0\). By (15) and (24), we have \(0=\varphi(0)\leq\varphi(x)+\varphi(0)=\varphi(x)+0=\varphi(x)\). Thus \(\varphi(x)=0\) for all \(x\in A\), that is, \(\varphi\) is a zero constant real-valued function on \(A\). By Theorem 2, we have \(\varphi\) is a \(0\)-weak pseudo-valuation, a near pseudo-valuation, and a pseudo-valuation on \(A\).
In this section, we induce a pseudo-metric without triangle inequality, a quasi pseudo-metric, a pseudo-metric, and a metric by some these mappings on a UP-algebra. We also prove that the binary operation defined on a UP-algebra is uniformly continuous under the induced metric by a valuation in some conditions.
Definition 7. Let \(A\) be a nonempty set. A real-valued function \(d\) on \(a\times A\) is called
Theorem 23. Let \(\varphi\) be a \(0\)-weak pseudo-valuation (resp., weak valuation, near pseudo-valuation, near valuation, pseudo-valuation, valuation) on \(A\) and \(r\) be a positive real number. Then the real-valued function \(d^{r}_\varphi\) on \(a\times A\) defined by
Proof.
Theorem 24. Let \(\varphi\) be a pseudo-valuation (resp., valuation) on \(A\) and \(r\) be a positive real number. Then the real-valued function \(d^{r}_\varphi : A\times A\rightarrow\mathbb{R}\) which is defined in (27) is a pseudo-metric on \(A\), called a pseudo-metric induced by a pseudo-valuation (resp., valuation) \(\varphi\).
Proof. By Theorem 23, it suffices to prove (M-4).
Theorem 25. Let \(\varphi\) be a valuation on \(A\) and \(r\) be a positive real number. Then the real-valued function \(d^{r}_\varphi : A\times A\rightarrow\mathbb{R}\) which is defined in (27) is a metric on \(A\), called a metric induced by a valuation \(\varphi\).
Proof. By Theorem 24, it suffices to prove (M-5).
Theorem 26. Let \(\varphi\) be a \(0\)-weak pseudo-valuation (resp., weak valuation, near pseudo-valuation, near valuation, pseudo-valuation, valuation) on \(A\) and \(r\) be a positive real number. Then the real-valued function \(d^{r}_\varphi : A\times A\rightarrow\mathbb{R}\) defined by
Proof.
Theorem 27. Let \(\varphi\) be a pseudo-valuation (resp., valuation) on \(A\) and \(r\) be a positive real number. Then the real-valued function \(a^{r}_\varphi : A\times A\rightarrow\mathbb{R}\) defined by
Proof.
Proposition 2. Let \(\varphi\) be a pseudo-valuation on \(A\). Then
Proof. Let \(x, y, a \in A\). By (UP-1) and Proposition 1 (2), we have \(\varphi((a\cdot y)\cdot (a\cdot x))\leq \varphi(y\cdot x)\) and \(\varphi((a\cdot x)\cdot (a\cdot y))\leq \varphi(x\cdot y)\). Thus \begin{align*} d^{r}_\varphi(x, y) &= \dfrac{\varphi(x\cdot y)+\varphi(y\cdot x)}{r}\\ &\geq \dfrac{\varphi((a\cdot x)\cdot (a\cdot y))+\varphi((a\cdot y)\cdot (a\cdot x))}{r}\\ &=d^{r}_\varphi(a\cdot x, a\cdot y). \end{align*}
The following lemma is easily proved.Lemma 2. Let \(a_1, a_2, b_1, b_2\) be real numbers. Then
Theorem 28. Let \(d\) be a real-valued function on \(a \times A\). Define the real-valued functions \(d^{\circ}\) and \(d_{\circ}\) on \((A \times A)\times(A \times A)\) by
Proof.
Theorem 29. Let \(d\) be a real-valued function on \(A\times A\). Then
Proof. It is straightforward from Theorem 28.
Corollary 30. If \(\varphi\) is a \(0\)-weak pseudo-valuation (resp., weak valuation, near pseudo-valuation, near valuation, pseudo-valuation, valuation) on \(A\) and \(r\) is a positive real number, then \((d^{r}_\varphi)^{\circ}, (d^{r}_\varphi)_{\circ}, (D^{r}_\varphi)^{\circ}\), and \((D^{r}_\varphi)_{\circ}\) are pseudo-metrics without triangle inequality on \(A\times A\).
Proof. It is straightforward from Theorems 23,26 and 29(1).
Corollary 31. If \(\varphi\) is a pseudo-valuation (resp., valuation) on \(A\) and \(r\) is a positive real number, then \((d^{r}_\varphi)^{\circ}\) is a pseudo-metric and \((A^{r}_\varphi)^{\circ}\) is a quasi pseudo-metric on \(A\times A\).
Proof. It is straightforward from Theorems 24,27,29(2) and 29(3).
Corollary 32. If \(\varphi\) is a valuation on \(A\) and \(r\) is a positive real number, then \((d^{r}_\varphi)^{\circ}\) is a metric on \(A\times A\).
Proof. It is straightforward from Theorems 25 and 29(4).
We recall the definition of a uniformly continuous function of metric spaces:
Definition 8. Let metric spaces \((X, d_1)\) and \((Y, d_2)\), a function \(f : X \rightarrow Y\) is said to be uniformly continuous if for every real number \(\varepsilon > 0\) there exists a real number \(\delta > 0\) such that \begin{equation*} (\forall x,y\in X)(d_1(x, y) < \delta\Rightarrow d_2(f(x), f(y)) < \varepsilon). \end{equation*}
Theorem 33. If \(\varphi\) is a valuation on \(A\) with \(\inf\{(d^{r}_\varphi)^{\circ}((x,y), (a, b))\mid(d^{r}_\varphi)^{\circ}((x,y), (a, b))>0\}>0\) exists, then the binary operation \(\cdot\) on \(A\) is uniformly continuous.
Proof. Assume that \(\varphi\) is a valuation on a finite UP-algebra \(A\) with more than one element. By Theorem 25 and Corollary 32, we have \((A, d^{r}_\varphi)\) and \((A\times A, (d^{r}_\varphi)^{\circ})\) are metric spaces. Let \(\varepsilon>0\). Choose \(\delta=\inf\{(d^{r}_\varphi)^{\circ}((x,y), (a, b))\mid(d^{r}_\varphi)^{\circ}((x,y), (a, b))>0\}\). Let \((x,y), (a, b)\in A\times A\) be such that \((d^{r}_\varphi)^{\circ}((x,y), (a, b))< \delta\). Then \((d^{r}_\varphi)^{\circ}((x,y), (a, b))=0\). By (M-5), we have \((x,y)=(a, b)\) and so \(x=a\) and \(y=b\). Thus, by (M-2), we have \(d^{r}_\varphi(\cdot(x,y), \cdot(a, b))=d^{r}_\varphi(\cdot(x,y), \cdot(x, y))=d^{r}_\varphi(x\cdot y, x\cdot y)=0< \varepsilon\). Hence, the binary operation \(\cdot\) on \(A\) is uniformly continuous.
Theorem 34. If \(\varphi\) is a valuation on a finite UP-algebra \(A\) with more than one element, then the binary operation \(\cdot\) on \(A\) is uniformly continuous.
Proof. Assume that \(\varphi\) is a valuation on a finite UP-algebra \(A\) with more than one element. By (M-1) and (M-5) and \(A\times A\) has more than one element, we have \(\{(d^{r}_\varphi)^{\circ}((x,y), (a, b))\mid(d^{r}_\varphi)^{\circ}((x,y), (a, b))>0\}\) is a finite nonempty subset of \(\mathbb{R}\). Thus \(\inf\{(d^{r}_\varphi)^{\circ}((x,y), (a, b))\mid(d^{r}_\varphi)^{\circ}((x,y), (a, b))>0\}=\min\{(d^{r}_\varphi)^{\circ}((x,y), (a, b))\mid(d^{r}_\varphi)^{\circ}((x,y), (a, b))>0\}\) exists. By Theorem 33, we have the binary operation \(\cdot\) on \(A\) is uniformly continuous.