Super cyclic antimagic covering for some families of graphs

1. Introduction and definitions

In the present paper all graphs are finite simple and we follow the notion and terminology from the book [1]. For the cardinality of vertex set and edge set, we use \(n\) and \(m\) respectively. Graph labeling is a mapping which assigns labels to vertices or edges or both from the set of positive integers. Usually if we assign label to vertices then corresponding labeling called vertex labeling, similarly if we assign label to edges then that is called edge labeling and to assign label to both vertices and edges then such labeling called total labeling. The weight of a vertex under a labeling is the sum of labels assign to that vertex(if present) and label of edges(if present) incident to that vertex. The weight of an edge is the sum of labels assign to that edge(if present) and labels of end vertices(if present) of that edge. Throughout the paper we consider total labeling a bijective function from the set \(V(G) \cup E(G)\) into the set \(\{1,2,3,…,n+m\}\). We give the following definitions of our interest:

Definition 1. [2] A total labeling \(f\) is called \((a,d)\)-edge-antimagic total labeling if the set of all edge weights is \(\{a,a+d,a+2d,a+3d,…,a+(m-2)d,a+(m-1)d\},\) where \(a > 0\) and \(d\geq0\) are two integers.

The \((a,d)\)-edge-antimagic total labeling was first defined by Simanjuntak et al., in [2]. If in such type of labeling we assign smallest possible labels to vertices then it is called super \((a,d)\)-edge-antimagic total labeling. For the case of \(d=0\) the corresponding \((a,0)\)-edge-antimagic total labeling is edge-magic total labeling. In above definition the idea of edges weight is used, in particular we covered any graph by edges. Gutierrez and Llado in [3,4] used idea of covering and extended the theory of edge-magic total labeling into a magic total covering.

Definition 2. [3,4] For a graph \(G\) a family of subgraphs \(K_i\), \(1\leq i \leq s\) is called an edge covering of \(G\) if every edge of \(G\) belong to some \(K_i\). More precisely we say that \(G\) admit \((K_1,K_2,K_3,…,K_s)\)-covering. In the case when all \(K_i\) isomorphic to some given graph \(K\) then we called that \(G\) has \(K\)-covering.

Definition 3. [3,4] If we have a graph \(G\) which admits \(K\)-covering and \(f\) is a total mapping on graph \(G\) then weight of the subgraph \(K\) is denoted by \(W(K)\) and is: \[W(K)= \sum_{x\in V(K)}f(v)+\sum_{y\in E(K)}f(y).\] If the weight set of all subgraphs \(K_i, \ \ 1\leq i \leq s\) isomorphic to \(K\) is a given constant then we say that \(G\) admits \(K\)-magic total covering. When the label of vertices taken from the \(\{1,2,3,…,n\}\) then \(K\)-magic total covering called \(K\)-supermagic total covering.

Some results on \(K\)-supermagic total covering can be seen in [3,4,5,6,7,8,9]. Inayah et al., [10] extend the theory of \(K\)-supermagic total covering to super \((a,d)\)-\(K\)-antimagic total covering. Ali et al., in [11] proposed Super Edge-Magicness of Stars Like Graphs and H-groupmagic total labelings of families of fangraphs in [12].

Definition 4. [10] For a given graph \(G\) the total mapping \(f\) is called \((a,d)\)-\(K\)-antimagic total covering, if the weights of all subgraphs \(K_i\) isomorphic to \(K\) form and arithmetic sequence starts from a positive non-zero integer \(a\) and vary with difference \(d\geq 0\) where \(d\) is also an integer. If vertices label from the set \(\{1,2,3,…,n\}\) then such labeling called super \((a,d)\)-\(K\)-antimagic total covering.

In [10] the authors showed that shackle of \(p\) copies of any graph \(K\) can be covered by \(p\) subgraphs isomorphic to \(K\) is \(K\)-super antimagic. Recently, Fenovcikova et al., [13] proved that wheels are cycle antimagic. Some more result on super \((a,d)\)-\(K\)-antimagic labeling can be found in [14] but still this topic remains widely open. In the present paper, we find necessary conditions for the octagonal planner map and multiple wheel graph to be super cyclic antimagic cover and then discuss their super cyclic antimagic covering.

2. Super cyclic \((a,d)\)-antimagic covering of octagonal planner map

The octagonal planner map is a plane graph which is constructed from an octagon. If we have octagons in the plane then we join these octagons in such a way that they cover the plane and called that octagonal planner map. In octagonal planner map the plane is covered by octagons and squares. Let \(l\) be the number of columns and \(k\) be the number of rows in octagonal planner map then we denote the octagonal planner map by \(O_{l}^{k}\) shown in Figure 1. The vertex set \(V(O_{l}^{k})\) and edge set \(E(O_{l}^{k})\) of octagonal planner maps are: \(V (O_{k}^{l}) = \big\{e_{i}^{j},\, f_{i}^{j},\, 1\leq i\leq l, \ \ 1\leq j\leq k+1 \big\}\cup \{g_{i}^{j},\, h_{i}^{j}, \ \ 1\leq i\leq l+1, \ \ 1\leq j\leq k \big\},\) \(E(O_{k}^{l}) = \big\{e_{i}^{j}f_{i}^{j}, \ \ 1\leq i\leq l, \ \ 1\leq j\leq k+1 \big \} \cup \big \{g_{i}^{j}h_{i}^{j}, 1\leq i\leq l+1, \ \ 1\leq j\leq k \big \}\cup \big \{ f_{i}^{j}g_{i+1}^{j},e_{i}^{j}g_{i}^{j},h_{i}^{j}e_{i}^{j+1},f_{i}^{j+1}g_{i+1}^{j},1\leq i\leq l, \ \ 1\leq j\leq k \big\}.\)

However the cardinality of \(|V(O_{k}^{l})|=4kl+2l+2k\) and \(|E(O_{k}^{l})|=6kl+l+k\).

We can cover the octagonal planner map \(O_{l}^{k}\) by the 8-sided cycles \(C_{8,i}^{j}\), for \(1 \leq j \leq k\), \(1 \leq i \leq l\), having following vertex set and edge set: \[V(C_{8,i}^{j})=\big\{e_{i}^{j},\, f_{i}^{j},\, g_{i+1}^{j},\, h_{i+1}^{j},\, f_{i}^{j+1},\, e_{i}^{j+1},\, h_{i}^{j},\, g_{i}^{j}; 1 \leq i \leq l, 1 \leq j \leq k \big\}\] and \[E(C_{8,i}^{j})=\big\{e_{i}^{j}f_{i}^{j},\,f_{i}^{j}g_{i+1}^{j},\,g_{i+1}^{j}h_{i+1}^{j},\,f_{i}^{j+1}h_{i+1}^{j},\,e_{i}^{j+1}f_{i}^{j+1},\,e_{i}^{j+1}h_{i}^{j}, g_{i}^{j}h_{i}^{j},\,e_{i}^{j}g_{i}^{j} ;1 \leq i \leq l, 1 \leq j \leq k \big\}.\] The upper bound for the parameter \(d\) under super \((a,d)\)-\(C_8\)-antimagic covering of \(O_{l}^{k}\) is computed as following:

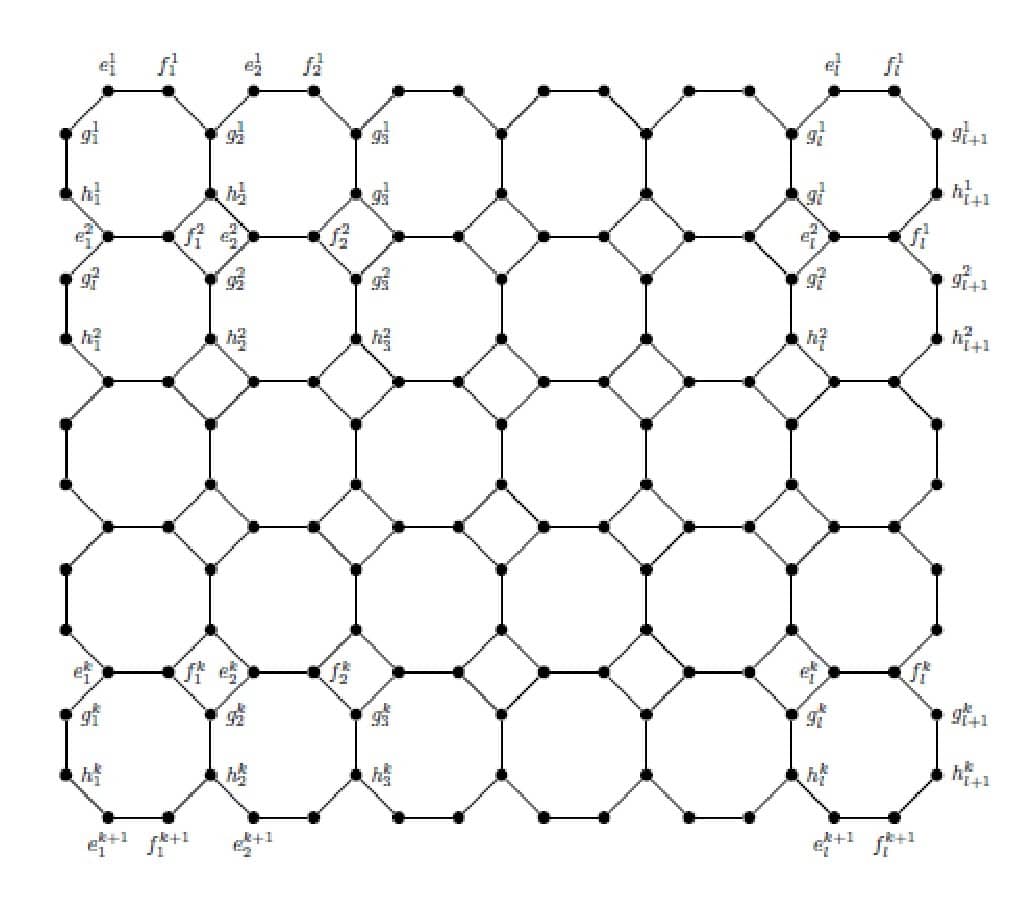
Theorem 1. The parameter \(d\) satisfy following relation under a super \((a,d)\)-\(C_8\)-antimagic covering of \(O_{l}^{k}\) \begin{equation*} d \leq 80+\bigg \lceil\frac{24l+24k-48}{kl-1}\bigg \rceil. \end{equation*}

Proof. Let \(\phi\) be a super \((a,d)\)-\(C_8\)-antimagic covering of the graph \(O_{l}^{k}\) then minimum possible weight of \(C_8\) is atleast \begin{equation*} \sum_{i=1}^{8}i+\sum_{i=1}^{8}(4kl+2l+2k+i)=32kl+16l+16k+72. \end{equation*} From the above inequality we have, \begin{equation*} a \geq 32kl+16l+16k+72 \end{equation*} and the largest weight of \(C_8\) is no more than \begin{equation*} \sum_{i=1}^{8}{(4kl+2l+2k+1-i)}+\sum_{i=1}^{8}{(10kl+3l+3k+1-i)}=112kl+40l+40k-56. \end{equation*} Thus \begin{equation*} a+(kl-1)d \leq 112kl+40l+40k-56. \end{equation*} By using above two inequalities we get, \begin{equation*} d \leq 80+\bigg \lceil\frac{24l+24k-48}{kl-1}\bigg \rceil. \end{equation*} For every \(k \geq 25\) and \( l \geq 25\), we get \(d \leq 81\).

Theorem 2. The octagonal planner map \(O_{l}^{k}\) admits super \((a,d)\)-\(C_{8}\)-antimagic covering for \(d \in \{2,4,6,8,10,12,14,16\},\) and \(k,l\geq 2.\)

Proof. For every \(d \in \{2,4,6,8,10,12,14,16\}\) and for every \(1\leq i\leq l, \ \ 1\leq j\leq k\) define a total labeling \(\phi_d\) of \(O_{l}^{k}\) as follow:

• \(\phi_2\Big(e_{i}^{j}g_{i}^{j} \Big)=\phi_6\Big(e_{i}^{j}g_{i}^{j} \Big)=\phi_{10}\Big(e_{i}^{j}g_{i}^{j} \Big)=\phi_{14}\Big(e_{i}^{j}g_{i}^{j} \Big)=3(k+1)l+2k(l+1)+(j-1)l+i ,\)
• \(\phi_4\Big(e_{i}^{j}g_{i}^{j} \Big)=\phi_8\Big(e_{i}^{j}g_{i}^{j} \Big)=\phi_{12}\Big(e_{i}^{j}g_{i}^{j}\Big)= \phi_{16}\Big(e_{i}^{j}g_{i}^{j} \Big)= 3(k+1)l+2k(l+1)+(k-j)l+i,\)
• \(\phi_2\Big(f_{i}^{j}g_{i+1}^{j} \Big)=\phi_6\Big(f_{i}^{j}g_{i+1}^{j} \Big)=\phi_{10}\Big(f_{i}^{j}g_{i+1}^{j} \Big)=\phi_{14}\Big(f_{i}^{j}g_{i+1}^{j} \Big)= 3(k+1)l+2k(l+1)+kl+(k+1-j)l\\+1-i,\)
• \(\phi_4\Big(f_{i}^{j}g_{i+1}^{j} \Big)=\phi_8\Big(f_{i}^{j}g_{i+1}^{j} \Big)=\phi_{12}\Big(f_{i}^{j}g_{i+1}^{j} \Big)=\phi_{16}\Big(f_{i}^{j}g_{i+1}^{j} \Big)= 3(k+1)l+2k(l+1)+kl+(k-j)l+i,\)
• \(\phi_2\Big(h_{i}^{j}e_{i}^{j+1} \Big)=\phi_4\Big(h_{i}^{j}e_{i}^{j+1} \Big)=\phi_6\Big(h_{i}^{j}e_{i}^{j+1} \Big)=\phi_{8}\Big(h_{i}^{j}e_{i}^{j+1} \Big)=\phi_{10}\Big(h_{i}^{j}e_{i}^{j+1} \Big)=\phi_{12}\Big(h_{i}^{j}e_{i}^{j+1} \Big)\\= 3(k+1)l+2k(l+1)+2kl+(k+1-j)l+1-i,\)
• \(\phi_{14}\Big(h_{i}^{j}e_{i}^{j+1} \Big)=\phi_{16}\Big(h_{i}^{j}e_{i}^{j+1} \Big)= 3(k+1)l+2k(l+1)+kl+(k-j)l+i,\)
• \(\phi_2\Big(h_{i+1}^{j}f_{i}^{j+1} \Big)=\phi_4\Big(h_{i+1}^{j}f_{i}^{j+1} \Big)=\phi_6\Big(h_{i+1}^{j}f_{i}^{j+1} \Big)=\phi_{8}\Big(h_{i+1}^{j}f_{i}^{j+1} \Big)=\phi_{10}\Big(h_{i+1}^{j}f_{i}^{j+1} \Big)=\phi_{12}\Big(h_{i+1}^{j}f_{i}^{j+1} \Big)\\= 3(k+1)l+2k(l+1)+3kl+(k+1-j)l+1-i,\)
• \(\phi_{14}\Big(h_{i+1}^{j}f_{i}^{j+1} \Big)=\phi_{16}\Big(h_{i+1}^{j}f_{i}^{j+1} \Big)= 3(k+1)l+2k(l+1)+3kl+(k-j)l+i.\)

For every \(1\leq i\leq l, 1\leq j\leq k+1\)

• \(\phi_2\Big(e_{i}^{j} \Big)=\phi_4\Big(e_{i}^{j} \Big)=\phi_6\Big(e_{i}^{j} \Big)=\phi_8\Big(e_{i}^{j} \Big)= (j-1)l+i,\)
• \(\phi_{10}\Big(e_{i}^{j} \Big)=\phi_{12}\Big(e_{i}^{j} \Big)=\phi_{14}\Big(e_{i}^{j} \Big)=\phi_{16}\Big(e_{i}^{j} \Big)= (k-j)l+i,\)
• \(\phi_2\Big(f_{i}^{j} \Big)=\phi_4\Big(f_{i}^{j} \Big)= (k+1)l+(k+1-j)l+1-i,\)
• \(\phi_6\Big(f_{i}^{j} \Big)=\phi_8\Big(f_{i}^{j} \Big)=\phi_{10}\Big(f_{i}^{j} \Big)=\phi_{12}\Big(f_{i}^{j} \Big)=\phi_{14}\Big(f_{i}^{j} \Big)=\phi_{16}\Big(f_{i}^{j} \Big)= (k+1)l+(k-j)l+i,\)
• \(\phi_2(e_{i}^{j}f_{i}^{j})=\phi_4(e_{i}^{j}f_{i}^{j})=\phi_{6}(e_{i}^{j}f_{i}^{j})=\phi_{8}(e_{i}^{j}f_{i}^{j})=\phi_{10}(e_{i}^{j}f_{i}^{j})=\phi_{12}(e_{i}^{j}f_{i}^{j})= 2(k+1)l+2k(l+1)+(j-1)l+i,\)
• \(\phi_{14}(e_{i}^{j}f_{i}^{j})=\phi_{16}(e_{i}^{j}f_{i}^{j})= 2(k+1)l+2k(l+1)+(k+1-j)l+i.\)

For every \(1\leq i\leq l+1, 1\leq j\leq k\)

• \(\phi_2\Big(g_{i}^{j} \Big)=\phi_4\Big(g_{i}^{j} \Big)= 2(k+1)l+(j-1)(l+1)+i,\)
• \(\phi_6\Big(g_{i}^{j} \Big)=\phi_8\Big(g_{i}^{j} \Big)=\phi_{10}\Big(g_{i}^{j} \Big)=\phi_{12}\Big(g_{i}^{j} \Big)=\phi_{14}\Big(g_{i}^{j} \Big)=\phi_{16}\Big(g_{i}^{j} \Big)= 2(k+1)l+(k-j)(l+1)+i,\)
• \(\phi_2\Big(h_{i}^{j} \Big)=\phi_4\Big(h_{i}^{j} \Big)=\phi_6\Big(h_{i}^{j} \Big)=\phi_8\Big(g_{i}^{j} \Big)= 2(k+1)l+k(l+1)+(k+1-j)(l+1)+1-i, \)
• \(\phi_{10}\Big(h_{i}^{j} \Big)=\phi_{12}\Big(h_{i}^{j} \Big)=\phi_{14}\Big(h_{i}^{j} \Big)=\phi_{16}\Big(h_{i}^{j} \Big)= 2(k+1)l+k(l+1)+(k-j)(l+1)+i,\)
• \(\phi_{d}\Big(g_{i}^{j}h_{i}^{j} \Big)= 3(k+1)l+2k(l+1)+4kl+(j-1)(l+1)+i. \)

The total labeling \(\phi_d\) label the vertices \(e_i^j\),\(f_i^j\),\(g_i^j\) and \(h_i^j\) from the set \(\{1,2,….,4kl+2l+2k\}\), where each label is used once and covers all the labels used. All the edges of the graph \(O_{l}^{k}\) labeled from the set \(\{4kl+2l+2k+1,4kl+2l+2k+2,….,10kl+3l+3k\}\), where each label used once and all the labels used from the mentioned set. This shows that the total labeling \(\phi_d\) is a bijective function from the set \(V(O_{l}^{k})\bigcup E(O_{l}^{k})\) into the set \(\{1,2,….,10kl+3l+3k\}.\)

Under the labeling \(\phi_d\) weight of the cycles \(C_{8,i}^{j}\), where \(1\leq i \leq l\) and \(1 \leq j \leq k\) are:

\begin{align*} &wt_d(C_{8,i}^{j})=\phi_d\Big(e_{i}^{j}\Big)+\phi_d\Big(f_{i}^{j}\Big)+\phi_d\Big(g_{i+1}^{j}\Big)+\phi_d\Big(h_{i+1}^{j}\Big)+ \phi_d\Big(f_{i}^{j+1}\Big)+\phi_d\Big(e_{i}^{j+1}\Big)+\phi_d\Big(h_{i}^{j}\Big)+\phi_d\Big(g_{i}^{j}\Big)+\phi_d\Big(e_{i}^{j}f_{i}^{j-1}\Big)\\ &\;\;\;+ \phi_d\Big(f_{i}^{j}g_{i+1}^{j}\Big)+\phi_d\Big(g_{i+1}^{j}h_{i+1}^{j}\Big)+\phi_d\Big(h_{i+1}^{j}f_{i}^{j+1}\Big)+\phi_d\Big(e_{i}^{j+1}f_{i}^{j+1}\Big) +\phi_d\Big(h_{i}^{j}e_{i}^{j+1}\Big)+\phi_d\Big(g_{i}^{j}h_{i}^{j}\Big)+\phi_d\Big(g_{i}^{j}e_{i}^{j}\Big). \end{align*} \[wt_d(C_{8,i}^{j})= \left\{ \begin{array}{ll} 71kl+31l+20k+7-2lj+2i, & for \ \ d=2, \\ 72kl+31l+20k+6-4lj+4i, & for \ \ d=4, \\ 73kl+31l+22k+7-6lj+6i, & for \ \ d=6, \\ 74kl+31l+22k+6-8lj+8i, & for \ \ d=8, \\ 75kl+29l+22k+5-10lj+10i, & for \ \ d=10, \\ 76kl+29l+22k+4-12lj+12i, & for \ \ d=12, \\ 74kl+29l+22k+3-14lj+14i, & for \ \ d=14, \\ 75kl+29l+22k+2-16lj+16i, & for \ \ d=16. \end{array} \right.\]

For the cases \(d=\{2,4,6,8,10,12,14,16\}\), when we put values of \(i\) and \(j\) from \(1\leq i \leq l\) and \(1\leq j \leq k\) in \(wt_d(C_{8,i}^{j})\), we get the sets \(\{69kl+31l+20k+9,69kl+31l+20k+11,69kl+31l+20k+13,….,71kl+31l+20k+7\}\), \(\{68kl+31l+20k+10,68kl+31l+20k+14,68kl+31l+20k+18,….,72kl+31l+20k+6\}\), \(\{67kl+31l+22k+13,67kl+31l+22k+19,67kl+31l+22k+25,….,73kl+31l+22k+7\}\), \(\{66kl+31l+22k+14,66kl+31l+22k+22,66kl+31l+22k+30,….,74kl+31l+22k+6\}\), \(\{65kl+29l+22k+15,65kl+29l+22k+25,65kl+29l+22k+35,….,75kl+29l+22k+5\}\), \(\{64kl+29l+22k+16,66kl+29l+22k+28,64kl+29l+22k+40,….,76kl+29l+22k+4\}\), \(\{60kl+29l+22k+17,60kl+29l+22k+31,60kl+29l+22k+45,….,74kl+29l+22k+3\}\) and \(\{59kl+29l+22k+18,59kl+29l+22k+34,59kl+29l+22k+50,….,75kl+29l+22k+2\}\) which showed that weights of the cycles \(C_{8,i}^{j}\) form an arithmetic sequence with differences \(2,4,6,8,10,12,14\) and \(16.\)

3. Super \((a,d)\)-\(C_3\)-antimagic covering of multiple-wheel graph \(mW_n\)

A multiple-wheel graph \(mW_n\) of size \(n\) can be composed of \(mC_n + K_1,\) that is it consists of \(m\) cycles of size \(n,\) where the vertices of the \(m\) cycles are all connected to a common hub. For \(m=2\) the multiple-wheel graph is called double-wheel graph, the graceful labeling of double-wheel graph were discussed in [15]. Let the vertex set and edge set of \(mW_n\) be define as follows: \begin{eqnarray*} V(mW_n)&=&\{u_i^j; \,\,\, 0 \leq i \leq n-1, \,\,\, 0 \leq j \leq m-1\} \cup \{c\},\\ E(mW_n)&=&\{ cu_i^j; 0 \leq i \leq n-1, \,\, 0 \leq j \leq m-1 \} \cup \{ u_i^ju_{i+1}^j; \,\,\, 0 \leq i \leq n-1, 0 \leq j \leq m-1\}, \end{eqnarray*} where \(|V(mW_n)|=1+mn\) and \(|E(mW_n)|=2mn\) be the cardinality of vertex set and edge set respectively.

The multiple-wheel graph \(mW_n\) shown in Figure 2 can be cover with cycle \(C_3\). We denote the cycles \(C_3\) by \(C_{3,i}^{j}\) having vertex set and edge set as follows: \begin{align*} V(C_{3,i}^{j})&=\{c,u_i^j, u_{i+1}^j\},\\ E(C_{3,i}^{j})&=\{ cu_i^j,u_{i}^{j}u_{i+1}^{j},cu_i^j\}. \end{align*} The upper bound for the parameter \(d\) under super \((a,d)\)-\(C_3\)-antimagic covering of \(mW_n\).

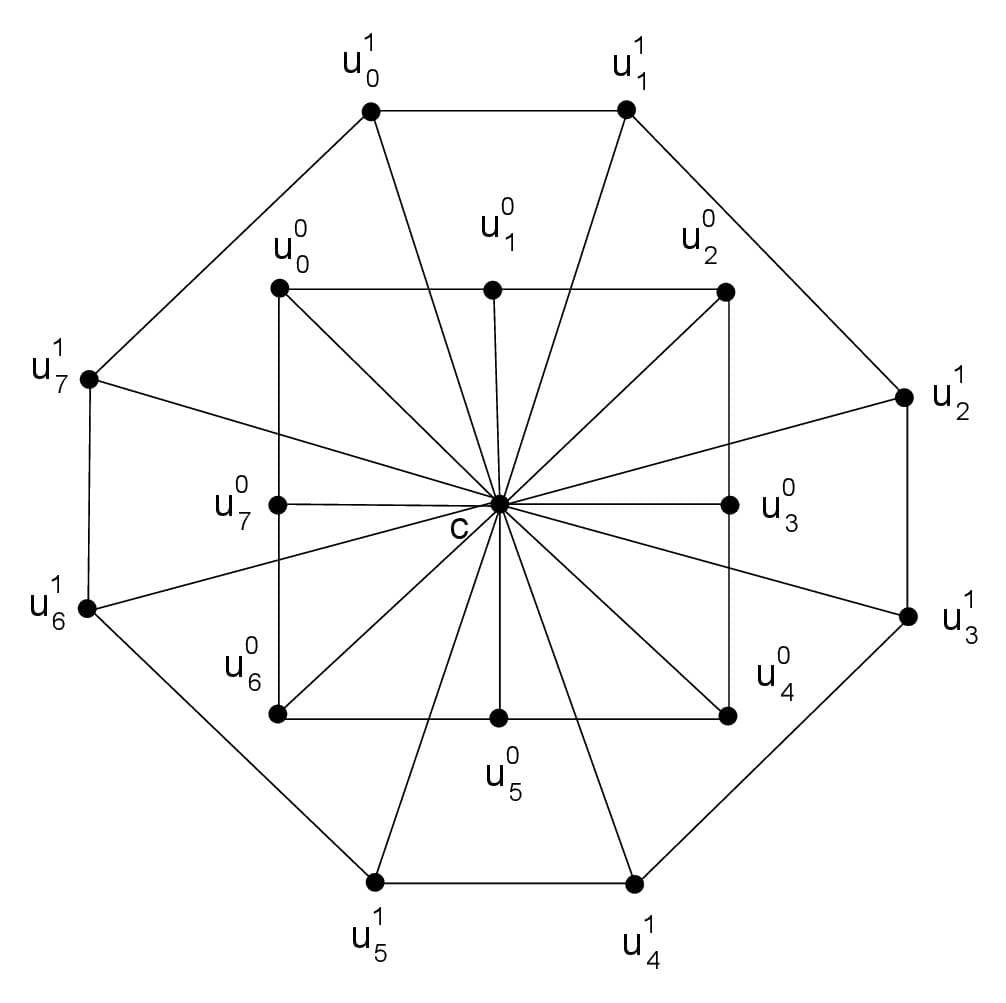
Theorem 3. For every \(m\geq 2\) and \(n\geq 3\), the parameter \(d\leq 9\) for a super \((a,d)\)-\(C_3\)-antimagic covering of \(mW_n\).

Proof. Let \(\xi\) be a super \((a,d)\)-\(C_3\)-antimagic covering of the graph \(mW_n\) then minimum possible weight of \(C_3\) is atleast \( \sum_{i=1}^{3}i+\sum_{i=1}^{3}(mn+1+i)=3mn+15 \) and the largest weight of \(C_3\) is no more than \( \sum_{i=1}^{3}{(mn+2-i)}+\sum_{i=1}^{3}{(3mn+2-i)}=12mn. \) Thus \( a+(mn-1)d \leq 12mn \) and \( d \leq \bigg\lceil9-\frac{6}{mn-1}\bigg\rceil. \) For \(m\geq 2\) and \(n \geq 3\), we get \(d \leq 9.\)

Theorem 4. For every \(n\ge3\) and \( m\ge 2\), the graph \(mW_n\) admits a super \((a,d)\)-\(C_3\)-antimagic total labeling for \(d=\{1,3\}\).

Proof. Let \(f_d:V(mW_n) \cup E(mW_n) \rightarrow \{1, 2, 3, …, 3mn+1\}\) is a total labeling define as: \begin{align*} f_d(c)&=1, &\nonumber\\ f_1(u_i^j)&=jn+2+i, & \hbox{for}\,\,\, 0\le i\le n-1,\,\,\, 0\le j\le m-1,\nonumber\\ f_1(cu_i^j)&=mn+(m-j)n+1-i, & \hbox{for}\,\,\, 0\le i\le n-1,\,\,\, 0\le j\le m-1, \nonumber\end{align*} \begin{align*}f_1(u_i^ju_{i+1}^j)&=2mn+jn+2+i, & \hbox{for}\,\,\, 0\le i\le n-1,\,\,\, 0\le j\le m-1,\end{align*} \begin{align*}f_3(u_i^j)&= \begin{cases} mn-2m+2+j, & \hbox{for}\,\,\, 0\le j\le m-1, \\ 2m+1-j, & \hbox{for}\,\,\, i=1 ,\,\, 0\le j\le m-1, \\ 2+j, & \hbox{for}\,\,\, i=n-2,\,\, 0\le j\le m-1,\\ im+2+j, & \hbox{for}\,\,\,2\leq i \leq n-3, \,\, 0\le j\le m-1,\\ (n-1)m+2+j, & \hbox{for}\,\,\, i=n-1,\,\, 0\le j\le m-1, \end{cases}\\ &\\ f_3(u_i^ju_{i+1}^j)&= \begin{cases} 3mn+1-j, & \hbox{for}\,\,\, i=n-3, \,\, 0\le j\le m-1, \\ 3mn-m+1-j, & \hbox{for}\,\,\, i=n-2, \,\, 0\le j\le m-1, \\ 2mn+2m+1-j, & \hbox{for}\,\,\, i=n-1, \,\, 0\le j\le m-1,\\ mn+2+j, & \hbox{for}\,\,\, i=0, \,\, 0\le j\le m-1, \\ 3mn-3m+2+j, & \hbox{for}\,\,\, i=1, \,\, 0\le j\le m-1,\\ 2mn+(n-1-i)m+1-j, & \hbox{for}\,\,\, 2 \leq i\leq n-4, \,\, 0\le j\le m-1, \end{cases}\\ &\\ f_3(cu_i^j)&= \begin{cases} mn+im+2+j, & \hbox{for}\,\,\, 1 \leq i \leq n-1, \,\, 0\le j\le m-1, \\ 2mn+2+j, & \hbox{for}\,\,\, i=0, \,\, 0\le j\le m-1. \end{cases} \end{align*} For every \( 0\leq i \leq n-1\) and \( 0\leq j \leq m-1\) the weights of \(C_{3,i}^j\) are as follows: \begin{align*} wt_d(C_{3,i}^j)&=f_d(c)+f_d(u_i^j)+f_d(u_{i+1}^j)+f_d(cu_i^j)+f_d(u_i^ju_{i+1}^j+f_d(cu_{i+1}^j),\\ wt_d(C_{3,i}^j)&= \begin{cases} jn+i+6mn+9, & \hbox{for}\,\,\, d=1, \\ 5mn+m+3j+3im+10, & \hbox{for}\,\,\, d=3. \end{cases} \end{align*} When we put values of \(i\) and \(j\) from \(0\leq i \leq n-1\) and \(0\leq j \leq m-1\) in \(wt_d(C_{3,i}^j)\), we get the sets \(\{6mn+9,6mn+10,6mn+11,….,7mn+8\}\) and \(\{5mn+m+10,5mn+m+13,5mn+m+16,….,8mn+m+7\}\) form an arithmetic sequence with differences \(1\) and \(3.\)

4. Conclusion

In this paper, we construct upper bound for the parameter \(d\) and examine the existence of \((a,d)\)-\(C_8\)-supermagic labelings for octagonal grid graph \(O_m^n\) for all \( m \ge3\) , \(n \ge 2\) and for \(d \in \{2,4,6,8,10,12,14,16\}\). Moreover we showed that the multiple wheel graph \(mW_n\) for \(m\geq 2\) and \(n\geq 3\) admits \((a,d)\)-\(C_3\)-supermagic labeling for \( d \in \{1, 3\}\).

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest

The authors declare no conflict of interest.