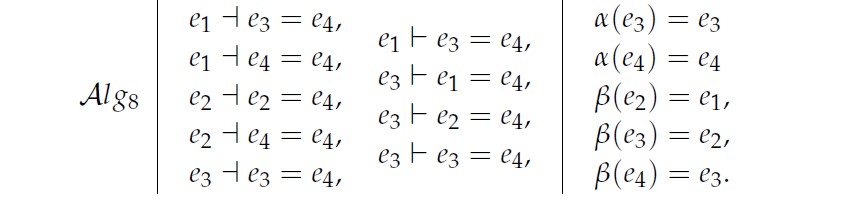The aim of this paper is to introduce and study BiHom-associative dialgebras. We give various constructions and study their connections with BiHom-Leibniz algebras and BiHom-Poisson dialgebras. Next, we discuss the central extensions of BiHom-associative dialgebras and we describe the classification of \(n\)-dimensional BiHom-associative dialgebras for \(n\leq 4\).
The diassociative algebras, also known as associative dialgebras, were introduced by Loday in 1990 as a generalization of associative algebras and were further developed in detail in [1,2,3,4,5,6,7,8,9]. They are a generalization of associative algebras in the sense that they possess two associative multiplications and obey three other conditions. When the two associative laws are equal, we recover associative algebras. One of his motivations was to find an algebra whose commutator gives rise to a Leibniz algebra, as is the case in the relation between associative algebra and Lie algebra. Another motivation comes from the research of an obstruction to periodicity in algebraic K-theory. Nowadays, these algebras have found their applications in classical geometry, non-commutative geometry, and physics.
However, the centroid occurs naturally in the study of derivations of an algebra and plays an important role in understanding forms of an algebra. It is also a key element in the classification of associative and diassociative algebras. Furthermore, averaging operators [10] are used in the deformation of an algebra to generate another algebraic structure. The Nijenhuis operator on an associative algebra was introduced in [11] to study quantum bi-Hamiltonian systems, while the notion of the Nijenhuis operator on a Lie algebra originated from the concept of the Nijenhuis tensor, which was introduced by Nijenhuis in the study of pseudo-complex manifolds and was related to the well-known concepts of the Schouten-Nijenhuis bracket, the Frolicher-Nijenhuis bracket [12], and the Nijenhuis-Richardson bracket. The associative version of the Nijenhuis relation may be regarded as the homogeneous version of the Rota-Baxter relation [13].
Recently, BiHom-algebraic structures were introduced by Graziani et al. in [14] from a categorical approach as an extension of the class of Hom-algebras. Since then, other interesting BiHom-type algebraic structures of many Hom-algebraic structures have been intensively studied, such as BiHom-Lie color algebra structures [15], representations of BiHom-Lie algebras [16], construction of BiHom-post-Lie algebras [17]HTS}, BiHom-Lie superalgebra structures [18], \({\sigma, \tau}\)-Rota-Baxter operators, infinitesimal Hom-bialgebras, and the associative (Bi)Hom-Yang-Baxter equation [19]. Additionally, the construction and deformation of BiHom-Novikov algebras [20], the n-ary generalization of BiHom-Lie algebras and BiHom-associative algebras [21], Rota-Baxter operators on BiHom-associative algebras and related structures [22], and constructions and generalized derivations of multiplicative \(n\)-BiHom-Lie color algebras [23] have also been studied.
The goal of this paper is to introduce, classify, and study structures and central extensions of BiHom-associative dialgebras. The paper is organized as follows. In S2, we define BiHom-associative dialgebras, give some constructions using twisting, direct sum, elements of the centroid, averaging operator, Nijenhuis operator, and Rota-Baxter relation. We establish a connection between BiHom-associative dialgebras and BiHom-Leibniz algebras. We introduce the action of a BiHom-Leibniz algebra on another one and give a Leibniz structure on the semidirect sum. Then, we show that the semidirect product of BiHom-Leibniz algebras associated with BiHom-associative dialgebras is the same as the BiHom-Leibniz algebra associated with the semidirect product of BiHom-associative dialgebras. Finally, we introduce BiHom-Poisson dialgebras and show that any BiHom-associative dialgebra carries a structure of a BiHom-Poisson dialgebra.
In S3, we introduce the notion of a central extension of BiHom-associative dialgebras and define \(2\)-cocycles and \(2\)-coboundaries of BiHom-associative dialgebras with coefficients in a trivial BiHom-module. Then, we establish the relationship between \(2\)-cocycles and central extensions. Section 4 is devoted to the classification of \(n\)-dimensional BiHom-associative dialgebras for \(n\leq 4\).
Definition 1. A BiHom-associative dialgebra is a 5-tuple \((A, \dashv, \vdash, \alpha, \beta)\) consisting of a linear vector space \(A\), two bilinear maps \(\dashv, \vdash: A\times A \longrightarrow A\), and two linear maps \(\alpha, \beta : A\longrightarrow A\) satisfying, for all \(x, y, z\in A\), the following conditions: \begin{eqnarray} \alpha\circ\beta&=&\beta\circ\alpha,\tag{1}\\ (x\dashv y)\dashv\beta(z)&=&\alpha(x)\dashv(y\dashv z),\tag{2}\label{eq4}\\ (x\dashv y)\dashv\beta(z)&=&\alpha(x)\dashv(y\vdash z),\tag{3}\label{eq5}\\ (x\vdash y)\dashv\beta(z)&=&\alpha(x)\vdash(y\dashv z),\tag{4}\label{eq6}\\ (x\dashv y)\vdash\beta(z)&=&\alpha(x)\vdash(y\vdash z),\tag{5}\label{eq7}\\ (x\vdash y)\vdash\beta(z)&=&\alpha(x)\vdash(y\vdash z).\tag{6}\label{eq8} \end{eqnarray}
We call \(\alpha\) and \(\beta\) (in this order) the structure maps of \(A\). If \(\alpha\) and \(\beta\) are bijections, then \((A, \dashv, \vdash, \alpha, \beta)\) is said to be a semi-regular BiHom-associative dialgebra.Example 1. Any Hom-associative dialgebra [29] or any associative dialgebra is a BiHom-associative dialgebra by setting \(\beta = \alpha\) or \(\alpha=\beta=id\), respectively.
Example 2. Let \((A, \dashv, \vdash, \alpha, \beta)\) be a BiHom-associative dialgebra. Consider the vector space of \(n\times n\) matrices \(\mathcal{M}n(D)=\mathcal{M}n(\mathbb{K})\otimes D\) with the linear maps \(\boldsymbol{\alpha} (A)=(\alpha(a{ij}))\), \({\boldsymbol{\beta}}(A)=(\beta(a{ij}))\) for all \(A\in \mathcal{M}n(D)\) and the products \((a\triangleleft b){ij}=\sum_{k}a_{ik}\dashv b_{kj}\) and \((a\triangleright b){ij}=\sum{k}a_{ik}\vdash b_{kj}\). Then, \((\mathcal{M}_n(D), \triangleleft, \triangleright, {\boldsymbol{\alpha}}, {\boldsymbol{\beta}})\) is a BiHom-associative dialgebra.
Definition 2. A morphism of BiHom-associative dialgebras is a linear map \(f : A \longrightarrow B\) satisfying \[f : ({D}, \dashv, \vdash, \alpha, \beta)\rightarrow({D}’, \dashv’,\vdash’, \alpha’, \beta’)\] such that \[\alpha’\circ f =f\circ\alpha,\;\; \beta’\circ f=f\circ\beta\] and \begin{eqnarray} f(x\dashv y)&=&f(x)\dashv’f(y)\nonumber\\ f(x\vdash y)&=&f(x)\vdash’f(y),\nonumber \end{eqnarray} for all \(x, y \in {D}.\)
Definition 3. A BiHom-associative dialgebra \((A, \dashv, \vdash, \alpha, \beta)\) in which \(\alpha\) and \(\beta\) are morphisms is said to be a multiplicative BiHom-associative dialgebra. Moreover, if \(\alpha\) and \(\beta\) are bijectives (i.e. automorphisms), then \((A, \dashv, \vdash, \alpha, \beta)\) is said to be a regular BiHom-associative dialgebra.
Remark 1. Any regular BiHom-associative dialgebra is a semi-regular BiHom-associative dialgebra whose structure maps are morphisms.
In the following theorem, we prove that any BiHom-associative dialgebra turns to another one via endomorphisms.Theorem 1. Let \((D, \dashv, \vdash, \alpha, \beta )\) be a BiHom-associative dialgebra and \(\alpha’, \beta’ : D\rightarrow D\) be two commuting endomorphisms. Then, \[D_(\alpha’, \beta’)=(D, \triangleleft:=\dashv(\alpha’\otimes\beta’), \triangleright:=\vdash(\alpha’\otimes\beta’), \alpha\alpha’, \beta\beta’)\] is a BiHom-associative dialgebra.
Proof. We only prove one axiom and leave the rest to the reader. So, for any \(x, y, z\in D\), \begin{eqnarray} (x\triangleleft y)\triangleleft\beta\beta'(z)- \alpha\alpha'(x)\triangleleft(y\triangleright z)&= &\alpha'(\alpha'(x)\dashv\beta'(y))\dashv\beta’\beta\beta'(z)-\alpha’\alpha\alpha'(x)\dashv\beta'(\alpha'(y)\vdash\beta'(z))\nonumber\\ &=&(\alpha’\alpha'(x)\dashv\alpha’\beta'(y))\dashv\beta\beta’\beta'(z)-\alpha\alpha’\alpha'(x)\dashv(\alpha’\beta'(y)\vdash\beta’\beta'(z)).\nonumber \end{eqnarray} The left hand side vanishes by (3). And, this ends the proof.
We have the following sequence of corollaries.Corollary 2. Let us consider the multiplicative BiHom-associative dialgebra \((D, \dashv, \vdash, \alpha, \beta )\). Then, \[(D, \dashv\circ(\alpha^n\otimes\beta^n), \vdash\circ(\alpha^n\otimes\beta^n), \alpha^{n+1}, \beta^{n+1})\] is also a multiplicative BiHom-associative dialgebra.
Proof. It suffices to take \(\alpha’=\alpha^n\) and \(\beta’=\beta^n\) in Theorem 1.
Corollary 3. Let \((D, \dashv, \vdash, \alpha)\) be a multiplicative Hom-associative dialgebra and \(\beta : D\rightarrow D\) be an endomorphism of \(D\). Then, \[(D, \dashv\circ(\alpha\otimes\beta), \vdash\circ(\alpha\otimes\beta), \alpha^{2}, \beta)\] is also a Hom-associative dialgebra.
Proof. It suffices to take \(\alpha’=\alpha\) and replace \(\beta\) by \(Id_D\), and \(\beta’\) by \(\beta\) in Theorem 1.
The next corollary states that any regular BiHom-associative dialgebra give rises to an associative dialgebra.Corollary 4. If \((D, \dashv, \vdash, \alpha, \beta)\) is a regular BiHom-associative dialgebra, then \[(D, \dashv\circ(\alpha^{-1}\otimes\beta^{-1}), \vdash\circ(\alpha^{-1}\otimes\beta^{-1}))\] is an associative dialgebra.
Proof. We have to take \(\alpha’=\alpha^{-1}\) and \(\beta’=\beta^{-1}\) in Theorem 1.
Corollary 5. Let \((D, \dashv, \vdash)\) be an associative dialgebra and \(\alpha : D\rightarrow D\) and \(\beta : D\rightarrow D\) a pair of commuting endomorphisms of \(D\). Then, \[(D, \dashv\circ(\alpha\otimes\beta), \vdash\circ(\alpha\otimes\beta), \alpha, \beta)\] is a BiHom-associative dialgebra.
Proof. We have to take \(\alpha=\beta=Id_D\) and replace \(\alpha’\) by \(\alpha\), and \(\beta’\) by \(\beta\) in Theorem 1.
Now, we introduce centroid for BiHom-associative dialgebras.Definition 4. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a BiHom-associative dialgebra. For any non negative integers \(k, l\), a linear map \(\theta : D\rightarrow D\) is called an element of \((\alpha^k, \beta^l)\)-element of centroid on \(D\) if, for all \(x, y\in D\), \begin{eqnarray} \alpha\circ\theta&=&\theta\circ\alpha, \beta\circ\theta=\theta\circ\beta,\tag{7}\\ \theta(x)\dashv \alpha^k\beta^l(y)&=&\theta(x)\dashv\theta(y)=\alpha^k\beta^l(x)\dashv \theta(y),\tag{8}\\ \theta(x)\vdash \alpha^k\beta^l(y)&=&\theta(x)\vdash \theta(y)=\alpha^k\beta^l(x)\vdash \theta(y)\tag{9}. \end{eqnarray} The set of all \((\alpha^k, \beta^l)\)-elements of centroid of \(D\) is denoted \(Cent_(\alpha^k, \beta^l)(D)\). The centroid of \(D\) is denoted \(Cent(D)\) and defined by \(Cent(D)=\oplus_{k, l} Cent_(\alpha^k, \beta^l)(D)\).
Proposition 1. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a BiHom-associative dialgebra, \(\phi : D\rightarrow D\) and \(\psi : D\rightarrow D\) be two commuting elements of cenroid. Let us define \[x\triangleleft y:=\phi(x)\dashv y \mbox{and} x\triangleright y:=\psi(x)\vdash y.\] Then, \((D, \triangleleft, \triangleright, \alpha, \beta)\) is a BiHom-associative dialgebra if and only if \[Im(\phi-\psi)\in Z_{\dashv}(D):=\{x\in D/x\dashv y=0, \forall y\in D\}\] and \[Im(\phi-\psi)\in Z_{\vdash}(D):=\{x\in D/y\vdash x=0, \forall y\in D\}.\]
Proof. We only prove axioms (3) and (5), the three others come from BiHom-associativity. So, for any \(x, y, z\in D\), \begin{eqnarray} (x\triangleleft y)\triangleleft\beta(z)-\alpha(x)\triangleleft(y\triangleright z) &=&(\phi(x)\dashv y)\dashv\phi\beta(z)-\phi\alpha(x)\dashv(y\vdash\psi(z))\nonumber\\ &=&(\phi(x)\dashv y)\dashv\beta\phi(z)-\alpha\phi(x)\dashv(y\vdash\psi(z))\nonumber\\ & \stackrel(3){=}&(\phi(x)\dashv y)\vdash\beta\phi(z)-(\phi(x)\dashv y)\vdash\beta\psi(z))\nonumber\\ &=&(\phi(x)\dashv y)\vdash\beta(\phi-\psi)(z)\nonumber\\ &=&\alpha\phi(x)\dashv (y\vdash(\phi-\psi)(z))\nonumber, \end{eqnarray} and \begin{eqnarray} (x\triangleleft y)\triangleright \beta(z)-\alpha(x)\triangleright(y\triangleright z) &=&(\phi(x)\dashv y)\vdash\beta\psi(z)-\psi\alpha(x)\vdash(y\vdash\psi(z))\nonumber\\ &=&(\phi(x)\dashv y)\vdash\beta\psi(z)-\alpha\psi(x)\vdash(y\vdash\psi(z))\nonumber\\ &\stackrel(5){=}&(\phi(x)\dashv y)\vdash\beta\psi(z)-(\psi(x)\dashv y)\vdash\beta\psi(z)\nonumber\\ &=&[(\phi(x)-\psi(x))\dashv y]\vdash\beta\psi(z)\nonumber. \end{eqnarray} A study of cancellation of the two equalities allows to conclude.
Proposition 2. Let \((A, \cdot, \alpha, \beta)\) be a BiHom-associative algebra, and \(\phi : A\rightarrow A\) and \(\psi : A\rightarrow A\) be a paire of commuting elements of cenroid. Let us define \[x\dashv y:=\phi(x)\cdot y \mbox{and} x\vdash y:=\psi(x)\cdot y.\] Then, \((A, \dashv, \vdash, \alpha, \beta)\) is a BiHom-associative dialgebra if and only if \(Im(\phi-\psi)\) is contained in the set of isotropic vectors.
Proof. We only prove axioms (3) and (5), the three other come from BiHom-associativity. So for any \(x, y, z\in A\), \begin{eqnarray} (x\dashv y)\dashv\beta(z)-\alpha(x)\dashv(y\vdash z) &=&(\phi(x)y)\phi\beta(z)-\phi\alpha(x)(y\psi(z))\nonumber\\ &=&(\phi(x)y)\beta\phi(z)-\alpha\phi(x)(y\psi(z))\nonumber\\ &=&(\phi(x)y)\beta\phi(z)-(\phi(x)y)\beta\psi(z))\nonumber\\ &=&(\phi(x)y)\beta(\phi-\psi)(z)\nonumber\\ &=&\alpha\phi(x)(y(\phi-\psi)(z))\nonumber. \end{eqnarray} and \begin{eqnarray} (x\dashv y)\vdash \beta(z)-\alpha(x)\vdash(y\vdash z) &=&(\phi(x)y)\beta\psi(z)-\psi\alpha(x)(y\psi(z))\nonumber\\ &=&(\phi(x)y)\beta\psi(z)-\alpha\psi(x)(y\psi(z))\nonumber\\ &=&(\phi(x)y)\beta\psi(z)-(\psi(x)y)\beta\psi(z)\nonumber\\ &=&[(\phi(x)-\psi(x))y]\beta\psi(z)\nonumber. \end{eqnarray} A study of cancelation of the two equalities allow to conclude.
Remark 2. Proposition 2 may be seen as a corollary of Proposition 1.
Proposition 3. Let us consider a BiHom-associative algebra \((A, \cdot, \alpha, \beta)\) and \((M, \ast_L, \ast_R, \alpha_M, \beta_M)\) an \(A\)-BiHom-bimodule i.e. \(M\) is a vector space, \(\alpha_M :M\rightarrow M\) and \(\beta_M : M\rightarrow M\) are two linear maps, and \(\ast_L : A\times M\rightarrow M\) and \(\ast_R : M\times A\rightarrow M\) two bilinear maps such that for any \(x, y\in A\) and \(m\in M\), \begin{eqnarray} \alpha(x)\ast_L(y\ast_L m)&=&(x\cdot y)\ast_L\beta_M(m),\nonumber\\ \alpha(x)\ast_L(m\ast_R y)&=&(x\ast_L m)\ast_R\beta(y),\tag{10}\label{m2}\\ \alpha_M(m)\ast_R(x\cdot y)&=&(m\ast_R x)\ast_R\beta(y).\nonumber \end{eqnarray} Suppose that \(f :M\rightarrow A\) is a morphism of \(A\)-BiHom-bimodule i.e. \(f\) is linear such that \(\alpha\circ f=f\circ\alpha_M\), \(\beta\circ f=f\circ\beta_M\) and \begin{eqnarray} f(x\ast_L m)&=&x\cdot f(m) \nonumber\\ f(m\ast_R x)&=&f(m)\cdot x.\nonumber \end{eqnarray} Then, \((M, \triangleleft, \triangleright, \alpha_M, \beta_M)\) is a BiHom-associative dialgebra with \[m\triangleleft n=f(m)\ast_L n\mbox{and} m\triangleright n=m\ast_Rf(n),\] for all \(m, n\in M\).
Proof. We only prove axiom (6), the other being proved similarly. For any \(m, n, p\in M\), \begin{eqnarray} (m\triangleleft n)\triangleright \beta_M(p) &=&(f(m)\ast_L n)\ast_R f\beta_M(p)\nonumber\\ &=&(f(m)\ast_L n)\ast_R \beta f(p)\nonumber. \end{eqnarray} By (10), \begin{eqnarray} (m\triangleleft n)\triangleright \beta_M(p) &=&\alpha f(m)\ast_L (n\ast_R f(p))\nonumber\\ &=& f\alpha_M(m)\ast_L (n\triangleright p)\nonumber\\ &=& \alpha_M(m)\triangleleft(n\triangleright p)\nonumber. \end{eqnarray} This completes the proof.
Remark 3. In the above proposition, \(A\) is seen as an \(A\)-BiHom-module over itself.
Now, we can observe that any \((\alpha^0, \beta^0)\)-element of centroid of a BiHom-associative algebra \(A\) is a morphism of \(A\)-BiHom-bimodule. Therefore, we have what follows :Corollary 6. Let \((A, \cdot, \alpha, \beta)\) be a BiHom-associative algebra and let \(\theta : A\rightarrow A\) be an \((\alpha^0, \beta^0)\)-element of cenroid on \(A\). Then, \((A, \triangleleft, \triangleright, \alpha, \beta)\) is a BiHom-associative dialgebra with \[x\triangleleft y=\theta(x)\cdot y\mbox{and} x\triangleright y=x\cdot \theta(y),\] for any \(x, y\in A.\)
Now, let us recall the definition of BiHom-Lie algebra.Definition 5.[14] A BiHom-Lie algebra is a quadruple \((L, \left[\cdot, \cdot\right], \alpha,\beta)\) in which L is linear vector space, \(\alpha, \beta : A\rightarrow A \) are linear maps and \([-, -] : L\otimes L\rightarrow L\) is a bilinear map such that for all \(x, y, z\in L\) : \begin{equation} \alpha\circ\beta=\beta\circ\alpha, \nonumber \end{equation} \begin{equation} \alpha(\left[x, y\right])=\left[\alpha(x), \alpha(y)\right]\,\text{and}\,\;\beta(\left[x, y\right])=\left[\beta(x), \beta(y)\right],\nonumber \end{equation} \begin{equation} \left[\beta(x),\alpha(y)\right])=-\left[\beta(y), \alpha(x)\right]\, (\text{BiHom-skew-symmetry}),\nonumber \end{equation} \begin{equation} \left[\beta^2(x),\left[\beta(y),\alpha(z)\right]\right]+\left[\beta^2(y),\left[\beta(z),\alpha(x)\right]\right] +\left[\beta^2(z),\left[\beta(x),\alpha(y)\right]\right]=0,\, (\text{BiHom-Jacobi identity}).\nonumber \end{equation}
The maps \(\alpha\) and \(\beta\) (in this order) are called the structure maps of \(L.\) When the structure maps are bijectives \(L\) is said to be a semi-regular BiHom-Lie algebra.Definition 6. Given two BiHom-Lie algebras \(L\) and \(L’\), a morphism \(f\) from \((L, [-, -], \alpha, \beta)\) onto \((L’, [-, -]’, \alpha’, \beta’)\) is a linear map \(f : L\rightarrow L’\) such that \[\alpha’\circ f=f\circ\alpha,\, \beta’\circ f=f\circ\beta\] and \[f(\left[x, y\right])=\left[f(x), f(y)\right]’, \forall x, y \in L.\]
The following lemma asserts that the commutator of any semi-regular BiHom-associative algebra gives rise to BiHom-Lie algebra.Lemma 1.[14] Let \((A, \cdot, \alpha, \beta )\) be a semi-regular BiHom-associative algebra. Then \[L(A)=(A, [-, -], \alpha, \beta)\] is a semi-regular BiHom-Lie algebra, with \[[x, y]=x\cdot y-\alpha^{-1}\beta(y)\cdot\alpha\beta^{-1}(x),\] for any \(x, y\in A.\)
Proposition 4. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a BiHom-associative dialgebra and \(R: D\rightarrow D\) be a Rota-Baxter operator of weight \(0\) on \(D\) i.e. \(R\) is linear and commutes with both \(\alpha\) and \(\beta\), and \begin{eqnarray} R(x)\dashv R(y)&=&R(R(x)\dashv y+x\dashv R(y))\tag{11}\\ R(x)\vdash R(y)&=&R(R(x)\vdash y+x\vdash R(y))\tag{12}. \end{eqnarray} Then, \((D, \triangleleft, \triangleright, \alpha, \beta)\) is also a BiHom-associative dialgebra with \begin{eqnarray} x\triangleleft y=R(x)\dashv y+x\dashv R(y),\tag{13}\\ x\triangleright y=R(x)\vdash y+x\vdash R(y),\tag{14} \end{eqnarray} for all \(x, y\in D\). Moreover, \(R\) is a Rota-Baxter operator on \((D, \triangleleft, \triangleright, \alpha, \beta)\).
Proof. We only prove axiom (3), the other being proved in a similar way. Thus, for any \(x, y, z\in D\), \begin{eqnarray} (x\triangleleft y)\triangleleft \beta(z)-\alpha(x)\triangleleft(y\triangleright z)&=&(x\dashv R(y)+R(x)\dashv y)\dashv R\beta(z)+R(R(x)\dashv y+x\dashv R(y))\dashv\beta(z)\nonumber\\ &&-\alpha(x)\dashv R(R(y)\vdash z+y\vdash R(z))-R\alpha(x)\dashv(R(y)\vdash z+y\vdash R(z))\nonumber\\ &=&(x\dashv R(y))\dashv \beta R(z)+(R(x)\dashv y)\dashv\beta R(z)+(R(x)\dashv R(y))\dashv \beta(z)\nonumber\\ &&-\alpha(x)\dashv(R(y)\vdash R(z))-\alpha R(x)\dashv(y\vdash R(z))-\alpha R(x)\dashv(R(y)\vdash z).\nonumber \end{eqnarray} The left hand side vanishes by axiom (3). This ends the proof.
Corollary 7. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a BiHom-associative dialgebra and \(R: D\rightarrow D\) be a Rota-Baxter operator of weight \(0\) on \(D\). Then, \((D, \ast, \alpha, \beta)\) is a BiHom-associative algebra with \[x\ast y=R(x)\triangleleft y+x\triangleright R(y),\] for all \(x, y, z\in D\).
Corollary 8. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a semi-regular BiHom-associative dialgebra and \(R: D\rightarrow D\) be a Rota-Baxter operator of weight \(0\) on \(D\). Then, \((D, [-, -], \alpha, \beta)\) is a semi-regular BiHom-Lie algebra with \[[x, y]=x\ast y-\alpha^{-1}\beta(y)\ast\alpha\beta^{-1}(x),\] with \(x\ast y=R(x)\triangleleft y+x\triangleright R(y)\), for all \(x, y, z\in D\).
It is well known that a Nijenhuis operator on an associative algebra allows to define another associative algebra. In the next result, we establish that a Nijenhuis operator on a BiHom-associative dialgebra give rises to another BiHom-associative dialgebra.Proposition 5. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a BiHom-associative dialgebra and \(N: D\rightarrow D\) be a Nijenhuis operator on \(D\) i.e. \(N\) is a linear map such that \begin{eqnarray} \alpha\circ N&=&N\circ\alpha,\tag{15}\label{n3}\\ \beta\circ N&=&N\circ\beta,\tag{16}\label{n4}\\ N(x)\dashv N(y)&=&N(N(x)\dashv y+x\dashv N(y)-N(x\dashv y)),\tag{17}\label{n1}\\ N(x)\vdash N(y)&=&N(N(x)\vdash y+x\vdash N(y)-N(x\vdash y))\tag{18}\label{n2}. \end{eqnarray} Then, \((D, \triangleleft, \triangleright, \alpha, \beta)\) is also a BiHom-associative dialgebra with \begin{eqnarray} x\triangleleft y=N(x)\dashv y+x\dashv N(y)-N(x\dashv y), \tag{19}\label{nm1}\\ x\triangleright y=N(x)\vdash y+x\vdash N(y)-N(x\vdash y),\tag{20}\label{nm2} \end{eqnarray} for all \(x, y\in D\).
Proof.
We only prove axiom (4) for the products \(\triangleleft\) and \(\triangleright\). The others are left to the reader.
\(
(x\triangleright y)\triangleleft \beta(z)-\alpha(x)\triangleright(y\triangleleft z)= N\Big(N(x)\vdash y+x\dashv N(y)-N(x\dashv y)\Big)\dashv \beta(z)+\Big(N(x)\dashv y+x\vdash N(y)-N(x\vdash y)\Big)\dashv N\beta(z)-N\Big((N(x)\vdash y+x\vdash N(y)-N(x\vdash y))\dashv\beta(z)\Big)-N\alpha(x)\vdash\Big(N(y)\dashv z+y\dashv N(z)-N(y\dashv z)\Big)-\alpha(x)\vdash N\Big(N(y)\dashv z+y\dashv N(z)-N(y\dashv z)\Big)+N\Big(\alpha(x)\vdash(N(y)\dashv z+y\dashv N(z)-N(y\dashv z))\Big).\)
By (15), (16), (17) and (18), it comes
\(
(x\triangleright y)\triangleleft \beta(z)-\alpha(x)\triangleright(y\triangleleft z)=(N(x)\vdash N(y))\dashv \beta(z)+(N(x)\dashv y)\dashv \beta N(z)+(x\vdash N(y))\dashv \beta N(z)
-N(x\vdash y)\dashv N\beta(z)-N\Big((N(x)\vdash y)\dashv\beta(z)\Big)-N\Big((x\vdash N(y))\dashv\beta(z)\Big)+N\Big(N(x\vdash y)\dashv\beta(z)\Big)-\alpha N(x)\vdash(N(y)\dashv z)-\alpha N(x)\vdash(y\dashv N(z))+N\alpha(x)\vdash N(y\dashv z)-\alpha(x)\vdash (N(y)\dashv N(z))+N\Big(\alpha(x)\vdash(N(y)\dashv z)\Big)+N\Big(\alpha(x)\vdash(y\dashv N(z))\Big)-N\Big(\alpha(x)\vdash N(y\dashv z)\Big).
\)
By (4), it follows that
\((x\triangleright y)\triangleleft \beta(z)-\alpha(x)\triangleright(y\triangleleft z)=-N(x\vdash y)\dashv N\beta(z)-N\Big((N(x)\vdash y)\dashv\beta(z)\Big)-N\Big((x\vdash N(y))\dashv\beta(z)\Big)
+N\Big(N(x\vdash y)\dashv\beta(z)\Big)+N\alpha(x)\vdash N(y\dashv z)+N\Big(\alpha(x)\vdash(N(y)\dashv z)\Big)
+N\Big(\alpha(x)\vdash(y\dashv N(z))\Big)-N\Big(\alpha(x)\vdash N(y\dashv z)\Big).
\)
Using again (17) and (18), it comes
\(
(x\triangleright y)\triangleleft \beta(z)-\alpha(x)\triangleright(y\triangleleft z)=-N\Big(N(x\vdash y)\dashv\beta(z)+ (x\vdash y)\dashv\beta N(z)-N((x\vdash y)\dashv\beta(z))\Big)
-N\Big((N(x)\vdash y)\dashv\beta(z)\Big)-N\Big((x\vdash N(y))\dashv\beta(z)\Big)+N\Big(N(x\vdash y)\dashv\beta(z)\Big)
+N\Big(N\alpha(x)\vdash(y\dashv z)+\alpha(x)\vdash N(y\dashv z)-N(\alpha(x)\vdash (y\dashv z))\Big)
+N\Big(\alpha(x)\vdash(N(y)\dashv z)\Big)+N\Big(\alpha(x)\vdash(y\dashv N(z))\Big)-N\Big(\alpha(x)\vdash N(y\dashv z)\Big).
\)
The left hand side vanishes by (4).
Corollary 9. If \((D, \dashv, \vdash, \alpha)\) is a Hom-associative dialgebra and \(N: D\rightarrow D\) a Nijenhuis operator on \(D\), then \((D, \triangleleft, \triangleright, \alpha)\) is also a Hom-associative dialgebra with the multiplications (19) and (20).
Corollary 10. If \((D, \dashv, \vdash)\) is an associative dialgebra and \(N: D\rightarrow D\) a Nijenhuis operator on \(D\), then \((D, \triangleleft, \triangleright)\) is also an associative dialgebra with the products (19) and (20).
Now, we have Nijenhuis operator on BiHom-Lie algebras.Proposition 6. Let \((L, [-, -], \alpha,\beta)\) be a BiHom-Lie algebra and \(N : L\rightarrow L\) be a Nijenhuis operator on \(L\) i.e. \(\alpha\circ N=N\circ\alpha\), \(\beta\circ N=N\circ\beta\) and \begin{eqnarray} [N(x), N(y)]=N([N(x), y]+[x, N(y)]-N([x, y]))\nonumber \end{eqnarray} for any \(x, y\in L\). Then, \(L_N=(L, [-, -]_N, \alpha,\beta)\) is a BiHom-Lie algebra with \begin{eqnarray} [x, y]_N=[N(x), y]+[x, N(y)]-N([x, y])\nonumber \end{eqnarray} for all \(x, y\in L\).
Proof. It follows from direct computation.
Corollary 11. Let \((A, \cdot, \alpha,\beta)\) be a semi-regular BiHom-associative algebra and \(N : A\rightarrow A\) be a Nijenhuis operator on \(A\) i.e. \(\alpha\circ N=N\circ\alpha\), \(\beta\circ N=N\circ\beta\) and \begin{eqnarray} N(x)\cdot N(y)=N(N(x)\cdot y+x\cdot N(y)-N(x\cdot y))\nonumber \end{eqnarray} for any \(x, y\in A\). Let us denote by \(L(A)\) the BiHom-Lie algebra associated with \(A\) as in Lemma 1. Then, \(L_N(A)=(A, [-, -]_N, \alpha,\beta)\) is a BiHom-Lie algebra.
Corollary 12. Let \((A, \cdot, \alpha,\beta)\) be a semi-regular BiHom-associative algebra and \(N : A\rightarrow A\) be a Nijenhuis operator on \(A\) i.e. \(\alpha\circ N=N\circ\alpha\), \(\beta\circ N=N\circ\beta\) and \begin{eqnarray} N(x)\cdot N(y)=N(N(x)\cdot y+x\cdot N(y)-N(x\cdot y))\nonumber \end{eqnarray} for any \(x, y\in A\). Then, \((A, \{-, -\}, \alpha,\beta)\) is a BiHom-Lie algebra with \begin{eqnarray} \{x, y\}= x\ast_N y-\alpha^{-1}\beta(y)\ast_N\alpha\beta^{-1}(x),\nonumber \end{eqnarray} where \begin{eqnarray} x\ast_Ny= N(x)\cdot y+x\cdot N(y)-N(x\cdot y)\nonumber \end{eqnarray} for all \(x, y\in A\).
Proof. It is similar to that of Proposition 5. And the Lemma 1 will end the proof.
Remark 4.
The BiHom-Lie algebra arising from Corollary 11 and Corollary 12 are equals. In other words, the below diagram of categories
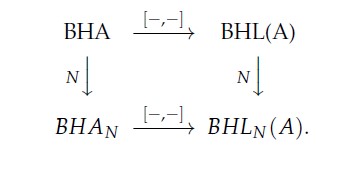
Proposition 7. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a semi-regular BiHom-associative dialgebra. Then, for all \(x, y\in D\), the bracket \([-, -] : D\times D\rightarrow D\) defined by \[[x, y]=[x, y]_L+[x, y]_R,\] where \begin{eqnarray} [x, y]_L&=&x\dashv y-\alpha^{-1}\beta(y)\dashv\alpha\beta^{-1}(x),\nonumber\\ {[x, y]_R}&=&x\vdash y-\alpha^{-1}\beta(y)\vdash\alpha\beta^{-1}(x),\nonumber \end{eqnarray} is a BiHom-Lie bracket if and only if \begin{eqnarray} \alpha(x)\dashv(y\vdash z)=(x\dashv y)\vdash\beta(z),\tag{21}\label{dil1}\\ \alpha(x)\dashv(y\dashv z)=(x\vdash y)\vdash\beta(z).\tag{22}\label{dil2} \end{eqnarray}
Proof. It is essentialy based on Lemma 1. The skew-symmetry is trivial and an expansion of BiHom-Jacobi identity leads to \(48\) terms including \(8\) terms which cancel pairewise by axiom (2), \(4\) terms cancel pairewise by axiom (3), \(12\) terms cancel pairewise by axiom (4), \(6\) terms cancel pairewise by axiom (5) and \(6\) terms cancel pairewise by axiom (6). For the rest of the \(12\) terms, \(8\) terms cancel pairewise by axiom (21) and \(4\) terms cancel pairewise by axiom (22).
The next proposition asserts that the twist of the products of any BiHom-associative dialgebra by an averaging operator leads to another BiHom-associative dialgebra.Proposition 8. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a BiHom-associative dialgebra and \(\theta: D\rightarrow D\) be an injective averaging operator on \(D\) i.e. \(\theta\) is an injective linear map such that \(\alpha\circ \theta=\theta\circ\alpha\) , \(\beta\circ \theta=\theta\circ\beta\), and \begin{eqnarray} \theta(x)\dashv\theta(y)&=&\theta(\alpha^k\beta^l(x)\dashv\theta(y))=\theta(\theta(x)\dashv\alpha^k\beta^l(y)),\tag{23}\label{c1}\\ \theta(x)\vdash\theta(y)&=&\theta(\alpha^k\beta^l(x)\vdash\theta(y))=\theta(\theta(x)\vdash\alpha^k\beta^l(y)),\tag{24}\label{c2} \end{eqnarray} for any \(x, y\in D\). Then, \((D, \triangleleft, \triangleright, \alpha, \beta)\) is also a BiHom-associative dialgebra with \begin{eqnarray} x\triangleleft y=\theta(x)\dashv\alpha^k\beta^l(y))\tag{25}\\ x\triangleright y=\theta(x)\vdash\alpha^k\beta^l(y)\tag{26}, \end{eqnarray} for all \(x, y\in D\).
Proof. We only prove one identity, the others have a similar proof. For any \(x, y, z\in D\), one has : \begin{eqnarray} \theta[(x\triangleleft y)\triangleright\beta(z)-\alpha(x)\triangleright(y\triangleleft z)]&=&\theta[\theta(\theta(x)\dashv\alpha^k\beta^l(y))\vdash\alpha^k\beta^{l+1}(z)) -\theta\alpha(x)\vdash\alpha^k\beta^l(\theta(y)\dashv\alpha^k\beta^l(z))]\nonumber\\ &=&\theta[(\theta(x)\dashv\theta(y))\vdash\alpha^k\beta^{l+1}(z)] -\theta\alpha(x)\vdash\theta(\theta(y)\dashv\alpha^k\beta^l(z))\nonumber\\ &=&(\theta(x)\vdash\theta(y))\dashv\beta\theta(z)-\alpha\theta(x)\vdash(\theta(y)\dashv\theta(z))\nonumber. \end{eqnarray} Which vanishes by axiom (4), and the conclusion holds by injectivity.
Now, we have the following definition.Definition 7. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a BiHom-associative dialgebra and \(D_o\) a subset of \(D\). We say that \(D_o\) is a BiHom-subalgebra of \(D\) if \(D_o\) is stable under \(\alpha\) and \(\beta\), and \(x\dashv y, x\vdash y\in D_o\), for any \(x, y\in D_o\).
Example 3. If \(\varphi : D_1\rightarrow D_2\) is a morphism of BiHom-associative dialgebras, the image \(Im\varphi\) is a BiHom-subalgebra of \(D_2\).
In the below proposition, we prove that BiHom-associative dialgebras are closed under direct sum, and give a condition for which a linear map becomes a morphism of direct sum of BiHom-associative dialgebras.Proposition 9. Let \(({A}, \dashv_{A}, \vdash_{A}, \alpha_{A}, \beta_{A})\) and \(({B}, \dashv_{B}, \vdash_{B}, \alpha_{B}, \beta_{B})\) be two BiHom-associative dialgebras. Then, there exists a BiHom-associative dialgebra structure on \({A}\oplus{B}\) with the bilinear maps \(\triangleleft, \triangleright : ({A}\oplus{B})^{\otimes 2}\rightarrow {A}\oplus{B}\) given by \[(a_1+b_2)\dashv(a_2+b_2) :=a_1\dashv_{A}a_2+b_2\dashv_{B}b_2,\] \[(a_1+b_1)\vdash(a_2+b_2) :=a_1\vdash_{A}a_2+b_{A}\vdash_{B}b_2\] and the linear maps \(\alpha=\alpha_{A}+\alpha_{B},\, \beta=\beta_{A}+\beta_{B} : {A}\oplus{B}\rightarrow {A}\oplus{B}\) given by \[(\alpha_{A}+\alpha_{B})(a+b) :=\alpha_{A}(a)+\alpha_{B}(b),\, (\beta_{A}+\beta_{B})(a+b) :=\beta_{A}(a)+\beta_{B}(b),\, \forall(a,b)\in {A}\times{B}. \] Moreover, if \(\xi : {A}\rightarrow {B}\) is a linear map. Then, \[ \xi : ({A}, \dashv_{A}, \vdash_{A}, \alpha_A, \beta_A) \rightarrow({B}, \dashv_{B}, \vdash_{B}, \alpha_B, \beta_B)\] is a morphism if and only if its graph \(\Gamma_\xi=\{x, \xi(x)), x\in A\}\) is a BiHom-subalgebra of \(({A}\oplus{B}, \triangleleft, \triangleright, \alpha, \beta)\).
Proof.
The proof of the first part comes from a direct computation, so we omit it. Now,
let us suppose that \(\xi : ({A}, \dashv_{A}, \vdash_{A},\alpha_A, \beta_A)\rightarrow({B}, \dashv_{B}, \vdash_{B},\alpha_B, \beta_B)\) is a
morphism of BiHom-associative dialgebras.
Then \[(u+\xi(u))\dashv(v+\xi(v))=(u\dashv_{A}v+\xi(u)\dashv_{B}\xi(v))=u\dashv_{A}v+\xi(u\dashv_{A}v),\]
\[(u+\xi(u))\vdash(v+\xi(v))=(u\vdash_{A}v+\xi(u)\vdash_{B}\xi(v))=u\vdash_{A}v+\xi(u\vdash_{A}v).\]
Thus the graph \(\Gamma_\xi\) is closed under the operations \(\dashv\) and \(\vdash\).
Furthermore, since \(\xi\circ\alpha_A=\alpha_B\circ\xi,\) and \(\xi\circ\beta_A=\beta_B\circ\xi,\) we have
\[
(\alpha_A\oplus\alpha_B)(u, \xi(u))=(\alpha_A(u), \alpha_B\circ\xi(u))=(\alpha_A(u), \xi\circ\alpha_A(u)),
\]
and
\[
(\beta_A\oplus\beta_B)(u, \xi(u))=(\beta_A(u), \beta_B\circ\xi(u))=(\beta_A(u), \xi\circ\beta_A(u)).
\]
Which implie that \(\Gamma_\xi\) is closed \(\alpha_A\oplus\alpha_B\) and \(\beta_A\oplus\beta_B.\)
Thus, \(\Gamma_\xi\) is a BiHom-subalgebra of
\(({A}\oplus{B}, \dashv, \vdash, \alpha, \beta).\)
Conversely, if the graph \(\Gamma_\xi\subset{A}\oplus{B}\) is a BiHom-subalgebra of
\(({A}\oplus{B}, \dashv, \vdash, \alpha, \beta)\) then we
\[(u+\xi(u))\dashv(v+\xi(v))=(u\dashv_{A}v+\xi(u)\dashv_{B}\xi(v))\in \Gamma_\xi, \]
\[(u+\xi(u))\vdash(v+\xi(v))=(u\vdash_{A}v+\xi(u)\vdash_{B}\xi(v))\in \Gamma_\xi.\]
Furthermore, \((\alpha_A\oplus\alpha_B)(\Gamma_\xi)\subset \Gamma_\xi,\, (\beta_A\oplus\beta_B)(\Gamma_\xi)\subset \Gamma_\xi,\) implies
\[
(\alpha_A\oplus\alpha_B)(u, \xi(u))=(\alpha_A(u),\alpha_B\circ\xi(u))\in \Gamma_\xi,\,(\beta_A\oplus\beta_B)(u, \xi(u))
=(\beta_A(u),\beta_B\circ\xi(u))\in \Gamma_\xi,
\]
which is equivalent to the condition \(\alpha_B\circ\xi(u)=\xi\circ\alpha_A(u),\) i.e. \(\alpha_B\circ\xi=\xi\circ\alpha_A.\) Similary,
\(\beta_B\circ\xi=\xi\circ\beta_A\). Therefore, \(\xi\) is a
morphism of BiHom-associative dialgebras.
Definition 8. Given a BiHom-associative dialgebra \((D, \dashv, \vdash, \alpha, \beta)\), a BiHom-subalgebra \(I\) of \(D\) is said to be a:
Example 4.
Proposition 10. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a BiHom-associative dialgebra and \(I\) be a two sided BiHom-ideal of \((D,\dashv, \vdash, \alpha, \beta)\). Then, \((D/I,\overline{\dashv}, \overline{\vdash}, \overline{\alpha}, \overline{\beta})\) is a BiHom-associative dialgebra where $$ \overline{\alpha}(\overline{x}):=\overline{\alpha(x)},\quad \overline{\beta}(\overline{x}):=\overline{\beta(x)},\quad \overline{x}\;\overline{\dashv}\;\overline{y}:=\overline{x\dashv y},\quad \mbox{and}\quad \overline{x}\;\overline{\vdash}\;\overline{y}:=\overline{x\vdash y}, $$ for all \(\overline{x}, \overline{y}\in A/I.\)
Proof. We only prove right associativity, the other being proved similarly. For all \(\overline{x}, \overline{y}, \overline{z}\in D/I\), we have \begin{eqnarray} (\overline{x}\overline{\vdash}\overline{y})\overline{\vdash}\overline{\beta}(\overline{z}) -\overline{\alpha}(\overline{x})\overline{\vdash}(\overline{y}\overline{\vdash}\overline{z}) =\overline(x\vdash y)\vdash\beta(z)-\alpha(x)\vdash(y\vdash z) =0.\nonumber \end{eqnarray} Then, \((D/I, \overline{\dashv}, \overline{\vdash}, \overline{\alpha}, \overline{\beta})\) is BiHom-associative dialgebra.
Here, we recall definition of BiHom-Leibniz algebras [27].Definition 9. A (right) BiHom-Leibniz algebra is a quadruple \((L, \left[-, -\right], \alpha, \beta)\), where L is a linear vector space, \(\left[-, -\right] : L \times L\rightarrow L\) is a bilinear map and \(\alpha, \beta : L\rightarrow L\) are two linear maps satisfying \begin{equation}\tag{27} \left[\left[x, y\right], \alpha\beta(z)\right]=\left[\left[x, \beta(z)\right], \alpha(y)\right]+\left[\alpha(x),\left[y, \alpha(z)\right]\right], \end{equation} for all \(x, y, z\in L\).
Example 5. Let \(L\) be a two-dimensional vector space and \(\left\{e_1, e_2\right\}\) be a basis of \(L\). Then, \((L, [-, -], \alpha, \beta)\) is a BiHom-Leibniz algebra with : \[\left[e_1, e_2\right]=ae_1, \left[e_2, e_2\right]=be_1,\; \alpha(e_1)=\beta(e_1)=0,\; \alpha(e_2)=\beta(e_2)=e_1, \; a, b\in \mathbb{R}.\]
Theorem 13. Let \(({D}, \dashv, \vdash, \alpha, \beta)\) be a regular BiHom-associative dialgebra. Then, for any \(x, y\in D\), the bracket defined by \[\left[x, y\right]=x \dashv y-\alpha^{-1}\beta(y)\vdash\alpha\beta^{-1}(x)\] defines a structure of BiHom-Leibniz algebra on \({D}\), and denoted \({\boldsymbol{Lb}}(D)\).
Proof. For any \(x, y, z\in {D}\), we have \begin{eqnarray} [[x, y], \alpha\beta(z)] &=&(x\dashv y-\alpha^{-1}\beta(y)\vdash\alpha\beta^{-1}(x))\dashv\alpha\beta(z)\nonumber\\ &&-\alpha^{-1}\beta\alpha\beta(z)\vdash(x\dashv y-\alpha^{-1}\beta(y)\vdash\alpha\beta^{-1})\nonumber\\ &=&(x\dashv y)\dashv\alpha\beta(z)-(\alpha^{-1}\beta(y)\vdash\alpha\beta^{-1}(x))\dashv\alpha\beta(z)\nonumber\\ &&-\beta^2(z)\vdash(\alpha\beta^{-1}(x)\dashv\alpha\beta^{-1}(y) +\beta^2(z)\vdash(y\vdash\alpha^2\beta^{-2}(x)).\nonumber\\ {[[x, \beta(z)], \alpha(y)]} &=&(x\dashv\beta(z)-\alpha^{-1}\beta^2(z)\vdash\alpha\beta^{-1}(x)\dashv\alpha(y)\nonumber\\ &&-\alpha^{-1}\beta\alpha(z)\vdash(\alpha\beta^{-1}(x\dashv y+\alpha^{-1}\beta(y)\vdash\alpha\beta^{-1})\nonumber\\ &=&(x\dashv\beta(z))\dashv\alpha(y)-(\alpha^{-1}\beta^2(z)\vdash\alpha\beta^{-1}(x))\dashv\alpha(y)\nonumber\\ &&-\beta(y)\vdash(\alpha\beta^{-1}(x)\dashv\alpha(z)) +\beta(y)\vdash(\beta(z)\vdash\alpha^2\beta^{-2}(x))\nonumber.\\ {[\alpha(x), [y, \alpha(z)]]} &=&\alpha(x)\dashv(y\dashv\alpha(z)-\alpha^{-1}\beta\alpha(z)\vdash\alpha\beta^{-1}(y)) -\alpha^{-1}\beta(y\dashv\alpha(z)\nonumber\\ &&-\beta(z)\vdash\alpha\beta^{-1}(y))\vdash\alpha\beta^{-1}\alpha(x)\nonumber\\ &=&\alpha(x)\dashv(y\dashv\alpha(z))-\alpha(x)\dashv(\beta(z)\vdash\alpha\beta^{-1}(y))\nonumber\\ &&-(\alpha^{-1}\beta(y)\dashv\beta(z))\vdash\alpha^2\beta^{-1}(x) -(\alpha^{-1}\beta^2(z)\vdash y)\vdash\alpha^2\beta^{-1}(x)\nonumber. \end{eqnarray} By axioms in Definition 1, the conclusion holds.
Now, we introduce BiHom-Poisson dialgebras as a generalization of Hom-Poisson dialgebras [29] and we study their connections with BiHom-associative dialgebras.Definition 10. A BiHom-Poisson dialgebra is a BiHom-associative dialgebra \(({P}, \dashv, \vdash, \alpha, \beta )\) and a BiHom-Leibniz algebra \(({P}, [-, -], \alpha, \beta )\) such that \begin{eqnarray} {[x\dashv y, \alpha\beta(z)]}&=&\alpha(x)\dashv[y, \alpha(z)]+[x, \beta(z)]\dashv\alpha(y),\nonumber\\ {[x\vdash y, \alpha\beta(z)]}&=&\alpha(x)\vdash[y, \alpha(z)]+[x, \beta(z)]\vdash\alpha(y),\nonumber\\ {[\alpha\beta(x), y\dashv z]}&=&\beta(y)\vdash[\alpha(x), z]+[\beta(x), y]\dashv\beta(z)=[\alpha\beta(x), y\vdash z],\nonumber \end{eqnarray} are satisfied for \(x, y, z\in{P}\).
Theorem 14. Let \(({D}, \dashv, \vdash, \alpha, \beta)\) be a semi-regular BiHom-associative dialgebra. Then, \[P(D)=(D, \dashv, \vdash,[-, -], \alpha, \beta)\] is a semi-regular BiHom-Poisson dialgebra, where \[[x, y]=x \dashv y-\alpha^{-1}\beta(y)\vdash \alpha\beta^{-1}(x),\] for any \(x, y\in {D}\).
Proof. By Theorem 13, \(P(D)\) is a BiHom-Leibniz algebra. Moreover, for any \(x, y, z\in D\), \begin{align} [x\dashv y, \alpha\beta(z)]&-\alpha(x)\dashv[y, \alpha(z)]-[x, \beta(z)]\dashv\alpha(y)\nonumber\\ =&(x\dashv y)\dashv\alpha\beta(z)-\alpha^{-1}\beta\alpha\beta(z)\vdash\alpha\beta^{-1}(x\dashv y)-\alpha(x)\dashv(y\dashv\alpha(z)\nonumber\\ &-\alpha^{-1}\beta\alpha(z)\vdash\alpha\beta^{-1}(y))-(x\dashv\beta(z)-\alpha^{-1}\beta\beta(z)\vdash\alpha\beta^{-1}(x))\dashv\alpha(y)\nonumber\\ =&(x\dashv y)\dashv\alpha\beta(z)-\beta^2(z)\vdash(\alpha\beta^{-1}(x)\dashv \alpha\beta^{-1}(y))-\alpha(x)\dashv(y\dashv\alpha(z)\nonumber\\ &+\alpha(x)\dashv(\beta(z)\vdash\alpha\beta^{-1}(y))- (x\dashv\beta(z))\dashv\alpha(y)+(\alpha^{-1}\beta^2(z)\vdash\alpha\beta^{-1}(x))\dashv\alpha(y)\nonumber. \end{align} The last three axioms are proved analogously. This completes the proof.
Theorem 15. Let \((P, \dashv, \vdash, [-, -], \alpha, \beta )\) be a BiHom-Poisson dialgebra and \(\alpha’, \beta’ : P\rightarrow P\) be two endomorphisms of BiHom-Poisson dialgebras such that the maps \(\alpha, \alpha’, \beta, \beta’\) commute pairewise. Then, \[P_(\alpha’, \beta’)=(P, \, \triangleleft:=\dashv(\alpha’\otimes\beta’),\; \triangleright:=\vdash(\alpha’\otimes\beta’),\; \{-, -\}:=[-, -](\alpha’\otimes\beta’),\; \alpha\alpha’,\; \beta\beta’),\] is a BiHom-Poisson dialgebra.
Proof. It is essentialy based on that of Theorem 1.
Remark 5. One may have a sequence of corollaries of this theorem like in Theorem 1.
Now, we introduce action of BiHom-Leibniz algebra on another one.Definition 11. Let \(D\) and \(L\) be two BiHom-Leibniz algebras. An action of \(D\) on \(L\) consists of a pair of bilinear maps, \(D\times L\rightarrow L, (x, a)\mapsto [a, x]\) and \(L\times D\rightarrow L, (x, a)\mapsto [x, a]\), such that \begin{eqnarray} \left[\alpha(x),\left[a, \alpha(b)\right]\right]&=&\left[\left[x, a\right], \alpha\beta(b)\right] -\left[\left[x, \beta(b)\right], \alpha(a)\right]\tag{28}\label{la1}\\ \left[\alpha(a),\left[x, \alpha(b)\right]\right]&=&\left[\left[a, x\right], \alpha\beta(b)\right] -\left[\left[a, \beta(b)\right], \alpha(x)\right]\tag{29}\\ \left[\alpha(a),\left[b, \alpha(x)\right]\right]&=&\left[\left[a, b\right], \alpha\beta(x)\right] -\left[\left[a, \beta(x)\right], \alpha(b)\right]\tag{30}\\ \left[\alpha(a),\left[x, \alpha(y)\right]\right]&=&\left[\left[a, x\right], \alpha\beta(y)\right] -\left[\left[a, \beta(y)\right], \alpha(x)\right]\tag{31}\\ \left[\alpha(x),\left[a, \alpha(y)\right]\right]&=&\left[\left[x, a\right], \alpha\beta(y)\right] -\left[\left[x, \beta(y)\right], \alpha(a)\right]\tag{32}\\ \left[\alpha(x),\left[y, \alpha(a)\right]\right]&=&\left[\left[x, y\right], \alpha\beta(a)\right] -\left[\left[x, \beta(a)\right], \alpha(y)\right]\tag{33} \end{eqnarray} for all \(a, b\in D, x, y\in L\).
Lemma 2. Let \(D\) and \(L\) be two BiHom-Leibniz algebras. Given a BiHom-Leibniz action of \(D\) on \(L\), we can consider the semidirect product Leibniz algebra \(L\rtimes D\), which consists of vector space \(L\oplus D\) together with the linear maps \begin{eqnarray}\tag{34} \alpha=\alpha_L+\alpha_D\mbox{and}\beta=\beta_L+\beta_D, \end{eqnarray} and the Leibniz bracket given by \begin{eqnarray}\tag{35} [(x, a), (y, b)]=([x, y]+[x, b]+[a, y], [a, b]), \end{eqnarray} for all \((x, a), (y, b)\in L\times D\).
Proof.
We have successively, for any \(a, b, c\in D, x, y, z\in L\),
\(
[\alpha(x, a), [(y, b), \alpha(z, c)]]=[(\alpha(x), \alpha(a)), ([y, \alpha(z)]+[y, \alpha(c)]+[b, \alpha(z)], [b, \alpha(c)])]
=\Big([\alpha(x), [y, \alpha(z)]]+[\alpha(x), [y, \alpha(c)]]+[\alpha(x), [b, \alpha(z)]]+[\alpha(x), [b, \alpha(c)]]
+[\alpha(a), [y, \alpha(z)]]+[\alpha(a), [y, \alpha(z)]]+[\alpha(a), [y, \alpha(c)]]
+[\alpha(a), [b, \alpha(z)], [\alpha(a), [b, \alpha(c)]]\Big),
\)
\(
{[[(x, a), (y, b)], \alpha\beta(z, c)]}=[([x, y]+[x, b]+[a, y]), [a, b]), (\alpha\beta(z), \alpha\beta(c))]
=([[x, y], \alpha\beta(z)]+[[x, b], \alpha\beta(z)]+[[a, y], \alpha\beta(z)]+[[x, y], \alpha\beta(c)]
+[[x, b], \alpha\beta(c)]
+[[a, y], \alpha\beta(c)]+[[a, b], \alpha\beta(c)], [[a, b], \alpha\beta(c)],
\)
and
\(
{[[(x, a), \beta(z, c)], \alpha(y, b)]}=[([x, \beta(z)]+[x, \beta(c)]+[a, \beta(z)], [a, \beta(c)]), (\alpha(y), \alpha(b))]=([[x, \beta(z)], \alpha(y)]+[[x, \beta(c)], \alpha(y)]+[[a, \beta(z)], \alpha(y)]+[[x, \beta(z)], \alpha(b)]
+[[x, \beta(c)], \alpha(b)]+[[a, \beta(z)], \alpha(b)]+[[a, \beta(c)], \alpha(y)], [[a, \beta(c)], \alpha(b)]).
\)
Using axioms in Definition 11, it follows that
\[{[[(x, a), (y, b)], \alpha\beta(z, c)]}={[[(x, a), \beta(z, c)], \alpha(y, b)]}+[\alpha(x, a), [(y, b), \alpha(z, c)]].\]
Which proves the proposition.
Definition 12. Let \(D\) and \(L\) be two BiHom-associative dialgebras. An action of \(D\) on \(L\) consists of four linear maps, two of them denoted by the symbol \(\dashv\) and other two by \(\vdash\), \begin{eqnarray} \dashv : D\otimes L\rightarrow L, & & \dashv : L\otimes D\rightarrow L,\nonumber\\ \vdash : D\otimes L\rightarrow L, & & \vdash : L\otimes D\rightarrow L\nonumber \end{eqnarray} such that the following \(30\) equalities hold:
| \((01) (x\dashv a)\dashv\beta(b)=\alpha(x)\dashv(a\dashv b) \), | \((16) (a\dashv x)\dashv\beta(y)=\alpha(a)\dashv(x\dashv y)\), |
|---|---|
| \((02) (x\dashv a)\dashv\beta(b)=\alpha(x)\dashv(a\vdash b)\), | \( (17) (a\dashv x)\dashv\beta(y)=\alpha(a)\dashv(x\vdash y)\), |
| \((03) (x\vdash a)\dashv\beta(b)=\alpha(x)\vdash(a\dashv b)\), | \( (18) (a\vdash x)\dashv\beta(y)=\alpha(a)\vdash(x\dashv y)\), |
| \((04) (x\dashv a)\vdash\beta(b)=\alpha(x)\vdash(a\vdash b)\), | \( (19) (a\dashv x)\vdash\beta(y)=\alpha(a)\vdash(x\vdash y)\), |
| \((05) (x\vdash a)\vdash\beta(b)=\alpha(x)\vdash(a\vdash b)\), | \( (20) (a\vdash x)\vdash\beta(y)=\alpha(a)\vdash(x\vdash y)\), |
| \((06) (a\dashv x)\dashv\beta(b)=\alpha(a)\dashv(x\dashv b)\), | \( (21) (x\dashv a)\dashv\beta(y)=\alpha(x)\dashv(a\dashv y)\), |
| \((07) (a\dashv x)\dashv\beta(b)=\alpha(a)\dashv(x\vdash b)\), | \((22) (x\dashv a)\dashv\beta(y)=\alpha(x)\dashv(a\vdash y)\), |
| \((08) (a\vdash x)\dashv\beta(b)=\alpha(a)\vdash(x\dashv b)\), | \( (23) (x\vdash a)\dashv\beta(y)=\alpha(x)\vdash(a\dashv y)\), |
| \((09) (a\dashv x)\vdash\beta(b)=\alpha(a)\vdash(x\vdash b)\), | \((24) (x\dashv a)\vdash\beta(y)=\alpha(x)\vdash(a\vdash y)\), |
| \((10) (a\vdash x)\vdash\beta(b)=\alpha(a)\vdash(x\vdash b)\), | \( (25) (x\vdash a)\vdash\beta(y)=\alpha(x)\vdash(a\vdash y)\), |
| \((11) (a\dashv b)\dashv\beta(x)=\alpha(a)\dashv(b\dashv x)\), | \( (26) (x\dashv y)\dashv\beta(a)=\alpha(x)\dashv(y\dashv a)\), |
| \((12) (a\dashv b)\dashv\beta(x)=\alpha(a)\dashv(b\vdash x)\), | \( (27) (x\dashv y)\dashv\beta(a)=\alpha(x)\dashv(y\vdash a)\), |
| \((13) (a\vdash b)\dashv\beta(x)=\alpha(a)\vdash(b\dashv x)\), | \( (28) (x\vdash y)\dashv\beta(a)=\alpha(x)\vdash(y\dashv a)\), |
| \((14) (a\dashv b)\vdash\beta(x)=\alpha(a)\vdash(b\vdash x)\), | \((29) (x\dashv y)\vdash\beta(a)=\alpha(x)\vdash(y\vdash a)\), |
| \((15) (a\vdash b)\vdash\beta(x)=\alpha(a)\vdash(b\vdash x)\), | \((30) (x\vdash y)\vdash\beta(a)=\alpha(x)\vdash(y\vdash a)\), |
Example 6.
i) Any BiHom-associative dialgebra may be seen as acting on itself.
ii) Given a morphism \(\varphi : D\rightarrow L\) of BiHom-associative dialgebras, then there is an action of \(D\) on \(L\) via the maps
\[x\triangleleft a:=\varphi(x)\dashv a,\; x\triangleright a:=\varphi(x)\vdash a,\;
a\triangleleft x:=a\dashv\varphi(x)\;\;\mbox{and}\;\; a\triangleright x:=a\vdash\varphi(x).\]
iii) If \(\psi : L\rightarrow D\) is an isomorphism of BiHom-associative dialgebras, then there is an action of \(D\) on \(L\) via the maps
\[x\triangleleft a:=\psi^{-1}(x)\vdash a,\; x\triangleright a:=\psi^{-1}(x)\vdash a,\;
a\triangleleft x:=a\dashv\psi^{-1}(x)\;\;\mbox{and}\;\; a\triangleright x:=a\vdash\psi^{-1}(x).\]
iv) If \(I\) is a BiHom-ideal of \(D\), then the left and the right products yield an action of \(D\) on I.
Lemma 3. Given two semi-regular BiHom-associative dialgebras \(D\) and \(L\) together with an action of \(D\) on \(L\), there is an action of \({\boldsymbol{ Lb}} (D)\) on \({\boldsymbol{Lb}} (L)\) given by \begin{eqnarray} [x, a]&=&x\dashv a-\alpha^{-1}\beta(a)\dashv\alpha\beta^{-1}(x),\nonumber\\ {[a, x]}&=&a\vdash x-\alpha^{-1}\beta(x)\vdash\alpha\beta^{-1}(a),\nonumber \end{eqnarray} for all \(x\in {\boldsymbol{Lb}} (D)\), \(a\in {\boldsymbol{Lb}} (L)\).
Proof. For all \(x\in {\boldsymbol{Lb}} (D)\), \(a\in {\boldsymbol{Lb}} (L)\), \begin{eqnarray} [[x, a], \alpha\beta(b)] &=&(x\dashv a-\alpha^{-1}\beta(a)\vdash\alpha\beta^{-1}(x))\dashv\alpha\beta(b)\nonumber\\ &&-\alpha^{-1}\beta\alpha\beta(b)\vdash\alpha\beta^{-1}(x\dashv a-\alpha^{-1}\beta(a)\vdash\alpha\beta^{-1}(x))\nonumber\\ &=&(x\dashv a)\dashv\beta\alpha(b)-(\alpha^{-1}\beta(a)\vdash\alpha\beta^{-1}(x))\dashv\beta\alpha(b)\nonumber\\ &&-\beta^2(b)\vdash(\alpha\beta^{-1}(x)\dashv\beta^{-1}\alpha(a)) +\beta^2(b)\vdash(a\vdash\alpha^2\beta^{-2}(x))\nonumber. \end{eqnarray} Furthermore, \begin{eqnarray} &&[[x, \beta(b)], \alpha(a)]+[\alpha(x), [a, \alpha(b)]] =\Big(x\dashv\beta(b)-\alpha^{-1}\beta^2(b)\vdash\alpha\beta^{-1}(x)\Big)\dashv\alpha(a)\nonumber\\ &&-\alpha^{-1}\beta\alpha(a)\vdash\alpha\beta^{-1}\Big(x\dashv\beta(b)-\alpha^{-1}\beta^2(b)\vdash\alpha\beta^{-1}(x)\Big) +\alpha(x)\dashv\Big(a\dashv \alpha(b)-\alpha^{-1}\beta\alpha(b)\vdash\alpha\beta^{-1}(a)\Big)\nonumber\\ &&-\alpha^{-1}\beta\Big(a\dashv \alpha(b)-\alpha^{-1}\beta\alpha(b)\vdash\alpha\beta^{-1}(a)\Big)\vdash\alpha\beta^{-1}\alpha(x)\nonumber\\ &&=(x\dashv\beta(b))\dashv\alpha(a)-(\alpha^{-1}\beta^2(b)\vdash\alpha\beta^{-1}(x))\dashv\alpha(a) -\beta(a)\vdash (\alpha\beta^{-1}(x)\dashv\alpha(b))\nonumber\\ &&+\beta(a)\vdash(\beta(b)\vdash\alpha^2\beta^{-2}(x))+\alpha(x)\dashv(a\dashv\alpha(b))-\alpha(x)\dashv(\beta(b)\vdash\alpha\beta^{-1}(a))\nonumber\\ &&-(\alpha^{-1}\beta(a)\dashv\beta(b))\vdash\beta^{-1}\alpha^2(x)+(\alpha^{-1}\beta^2(b)\vdash a)\vdash\beta^{-1}\alpha^2(x)\nonumber. \end{eqnarray} Using axioms (3), (5) in Definition 12, it comes \begin{eqnarray} [[x, \beta(b)], \alpha(a)]+[\alpha(x), [a, \alpha(b)]]&=&-(\alpha^{-1}\beta^2(b)\vdash\alpha\beta^{-1}(x))\dashv\alpha(a)-\beta(a)\vdash (\alpha\beta^{-1}(x)\dashv\alpha(b))\nonumber\\ &&+\alpha(x)\dashv(a\dashv\alpha(b)) +(\alpha^{-1}\beta^2(b)\vdash a)\vdash\alpha^2\beta^{-1}(x)\nonumber. \end{eqnarray} By comparing, we get the desired result. The five other axioms are proved in the same way.
Lemma 4. Let \(D\) and \(L\) be two semi-regular BiHom-associative dialgebras together with an action of \(D\) on \(L\). Then, there is a BiHom-associative dialgebra structure on \(L\rtimes D\) which consists with vector space \(L\oplus D\), the linear maps \begin{eqnarray}\tag{36} \alpha=\alpha_L+\alpha_D\mbox{and}\beta=\beta_L+\beta_D, \end{eqnarray} and the multiplications \begin{eqnarray} (a, x)\triangleleft (b, y)&=&(a\dashv b+a\dashv y+x\dashv b, x\dashv y)\nonumber,\\ (a, x)\triangleright (b, y)&=&(a\vdash b+a\vdash y+x\vdash b, x\vdash y)\nonumber, \end{eqnarray} for any \((a, x), (b, y)\in L\times D.\)
Proof. For any \(a, b, c\in L, x, y, z\in D\), one has \begin{eqnarray} &&\Big((a, x)\triangleleft(b, y)\Big)\triangleleft\beta(c, z)-\alpha(a, x)\triangleleft\Big((b, y)\triangleright(c, z)\Big)\nonumber\\ &&=(a\dashv b+a\dashv y+x\dashv b, x\dashv y)\triangleleft(\beta(c), \beta(z)) -(\alpha(a), \alpha(x))\triangleleft (b\vdash c+b\vdash z+y\vdash c, y\vdash z)\nonumber\\ &&=\Big((a\dashv b+a\dashv y+x\dashv b)\dashv\beta(c) +(a\dashv b+a\dashv y+x\dashv b)\dashv\beta(z) +(x\dashv y)\dashv\beta(c),\;\; (x\dashv y)\dashv\beta(z)\Big)\nonumber\\ &&-\Big(\alpha(a)\dashv(b\vdash c+b\vdash z+y\vdash c)+\alpha(a)\dashv(y\vdash z) +\alpha(x)\dashv(b\vdash c+b\vdash z+y\vdash c),\;\; \alpha(x)\dashv(y\vdash z)\Big)\nonumber\\ &&=\Big((a\dashv b)\dashv\beta(c)+(a\dashv y)\dashv\beta(c)+(x\dashv b)\dashv\beta(c)+(a\dashv b)\dashv\beta(z)\nonumber\\ &&+(a\dashv y)\dashv\beta(z)+(x\dashv b)\dashv\beta(z)+(x\dashv y)\dashv\beta(c)-\alpha(a)\dashv(b\vdash c)\nonumber\\ &&-\alpha(a)\dashv(b\vdash z)-\alpha(a)\dashv(y\vdash c)-\alpha(a)\dashv(y\vdash z) -\alpha(x)\dashv(b\vdash c)\nonumber\\ &&-\alpha(x)\dashv(b\vdash z)-\alpha(x)\dashv(y\vdash c),\;\; (x\dashv y)\dashv\beta(z)-\alpha(x)\dashv(y\vdash z)\Big)\nonumber. \end{eqnarray} The left hand side vanishes by axiom (3) and axioms (02), (07), (12), (17), (22) and (27) of Definition 12. The other axioms are proved in the same way.
Remark 6. The bijectivity of the structure maps in Lemma 4 are not essentials.
Theorem 5. Let \(D\) and \(L\) be two semi-regular BiHom-associative dialgebras together with an action of \(D\) on \(L\). Then, \({\boldsymbol{Lb}}(L\rtimes D)={\boldsymbol{Lb}}(L)\rtimes{\boldsymbol{Lb}}(D)\).
Proof. By Lemma \(3\), \({\boldsymbol{Lb}}(D)\) acts on \({\boldsymbol{Lb}}(L)\), so it makes sense to consider the semidirect product Leibniz algebra \({\boldsymbol{Lb}}(L)\rtimes{\boldsymbol{Lb}}(D)\). It is clear that \({\boldsymbol{Lb}}(L\rtimes D)\) and \({\boldsymbol{Lb}}(L)\rtimes{\boldsymbol{Lb}}(D)\) are egal as vector space, so we only need to verify that they share the same bracket. Let \((a, x), (b, y)\in L\times D\). If we use the bracket in \({\boldsymbol{Lb}}(L)\rtimes{\boldsymbol{Lb}}(D)\), we get : \begin{eqnarray} [(a, x), (b, y)] &=&([a, b]+[x, b]+[a, y], [x, y])\nonumber\\ &=&(a\dashv y-b\vdash+x\dashv b-b\vdash x+a\dashv y-y\vdash a, x\dashv y-y\vdash x).\nonumber \end{eqnarray} On the other hand, if we use the Leibniz bracket in \({\boldsymbol{Lb}}(L\rtimes D)\) [Lemma 4], we get \begin{eqnarray} \{a, x), (b, y)\} &=&(a, x)\triangleleft(b, y)-(b, y)\triangleright (a, x)\nonumber\\ &=&(a\dashv b+x\dashv b+a\dashv y, x\dashv y)-(b\vdash a+y\vdash a+b\vdash x, y\vdash x)\nonumber. \end{eqnarray} Thus, the two brackets are equals.
Definition 13. Let \((D_i, \dashv_i, \vdash_i, \alpha_i, \beta_i), i=1,2,3\) be three BiHom-associative dialgebras. The BiHom-associative dialgebra \(D_2\) is called the extension of \(D_3\) by \(D_1\) if there are morphisms \(\phi : D_1\rightarrow D_2\) and \(\psi : D_2\rightarrow D_3\) such that the following sequence \[0\longrightarrow D_1\stackrel{\phi}{\longrightarrow}D_2\stackrel{\psi}{\longrightarrow}D_3\longrightarrow0\] is exact.
Definition 14. An extension is called trivial if there exists a BiHom-ideal \(I\) of \(D_2\) complementary to \(Ker\psi\) i.e. \[D_2=Ker\psi\oplus I.\]
It may happen that there exist several extensions of \(D_3\) by \(D_1\). To classify extensions, the notion of equivalent extensions is defined.Definition 15. Two sequences \[0\longrightarrow D_1\stackrel{\phi}{\longrightarrow}D_2\stackrel{\psi}{\longrightarrow}D_3\longrightarrow0\] and \[0\longrightarrow D_1\stackrel{\phi’}{\longrightarrow}D’_2\stackrel{\psi’}{\longrightarrow}D_3\longrightarrow0\] are equivalent extensions if there exists a BiHom-associative dialgebra isomorphism \(f : D_2\rightarrow D’_2\) such that \[f\circ\phi=\phi’\mbox{and} \psi’\circ f=\psi.\]
Definition 16. An extension \[0\longrightarrow D_1\stackrel{\phi}{\longrightarrow}D_2\stackrel{\psi}{\longrightarrow}D_3\longrightarrow0\] is called central if the kernel of \(\psi\) is contained in the center \(Z(D_2)\) of \(D_2\), i.e. \(Ker\psi\subset Z(D_2)\).
Now, we introduce \(2\)-cocycle on BiHom-associative dialgebras with values in a BiHom-module.Definition 17. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a BiHom-associative dialgebra and \((M, \alpha_M, \beta_M)\) be a BiHom-module i.e. \(M\) is a linear vector space, \(\alpha_M : M\rightarrow M\) and \(\beta_M : M\rightarrow M\) are two linear maps. A pair \(\Theta=(\theta_1, \theta_2)\) of bilinear maps \(\theta_1 : D\times D\rightarrow M\) and \(\theta_2 : D\times D\rightarrow M\) is called a \(2\)-cocycle on \(D\) with values in \(M\) if \(\theta_1\) and \(\theta_2\) satisfy \begin{eqnarray} \theta_i(\alpha\otimes\alpha)&=&\alpha_M\circ\theta_i, i=1, 2,\tag{37}\\ \theta_1(x\dashv y, \beta(z))&=&\theta_1(\alpha(x), y\dashv z), \tag{38}\label{cc1}\\ \theta_1(x\dashv y, \beta(z))&=&\theta_1(\alpha(x), y\vdash z),\tag{39} \\ \theta_2(x\vdash y, \beta(z))&=&\theta_2(\alpha(x), y\vdash z),\tag{40} \\ \theta_2(x\dashv y, \beta(z)) &=& \theta_2(\alpha(x), y\vdash z), \tag{41}\\ \theta_1(x\vdash y, \beta(z))&=&\theta_2(\alpha(x), y\dashv z),\tag{42} \end{eqnarray} for all \(x, y, z\in D\).
The set of all \(2\)-cocycles on \(D\) with values in \(M\) is denoted \(Z^2(D, M)\), which is a vector space. In the below lemma, we give a special type of \(2\)-cocycles which are called \(2\)-coboundaries.Lemma 5. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a multiplicative BiHom-associative dialgebra, \(\nu : D\rightarrow M\) be a linear map such that \(\nu\beta=\alpha_M\nu\) and \(\nu\beta=\beta_M\nu\). Let us define \(\varphi_1(x, y)=\nu(x\dashv y)\) and \(\varphi_2(x, y)=\nu(x\vdash y)\). Then, \(\Phi=(\varphi_1, \varphi_2)\) is a \(2\)-cocycle on \(D\).
Proof. We will prove one equality, the others being proved in the same way. For any \(x, y, z\in D\), one has \begin{eqnarray} \varphi_1(\alpha(x), y\dashv z)&=&\nu(\alpha(x)\dashv(y\dashv z))=\nu((x\dashv y)\dashv\beta(z))\nonumber\\ &=&\nu(\alpha(x)\dashv(y\vdash z))=\varphi_1(\alpha(x), y\vdash z).\nonumber \end{eqnarray} This finishes the proof.
The set of all \(2\)-coboundaries is denoted by \(B^2(D, M)\) and it is a subgroup of \(Z^2(D, M)\). The group \(H^2(D, M)=Z^2(D, M)/B^2(D, M)\) is said to be the second cohomology group of \(D\) with values in \(M\). Two cocycles \(\Theta_1\) and \(\Theta_2\) are said to be cohomologous cocycles if \(\Theta_1-\Theta_2\) is a coboundary.Theorem 17. Let \((D, \dashv, \vdash, \alpha_D, \beta_D)\) be a multiplicative BiHom-associative dialgebra, \((M, \alpha_M, \beta_M)\) be a BiHom-module, \[\theta_1 : D\times D\rightarrow M\mbox{and} \theta_2 : D\times D\rightarrow M\] be bilinear maps as in Lemma 5. Let us set \(D_\Theta=D\oplus M\), where \(\Theta=(\theta_1, \theta_2)\). For any \(x, y\in D\), \(v, w\in M\), let us define \begin{eqnarray}\tag{43} (\alpha\oplus \alpha_M)(x+u)=\alpha_D(x)+\alpha_M(u),\qquad (x+u)\triangleleft(y+v)=x\dashv y+\theta_1(x, y),\nonumber\\ (\beta\oplus \beta_M)(x+u)=\beta_D(x)+\beta_M(u)\mbox{and} (x+u)\triangleright(y+v)=x\vdash y+\theta_2(x, y).\nonumber\\ \end{eqnarray} Then, \((D_\Theta, \triangleleft, \triangleright, \alpha_D\oplus \alpha_M, \beta_D\oplus \beta_M)\) is a multiplicative BiHom-associative dialgebra if and only if \(\Theta\) is a \(2\)-cocycle.
Proof. For any \(x, y, z\in D, u, v, w\in M\), we have \begin{eqnarray} && ((x+v)\triangleleft(y+w))\triangleleft(\beta_D(z)+w)-(\alpha_D(x)+v)\triangleleft((y+w)\triangleleft(z+w))\nonumber\\ &&=((x+v)\triangleleft(y+w))\triangleleft(\beta_D(z)+w)-(\alpha_D(x)+ v)\triangleleft((y\dashv z)+\theta_1(y, z))\nonumber\\ &&=((x\dashv y)\dashv \beta_D(z))+\theta_1(x\dashv y, \beta_D(z))-(\alpha_D(x)\dashv (y\dashv z))-\theta_1(\alpha_D(x), y\dashv z).\nonumber \end{eqnarray} The left hand vanishes by axioms (2) and (38). The other axioms are proved analagously.
Lemma 6. Let \((D, \dashv, \vdash, \alpha, \beta)\) be a multiplicative BiHom-associative dialgebra, \(\Theta\) be a \(2\)-cocycle and \(\Phi\) a \(2\)-coboundary. Then, \(D_{\Theta+\Phi}\) is a BiHom-associative dialgebra with \begin{eqnarray} (x+u)\unlhd(y+v)=x\dashv y+\varphi_1(x, y)+\theta_1(x, y),\nonumber\\ (x+u)\unrhd(y+v)=x\vdash y+\varphi_2(x, y)+\theta_2(x, y),\nonumber \end{eqnarray} and \begin{eqnarray} (\alpha\oplus \alpha_M)(x+u)=\alpha(x)+\alpha_M(u)\mbox{and} (\beta\oplus \beta_M)(x+u)=\beta(x)+\beta_M(u)\nonumber, \end{eqnarray} any \(x, y\in D, u, v\in M\). Moreover, \(D_\Theta\cong D_{\Theta+\Phi}\).
Proof. First, we have to show that \(D_{\Theta+\Phi}\) is a multiplicative BiHom-associative dialgebra. So, for any \(x+u, y+v, z+w\in D\oplus M\), \begin{eqnarray} &&((x+u)\unlhd(y+v))\unlhd\beta(z+w)-\alpha(x+u)\unlhd((y+v))\unlhd(z+w))\nonumber\\ &&=(x\dashv y+\varphi_1(x, y)+\theta_1(x, y))\unlhd(\beta(z)+\beta(w)) -(\alpha(x)+\alpha(u))\unlhd(y\dashv z+\varphi_1(y, z)+\theta_1(y, z))\nonumber\\ &&=(x\dashv y)\dashv\beta(z)+\varphi_1(x\dashv y,\beta(z))+\theta_1(x\dashv y,\beta(z)) -\alpha(x)\dashv (y\dashv z)-\varphi_1(\alpha(x), y\dashv z)+\theta_1(\alpha(x), y\dashv z)\nonumber. \end{eqnarray} The left hand side vanishes by (2) and (38). The proofs of the rest of axioms are left to the reader. Next, the isomorphism \(f : D_\Theta\rightarrow D_{\Theta+\Phi}\) is given by \[f(x+v)=x+\nu(x)+v.\] In fact, it is clear that \(f\) is a bijective linear map and \begin{eqnarray} f(\alpha+\alpha_M)(x+v)&=&f(\alpha(x)+\alpha_M(v))\nonumber\\ &=&\alpha(x)+\nu\alpha(x)+\alpha_M(v)\nonumber\\ &=&\alpha(x)+\alpha_M\nu(x)+\alpha_M(v)\nonumber\\ &=&(\alpha+\alpha_M)(x+\nu(x)+v)\nonumber\\ &=&(\alpha+\alpha_M) f(x+v).\nonumber \end{eqnarray} Thus, \(f\) commutes \(\alpha_D+\alpha_M\), and similarly with \(\beta_D+\beta_M\). Then, \begin{eqnarray} f((x+v)\triangleleft (y+w)) &=&f(x\dashv y+\theta_1(x, y))\nonumber\\ &=&f(x\dashv y)+f(\theta_1(x, y))\nonumber\\ &=&x\dashv y+\nu(x\dashv y)+\theta_1(x, y)\nonumber\\ &=&x\dashv y+\varphi_1(x, y)+\theta_1(x, y)\nonumber, \end{eqnarray} and \begin{eqnarray} f(x+v)\unlhd f(y+w) &=&(x+\nu(x)+v)\unlhd(y+\nu(y)+w)\nonumber\\ &=&x\dashv y+\varphi_1(x, y)+\theta_1(x, y).\nonumber \end{eqnarray}
Corollary 18. Let \(\Theta_1, \Theta_2\) be two cohomologous \(2\)-cocycles on a multiplicative BiHom-associative dialgebra \(D\), and \(D_1, D_2\) be the central extensions constructed with these \(2\)-cocycles, respectively. The central extensions \(D_1\) and \(D_2\) are equivalent extensions. In particular a central extension defined by a coboundary is equivalent with a trivial central extension.
The following theorem is proved Mutatis Mutandis as ([30], Theorem 4.1). So, we omitted the proof.Theorem 19. There exists one to one correspondence between elements of \(H^2(D, M)\) and nonequivalents central extensions of a multiplicative BiHom-associative dialgebra \(D\) by \(M\).
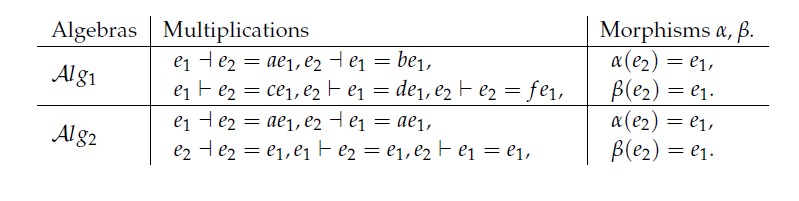

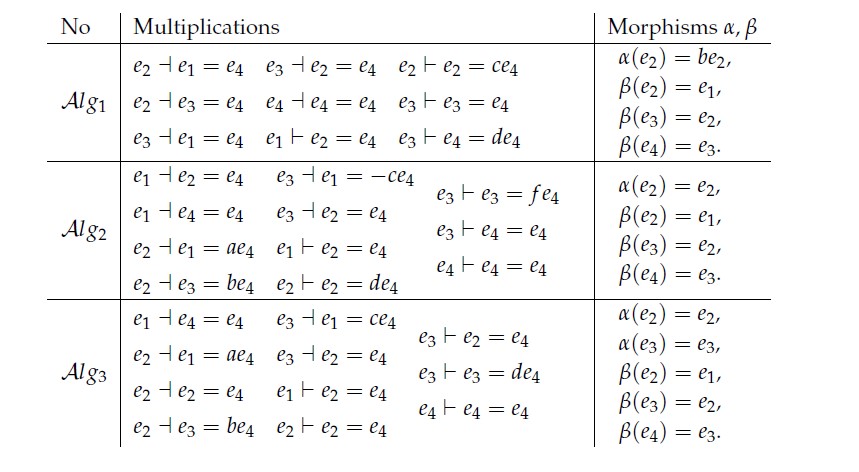
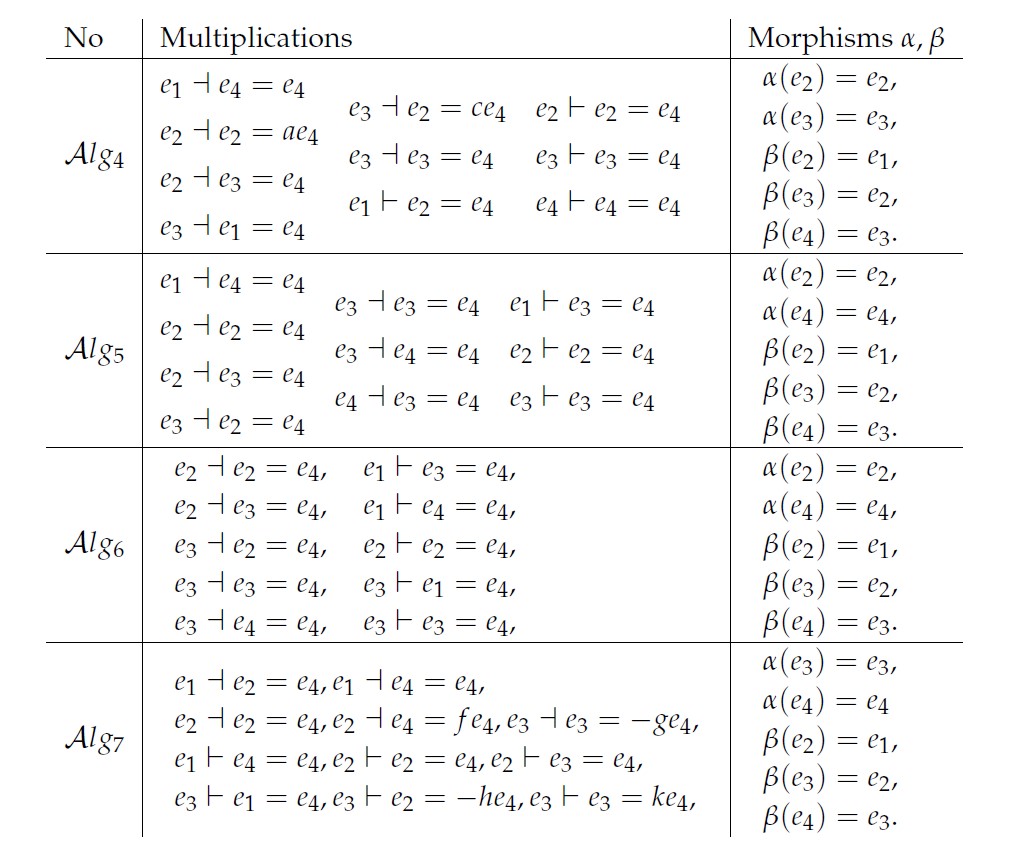
Remark 7. In two dimensional, all of the BiHom-associative dialgebras are Hom-diassociatives.