Motivated by Euler-Goldbach and Shallit-Zikan theorems, we introduce zeta-one functions with infinite sums of \(n^{s}\pm1\) as an analogy of the Riemann zeta function. Then we compute values of these functions at positive even integers by the residue theorem.
Theorem 1.[Euler-Goldbach] \[ \sum_{p:\text{perfect power}}\frac{1}{p-1}=1. \]
See Bibiloni-Paradis-Viader [1] for history of this theorem. Recently, Shallit-Zikan [2] (1983) reinterpreted it in terms of Riemann’s zeta function: the infinite series \begin{align*} \zeta(s)&=\sum_{n=1}^{\infty}\frac{1}{n^{s}}= \frac{1}{1^{s}}+\frac{1}{2^{s}}+\frac{1}{3^{s}}+\frac{1}{4^{s}}+\frac{1}{5^{s}}+\cdot\cdot\cdot \end{align*} is convergent for all complex numbers \(s\) such that Re\({(s)}>1\). Indeed, Euler proved that \[ \zeta(2k)=-\frac{1}{2}\frac{(2\pi i)^{2k}}{(2k)!}B_{2k}\,, \] where \(\{B_{n}\}\) are signed Bernoulli numbers; refer to Ayoub [3] for history of this function. Since \(\zeta(s)=1+\frac{1}{2^{s}}+\cdot\cdot\cdot>1\) and \[ 2> \frac{\pi^{2}}{6}=\zeta(2)>\zeta(3)>\zeta(4)>\zeta(5)>\cdot\cdot\cdot, \] we have \(1< \zeta(s)< 2\) for all \(s \ge 2 \). That is, \(\zeta(s)-1\) is the fractional part of \(\zeta(s)\). For example, \begin{align*} \zeta (2)-1&=0.6449\dots,\\ \zeta (3)-1&=0.2020\dots,\\ \zeta (4)-1&=0.0823\dots,\\ \zeta (5)-1&=0.0369\dots. \end{align*}Theorem 2.Shallit-Zikan [2] \begin{align*} \sum_{k=2}^{\infty}(\zeta(k)-1)&=1. \end{align*}
Let us now see a similar result.Theorem 3. See J.M. Borwein-Bradley-Crandall [4] \[ \sum_{k=1}^{\infty}(\zeta(2k)-1)=\frac{3}{4}. \]
Here we give a proof since it suggests some ideas for our main results.Proof. Consider the double sequence \(a_{nk}=\left(\frac{1}{n^{2k}}\right)_{n\ge2, k\ge1}\) and positive series \(\sum\limits_{n\ge2, k\ge1}a_{nk}\). We find that \begin{align*} \sum_{n=2}^{\infty} \sum_{k=1}^{\infty}\frac{1}{n^{2k}} &= \sum_{n=2}^{\infty} \frac{1}{n^{2}} \sum_{k=0}^{\infty}\left(\frac{1}{n^{2}}\right)^{k} \\&=\sum_{n=2}^{\infty} \frac{1}{n^{2}} \frac{1}{1-\frac{1}{n^{2}}} = \sum_{n=2}^{\infty} \frac{1}{n^{2}-1} \\&= \frac{1}{2} \sum_{n=2}^{\infty} \left(\frac{1}{n-1}-\frac{1}{n+1}\right)= \frac{3}{4}\,, \end{align*} so that we can freely switch order of this series. As a consequence, $$\sum_{k=1}^{\infty}\left(\zeta(2k)-1\right)=\sum_{k=1}^{\infty}\sum_{n=2}^{\infty}\frac{1}{n^{2k}}=\sum_{n=2}^{\infty} \sum_{k=1}^{\infty}\frac{1}{n^{2k}}=\frac{3}{4}. $$
In this proof, the infinite series \(\sum\limits_{n=2}^{\infty} \frac{1}{n^{2}-1}\) appeared. It is now natural to think of analogous sums \(\sum\frac{1}{n^{s}\pm1}\). With this simple idea, this article introduces zeta-one functions \(\zeta_{+1}(s)\), \(\zeta_{-1}(s)\) and we compute values of \(\zeta_{+1}(2m)\) and \(\zeta_{-1}(2m)\) as main Theorems 4 and 5.Theorem 4. \begin{align*} \zeta_{+1}(2m)&= -\frac{1}{2}+\frac{1}{2m}\sum_{k=1}^{m} \pi\alpha^{2k-1}\cot(\pi \alpha^{2k-1}). \end{align*}
Theorem 5. \[ \zeta_{-1}(2m)= \frac{\,1\,}{2}+\frac{2m-1}{4m}- \frac{\pi}{4m} \sum_{1\le k\le 2m-1, k\ne m} \beta^{k}\cot(\pi \beta^{k}). \]
Definition 1. Define the zeta-one functions by \[ \zeta_{+1}(s)=\sum_{n=1}^{\infty}\frac{1}{n^{s}+1} \;\;\text{and}\;\; \zeta_{-1}(s)= \sum_{n=2}^{\infty} \frac{1}{n^{s}-1}\,. \] (For \(s\ge2\), these sums are indeed convergent as mentioned below). Call each zeta-plus-one and zeta-minus-one function, respectively.
Example 1. As seen above, \(\zeta_{-1}(2)=\frac{3}{4}\). Moreover, since \[ \coth(\pi z)=\frac{1}{\pi z}+\frac{1}{\pi} \sum_{n=1}^{\infty}\frac{2z}{z^{2}+n^{2}}, \;\; z\in\mathcal{C}, \] the substitution \(z=1\) implies that \[ \zeta_{+1}(2)= \sum_{n=1}^{\infty}\frac{1}{n^{2}+1}= -\frac{1}{2}+\frac{\pi}{2}\coth(\pi). \] As a consequence, \[ \zeta_{+1}(s)\le \zeta_{+1}(2)<\infty, \;\; \zeta_{-1}(s)\le \zeta_{-1}(2)<\infty \] for all \(s\ge2\).
Lemma 1. For \(n=0, \pm1, \pm2, \pm3, \dotsb\), we have \[ \text{Res}(f, n)=\frac{1}{\pi(n^{2m}+1)}, \] and for \(1\le k\le m\), \[ \text{Res}(f,\pm\alpha^{2k-1})= – \frac{\alpha^{2k-1}{\cot(\pi \alpha^{2k-1})}}{2m}. \]
Proof. First, we have \begin{align*} \text{Res}(f,n)=&\lim_{z\to n}(z-n)f(z){}= \lim_{z\to n}\frac{z-n}{\sin\pi (z-n)}\cdot\frac{\cos(\pi z)}{z^{2m}+1}{} =\frac{1}{\pi (n^{2m}+1)}. \end{align*} Second, for \(1\le k\le m\), \begin{align*} \text{Res}(f,\alpha^{2k-1})&= \lim_{z\to \alpha^{2k-1}}(z-\alpha^{2k-1})f(z) \\&= \lim_{z\to \alpha^{2k-1}}(z-\alpha^{2k-1})\frac{\cot(\pi z)}{ z^{2m}+1} \\&= \lim_{z\to \alpha^{2k-1}}\cot(\pi z) \lim_{z\to \alpha^{2k-1}}\frac{z-\alpha^{2k-1}}{ z^{2m}+1} \\&= {\cot(\pi \alpha^{2k-1})} \lim_{z\to \alpha^{2k-1}}\frac{1}{ 2mz^{2m-1}} \;\; \text{(L’Hopital’s rule)} \\&= {\cot(\pi \alpha^{2k-1})} \frac{1}{ 2m(\alpha^{2k-1})^{2m-1}} \\&=- \frac{\alpha^{2k-1}{\cot(\pi \alpha^{2k-1})}}{2m} \;\;{\left((\alpha^{2k-1})^{2m}=-1\right)}. \end{align*} It is quite similar to show that \[ \text{Res}(f, -\alpha^{2k-1})=-\frac{\alpha^{2k-1}\cot(\pi\alpha^{2k-1})}{2m}. \]
Lemma 2.
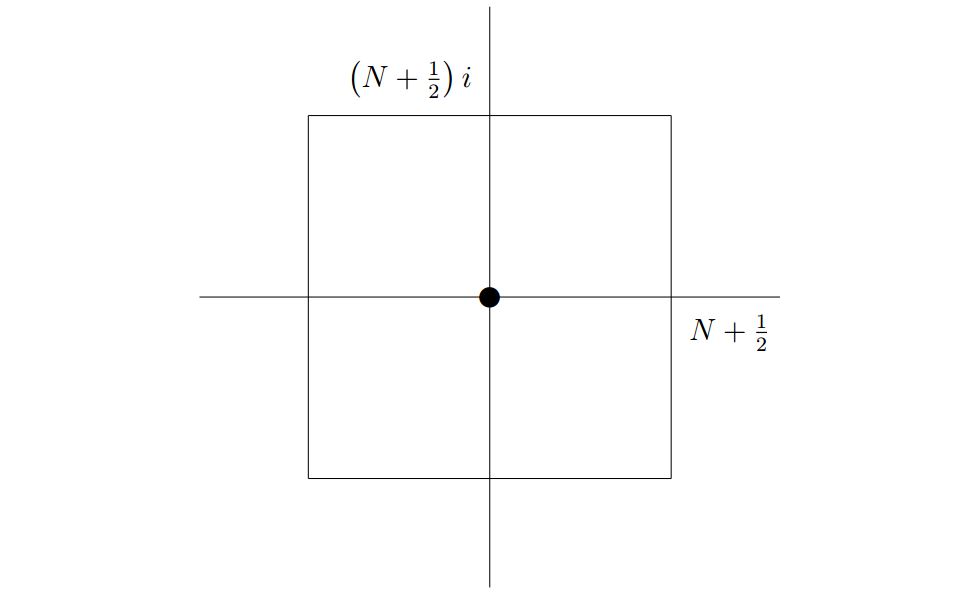
For a positive integer \(N\), consider line segments on the complex plane
\begin{align*}
C_{1}(N)&=
\left\{\left(N+\frac{1}{2}\right)+yi
\right\}{-\left(N+\frac{1}{2}\right)\le y\le {N+\frac{1}{2}}},
\\C_{2}(N)&=
\left\{x+\left(N+\frac{1}{2}\right)i
\right\}{-\left(N+\frac{1}{2}\right)\le x\le {N+\frac{1}{2}}},
\\C_{3}(N)&=
\left\{-\left(N+\frac{1}{2}\right)+yi
\right\}{-\left(N+\frac{1}{2}\right)\le y\le {N+\frac{1}{2}}},
\\C_{4}(N)&=
\left\{x-\left(N+\frac{1}{2}\right)i
\right\}{-\left(N+\frac{1}{2}\right)\le x\le {N+\frac{1}{2}}}\,,
\end{align*}
and set \(C(N)=C_{1}(N)\cup C_{2}(N)\cup C_{3}(N)\cup
C_{4}(N).\)
Proof.
Proof.[Proof of Theorem 4] Let \(s\) be a positive even integer, say \(s=2m\), \(m\ge1\). Further, let \(\alpha=\alpha_{2m}=\exp\left(\frac{\pi i}{2m}\right)\) for convenience. View \(C(N)=C_{1}(N)+C_{2}(N)+C_{3}(N)+C_{4}(N)\) above as the sum of four paths with counterclockwise orientation. Notice that any pole of \(f\) does not lie on \(C(N)\). We are going to compute the integral \[ I_{N}=\int_{C(N)}f(z)dz. \] Let \(D(N)\) be the domain enclosed by \(C(N)\). Then, the residue theorem with Lemma 1 claims that \begin{align*} I_{N}&=\int_{C{(N)}}f(z)dz \\&= 2\pi i \sum_{a: \text{pole of} f(z)| a\in D(N)} \text{Res}(f, a) \\&= 2\pi i \left(\text{Res}(f, 0)+ \sum_{n=1}^{N} \left(\text{Res}(f, n)+\text{Res}(f, -n)\right) + \sum_{k=1}^{m} \left(\text{Res}(f, \alpha^{2k-1})+\text{Res}(f, -\alpha^{2k-1})\right)\right) \\&= 2\pi i \left(\frac{1}{\pi}+2 \sum_{n=1}^{N}\frac{1}{\pi(n^{2m}+1)}+2\left(-\sum_{k=1}^{m}\frac{\alpha^{2k-1}\cot(\pi\alpha^{2k-1})}{2m} \right)\right)\,, \end{align*} while Lemma 2 implies \begin{align*} |I_{N}|&=\left|\int_{C{(N)}}f(z)dz\right| \le \int_{C{(N)}}|f(z)|dz \le \frac{\coth\frac{3}{2}\pi}{ \left(N+\frac{1}{2}\right)^{2m}-1 } \int_{C{(N)}}dz \\&=\frac{\coth\frac{3}{2}\pi}{ \left(N+\frac{1}{2}\right)^{2m}-1 }\cdot 8\left(N+\frac{1}{2}\right)\to 0 \;\; (N\to \infty). \end{align*} Therefore, taking the limit \(N\to\infty\) for \(I_{N}\) yields \[ 0= 2\pi i \left(\frac{1}{\pi}+\frac{2}{\pi}\zeta_{+1}(2m)-2 \sum_{k=1}^{m}\frac{\alpha^{2k-1}\cot(\pi\alpha^{2k-1})}{2m}\right) . \] Conclude that \[ \zeta_{+1}(2m)= -\frac{1}{2}+\frac{1}{2m}\sum_{k=1}^{m} \pi\alpha^{2k-1}\cot(\pi \alpha^{2k-1}). \]
Of course, \(\zeta_{+1}(2m)\) is a real number so that there should be some expression of \(\zeta_{+1}(2m)\) in terms of only real trigonometric functions.Example 2. Let \(s=4, m=2\) and \(\alpha=\alpha_{4}=\exp\left(\frac{\pi i}{4}\right)\). Then \begin{align*} \zeta_{+1}(4)=\sum_{n=1}^\infty \frac{1}{n^{4}+1}&=-\frac{1}{2}+\frac{\pi}{4}\sum_{k=1}^2 \alpha^{}\cot(\pi \alpha^{}){}\\ &=-\frac{1}{2}+\frac{\pi}{4} \left(\alpha \cot(\pi \alpha^{})+\alpha^{3} \cot(\pi \alpha^{3})\right) {}\\ &=-\frac{1}{2}+\frac{\pi}{4} \left(\alpha \cot(\pi \alpha)+\alpha^{-1} \cot(\pi \alpha^{-1})\right) .\end{align*} Now, it follows from the facts \[\pi \exp\left(\frac{\pi i}{4}\right) =\frac{1\pm i}{\sqrt2} \pi \;\; \text{and} \;\; \cot(x+yi)=\frac{\sin2x-i\sinh2y}{\cosh2y-\cos2x} \;\; x, y\in \mathcal{R} \,,\] that \begin{align*} \zeta_{+1}(4)&= -\frac{1}{2}+\frac{\pi}{4} \left(\alpha \cot(\pi \alpha)+\alpha^{-1} \cot(\pi \alpha^{-1})\right) \\&= -\frac{1}{2}+ \frac{\pi}{4} \left( \frac{1+i}{\sqrt{2}}\cdot\frac{\sin\sqrt{2}\pi-i\sinh\sqrt{2}\pi}{\cosh\sqrt{2}\pi-\cos\sqrt{2}\pi} + \frac{1-i}{\sqrt{2}}\cdot\frac{\sin\sqrt{2}\pi+i\sinh\sqrt{2}\pi}{\cosh\sqrt{2}\pi-\cos\sqrt{2}\pi} \right) \\&= -\frac{1}{2}+\frac{\sqrt2 \pi}{4} \left(\frac{ \sin\sqrt2 \pi+ \sinh\sqrt2 \pi}{\cosh\sqrt2 \pi-\cos\sqrt2 \pi}\right). \end{align*} Let \(s=6\), \(m=3\) and \(\alpha=\alpha_{6}=\exp\left(\frac{\pi i}{6}\right)=\frac{\sqrt{3}+i}{2}\). With \(\alpha^{3}=i\), \(\alpha^{5}=\alpha^{-1}=\frac{\sqrt{3}-i}{2}\) and \(i\cot(\pi i)=\coth(\pi) \), we observe that \begin{align*} \zeta_{+1}(6)&= -\frac{1}{2}+\frac{\pi}{6} \left(\alpha\cot(\pi \alpha)+ {\alpha^{3}\cot(\pi \alpha^{3})} +\alpha^{5}\cot(\pi \alpha^{5})\right) \\ &= -\frac{1}{2}+\frac{\pi}{6} \left(\alpha\cot(\pi \alpha)+ \alpha^{-1}\cot(\pi \alpha^{-1}) + i\cot(\pi i) \right) \\ &= -\frac{1}{2}+\frac{\pi}{6} \left( \frac{\sqrt{3}+i}{2}\cdot \frac{\sin\sqrt{3}\pi-i\sinh\pi}{\cosh\pi-\cos\sqrt{3}\pi} + \frac{\sqrt{3}-i}{2}\cdot \frac{\sin\sqrt{3}\pi+i\sinh\pi}{\cosh\pi-\cos\sqrt{3}\pi} +\coth(\pi) \right) \\&= -\frac{1}{2}+\frac{\pi}{6}\left( \frac{\sqrt3 \sin\sqrt3 \pi+\sinh\pi}{\cosh\pi-\cos\sqrt3 \pi }+\coth(\pi)\right). \end{align*}
Lemma 3. For \(n=0, \pm2, \pm3, \dots\), we have \[ \text{Res}(g, n)=\frac{1}{\pi(n^{2m}-1)}, \] for \(1\le k\le 2m-1, k\ne m\), \[\text{Res}(\pi, \beta^{k})=\frac{\beta^{k}}{2m}\cot(\pi \beta^{k}) \,,\] and moreover \[ \text{Res}(g, \pm1)=-\frac{2m-1}{4m\pi}. \]
Proof. The proofs of the first two equalities are almost similar to ones for Lemma 1. Thus we only need to show \(\text{Res}(g, \pm1)=-\frac{2m-1}{4m\pi}\). Let \(\phi(z)= \sum\limits_{k=0}^{2m-1}z^{k}\). Notice that \(\phi(z)=(z^{2m+1}-1)/(z-1)\). Then \begin{align*} \text{Res}(g, 1)&=\lim_{z\to 1}{ \frac{d}{dz}(z-1)^{2}g(z)} \\&=\lim_{z\to 1}{ \frac{d}{dz}(z-1)\cot(\pi z)\cdot\frac{1}{\phi(z)}} \\&= \lim_{z\to 1}\left( \frac{\cot(\pi z)-\pi(z-1)(\cot^{2}\pi z+1)}{\phi(z)} – (z-1)\cot(\pi z)\frac{\phi'(z)}{\phi(z)^{2}} \right). \end{align*} Let us see the first term. Immediately, \(\lim_{z\to 1}\phi(1)=2m\) and \begin{align*} \lim_{z\to 1} \left( \cot(\pi z)-\pi(z-1)(\cot^{2}\pi z+1)\right) & = \lim_{w\to 0}\left( \cot(\pi w)-\pi w(\cot^{2}\pi w+1)\right) \\&= \lim_{w\to 0} \left( \cot(\pi w)(1-\pi w\cot(\pi w))\right) -\lim_{w\to 0}{\pi w} \\&= \lim_{w\to 0} { \frac{\tan(\pi w)-\pi w}{\tan^{2}\pi w}} -0 \\&= \lim_{w\to 0}{ \frac{\pi (1+\tan^{2}\pi w)-\pi} {2\pi \tan \pi w(1+\tan^{2}\pi w)} } =0. \;\; \text{(L’H\opital’s rule)} \end{align*} In addition, since \[ \phi'(1)= \sum_{k=0}^{2m-1}k =m(2m-1), \] the limit \(z\to1\) for the second term is \begin{align*} \lim_{z\to 1}{ \left(-(z-1)\cot(\pi z)\frac{\phi'(z)}{\phi(z)^{2}}\right) } &=- \lim_{w\to 0} {w\cot(\pi w) \frac{\phi'(w-1)}{\phi(w-1)^{2}} } \\&=-\frac{1}{\pi}\frac{m(2m-1)}{(2m)^{2}} =-\frac{2m-1}{4m\pi}. \end{align*}
Proof.[Proof of Theorem 5] Let \(\beta=\exp(\frac{\pi i}{m})\) be as above. Further, let \(N, C(N), D(N)\) be as in the previous section. Again, the residue theorem claims that \[ \int_{C(N)}{g(z)}\,dz= 2\pi i \sum_{ \substack{\text{\(a\):pole of \(g\)}\\ a\in D(N)} }\text{Res}(g, a). \] Taking the limit \(N\to \infty\), the integral converges to 0 likewise. It follows from Lemma 3 that \begin{align*} 0&=2\pi i \sum_{a:\text{pole of \(g\)}}\text{Res}(g, a), \end{align*} \begin{align*}0&= \text{Res}(g, 0)+\text{Res}(g, 1)+\text{Res}(g, -1)+ \sum_{n=2}^{\infty} \left(\text{Res}(g, n)+ \text{Res}(g, -n)\right) + \sum_{1\le k\le 2m-1, k\ne m} \frac{\pi }{2m} \beta^{k}\cot(\pi \beta^{k}) \\&= -\frac{1}{\pi }-\frac{2m-1}{2m}\pi +\frac{2}{\pi }\zeta_{-1}(2m)+ \sum_{1\le k\le 2m-1, k\ne m} \frac{\pi }{2m} \beta^{k}\cot(\pi \beta^{k}). \end{align*} Conclude that \[ \zeta_{-1}(2m)= \frac{\,1\,}{2}+\frac{2m-1}{4m}- \frac{\pi}{4m} \sum_{1\le k\le 2m-1, k\ne m} \beta^{k}\cot(\pi \beta^{k}). \]
Example 3. For \(s=4, m=2, \beta=\exp\left(\frac{\pi i}{2}\right)=i\), an expression of real trigonometric function for \(\zeta_{-1}(4)\) is \[ \zeta_{-1}(4)= \frac{1}{2}+\frac{3}{8}-\frac{\pi}{8} \left(i\cot(\pi i)+i^{3}\cot(\pi i^{3})\right) = \frac{7}{8}-\frac{\pi}{4}\coth(\pi). \] Notice that this also shows that \[ \sum_{k=1}^{\infty}\left(\zeta(4k)-1\right) =\frac{7}{8}-\frac{\pi}{4}\coth(\pi) \] as in [4, 263]. For \(s=6, m=3, \beta=\exp\left(\frac{\pi i}{3}\right)\), we see that \begin{align*} \zeta_{-1}(6)& =\frac{1}{2}+\frac{5}{12} -\frac{\pi}{12} \left( e^{\pi i/3}\cot(\pi e^{\pi i/3}) + e^{-\pi i/3}\cot(\pi e^{-\pi i/3} ) + e^{2\pi i/3}\cot(\pi e^{2\pi i/3}) + e^{-2\pi i/3}\cot(\pi e^{-2\pi i/3} )\right)\\ &= \frac{11}{12}-\frac{\pi}{12} \left( \frac{\sqrt{3}\sinh \sqrt{3}\pi}{\cosh\sqrt{3}\pi+1} + \frac{\sqrt{3}\sinh \sqrt{3}\pi}{\cosh\sqrt{3}\pi+1} \right)\\ &= \frac{11}{12}-\frac{\pi}{12} \left( \,2\sqrt{3}\, \frac{2\sinh \frac{\sqrt{3}}{2}\pi\cosh \frac{\sqrt{3}}{2}\pi} {2\cosh^{2} \frac{\sqrt{3}}{2}\pi} \right)\\ &=\frac{11}{12}-\frac{\sqrt{3}}{6}\pi\tanh{\frac{\sqrt{3}}{2}\pi}. % =0.017593\cd. \end{align*}