This study employs dynamic modeling and simulation to provide theoretical insights into the systemic behaviors underlying diphtheria pathogenesis. A Boolean network model was developed to formalize the hypothesized interactions among eight genes identified in the literature as central to toxin production, immune response, and disease transmission. Computational exploration of the state-space dynamics within this model revealed three distinct attractors, each hypothesized to represent key disease states. Structural analysis of these attractors and their basins of attraction offered insights into network architectures potentially responsible for bistable switches between chronic infection and recovery, endogenous inflammatory oscillations reflective of periodic fever cycles, and modular topologies enabling alternative developmental pathways. These findings demonstrate the utility of Boolean modeling in uncovering organizing principles—such as periodicity, bistability, and evolvability—that govern disease emergence in complex systems. The study highlights testable network signatures that could refine our understanding of diphtheria and similar pathologies, and while preliminary, it underscores the potential of iterative computational and experimental approaches to inform more effective control strategies.
Gene regulation is a fundamental process that guides cell function and differentiation through precisely orchestrated patterns of gene expression [1-3]. At the core of gene regulation are gene regulatory networks (GRNs), complex webs of interactions where gene products activate or repress one another’s transcription [4-7]. Stable states of consistent gene expression are vital for maintaining cell identity and facilitating appropriate responses to stimuli [8-10]. Perturbations to stable expression patterns have been implicated in various diseases [11-13], underscoring the importance of characterizing the stable states attainable within GRNs.
However, the high dimensionality and nonlinearity of real molecular-scale GRNs pose major challenges to quantitative dynamical analysis [14-16]. Boolean network (BN) models provide a simplified abstract model that has proven useful in studying qualitative system-level properties like stable expression patterns [17-19]. In Boolean network modeling, genes are represented as network nodes that can be either active/ON or inactive/OFF [20-23]. Interactions between genes are encoded by edges updated according to logical Boolean functions [24-26]. While offering a coarse-grained approximation, BNs allow exploring how network structure and updating schemes influence a system’s long-term attractors [27-29].
Diphtheria is caused by Corynebacterium diphtheriae, which produces a potent exotoxin known to be the primary virulence factor. The exotoxin works by inhibiting protein synthesis through NAD-dependent diphtheria toxin-catalyzed ADP-ribosylation of elongation factor 2 (EF-2), leading to cell death [30,31]. The pathogenesis progresses as the bacteria colonize and create a pseudomembrane in the upper respiratory tract. Toxin production is initiated upon contact between the bacteria and host epithelial cells. This suggests cell-cell signaling plays a role in regulating toxin gene (toxT) expression [32].
Toxin production triggers an acute inflammatory response attempting to clear the infection. However, the pathogen has evolved mechanisms to subvert this. For example, the toxin itself suppresses antigen presentation and delays neutrophil recruitment, aiding bacterial survival [33].
A complex interplay between host immunity and bacterial virulence factors determines disease outcomes. Animal models have helped elucidate key cytokine pathways, demonstrating their role in mediating fever cycles often seen in clinical diphtheria. Adaptive immune responses also contribute to usually long-term immunity following recovery [34].
Mathematical models provide another lens to study the dynamical interdependencies governing disease emergence and progression [35]. This work extends such approaches through Boolean modeling to generate hypotheses reflecting pathogenic mechanisms orchestrated at the systemic network-level scale. It systematically determines the fixed points and attractor basins achievable within BN models of GRNs under a synchronous updating scheme, where all nodes update simultaneously at each discrete time step. Characterizing stable expression patterns in this basic modeling scenario lays foundation for further refinements incorporating regulatory details on molecule concentrations and timing. Understanding how fixed points are shaped by network architecture also provides insights applicable to GRN engineering and control.
In this work, Boolean network (BN) modelling is employed to investigate mechanisms of stable gene expression patterning within gene regulatory networks (GRNs). BNs provide a simplified discrete abstraction of GRNs that has proven fruitful for qualitative dynamical analysis despite biological simplifications. In BN representation, genes are denoted as nodes of a directed network, with binary states \(z_i = 1\) (Active/On) or \(z_i = 0\) (Inactive/Off) indicating expression levels. Directed edges between nodes encode regulatory interactions, with an edge from node \(j\) to \(i\) indicating \(j\) helps determine the state of \(i\).
Here are some preliminary definitions to understand the core concepts employed for modelling gene regulatory networks (GRNs) through Boolean networks (BNs):
Boolean network: A boolean network \(B(V,E)\) consists of a set of nodes (boolean variables), each variable can take on one of two values: true (represented by 1) or false (represented by 0), and a set of logical functions that determine the state of each variable based on the states of other variables. These logical functions are often defined using logical operators such as AND (\(\land\)), OR (\(\lor\)), and NOT (\(\lnot\)) [23].
Boolean Transition Function (Update Function): To formally encapsulate the logical relationships governing node state dynamics in Boolean network models, a Boolean transition function is defined for each node (represented by a boolean variable), where the state of variable \(z_i\) at time step \(t+1\) is determined by the logical function \(g_i: \left\lbrace 0,1 \right\rbrace^k \longrightarrow \left\lbrace 0,1 \right\rbrace^k\), which depends on the states of variables \(\left\lbrace z_1, z_2,\ldots, z_n \right\rbrace\) at time step \(t\) [36]. We can represent this relationship mathematically as: \[\label{key} \begin{cases} z_1(t+1) = g_1(z_1(t), z_2(t), \ldots, z_n(t)), \\ z_2(t+1) = g_2(z_1(t), z_2(t), \ldots, z_n(t)), \\ \quad \vdots \\ z_n(t+1) = g_n(z_1(t), z_2(t), \ldots, z_n(t)). \end{cases}\tag{1}\] Here, \(z_n(t+1)\) represents the state of variable \(z_i\) at time step \(t+1\), and \(g_n(z_1(t), z_2(t), \ldots, z_n(t))\) represents the logical function that determines the state of \(z_i\) based on the states of other variables at time step \(t\).
Gene Regulatory Network (GRN): A network of interactions between DNA-binding transcription factors and the genes they regulate [36].
Node (Boolean Variable): The representation of a single gene or transcription factor as a basic discrete variable in a Boolean network model.
Edge: A directed connection from one node to another in the network, representing a regulatory interaction where the source node helps determine the target’s state.
Wiring Diagram: The wiring diagram depicts the regulatory interconnections between network nodes through directed edges. It encodes the topological features and connectivity architecture that dictate qualitative dynamical constraints [36].
State: The value assumed by a node at any given time step, either ON (1) or OFF (0) in a binary Boolean system [36].
Attractor: A repeating pattern of node state configurations into which the dynamics will eventually settle, such as a fixed point or limit cycle.
Fixed Point: A state configuration constituting an attractor where the system’s state remains constant under further updates [36]. For an update function \(g : \mathbb{G}^n_2 \rightarrow \mathbb{G}^n_2\) the set of fixed points can be formally expressed as: \[Fix(g) = \{ z \in \mathbb{G}^n_2 | g(z) = z \}.\tag{2}\]
Limit Cycle: A limit cycle can be defined as a closed finite set of state configurations \(C = \{c_1, c_2, \ldots , c_n\}\) such that applying the system’s update rules will cycle sequentially through each configuration in \(C\) indefinitely. That is, beginning from any configuration \(c_k\) in \(C\), repeated application of the update functions will lead to configurations \(c_{k+1}\), \(c_{k+2}\), and so on until returning to the initial configuration and restarting the cycle [36].
Basin of Attraction: The set of initial states from which the dynamics will evolve into a given attractor under repeated updates.
State Space: Refers to the set of all possible discrete state configurations the system can take on at any given time step. For a network with N nodes that can be in either state 0 or 1, the state space contains \(2^N\) elements [37].
State Transition Graph: A graphical representation of state space dynamics where nodes denote unique system states and directed edges indicate possible state transitions under applying the update functions. The graph structure illuminates attractor structure and basin organization [36].
Circuits (feedback loops): This refers to interconnected pathways that regulate cellular processes and interactions, functioning similarly to electrical circuits in that they transmit signals and feedback to maintain homeostasis within the system. These feedback loops are crucial for understanding stability, oscillations, and bistability in biological systems, particularly in the context of diseases such as diphtheria. While Feedback refers to the process by which the output of a system influences its input, thereby affecting its future behavior [38].
Set of Transient States: One of the important phases in anallyzing a Boolean network model’s dynamics is characterizing the set of transient states. These represent the states that the network will pass through before ultimately settling into an attractor cycle or fixed point [36]. Suppose \((Z, G)\) is a Boolean network having the global update function \(g : \mathbb{G}^n_2 \rightarrow \mathbb{G}^n_2\), then the transient states of \(g\) can be expressed as: \[Trans(g) = \{ z \in \mathbb{G}^n_2 \ | \ g^{(k)} (z) \ne z \quad \forall \ k \ge 1\},\tag{3}\]
Set of Periodic points: The set of periodic points denoted as \(Per(g)\), encompasses any states that directly return to themselves after some number of time steps via the transition function [36]. This includes both stable limit cycles as well as unstable repeating patterns. It is expressed mathematically as: \[Per(g) = \{z \in \mathbb{G}^n_2 \ | \ g^{(k)} (z) = z \ \text{for some} \ k > 1\}.\tag{4}\]
Garden of Eden State: A garden-of-Eden state is defined as a network configuration that maps to other states under iterative application of the function, but is not mapped to itself and cannot be re-derived through successive updates [36]. Mathematically, it is the set: \[GoE(g) = \{z \in \mathbb{G}^n_2 \ | \ \nexists \ w \in \mathbb{G}^n_2 \ \text{such that} \ g(w) = z \}.\tag{5}\]
This preliminary definitional paradigm establishes the key modeling abstractions, structural elements and analytical concepts that will be systematically investigated through BN simulations of GRNs under different architectural constraints.
Diphtheria infection is initiated upon binding of Corynebacterium diphtheriae toxin (DtxR) to epidermal growth factor receptors on host cells. This leads to MAPK cascade activation and up-regulation of pro-inflammatory cytokines like IL-6 and TNF\(\alpha\). Toll-like receptors (TLRs) also sense lipoproteins and lipopolysaccharides from the bacteria. TLR4 in particular triggers the MyD88-dependent pathway inducing NF-\(\kappa\)B, which drives expression of additional cytokines, costimulatory molecules and interferons [30].
Interferons then signal via JAK-STAT to induce hundreds of antiviral effector genes including Mx proteins, PKR, and OAS. This helps override DtxR-mediated repression of MHC expression and clear the infection. Nrf2 and AP-1 regulate oxidative stress response and coordinately protect cells from reactive oxygen species accompanying heavy metal dysregulation during illness. They may modulate cytokine storm severity. While diphtheria pathogenesis has long been observed clinically, quantitative modelling of the underlying genetic interactions remains under-explored. Previous systems-level analyses have largely focused on continuous differential equation approaches or data-driven correlations, overlooking the logic of transcriptional control crucial to dynamical behaviors. To begin investigating dynamical behaviors under the synchronous update scheme, we propose a 8-node prototype Boolean network model to explore genetic regulatory dynamics underlying diphtheria pathogenesis progression (see Table 2 and 3).
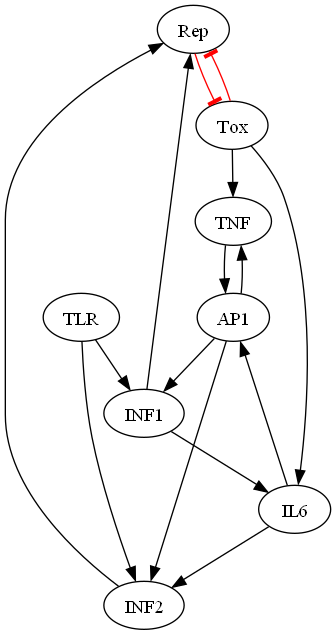
The 8-node prototype network (see Figure 1) represents the first attempt to formally conceptualize how key genetic components in the diphtheria system operate together as an integrated whole according to combinatorial input rules. By drawing upon current pathway knowledge, we distilled the complexity into a simplified yet rigorously defined structure upon which hypotheses about disease emergence and progression can be systematically generated. This innovation sets the stage for new theoretical investigations into mechanisms of toxin production, host immune responses, and inflammatory feedbacks through simulation.
The figure 1 illustrates the intricate transduction involved in the immune response. Each node represents a key protein or signaling molecule, including Rep (regulator), Tox (toxin), INF1 and INF2 (interferons), TLR (Toll-like receptor), TNF (tumor necrosis factor), AP1 (activator protein 1), and IL6 (interleukin 6). Arrows indicate the direction of activation, with black lines showing direct interactions and a red lines denoting feedback inhibition from Rep to Tox [31]. In this network, TLR senses pathogen-associated molecular patterns, leading to the activation of INF1 and INF2 [39], which are crucial for antiviral defense. TNF activates AP1 [40], that is enhanced by IL6 [41], and AP1 also interacts with INF1 [42] and INF2 [43], which plays a crucial role in the body’s defense mechanisms by helping to regulate the immune response. Elevated levels of Rep modulate the network by inhibiting Tox [44], thereby fine-tuning the immune response (see Table 1). This feedback loop is essential for maintaining homeostasis in immune signaling, allowing the body to respond appropriately to infections while preventing excessive inflammation.
The model necessarily retains abstraction but establishes a proof-of-principle for discrete modeling in this under-explored application domain. Phenomena such as multistability, oscillations, and phase transitions emerging from cooperativity across network elements can now be explored in silico, guiding wet-lab validation efforts. In proposing this admittedly nascent model, our goal is to spark new conceptual perspectives and drive future model refinement. With increased biological realism and testing against time-series data, such efforts may one day support precision diagnostics and therapy. Fundamentally, our contribution introduces a paradigm for advancing systems-level comprehension of this important infectious disease.
In BNs, each node’s discrete dynamic behavior is encapsulated by an associated Boolean function (BF) defining its next state based on the present states of incoming regulatory inputs. Synchronous updating [45] allows all nodes in the network to be updated simultaneously, which generates deterministic dynamics. This means that from any given state, there is a unique successor state, making it easier to analyze and predict the system’s behavior over time. In contrast, asynchronous updating introduces stochasticity, leading to multiple possible successor states depending on the order of updates, which complicates the analysis. While asynchronous models are often considered more biologically realistic due to their representation of individual component updates, they can misrepresent timing in biological processes. For instance, if a biological event takes minutes, an asynchronous model might imply that downstream genes remain inactive for days, which is unrealistic. Synchronous models can better capture the interdependencies of biological processes where multiple components influence each other simultaneously. In this study, synchronous updating will be used as defined by the global state transition function: \[Y(z(t),z(t+1)) = \bigwedge^{n}_{i=1} \left( z_i (t+1) \leftrightarrow g_i(z_1(t), z_2(t), \ldots, z_n(t)) \right) .\tag{6}\] The update procedure would involve iterating through the following discrete time steps:
Determine the current global expression state vector \(Z(t)\) consisting of all genes’ expression levels (\(0\) or \(1\)).
Synchronously update each gene \(n\) according to its transition function \(g_n\): \[z_n(t+1) = g_n (z_1(t), z_2(t),\ldots, z_n(t)) ,\tag{7}\] where \(z_n(t)\) refers to the expression levels of genes regulating \(n\) at time \(t\).
Advance the global state: \[Z(t+1) = \left[ z_1(t+1), s_2(t+1),\ldots,s_n(t+1) \right].\tag{8}\]
Record \(Z(t+1)\) and repeat steps \(2-3\), continually updating all genes in unison based on the previous state.
Iterate until a fixed point attractor is reached where \(Z(t+X) = Z(t+X+1)\), or a periodic cycle is detected.
Repeat for all possible initial conditions to exhaustively explore dynamics.
This simulation-based approach allows investigating how specific network architectures, logical rules, and perturbations influence long-term expression patterns emerging from synchronous discrete updates. Moving forward and formally modeling the 8–node diphtheria genetic regulatory network (1) using Boolean transition function. Let \(z_1(t)\) represent expression of the toxin gene Tox, \(z_2(t)\) the repressor gene Rep, \(z_3(t)\) for INF1, \(z_4(t)\) for INF2, \(z_5(t)\) for TLR, \(z_6(t)\) for AP1, \(z_7(t)\) for IL6 and \(z_8(t)\) for tumor necrosis factor TNF: \[\label{first} \begin{cases} z_1 (t+1) = \lnot z_2 (t) \ \ \ \ \ \ \ \ \ \ \ \\ z_2 (t+1) = \lnot z_1 (t) \land (z_3 (t) \lor z_4 (t)) \\ z_3 (t+1) = z_5 (t) \lor z_6 (t) \ \ \ \ \ \ \ \\ z_4 (t+1) = z_5 (t) \lor z_6 (t) \lor z_7 (t) \ \ \\ z_5 (t+1) = 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ z_6 (t+1) = z_8 (t) \lor z_7 (t) \ \ \ \ \ \ \ \\ z_7 (t+1) = z_1 (t) \lor z_3 (t) \ \ \ \ \ \ \ \\ z_8 (t+1) = z_1 (t) \lor z_6(t) \ \ \ \ \ \ \ \end{cases}\tag{9}\]
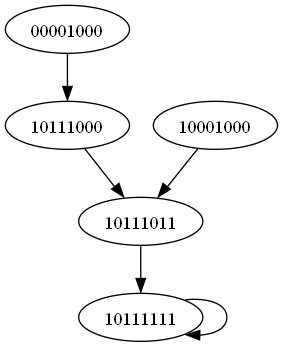
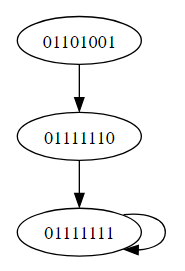
This captures the system dynamics succinctly in discrete time and logic. Now let, we could also convert this boolean transition function into a rather polynomial form so that, where \(h(y,z) = y \lor z = y + z + y \cdot z\), \(h(y,z) = y \land z = y\cdot z\), \(h(y) = \lnot y = 1 + y\), \(h(y) = y \land y = y^2 = y\) and \(h(y) = \alpha \cdot y = 0 \ \forall \ \alpha \in \Re\), then equation (9), becomes: \[\label{second} \begin{cases} z_1 (t+1) = 1 + z_2 (t) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad\\ z_2 (t+1) = (1 + z_1 (t)) \cdot (z_3 (t) + z_4 (t) + z_3(t) \cdot z_4(t)) \quad \quad \quad \quad \\ z_3 (t+1) = z_5 (t) + z_6 (t) + z_5 (t) \cdot z_6 (t) \quad \quad \quad \quad \quad \quad \quad \quad \\ z_4 (t+1) = z_5 (t) + \left( z_6 (t) + z_7 (t) + z_6 (t) \cdot z_7 (t) \right) + z_5(t) \cdot \left( z_6 (t) + z_7 (t) + z_6 (t) \cdot z_7 (t) \right) \ \ \\ z_5 (t+1) = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ z_6 (t+1) = z_8 (t) + z_7 (t) + z_8 (t) \cdot z_7 (t) \quad \quad \quad \quad \quad \quad \quad \quad \\ z_7 (t+1) = z_1 (t) + z_3 (t) + z_1 (t) \cdot z_3 (t) \quad \quad \quad \quad \quad \quad \quad \quad \\ z_8 (t+1) = z_1 (t) + z_6(t) + z_1 (t) \cdot z_6(t) \quad \quad \quad \quad \quad \quad \quad \quad \end{cases}\tag{10}\] Then to simulate Eq. (10), synchronously, we begin with a hypothetical scenario where the pathogen has just entered the host cell and initiated an immune response. This translates to an initial state vector of: \(z_n^{(0)} =\left[ z_1^{(0)}, z_2^{(0)}, z_3^{(0)}, z_4^{(0)}, z_5^{(0)}, z_6^{(0)}, z_7^{(0)}, z_8^{(0)} \right] = \left[ 1, 0, 0, 0, 1, 0, 0, 0 \right]\), where \(z_1(t)\) “Toxin” is activated, representing presence of the bacteria. \(z_5(t)\) “TLR” is also ON as it detects microbial signals. Applying the update rules, we calculate \(z_n^{(1)}\): \[\label{third} \begin{cases} z_1^{(1)} = 1 + z_2^{(0)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad\\ z_2^{(1)} = (1 + z_1^{(0)}) \cdot (z_3^{(0)} + z_4^{(0)} + z_3^{(0)} \cdot z_4^{(0)}) = 0 \quad \quad \quad \quad \\ z_3^{(1)} = z_5^{(0)} + z_6^{(0)} + z_5^{(0)} \cdot z_6^{(0)} = 1\quad \quad \quad \quad \quad \quad \quad \quad \\ z_4^{(1)} = z_5^{(0)} + \left( z_6^{(0)} + z_7^{(0)} + z_6^{(0)} \cdot z_7^{(0)} \right) + z_5^{(0)} \cdot \left( z_6^{(0)} + z_7^{(0)} + z_6^{(0)} \cdot z_7^{(0)} \right) = 1 \ \ \\ z_5^{(1)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ z_6^{(1)} = z_8^{(0)} + z_7^{(0)} + z_8^{(0)} \cdot z_7^{(0)} = 0 \quad \quad \quad \quad \quad \quad \quad \quad \\ z_7^{(1)} = z_1^{(0)} + z_3^{(0)} + z_1^{(0)} \cdot z_3^{(0)} = 1\quad \quad \quad \quad \quad \quad \quad \quad \\ z_8^{(1)} = z_1^{(0)} + z_6^{(0)} + z_1^{(0)} \cdot z_6^{(0)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \end{cases}\tag{11}\] For the next iteration, we have; \[\label{Fourth} \begin{cases} z_1^{(2)} = 1 + z_2^{(1)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad\\ z_2^{(2)} = (1 \cdot z_1^{(1)}) \cdot (z_3^{(1)} + z_4^{(1)} + z_3^{(1)} \cdot z_4^{(1)}) = 0 \quad \quad \quad \quad \\ z_3^{(2)} = z_5^{(1)} + z_6^{(1)} + z_5^{(1)} \cdot z_6^{(1)} = 1\quad \quad \quad \quad \quad \quad \quad \quad \\ z_4^{(2)} = z_5^{(1)} + ( z_6^{(1)} + z_7^{(1)} + z_6^{(1)} \cdot z_7^{(1)}) + z_5^{(1)} \cdot \left( z_6^{(1)} + z_7^{(1)} + z_6^{(1)} \cdot z_7^{(1)}\right) = 1 \ \ \\ z_5^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ z_6^{(2)} = z_8^{(1)} + z_7^{(1)} + z_8^{(1)} \cdot z_7^{(1)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \\ z_7^{(2)} = z_1^{(1)} + z_3^{(1)} + z_1^{(1)} \cdot z_3^{(1)} = 1\quad \quad \quad \quad \quad \quad \quad \quad \\ z_8^{(2)} = z_1^{(1)} + z_6^{(1)} + z_1^{(1)} \cdot z_6^{(1)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \end{cases}\tag{12}\] The next iteration becomes; \[\label{Five} \begin{cases} z_1^{(3)} = 1 + z_2^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad\\ z_2^{(3)} = (1 \cdot z_1^{(2)}) \cdot (z_3^{(2)} + z_4^{(2)} + z_3^{(2)} \cdot z_4^{(2)}) = 0 \quad \quad \quad \quad \\ z_3^{(3)} = z_5^{(2)} + z_6^{(2)} + z_5^{(2)} \cdot z_6^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \\ z_4^{(3)} = z_5^{(2)} + ( z_6^{(2)} + z_7^{(2)} + z_6^{(2)} \cdot z_7^{(2)}) + z_5^{(2)} \cdot ( z_6^{(2)} + z_7^{(2)} + z_6^{(2)} \cdot z_7^{(2)}) = 1 \ \ \\ z_5^{(3)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ z_6^{(3)} = z_8^{(2)} + z_7^{(2)} + z_8^{(2)} \cdot z_7^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \\ z_7^{(3)} = z_1^{(2)} + z_3^{(2)} + z_1^{(2)} \cdot z_3^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \\ z_8^{(3)} = z_1^{(2)} + z_6^{(2)} + z_1^{(2)} \cdot z_6^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \end{cases}\tag{13}\] Since iteration 2 and 3 are the same the solution is said to converge and 10111111 is a fixed point of the system, the transient state of this attractor is seen in Figure (2). As oppose our first initial state, lets consider a vector of: \(z_n^{(0)} =\left[ z_1^{(0)}, z_2^{(0)}, z_3^{(0)}, z_4^{(0)}, z_5^{(0)}, z_6^{(0)}, z_7^{(0)}, z_8^{(0)} \right] = \left[ 0, 0, 0, 0, 1, 0, 0, 0 \right]\), where \(z_1(t)\) “Toxin” is deactivated, representing presence of the bacteria. \(z_5(t)\) “TLR” is only ON as it detects microbial signals, we have: \[\label{Seven} \begin{cases} z_1^{(1)} = 1 + z_2^{(0)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad\\ z_2^{(1)} = (1 + z_1^{(0)}) \cdot (z_3^{(0)} + z_4^{(0)} + z_3^{(0)} \cdot z_4^{(0)}) = 0 \quad \quad \quad \quad \\ z_3^{(1)} = z_5^{(0)} + z_6^{(0)} + z_5^{(0)} \cdot z_6^{(0)} = 1\quad \quad \quad \quad \quad \quad \quad \quad \\ z_4^{(1)} = z_5^{(0)} + \left( z_6^{(0)} + z_7^{(0)} + z_6^{(0)} \cdot z_7^{(0)} \right) + z_5^{(0)} \cdot \left( z_6^{(0)} + z_7^{(0)} + z_6^{(0)} \cdot z_7^{(0)} \right) = 1 \ \ \\ z_5^{(1)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ z_6^{(1)} = z_8^{(0)} + z_7^{(0)} + z_8^{(0)} \cdot z_7^{(0)} = 0 \quad \quad \quad \quad \quad \quad \quad \quad \\ z_7^{(1)} = z_1^{(0)} + z_3^{(0)} + z_1^{(0)} \cdot z_3^{(0)} = 0\quad \quad \quad \quad \quad \quad \quad \quad \\ z_8^{(1)} = z_1^{(0)} + z_6^{(0)} + z_1^{(0)} \cdot z_6^{(0)} = 0 \quad \quad \quad \quad \quad \quad \quad \quad \end{cases}\tag{14}\] For the next iteration, we have; \[\label{Six} \begin{cases} z_1^{(2)} = 1 + z_2^{(1)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad\\ z_2^{(2)} = (1 \cdot z_1^{(1)}) \cdot (z_3^{(1)} + z_4^{(1)} + z_3^{(1)} \cdot z_4^{(1)}) = 0 \quad \quad \quad \quad \\ z_3^{(2)} = z_5^{(1)} + z_6^{(1)} + z_5^{(1)} \cdot z_6^{(1)} = 1\quad \quad \quad \quad \quad \quad \quad \quad \\ z_4^{(2)} = z_5^{(1)} + ( z_6^{(1)} + z_7^{(1)} + z_6^{(1)} \cdot z_7^{(1)}) + z_5^{(1)} \cdot \left( z_6^{(1)} + z_7^{(1)} + z_6^{(1)} \cdot z_7^{(1)}\right) = 1 \ \ \\ z_5^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ z_6^{(2)} = z_8^{(1)} + z_7^{(1)} + z_8^{(1)} \cdot z_7^{(1)} = 0 \quad \quad \quad \quad \quad \quad \quad \quad \\ z_7^{(2)} = z_1^{(1)} + z_3^{(1)} + z_1^{(1)} \cdot z_3^{(1)} = 1\quad \quad \quad \quad \quad \quad \quad \quad \\ z_8^{(2)} = z_1^{(1)} + z_6^{(1)} + z_1^{(1)} \cdot z_6^{(1)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \end{cases}\tag{15}\] Iterating again gives; \[\label{Eight} \begin{cases} z_1^{(3)} = 1 + z_2^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad\\ z_2^{(3)} = (1 \cdot z_1^{(2)}) \cdot (z_3^{(2)} + z_4^{(2)} + z_3^{(2)} \cdot z_4^{(2)}) = 0 \quad \quad \quad \quad \\ z_3^{(3)} = z_5^{(2)} + z_6^{(2)} + z_5^{(2)} \cdot z_6^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \\ z_4^{(3)} = z_5^{(2)} + ( z_6^{(2)} + z_7^{(2)} + z_6^{(2)} \cdot z_7^{(2)}) + z_5^{(2)} \cdot ( z_6^{(2)} + z_7^{(2)} + z_6^{(2)} \cdot z_7^{(2)}) = 1 \ \ \\ z_5^{(3)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ z_6^{(3)} = z_8^{(2)} + z_7^{(2)} + z_8^{(2)} \cdot z_7^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \\ z_7^{(3)} = z_1^{(2)} + z_3^{(2)} + z_1^{(2)} \cdot z_3^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \\ z_8^{(3)} = z_1^{(2)} + z_6^{(2)} + z_1^{(2)} \cdot z_6^{(2)} = 1 \quad \quad \quad \quad \quad \quad \quad \quad \end{cases}\tag{16}\]
Hence another iteration gives you same state, therefore 10111111 is a fixed point of the system (see Figure (2)) for the transient state of the attractor.
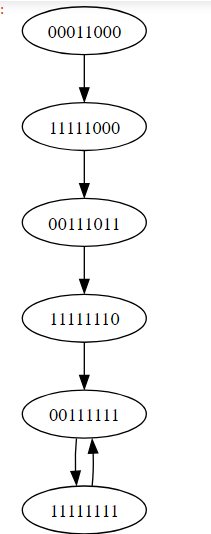
The synchronous update approach described above was used to systematically analyze the long-term dynamical behavior (see Appendix Table (4)) and attractors exhibited by the disease transmission model. By iteratively updating the state variables in lockstep according to the defined logic and polynomial equations, the asymptotic trajectories and basins of attraction was be characterized (see result). This provided insights into the equilibrium points and cycles representing endemic and disease-free states. However, it is acknowledged that synchronous updating schemes may yield different attractor structures due to effects not captured under asynchronization.
Upon conducting a thorough investigation of the network dynamics using computational modeling and Boolean simulation techniques, several noteworthy attractors within the state space were identified. These stable expression patterns provide important hypotheses about core pathogenic mechanisms and disease trajectories which now warrant further exploration. Specifically, the analysis uncovered the existence of three key attractors that may provide useful insights into diphtheria progression at a system-wide level. The first attractor (10111111) consisted of a simple fixed point involving repression of key genes associated with toxin production. A second fixed point attractor (01111111) likewise demonstrated repressed expression, but in this case without toxin. Most intriguingly, a cyclic attractor (11111111, 00111111) was observed oscillating between two states of differential inflammation gene expression over time. Such dynamical behavior hints at underlying periodicity in disease symptoms and immune response modulation. Together, these in silico predictions represent theoretically grounded proposals for empirically examining diphtheria pathogenesis through a higher-order network perspective. In the following sections, We aim to characterize each attractor in detail and discuss their potential biological relevance based on existing knowledge of associated gene functions and protein interactions. By rendering the model’s emergent properties visible and subject to investigation, we embark on an promising program of computational validation through experimentation.
The Table 4 (see Appendix) provides insight into the structure and stability of the basin of attraction for Attractor 1. We can observe that 40 total states map to this fixed point, with the majority (32 states) transitioning to it in just 1-3 updating steps. This suggests Attractor 1 exerts a strong pulls on the state space dynamics. States farther from the attractor take slightly longer to converge onto its cycle, like 00001000 requiring 3 transitions. But all reachable states ultimately settle into the stable pathogenic expression profile of Attractor 1.
Notably, the Attractor 1 state itself 10111111 is also listed, confirming it is an absorbing fixed point that remains in the basin once entered. Overall, this exploration of the basin portrait reinforces conclusions about Attractor 1 representing a robust infectious phenotype governed by toxin production. The wide and topologically concentrated basin endows this configuration with considerable influence over system trajectories.
Furthermore, examining the basin structure of Attractor 2 (Table 5) provides additional insights into its dynamical properties and stability. We observe that its basin encompasses 24 total states that map to the fixed point configuration 01111111. Similar to Attractor 1, most of these states (16 out of 24) converge to the attractor within just 1-4 timesteps according to the network functions. This suggests Attractor 2 exerts a dominant pull on a notable region of phase space.
Interestingly, the average number of steps taken to reach Attractor 2 from its basin states appears slightly greater than for Attractor 1. This could point to Attractor 2 representing a more precarious expression profile that is slightly more perturbation-sensitive once infections are resolved without toxin.
Nonetheless, its basin remains reasonably concentrated and topologically close to the fixed point itself, endowing Attractor 2 with considerable stability against stochastic fluctuations once attained. This accords with its posited role in modeling disease resolution or asymptomatic carriage upon toxin clearance.
Analyzing the basin structure of Attractor 3 (Table 6 – 7), the dynamical 2-state cyclic attractor, provides useful insights into its propensity to emerge across trajectories of the disease network model.
We see its basin encompasses the largest region of the phase space at 64 states. Many are centered closely around the limit cycle itself, transitioning to it within 1-4 timesteps as expected for a dominant emergent behavior.
However, some states mapped to the cycle require traversing longer paths. For example, 00011000 takes 4 transitions, hinting at how small variations could impact the cyclic inflammation profile. Overall, the cyclic attractor appears well-embedded within the landscape, influencing a broad domain susceptibly to periodic oscillations in inflammatory genes over infection timescales. This quantitative portrait lends theoretical plausibility to Attractor 3 representing a robust and flexible endogenous response mechanism governing recurring fever cycles etc. Its prominence as a attractor could also explain how innate immune fluctuations may persist even after adaptive resolution via other fixed points. These analysis further elucidate the postulated bistability between chronic infection versus recovery/healthy dynamics governed by this network model. They demonstrate the properties expected of biologically meaningful hypotheses warranting experimental interrogation.
In all the attractors identified in this Boolean model provide biologically meaningful insights into diphtheria pathogenesis, though certain caveats regarding the abstraction level apply: Fixed point attractors likely correlate with stable gene expression profiles achievable in vivo through various molecular interactions. While overlooking finer dynamics, attractors provide testable global hypotheses about stable disease/healthy states emergent from network architecture. For example, the robust toxin/infammation fixed points may reflect bistable switches governed by stabilized feedback at a higher organizational level than single bindings. However, the model abstracts away details of transcription, translation, protein complexes and real-valued expression inherent to molecular regulation. Future refinements incorporating such mechanism could garner closer agreement with wet-lab data.
Notably, the attractors demonstrated resilience within their basins against state perturbations, hinting at how stabilized expression patterns may withstand internal/external fluctuations in the real system. Experimental perturbation of specific network nodes mapped in attractor basins could validate such computational predictions of expression profile robustness conferring pathodynamics. While idealized, Boolean models offer a complementary perspective to reductionist approaches by focusing on emergent organizational principles beneath cellular complexity. Their hypotheses warrant testing to iteratively refine system-level understanding of signalling networks.
A Boolean network model has been developed to detail the interactions among eight essential genes involved in toxin production, immune response, and transmission. The model offers a valuable basis for exploring the systemic behaviors associated with diphtheria pathogenesis. The attractors identified in this study are encoded in the format Tox, Rep, INF1, INF2, TLR, AP1, IL6, TNF, and each offers unique contributions to our understanding of diphtheria pathogenesis.
The attractor 10111111 provides a comprehensive view of a significant disease state associated with active diphtheria infection and a strong immune response. This state is marked by the activation of the diphtheria toxin gene (Tox) alongside the repression of the toxin repressor gene (Rep), indicating a phase where toxin production by the bacteria is not regulated. Such unregulated production is a key feature of active diphtheria infections, leading to symptoms like pseudomembrane formation in the respiratory tract and systemic toxicity. At the same time, the activation of interferon response genes (INF1 and INF2) suggests that the host’s immune system is actively engaging with the infection. Interferons are crucial components of the innate immune response, enhancing antiviral defenses and modulating immune activity, which indicates that the host is attempting to counteract the bacterial invasion. The activation of toll-like receptors (TLR) further emphasizes this immune engagement, as TLRs are essential for recognizing pathogen-associated molecular patterns (PAMPs) and triggering inflammatory responses.
The transcription factor AP1’s activation within this attractor points to ongoing transcriptional activity related to immune responses and inflammation. AP1 serves as a vital regulator of gene expression, likely activated by upstream signals from TLRs and other immune receptors. Additionally, the presence of interleukin 6 (IL6) and tumor necrosis factor (TNF) reflects a vigorous inflammatory response. IL6 plays a role in activating immune cells during infections, while TNF is critical for initiating inflammation and activating various immune responses. This attractor encapsulates a phase of acute infection where the host’s immune system is actively working to combat the bacterial infection and mitigate toxin effects. The interplay between the bacterial pathogen and the host’s immune response highlighted by this attractor offers valuable insights into the systemic behaviors associated with diphtheria pathogenesis. The combination of unchecked toxin production and a robust immune response illustrates how crucial the host’s defenses are in managing infection.
The second attractor, 01111111, reveals a unique and noteworthy state within the Boolean gene regulation model of diphtheria pathogenesis. This attractor is defined by the inactivation of the diphtheria toxin gene (Tox) and the activation of the toxin repressor gene (Rep), indicating that toxin production is effectively inhibited. This inhibition is a crucial element of the host’s defense strategy, aimed at minimizing the harmful effects of the diphtheria toxin. Even in the absence of toxin production, immune response genes remain active. The activation of interferon response genes (INF1 and INF2) suggests that the host’s immune system continues to be alert and ready to address any potential threats. The toll-like receptor (TLR) is also engaged, signifying that the immune system is persistently detecting pathogen-associated molecular patterns (PAMPs), even without active toxin production. This ongoing TLR activity emphasizes the host’s preparedness to initiate an immune response if necessary. The activation of the transcription factor AP1 indicates that the host cells are actively transcribing genes related to immune responses and inflammation. This transcriptional activity helps ensure that the host is ready to combat any potential resurgence of infection. Furthermore, the presence of interleukin 6 (IL6) and tumor necrosis factor (TNF) signifies a continuous inflammatory state. Both IL6 and TNF are critical pro-inflammatory cytokines involved in activating immune cells and initiating inflammation, suggesting that the immune system remains in a heightened state of alertness despite suppressed toxin production. This attractor likely represents a chronic infection phase or a recovery state where the host has effectively controlled toxin production while remaining actively engaged in immune defense. The persistent activation of immune response genes and inflammatory cytokines indicates that the host is still prepared to respond to any potential resurgence of infection. This scenario illustrates the bistable nature of the network architecture, allowing for transitions between chronic infection and recovery.
The third attractor, (11111111, 00111111), introduces an oscillatory and dynamic state within the Boolean gene regulation model of diphtheria pathogenesis. This attractor is defined by periodic transitions between two different states, each exhibiting distinct gene activation patterns. These oscillations offer significant insights into the temporal dynamics of gene expression and the immune response during diphtheria infections. In the first state (11111111), both the diphtheria toxin gene (Tox) and the toxin repressor gene (Rep) are active. This simultaneous activation indicates a temporary phase in which the bacterial pathogen is producing toxin while the host’s regulatory mechanisms are working to suppress it. The active interferon response genes (INF1 and INF2), toll-like receptor (TLR), transcription factor AP1, interleukin 6 (IL6), and tumor necrosis factor (TNF) signify a strong immune response. This state likely corresponds to an active infection phase where the host’s immune system is vigorously combating toxin production. In contrast, the second state (00111111) shows both the toxin gene (Tox) and the repressor gene (Rep) inactive. Despite this lack of toxin production, immune response genes remain engaged. The continued activation of INF1, INF2, TLR, AP1, IL6, and TNF suggests that the host’s immune system is in a heightened state of readiness, prepared to respond to any potential resurgence of infection. This state likely represents a phase of immune surveillance, where the immune system remains vigilant even without active toxin production. The cyclic nature of this attractor mirrors the endogenous inflammatory oscillations and periodic fever cycles often seen in patients with diphtheria. The transitions between states of high and low inflammation illustrate the dynamic relationship between toxin production and the host’s immune response. This periodic behavior indicates that the immune system is continuously adapting to the presence of the bacterial pathogen, alternating between active responses and surveillance.
Boolean modeling is a powerful tool for studying diphtheria pathogenesis, but it has several limitations that must be understood to accurately interpret results and guide future research. One significant limitation of Boolean modeling is its oversimplification of biological complexity. These models represent gene activities in binary terms—either “on” (1) or “off” (0)—which fails to capture the nuanced and continuous nature of gene expression. In reality, gene expression occurs at varying levels rather than in a strict on/off manner, meaning that important regulatory details may be overlooked. Another drawback is that Boolean models typically do not incorporate the temporal dynamics of gene expression and regulatory processes. Biological systems are inherently dynamic, with gene expression levels fluctuating over time in response to various stimuli. Since Boolean models often assume synchronous updates of gene states, they may not accurately reflect the asynchronous and stochastic nature of biological processes, which is particularly important in infectious diseases like diphtheria.
Biological systems are influenced by stochastic effects, where random fluctuations can impact gene expression and regulatory outcomes. Boolean models are deterministic and do not account for these random variations, potentially leading to an incomplete understanding of the variability seen in biological systems. In diphtheria pathogenesis, such stochastic effects can significantly affect both the host’s immune response and the behavior of the bacterial pathogen. Boolean models often simplify the complex interactions among genes and proteins. In reality, these interactions involve feedback loops, cross-talk between pathways, and context-dependent regulation. Boolean models may fail to capture these intricate relationships, resulting in an oversimplified view of the regulatory network. For example, the relationship between the diphtheria toxin gene (Tox) and its repressor gene (Rep) is likely influenced by multiple factors that a Boolean model may not fully represent. Boolean models generally assume homogeneity within cell populations, neglecting the variability that exists among different cells. Cells within a population can exhibit diverse gene expression patterns and regulatory behaviors, which can influence the overall response to infection. This heterogeneity is not accounted for in Boolean models, potentially leading to an incomplete understanding of system behavior. Biological regulation is often context-dependent; genes and proteins can behave differently under varying conditions. Boolean models may not adequately capture this variability since they typically apply a fixed set of rules without considering the biological context. This limitation is particularly relevant in infectious diseases, where both the host’s immune response and the pathogen’s behavior can vary significantly based on circumstances.
Boolean models rely on hypothesized interactions and rules derived from existing literature, which may not always be experimentally validated. The absence of direct validation can limit the reliability of predictions made by these models. Integrating Boolean modeling with experimental data is crucial for confirming assumptions and refining predictions, though this process can be challenging and requires iterative cycles of modeling and experimentation.
In closing, this paper has demonstrated the utility of applying Boolean modeling and dynamical systems analysis to generate testable insights into the system-level behavior governing diphtheria pathogenesis. Through simulating the hypothesized gene regulatory network, our computational exploration uncovered three distinct attractors hypothesized to capture key disease states and endogenous dynamics. Analyzing aspects such as basin structures associated with attractors provided quantitative characterizations of their postulated roles and influences over systemic trajectories. Though, further research is still required to rigorously validate these in silico predictions. Experimental confirmation or refinement of attractor configurations, stabilization of hypothesized expression profiles under perturbation, and reconstruction of alternative trajectories corresponding to Garden of Eden states represent crucial next steps. Dynamical modeling must also be integrated with ongoing advancement of molecular-scale regulatory mechanisms. Nonetheless, even at this early stage, our work has illuminated potential organizational blueprints within the disease network topology that warrant targeted investigation. It establishes this Boolean model as a valuable tool for generating new hypotheses regarding bistability, cyclic behaviors, evolutionary flexibility and other emergent phenomena beyond traditional reductionist views. Continuing this iterative dialogue between computational abstraction and wet-lab experimentation holds promise to transform our understanding of diphtheria and other pathologies at a higher network level. With refinement, such approaches may eventually inform disease subtyping, control strategies, and therapeutic interventions. Overall, this paper demonstrates the nascent power of dynamical modeling to open new theoretical windows into intrinsic organizational capacities encoded within biological regulatory network. It is recommended that future studies consider incorporating perturbation analyses, such as gain-of-function or loss-of-function studies, to enhance the understanding of the model’s dynamics. While this work focused on determining fixed points and attractors within a deterministic basis, the introduction of perturbation analyses could provide valuable insights, despite the potential complexity and additional variables they may introduce. Furthermore, acknowledging the limitations inherent in the current Boolean model, subsequent research could explore how these perturbations might impact the core dynamics. By integrating such analyses, future researchers could uncover how manipulating gene functions influences the behavior of the system. This approach would contribute to a more comprehensive understanding of synchronously updated fixed points and attractors, ultimately enriching the interpretability and robustness of the findings within the broader context of the model.
Boolean network model and its function according to the proposed transition rules:
Tox: Represents expression of the diphtheria toxin gene. Self-represses based on interaction with Rep.
Rep: Encodes the toxin repressor protein. Activated indirectly by INF1/INF2 and directly represses Tox. Provides negative feedback on toxin production.
INF1/INF2 : Capture interferon response genes, which help clear the infection. INF1 activates in response to TLR signaling or inflammatory AP1 pathway. INF2 further induced by IL6 in positive feedback.
TLR : Toll-like receptor sensor of PAMPs that triggers innate immunity cascade. Functionally fixed “on” in this simplified model.
AP1 : Inflammatory transcription factor complex. Upregulated cooperatively by TNF/IL6 signals in positive feedback loop amplifying inflammation.
IL6/TNF: Pro-inflammatory cytokine genes in later response. IL6 induced directly by toxin or INF1. TNF activated by toxin or AP1 pathways.
| Source Node | Target Node | Interaction Type | Reference |
|---|---|---|---|
| Tox | Rep | Inhibition | Boyd et. al., 1990 [44] |
| Rep | Tox | Inhibition | Holmes, 2000[31] |
| Tox | TNF | Activation | Morimoto et al., 1991[46] |
| TNF | AP1 | Activation | Westwick et al., 1994[40] |
| AP1 | TNF | Activation | Granet et al., 2004[47] |
| Tox | IL6 | Activation | Kashiwagi et al., 2014 [48] |
| IL6 | AP1 | Activation | Hungness et al., 2000 [41] |
| AP1 | INF1 | Activation | Atsaves et al., 2019[42] |
| AP1 | INF2 | Activation | Bartolini et al., 2016[43] |
| IL6 | INF2 | Activation | Moehring et al., 1971[49] |
| INF1 | IL6 | Activation | Nash et al., 2023[50] |
| INF1 | Rep | Activation | Schmitt et al., 1992[51] |
| TLR | INF1 | Activation | Severa & Fitzgerald., 2007[52] |
| TLR | INF2 | Activation | Kawai & Akira, 2010[39] |
| INF2 | Rep | Activation | Fourel et al., 1989[53] |
| Node | Gene Name |
|---|---|
| Tox | Diphtheria toxin gene |
| Rep | Tox repressor gene |
| INF1 | Interferon response gene 1 |
| INF2 | Interferon response gene 2 |
| TLR | Toll-like receptor, immune sensor |
| AP1 | Transcription factor activating pro-inflammatory genes |
| IL6 | Interleukin 6 cytokine gene |
| TNF | Tumor necrosis factor cytokine gene |
Together, these rules aim to distill the key genetic interactions governing progression from bacterial toxin initiation, to host defense, and resolution versus hyper-inflammation (see Table (3)).
| Node | Boolean Transition Rules |
|---|---|
| Tox | NOT Rep |
| Rep | NOT Tox AND (INF1 OR INF2) |
| INF1 | TLR OR AP1 |
| INF2 | TLR OR AP1 OR IL6 |
| TLR | 1 |
| AP1 | TNF OR IL6 |
| IL6 | Tox OR INF1 |
| TNF | Tox OR AP1 |
| State | Next state | Attr. basin | # trans. to attr. |
|---|---|---|---|
| 10001000 | 10111011 | 1 | 2 |
| 10101000 | 10111011 | 1 | 2 |
| 10011000 | 10111011 | 1 | 2 |
| 10111000 | 10111011 | 1 | 2 |
| 10001100 | 10111011 | 1 | 2 |
| 10101100 | 10111011 | 1 | 2 |
| 10011100 | 10111011 | 1 | 2 |
| 10111100 | 10111011 | 1 | 2 |
| 10001111 | 10111111 | 1 | 1 |
| 10101111 | 10111111 | 1 | 1 |
| 10011111 | 10111111 | 1 | 1 |
| 10111111 | 10111111 | 1 | 0 |
| 10001011 | 10111111 | 1 | 1 |
| 10101011 | 10111111 | 1 | 1 |
| 10011011 | 10111111 | 1 | 1 |
| 10111011 | 10111111 | 1 | 1 |
| 10001101 | 10111111 | 1 | 1 |
| 10101101 | 10111111 | 1 | 1 |
| 10011101 | 10111111 | 1 | 1 |
| 10111101 | 10111111 | 1 | 1 |
| 10001001 | 10111111 | 1 | 1 |
| 10101001 | 10111111 | 1 | 1 |
| 10011001 | 10111111 | 1 | 1 |
| 10111001 | 10111111 | 1 | 1 |
| 10001110 | 10111111 | 1 | 1 |
| 10101110 | 10111111 | 1 | 1 |
| 10011110 | 10111111 | 1 | 1 |
| 10111110 | 10111111 | 1 | 1 |
| 10001010 | 10111111 | 1 | 1 |
| 10101010 | 10111111 | 1 | 1 |
| 10011010 | 10111111 | 1 | 1 |
| 10111010 | 10111111 | 1 | 1 |
| 00001010 | 10111100 | 1 | 3 |
| 00001001 | 10111100 | 1 | 3 |
| 00001011 | 10111100 | 1 | 3 |
| 00001110 | 10111101 | 1 | 2 |
| 00001101 | 10111101 | 1 | 2 |
| 00001111 | 10111101 | 1 | 2 |
| 00001100 | 10111001 | 1 | 2 |
| 00001000 | 10111000 | 1 | 3 |
| State | Next state | Attr. basin | # trans. to attr. |
|---|---|---|---|
| 01101000 | 01111010 | 2 | 3 |
| 01111000 | 01111010 | 2 | 3 |
| 01101100 | 01111011 | 2 | 3 |
| 01111100 | 01111011 | 2 | 3 |
| 01101010 | 01111110 | 2 | 2 |
| 01101001 | 01111110 | 2 | 2 |
| 01111001 | 01111110 | 2 | 2 |
| 01101011 | 01111110 | 2 | 2 |
| 01111011 | 01111110 | 2 | 2 |
| 01111010 | 01111110 | 2 | 2 |
| 01101110 | 01111111 | 2 | 1 |
| 01111110 | 01111111 | 2 | 1 |
| 01101101 | 01111111 | 2 | 1 |
| 01111101 | 01111111 | 2 | 1 |
| 01101111 | 01111111 | 2 | 1 |
| 01111111 | 01111111 | 2 | 0 |
| 01011111 | 01111101 | 2 | 2 |
| 01011101 | 01111101 | 2 | 2 |
| 01011110 | 01111101 | 2 | 2 |
| 01011010 | 01111100 | 2 | 4 |
| 01011001 | 01111100 | 2 | 4 |
| 01011011 | 01111100 | 2 | 4 |
| 01011100 | 01111001 | 2 | 3 |
| 01011000 | 01111000 | 2 | 4 |
| State | Next state | Attr. basin | # trans. to attr. |
|---|---|---|---|
| 00011101 | 11111101 | 3 | 2 |
| 00011111 | 11111101 | 3 | 2 |
| 00011110 | 11111101 | 3 | 2 |
| 01001110 | 00111101 | 3 | 2 |
| 01001101 | 00111101 | 3 | 2 |
| 01001111 | 00111101 | 3 | 2 |
| 01001000 | 00111000 | 3 | 3 |
| 00011000 | 11111000 | 3 | 4 |
| 01001100 | 00111001 | 3 | 3 |
| 00011100 | 11111001 | 3 | 2 |
| 00101110 | 11111111 | 3 | 1 |
| 00111110 | 11111111 | 3 | 1 |
| 00101101 | 11111111 | 3 | 1 |
| 00111101 | 11111111 | 3 | 1 |
| 00101111 | 11111111 | 3 | 1 |
| 00111111 | 11111111 | 3 | 0 |
| State | Next state | Attr. basin | # trans. to attr. |
|---|---|---|---|
| 11001000 | 00111011 | 3 | 3 |
| 11101000 | 00111011 | 3 | 3 |
| 11011000 | 00111011 | 3 | 3 |
| 11111000 | 00111011 | 3 | 3 |
| 11001100 | 00111011 | 3 | 3 |
| 11101100 | 00111011 | 3 | 3 |
| 11011100 | 00111011 | 3 | 3 |
| 11111100 | 00111011 | 3 | 3 |
| 00101100 | 11111011 | 3 | 2 |
| 00111100 | 11111011 | 3 | 2 |
| 11001010 | 00111111 | 3 | 1 |
| 11101010 | 00111111 | 3 | 1 |
| 11011010 | 00111111 | 3 | 1 |
| 11111010 | 00111111 | 3 | 1 |
| 11001110 | 00111111 | 3 | 1 |
| 11101110 | 00111111 | 3 | 1 |
| 11011110 | 00111111 | 3 | 1 |
| 11111110 | 00111111 | 3 | 1 |
| 11001001 | 00111111 | 3 | 1 |
| 11101001 | 00111111 | 3 | 1 |
| 11011001 | 00111111 | 3 | 1 |
| 11111001 | 00111111 | 3 | 1 |
| 11001101 | 00111111 | 3 | 1 |
| 11101101 | 00111111 | 3 | 1 |
| 11011101 | 00111111 | 3 | 1 |
| 11111101 | 00111111 | 3 | 1 |
| 11001011 | 00111111 | 3 | 1 |
| 11101011 | 00111111 | 3 | 1 |
| 11011011 | 00111111 | 3 | 1 |
| 11111011 | 00111111 | 3 | 1 |
| 11001111 | 00111111 | 3 | 1 |
| 11101111 | 00111111 | 3 | 1 |
| 11011111 | 00111111 | 3 | 1 |
| 11111111 | 00111111 | 3 | 0 |
| 01001010 | 00111100 | 3 | 3 |
| 01001001 | 00111100 | 3 | 3 |
| 01001011 | 00111100 | 3 | 3 |
| 00101010 | 11111110 | 3 | 2 |
| 00111010 | 11111110 | 3 | 2 |
| 00101001 | 11111110 | 3 | 2 |
| 00111001 | 11111110 | 3 | 2 |
| 00101011 | 11111110 | 3 | 2 |
| 00111011 | 11111110 | 3 | 2 |
| 00101000 | 11111010 | 3 | 2 |
| 00111000 | 11111010 | 3 | 2 |
| 00011011 | 11111100 | 3 | 4 |
| 00011001 | 11111100 | 3 | 4 |
| 00011010 | 11111100 | 3 | 4 |