Squares of odd index Fibonacci polynomials are used to define a new function \(\Phi\left(10^{n}\right)\) to approximate the number \(\pi\left(10^{n}\right)\) of primes less than \(10^{n}\). Multiple of 4 index Fibonacci polynomials are further used to define another new function \(\Psi\left(10^{n}\right)\) to approximate the number \(\Delta\left(\pi\left(10^{n}\right)\right)\) of primes having \(n\) digits and compared to a third function \(\Psi’\left(10^{n}\right)\) defined as the difference of the first function \(\Phi\left(10^{n}\right)\) based on odd index Fibonacci polynomials. These three functions provide better approximations of \(\pi\left(10^{n}\right)\) than those based on the classical \(\left(\frac{x}{log\left(x\right)}\right)\), Gauss’ approximation \(Li\left(x\right)\), and the Riemann \(R\left(x\right)\) functions.
The Prime Number Theorem states (see e.g. [1]) that if \(\pi\left(x\right)\) is the number of primes \(\leq x\) (\(x\in\mathbb{Z}^{+}\)), then \[\lim_{x\rightarrow\infty}\left(\frac{\pi(x)}{\frac{x}{log\left(x\right)}}\right)=1\label{eq:1}\tag{1}\] which means in all generality that the relative error of the approximation of \(\pi(x)\) by \(\left(\frac{x}{log\left(x\right)}\right)\) approaches \(0\) as \(x\) approaches infinity. Several better approximations to \(\pi(x)\) are given for example by Gauss’ approximation, i. e. the offset logarithmic integral or Eulerian logarithmic integral (see e.g. [2]) \[Li(x)=li\left(x\right)-li\left(2\right)=\intop_{2}^{x}\frac{dt}{log\left(t\right)}\label{eq:2}\tag{2}\] in function of the logarithmic integral \(li(x)=\intop_{0}^{x}\frac{dt}{log\left(t\right)}\), or by the Riemann function (see e.g. [3]) \[R\left(x\right)=\sum_{i=1}^{\infty}\frac{\mu\left(i\right)}{i}li\left(x^{\frac{1}{i}}\right),\label{eq:3}\tag{3}\] where \(\mu\left(i\right)\) is the Moebius function and \(i\in\mathbb{Z}^{+}\), or by an even better function \[R\left(x\right)-\frac{1}{log\left(x\right)}+\frac{1}{\pi}arctan\left(\frac{\pi}{log\left(x\right)}\right)\label{eq:4}.\tag{4}\] Interestingly when looking at the first values of \(\pi\left(10^{n}\right)\) for \(1\leq n\leq4\) (\(n\in\mathbb{Z}^{+}\)), it appears that they are equal or close to the square of odd index Fibonacci numbers \(F_{2n+1}\), while the number of prime numbers having \(n\) digits, i.e. the difference \(\pi\left(10^{n}\right)-\pi\left(10^{n-1}\right)\), is equal or close to Fibonacci numbers \(F_{4n}\) of indices multiple of 4.
We propose in this paper new functions giving a better representation of the sequence of \(\pi\left(10^{n}\right)\) based on the square of odd index Fibonacci polynomials of a function \(\xi\) of \(n\) and two other representations based on Fibonacci polynomials for the difference \(\pi\left(10^{n}\right)-\pi\left(10^{n-1}\right)\).
The values of \(\pi\left(10^{n}\right)\) are known for \(1\leq n\leq29\) (see [4]).
| \(n\) | \(\pi\left(10^{n}\right)\) | \(F_{2n+1}^{2}\) | \(\Delta\left(\pi\left(10^{n}\right)\right)\) | \(F_{4n}\) |
|---|---|---|---|---|
| \(1\) | \(4\) | \(4\) | \(4\) | \(3\) |
| \(2\) | \(25\) | \(25\) | \(21\) | \(21\) |
| \(3\) | \(168\) | \(169\) | \(143\) | \(144\) |
| \(4\) | \(1229\) | \(1156\) | \(1061\) | \(987\) |
| \(5\) | \(9592\) | \(7921\) | \(8363\) | \(6765\) |
The second column of Table 1 gives the first five values of \(\pi\left(10^{n}\right)\). Interestingly,the first two terms of the sequence of \(\pi\left(10^{n}\right)\) are integer squares while following terms are close to squares. With the notation \(\left|\left[x\right]\right|=\text{round}\left(x\right)\), taking the nearest integer \(\rho_{n}\) to the square root of \(\pi\left(10^{n}\right)\) for \(1\leq n\leq29\) \[\rho_{n}=\left|\left[\sqrt{\pi\left(10^{n}\right)}\right]\right|\label{eq:5}\tag{5}\] yields then the values 2, 5, 13, 35, 98, 280, …. [5].The first values are equal or close to those of odd index Fibonacci numbers \(F_{2n+1}\), i.e. 2, 5, 13, 34, 89, 233, … [6](see third column of Table 1). However, they diverge quite rapidly thereafter and \(F_{2n+1}<\pi\left(10^{n}\right)\) for larger values of \(n\). Figure 1 shows, for \(1 \leq n \leq25\), the of the relative difference \[\delta_{n}=\frac{\rho_{n}-F_{2n+1}}{\rho_{n}}\label{eq:6}.\tag{6}\]
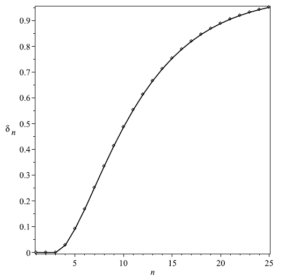
On the other hand, if the first values of \(\pi\left(10^{n}\right)\) can be represented by the square of odd index Fibonacci numbers \(F_{2n+1}\), and as \[F_{4n}=F_{2n+1}^{2}-F_{2n-1}^{2}\label{eq:7-3},\tag{7}\] (see e.g. [7]), one can expect that the difference of two successive values of \(\pi\left(10^{n}\right)\), i.e., \[\Delta\left(\pi\left(10^{n}\right)\right)=\pi\left(10^{n}\right)-\pi\left(10^{n-1}\right)\label{eq:7-1}\tag{8}\] can be represented by multiple of 4 index Fibonacci numbers \(F_{4n}\),i.e., 3, 21, 144, 987, 6765, … . In fact, \(\Delta\left(\pi\left(10^{n}\right)\right)\) gives the number of primes between \(10^{n}\) and \(10^{n-1}\) or the number of primes with \(n\) digits ([8], see fourth column of Table 1 (with \(\pi\left(1\right)=0\)), i.e. there are 4 primes between \(1\) and \(10\), 21 primes between \(11\) and \(100\), 143 primes between \(101\) and \(1000\), etc. And these values are indeed equal or close to the first Fibonacci numbers \(F_{4n}\) of indices multiple of 4 (fifth column of Table 1). Again, they diverge quite rapidly thereafter and \(F_{4n}<\Delta\left(\pi\left(10^{n}\right)\right)\) for larger values of \(n\).
Next, we ask whether the square of odd index Fibonacci polynomials \(F_{2n+1}\left(x\right)\) (see e.g. [9]) (with now \(x\in\mathbb{R}\) onward) could approximate better the sequence of values of \(\pi\left(10^{n}\right)\). The first odd index Fibonacci polynomials \(F_{2n+1}\left(x\right)\) are given in Table 2.
| \(n\) | \(F_{2n+1}\left(x\right)\) |
|---|---|
| \(1\) | \(x^{2}+1\) |
| \(2\) | \(x^{4}+3x^{2}+1\) |
| \(3\) | \(x^{6}+5x^{4}+6x^{2}+1\) |
| \(4\) | \(x^{8}+7x^{6}+15x^{4}+10x^{2}+1\) |
| \(5\) | \(x^{10}+9x^{8}+28x^{6}+35x^{4}+15x^{2}+1\) |
The roots of \[F_{2n+1}\left(x\right)-\sqrt{\pi\left(10^{n}\right)}=0\label{eq:7}\tag{9}\] are then computed1 for \(1\leq n\leq25\). All polynomials (9) have two real roots, one positive and one negative, and \(2\left(n-1\right)\) complex roots of no interest here. Only the positive real root \(x_{n}^{+}\) is considered in each case and, remarkably, all are close to unity, slowly increasing with increasing \(n\), \(1\lesssim x_{n}^{+}\lesssim1.13…\) (see Figure 2).
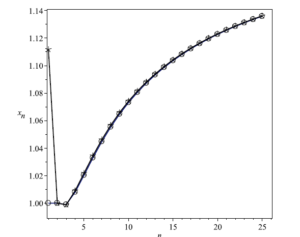
The next step is to find a function that can approximate the sequence of real roots \(x_{n}^{+}\) in function of \(n\). Using a nonlinear regression curve fitting algorithm, such a function is given by
\[\xi\left(n\right)=\sum_{i=0}^{2}C_{i}\left(log\left(log\left(A\left(B+n^{2}\right)\right)\right)\right)^{2i}\label{eq:8},\tag{10}\] where \(i\in\mathbb{Z}^{+}\), \(A\), \(B\), \(C_{i}\in\mathbb{R}\) with \(A=0.1641239\), \(B=10.0861\), \(C_{0}=0.9976796712309498\), \(C_{1}=7.445960495\times10^{-2}\), \(C_{2}=-6.73751166802\times10^{-3}\). Then the distribution of \(\pi\left(10^{n}\right)\) can be approximated by \[\Phi\left(10^{n}\right)=\left|\left[\left(F_{2n+1}\left(\xi\left(n\right)\right)\right)^{2}\right]\right|\label{eq:9}.\tag{11}\] This function \(\Phi\left(10^{n}\right)\) gives exactly the first four values of \(\pi\left(10^{n}\right)\) for \(1\leq n\leq4\) and quite closely the following values (see [10]).
For the difference \(\Delta\left(\pi\left(10^{n}\right)\right)\), we verify whether similarly Fibonacci polynomials \(F_{4n}\left(x\right)\) of indices multiple of 4 could similarly approximate the sequence of values of \(\Delta\left(\pi\left(10^{n}\right)\right)\). The first Fibonacci polynomials \(F_{4n}\left(x\right)\) are shown in Table 3.
| \(n\) | \(F_{4n}\left(x\right)\) |
|---|---|
| \(1\) | \(x^{3}+2x\) |
| \(2\) | \(x^{7}+6x^{5}+10x^{3}+4x\) |
| \(3\) | \(x^{11}+10x^{9}+36x^{7}+56x^{5}+35x^{3}+6x\) |
| \(4\) | \(x^{15}+14x^{13}+78x^{11}+220x^{9}+330x^{7}+252x^{5}+84x^{3}+8x\) |
| \(5\) | \(x^{19}+18x^{17}+136x^{15}+560x^{13}+1365x^{11}+2002x^{9}+1716x^{7}+792x^{5}+165x^{3}+10x\) |
However, relation (7) does not hold for Fibonacci polynomials. The correct relation is \[xF_{4n}\left(x\right)=F_{2n+1}^{2}\left(x\right)-F_{2n-1}^{2}\left(x\right)\label{eq:12}.\tag{12}\] Therefore we use the product \(xF_{4n}\left(x\right)\) instead of \(F_{4n}\left(x\right)\), and the roots of \[xF_{4n}\left(x\right)-\Delta\left(\pi\left(10^{n}\right)\right)=0\label{eq:7-2}\tag{13}\] are computed2 for \(1\leq n\leq25\). All polynomials (13) have two real roots, one positive and one negative, two imaginary roots and \(4\left(n-1\right)\) complex roots of no interest here. Again, all 25 real positive roots \(x_{n}^{'+}\) are close to unity; except for the first value (for \(n=1\)), all values of \(x_{n}^{'+}\) are slowly increasing with increasing \(n\), \(1\lesssim x_{n}^{'+}\lesssim1.13…\) (see Figure 2). A function approximating the sequence of roots \(x_{n}^{'+}\) in function of \(n\) is found to be
\[\xi'\left(n\right)=\sum_{i=0}^{3}C_{i}\left(log\left(log\left(A\left(B+n^{2}\right)\right)\right)\right)^{i}\label{eq:8-1},\tag{14}\] where \(i\in\mathbb{Z}^{+}\), \(A\), \(B\), \(C_{j}\in\mathbb{R}\) with \(A=5.55206477803854105\times10^{-3}\), \(B=179.5601349965941682\), \(C_{0}=1.115263992333283653\), \(C_{1}=5.11592774905246001\times10^{-2}\), \(C_{2}=0\), \(C_{3}=-1.4047014763335134\times10^{-3}\). The distribution of \(\Delta\left(\pi\left(10^{n}\right)\right)\) can then be approximated by \[\Psi\left(10^{n}\right)=\left|\left[\xi'\left(n\right)F_{4n}\left(\xi'\left(n\right)\right)\right]\right|\label{eq:9-1}.\tag{15}\] This function \(\Psi\left(10^{n}\right)\) gives exactly the first three values of \(\Delta\left(\pi\left(10^{n}\right)\right)\) for \(1\leq n\leq3\) and quite closely the following values.
Another function \(\Psi'\left(10^{n}\right)\) approximating \(\Delta\left(\pi\left(10^{n}\right)\right)\) can be obtained by successive values of \(\Phi\left(10^{n}\right)\), i.e., \[\Psi'\left(10^{n}\right)=\Phi\left(10^{n}\right)-\Phi\left(10^{n-1}\right)=\left|\left[\left(F_{2n+1}\left(\xi\left(n\right)\right)\right)^{2}\right]\right|-\left|\left[\left(F_{2n-1}\left(\xi\left(n-1\right)\right)\right)^{2}\right]\right|.\tag{16}\]
The first value for \(n=1\) is not well represented as \(\Psi'\left(10\right)=3\) (with \(\left|\left[\left(F_{1}\left(\xi\left(0\right)\right)\right)^{2}\right]\right|=1\) and \(\xi\left(0\right)=1.0311467…\)) while \(\Delta\left(\pi\left(10\right)\right)=4\). However \(\Psi'\left(10^{n}\right)\) gives exactly the following three values of \(\Delta\left(\pi\left(10^{n}\right)\right)\) for \(2\leq n\leq4\) and approximates well the following values up to \(n=25\), much closer than \(\Psi\left(10^{n}\right)\) (see further discussion).
For the distribution of \(\pi\left(10^{n}\right)\), it is interesting to compare the values obtained with \(\Phi\left(10^{n}\right)\) to the nearest integers to those values obtained with the approximating functions of Section 1.
| \(n\) | \(\pi\left(10^{n}\right)\) | \(\left|\left[\frac{10^{n}}{log\left(10^{n}\right)}\right]\right|\) | \(\left|\left[Li\left(10^{n}\right)\right]\right|\) | \(\left|\left[R\left(10^{n}\right)\right]\right|\) | \(\Phi\left(10^{n}\right)\) |
|---|---|---|---|---|---|
| \(1\) | \(4\) | \(4\) | \(5\) | \(5\) | \(4\) |
| \(2\) | \(25\) | \(22\) | \(29\) | \(26\) | \(25\) |
| \(3\) | \(168\) | \(145\) | \(177\) | \(168\) | \(168\) |
| \(4\) | \(1229\) | \(1086\) | \(1245\) | \(1227\) | \(1229\) |
| \(5\) | \(9592\) | \(8686\) | \(9629\) | \(9587\) | \(9595\) |
| \(6\) | \(78498\) | \(72382\) | \(78627\) | \(78527\) | \(78527\) |
| \(7\) | \(664579\) | \(620421\) | \(664917\) | \(664667\) | \(664408\) |
| \(8\) | \(5761455\) | \(5428681\) | \(5762208\) | \(5761552\) | \(5759130\) |
| \(9\) | \(50847534\) | \(48254942\) | \(50849234\) | \(50847455\) | \(50833725\) |
| \(10\) | \(455052511\) | \(434294482\) | \(455055614\) | \(455050683\) | \(455019102\) |
Table 4 shows the first ten values of \(\pi\left(10^{n}\right)\), \(\left|\left[\frac{10^{n}}{log\left(10^{n}\right)}\right]\right|\) (see [11]), \(\left|\left[Li\left(10^{n}\right)\right]\right|\) (from (2), see [12]), \(\left|\left[R\left(10^{n}\right)\right]\right|\) (from (3), see [13]), or \[f\left(n\right)=\text{either}\left|\left[\frac{10^{n}}{log\left(10^{n}\right)}\right]\right|\,\text{or}\,\left|\left[Li\left(10^{n}\right)\right]\right|\,\text{or}\,\left|\left[R\left(10^{n}\right)\right]\right|\label{eq:16},\tag{17}\] and \(\Phi\left(10^{n}\right)\) (11). Note that in calculating \(R\left(10^{n}\right)\), the summation in (3) is made for \(1\leq i\leq1000\), as the value of \(R\left(10^{n}\right)\) does not change for higher values of \(i\), due mainly to the operation of rounding to the nearest integer. The function (4) is not considered as the values obtained by rounding to the nearest integer the function (4) does not differ (except for \(n=1\)) from those obtained by rounding \(R\left(10^{n}\right)\) for the same reason.
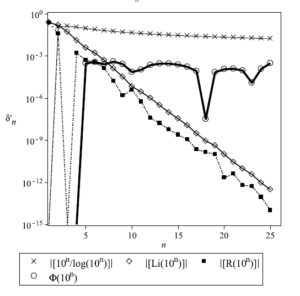
Computing the absolute value of the relative differences \[\delta_{n}^{'}=\left|\frac{\pi\left(10^{n}\right)-d'\left(n\right)}{\pi\left(10^{n}\right)}\right|\label{eq:10}\tag{18}\] for \(1\leq n\leq25\), where \(d'\left(n\right)\) is either \(f\left(n\right)\) (17) or \(\Phi\left(10^{n}\right)\) (11), Figure 3 shows the , in function of \(n\), of \(\delta_{n}^{'}\) for these four distributions on a log scale (recall that the first four values of \(\delta_{n}^{'}\) are for \(\Phi\left(10^{n}\right)\)) and Table 5 shows the averages \(\mu\left(\delta_{n}^{'}\right)\) and standard deviations \(\sigma\left(\delta_{n}^{'}\right)\) of \(\delta_{n}^{'}\) for \(1\leq n\leq25\) for the four distributions.
| \(d'\left(n\right)\) | \(\left|\left[\frac{10^{n}}{log\left(10^{n}\right)}\right]\right|\) | \(\left|\left[Li\left(10^{n}\right)\right]\right|\) | \(\left|\left[R\left(10^{n}\right)\right]\right|\) | \(\Phi\left(10^{n}\right)\) |
|---|---|---|---|---|
| \(\mu\left(\delta_{n}^{'}\right)\) | \(4.65309\times10^{-2}\) | \(1.93110\times10^{-2}\) | \(1.17069\times10^{-2}\) | \(1.58269\times10^{-4}\) |
| \(\sigma\left(\delta_{n}^{'}\right)\) | \(3.60695\times10^{-2}\) | \(5.83932\times10^{-2}\) | \(5.02812\times10^{-2}\) | \(1.28997\times10^{-4}\) |
It is seen that the distribution \(\left|\left[\frac{10^{n}}{log\left(10^{n}\right)}\right]\right|\) provides a relatively poor approximation for small and large value (up to \(n=25\)) of \(\pi\left(10^{n}\right)\). The distributions \(\left|\left[Li\left(10^{n}\right)\right]\right|\) and \(\left|\left[R\left(10^{n}\right)\right]\right|\) provide both a relatively poor approximation of \(\pi\left(10^{n}\right)\) for small values of \(n\), but increasingly better with increasing values of \(n\). The distribution \(\Phi\left(10^{n}\right)\) gives a better approximation of \(\pi\left(10^{n}\right)\) for small values of \(n\leq6\) but not as good as \(\left|\left[Li\left(10^{n}\right)\right]\right|\) and \(\left|\left[R\left(10^{n}\right)\right]\right|\) for larger values of \(n\). However the distribution \(\Phi\left(10^{n}\right)\) gives on average a better approximation of the 25 values of \(\pi\left(10^{n}\right)\) than the \(\left(\frac{x}{log\left(x\right)}\right)\) function, the Gauss’ approximation \(Li\left(x\right)\) and the Riemann function \(R\left(x\right)\) as shown by the average and standard deviation values given in Table 4 (\(\mu\left(\delta_{n}^{'}\right)\) and \(\sigma\left(\delta_{n}^{'}\right)\) for \(\Phi\left(10^{n}\right)\) are approximately two orders of magnitude less that the other values), due to the fact that \(\Phi\left(10^{n}\right)\) gives exactly the first four values of \(\pi\left(10^{n}\right)\).
Comparing now the values for the difference \(\Delta\left(\pi\left(10^{n}\right)\right)\) obtained by subtracting successive values of the functions of section 1, i.e., \[g\left(n\right)=f\left(n\right)-f\left(n-1\right)=\Delta\left(f\left(n\right)\right)\label{eq:17}\tag{19}\] with \(f\left(n\right)\) (17), to those of \(\Psi\left(10^{n}\right)\) and \(\Psi'\left(10^{n}\right)\), Table 6 gives the first ten values of \(\Delta\left(\pi\left(10^{n}\right)\right)\), \(g\left(n\right)\) (19), \(\Psi\left(10^{n}\right)\) and \(\Psi'\left(10^{n}\right)\). Note that the values of the three distributions \(g\left(n\right)\) (19) are not defined for \(n=1\), as \(f\left(n-1\right)=f(0)\) is not defined and, for the sake of the argument, the values of \(\left|\left[\frac{1}{log\left(1\right)}\right]\right|\), \(\left|\left[Li\left(1\right)\right]\right|\), \(\left|\left[R\left(1\right)\right]\right|\) have been arbitrarily put equal to \(0\).
| \(n\) | \(\Delta\left(\pi\left(10^{n}\right)\right)\) | \(\Delta\left(\left|\left[\frac{10^{n}}{log\left(10^{n}\right)}\right]\right|\right)\) | \(\Delta\left(\left|\left[Li\left(10^{n}\right)\right]\right|\right)\) | \(\Delta\left(\left|\left[R\left(10^{n}\right)\right]\right|\right)\) | \(\Psi\left(10^{n}\right)\) | \(\Psi'\left(10^{n}\right)\) |
|---|---|---|---|---|---|---|
| \(1\) | \(4\) | \(4\) | \(5\) | \(5\) | \(4\) | \(3\) |
| \(2\) | \(21\) | \(18\) | \(24\) | \(21\) | \(21\) | \(21\) |
| \(3\) | \(143\) | \(123\) | \(148\) | \(142\) | \(143\) | \(143\) |
| \(4\) | \(1061\) | \(941\) | \(1068\) | \(1059\) | \(1063\) | \(1061\) |
| \(5\) | \(8363\) | \(7600\) | \(8384\) | \(8360\) | \(8385\) | \(8366\) |
| \(6\) | \(68906\) | \(63696\) | \(68998\) | \(68940\) | \(68929\) | \(68932\) |
| \(7\) | \(586081\) | \(548039\) | \(586290\) | \(586140\) | \(584467\) | \(585881\) |
| \(8\) | \(5096876\) | \(4808260\) | \(5097291\) | \(5096885\) | \(5074924\) | \(5094722\) |
| \(9\) | \(45086079\) | \(42826261\) | \(45087026\) | \(45085903\) | \(44885325\) | \(45074595\) |
| \(10\) | \(404204977\) | \(386039540\) | \(404206380\) | \(404203228\) | \(402777151\) | \(404185377\) |
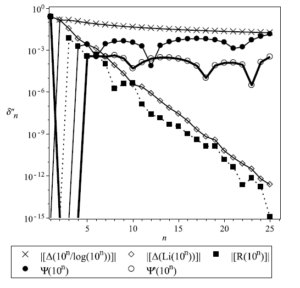
Figure 4 shows the of the absolute value of the relative differences \[\delta_{n}^{"}=\left|\frac{\Delta\left(\pi\left(10^{n}\right)\right)-d"\left(n\right)}{\Delta\left(\pi\left(10^{n}\right)\right)}\right|\label{eq:10-1}\tag{20}\] in function of \(n\) for \(1\leq n\leq25\), where \(d"\left(n\right)\) is either \(g\left(n\right)=\Delta\left(f\left(n\right)\right)\), or \(\Psi\left(10^{n}\right)\) or \(\Psi'\left(10^{n}\right)\), and Table 7 shows the averages \(\mu\left(\delta_{n}^{"}\right)\) and standard deviations \(\sigma\left(\delta_{n}^{"}\right)\) of \(\delta_{n}^{"}\) for the five distributions with and without the first value for \(n=1\) (i.e. respectively for \(1\leq n\leq25\) and for \(2\leq n\leq25\)).
| \(1\leq n\leq25\) | \(2\leq n\leq25\) | |||
|---|---|---|---|---|
| \(d"\left(n\right)\) | \(\mu\left(\delta_{n}^{"}\right)\) | \(\sigma\left(\delta_{n}^{"}\right)\) | \(\mu\left(\delta_{n}^{"}\right)\) | \(\sigma\left(\delta_{n}^{"}\right)\) |
| \(\Delta\left(\left|\left[\frac{10^{n}}{log\left(10^{n}\right)}\right]\right|\right)\) | \(4.69094\times10^{-2}\) | \(3.80699\times10^{-2}\) | \(4.88640\times10^{-2}\) | \(3.75855\times10^{-2}\) |
| \(\Delta\left(\left|\left[Li\left(10^{n}\right)\right]\right|\right)\) | \(1.75493\times10^{-2}\) | \(5.64517\times10^{-2}\) | \(7.86383\times10^{-3}\) | \(2.96342\times10^{-2}\) |
| \(\Delta\left(\left|\left[R\left(10^{n}\right)\right]\right|\right)\) | \(1.03936\times10^{-2}\) | \(4.99384\times10^{-2}\) | \(4.10042\times10^{-4}\) | \(1.45666\times10^{-3}\) |
| \(\Psi\left(10^{n}\right)\) | \(3.75342\times10^{-3}\) | \(3.32007\times10^{-3}\) | \(3.90981\times10^{-3}\) | \(3.29607\times10^{-3}\) |
| \(\Psi'\left(10^{n}\right)\) | \(1.01657\times10^{-2}\) | \(4.99657\times10^{-2}\) | \(1.72564\times10^{-4}\) | \(1.36990\times10^{-4}\) |
Again, both functions based on Fibonacci polynomials of a function of \(n\) approximate on average better the distribution of the number of primes of \(n\) digits, mainly because the first values of \(\Delta\left(\pi\left(10^{n}\right)\right)\) are exactly or closely represented. If the first value for \(n=1\) is included, the representation of \(\Delta\left(\pi\left(10^{n}\right)\right)\) by the function \(\Psi\left(10^{n}\right)\) of Fibonacci polynomials \(\left(\xi'\left(n\right)F_{4n}\left(\xi'\left(n\right)\right)\right)\) of a function \(\xi'\left(n\right)\) of \(n\) (with \(\xi'\left(n\right)\thickapprox1\)) is better than by the \(\left(\frac{x}{log\left(x\right)}\right)\) function, the Gauss’ approximation \(Li\left(x\right)\) and the Riemann function \(R\left(x\right)\), with an average \(\mu\left(\delta_{n}^{"}\right)\) and a standard deviation \(\sigma\left(\delta_{n}^{"}\right)\) for \(\Psi\left(10^{n}\right)\) approximately one order of magnitude less than those for the other functions. If the first value for \(n=1\) is discarded, the representation of \(\Delta\left(\pi\left(10^{n}\right)\right)\) by the function \(\Psi'\left(10^{n}\right)\) of the difference of the square of odd index Fibonacci polynomials \(F_{2n+1}\left(\xi\left(n\right)\right)\) of a function \(\xi\left(n\right)\) of \(n\) (with \(\xi\left(n\right)\thickapprox1\)) is better than by the \(\left(\frac{x}{log\left(x\right)}\right)\) function, the Gauss’ approximation \(Li\left(x\right)\) and the Riemann function \(R\left(x\right)\) (with \(\mu\left(\delta_{n}^{"}\right)\) and \(\sigma\left(\delta_{n}^{"}\right)\) for \(\Psi'\left(10^{n}\right)\) approximately two orders of magnitude less than for\(\left(\frac{x}{log\left(x\right)}\right)\) and \(Li\left(x\right)\) and \(\mu\left(\delta_{n}^{"}\right)\) and \(\sigma\left(\delta_{n}^{"}\right)\) for \(\Psi'\left(10^{n}\right)\) respectively less than and one order of magnitude less than for \(R\left(x\right)\)).
A function \(\Phi\left(10^{n}\right)\) of odd index Fibonacci polynomials \(F_{2n+1}\left(\xi\left(n\right)\right)\) of a function \(\xi\left(n\right)\) of \(n\) was found to approximate the distribution of the number \(\pi\left(10^{n}\right)\) of primes less than \(10^{n}\). Two functions \(\Psi\left(10^{n}\right)\) and \(\Psi'\left(10^{n}\right)\) were found to approximate the distribution of the number \(\Delta\left(\pi\left(10^{n}\right)\right)\) of primes having \(n\) digits, where \(\Psi\left(10^{n}\right)\) is a function of multiple of 4 index Fibonacci polynomials \(\left(\xi'\left(n\right)F_{4n}\left(\xi'\left(n\right)\right)\right)\) of a function \(\xi'\left(n\right)\) of \(n\) and \(\Psi'\left(10^{n}\right)=\Phi\left(10^{n}\right)-\Phi\left(10^{n-1}\right)\) is a function of the difference of odd index Fibonacci polynomials \(F_{2n+1}\left(\xi\left(n\right)\right)\) for successive values of \(n\).
On average these three functions provide better approximations of one or two orders of magnitude in the averages of relative absolute differences of the exact and calculated values than classical functions, i.e. the \(\left(\frac{x}{log\left(x\right)}\right)\) function, the Gauss’ approximation \(Li\left(x\right)\) and the Riemann function \(R\left(x\right)\).
Note that these results do not disprove the Prime Number Theorem, but provide better representations of \(\pi\left(10^{n}\right)\) and \(\Delta\left(\pi\left(10^{n}\right)\right)\).