We show that Euler’s relation and the Taxi-Cab relation are both solutions of the same equation. General solutions of sums of two consecutive cubes equaling the sum of two other cubes are calculated. There is an infinite number of relations to be found among the sums of two consecutive cubes and the sum of two other cubes, in the form of two families. Their recursive and parametric equations are calculated.
The remarkable relation \[3^{3}+4^{3}+5^{3}=6^{3}\label{eq:1}\tag{1}\] among the cubes of four successive integers is often attributed to Euler, while in fact it was already known to P. Bungus in the XVIth century [1,2]. No other similar relation can be found between cubes of four successive integers. Another well-known relation involving two different sums of two cubes is \[1729=9^{3}+10^{3}=12^{3}+1^{3}\label{eq:2}\tag{2}\] often call the taxi-cab number or taxi-cab relation and attributed to Indian mathematician Ramanujan after he mentioned in 1919 to fellow British mathematician Hardy that this number is remarkable in the fact that it is the smallest integer that can be written as the sum of two positive cubes in two ways (see historical account in e.g., [3]). However, this relation was already mentioned by French mathematician Frenicle in the XVIIth century [2,4]. Nevertheless, we will refer in this paper to (1) and (2) as Euler’s relation and Ramanujan’s taxi-cab relation. In fact, both relations can be deduced from a same equation, as we show in this paper. It is simple to see that one can find other taxi-cab numbers smaller than Ramanujan’s by transferring one term from left to right of (1), introducing negative integers and yielding successively \[ 91 =3^{3}+4^{3}=6^{3}+\left(-5\right)^{3},\label{eq:3-1}\tag{3}\]\[ 152 =3^{3}+5^{3}=6^{3}+\left(-4\right)^{3},\label{eq:4-1}\tag{4}\]\[ 189 =4^{3}+5^{3}=6^{3}+\left(-3\right)^{3},\label{eq:5-1}\tag{5} \] and so on. Other taxi-cab numbers can be found by multiplying each relations (3) to (5) by \(k^{3}\), i.e., the cube of any integer \(k\). Sequences A001235 and A051347 in the OEIS [5] list all taxi-cab numbers for respectively only positive integers and for positive and negative integers. Numerous mathematicians and authors have worked on sums of cubes and equal sums of cubes. Excellent summaries and numerous results can be found e.g., in [2,6].
In this paper, our interest is in numbers that can be written as sums of two cubes in at least two ways, one of them involving two consecutive cubes. In Section, 2 we show first that Euler’s and the Taxi-Cab relations are solutions of the same equation. We calculate then the general case of the sum of two consecutive cubes equal to the sum of two other cubes. In Section 3, we characterize two infinite families of solutions of the sum of two consecutive cubes equaling the sum of two other cubes.
We show first that (1) and (2) are both solutions of the same equation. If one observes that the first term on the right-hand side in (2) and (3) is three units larger than the first term on the left-hand side, we can write \[N=n^{3}+\left(n+1\right)^{3}=\left(n+3\right)^{3}+\left(n+\alpha\right)^{3}\label{eq:10}\tag{6}\] with \(\alpha\) integer and \(N\) the positive integer that can be represented in (at least) two ways by sums of two consecutive cubes and of two other cubes, one of which possibly negative. Eq. (6) yields the two general solutions \[n=\frac{-3\left(\alpha^{2}+8\right)\pm\sqrt{-3\left(\alpha^{4}+8\left(\alpha^{3}-6\alpha^{2}+13\alpha+2\right)\right)}}{6\left(\alpha+2\right)},\label{eq:11}\tag{7}\] which produces integer solutions for \(\alpha=-8\), giving \(n_{+}=3\) and \(n_{-}=9\). Equation (6) yields then respectively (3) and (2), showing that (6) yields both Euler’s relation and Ramanujan’s taxi-cab number relation. Let us consider now the general equation \[N=n^{3}+\left(n+1\right)^{3}=\left(n+a\right)^{3}+\left(n+b\right)^{3},\label{eq:3}\tag{8}\] with \(a\) and \(b\) integers, \(a>0\) and \(b<0\). Solving for \(n\), the third degree equation defined by the second equality in (8) reduces to a second degree equation \[3n^{2}\left(a+b-1\right)+3n\left(a^{2}+b^{2}-1\right)+\left(a^{3}+b^{3}-1\right)=0,\label{eq:4}\tag{9}\] whose discriminant reads \[D=3\left(\left(a-b\right)^{4}-\left(a^{4}+b^{4}+\left(a-1\right)^{4}+\left(b-1\right)^{4}\right)+1\right)\label{eq:5}\tag{10}\] providing two real solutions for \(D>0\), namely \[n=\frac{-3\left(a^{2}+b^{2}-1\right)\pm\sqrt{3\left(\left(a-b\right)^{4}-\left(a^{4}+b^{4}+\left(a-1\right)^{4}+\left(b-1\right)^{4}\right)+1\right)}}{6\left(a+b-1\right)}.\label{eq:6}\tag{11}\] As \(N\) must be positive, we limit our search to \(b<0<a<\left|b\right|\) and discrete solutions of (8) or (9) are found, as shown in Table 1 for \(n<1000\), and arranged in increasing order of \(N\).
| \(a\) | \(b\) | \(n_{+}\) | \(n_{-}\) | \(N=n^{3}+\left(n+1\right)^{3}=\left(n+a\right)^{3}+\left(n+b\right)^{3}\) |
|---|---|---|---|---|
| 3 | -8 | 3 | – | \(91=3^{3}+4^{3}=6^{3}+(-5)^{3}\) |
| 2 | -7 | 4 | – | \(189=4^{3}+5^{3}=6^{3}+(-3)^{3}\) |
| 3 | -8 | – | 9 | \(1729=9^{3}+10^{3}=12^{3}+1^{3}\) |
| 10 | -39 | 18 | – | \(12691=18^{3}+19^{3}=28^{3}+(-21)^{3}\) |
| 9 | -38 | – | 32 | \(68705=32^{3}+33^{3}=41^{3}+(-6)^{3}\) |
| 10 | -39 | – | 36 | \(97309=36^{3}+37^{3}=46^{3}+(-3)^{3}\) |
| 105 | -194 | 46 | – | \(201159=46^{3}+47^{3}=151^{3}+(-148)^{3}\) |
| 32 | -127 | 58 | – | \(400491=58^{3}+59^{3}=90^{3}+(-69)^{3}\) |
| 64 | -243 | 107 | – | \(2484755=107^{3}+108^{3}=171^{3}+(-136)^{3}\) |
| 73 | -258 | 108 | – | \(2554741=108^{3}+109^{3}=181^{3}+(-150)^{3}\) |
| 32 | -103 | – | 121 | \(3587409=121^{3}+122^{3}=153^{3}+18^{3}\) |
| 248 | -481 | 121 | – | \(3587409=121^{3}+122^{3}=369^{3}+(-360)^{3}\) |
| 37 | -192 | – | 123 | \(3767491=123^{3}+124^{3}=160^{3}+(-69)^{3}\) |
| 43 | -168 | – | 163 | \(8741691=163^{3}+164^{3}=206^{3}+(-5)^{3}\) |
| 91 | -360 | 163 | – | \(8741691=163^{3}+164^{3}=254^{3}+(-197)^{3}\) |
| 819 | -1208 | 197 | – | \(15407765=197^{3}+198^{3}=1016^{3}+(-1011)^{3}\) |
| 57 | -128 | – | 235 | \(26122131=235^{3}+236^{3}=292^{3}+107^{3}\) |
| 184 | -597 | 235 | – | \(26122131=235^{3}+236^{3}=419^{3}+(-362)^{3}\) |
| 77 | -208 | – | 301 | \(54814509=301^{3}+302^{3}=378^{3}+93^{3}\) |
| 120 | -629 | 393 | – | \(121861441=393^{3}+394^{3}=513^{3}+(-236)^{3}\) |
| 120 | -629 | – | 411 | \(139361059=411^{3}+412^{3}=531^{3}+(-218)^{3}\) |
| 393 | -1178 | 438 | – | \(168632191=438^{3}+439^{3}=831^{3}+(-740)^{3}\) |
| 152 | -793 | 481 | – | \(223264809=481^{3}+482^{3}=633^{3}+(-312)^{3}\) |
| 128 | -511 | – | 490 | \(236019771=490^{3}+491^{3}=618^{3}+(-21)^{3}\) |
| 3225 | -4274 | 528 | – | \(295233841=528^{3}+529^{3}=3753^{3}+(-3746)^{3}\) |
| 148 | -687 | – | 562 | \(355957875=562^{3}+563^{3}=710^{3}+(-125)^{3}\) |
| 2258 | -3367 | 562 | – | \(355957875=562^{3}+563^{3}=2820^{3}+(-2805)^{3}\) |
| 512 | -1591 | 607 | – | \(448404255=607^{3}+608^{3}=1119^{3}+(-984)^{3}\) |
| 777 | -1952 | 633 | – | \(508476241=633^{3}+634^{3}=1410^{3}+(-1319)^{3}\) |
| 190 | -999 | – | 640 | \(525518721=640^{3}+641^{3}=830^{3}+(-359)^{3}\) |
| 442 | -1767 | 804 | – | \(1041378589=804^{3}+805^{3}=1246^{3}+(-963)^{3}\) |
Note also that similar relations but with coefficients having opposite signs are obtained for negative values of \(a\) and for \(a^{\prime}=-b+1\), \(b^{\prime}=-a+1\), and \(n^{\prime}=-n-1\).
It is seen also that three sums of two cubes are found for \(n=121,163,235,562.\) Other relations are given in OEIS [] Sequences A352133 to A352136 and cases with three sums of two cubes are given in Sequences A352220 to A352225.
Figure 1 shows a plot of the couples \(\left(n,n+a\right)\) for \(0<n\leq275\) (data are from OEIS [5] Sequences A352135, A352136, A352222, A352223, A352224, A352225). Two families are clearly visible along two curves.
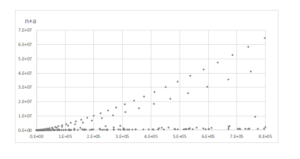
The first top curve (or first family) includes all couples \(\left(n,n+a\right)\) such that \(\eta=\left(n+a\right)+\left(n+b\right)=2n+a+b\) are regularly increasing odd integers as shown in Table 2 for the first twenty cases, while for the second below curve (or second family), \(\eta=2n+a+b\) are regularly increasing odd multiples of \(3\).
| First family | Second family | |||||||
|---|---|---|---|---|---|---|---|---|
| \(i\) | \(n\) | \(n+a\) | \(n+b\) | \(\eta\) | \(n\) | \(n+a\) | \(n+b\) | \(\eta\) |
| 1 | 3 | 6 | -5 | 1 | 4 | 6 | -3 | 3 |
| 2 | 46 | 151 | -148 | 3 | 121 | 369 | -360 | 9 |
| 3 | 197 | 1016 | -1011 | 5 | 562 | 2820 | -2805 | 15 |
| 4 | 528 | 3753 | -3746 | 7 | 1543 | 10815 | -10794 | 21 |
| 5 | 1111 | 10090 | -10081 | 9 | 3280 | 29538 | -29511 | 27 |
| 6 | 2018 | 22331 | -22320 | 11 | 5989 | 65901 | -65868 | 33 |
| 7 | 3321 | 43356 | -43343 | 13 | 9886 | 128544 | -128505 | 39 |
| 8 | 5092 | 76621 | -76606 | 15 | 15187 | 227835 | -227790 | 45 |
| 9 | 7403 | 126158 | -126141 | 17 | 22108 | 375870 | -375819 | 51 |
| 10 | 10326 | 196575 | -196556 | 19 | 30865 | 586473 | -586416 | 57 |
| 11 | 13933 | 293056 | -293035 | 21 | 41674 | 875196 | -875133 | 63 |
| 12 | 18296 | 421361 | -421338 | 23 | 54751 | 1259319 | -1259250 | 69 |
| 13 | 23487 | 587826 | -587801 | 25 | 70312 | 1757850 | -1757775 | 75 |
| 14 | 29578 | 799363 | -799336 | 27 | 88573 | 2391525 | -2391444 | 81 |
| 15 | 36641 | 1063460 | -1063431 | 29 | 109750 | 3182808 | -3182721 | 87 |
| 16 | 44748 | 1388181 | -1388150 | 31 | 134059 | 4155891 | -4155798 | 93 |
| 17 | 53971 | 1782166 | -1782133 | 33 | 161716 | 5336694 | -5336595 | 99 |
| 18 | 64382 | 2254631 | -2254596 | 35 | 192937 | 6752865 | -6752760 | 105 |
| 19 | 76053 | 2815368 | -2815331 | 37 | 227938 | 8433780 | -8433669 | 111 |
| 20 | 89056 | 3474745 | -3474706 | 39 | 266935 | 10410543 | -10410426 | 117 |
The values of \(n\), \(n+a\) and \(n+b\) of both the first and second families can be found by the recurrence relations \[ n_{i} =3n_{i-1}-3n_{i-2}+n_{i-3}+\kappa\label{eq:12}\tag{12}\]\[ \left(n+a\right)_{i} =3\left(n+a\right)_{i-1}-3\left(n+a\right)_{i-2}+\left(n+a\right)_{i-3}+\lambda\label{eq:12-1}\tag{13}\]\[ \left(n+b\right)_{i} =3\left(n+b\right)_{i-1}-3\left(n+b\right)_{i-2}+\left(n+b\right)_{i-3}-\lambda\label{eq:12-2}\tag{14}\] with \(\kappa=72\) and \(216\) and \(\lambda=576\left(i-2\right)\) and \(1728\left(i-2\right)\) for respectively the first and second families, and the first three values of \(n_{i}\), \(\left(n+a\right)_{i}\) and \(\left(n+b\right)_{i}\) from Table 2.
We see from Table 2 that the fourth term \(n+b\) of (8) is negative and is decreasing regularly with increasing \(n\). So, let us pose \(n+b=-\left(n+a\right)+\beta\), yielding from (8) \[N=n^{3}+\left(n+1\right)^{3}=\left(n+a\right)^{3}-\left(n+a-\beta\right)^{3}.\label{eq:13}\tag{15}\] For specific relations between \(a\) and \(n\), one obtains two infinite families of solutions as shown in the following two theorems, giving parametric solutions for \(n\), \(N\), \(n+a\) and \(n+b\).
Theorem 1. For \(\forall i\in\mathbb{Z}_{0}^{+}\), \(\exists n,a,\beta\in\mathbb{Z}_{0}^{+}\), such that \[a=\left(\beta-1\right)n+\beta^{2}+\beta+1,\label{eq:15-1}\tag{16}\] and an infinite family of solutions of (15) exists for \(\beta\) odd, \[\beta=2i-1\label{eq:16-1}\tag{17}\] yielding \[ n =\frac{\left(2i-1\right)\left(3\left(2i-1\right)^{2}+4\right)-1}{2}\label{eq:17-1},\tag{18}\]\[ N =\frac{\left(2i-1\right)\left(3\left(2i-1\right)^{2}+4\right)\left(\left(2i-1\right)^{2}\left(3\left(2i-1\right)^{2}+4\right)^{2}+3\right)}{4}\label{eq:18-1},\tag{19}\]\[ n+a =\frac{3\left(2i-1\right)^{2}\left(\left(2i-1\right)^{2}+2\right)+2i+1}{2}\label{eq:18-2},\tag{20}\]\[ n+b =-\frac{3\left(2i-1\right)^{2}\left(\left(2i-1\right)^{2}+2\right)-2i+3}{2}\label{eq:18-3}\tag{21}.\]
Proof. Let \(n,a,\beta,i\in\mathbb{Z}_{0}^{+}\), and let \(a\), \(n\) and \(\beta\) satisfy (16). Relation (15) yields then the third degree equation \[n^{3}+\left(n+1\right)^{3}-\left(\beta n+\beta^{2}+\beta+1\right)^{3}+\left(\beta n+\beta^{2}+1\right)^{3}=0,\tag{22}\] that simplifies immediately in the product of a linear and a quadratic relations \[\left(2n-\beta\left(3\beta^{2}+4\right)+1\right)\left(n^{2}+\left(2\beta+1\right)n+\beta^{2}+\beta+1\right)=0.\tag{23}\] As the discriminant of the right quadratic polynomial is always negative, the quadratic equation yields two complex solutions of no interest here. The right linear equation yield the only real solution \[n=\frac{\beta\left(3\beta^{2}+4\right)+1}{2}.\tag{24}\] As \(n\) must be integer, \(\beta\) cannot be even and must be odd, \(\beta=2i-1\), yielding (18) to (21). ◻
Theorem 2. For \(\forall i\in\mathbb{Z}_{0}^{+}\), \(\exists n,a,\beta\in\mathbb{Z}_{0}^{+}\), such that \[a=\frac{\left(\beta-3\right)n+2\beta}{3}\label{eq:15-1-1},\tag{25}\] and an infinite family of solutions of (15) exists for \(\beta\equiv3\text{mod{6}}\), \[\beta=3\left(2i-1\right)\label{eq:16-1-1}\tag{26}\] yielding \[ n =\frac{9\left(2i-1\right)^{3}-1}{2}\label{eq:17-1-2}\tag{27},\]\[ N =\frac{27\left(2i-1\right)^{3}\left(27\left(2i-1\right)^{6}+1\right)}{4}\label{eq:17-2}\tag{28},\]\[ n+a =\frac{3\left(2i-1\right)\left(3\left(2i-1\right)^{3}+1\right)}{2}\label{eq:17-3}\tag{29},\]\[ n+b =-\frac{3\left(2i-1\right)\left(3\left(2i-1\right)^{3}-1\right)}{2}\label{eq:17-4}\tag{30}.\]
Proof. Let \(n,a,\beta,i\in\mathbb{Z}_{0}^{+}\), and let \(a\), \(n\) and \(\beta\) satisfy (25). Relation (15) yields then the third degree equation \[n^{3}+\left(n+1\right)^{3}-\left(\frac{\beta}{3}\left(n+2\right)\right)^{3}+\left(\frac{\beta}{3}\left(n-1\right)\right)^{3}=0\label{eq:18},\tag{31}\] that simplifies immediately in the product of a linear and a quadratic relations \[\frac{\left(6n-\beta^{3}+3\right)\left(n^{2}+n+1\right)}{3}=0\label{eq:19}.\tag{32}\] The right quadratic equation yields two complex solutions of no interest here. The right linear equation yield the only real solution \[n=\frac{\beta^{3}-3}{6}\label{eq:20}.\tag{33}\] As \(n\) must be integer, \(\beta\) must \(3\text{mod{6}}\), \(\beta=3\left(2i-1\right)\), yielding (27) to (30). ◻