This study looks at the worldwide behavior of a monkeypox epidemic model that includes the impact of vaccination. A mathematical model is created to analyse the vaccine impact, assuming that immunisation is administered to the susceptible population. The system’s dynamics are determined by the fundamental reproduction number, R0. When R0 < 1, the illness is expected to be eradicated, as evidenced by the disease-free equilibrium’s global asymptotic stability. When R0 > 1, the illness continues and creates a globally stable endemic equilibrium. Furthermore, we investigate the existence of traveling wave solutions, demonstrating that (i) a minimal wave speed, designated as c* > 0, exists when R0 > 1; (ii) when R0 ≤ 1, no nontrivial traveling wave solution exists. Additionally, for wave speeds c < c*, no nontrivial traveling wave solution is found, whereas when c ≥ c*, the system admits a nontrivial traveling wave solution with speed c. Numerical simulations are performed to further validate these theoretical results, confirming both the stability of the equilibrium points and the traveling wave solutions.
One important aspect of these models is the impact of vaccination, which is essential for containing disease spread. In this paper, we formulate and analyze a mathematical model that captures the global behavior and traveling wave solutions of a Monkeypox epidemic [6-8], incorporating vaccination as a key control strategy.
Traveling wave solutions are particularly significant as they represent the spatiotemporal spread of an infectious disease [9], thereby enhancing the understanding of disease front propagation. By studying such wave solutions, we can determine the speed and pattern of disease dissemination, identify critical thresholds that may be vital for disease eradication, and evaluate the long-term effectiveness of vaccination programs.
This paper analyzes the conditions for the existence of traveling wave solutions, as well as the stability and persistence of these waves. Within this framework, the model offers a robust approach to assess the potential outcomes of vaccination strategies, providing valuable insights for public health planning and response efforts against Monkeypox epidemics.
In light of the aforementioned issues, we present the following reaction-diffusion Monkeypox epidemic model incorporating the effects of vaccination.
\[\label{1} \left\{\begin{array}{lll} \frac{\partial S_{h}(x,t)}{\partial t} =& d_h \Delta S_h(x,t)+\Lambda-\beta_{ha}S_{h}(x,t) I_{a}(x,t)-\beta_{hh}S_{h}(x,t) I_{h}(x,t)-(\mu+\alpha) S_{h}(x,t) + \theta V_h(x,t) ,\\ \frac{\partial V_{h}(x,t)}{\partial t}=& y_h \Delta I_h(x,t)+\alpha S_{h}(x,t) -(\mu+\sigma+\theta) V_h(x,t), \\ \frac{\partial I_{h}(x,t)}{\partial t}=& q_h \Delta I_h(x,t)+\beta_{ha}S_{h}(x,t) I_{a}(x,t)+\beta_{hh}S_{h}(x,t) I_{h}(x,t)-(\mu +\gamma) I_{h}(x,t), \\ \frac{\partial R_{h}(x,t)}{\partial t}=& m_h \Delta R_h(x,t)+\gamma I_{h}(x,t) – \mu R_{h}(x,t) + \sigma V_h(x,t), \\ \frac{\partial S_{a}(x,t)}{\partial t}=& d_a \Delta S_a(x,t)+ A-\beta_{ah}S_{a}(x,t)I_{h}(x,t)-\beta_{aa}S_{a}(x,t)I_{a}(x,t)-\xi S_{a}(x,t), \\ \frac{\partial I_{a}(x,t)}{\partial t}=& q_h \Delta I_a(x,t)+ \beta_{ah}S_{a}(x,t)I_{h}(x,t)+\beta_{aa}S_{a}(x,t)I_{a}(x,t)-(\xi+\kappa )I_{a}(x,t),\\ \frac{\partial R_{a}(x,t)}{\partial t} =& m_a \Delta R_a(x,t)+\kappa I_a(x,t)-\xi R_a(x,t). \end{array} \right.\tag{1}\] We make the assumption
(A): \(d_h,d_a,y_h,q_h,q_a,m_h\) and \(m_a\) are positive.
with \(\beta_{hh}\) is the transmission rate of the susceptible human by infected human. \(\beta_{ha}\) is the transmission rate of the susceptible human by an infected animal. \(\beta_{ah}\) is the transmission rate of the susceptible animal by infected human. \(\beta_{aa}\) is the transmission rate of the susceptible animal by an infected animal. \(\mu\) is the natural mortality coefficient of the bovines. \(\gamma\) is the recovering rate of the infected human. \(\xi\) is the mortality coefficient of the animal. \(\Lambda\) is the constant birth rate of the susceptible human. \(\alpha\) is the vaccination rate. \(\theta\) is the return rate to susceptible population and \(\sigma)\) is the term of recovery. \(L\) represents the constant birth rate of susceptible animal and \(\kappa\) is the recovery rat of the animal population.
The system (1) can be rewritten in the following abstract form \[\frac{dX(t)}{dt}=f(X(t)),\] with \(X(t)=(S_h,V_h,I_h,R_h,S_a,I_a,R_a)\), and
\[f(X) = \left(\begin{array}{ccccc} f_{1}(X)\\ f_{2} (X)\\ f_{3} (X)\\ f_{4} (X)\\ f_{5}(X)\\ f_{6}(X)\\ f_{7}(X) \end{array} \right) = \left(\begin{array}{ccccc} \Lambda-\beta_{ha}S_{h}(t) I_{a}(t)-\beta_{hh}S_{h}(t) I_{h}(t)-(\mu+\alpha) S_{h}(t) + \theta V_h(t) \\ \alpha S_{h}(t) -(\mu+\sigma+\theta) V_h(t)\\ \beta_{ha}S_{h}(t) I_{a}(t)+\beta_{hh}S_{h}(t) I_{h}(t)-(\mu +\gamma) I_{h}(t) \\ \gamma I_{h}(t) – \mu R_{h}(t) + \sigma V_h(t)\\ A-\beta_{ah}S_{a}(t)I_{h}(t)-\beta_{aa}S_{a}(t)I_{a}(t)-\xi S_{a}(t) \\ \beta_{ah}S_{a}(t)I_{h}(t)+\beta_{aa}S_{a}(t)I_{a}(t)-(\xi+\kappa )I_{a}(t)\\ \kappa I_a(t)-\xi R_a(t) \end{array} \right).\]
Notice that \(f_{i}\) is of class \(C^{1}\) Then it is locally Lipschitz with respect to the second variable, hence according to the Cauchy Lipschitz theorem implies the existence and uniqueness of the solution. The positivity of the solution follows form the standard results of dynamical systems theory. Therefore, the system (1) admits a unique solution.
Next, we initial conditions \((S_{h}(0),V_h(0), I_{h}(0), R_{h}(0), S_{a}(0), I_{a}(0),T_a(0) )\) \(t \in \mathbb{R}_{+}^{7}\). At first, we introduce the following lemma.
Lemma 1. Suppose \(\Omega \subset\) \(\mathbb{R} \times \mathbb{C}^{n}\) is open,\(f_{i} \in \mathbb{C} (\Omega, \mathbb{R} )\), \(i=1,2,3…n\). If \(f_{i}|_{x_{i}=0 }X_{t} \in \mathbb{C}_{0+}^{n}\geq 0\), \(X_{t}=(x_{1t},x_{2t}, x_{3t}…. x_{1n})^{T}\), \(i=1,2,3…n\).then \(\mathbb{C}_{0+}^{n}\) is the invariant domain of the following equations: \[\frac{d x_{i}(t)} {dt} =f_{i}(t,X_{t} ) , \ \ t>\sigma , i=1,2…n .\]
Theorem 1. Each solution \((S_{h}(0),V_h(0), I_{h}(0), R_{h}(0), S_{a}(0), I_{a}(0),R_a(0) )\) of model ((1)) with the non-negative initial conditions for all \(t > 0\). Moreover, the following set \[\begin{array}{ccc} \Omega=\bigg\{ (S_h,V_h,I_h,R_h,S_h,I_h,R_h), S_h \geq 0, V_h \geq 0, I_h \geq 0, R_h \geq 0, S_a \geq 0, I_a \geq 0, R_a \geq 0,\\ S_h+V_h+I_h+R_h \leq \frac{\Lambda}{\mu} \ \ \mbox{and}\ \ S_a+I_a+R_a \leq \frac{A}{\xi} \bigg\},\end{array}\] is a positively invariant set.
Proof. Let \(X=(S_{h},V_h, I_{h}, R_{h}, S_{a}, I_{a},R_a )^{T}\) and \(f(X) = (f_{1} (X), f_{2} (X), f_{3} (X), f_{4} (X), f_{5} (X), f_{6} (X), f_{7} (X))^{T}\) then we can rewrite model (1) as:
\[\dot X= f_i(X)\] Note that \[\begin{array}{lllll} \frac{dS_{h} }{dt}|_{S_{h}=0 } =\Lambda + \theta V_h>0, \ \ \frac{dV_{h} }{dt}|_{V_{h}=0 } =\alpha S_h>0, \ \ \frac{dI_{h} } {dt}|_{I_{h}=0}=\beta_{ha}S_hI_a \geq 0,\\ \frac{dR_{h} } {dt}|_{R_{h}=0}= \gamma I_h+\sigma V_h \geq 0,\ \ \frac{dS_{a} } {dt}|_{S_{a}=0 }=A >0, \ \ \frac{dI_{a} } {dt}|_{I_{a}=0 }=\beta_{ah}S_{a}(t)I_{h}(t)\geq 0 \\ \frac{dR_{a} } {dt}|_{R_{a}=0 }=\kappa I_{a}(t) \geq 0. \end{array}\] The standard results of theory of differential equations implies that (1) has a unique positive solution. For showing that the solution is globally defined, we sum up the three equations of ((1)), for each \(i=1,2\), to obtain \[(S_h(t) +V_h(t)+ I_h(t) +R_h(t))' = \Lambda – \mu (S_h(t) +V_h(t)+ I_h(t) +R_h(t)),\] and \[(S_a(t) + I_a(t) +R_a(t))' = A – \xi (S_a(t)+ I_a(t) +R_a(t)),\] then \[\limsup_{t \rightarrow +\infty} (S_h(t) +V_h(t)+ I_h(t) +R_h(t)) \leq \frac{\Lambda}{\mu},\] and \[\limsup_{t \rightarrow +\infty} (S_a(t) + I_a(t) +R_a(t)) \leq \frac{A}{\xi}.\] Therefore, the solution is globally defined. Therefore, \[\limsup_{t \rightarrow +\infty} S_h(t) \leq \frac{\Lambda}{\mu},\] and \[\limsup_{t \rightarrow +\infty} S_a(t) \leq \frac{A}{\xi}.\] Then it follows from Lemma 1 that \(\Omega\) is invariant set. ◻
In this section, we investigate the temporal behavior. Clearly, the \(R_h\) and \(R_a-\)equations can be separated from the system (1). Therefore, we focus on studying the following ODE system
\[\label{11} \left\{\begin{array}{lll} S'_{h}(t) =&\Lambda-\beta_{ha}S_{h}(t) I_{a}(t)-\beta_{hh}S_{h}(t) I_{h}(t)-(\mu+\alpha) S_{h}(t) + \theta V_h(t) ,\\ V'_{h}(t)=& \alpha S_{h}(t) -(\mu+\sigma+\theta) V_h(t), \\ I'_{h}(t)=& \beta_{ha}S_{h}(t) I_{a}(t)+\beta_{hh}S_{h}(t) I_{h}(t)-(\mu +\gamma) I_{h}(t), \\ S'_{a}(t)=& A-\beta_{ah}S_{a}(t)I_{h}(t)-\beta_{aa}S_{a}(t)I_{a}(t)-\xi S_{a}(t), \\ I'_{a}(t)=& \beta_{ah}S_{a}(t)I_{h}(t)+\beta_{aa}S_{a}(t)I_{a}(t)-(\xi+\kappa )I_{a}(t). \end{array} \right.\tag{2}\]
Next, we derive the following results. The BRN, \(R_0\), associated to (2) is the spectral radius of \(\mathcal{J}\), that is, and we obtain that the basic reproduction number of system ((2)) at the disease-free equilibrium \((S_h^0,V_h^0,0,S_a^0,0)\), denoted by \(R_0\), can be expressed as \[R_0 = \rho(\mathcal{J})\] where \[\mathcal{J} = \begin{bmatrix} \frac{\beta_{hh} S_h^0}{(\mu +\gamma)} & \frac{\beta_{ha} S_h^0}{(\mu +\gamma)} \\ \\ \frac{\beta_{ah} S_a^0}{(\xi+\kappa)} & \frac{\beta_{aa} S_a^0}{(\xi+\kappa)} \end{bmatrix}\] and \(\rho(\mathcal{J})\) denotes the spectral radius of the matrix \(\mathcal{J}\). The equilibrium points of the system (2) satisfies \(S'_{h}=V_h=I'_{h}=S'_{a}=I'_{a}=0\). In this case, we will show that (2) admits two equilibrium \(E_0=(S_h^0,V_h^0,0,S_a^0,0)\) which corresponds to the Disease free equilibrium where \[S_h^0 = \frac{ \Lambda}{\mu(\mu+\sigma+\theta) + \alpha(\mu+\sigma) }, \ \ V_h^0= \frac{\alpha S_h^0}{(\mu+\sigma+\theta) } \ \ \mbox{and} \ \ S_a^0 =\frac{A}{\xi}.\] The second equilibrium points satisfies the following system
\[\label{111} \left\{\begin{array}{lll} 0 =&\Lambda-\beta_{ha}S_{h}^* I_{a}^*-\beta_{hh}S_{h}^* I_{h}^*-(\mu+\alpha) S_{h}^* + \theta V_h^* ,\\ 0 =& \alpha S_{h}^* -(\mu+\sigma+\theta) V_h^*, \\ 0=& \beta_{ha}S_{h}^* I_{a}^*+\beta_{hh}S_{h}^* I_{h}^*-(\mu +\gamma) I_{h}^*, \\ 0 =& A-\beta_{ah}S_{a}^*I_{h}^*-\beta_{aa}S_{a}^*I_{a}^*-\xi S_{a}^*, \\ 0 =& \beta_{ah}S_{a}^*I_{h}^*+\beta_{aa}S_{a}^*I_{a}^*-(\xi+\kappa )I_{a}^*. \end{array} \right.\tag{3}\] Motivated by [10], we let the following assumption.
Theorem 2. If \(R_0 < 1\), then the IFES, \(E_0=(S_h^0,V_h^0,0,S_a^0,0)\), is global asymptotically stable, and if \(R_0 > 1\), then the IFES is unstable, and ((2)) is uniformly persistent in \(\bar{\Omega}\), and admits a unique EES, \(E^*\), which is globally attractive. If \(R_0 > 1\), \(E^*\) is an arbitrary endemic equilibrium, then there exists a unique endemic equilibrium \(E^*\) for the system (2), and \(E^*\) is globally asymptotically stable.
Proof. We let \(E=(S_h,V_h,I_h,S_a,I_a)\) be an arbitrary equilibrium, then, the Jacobian matrix of the system (2) at \(E\) is given by \[J_E=\left(\begin{array}{cccccc} -\beta_{ha} I_{a}-\beta_{hh}I_h -(\mu+\alpha) & \theta & -\beta_{hh}S_h & 0 & -\beta_{ha}S_h \\ \alpha & -(\mu+\sigma+\theta)& 0 & 0 & 0\\ \beta_{ha} I_{a}+\beta_{hh}I_h & 0& \beta_{hh} S_h- (\mu+\gamma) & 0 & \beta_{ha}S_{h}\\ 0 & 0& – \beta_{ah} S_{a} & – \beta_{ah} I_{a}-\beta_{aa} I_a – \xi & -\beta_{aa} S_a \\ 0 & 0 &\beta_{ah}S_{a} & \beta_{ah} I_{a}+\beta_{aa} I_a & \beta_{aa} S_a – (\xi+\kappa) \end{array}\right) .\] First, we show the stability of the disease free equilibrium Therefore, we start wit the local stability analysis. By evaluating this Jacobian matrix at the disease-free equilibrium, we obtain \[J_{E_{0} } =\left(\begin{array}{cccccc} -(\mu+\alpha) & \theta & -\beta_{hh}S_h^0 & 0 & -\beta_{ha}S_h^0 \\ \alpha & -(\mu+\sigma+\theta)& 0 & 0 & 0\\ 0 & 0& \beta_{hh} S_h^0- (\mu+\gamma) & 0 & \beta_{ha}S_{h}^0\\ 0 & 0& – \beta_{ah} S_{a}^0 & – \xi & -\beta_{aa} S_a^0 \\ 0 & 0 &\beta_{ah}S_{a}^0 & 0 & \beta_{aa} S_a^0 – (\xi+\kappa) \end{array}\right) .\] We remark that \(l=-\xi\) is a negative eigenvalue. Then, we have \[J_{E_{0} } =\left(\begin{array}{cccccc} -(\mu+\alpha) & \theta & -\beta_{hh}S_h^0 & -\beta_{ha}S_h^0 \\ \alpha & -(\mu+\sigma+\theta)& 0 & 0\\ 0 & 0& \beta_{hh} S_h^0- (\mu+\gamma) & \beta_{ha}S_{h}^0\\ 0 & 0 &\beta_{ah}S_{a}^0 & \beta_{aa} S_a^0 – (\xi+\kappa) \end{array}\right) .\] The corresponding characteristic equation is given by \[p(\lambda) : = \bigg[(\beta_{hh} S_h^0- (\mu+\delta+\gamma)-\lambda)(\beta_{aa} S_a^0 – (\xi+\kappa)-\lambda) -\beta_{ha}S_{h}^0\beta_{ah}S_{a}^0\bigg]\bigg[(\mu+\alpha+\lambda)(\mu+\sigma+\theta+\lambda)-\alpha\theta\bigg] =0,\] then, we have \[\label{f} (\mu+\alpha+\lambda)(\mu+\sigma+\theta+\lambda)-\alpha\theta=0.\tag{4}\] Clearly, by the Dickarte sign rule wee get the equation (4) admits two negative eigenvalues. Then, we have \[\label{ff} \begin{array}{llll} 0 =& (\beta_{hh} S_h^0- (\mu+\delta+\gamma)-\lambda)(\beta_{aa} S_a^0 – (\xi+\kappa)-\lambda) -\beta_{ha}S_{h}^0\beta_{ah}S_{a}^0\\ =& \lambda^2-\bigg(\beta_{hh} S_h^0- (\mu+\gamma)+ \beta_{aa} S_a^0 – (\xi+\kappa)\bigg)l+( (\beta_{hh} S_h^0- (\mu+\gamma))(\beta_{aa} S_a^0 – (\xi+\kappa))-\beta_{ha}S_{h}^0\beta_{ah}S_{a}^0. \end{array}\tag{5}\]
Therefore, the disease-free equilibrium \(E_{0}\) is locally asymptotically stable if the Routh-Hurwitz condition are satisfy where \(R_0<1\) and unstable if \(R_0 >1\). The following conditions are met: \[\left\{\begin{array}{rcl} a_{1} > 0,\\ a_{1} a_{2} >0. \end{array}\right.\]
Next, we turn our attention into the global stability of the \(E_0\) if \(R_0<1\). By the first and the third equations of (2), and if we rewrite the system as follow \[\label{new} \left\{\begin{array}{lll} S'_{h}(t) =&\Lambda-\beta_{ha}S_{h}(t) I_{a}(t)-\beta_{hh}S_{h}(t) I_{h}(t)-(\mu+\alpha) S_{h}(t) + \theta V_h(t) ,\\ S'_{a}(t)=& A-\beta_{ah}S_{a}(t)I_{h}(t)-\beta_{aa}S_{a}(t)I_{a}(t)-\xi S_{a}(t), \\ V'_{h}(t)=& \alpha S_{h}(t) -(\mu+\sigma+\theta) V_h(t), \\ \frac{d I_i(t)}{dt} =& \displaystyle\sum_{j=1}^2 F_{ij}(S_{i}(t),I_j(t)) – (\mu_i +\varrho_i)I_i(t), \end{array} \right.\tag{6}\] where \((i= 1,2)\) and if \(i=1\) represent the human compartment and \(i=2\) the animal compartment and \(F_{ij}(S_{i}(t),I_j(t))= \beta_{ij} S_i(t)I_j(t)\). Then, motivated by [11], [10] and [12]. From the well known Perron–Frobenius Theorem, \(\mathcal{J}\) has a positive principal eigenvector \(w = (w_1, w_2)\) with \(w_i > 0\), \(i = 1, 2\), and \(w · \rho(\mathcal{J}) = w · \mathcal{J}\). First, we start with the global stability of the IFES. Let the Lyapunov function \(V_i(t)\), with \[V_i(t)= \displaystyle\sum_{i=1}^{2} \frac{w_i}{\mu_i+\varrho_i}I_i(t).\]
Then we have \[\begin{array}{lllll} V_i^{'}(t) =& \displaystyle\sum_{i=1}^{2} \frac{w_i}{\mu_i+\varrho_i}I_i'(t)\\ =& \displaystyle\sum_{i=1}^{2} \frac{w_i}{\zeta_i+\varrho_i}\bigg[F_{i1}(S_i(t),I_1(t))+F_{i2}(S_i(t),I_2(t)) – (\mu_i +\varrho_i)I_i(t)\bigg]. \end{array}\]
Therefore, we get \[\begin{array}{lllll} V_i'(t) =& \displaystyle\sum_{i=1}^{2} \frac{w_i}{\mu_i+\varrho_i}\bigg[F_{i1}(S(t),I_1(t))+F_{i2}(S_i(t),I_2(t)) – (\mu_i +\varrho_i)I_i(t)\bigg] \\ \leq& \displaystyle\sum_{i=1}^{2} \frac{w_i}{\mu_i+\varrho_i}\bigg[\frac{dF_{i1}(S_i^0,0)}{dI_1}I_1(t)+\frac{dF_{i2}(S_i^0,0)}{dI_2}I_2(t) – (\mu_i +\varrho_i)I_i(t)\bigg] \\ =& w.[\mathcal{J} I(t) -I(t)] = [\rho(\mathcal{J})-1]w.I(t) \\ \leq& 0, \end{array}\] if and only if \(\rho(\mathcal{J}) =R_0 < 1\). Here, \(I = diag(I_1, I_2)\). If \(\rho(\mathcal{M}) < 1\), then \(V_i' = 0\) if and only if \(I = 0\). If \(\rho(\mathcal{J}) = 1\), hence \(V_i' = 0\) yields
\[\label{I0} \begin{array}{lll} \displaystyle\sum_{i=1}^{2} \frac{w_i}{\mu_i+\varrho_i}\bigg[F_{i1}(S_i(t),I_1(t))+F_{i2}(S_i(t),I_2(t)) \bigg] = \sum_{i=1}^{2} w_i I_i. \end{array}\tag{7}\] If at least for one \(i= 1, 2, S_i \neq 1\) then
\[\begin{array}{lll} \displaystyle\sum_{i=1}^{2} \frac{w_i}{\mu_i+\varrho_i}\bigg[F_{i1}(S_i(t),I_1(t))+F_{i2}(S_i(t),I_2(t)) \bigg] =& \displaystyle\sum_{i=1}^{2} w_i I_i\\ &<& \displaystyle\sum_{i=1}^{2} \frac{w_i}{\mu_i+\varrho_i}\bigg[\frac{dF_{i1}(S_i^0,0)}{dI_1}I_1(t)+\frac{F_{i2}(S_i^0,0)}{dI_2}I_2(t) \bigg] \\ =& w.\mathcal{J} I = \rho(\mathcal{J})I. w = w.I, \end{array}\] which implies that (7) and only if \(I = 0\) or \(S_i = 1\) for all \(i=1,2\). Provided that \(\rho(\mathcal{J}) < 1\). Clearly, \(V_i' = 0\) contains only the singleton \(\{E_0\}\). Consequently, LaSalle’s Invariance Principle [13], implies the global asymptotic stability of \(E_0\) for \(R_0 < 1\). Now, assume that \(R_0 > 1\), hence \(I_i \neq 0\), then we have
\[w.\mathcal{J} I = \rho(\mathcal{M})I. w > 0,\] and thus by continuity \[\displaystyle\sum_{i=1}^{2} \frac{w_i}{\mu_i+\varrho_i}\bigg[\frac{dF_{i1}(S_i^0,0)}{dI_1}I_1(t)+\frac{dF_{i2}(S_i^0,0)}{dI_2}I_2(t) – (\mu_i +\varrho_i)I_i(t)\bigg] > 0.\] In a neighborhood of \(E_0\) in \(\bar{\Omega}\). This ensures that \(E_0\) is unstable. The uniform persistence results, e.g. [14], and a similar argument as in the proof of [15] implies that the system (6) is uniformly persistent if \(R_0 > 1\), which it can be deduced from the instability of \(E_0\). Furthermore, by [16] we ensure that there exists at least one EESS.
To show the uniqueness of the EESS, we will show its global stability, which it can imply that it is unique using the uniqueness of the limit.
Now, we move to prove the second part of the theorem 2. We employ a Lyapunov function to obtain the global stability of \(E^*\) when ever exists. We consider the following function:
\[\label{lya} \begin{array}{rcl} V(t) = S_{h}^{*}h(\frac{S_{h}}{S_{h}^{*}}) +V_{h}^{*}h(\frac{V_{h}}{V_{h}^{*}})+ I_{h}^{*}h(\frac{I_{h}}{I_h^{*}}) + cS_{a}^{*}h(\frac{S_{a}}{S_{a}^{*}}) + cI_{a}^{*}h(\frac{I_{a}}{I_{a}^{*}}), \end{array}\tag{8}\] where \(h\) is Volterra function \(h(x) = 1 – x – ln(x)\) , \(x\) \(\in\) \(\mathbb{R}^{+}\), and the positive constant \(c\) will be determined later. Recall that the endemic equilibrium \(E_{*}\) satisfies \[\label{12} \left\{\begin{array}{lll} \Lambda =&\beta_{ha}S_{h}^* I_{a}^*+\beta_{hh}S_{h}^* I_{h}^*+(\mu+\alpha) S_{h}^* – \theta V_h^* ,\\ (\mu+\sigma+\theta) V_h^* =& \alpha S_{h}^* , \\ (\mu +\gamma) I_{h}^*=& \beta_{ha}S_{h}^* I_{a}^*+\beta_{hh}S_{h}^* I_{h}^*, \\ A =& \beta_{ah}S_{a}^*I_{h}^*+\beta_{aa}S_{a}^*I_{a}^*+\xi S_{a}^*, \\ (\xi+\kappa )I_{a}^* =& \beta_{ah}S_{a}^*I_{h}^*+\beta_{aa}S_{a}^*I_{a}^*. \end{array} \right.\tag{9}\] The derivative of \(V(t)\) with respect to \(t\), we obtain \[\begin{array}{llll} V'(t) =& \bigg(1-\frac{S_h^*}{S_h(t)}\bigg)S'_h(t)+\bigg(1-\frac{V_h^*}{V_h(t)}\bigg)V'_h(t)+\bigg(1-\frac{I_h^*}{I_h(t)}\bigg)I'_h(t)+\bigg(1-\frac{S_a^*}{S_a(t)}\bigg)S'_a(t)+\bigg(1-\frac{I_a^*}{I_a(t)}\bigg)I'_a(t). \end{array}\] Some simplifications and applied the equations of the system (9), gives \[\begin{aligned} V'(t) =& \mu S_h^*\bigg(1-\frac{S_h^*}{S_h(t)}\bigg)\bigg(1-\frac{S_h(t)}{S_h^*}\bigg) \\&+ \beta_{ha }S_h^* I_a^*\bigg(2+\frac{I_a(t)}{I_a^*}-\frac{S_h^*}{S_h(t)}-\frac{S_h(t)I_a(t)I_h^*}{S_h^*I_a^* I_h(t)}-\frac{I_h(t)}{I_h^*}+\frac{I_a^*}{I_a(t)}-\frac{I_a^*}{I_a(t)}+2-2\bigg) \\& +\beta_{hh }S_h^* I_h^*\bigg(2-\frac{S_h^*}{S_h(t)}-\frac{S_h(t)}{S_h^*}\bigg)+\alpha S_h^*\bigg(3-\frac{S_h^*}{S_h(t)}-\frac{S_h(t)V_h^*}{S_h^* V_h(t)}-\frac{V_h(t)}{V_h^*}\bigg)\\&+\theta V_h^* \bigg(-1-\frac{V_h(t)S_h^*}{V_h^*S_h(t)}+\frac{S_h^*}{S_h(t)}+\frac{V_h(t)}{V_h^*}+\frac{V_h^*S_h(t)}{S_h^*V_h(t)}-\frac{V_h^*S_h(t)}{S_h^*V_h(t)}+2-2\bigg) +c(\xi+\beta_{aa}I_a^*) S_a^* \\&\times \bigg(1-\frac{S_a^*}{S_a(t)}\bigg)\bigg(1-\frac{S_a(t)}{S_a^*}\bigg)\\&+c\beta_{ah} S_a^*I_h^*\bigg(\frac{I_h(t)}{I_h^*}+2-\frac{S_a^*}{S_a(t)}-\frac{S_a(t)I_h(t)I_a^*}{S_a^*I_h^*I_a(t)}-\frac{I_a(t)}{I_a^*}-\frac{I_h^*}{I_h(t)}+\frac{I_h^*}{I_h(t)}+2-2\bigg)\\ =& \mu S_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)}{S_h^*}\bigg)\bigg)\\& + \beta_{ha }S_h^* I_a^*\bigg(h\bigg(\frac{I_a(t)}{I_a^*}\bigg)-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)I_a(t)I_h^*}{S_h^*I_a^* I_h(t)}\bigg)-h\bigg(\frac{I_h(t)}{I_h^*}\bigg)\bigg) \\& +\beta_{hh }S_h^* I_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)}{S_h^*}\bigg)\bigg)+\alpha S_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)V_h^*}{S_h^* V_h(t)}\bigg)-h\bigg(\frac{V_h(t)}{V_h^*}\bigg)\bigg)\\&+\theta V_h^* \bigg(-h\bigg(\frac{V_h(t)S_h^*}{V_h^*S_h(t)}\bigg)+h\bigg(\frac{S_h^*}{S_h(t)}\bigg)+h\bigg(\frac{V_h(t)}{V_h^*}\bigg)\bigg)+c(\xi+\beta_{aa}I_a^*) S_a^*\bigg(-h\bigg(\frac{S_a^*}{S_a(t)}-h\bigg(\frac{S_a(t)}{S_a^*}\bigg)\bigg)\\&+c\beta_{ah} S_a^*I_h^*\bigg(h\bigg(\frac{I_h(t)}{I_h^*}\bigg)-h\bigg(\frac{S_a^*}{S_a(t)}\bigg)-h\bigg(\frac{S_a(t)I_h(t)I_a^*}{S_a^*I_h^*I_a(t)}\bigg)-h\bigg(\frac{I_a(t)}{I_a^*}\bigg)\bigg), \end{aligned}\] if we take \(c = \frac{\beta_{ha }S_h^*I_h^*}{\beta_{ah} S_a^*I_h^*}\), then we get \[\begin{array}{llll} V'(t) =& \mu S_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)}{S_h^*}\bigg)\bigg) + \beta_{ha }S_h^* I_a^*\bigg[h\bigg(\frac{I_a(t)}{I_a^*}\bigg)-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)I_a(t)I_h^*}{S_h^*I_a^* I_h(t)}\bigg)\\&-h\bigg(\frac{I_h(t)}{I_h^*}\bigg)+h\bigg(\frac{I_h(t)}{I_h^*}\bigg)-h\bigg(\frac{S_a^*}{S_a(t)}\bigg)-h\bigg(\frac{S_a(t)I_h(t)I_a^*}{S_a^*I_h^*I_a(t)}\bigg)-h\bigg(\frac{I_a(t)}{I_a^*}\bigg)\bigg] +\\&\beta_{hh }S_h^* I_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)}{S_h^*}\bigg)\bigg)+\alpha S_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)V_h^*}{S_h^* V_h(t)}\bigg)-h\bigg(\frac{V_h(t)}{V_h^*}\bigg)\bigg) +\\&\theta V_h^* \bigg[-h\bigg(\frac{V_h(t)S_h^*}{V_h^*S_h(t)}\bigg)+h\bigg(\frac{S_h^*}{S_h(t)}\bigg)+h\bigg(\frac{V_h(t)}{V_h^*}\bigg)\bigg]+\frac{\beta_{ha }S_h^*I_h^*}{\beta_{ah} S_a^*I_h^*}(\xi+\beta_{aa}I_a^*) S_a^*\bigg(-h\bigg(\frac{S_a^*}{S_a(t)}-h\bigg(\frac{S_a(t)}{S_a^*}\bigg)\bigg)\\ =& \mu S_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)}{S_h^*}\bigg)\bigg) + \beta_{ha }S_h^* I_a^*\bigg[-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)I_a(t)I_h^*}{S_h^*I_a^* I_h(t)}\bigg)\\&-h\bigg(\frac{S_a^*}{S_a(t)}\bigg)-h\bigg(\frac{S_a(t)I_h(t)I_a^*}{S_a^*I_h^*I_a(t)}\bigg)\bigg] +\beta_{hh }S_h^* I_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)}{S_h^*}\bigg)\bigg)+\\&\alpha S_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)V_h^*}{S_h^* V_h(t)}\bigg)-h\bigg(\frac{V_h(t)}{V_h^*}\bigg)\bigg) -\theta V_h^*h\bigg(\frac{V_h(t)S_h^*}{V_h^*S_h(t)}\bigg)\\& \theta V_a^*\bigg[h\bigg(\frac{S_h^*}{S_h(t)}\bigg)+h\bigg(\frac{V_h(t)}{V_h^*}\bigg)\bigg]+\frac{\beta_{ha }S_h^*I_h^*}{\beta_{ah} S_a^*I_h^*}(\xi+\beta_{aa}I_a^*) S_a^*\bigg(-h\bigg(\frac{S_a^*}{S_a(t)}-h\bigg(\frac{S_a(t)}{S_a^*}\bigg)\bigg). \end{array}\] We replace \(\theta V^*\) by \(\alpha S_a^*-(\mu+\sigma)V_h^*\), we get \[\begin{array}{llll} V'(t) =& \mu S_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)}{S_h^*}\bigg)\bigg) + \beta_{ha }S_h^* I_a^*\bigg[-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)I_a(t)I_h^*}{S_h^*I_a^* I_h(t)}\bigg)\\&-h\bigg(\frac{S_a^*}{S_a(t)}\bigg)-h\bigg(\frac{S_a(t)I_h(t)I_a^*}{S_a^*I_h^*I_a(t)}\bigg)\bigg] +\beta_{hh }S_h^* I_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)}{S_h^*}\bigg)\bigg)+\\&\alpha S_h^*\bigg(h\bigg(\frac{S_h^*}{S_h(t)}\bigg)+h\bigg(\frac{V_h(t)}{V_h^*}\bigg)-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)V_h^*}{S_h^* V_h(t)}\bigg)-h\bigg(\frac{V_h(t)}{V_h^*}\bigg)\bigg) -\theta V_h^*h\bigg(\frac{V_h(t)S_h^*}{V_h^*S_h(t)}\bigg)\\& -(\mu+\sigma) V_a^*\bigg[h\bigg(\frac{S_h^*}{S_h(t)}\bigg)+h\bigg(\frac{V_h(t)}{V_h^*}\bigg)\bigg]+\frac{\beta_{ha }S_h^*I_h^*}{\beta_{ah} S_a^*I_h^*}(\xi+\beta_{aa}I_a^*) S_a^*\bigg(-h\bigg(\frac{S_a^*}{S_a(t)}-h\bigg(\frac{S_a(t)}{S_a^*}\bigg)\bigg)\\ =& \mu S_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)}{S_h^*}\bigg)\bigg) + \beta_{ha }S_h^* I_a^*\bigg[-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)I_a(t)I_h^*}{S_h^*I_a^* I_h(t)}\bigg)\\&-h\bigg(\frac{S_a^*}{S_a(t)}\bigg)-h\bigg(\frac{S_a(t)I_h(t)I_a^*}{S_a^*I_h^*I_a(t)}\bigg)\bigg] +\beta_{hh }S_h^* I_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(t)}\bigg)-h\bigg(\frac{S_h(t)}{S_h^*}\bigg)\bigg)-\alpha S_h^*h\bigg(\frac{S_h(t)V_h^*}{S_h^* V_h(t)}\bigg) \\&-\theta V_h^*h\bigg(\frac{V_h(t)S_h^*}{V_h^*S_h(t)}\bigg) -(\mu+\sigma) V_a^*\bigg[h\bigg(\frac{S_h^*}{S_h(t)}\bigg)+h\bigg(\frac{V_h(t)}{V_h^*}\bigg)\bigg]+\frac{\beta_{ha }S_h^*I_h^*}{\beta_{ah} S_a^*I_h^*}(\xi+\beta_{aa}I_a^*) S_a^*\bigg(-h\bigg(\frac{S_a^*}{S_a(t)}\\&-h\bigg(\frac{S_a(t)}{S_a^*}\bigg)\bigg),\\ \leq& 0. \end{array}\] and equality holds if and only if \(S_h(t)=S_h ^*\), \(V_h(t)-V_h^*\), \(I_h(t)=I_h^*\), \(S_a(t)=S_a^*\), \(I_(t)=I_a^*\). Which implies that \(E^{*}\) is globally attractive. ◻
In this section, we will always assume that \(R_0>1\). In this case, (2) have two equilibria \(E_0\), \(E^*\). Our main interest is to study the existence (resp. nonexistence) of a TWS of (2) that connects \(E_0\), and \(E^*\). A TWS of (2) is a particular solution of the form \[\label{hk} (S_h(z),V_h(z),I_h(z),S_a(z),I_a(z)),~~~z=x + ct \in \mathbb{R} .\tag{10}\] Plugging (10) into (2) to obtain
\[\label{tra} \left\{\begin{array}{lll} cS'_h(z) =& d_h S''_h(z)+\Lambda-\beta_{ha}S_{h}(z) I_{a}(z)-\beta_{hh}S_{h}(z) I_{h}(z)-(\mu+\alpha) S_{h}(z) + \theta V_h(z) ,\\ cV'_h(z)=& y_h V''_h(z)+\alpha S_{h}(z) -(\mu+\sigma+\theta) V_h(z), \\ cI'_h(z)=& q_h I''_h(z)+\beta_{ha}S_{h}(z) I_{a}(z)+\beta_{hh}S_{h}(z) I_{h}(z)-(\mu +\gamma) I_{h}(z), \\ cS'_a(z)=& d_a S''_a(z)+ A-\beta_{ah}S_{a}(z)I_{h}(z)-\beta_{aa}S_{a}(z)I_{a}(z)-\xi S_{a}(z), \\ cI'(z)=& q_h I''_a(z)+ \beta_{ah}S_{a}(z)I_{h}(z)+\beta_{aa}S_{a}(z)I_{a}(z)-(\xi+\kappa )I_{a}(z).\\ \end{array} \right.\tag{11}\] We can also write as follow \[\label{tra1} \left\{\begin{array}{lll} cS'_h(z) =& d_h S''_h(z)+\Lambda-\beta_{ha}S_{h}(z) I_{a}(z)-\beta_{hh}S_{h}(z) I_{h}(z)-(\mu+\alpha) S_{h}(z) + \theta V_h(z) ,\\ cS'_a(z)=& d_a S''_a(z)+ A-\beta_{ah}S_{a}(z)I_{h}(z)-\beta_{aa}S_{a}(z)I_{a}(z)-\xi S_{a}(z),\\ cV'_h(z)=& y_h V''_h(z)+\alpha S_{h}(z) -(\mu+\sigma+\theta) V_h(z), \\ cI'_i(z)=& q_i I''_i(z)+\beta_{ih}S_{i}(z) I_{h}(z)+\beta_{ia}S_{i}(z) I_{a}(z)-(\mu_i +\gamma_i) I_{i}(z). \\ \end{array} \right.\tag{12}\] Where \(i= h, a\), \(\mu_h= \mu\), \(\mu_a = \xi\), \(\gamma_h= \gamma\), \(\gamma_a =\kappa\) and with the boundary conditions \[\label{pl} \begin{array}{lll} (S_h(z),V_h(z),I_h(z),S_a(z),I_a(z))(-\infty) = (S_h^0,V_h^0,0,S_a^0,0), \\ (S_h(z),V_h(z),I_h(z),S_a(z),I_a(z))(+\infty) = (S_h^*,V_h^*,I_h^*,S_a^*,I_a^*). \end{array}\tag{13}\] We intend to establish a positive solution of (11) that satisfies the boundary condition (13). The linearized equations of the third and forth equation of (11) at \(E_0\) is as follows
\[\label{lin} \left\{ \begin{array}{lll} cI'_h(z)=& q_h I''_h(z)+\beta_{ha}S_{h}(z) I_{a}(z)+\beta_{hh}S_{h}(z) I_{h}(z)-(\mu +\gamma) I_{h}(z), \\ cI'(z)=& q_h I''_a(z)+ \beta_{ah}S_{a}(z)I_{h}(z)+\beta_{aa}S_{a}(z)I_{a}(z)-(\xi+\kappa )I_{a}(z).\\ \end{array}\right .\] Letting \(I_h(z) = \omega _1 \exp^{\lambda z}\), and \(I_a(z) = \omega _2 \exp^{\lambda z}\), we get
\[\label{lin2} \left\{ \begin{array}{lll} c \omega _1 \lambda =& q_h i\omega _1 \lambda^2+ \beta_{ha}S_{h}^0\omega _2+\beta_{hh}S_{h}^0\omega _1-(\mu +\gamma) \omega _1\\ c \omega _2 \lambda =& q_a \omega _2 \lambda^2+ \beta_{ah}S_{a}^0\omega _1+\beta_{aa}S_{a}^0\omega _2-(\xi+\kappa )\omega _2.\\ \end{array}\right .\tag{14}\] Let \[\mathcal{A}=\begin{bmatrix} q_h & 0\\0 & q_a \end{bmatrix}, \ \ \mathcal{B}=\begin{bmatrix} c & 0\\0 & c \end{bmatrix}, \ \ \mathcal{D}=\begin{bmatrix} \mu +\gamma& 0\\0 & \xi+\kappa \end{bmatrix},\] and \[\mathcal{E}=\begin{bmatrix} \beta_{hh}S_{h}^0& \beta_{ha}S_{h}^0 \\ \\ \beta_{ah}S_{a}^0 & \beta_{aa}S_{a}^0 \end{bmatrix}.\]
Denote \(p(\lambda,c) = \lambda^2 \mathcal{A}-\lambda \mathcal{B}-\mathcal{D}+\mathcal{E}\). Then, the system (14) reduces to \[p(\lambda,c)\bigg(\begin{matrix} \kappa_1 \\ \kappa_2 \end{matrix}\bigg) =0.\] Let \(A'=\mathcal{D}'^{-1}\mathcal{A}, B'=\mathcal{D}'^{-1}\mathcal{B}\) and \(F'=\mathcal{D}'^{-1}\mathcal{F}\), thus \(p(\vartheta,c)\) becomes \[\label{15} (-A' \lambda^2+B'\lambda +I)^{-1}F'\omega = \omega\tag{15}\] where \(\omega = \bigg(\begin{matrix} \omega _1 \\ \omega _2 \end{matrix} \bigg)\), \(m_h(\lambda,c)= -q_h\lambda^2+c\lambda +(\mu +\gamma)\), \(m_a(\lambda,c)= -q_a\lambda^2+c\lambda +(\xi +\kappa)\) and \[(-A' \vartheta^2+B'\vartheta +I)^{-1}F' = \begin{bmatrix} \frac{\beta_{hh}S_h^0}{m_h(\lambda,c)} & \frac{\beta_{ha}S_h^0 }{m_h(\lambda,c)}\\ \frac{ \beta_{ah}S_a^0}{m_a(l;c)} & \frac{\beta_{aa}S_a^0}{m_a(\lambda,c)} \end{bmatrix}.\] Let \(N(\lambda,c) = (-A' \lambda^2+B'\lambda +I)^{-1}F'\), then (1) becomes \[N(\lambda,c) \omega = \omega .\]
Let \(L(\omega , c)\) be the principal eigenvalue of \(N(\omega , c)\). Now, we solve \(m_{h}(\lambda,c)=0\) and \(m_{a}(\lambda,c)=0\) in \(\lambda\). Clearly, \(m_{h}(0,c)=(\mu +\gamma)>0\), \(m_{a}(0,c)=(\xi +\kappa)>0\), \(m_{h,a}(+\infty,c)=-\infty\) and \[\frac{\partial m_h(\lambda,c)}{\partial \lambda}\bigg|_{\lambda=0}=c>0,~~\frac{\partial^2 m_h(\lambda,c)}{\partial \lambda^2}=-2q_h<0.\] We applied the same calculation in the \(m_a(\lambda,c)\). Therefore, there is always \(\lambda_c^h >0\) and \(\lambda_c^a > 0\) satisfying \(m_h(\lambda_c^h ,c)=0\) and \(m_a(\lambda_c^a ,c)=0\), for all \(c>0\). We let \(\lambda_c = \min \bigg\{ \frac{c+\sqrt{c^2+4q_h (\mu +\gamma)}}{2q_h} ,\frac{c+\sqrt{c^2+4q_a (\xi +\kappa)}}{2q_a} \bigg\}\). If \(c \geq 0\), \(\lambda\in [0, \lambda_c)\), some calculations gives
\[\label{2} L(\vartheta,c)=\frac{1}{2}\bigg[\bigg(\frac{\beta_{ha}S_h^0}{m_a(\lambda,c)}+\frac{\beta_{hh}S_h^0}{m_a(\lambda,c)}\bigg)+\biggl\{\bigg(\frac{\beta_{hh} S_h^0}{m_h(\lambda,c)}-\frac{\beta_{aa}S_a^0}{m_a(\lambda,c)}.\bigg)^2+\frac{4\beta_{ha}S_h^0 \beta_{ah}S_a^0}{m_h(\lambda,c)m_a(\lambda,c)}\biggr\}^{\frac{1}{2}}\bigg].\]
Proposition 1. The three claims that follow are true:
\(\lambda_c\) is increasing in \(c \in [0, +\infty)\), and \(\lim_{c\rightarrow +\infty} \lambda_c = +\infty\).
\(L(0,c) = R_0\), \(\forall c \in [0, +\infty)\), \(L(\lambda,c)\) is increasing in \(\lambda \in [0, \lambda_0)\), and \(\lim_{l\rightarrow\lambda_c} L(\lambda,c) = +\infty\), \(\forall c \geq 0\).
\(\forall \lambda \in (0,\lambda_c)\), \(\frac{\partial}{\partial c} L(\lambda,c) < 0\).
For the sake of proving this proposition (we refer Proposition 3.1 in
[6]). Let \[\tilde{\lambda}(c) = \min_{\lambda \in [0,
\lambda_c)} L(\lambda, c) \ \ for \ \ c \geq 0.\] Thus \(\tilde{\lambda}(0)= R_0\), \(\lim_{c\rightarrow +\infty}\tilde{\lambda}(c) =
0\) and \(\tilde{\lambda}(c)\)
is continuous and decreasing in \(c \in [0,
\infty)\). When \(R_0 > 1\),
thus there is a constant \(c^* > 0\)
verifying \(\tilde{\lambda}(c^*) = 1,
\tilde{\lambda}(c) > 1\), \(\forall
c \in [0, c^*)\) and \(\tilde{\lambda}(c) < 1\), \(\forall c \in (c^*, \infty)\).
Let \[\lambda^*=\inf\biggl\{\lambda \in [0,
\lambda_{c^*} ) : L(\lambda, c) = 1 \biggr\}.\] Hence, \(L(\lambda^*, c^*) = 1\), \(l(\lambda^*, c) < 1\), \(\forall c > c^*\). Denote \[\lambda_1(c) = \sup \{ \lambda \in (0, \lambda^*)
: L(\lambda, c) = 1, L(\lambda', c) \geq 1 \ \ \forall \lambda'
\in (0, \lambda)\}.\]
As \(L(\lambda^*, c) < 1\), \(\forall c > c^*\), the following results are satisfied
Proposition 2. If \(R_0 > 1\), then there is \(c^* > 0\), \(\lambda^* \in (0, \lambda_{c^*})\) satisfying
\(L(\lambda, c) > 1\), \(\forall 0 \leq c < c^*\), \(\forall \lambda \in (0, \lambda_c)\), where \(\lambda_c \in [0, +\infty);\)
\(L(\lambda^*, c^*) = 1\), \(L(\lambda, c^*) > 1\) when \(\lambda \in (0, \lambda^*)\), and \(L(\lambda, c^*) \geq 1\) when \(\lambda \in (0, \lambda_{c^*});\)
\(\forall c > c^*\), there is \(\lambda_1(c) \in (0, \lambda^*)\) satisfies \(L(\lambda_1(c), c) = 1\), \(L(\lambda, c) \geq 1\) for \(\lambda\in (0, \lambda_1(c))\), and \(L(\lambda_1(c)+\varepsilon_n(c), c) < 1\) for some decreasing sequences \(\{\varepsilon_n(c)\}\) verifying \(\lim_{n\rightarrow\infty} \varepsilon_n = 0\) and \(\varepsilon_n + \lambda1(c) < \vartheta^*\), \(\forall n \in \mathbb{N}\). Particularly, \(\lambda_1(c)\) decreases in \(c \in (c^*, \infty)\).
As \(N(\lambda, c)\) is irreducible nonnegative matrix for \(\lambda \in [0, \lambda_c)\), we obtain by applying the Perron–Frobenius theorem.
Proposition 3. Suppose that \(R_0 > 1\). When \(c > c^*\), there exists positive unit vectors \(\omega (c) = (\omega _1(c), \omega _2(c))^T\) and \(\xi^n(c) = (\xi_1^n(c), \xi_2^n(c))^T (n \in \mathbb{N})\) verifying \[N(\lambda_1(c), c)\omega (c) = \omega (c),\] \[N(\lambda_1(c) + \varepsilon_n(c), c)\xi^n(c) = L(\lambda_1(c) + \varepsilon_n(c), c)\xi^n(c), n \in \mathbb{N}.\]
Now, let fix \(c > c^*\). Suppose that \(\lambda_1(c), \omega (c) = (\omega _1(c), \omega _2(c))^T , \varepsilon_n(c)\), and \(\xi^n(c) = (\xi_1^n(c), \xi_2^n(c))^T (n \in \mathbb{N})\) are mentioned in Propositions 2 and 3. Without loss of generality, we substitute \(\omega _1(c), \omega (c) = (\omega _1(c), \omega _2(c))^T , \varepsilon_n(c)\), and \(\xi^n(c) = (\xi_1^n(c), \xi_2^n(c))^T (n \in \mathbb{N})\) for \(\lambda_1, \omega = (\omega _1, \omega _2)^T\), \(\varepsilon_n\) and \(\xi^n(c) = (\xi_1^n(c), \xi_2^n(c))^T (n \in \mathbb{N})\). Given that \(L(\vartheta_1 + \varepsilon_n, c) < 1\), Proposition 3 implies that \[ \left\{ \begin{array}{lll} -m_h(\lambda_1, c) \omega _1 ++\bigg(\beta_{ha}S_h^0\omega _1 +\beta_{hh}S_h^0 \omega _2 \bigg) =& 0,\\ -m_a(\lambda_1, c)\omega _2 + \bigg(\beta_{ah}S_a^0\omega _1 +\beta_{aa}S_a^0 \omega _2 \bigg) =& 0,\\ \end{array}\right .\] and \[\label{3} \left\{ \begin{array}{lll} -m_h(\lambda_1+\varepsilon_n, c) \xi_1^n +\bigg(\beta_{ha}S_h^0\omega _1 +\beta_{hh}S_h^0 \omega _2 \bigg)&<& 0,\\ -m_a(\lambda_1+\varepsilon_n, c)\xi_2^n + \bigg(\beta_{ah}S_a^0\omega _1 +\beta_{aa}S_a^0 \omega _2 \bigg) &<& 0 , \end{array}\right .\] for any \(n\in \mathbb{N}\).
Lemma 2. The vector function \(K(z) = (o_1(z), o_2(z))^T\) with \(o_i(z) = \omega _i\exp^{l1 z}\) satisfies
\[\left\{ \begin{array}{lll} c p_1'(z) =& q_h p_1''(z)+ \beta_{ha}S_h^0p_1(z) +\beta_{hh}S_h^0p_2(z) – (\mu +\gamma)p_1(z),\\ c p_2'(z) =& q_a p_2''(z)+ \beta_{ah}S_a^0p_1(z)+ \beta_{aa}S_a^0p_2(z)- (\xi +\kappa)p_2(z), \end{array}\right.\] for any \(z \in \mathbb{R}\).
In this subsection, we assume that \(R_0 < 1\), then we by the contradiction we prove the non-existence of TWS for (2).
Theorem 3. Assume that \(R_0 < 1\). Thus, there exists no nonnegative bounded solution
\((S_h(z),V_h(z),I_h(z),S_a(z),I_a(z)),\) of ((11)) satisfying ((13)).
Proof. Assume that there is \((S_h(z),V_h(z),I_h(z),S_a(z),I_a(z))\) that solves ((11))-(13). Let \((I_h)_{sup} = \sup_{z\in \mathbb{R}} I_h(z)\) and \((I_a)_{sup} = \sup_{z\in \mathbb{R}} I_a(z)\) . By (11) \[\label{22} \left\{\begin{array}{lllll} cI'_h(z)=& q_h I''_h(z)+\beta_{ha}S_{h}^0 (I_a)_{sup}(z)+\beta_{hh}S_{h}^0 (I_h)_{sup}(z)-(\mu +\gamma) I_{h}(z), \\ cI'(z)=& q_h I''_a(z)+ \beta_{ah}S_{a}^0(I_h)_{sup}(z)+\beta_{aa}S_{a}^0(I_a)_{sup}(z)-(\xi+\kappa )I_{a}(z). \end{array}\right.\] The comparison principle implies that \[\bigg(\begin{matrix} I_h(z)\\I_a(z) \end{matrix}\bigg)\leq \mathcal{M} \bigg(\begin{matrix} (I_h)_{sup}(z)\\(I_a)_{sup}(z) \end{matrix}\bigg) \ \ \ \forall z \in \mathbb{R},\] by the definition of \(\mathcal{J}\) and \(R_0\) in the section 2. Clearly, \(\mathcal{J}\) is nonnegative and irreducible. The Perron-Frobenius theorem ensures the existence of a vector \(P = (p_1, p_2)^T \in \mathbb{R}^2\), \(p_1 > 0\), \(p_2 > 0\), satisfies \(\mathcal{J} P = R_0P\). Noting that there is a constant \(\epsilon > 0\) large enough, that satisfy \[\bigg(\begin{matrix} (I_h)_{sup}\\(I_a)_{sup} \end{matrix}\bigg) \leq R_0 P,\] \[\bigg(\begin{matrix} (I_h)_{sup}\\(I_a)_{sup} \end{matrix}\bigg) \leq \mathcal{J}^n\bigg(\begin{matrix} (I_h)_{sup}\\(I_a)_{sup} \end{matrix}\bigg) \leq \epsilon \mathcal{J}^n P = \epsilon R_0^n P \rightarrow 0,\] for \(n \rightarrow \infty\), that is a contradiction with \(I_h(z) > 0\) and \(I_a(z) > 0\), \(\forall z \in \mathbb{R}\). ◻
The next theorem we show the case when (11) do not admits a TWS.
Theorem 4. Assume that \(R_0 > 1\) and \(0 < c < c^*\). Thus, (11) has no TWS of the form \((S_h(z),V_h(z),I_h(z),S_a(z),I_a(z))\) that satisfies (13).
Proof. We argue by contradiction. Fixing \(0<c< c^*\), and assume that there is a positive solution \((S_h(z),V_h(z),I_h(z),S_a(z),I_a(z))\) of ((11)) the verifies ((13)). By [6] there exists \(\mu_0 > 0\) satisfying
\[\sup_{z \in \mathbb{R}} |I_h(\xi) e^{-\mu_0 z}| < +\infty,\ \ |I_a(\xi) e^{-\mu_0 z}| < +\infty\] \[\sup_{z \in \mathbb{R}} |I_h'(z) e^{-\mu_0 z}| < +\infty, \ \ |I_a'(z) e^{-\mu_0 z}| < +\infty,\] \[\sup_{z \in \mathbb{R}} |I_h''(z) e^{-\mu_0 z}| < +\infty, \ \ |I_a''(z) e^{-\mu_0 z}| < +\infty.\]
Consider \(p_1(z) := 1 – S_h(z)\). Then \(p_1(z)\) satisfies \[c p_1'(z) = q_h p_1''(z) – (\mu +\gamma) p_1(z) +\beta_{ha}S_{h}(z) I_a(z)+\beta_{hh}S_{h}(z)I_h(z).\]
By the inequality \[\|p_1'\|_{L^\infty((-\infty,0])} \leq 2 \sqrt{\|p_1\|_{L^\infty((-\infty,0])} \|p_1''\|_{L^\infty((-\infty,0])}}\] and \[\lim_{z \to -\infty} p_1(z) = 0,\] we obtain that \[\label{q} \lim_{z \to -\infty} p_1'(z) = 0.\]
Furthermore, as \(p_1'(z)\) is bounded by \(S_h(z)\) for \(z \in \mathbb{R}\) and ((17)), we integrate the above inequality between \(-\infty\) and \(z, (z < 0)\), then there is a constant \(G > 0\) that satisfy \[(\mu+\gamma) \int_{-\infty}^z p_1(\eta) d\eta = -c p_1(z) + q_h p_1'(z) + \int_{-\infty}^z \beta_{ha}S_{h}(\eta) I_a(\eta)+\beta_{hh}S_{h}(\eta)I_h(\eta) d\eta \leq G, \quad z \leq 0.\]
Let \[E_1(z) = \int_{-\infty}^{z} \beta_{hh}S_{h}(\eta)I_h(\eta) +\int_{-\infty}^z \beta_{ha}S_{h}(\eta) I_a(\eta) d\eta\] and \[B_1(z) = [\mu+\gamma] \int_{-\infty}^z p_1(\eta) d\eta, ~~\forall z<0.\] Therefore, \(E_1(z) \leq C_M e^{\mu_0 z}\), \(\forall z \in \mathbb{R}\), with \(C_M > 0\) is a constant. By \(p_1(z)\), we obtain \[q_h p_1'(z) – c p_1(z) = B_1(z) – E_1(z), \quad z < 0.\]
Solving the last equation yields \[\begin{array}{lllll} &p_1(z) = \hat{C}_M e^{\frac{c}{q_h} z} + \frac{1}{q_h} e^{\frac{c}{q_h} z} \int_0^z e^{-\frac{c}{q_h} \eta} [E_1(\eta) – B_1(\eta)] d\eta,\\ &\leq \hat{C}_M e^{\frac{c}{q_h} z} + \frac{1}{q_h} e^{\frac{c}{q_h} z} \int_z^0 e^{-\frac{c}{q_h} \eta} E_1(\eta) d\eta, \quad z < 0, \end{array}\] where \(\hat{C}_M = p_1(0)\). According to \(E_1(z) = O(e^{\mu_0 z})\) as \(z \to -\infty\), it is obvious that \(p_1(z) = O(e^{\mu_0' z})\) as \(z \to -\infty\), with \(\mu_0' = \min\{\mu_0, \frac{c}{q_h}, \frac{c}{q_a}\}\). In the view of \(0 \leq p_1(z) \leq S_h^0\), one has \[\sup_{z \in \mathbb{R}} \{p_1(z) e^{-\mu_0' z} \} < +\infty.\]
Let \(p_2(z) := 1 – S_a(z), \, z \in \mathbb{R}\). Similarly, we have \[\sup_{z \in \mathbb{R}} \{p_2(z) e^{-\mu_0' z} \} < +\infty.\]
Since that \(\sup_{z \in \mathbb{R}} \{I_h(z) e^{-\mu_0' z} \} < +\infty\) and \(\{I_a(z) e^{-\mu_0' z} \} < +\infty\), we define the one-side Laplace transform of \(I_h\), \(I_a\) by \[T_i(\lambda) = \int_{-\infty}^0 e^{-\lambda z} I_i(z) dz, \quad i = 1, 2.\]
Next, let \(\lambda \in \mathbb{R}_+\). As \(I_h(z) > 0\), \(I_a(z) > 0\), \(\forall z \in \mathbb{R}\) and \(T_h(\cdot)\), \(T_a(\cdot)\) is increasing on \(\mathbb{R}_+\), either there is a constant \(\alpha_k > \mu_0\) satisfies \(T_i(\lambda) < +\infty\) for all \(0 < \lambda < \alpha_i\), with \(i=h,a\) and \(\lim_{\lambda \to \alpha_h – 0} T_h(\lambda) = +\infty\), \(\lim_{\lambda \to \alpha_a – 0} T_a(\lambda) = +\infty\), or \(T_h(\lambda) < +\infty\), \(T_a(\lambda) < +\infty\), \(\forall \lambda \geq 0\). Now, we let the two-sides Laplace transform of \(I_h\) and \(I_a\) as \[\mathcal{T}_i(\overline{\vartheta}) = \int_{-\infty}^{+\infty} e^{-\vartheta z} I_i(z) dz, \quad i = 1, 2.\]
Let \(\vartheta \in \mathbb{R}_+\). As \(I_i(z)\) is bounded in \(\mathbb{R}\) and \(i=h,a\), then \(\int_0^{+\infty} e^{-\vartheta z} I_i(z) dz < +\infty\) \(\forall \lambda > 0\). Hence, \(\mathcal{T}_h(\overline{\lambda})\), \(\mathcal{T}_a(overline{\lambda})\), and \(T_h(\lambda), T_a(\lambda)\) have the same properties in \(\lambda> 0\), either there is a constant \(\alpha_h > \mu_0\), \(\alpha_a > \mu_0\) satisfying \(\mathcal{T}_h(\overline{\lambda}) < +\infty\), \(\mathcal{T}_a(\overline{\lambda}) < +\infty\), \(\forall 0 < \lambda < \alpha_h\), \(\forall 0 < \lambda < \alpha_a\), and \(\lim_{\lambda \to \alpha_h – 0} \mathcal{T}_h(\overline{\lambda}) = +\infty\), or \(\mathcal{T}_h(\overline{\lambda}) < +\infty\) and and \(\lim_{\lambda \to \alpha_a – 0} \mathcal{T}_a(\overline{\lambda}) = +\infty\), or \(\mathcal{T}_a(\overline{\lambda}) < +\infty\), \(\forall\lambda > 0\).
First, we prove that there are \(\alpha_h , \alpha_a = +\infty\), satisfying, \(\mathcal{T}_h(\overline{\lambda}) < +\infty\),\(\mathcal{T}_a(\overline{\lambda}) < +\infty\), \(\forall \lambda > 0\). We argue by contradiction. Without loss of generality, let \(0 < \alpha_h < +\infty\) and \(\alpha_a \leq +\infty\) on the contrary. Then we have two cases: (1) \(0 < \alpha_a < +\infty\); (2) \(\alpha_h = +\infty\). For (1), let \(0 < \alpha_a < \alpha_h \leq +\infty\). In view of \[\begin{array}{lll} q_h I_1''(z) – c I_1'(z) – (\mu+\gamma) I_h(z) =& \epsilon_1 \beta_{hh}S_h^0 I_h(z) )+\beta_{ha} S_h^0 I_a(z))\\ =& \beta_{hh} (1- S_h(z ))I_h(z ) + \beta_{ha} (1- S_h(z)) I_a(z). \end{array}\] One has \[\label{z} \begin{array}{llllll} &\mathcal{T}_h(\overline{\vartheta}) (q_h\lambda^{2} – c\lambda – (\mu+\gamma) + \beta_{hh}S_h^0) + \mathcal{T}_a(\overline{\lambda}) \beta_{ha} S_h^0 \\ &\qquad= \int_{-\infty}^{+\infty} e^{-\overline{\lambda} z} \beta_{hh} ( 1- S_{h}(z))I_{h} (z) d z \int_{-\infty}^{+\infty} e^{-\overline{\lambda} z}\beta_{ha} ( 1 – S_{h}(z )) I_{a} (z) dz. \end{array}\tag{18}\] Similarly, we have \[\label{zz} \begin{array}{llllll} &\mathcal{T}_h(\overline{\lambda}) (q_a\lambda^{2} – c\lambda – (\kappa+\xi) + \beta_{ah}S_a^0 )+ \mathcal{T}_a(\overline{\lambda}) \beta_{aa} S_a^0 \\ &\qquad= \int_{-\infty}^{+\infty} e^{-\overline{\lambda} z} \beta_{ah} (( 1- S_{a}(z )I_{h} (z) )d z + \int_{-\infty}^{+\infty} e^{-\overline{\lambda} z}\beta_{aa}( 1 – S_{a}(z))I_{a} (z ) dz. \end{array}\tag{19}\] Since \(0 < 1 – S_{h}(z) \leq S_h^0\), \(0 < 1 – S_{a}(z) \leq S_a^0\) for any \(z \in \mathbb{R}\) and \(\sup_{z \in \mathbb{R}} \left\lbrace (1 – S_{h}(z)) e^{- \mu_{0} z} \right\rbrace < + \infty\), \(\sup_{z \in \mathbb{R}} \left\lbrace (1 – S_{a}(z)) e^{- \mu_{0} z} \right\rbrace < + \infty\), we obtain that \[\int_{-\infty}^{+\infty} e^{- \overline{\lambda} z} \beta_{hh} S_h(z)I_h(z) dz < + \infty, \quad \forall \vartheta \in (0, \alpha_{h} + \mu_{0}),\]
\[\int_{-\infty}^{+\infty} e^{- \overline{\lambda} z} \beta_{ah} S_a(z)I_h(z) dz < + \infty, \quad \forall \vartheta \in (0, \alpha_{h} + \mu_{0}),\]
\[\int_{-\infty}^{+\infty} e^{- \overline{\lambda} z} \beta_{ha} S_h(z)I_a(z) dz < + \infty, \quad \forall \vartheta \in (0, \alpha_{a} + \mu_{0}),\] and \[\int_{-\infty}^{+\infty} e^{- \overline{\lambda} z} \beta_{aa} S_a(z)I_a(z) dz < + \infty, \quad \forall \vartheta \in (0, \alpha_{a} + \mu_{0}).\]
In view of \(\alpha_{h} < \alpha_{a}\), letting \(\overline{\lambda} \rightarrow \alpha_{h} – 0\) in ((19)) that is a contradiction due to the fact that the first term tends to \(\infty\) and the other terms is bounded as \(\overline{\lambda} \rightarrow \alpha_{h} – 0\). It follows that the case \(0 < \alpha_{h} < \alpha_{a} \leq + \infty\) is not possible.
For (2), that is, assume that \(0 < \alpha_{h} = \alpha_{a} = \alpha_{0} \leq + \infty\). If one of inequalities \[q_h \alpha_{0}^{2} – c\alpha_{0} – (\mu+\gamma) + \beta_{hh} S_h^0 \geq 0,\] and \[q_a \alpha_{0}^{2} – c\alpha_{0} – (\xi,\kappa) +\beta_{aa} S_a^0 \geq 0,\] holds, then letting \(\overline{\lambda} \rightarrow \alpha_{h} – 0\) in (18) or ((19)) yields a contradiction. If both inequalities \[q_h \alpha_{0}^{2} – c\alpha_{0} – (\mu+\gamma) + \beta_{hh} S_h^0 < 0\] and \[q_a \alpha_{0}^{2} – c\alpha_{0} -(\xi, \kappa) + \beta_{aa} S_a^0 < 0,\] hold, then we rewrite (18) and (19) as \[N (\overline{\lambda}, c) \left(\begin{array}{llll} \mathcal{T}_{h}(\overline{\lambda}) \\ \mathcal{T}_{a}(\overline{\lambda})\end{array}\right) – \left( \begin{array}{llll}\mathcal{T}_{h}(\overline{\lambda}) \\\mathcal{T}_{a}(\overline{\lambda})\end{array} \right) = \left(\begin{array}{llll} \frac{h_{h}(\overline{\lambda})}{m_h(\tilde{\vartheta},c)} \\ \frac{h_{a}(\overline{\lambda})}{m_a(\tilde{\vartheta},c)} \end{array}\right) \ \ \ \overline{\lambda} \in (0, \alpha_{0}),\] where \(h_{h} (\overline{\lambda}) := \int_{-\infty}^{+\infty} e^{- \overline{\lambda} z} \beta_{ha}( (1 – I_{a} (z)) I_{h} (z) + \beta_{hh}( (1 – I_{h} (z)) I_{h} (z)+\beta_{ah}( (1 – I_{h} (z)) I_{a} (z) +\beta_{ha}( (1 – I_{a} (z)) I_{a} (z) d z\). Clearly, \(\alpha_{0} < \mu_{c}\) due to \[q_h \alpha_{0}^{2} – c\alpha_{0} – (\mu+\gamma) + \beta_{hh} S_h^0 < 0\] and \[q_a \alpha_{0}^{2} – c\alpha_{0} -(\xi+\kappa) + \beta_{aa} S_a^0 < 0 .\] (with \(N (\lambda, c)\) and \(L (\lambda, c)\) are defined in section 5). As \(0<c<c^{*}\), and \(R_{0} > 1\), then Proposition 2 ensures that \(\inf_{\overline{\lambda} \in [0, \alpha_{0})} \rho (\lambda, c) > 1\). As \(N (\lambda, c)\) is positive matrix, then we need to prove either \[\begin{aligned} \beta_{hh} S_h^0 \frac{\mathcal{T}_{h} (\overline{\lambda})}{m_{h} (\lambda, c)} +\beta_{ha } S_h^0 \frac{\mathcal{T}_{a} (\overline{\lambda})}{m_{h} (\lambda, c)} \geq L (\lambda, c) \mathcal{T}_{h} (\lambda), \lambda \in (0, \alpha_{0}), \end{aligned}\] is satisfied. Thus, for all \(\overline{\lambda} \in (0, \alpha_{0})\) there holds either \[\label{d} (L (\lambda, c) – 1) \mathcal{T}_{h} (\lambda) \leq \frac{h_{h} (\overline{\lambda})}{m_{h} (\lambda, c)},\tag{20}\] or \[\label{dd} (L(\lambda, c) – 1) \mathcal{T}_{a} (\lambda) \leq \frac{h_{a} (\lambda)}{m_{a} (\lambda, c)}.\tag{21}\]
Since \(\inf_{\bar{\lambda} \in [0,\alpha_0]} m_h(\bar{\lambda}, c) > 0, m_a(\bar{\lambda}, c) > 0\), \(h_h(\bar{\lambda})\), \(h_a(\bar{\lambda})\) are well posed in \([0, \alpha_0 +\mu_0')\), we let \(\bar{\lambda} \rightarrow \alpha_0 – 0\) in (20) and (21) yields a contradiction due to \(\lim_{\bar{\lambda}\rightarrow\alpha_0} \mathcal{T}_h( \bar{\lambda}) = +\infty\), \(\lim_{\bar{\lambda}\rightarrow\alpha_0} \mathcal{T}_a( \bar{\lambda}) = +\infty\). Consequently, \(0 < \alpha_{1} = \alpha_{a} = \alpha_{0} = + \infty\) is also not possible. \(L_{h}(\bar{\lambda}) < + \infty\), \(L_{a}(\bar{\lambda}) < + \infty\), \(\forall (\bar{\lambda} > 0)\). Therefore, we get \[\label{kk} \begin{array}{lll} & a_h I_{h}'' (z) – c I_{h}' (z) – (\mu+\gamma) I_{h} (z) +\beta_{ha}S_h^0 I_{a} (z)+ \beta_{hh} S_h^0 I_{h} (z ) \\ &\qquad=\beta_{ha } ((1 – S_{h} (z) I_{a} (z )) +\beta_{hh} (1- S_{h} (z )) I_{h} (z ) \\ &\qquad< \beta_{ha}S_h^0 I_{a} (z ) )+ \beta_{hh}S_h^0 I_{h} (z) ). \end{array}\tag{22}\] The same with \(I_a-equation\), \(\forall (\zeta \in \mathbb{R})\). Then we get
\[\begin{aligned} \label{n} \int_{-\infty}^{+\infty} e^{-\lambda z} I_{h} (z) \chi_{h} (\lambda) d z + \int_{-\infty}^{+\infty} e^{-\lambda z} I_{a} (z) \chi_{a} (\lambda) d z \leq 0, \quad \end{aligned}\tag{23}\] where \[\begin{aligned} \chi_{h} (\lambda) & := – m_{h} (\lambda, c) +\beta_{hh} S_h^0, \\ \chi_{a} (\lambda) & := – m_{a} (-\lambda, c) +\beta_{ha} S_h^0. \end{aligned}\]
However, letting \((\bar{\lambda} \rightarrow + \infty)\) in (23), that is a contradiction with the boundedness of the solution \((\lim_{\bar{\lambda} \rightarrow + \infty} \chi_{h} (\bar{\lambda}) = + \infty)\) and \((\lim_{\bar{\lambda} \rightarrow + \infty} \chi_{a} (\bar{\lambda}) = + \infty)\). ◻
In this section, we suppose that \(R_0>1\) and \(c > c^*\). The existence of a traveling wave solution is discussed through the following subsections.
For \(c > c^*\), we build a pair of upper and lower solutions of (12) by an iteration procedure. In particular, we build the \(S_{h,a}\)-component of the supper solution \(S_{h,a} ^+\) first, and then use that expression to build the \(V_h\)-component of the supper solution \(V_h^+\), and then use that expression to build the \(I_{h,a}\)-component of the supper solution \(I_i^+\) \((i=1,2)\). The lower solution \(S_{h,a}^-\) for \(S_{h,a}\)-component is then produced by using \(I_{h,a}^+\) in turn.The same for \(V_h^-\). Lastly, we build the \(I_{h,a}\)-component of the lower solution \(I_{h,a}^-\) using \(S_{h,a} ^-\). The concept behind such a building is
Definition 1. \((S_{h,a}^+, V_h^+, I_{h,a}^+)\) and \((S_{h,a}^-, V_h^-, I_{h,a}^-)\) stand for the pair of super- and sub-solutions of (11), respectively, and satisfy the following inequalities: \[ -c(S_h^+)'(z) + d_h (S_h^+)''(z) + \mathcal{L} – (\mu + \alpha) S_h^+(z) + \theta V_h^+(z) – \beta_{hh} S_h^+(z) I_h^-(z) – \beta_{ha} S_h^+(z) I_a^-(z) \leq 0, \tag{24}\] \[ -c(S_h^-)'(z) + d_h (S_h^-)''(z) + \mathcal{L} – (\mu + \alpha) S_h^-(z) + \theta V_h^+(z) – \beta_{hh} S_h^-(z) I_h^+(z) – \beta_{ha} S_h^-(z) I_a^+(z) \geq 0, \tag{25}\] \[ -c(S_a^+)'(z) + d_a (S_a^+)''(z) + A – \xi S_a^+(z) – \beta_{ah} S_a^+(z) I_h^-(z) – \beta_{aa} S_a^+(z) I_a^-(z) \leq 0, \tag{26}\]\[ -c(S_a^-)'(z) + d_a (S_a^-)''(z) + A – \xi S_a^-(z) + \alpha S_a^-(z) – \beta_{ah} S_a^-(z) I_h^+(z) – \beta_{aa} S_a^-(z) I_a^+(z) \geq 0, \tag{27}\]\[ c(V_h^+)'(z) = y_h (V_h^+)''(z) + \alpha S_h^+(z) – (\mu + \sigma + \theta) V_h^+(z) \leq 0, \tag{28}\]\[ c(V_h^-)'(z) = y_h (V_h^-)''(z) + \alpha S_h^-(z) – (\mu + \sigma + \theta) V_h^-(z) \geq 0, \tag{29}\]\[ -c(I_i^+)'(z) + q_i (I_i^+)''(z) + \beta_{ih} S_i^+(z) I_h^+(z) + \beta_{ia} S_i^+(z) I_a^+(z – c\tau) – (\mu_i + \gamma_i) I_i^+(z) \leq 0, \tag{30}\]\[ -c(I_i^-)'(z) + q_i (I_i^-)''(z) + \beta_{ih} S_i^-(z) I_h^-(z) + \beta_{ia} S_i^-(z) I_a^-(z) – (\mu_i + \gamma_i) I_i^-(z) \geq 0,\tag{31}\] except for finite points of \(z \in \mathbb{R}\).
In the remainder of this section, we assume that \(R_0 > 1\).
The following lemma illustrates the construction of the upper and lower solutions that satisfy (24)–(31).
Lemma 3. Suppose that \(R_0>1\), and \(c>c^*\). Let \[\begin{array}{lll} S_i^+(z)=S_i^0,& V_h^+(z)=V_h^0,,&I_i^+ = \kappa_i \exp^{\lambda_1 z}, \\ S_i^- = \max\biggl\{ 1-M_i\exp^{\rho z}, 0\biggr\},& V_h^- = \max\biggl\{ 1-K_i\exp^{\omega z}, 0\biggr\},&I_i^-(z)= \max\{\kappa_ie^{\lambda_1z}(1-J_ie^{\eta z}),0\}, \end{array}\] for some positive constants \(\gamma,J_i\) and \(M_i\) \((i=h,a)\) that will be determined later, then (24)–(31) are satisfied.
Proof. The proof is achieved through the following points
Clearly \(S_i^+ (z)= S_i^0\) satisfies \[\label{i} \begin{array}{rcl} -c(S_{h}^+)'(z) + d_h (S_h^+)''(z) +\Lambda – (\mu_i+\alpha) (S_h^+)(z)+\theta V_h^+(z)- \beta_{hh}S_i^+(z)I_h^-(z))-\beta_{ha}S_h^+(z)I_a^-(z) \leq 0,\\ -c(S_{a}^+)'(z) + d_a (S_a^+)''(z) +A – \xi (S_a^+)(z)- \beta_{ah}S_a^+(z)I_h^-(z))-\beta_{aa}S_a^+(z)I_a^-(z) \leq 0 \end{array}\] then, (24) and (26) are satisfied.
Clearly \(V_h^+ (z)= V_h^0\) satisfies \[\begin{array}{rcl} -c(V_h^+)'(z)= y_h (V_h^+)''(z)+\alpha S_{h}^+(z) -(\mu+\sigma+\theta) V_h^+(z) \leq 0 ,, \end{array}\] then, (28) is satisfied.
Clearly, for \(z<z_0\), with \(z_0=0\), we obtain \(I_i^+(z)=0\), Therefore, we have
\[-c(I_i^+)'(z) + q_i I_(i^+)''(z) + \beta_{ih} (S_i^+(z-c\tau))(z)I_h^+(z-c\tau)+\beta_{ia}S_i^+(z-c\tau)I_a^+(z-c\tau) – (\mu_i +\gamma_i)I_i^+(z)=0,\]
For \(z>z_0\), we obtain \(I_i^+ (z)= \kappa_i\exp^{\lambda_1 z}\), we show that \(I_i^+\) fulfills (30). It is easy to check that \[\begin{aligned} \label{6} -c(I_i^+)'(z) &+ q_i I_i(^+)''(z) + \beta_{ih}( S_i^+(z)I_h^+(z))+\beta_{ia}S_i^+(z) I_a^+(z) – (\mu_i +\gamma_i)I_i^+(z)\notag \\ &\leq -c(I_i^+)'(z) + q_i I_(i^+)''(z) +\beta_{ih}S_i^0 I_h^+(z)+\beta_{ia}S_i^0 I_a^+(z) – (\mu_i +\gamma_i)I_i^+(z)\notag\\ &= q_i\lambda_1^2\exp^{\lambda_1 z} + \beta_{ih}S_i^0 \kappa_h\exp^{\lambda_1 z}+\beta_{ia}S_i^0 \kappa_a\exp^{\lambda_1 z} – (\mu_i +\gamma_i)\kappa_i\exp^{\lambda_1 z}- c\kappa_i\exp^{\lambda_1 z}\notag\\ &= \exp^{\lambda_1 z} L(\lambda_1,c)\notag\\ & = 0, \end{aligned}\tag{32}\] by the definition of \(\lambda_1\) .
Choosing \(0 <\rho <\min\bigg\{ \lambda_1,\frac{c}{d_i}\bigg\}\). Suppose that \(z \neq \frac{1}{\rho}ln\frac{1}{M_i} := z^*\), and we claim that \(S_i^-\) satisfies \[ \begin{array}{rcl} -c(S_i^-)'(z) + d_i( S_i^-)''(z) +\Lambda_i- (\mu_i+\alpha) (S_i^-)(z)+\theta V_h^+(z)- \beta_{ih}S_i^-(z)I_h^+(z)-\beta_{ia}S_i^-(z)I_a^+(z) \geq 0,\\ -c(S_a^-)'(z) + d_a( S_a^-)''(z) +A – \xi+\alpha S_a^-(z)- \beta_{ah}(S_a^-(z)I_h^+(z))-\beta_{aa}(S_a^-(z), I_a^+(z)) \geq 0 . \end{array}\] We will prove the first equation and the second equation is in the same way. To prove this claim, we first suppose that \(z > z^*\), this implies that \(S_i^-(z) = 0\) in \((z^*,\infty)\), the inequality holds directly. If \(z < z^*\), we have \(S_i^-(z) = 1-M_ie^{\kappa z}\). Then, we have \(\beta_{ih}S_i^+(z)I_h^+(z)\leq \beta_{ih}S_i^0I_h^+(z)\) and \(\beta_{i2}S_i^+(z)I_a^+(z)\leq \beta_{i2}S_i^0I_a^+(z)\). Then, we have \[\begin{array}{rcl} &-c(S_h^-)'(z) + d_h( S_h^-)''(z) +\Lambda – (\mu+\alpha) (S_h^-)(z) +\theta V_h^+(z)- \beta_{hh}S_h^-(z)I_h^+(z)-\beta_{ha}S_h^-(z) I_a^+(z)\\ &\geq cM_h\rho \exp^{\rho z} -d_hM_h\rho^2 \exp^{\rho z} +(\mu+\alpha) M_h \exp^{\rho z}- \beta_{hh}S_h^0I_h^+(z) -\beta_{ha}S_h^0I_a^+(z)\\ &= cM_h\rho\exp^{\rho z} -d_hM_h\rho^2 \exp^{\rho z} +(\mu+\alpha) M_h \exp^{\rho z}- \beta_{hh}S_h^0\kappa_h\exp^{\lambda_1 z} – \beta_{ha}S_h^0\kappa_a\exp^{\lambda_1 z}\\ &=\exp^{\rho z}\bigg[ M_h\rho(c -d_h\rho) +(\mu+\alpha) M_i – \beta_{hh}S_h^0\kappa_h\exp^{(\lambda_1-\rho)z} -\beta_{ha}S_h^0\kappa_a\exp^{(\lambda_1-\rho)z}\bigg] \\ &\geq \exp^{\rho z}\bigg[ M_h\rho(c -d_h\rho)+(\mu+\alpha) M_h-\beta_{ia}S_h^0\kappa_h- \beta_{hh}S_h^0\kappa_a\bigg]\\ &\geq 0. \end{array}\] for \(M_h\) sufficiently large, and \(0 <\rho <\min\bigg\{ \lambda_1,\frac{c}{d_h}\bigg\}\). The claim is proved.
Choosing \(0 <\eta < \min\{\lambda_2-\lambda_1,\lambda_1\}\), and \(J_i>0\) sufficiently large. Then, we claim that \(I_i^-(z)\) satisfies \[\label{100} \begin{array}{lll} &-c(I_i^-)'(z) +q_i( I_i^-)''(z) + \beta_{ih}( S_i^-(z)I_h^-(z) + \beta_{ia}S_i^-(z) I_2^-(z)- (\mu_i +\gamma_i)I_i^-(z) \geq 0, \end{array}\] with \(z \neq z_2:=\frac{-ln J_i}{\eta}\).
We show this claim for two separated cases, that are, \(z >z_2\), and \(z <z_2\), respectively. If \(z >z_2\), thus \(I_i^-(z)=0\), which means that (33) is satisfied. If \(z < z_2\), we get \(I_i^-(z)= \kappa_ie^{\lambda_1z}(1-J_ie^{\eta z})\). In this case, we show that (33) holds for \(L\) sufficiently large, which it will be determined later. Notice that the inequality (33) can be expressed as follows \[\label{1c} \begin{array}{lllll} \beta_{ih}S_i^0I_h^-(z)+& \beta_{ia}S_i^0I_a^-(z) – \beta_{ih}S_i^-(z) I_h^-(z)-\beta_{ia} S_i(z I_a(z))\\&\leq -c(I_i^-)'(z) +q_i( I_i^-)''(z) \beta_{ih}S_i^0I_h^-(z)+ \beta_{ia}S_i^0I_a^-(z)- (\mu_i +\gamma_i)I_i^-(z)\\ &\leq -J_i p(\lambda_1+\eta, c)\kappa_i\exp^{(\lambda_1+\eta)z}. \end{array}\] For all \(\xi \in (0,max\{ \beta_{ih}S_i^0, \beta_{ia}S_i^0\})\), \(\beta_{ih}S_i\) and \(\beta_{ia} S_i(z)\) are a decreasing function on \((0,\infty)\). As \(I_i^-\) is a bounded function for \(z < z_2\), then there is \(\delta_0>0\) satisfies \(0 < I_i^- < \delta_0\) for all \(z < z_2\). The boundedness of \(I_i^-\) for \(z < z_2\), and the fact that \(\beta_{ih}S_i^0 , \beta_{ia}S_i^0>0\) implies the existence of \(\xi>0\) small as necessary in such a way the following inequality \[\beta_{ih}S_i^- \geq \beta_{ih}S_i^0-\xi>0,\] and \[\beta_{ia}S_i^- \geq\beta_{ia}S_i^0-\xi>0,\] hold for all \(0 < I_i^- < \delta_0\). Using the fact that \(0 < I_i^- < \delta_0\), we obtain
\[\label{101} \begin{array}{lllll} \beta_{ih}S_i^0I_h^-(z)+ \beta_{ia}S_i^0I_a^-(z) = \bigg( \beta_{ih}S_i^0I_h^-(z)+ \beta_{ia}S_i^0I_a^-(z)- \beta_{ih}S_i^-I_h^-(z)- \beta_{ia}S_i^-I_a^-(z),\\ \qquad \qquad \qquad \qquad \qquad \quad \leq \bigg(\frac{ \beta_{ih}S_i^0I_h^-(z)+ \beta_{ia}S_i^0I_a^-(z)- \beta_{ih}S_i^- – \beta_{ia}S_i^- +I_j^{-}(z)}{2}\bigg)^2\\\qquad \qquad \qquad \qquad \qquad \quad \leq \bigg[ \beta_{ih}S_i^-I_h^-(z)- \beta_{ia}S_i^-I_a^-(z)- \big( \beta_{ih}S_i^-I_h^-(z)-\xi – \beta_{ia}S_i^-I_a^-(z)-\xi \big);+I_j^{-}(z)^2\bigg]^2. \end{array}\]
Then, we have \[\beta_{ih}S_i^-I_h^-(z)+ \beta_{ia}S_i^-I_a^-(z)- \beta_{ih}S_i^-(z)I_h^-(z)-\beta_{ia}S_i^-(z)I_a^-(z) \leq (I_h^-(z))^2+ (I_a^-(z))^2.\] Therefore, to prove the inequality (33), it is sufficient to show that
\[\label{102} (I_h^-(z))^{2}+ (I_a^-(z))^{2}\leq -J_ip(\lambda_1+\eta, c)\kappa_i\exp^{(\lambda_1+\eta)z}.\tag{34}\] Noting that \(I_i^-\leq I_i^+\), then we have \((I_i^{-}(z))^2 \leq e^{2\lambda_1 z}\). To ensure (34), we show that \[\label{102d} e^{2\lambda_1 z} \leq -J_i p(\lambda_1+\eta, c)\kappa_i\exp^{(\lambda_1+\eta)z}.\tag{35}\] As the two sides of the inequality (35) are bounded for all \(z<z_2\), and both tends to \(0\) as \(z\to -\infty\), then the inequality (35) holds for \(J_i\) sufficiently large. The proof is completed.
◻
Next, for \(c > c^*\), we let the truncated problem
\[\label{tra11} \left\{ \begin{array}{lllll} cS'_h(z) = d_h S''_h(z)+\Lambda-\beta_{ha}S_{h}(z) I_{a}(z)-\beta_{hh}S_{h}(z) I_{h}(z)-(\mu+\alpha) S_{h}(z) + \theta V_h(z) \ \ z\in I_l =(-l,l) ,\\ cV'_h(z)= y_h V''_h(z)+\alpha S_{h}(z) -(\mu+\sigma+\theta) V_h(z) \ \ z\in I_l =(-l,l) , \\ cI'_h(z)= q_h I''_h(z)+\beta_{ha}S_{h}(z) I_{a}(z)+\beta_{hh}S_{h}(z) I_{h}(z)-(\mu +\gamma) I_{h}(z) \ \ z\in I_l =(-l,l) , \\ cS'_a(z)= d_a S''_a(z)+ A-\beta_{ah}S_{a}(z)I_{h}(z)-\beta_{aa}S_{a}(z)I_{a}(z)-\xi S_{a}(z) \ \ z\in I_l =(-l,l) , \\ cI'(z)= q_h I''_a(z)+ \beta_{ah}S_{a}(z)I_{h}(z)+\beta_{aa}S_{a}(z)I_{a}(z)-(\xi+\kappa )I_{a}(z), \ \ z\in I_l =(-l,l), \\ S_i(z) = S_i^-(z), V_h(z)= V_h^-(z), I_i(z) = I_i^-(z), \ \ z\in \mathbb{R}\setminus I_l, \end{array}\right .\tag{36}\] where \(l > -z_2\). We define the following spaces \[\mathcal{X} = C(\mathbb{R}) \times C(\mathbb{R}) \ \ \ \mbox{and}\ \ \mathcal{Y}= C^1(I_l) \times C^1(I_l).\] The Schauder fixed point theorem will be utilized to demonstrate the existence of a pair of functions \((S_i, V_h, I_i) \in X\cap Y\) that fulfill (36). Firstly, we define \[\label{e} \mathcal{E} = \{(S_i, V_h, I_i)\in \mathcal{X} / S_i^-\leq S_i\leq S_i^+ \ \ V_h^-\leq V_h\leq V_h^+ ~~\mbox{and}~~ I_i^- \leq I_i \leq I_i^+ ~~\mbox{in}~~ \mathbb{R}\},\tag{37}\] that is a closed convex set \(X\) equipped with the norm \(\|(f_1, f_2)\|_\mathcal{X} = \|f_1\|_{C(\mathbb{R})} + \|f_2\|_{C(\mathbb{R})}\). Then, we let \(\mathcal{F}:E\rightarrow E\) such that for all \(((S_i)_0,( V_h) _0, (I_i)_0) \in E\), \[\mathcal{F}((S_i)_0, ( V_h) _0, (I_i)_0) = (S_i, V_h, I_i),\] with \((S_i, I_i) \in X \cap Y\) that solves \[\label{tra2} \left\{ \begin{array}{llll} cS'_h(z) = d_h S''_h(z)+\Lambda-\beta_{ha}S_{h}(z) (I_{a})_0(z)-\beta_{hh}S_{h}(z) (I_{h})_0(z)-(\mu+\alpha) S_{h}(z) + \theta (V_h)_0(z) \ \ z\in I_l =(-l,l) ,\\ cV'_h(z)= y_h V''_h(z)+\alpha S_{h}(z) -(\mu+\sigma+\theta) V_h(z) \ \ z\in I_l =(-l,l) , \\ cI'_h(z)=q_h I''_h(z)+\beta_{ha}(S_{h})_0(z) (I_{a})_0(z)+\beta_{hh}(S_{h})_0(z) (I_{h})_0(z)-(\mu +\gamma) I_{h}(z) \ \ z\in I_l =(-l,l) , \\ cS'_a(z)= d_a S''_a(z)+ A-\beta_{ah}S_{a}(z)(I_{h})_0(z)-\beta_{aa}S_{a}(z)(I_{a})_0(z)-\xi S_{a}(z) \ \ z\in I_l =(-l,l) , \\ cI'(z)= q_h I''_a(z)+ \beta_{ah}(S_{a})_0(z)(I_{h})_0(z)+\beta_{aa}(S_{a})_0(z)(I_{a})_0(z)-(\xi+\kappa )I_{a}(z), \ \ z\in I_l =(-l,l) ,\\ S_i(z) = S_i^-(z), V_h(z)= V_h^-(z), I_i(z) = I_i^-(z), \ \ z\in \mathbb{R}\setminus I_l. \end{array}\right .\tag{38}\] Any fixed point of \(\mathcal{ F}\) is the pair \((S_i, I_i) \in \mathcal{X} \cap \mathcal{Y}\) that fulfill (38). Here, we shall confirm that the \(\mathcal{ F}\) meets the Schauder fixed point theorem’s conditions.
Lemma 4. For any \(((S_h)_0,(S_a)_0, (V_h)_0, (I_h)_0 (I_a)_0) \in E\), there is a unique solution \((S_h, S_a,V_h,I_h, I_a) \in \mathcal{X} \cap \mathcal{Y}\) fulfilling ((36)). Furthermore, \((S_h, S_a,V_h I_h, I_a)\in \mathcal{E}\) with \(i=1,2\).
Proof. As (38) is a system of decoupled inhomogeneous linear equations, then the existence and uniqueness of solutions to the (38) can be obtained from Theorem 3.1 in Chapter 12 of [7]. Moreover, since \(-cS'_h(z)+ d_h S''_h(z)-\beta_{ha}S_{h}(z) (I_{a})_0(z)-\beta_{hh}S_{h}(z) (I_{h})_0(z)-(\mu+\alpha) S_{h}(z) + \theta (V_h)_0(z) = -\Lambda \leq 0\) and \(-cS'_a(z)+ d_a S''_a(z)-\beta_{ah}S_{a}(z)(I_{h})_0(z)-\beta_{aa}S_{a}(z)(I_{a})_0(z)-\xi S_{a}(z) \leq A \leq 0\) on \(I_l\) and \(S_i(\pm l) = S_i^-(\pm l)\geq 0\), thus \(S > 0\) on \(I_l\) (by the maximum principle). Similarly, we get \(I_i > 0\) over \(I_l\). Next, we prove that \(S_i^-\leq S_i \leq S_i^+\) in \(I_l\). By the second equation of (36) and \((I_i)_0 \leq I_i^+\), we arrive at \[\begin{array}{rcl} -cS'_h(z)+ d_h S''_h(z)+\Lambda-\beta_{ha}S_{h}(z) (I_{a})_0(z)-\beta_{hh}S_{h}(z) (I_{h})_0(z)-(\mu+\alpha) S_{h}(z) + \theta (V_h)_0(z) \leq& 0 \end{array}\] and \[\begin{array}{rcl} -cS'_a(z)+ d_a S''_a(z)-\beta_{ah}S_{a}(z)(I_{h})_0(z)-\beta_{aa}S_{a}(z)(I_{a})_0(z)-\xi S_{a}(z) + A \leq& 0. \end{array}\] Together with (1), we notice that \((w_h)_1 = S_h- S_h^-\) verifies \(d_h (w_h)_1''(z) -c(w_h)_1'(z) -(\mu + \alpha+ \beta_{hh}I_h^+(z )+ \beta_{ha}I_a^+(z ))(w_h)_1(z)+\theta V_h^+(z) \leq 0\) and \((w_a)_1 = S_a- S_a^-\) verifies \(d_a (w_a)_1''(z) -c(w_a)_1'(z) -(\xi + \beta_{ah}I_h^+(z )+ \beta_{aa}I_a^+(z ))(w_a)_1(z) \leq 0\). In addition, from the third line of (36) and the fact \(S_i(z_1) > 0\) and \(S_i^-(z_0) = 0\), it is known that \((w_i)_1(z) > 0\) and \((w_i)_1(l) = 0\). Hence, the maximum principle gives \((w_i)_1\geq 0\) in \((-l, z_0)\), that implies \(S^- \leq S\) . Together with \(S_i^- = 0\) in \([z_1, l)\), yields \(S_i^-\leq S\) in \(I_l\). Next, showing that \(S_i \leq S_i^+\) , \(V_h \leq V_h^+\) in \(I_l\). Since \((I_i)_0 \geq I_i^-\), it follows that \[\begin{array}{rcl} -c(S_h)'(z) + d_h (S_h)''(z) +\Lambda -( \mu + \alpha) S_h(z)-\beta_{hh}S_h(z)I_h(z)-\beta_{ha}S_h(z)I_a(z) + \theta V_h(z) &\geq& 0 \ \ \mbox{in} \ \ I_l, \end{array}\] and \[\begin{array}{rcl} -c(S_a)'(z) + d_a (S_a)''(z) +A – \xi S_a(z)-\beta_{ah}S_a(z)I_h(z)-\beta_{aa}S_a(z)I_a(z) &\geq& 0 \ \ \mbox{in} \ \ I_l. \end{array}\] Similarly with the equation of \(S_h\) and \(S_a\) we get \(V_h(\pm l) \leq V_h^+(\pm l)\). Noting \(S_i(\pm l) \leq S_i^+(\pm l)\), then, by the maximum principle yield \(S_i \leq S_i^+\) in \(I_l\). Next, claiming that \(I_i^- \leq I_i \leq I_i^+\) in \(I_l\). Since \[\beta_{ih}S_i^-(z)I_h^-(z) \leq \beta_{ih}(S_i)_0(z)(I_h)_0(z) \leq \beta_{ih}S_i^+(z)I_h^+(z ),\] and \[\beta_{ia}S_i^-(z)I_a^-(z) \leq \beta_{ia}(S_i)_0(z)(I_a)_0(z) \leq \beta_{ia}S_i^+(z)I_a^+(z ),\] it follows that \[q_i I_i''(z) – cI_i'(z) +\beta_{ih}S_i^+(z)I_h^+(z)+ \beta_{ia}S_i^+(z)I_a^+(z )- (\mu_i +\gamma_i)I_i(z) \leq 0\] and \[q_i I_i''(z) – cI_i'(z) +\beta_{ih}S_i^+(z)I_h^+(z)+ \beta_{ia}S_i^+(z)I_a^+(z )- (\mu_i +\gamma_i)I_i(z) \geq 0 ,~~z\in I_l.\] Let \((w_i)_2 = I_i -I_i^-\). By the second equation of (36) and \(I_i(z^*) > 0\), \(I_i^-(z^*)\) = 0, we have \((w_i)_2(z^*) > 0\), \((w_i)_2(-l)\) = 0. Also, both 33, and \[q_i I_i''(z) – cI_i'(z) +\beta_{ih}S_i^+(z)I_h^+(z)+ \beta_{ia}S_i^+(z)I_a^+(z )- (\mu_i +\gamma_i)I_i(z) \leq 0,\] gives that \[(w_i)_2''(z) + c(w_i)_2'(z) – (\mu_i + \gamma_i)(w_i)_2(z) \leq 0,~~z \in (-l, z_2).\] Therefore, the maximum principle ensures that \((w_i)_2 \geq 0\) in \((-l, z^*)\), which means \(I_i^- \leq I_i\) in \((-l, z_2)\). Together with \(I_i^- = 0 \leq I_i\) in \([z_2, l)\), then \(I_i^- \leq I_i\) in \(I_l\). To prove \(I_i\leq I_i^+\) on \(I_l\), we let \(\bar{I}_i(z) = \kappa_i\exp^{\lambda_1z}\) satisfies
\[q_i\bar{I}_i''(z)-c\bar{I}_i'(z) + \beta_{ih}S_i^+(z)\bar{I}_h(z )+ \beta_{ia}S_i^+(z)\bar{I}_a(z ) -(\mu_i + \gamma_i)\bar{I}_i(z) = 0 \ \ \mbox{ in}\ \ I_l.\] Since \(\beta_{ih}(S_i)_0(z)(I_h)_0(z) \leq \beta_{ih}S_i^+(z)\bar{I}_h(z )\) and \(\beta_{ia}(S_i)_0(z)(I_a)_0(z) \leq \beta_{ia}S_i^+(z)\bar{I}_a(z )\), it follows that \[q_i I_i''(z)-cI_i'(z) \beta_{ih}S_i^+(z)\bar{I}_h^+(z)+ \beta_{ia}S_i^+(z)\bar{I}_a^+(z ) -(\mu_i + \gamma_i)I_i(z) \geq 0 \ \ \mbox{ in}\ \ I_l.\] Notice that \(I_i(\pm l) \leq \kappa_i \exp^{\lambda_1 z}\). The maximum principle implies \(I_i \leq \kappa_i \exp^{\lambda_1 z}\) in \(I_l\). Further, as \(I_i^+(z) = \kappa_i\exp^{\lambda_1 z}\) in \([z_0, l)\), then \(I_i \leq I_i^+\) in \([z_0, l)\). To show \(I_i \leq I_i^+\) in \((-l, z_0]\), notice that \(I_i(-l) \leq I_i^+(-l)\) and \(I_i(z_0) \leq \kappa_i\exp^{\lambda_1 z} = I_i^+(z_0)\). This result, (32), \[q_i I_i''(z)- cI_i'(z) + \beta_{ih}S_i^+(z)I_h^+(z)+ \beta_{ia}S_i^+(z)I_a^+(z ) -(\mu_i + \gamma_i)I_i(z) \geq 0\] and the maximum principle, we obtain \(I_i \leq I_i^+\) in \((-l, z_0]\). ◻
Before starting on showing the existence of a fixed point, we consider an axillary result that will be helpful in the proof of the existence of the fixed point, and the traveling wave solution. Letting the following problem \[\label{44} \begin{array}{rcl} w''(z) – Aw'(z)+f(z)w(z) = h(z) \end{array}\tag{39}\] with \(A\) is a positive constant, and \(f,h\in C([a,b])\), with \([a,b]\) is an arbitrary interval of \(\mathbb{R}\). The following lemma is the result of Lemma 3.1-3.3 in [8].
Lemma 5. Suppose that \(w \in C([a, b]) \cap C^2((a, b))\) satisfies the differential equation (39) in \((a, b)\) with the boundary conditions \(w(a) = w(b) = 0\). If \[-C_1 \leq f \leq 0 \ \ \mbox{and} \ \ | h| \leq C_2 \ \ \mbox{on} \ \ [a,b],\] for some constants \(C_1, C_2>0\), then there exists a positive constant \(C_3\), depending only on \(A\), \(C_1\), and \((b-a)\), such that \[\|w \|_{C([a,b])} +\|w'\|_{C([a,b])} \leq C_3.\]
Finally, it is possible to confirm that the mapping \(\mathcal{F}\) is continuous and precompact by arguing as the proofs of Lemma 4.4-4.5 in [8] and utilizing lemma 5. The fixed point \(((S_i)_l,( V_h)_l (I_i)_l) \in \mathcal{X}\cap \mathcal{Y}\) for \(\mathcal{F}\) is then determined by using the Schauder fixed point theorem. This pair satisfies (36) and \(S_i^-\leq (S_i)_l \leq S_i^+\), \(V_h^-\leq (V_h)_l \leq V_h^+\) and \(I_i^-\leq( I_i)_l \leq (I_i)^+\) on \(\mathbb{R}\). For the truncated problem (36), the existence result is as follows, based on the description above.
Lemma 6. There is \(((S_i)_l, (V_h)_l, (I_i)_l) \in \mathcal{X} \cap \mathcal{Y}\) satisfying (36). Moreover, \[0 \leq (S_i)^- \leq (S_i)_l \leq (S_i)^+ =S_i^0, \ \ 0 \leq (V_h)^- \leq (V_h)_l \leq (V_h)^+ =V_h^0 \ \ \mbox{and}\ \ 0 \leq I_i^- \leq( I_i)_l \leq I_i^+ \leq \mathcal{B}\] on \(\mathbb{R}\).
Lemma 7. There is \(((S_i)_l, (I_i)_l) \in \mathcal{X} \cap \mathcal{Y}\) satisfying (12). Moreover, \[0 \leq (S_i)^- \leq (S_i)_l \leq (S_i)^+ =1 \ \ \mbox{and}\ \ 0 \leq I_i^- \leq( I_i)_l \leq I_i^+ \leq \mathcal{B}\] on \(\mathbb{R}\).
In this step, we use the solution \(((S_i)_l,(V_h)_l, (I_i)_l)\) of (12) to show that \((S_i^+,V_h^+,I_i^+)\), and \((S_i^-,V_h^-,I_i^-)\) are the upper and lower solution of (12), respectively. Also, we will show that \((S_i,V_h,I_i)\to(S_i^+,V_h^*,I_i^*)\) as \(z\to +\infty\) by constructing a Lyapunov function with \(i=h,a\). At first, we show that
Lemma 8. The solution \((S_i,V_h,I_i)\) of the system (12) satisfies \((S_i,V_h,I_i)\in \mathcal{E}\) and is defined by (37). Moreover, \[0<S_i<S_i^0, \ \ 0<V_h<V_h^0,~~0<I_i< \kappa_i\exp^{\lambda_1 z},\] for all \(z\in \mathbb{R}\).
Proof. Let \(\{l_n\}_{n} \in \mathbb{N}\) be an increasing sequence in \((z_2,\infty)\) such that \(l_1 > \max\{-z_2, |z_0|\}\) and \(l_n \rightarrow +\infty\), and let \(((S_i)_n,(V_h)_n, (I_i)_n)\in \mathcal{X} \times \mathcal{Y}\), \(n \in \mathbb{N}\), solving (12) with \(l = l_n\) and 7 on \(\mathbb{R}\). For any \(N \in \mathbb{N}\), we have \[\{(S_i)_n\}_{n \geq N}, \ \ \mbox{ }\ \ \{(V_h)_n\}_{n \geq N}, \ \ \mbox{ }\ \ \{(I_i)_n\}_{n\geq N},\] are uniformly bounded in \([-l_N, l_N]\), we can use Lemma 5 to ensure that \[\{(S_i)'_n\}_{n\geq N}, \ \ \mbox{ }\ \ \{(V_h)'_n\}_{n \geq N}, \ \ \mbox{ }\ \ \{(I_i)'_n\}_{n\geq N}\] are also uniformly bounded in \([-l_N, l_N]\). By (12), we have that \((S_i)''_n\), \((V_h)''_n\) and \((I_i)''_n\) can be written terms of \((S_i)_n,(V_h)_n,( I_i)_n, (S_i)'_n\), \((V_h)'_n\) and \((I_i)'_n\). This means that \((S_i)''_n\), \((V_h)''_n\) and \((I_i)''_n\) are uniformly bounded in \([-l_N, l_N]\). By a differentiation of the equations of (12), and utilizing the boundedness of \((S_i)''_n\),\((V_h)''_n\), \((I_i)''_n\), \((S_i)_n,(V_h)_n (I_i)_n, (S_i)'_n, (V_h)'_n\), \((I_i)'_n\), we can ensure that \[\{(S_i)''_n\}_{n\geq N}, \{(V_h)''_n\}_{n\geq N}, \{(I_i)''_n\}_{n\geq N}, \{(S_i)'''_n\}_{n\geq N}, \ \ \{(V_h)'''_n\}_{n\geq N} \ \ \mbox{and} \ \ \{(I_i)'''_n\}_{n\geq N}\] are uniformly bounded in \([-l_N, l_N]\). The Arzela-Ascoli theorem, and diagonal process ensure that there is a subsequence \(\{((S_i)_{n_j}, (V_h)_{n_j}, (I_i)_{n_j} )\}\) of \(\{((S_i)_n, (V_h)_{n}, (I_i)_n)\}\) satisfies \[(S_i)_{n_j}\longrightarrow (S_i), (S_i)'_{n_j}\longrightarrow (S_i)',(S_i)''_{n_j}\longrightarrow (S_i)'',\] \[(V_h)_{n_j}\longrightarrow (V_h), (V_h)'_{n_j}\longrightarrow (V_h)',(V_h)''_{n_j}\longrightarrow (V_h)'',\] and \[(I_i)_{n_j}\longrightarrow I_i, (I_i)'_{n_j}\longrightarrow (I_i)',(I_i)''_{n_j}\longrightarrow (I_i)'',\] uniformly in any compact interval of \(\mathbb{R}\) as \(n \longrightarrow \infty\), for some \(S_i,V_h,I_i\) in \(C^2(\mathbb{R})\). the definitions of \(S_i^{\pm}\), \(V_h^{\pm}\) and \(I_i^{\pm}\) implies that \((S_i,V_h, I_i)\to (S_i^0, V_h^0,0)\) as \(z\to -\infty\). Next, we claim that \(0 < S_i < S_i^0\), \(0 < V_h < V_h^0\) and \(0 < I_i < \mathcal{B}_i\) on \(\mathbb{R}\). We prove this result by contradiction, we let \(I_i(\tilde{z}_2)\) = 0 for some \(\tilde{z}_2 \in \mathbb{R}\). Thus \(I_i(\tilde{z}'_2)\) = 0. Hence \(I_i \equiv 0\) (by the uniqueness), that is a contradiction with \(I_i \geq I_i^- >0\) on \((-\infty, z_2)\). To show that \(S_i < 1\) on \(\mathbb{R}\), assume by contradiction that \(S_i(\tilde{z}_3) = S_i^0\) for some \(\tilde{z}_3\in \mathbb{R}\). Then, \(S_i'(\tilde{z}_3)\) = 0 and \(S_i''(\tilde{z}_3) \leq 0\) and \(V_h(\tilde{z}_6) = V_h^0\) for some \(\tilde{z}_6\in \mathbb{R}\). Then, \(V_h'(\tilde{z}_6)\) = 0 and \(V_h''(\tilde{z}_6) \leq 0\).. Also a contradiction with the first and third equation of (12) \(z =\tilde{z}_3\), \(z =\tilde{z}_6\) and . The proof is complete. ◻
Remark 1. The first and second equations of (11) and the boundary conditions (13) . We have already shown that \(S_i, I_i\) are bounded for all \(z \in \mathbb{R}\).
The next step is to show that \(S_i', V_h', I_i'\) are also bounded. This will be used to prove \((S_i,V_h, I_i) \rightarrow (S_i^*,V_h^*, I_i^*)\) as \(z \rightarrow +\infty\) by using the Lyapunov-LaSalle Theorem. To prove the existence of non-critical traveling wave, we need to prove that \((S_h,S_a,V_h,I_h, I_a)\to (S_h^*,S_a^*,V_h^*,I_h^*,I_a^*)\) as \(z\to\infty\) by applying the Lyapunov-LaSalle Theorem. We define \[E= \left\{\begin{array}{lllllll} S_h(.),S_a(.),V_h(.),I_h(.), I_a(.) \in C^1(\mathbb{R}, (0, +\infty))\times C^1 (\mathbb{R}, (0, +\infty)),\\ S_h(.) > 0, \ \ S_a(.)> 0,\ \ V_h(.)> 0 ,\ \ I_h(.)> 0, \ \ I_a(.)> 0\\ \exists M> 0,\ \ \ \ \bigg|\frac{I_h'(z)}{I_h(z)}\bigg|+\bigg|\frac{I_a'(z)}{I_a(z)}\bigg| \leq M \end{array} \right\}.\] We construct the Lyapunov functional. \[\label{vv} \begin{array}{lllllll} V(z) =& c\bigg(S_{h}^{*}h(\frac{S_{h}(z)}{S_{h}^{*}}) +V_{h}^{*}h(\frac{V_{h}(z)}{V_{h}^{*}})+ I_{h}^{*}h(\frac{I_{h}(z)}{I_h^{*}}) + CS_{a}^{*}h(\frac{S_{a}(z)}{S_{a}^{*}}) + CI_{a}^{*}h(\frac{I_{a}(z)}{I_{a}^{*}})\bigg) \\ &-d_h S_h'(z)\bigg(1-\frac{S_h^*,}{S_h(z)}\bigg) -d_a S_a'(z)\bigg(1-\frac{S_a^*,}{S_a(z)}\bigg)-y_h V_h'(z)\bigg(1-\frac{V_h^*,}{V_h(z)}\bigg)\\ &-q_h I_h'(z)\bigg(1-\frac{I_h^*}{I_h(z)}\bigg)-q_a I_a'(z)\bigg(1-\frac{I_a^*}{I_a(z)}\bigg) \end{array}\tag{40}\] with \(h(x) = x – 1 – ln(x)\); \(x \in \mathbb{R}^+\), clearly \(h(x)>0\) for all \(x>0\). Then we claim the below lemma
Lemma 9. Let( \(\textbf{A}\)) be satisfied and \((S_h(.),S_a(.),V_h(.),I_h(.), I_a(.))\) be a positive solution of system (12) satisfying \[ \frac{1}{N} \leq S_i(z)\leq S_i^*,\tag{41}\]\[ V_h \leq N V_h^*, \tag{42}\] \[ I_i(z) \leq N I_i^*, \tag{43}\] and \[\begin{aligned} \bigg|\frac{I_h'(z)}{I_h(z)}\bigg|+\bigg|\frac{I_a'(z)}{I_a(z)}\bigg| \leq N,\label{gg} \end{aligned}\tag{44}\] for any \(z \in \mathbb{R}\) and \(i=h,a\), where \(N\) is a positive constant. Then, there exists a constant \(m > 0\) depending on \(N\), such that \[-m \leq V(z)< +\infty,\ \ \ \forall z \in \mathbb{R}.\] Where the map \(V(z)\) is defined as a formula (40). Moreover, the map \(V(z)\) is not increasing. In particular, \((S_h,S_a,V_h,I_h, I_a)\to (S_h^*,S_a^*,V_h^*,I_h^*,I_a^*)\) uniformly as \(z\to +\infty\). as the map \(V(z)\) is a constant.
Proof. The previous description has shown \(S_h\) and \(S_a\) are bonded in \(C^2(\mathbb{R})\). Via inequalities (41)–(44), we have \[\begin{array}{rcl} V^{'}(z) &=& \bigg(1-\frac{S_h^*}{S_h(z)}\bigg)(cS_h'(z) – d_h S_h''(z)) +\bigg(1-\frac{S_a^*}{S_a(z)}\bigg)(cS_a'(z) – d_a S_a''(z)) +\bigg(1-\frac{V_h^*}{V_h(z)}\bigg)(cV_h'(z) \\&&- y_h V_h''(z))+ \bigg(1-\frac{I_h^*}{I_h(z)}\bigg)(cI_h'(z)-q_h I_h''(z))+ \bigg(1-\frac{I_a^*}{I_a(z)}\bigg)(cI_a'(z)-q_a I_a''(z)) \\&&-d_h\frac{(S_h'(z))^2}{S_h^*}\bigg(\frac{S_h^*}{S_h(z)}\bigg)^2-d_a\frac{(S_a'(z))^2}{S_a^*}\bigg(\frac{S_a^*}{S_a(z)}\bigg)^2-y_h\frac{(V_h'(z))^2}{V_h^*}\bigg(\frac{V_h^*}{V_h(z)}\bigg)^2 -q_h\frac{(I_h'(z))^2}{I_h^*}\bigg(\frac{I_h^*}{I_h(z)}\bigg)^2 \\&&-q_a\frac{(I_a'(z))^2}{I_a^*}\bigg(\frac{I_a^*}{I_a(z)}\bigg)^2. \end{array}\]
By the proof of second part of Theorem 2, we obtain
\[\begin{array}{llll} V'(z) =&\mu S_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(z)}\bigg)-h\bigg(\frac{S_h(z)}{S_h^*}\bigg)\bigg) + \beta_{ha }S_h^* I_a^*\bigg[-h\bigg(\frac{S_h^*}{S_h(z)}\bigg)-h\bigg(\frac{S_h(z)I_a(z)I_h^*}{S_h^*I_a^* I_h(z)}\bigg)\\&-h\bigg(\frac{S_a^*}{S_a(z)}\bigg)-h\bigg(\frac{S_a(z)I_h(z)I_a^*}{S_a^*I_h^*I_a(z)}\bigg)\bigg] +\beta_{hh }S_h^* I_h^*\bigg(-h\bigg(\frac{S_h^*}{S_h(z)}\bigg)-h\bigg(\frac{S_h(z)}{S_h^*}\bigg)\bigg)-\alpha S_h^*h\bigg(\frac{S_h(z)V_h^*}{S_h^* V_h(z)}\bigg) \\&-\theta V_h^*h\bigg(\frac{V_h(z)S_h^*}{V_h^*S_h(z)}\bigg) -(\mu+\sigma) V_a^*\bigg[h\bigg(\frac{S_h^*}{S_h(z)}\bigg)+h\bigg(\frac{V_h(z)}{V_h^*}\bigg)\bigg]+\frac{\beta_{ha }S_h^*I_h^*}{\beta_{ah} S_a^*I_h^*}(\xi+\beta_{aa}I_a^*) S_a^*\bigg(-h\bigg(\frac{S_a^*}{S_a(z)}\\&-h\bigg(\frac{S_a(z)}{S_a^*}\bigg)\bigg)-d_h\frac{(S_h'(z))^2}{S_h^*}\bigg(\frac{S_h^*}{S_h(z)}\bigg)^2-d_a\frac{(S_a'(z))^2}{S_a^*}\bigg(\frac{S_a^*}{S_a(z)}\bigg)^2-y_h\frac{(V_h'(z))^2}{V_h^*}\bigg(\frac{V_h^*}{V_h(z)}\bigg)^2 -q_h\frac{(I_h'(z))^2}{I_h^*}\bigg(\frac{I_h^*}{I_h(z)}\bigg)^2 \\&-q_a\frac{(I_a'(z))^2}{I_a^*}\bigg(\frac{I_a^*}{I_a(z)}\bigg)^2\\ \leq& 0. \end{array}\]
Hence, \(V(z)\leq 0\), and \(V(z)= 0\) if and only if \(S_h= S_h^*\), \(S_a= S_a^*\),\(V_h=V_h^*\), \(I_h =I_h^*\) and \(I_a =I_a^*\).
Finally, we deduce that \((S_h,S_a,V_h,I_h, I_a)(\infty)= (S_h^*,S_a^*,V_h^*,I_h^*,I_a^*)\), We let the set \(D\) corresponding to (11) as follows: \[\begin{array}{lllll} D =& \bigg\{(S_h,S_a,V_h,I_h, I_a)|0 < S_h < S_h^0, ~~0 < S_a < S_a^0, ~~0 < V_h < V_h^0, ~~0 < I_h < I_h^+,~~0 < I_a < I_a^+, ~~ \\&-L_1 S_i(z) < S_i'(z) < L_2 S_i(z),\ \ \ \ -L_3 V_h(z) < V_h'(z) < L_4V_h(z),~~-L_5 I_i(z) < I_i'(z) < L_6 I_i(z).\bigg\}.\end{array}\] Then, Lemma 9 implies that \(D\) is is positively invariant for (12), for all \(z\geq0\). Remember that \(L\) has a non-positive orbital derivative along \(\varPsi(z)\). Furthermore, \(L\) is clearly continuous and bounded below on \(D\). This, and the Lyapunov-LaSalle Theorem indicates that \(\varPsi(z) \rightarrow (S_1^*,S_2^*,I_1^*,I_2^*)\) as \(z\rightarrow \infty\), and as a result, \((S_h,S_a,V_h,I_h, I_a)\to (S_h^*,S_a^*,V_h^*,I_h^*,I_a^*)\) as \(z\to+\infty\). This concludes the proof. ◻
It worth noting that Lemma 8 implies that the solution of (12) satisfies \(S_i^-\leq S_i\leq S_i^+\), and \(I_i^-\leq I_i\leq I_i^+\), and \((S_h,S_a,V_h,I_h, I_a)\to (S_1^0,S_2^0, V_h^0,0 ,0)\) as \(z\to – \infty\). By Lemma 9, we have \((S_h,S_a,V_h,I_h, I_a)\to (S_h^*,S_a^*,V_h^*,I_h^*,I_a^*)\) as \(z\to + \infty\). Therefore, we deduce that the system (11) admits a unique positive solution that satisfies the boundary conditions (13), which is the TWS of the system (11).
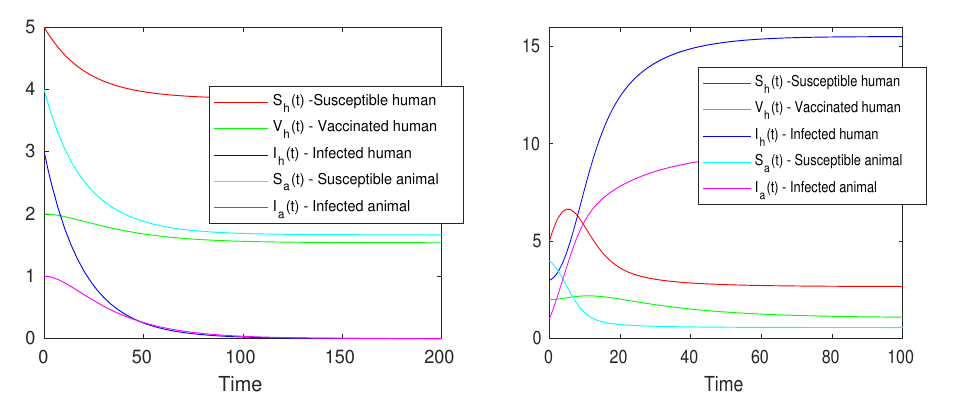
In this section, we investigate the model (2) numerically to determine the effect of the vaccination of the humans on the temporal behavior of the Monkeypox disease. In this simulation, we will focus only of the infected classes which have a direct effect on the evolution of the disease. In this figure, we consider the following set of parameters \[\mu = 0.01, \alpha = 0.02, \theta = 0.01; % \sigma = 0.03; % \gamma = 0.05; % \xi = 0.03; \kappa = 0.02;\] and the initial data \[S_h(0)=5,V_h=2,~S_a(0)=4,~I_h(0)=3,~I_a(0)=1,\] and for the right hand figure, we consider that \(\beta_{ha} = 0.02; \beta_{hh} = 0.01, \beta_{ah} =0.3, \beta_{aa} = 0.04\). In this case, we get \(R_0>1\). However, for \(\beta_{ha} = 0.002; \beta_{hh} = 0.001, \beta_{ah} =0.03, \beta_{aa} = 0.004\) Then, we obtain \(R_0<1\).
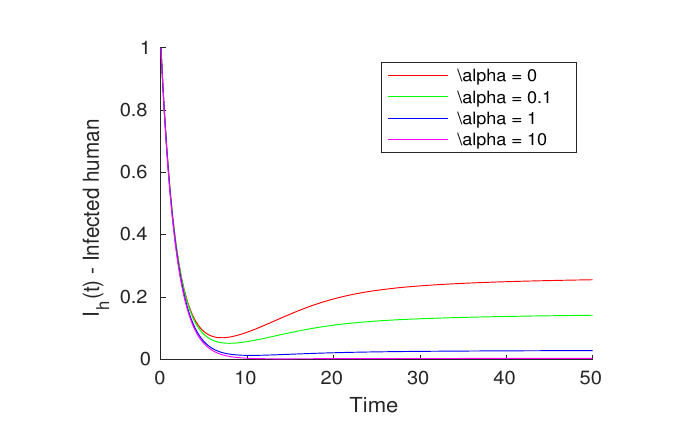
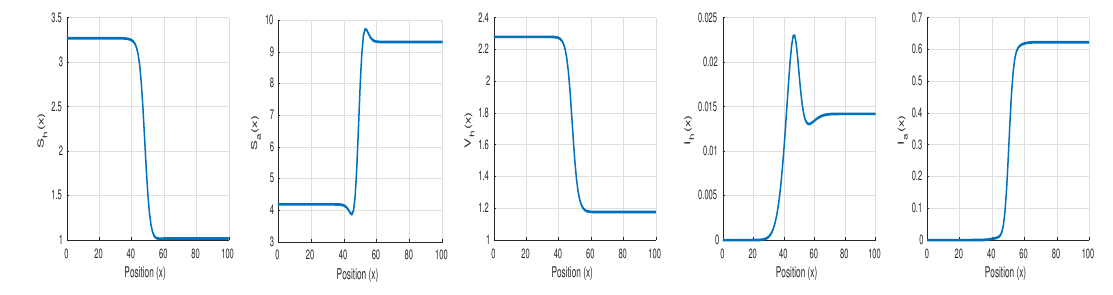
In this figure, we look at how vaccination rates affect the sick human population. As the “\(\alpha\)” parameter grows, the vulnerable human population falls quicker owing to increased vaccination rates. A higher “\(\alpha\)” value implies a more successful immunisation measure, limiting transmission of illness.
The graphic shows the development of the infected human population over time \((I_h(t))\). As “\(\alpha\)” grows, the infected population drops faster. Overall, raising the “\(\alpha\)” parameter stringent vaccination policy, which can assist minimise the spread of the virus by lowering the number of vulnerable and infected humans over time. Now, we focusing on the traveling wave solutions of system (11), we perform some numerical simulations. We also, consider the following initial conditions \[(S_h)_0(x)=\left\{\begin{array}{ll} 3.2&\text{ if }x\in [0,50],\\ 0.9&\text{ if }x\in [50,100[, \end{array} \right. \ \ \ ( V_h)_0(x)=\left\{\begin{array}{ll} 2.3&\text{ if }x\in [0,50],\\ 1&\text{ if }x\in [50,100[, \end{array} \right.\] \[(I_h)_0(x)=\left\{\begin{array}{ll} 0&\text{ if }x\in [0,50],\\ 0.01&\text{ if }x\in[50,100[, \end{array} \right.\ \ \ (S_a)_0(x)=\left\{\begin{array}{ll} 4&\text{ if }x\in [0,50],\\ 9&\text{ if }x\in [50,100[, \end{array} \right.\] \[(I_a)_0(x)=\left\{\begin{array}{ll} 0&\text{ if }x\in[0,50],\\ 0.6&\text{ if }x\in [50,100[, \end{array} \right.\]