In normed spaces, Birkhoff orthogonality and isosceles orthogonality can be used to characterize space structures, and many scholars have introduced geometric constants to quantitatively describe the relationship between these two types of orthogonality. This paper introduces a new orthogonal relationship – Skew orthogonality – and proposes a new geometric constant to measure the “distance” of difference between skew orthogonality and Birkhoff orthogonality in normed spaces. In the end, we provide some examples of specific spaces.
We consider a real normed space \(X\) with \(\operatorname{dim} X \geq 2\), equipped with the norm \(\|\cdot\|\), the unit ball denoted by \(B_X\), and the unit sphere denoted by \(S_X\). In the context of inner product spaces, orthogonality \((x \perp y)\) between elements \(x\) and \(y\) is defined when their inner product is zero. This concept of orthogonality has given rise to various related notions. Roberts [1] introduced Roberts orthogonality, denoted by \(x \perp_R y\), which holds for any \(x, y \in X\) if \[\forall \lambda \in \mathbb{R}, \quad\|x+\lambda y\|=\|x-\lambda y\|.\] Birkhoff [2] introduced Birkhoff orthogonality, denoted by \(x \perp_B y\), which holds for \(x, y \in X\) if \[\forall \lambda \in \mathbb{R}, \quad\|x+\lambda y\| \geq\|x\|.\] James [3] introduced isosceles orthogonality, denoted by \(x \perp_I y\), which holds for \(x, y \in X\) if \[\|x+y\|=\|x-y\|.\] Quantifying geometric properties with numerical constants offers an intuitive way to understand these properties in a given Banach space. Some of the most prominent geometric constants in this context include von Neumann-Jordan constant \[C_{N J}(X)=\sup \left\{\frac{\|x+y\|^2+\|x-y\|^2}{2\left(\|x\|^2+\|y\|^2\right)}: x, y \in X,(x, y) \neq(0,0)\right\},\] and James constant
\[J(X)=\sup \left\{\min \{\|x-y\|,\|x+y\|\}: x, y \in S_X\right\} .\]
In addition, building upon various orthogonal relationships, scholars have modified certain classical constants to investigate the distinctions between two types of orthogonality. For instance, Ji D. and Wu S. introduced the constants \(D(X)\) and \(D^{\prime}(X)\) in [4] to measure the distinction between Birkhoff orthogonality and isosceles orthogonality. Moreover, Papini P.L. and Baronti M. [5] explored the \(J_{\perp}(X)\) constant within the context of Birkhoff orthogonal relationships. These constants are listed below: \[\begin{aligned} J_{\perp}(X)=&\sup \left\{\min \{\|x-y\|,\|x+y\|\}: x, y \in S_X, x \perp_B y\right\},\\ D(X)=&\inf \left\{\inf _{\lambda \in \mathbb{R}}\|x+\lambda y\|: x, y \in S_X, x \perp_I y\right\},\\ D^{\prime}(X)=&\sup \{\|x+y\|-\|x-y\|: x, y \in S_X, x \perp_B y \}. \end{aligned}\]
Readers interested in the above content can refer to [4-7] and the references therein for detailed information.
Building upon the existing results, our aim is to delve deeper into the study by introducing a new asymmetric skew orthogonality relationship, denoted by \(x \perp_{\alpha-\beta} y\), defined as: \[\|\alpha x+\beta y\|=\|\beta x-\alpha y\|.\] We also propose a related geometric constant \(B_{\alpha-\beta}(X)\). This constant serves to estimate the difference between these two orthogonal pairs. In Section 2, we introduce the constant \(B_{\alpha-\beta}(X)\) and explore some of its basic properties, along with calculating its values for specific spaces. After that, we compare the relationship between the modulus of convexity \(\delta_X(\varepsilon)\) and \(B_{\alpha-\beta}(X)\). At the end of the article, we present results comparing other classical constants such as \(D^{\prime}(X)\) and \(J_{\perp}(X)\).
In this paper, we will first introduce an orthogonality concept based on Roberts orthogonality [1].
Definition 1. Let \(X\) be a real normed linear space of dimension at least two. If \(x, y \in X\), then \(x\) is said to be \(\alpha-\beta\) orthogonal to \(y\) (denoted by \(x \perp_{\alpha-\beta} y\) ) if \[\forall \alpha,\beta \in \mathbb{R}, \quad\|\alpha x+\beta y\|=\|\beta x-\alpha y\| .\]
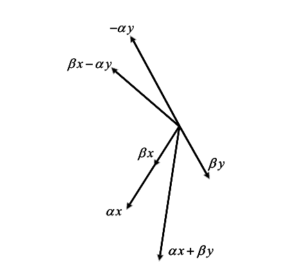
Example 1. Let \(X=\mathbb{R}^2\) endowed with the norm \[\left\|\left(x_1, x_2\right)\right\|=\max \left\{\left|x_1\right|,\left|x_2\right|\right\} .\] Choose \(x=(0,1), y=(1,0)\), we have \(\alpha x+\beta y=(\beta, \alpha)\) and \(\beta x-\alpha y=(-\alpha, \beta)\). It’s clear that \(\|\alpha x+\beta y\|=\|\beta x-\alpha y\|\).
We consider the constant \(B_{\alpha-\beta}(X)\) to measure the difference between Birkhoff orthogonality and \(\alpha-\beta\) orthogonality in the entire space \(X\):
for \(\alpha,\beta >0\), let
\[B_{\alpha-\beta}(X)=\sup \left\{\frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha}: x, y \in S_X, x \perp_B y\right\}.\]
Proposition 1. Let \(X\) be a Banach space. Then \[0 \leq B_{\alpha-\beta}(X) \leq 1.\]
Proof. It is trivial that \(0 \leq B_{\alpha-\beta}(X)\). On the other hand, \[\frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha} \leq \frac{\alpha+\beta-\beta}{\alpha}=1.\] Hence we obtain \(B_{\alpha-\beta}(X) \leq 1.\) ◻
Before delving into further discussions about the basic properties of \(B_{\alpha-\beta}(X)\), let’s first introduce two lemmas.
Lemma 1. [8] A normed space \(X\) is an inner product space if and only if \(\|x+t y\|=\|y+t x\|\) for all \(t \in \mathbb{R}\) and \(x, y \in X\) with \(\|x\|=\|y\|\).
Lemma 2. [8] A normed space \(X\) is an inner product space if and only if \(x \perp_B y \Leftrightarrow x \perp_I y\) for all \(x, y \in S_X\) .
The two lemmas establish connections between orthogonality and inner product spaces, and use these connections to prove the following theorem.
Theorem 1. For any \(\alpha,\beta > 0\), \(B_{\alpha-\beta}(X)=0\) if and only if \(X\) is an inner product space.
Proof. If \(X\) is an inner product space, according to Lemma 1, we have \[\|\alpha x+\beta y\|-\|\beta x-\alpha y\|=\|\alpha x+\beta y\|-\|\beta x+\alpha y\|=0\] for all \(\alpha, \beta> 0\) and \(x, y \in S_X\), and hence \(B_{\alpha-\beta}(X)=0.\)
Conversely, if \(B_{\alpha-\beta}(X)=0\). We can deduce that \(\|\alpha x+\beta y\| \leq\|\beta x-\alpha y\|\) for all \(\alpha,\beta > 0,x, y \in S_X, x \perp_B y\). So \[\|\alpha x-\beta y\| \leq\|\beta x+\alpha y\|\] also hold for all \(x \perp_B y\). This means \[\|\alpha x+\beta y\|=\|\beta x-\alpha y\|\] for all \(\alpha,\beta > 0,x, y \in S_X,\) and \(x \perp_B y\) also holds. Assuming we cannot achieve isosceles orthogonality, it would result in the contradiction shown below: \[\|\alpha x+\beta y\| \neq \|\beta x-\alpha y\|.\] Therefore, we deduce that \(x \perp_I y\). Applying Lemma 2, as desired. ◻
Example 2. Let \(X=\mathbb{R}^2\), \(\alpha\leq\beta\) and assign the following \(\ell_{\infty}-\ell_1\) norm \[\|x\|=\left\{\begin{array}{l} \|x\|_1,~~~~~ x_1 x_2 \leq 0, \\ \|x\|_{\infty},~~~~ x_1 x_2 \geq 0 . \end{array}\right.\] Then \(B_{\alpha-\beta}(X)=1\).
Considering the vectors \(x = (1, 0)\) and \(y = (0, -1)\), we can observe that \(x,y \in S_X\) and \(x \perp_B y\). Then \(\|\alpha x+\beta y\|=\alpha+\beta\), \(\|\beta x-\alpha y\|=\beta\), we have \[\frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha}=\frac{\alpha+\beta-\beta}{\alpha}=1.\]
Theorem 2. The upper bound 1 of \(B_{\alpha-\beta}(X)\) is attained by a pair of points of \(S_X\) if and only if there exist two points \(x, y \in S_X\) such that \([x, y]\) and \([x, x-\frac{2\alpha}{\beta} y]\) are both contained in \(S_X\). In this case, the length of the segment \([x, y]\) is at least 1 .
Proof. Let exist two points \(x,y \in S_X\) and a real number \(\alpha >0\) such that \(x \perp_B y\) and the following inequality holds: \[\frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha}=1.\] Since \[1=\frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha}\leq \frac{\alpha+\beta-\beta}{\alpha}=1,\] which implies that \[\|\alpha x+\beta y\|=\alpha+\beta\] and \[\|\beta x-\alpha y\|=\beta\] holds for \(\alpha,\beta >0\).
Then we have \(\bigg\|\frac{\alpha}{\alpha+\beta}x+\frac{\beta}{\alpha+\beta}y\bigg\|=1\) and hence \([x,y]\subset S_X\).
On the other hand, since \(\|\beta x-\alpha y\|=\beta\) holds for \(\alpha ,\beta >0\), so \[\bigg\|\frac{1}{2}x+\frac{1}{2}x-\frac{1}{2}\frac{2\alpha}{\beta}y\bigg\|=1,\] this means that the middle point of \(x, x-\frac{\alpha}{\beta} y\) which norm is \(1\). Then we can conclude that \([x, x-\frac{2\alpha}{\beta} y]\subset S_X\). Moreover, since \(x \perp_B y\), we have\(\|x-y\|\geq 1\).
Conversely, suppose that there exist two points \(x,y \in Sx\) such that \([x,y],[x, x-\frac{2\alpha}{\beta} y]\subset S_X\). We have \(\|\alpha x+\beta y\|=\alpha+\beta\) and \(\|\beta x-\alpha y\|=\beta\).
Hence \[\frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha}= \frac{\alpha+\beta-\beta}{\alpha}=1.\] ◻
Next, we show the relation between \(B_{\alpha-\beta}(X)\) and the modulus of convexity \(\delta_X(\varepsilon)\).
Definition 2. [9] Let \(X\) be a Banach space. For every \(\varepsilon \in[0,2]\), the modulus of convexity (or rotundity) of \(\|\cdot\|\) is defined as \[\delta_X(\varepsilon)=\inf \left\{1-\left\|\frac{x+y}{2}\right\|: x, y \in B_X,\|x-y\| \geq \varepsilon\right\}.\] The norm \(\|\cdot\|\) is called uniformly convex (UC) (or uniformly rotund (UR)) if \(\delta_X(\varepsilon)>0\) for all \(\varepsilon \in(0,2]\). The space \((X,\|\cdot\|)\) is then called a uniformly convex space.
Theorem 3. If \(B_{\alpha-\beta}(X)=1\) then \(\delta_X(1)=0\),
Proof. If \(B_{\alpha-\beta}(X)=1\), then, for each positive number \(k \in \mathbb{N}\), there exist two points \(x_k, y_k \in S_X\) satisfying \(x_k \perp_B y_k\) and a real number \(\alpha_k>0\) such that \[\frac{\|\alpha_k x_k+\beta_k y_k\|-\|\beta_k x_k-\alpha_k y_k\|}{\alpha_k}>1-\frac{1}{k} .\] By extracting subsequences if it is necessary we may assume that there exists a number \(\alpha > 0\) such that \(\alpha=\lim_{k \rightarrow \infty} \alpha_k\). In the following we distinguish two cases on \(\alpha\).
Case 1: \(\alpha \neq 1\). When \(k\) is sufficiently large we may assume that \(0<\alpha_k \leq \beta_k\). From the following inequality: \[\|\alpha_k x_k+\beta_k y_k\|\leq \alpha_k\|x_k+y_k\|+(\beta_k-\alpha_k)\|y_k\|\] We have: \[\begin{aligned} \alpha_k\|x_k+y_k\| \geq& \|\alpha_k x_k+\beta_k y_k\|-\|(\beta_k-\alpha_k)y_k\|\\ >&(1-\frac{1}{k})\alpha_k+\|\beta_k x_k-\alpha_k y_k\|-\beta_k+\alpha_k\\ \geq&(1-\frac{1}{k})\alpha_k+\beta_k-\beta_k+\alpha_k\\ =&(2-\frac{1}{k})\alpha_k. \end{aligned}\] Hence \(\left\|x_k+y_k\right\|>2-\frac{1}{k}\). Therefore \[\lim _{k \rightarrow \infty}\left(1-\frac{1}{2}\left\|x_k+y_k\right\|\right)=0,\] which implies that \(\delta_X(1)=0\).
Case 2: \(\alpha=1\). In this case we can find a subsequence of \(\left\{\alpha_k\right\}_{k=1}^{\infty}\) contained either in \([0,1]\) or in \((1,+\infty]\). With a similar technique as in the foregoing two cases we can show that \(\delta_X(1)=0\). This completes the proof. ◻
Theorem 4. Let \(X\) be Banach space with \(\delta_X(1)>0\). If \(0<\alpha \leq \beta\), then \(B_{\alpha-\beta}(X) \leq \frac{1}{1+\delta_X(1)}\).
Proof. For each pair of points \(x, y \in S_X\) satisfying \(x \perp_{B y}\), we have \(\|x-y\| \geq 1\), and combined with facts, we have \(\|\beta x-\alpha y\| \geq \beta\). According to the definition of \(\delta_X(1),\|x+y\| \leq 2(1-\delta_X(1))\) hold.
So, \[\begin{aligned} \|\alpha x+\beta y\|= & \|\alpha x+\alpha y+\beta y-\alpha y\| \\ & =\|\alpha(x+y)\|+\|(\beta-\alpha) y\| \\ & \leq \alpha\|x+y\|+\beta-\alpha \\ & \leq 2 \alpha\left(1-\delta_X(1)\right)+\beta-\alpha . \end{aligned}\] Thus \[\begin{aligned} \frac{\|\alpha x+\beta y\|-\|\beta x-\alpha\|}{\alpha} & \leq \frac{\alpha-2 \alpha \delta_X(1)+\beta-\beta}{\alpha} \\ & =1-2 \delta_X(1) \\ & <1-\delta_X(1) \\ & <\frac{1}{1+\delta_X(1)} . \end{aligned}\] ◻
We will demonstrate the respective connections between \(J_{\perp}(X)\), \(D^{\prime}(X)\) and \(B_{\alpha-\beta}(X).\)
Proposition 2. For any non-trivial Banach space \(X\) with dim \(X \geq 2\), we have \[B_{\alpha-\beta}(X)\leq J_{\perp}(X)-1.\]
Proof. We may assume without loss of generality that \(\alpha \leq \beta\), then \[\begin{aligned} \frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha} & \leq \frac{\alpha\|x+y\|+|\alpha-\beta|\|y\|-\beta}{\alpha} \\ &= \frac{\alpha\|x+y\|+\beta-\alpha-\beta}{\alpha} \\ &=\|x+y\|-1. \end{aligned}\] Similarly, \[\begin{aligned} \frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha} \leq \|x-y\|-1. \end{aligned}\] So,\[B_{\alpha-\beta}(X)\leq J_{\perp}(X)-1.\] ◻
Theorem 5. Let \(X\) be Banach space, then \[\frac{(\alpha+\beta)D^\prime(X)-2|\beta-\alpha|}{2\alpha}\leq B_{\alpha-\beta}(X) \leq \frac{\beta D^\prime(X)+2|\alpha-\beta|}{\alpha}.\]
Proof. Consider the following relationships, \[\begin{aligned} \frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha} & \leq \frac{(\beta\|x+y\|+|\alpha-\beta|\|x\|)-(\beta\|x-y\|-|\alpha-\beta|\|y\|)}{\alpha} \\ & =\frac{(\beta\|x+y\|+|\alpha-\beta|)-(\beta\|x-y\|-|\alpha-\beta|)}{\alpha} \\ & =\frac{\beta(\|x+y\|-\|x-y\|)+2|\alpha-\beta|}{\alpha}. \end{aligned}\] So, \[\sup \left\{\frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha}\right\} \leq \sup \left\{\frac{\beta(\|x+y\|-\|x-y\|)+2|\alpha-\beta|}{\alpha}\right\}.\]
On the other hand, \[\begin{aligned} \frac{\|\alpha x+\beta y\|-\|\beta x-\alpha y\|}{\alpha} & \geq \frac{\left(\left\|\frac{\alpha+\beta}{2}(x+y)\right\|-\left\|\frac{\alpha-\beta}{2}(x-y)\right\|\right)-(\alpha\|x-y\|+|\beta-\alpha|\|x\|)}{\alpha} \\ & =\frac{\frac{\alpha+\beta}{2}\|x+y\|-\frac{\alpha+\beta}{2}\|x-y\|-|\beta-\alpha|}{\alpha}. \end{aligned}\] Hence, \[\begin{aligned} B_{\alpha-\beta}(X) \geq& \frac{\alpha+\beta}{2\alpha}\sup\{(\|x+y\|-\|x-y\|)\}-\frac{|\beta-\alpha|}{\alpha}\\ \geq&\frac{\alpha+\beta}{2\alpha}D^\prime(X)-\frac{|\beta-\alpha|}{\alpha}. \end{aligned}\] In summary, we have \[\frac{(\alpha+\beta)D^\prime(X)-2|\beta-\alpha|}{2\alpha}\leq B_{\alpha-\beta}(X) \leq \frac{\beta D^\prime(X)+2|\alpha-\beta|}{\alpha}.\] ◻
Definition 3. Let \(U\) be an ultrafilter on \(\mathbb{N}\). A sequence \(\left\{x_n\right\}\) in \(X\) converges to \(x\) with respect to \(\mathcal{U}\), denoted as \(\lim_\mathcal{U} x_n = x\), if for every neighborhood \(U\) of \(x\), the set \(\{i \in \mathbb{N}: x_i \in U\} \in \mathcal{U}\). The ultrapower of \(X\), denoted as \(\tilde{X}\), is formed as the quotient space \(l_{\infty}(X) / N_{\mathcal{U}}(X)\) equipped with the quotient norm, where:
\[\begin{aligned} & l_{\infty}(X) = \left\{(x_n) \subset X : \left\| (x_n) \right\| = \sup_{n \in \mathbb{N}} \|x_n\| < \infty \right\}, \\ & N_\mathcal{U}(X) = \left\{(x_n) \in l_{\infty}(X): \lim_\mathcal{U} \|x_n\| = 0 \right\}, \end{aligned}\]
and \(\|\tilde{x}\| = \lim_\mathcal{U} \|x_n\|\) for \(\tilde{x} = (x_n)_\mathcal{U} \in \tilde{X}\).
In this definition, for more information about ultra-techniques in
Banach space theorem, please refer to [11].
The following lemma has been proven by Papini and Wu in [10].
Lemma 3. Let \(X\) be a uniformly convex Banach space, \({\tilde{x}}=(x_{n})\) and \({\tilde{y}}=(y_{n})\) be two unit vectors in \(\tilde{X}\) satisfying \(\tilde{x} \perp_{B} {\hat{y}}\) Then there exist two sequences \(\{u_{n}\}_{n=1}^{\infty},\{v_{n}\}_{n=1}^{\infty}\subset S_{X}\) such that \(u_{n}\perp_{B} v_{n}\) holds for each \(n\in\mathbb{N}\) and that \({\tilde{x}}=(u_{n})\) and \({\tilde{y}}=(v_{n}).\)
Theorem 6. If \(X\) is a uniformly convex space then \(B_{\alpha-\beta}(X)=B_{\alpha-\beta}(\tilde{X})\) .
Proof. Because \(X\) is isometric to a subspace of \(\tilde{X}\), we only need to prove that \(B_{\alpha-\beta}(X) \leq B_{\alpha-\beta}(\tilde{X})\).
By Lemma 3, there exist two sequences \(\left\{u_n\right\}_{n=1}^{\infty}\) and \(\left\{v_n\right\}_{n=1}^{\infty}\) of unit vectors such that \(u_n \perp_B v_n\) for each \(n \in \mathbb{N}\) and that \(\tilde{x}=\left(u_n\right)\) and \(\tilde{y}=\left(v_n\right)\). Then
\[\begin{aligned} B_{\alpha-\beta}(\tilde{X})-\varepsilon & <\frac{\|\alpha\tilde{x}+\beta \tilde{y}\|-\|\beta\tilde{x}-\alpha \tilde{y}\|}{\alpha} \\ & =\lim _\mathcal{U} \frac{\left\|\alpha u_n+\beta v_n\right\|-\left\|\beta u_n-\alpha v_n\right\|}{\alpha} \\ & \leq B_{\alpha-\beta}(X) . \end{aligned}\] ◻
Birkhoff, G. (1935). Orthogonality in linear metric spaces. Duke Mathematical Journal, 1, 169-172.
James, R.C. (1945). Orthogonality in normed linear spaces. Duke Mathematical Journal, 12, 291-301. P. Jordan and J. von Neumann
Kato, M., Maligranda, L., & Takahashi, Y. (2001). On James and Jordan–von Neumann constants and the normal structure coecient of Banach spaces. Studia Mathematica, 144, 275–295.
Papadopoulos. (2022). A. Surveys in Geometry I. Gewerbestrasse 11, 6330 Cham, Switzerland: Springer Nature Switzerland AG.
Yang, C.S., & Zuo, H.L. (2001). An application of Hahn-Banach’s theorem to modulus of convexity. Acta Mathematiea Scientia, 21(1), 133-137.
Papini, P.L., & Wu, S. (2013). Measurements of differences between orthogonality types. Journal of Mathematical Analysis and Applications, 397, 285–291.
Aksoy, A.G., & Khamsi, M.A. (1990). Nonstandard Methods in Fixed Point Theory. Springer-Verlag, New York.