For an undirected graph \(G\), a zero-sum flow is an assignment of nonzero integers to the edges such that the sum of the values of all edges incident with each vertex is zero, and we call it a zero-sum \(k\)-flow if the absolute values of edges are less than \(k\). We define the zero-sum flow number of \(G\) as the least integer \(k\) for which \(G\) admitting a zero sum \(k\)-flow. In this paper we gave complete zero-sum flow and zero sum number for octagonal grid, generalized prism and book graph.
The nowhere-zero flows were defined by Tutte in [1]. The definition of nowhere-zero flows on signed graphs naturally comes from the study of embedding of graphs in non-orientable surfaces, where nowhere-zero flows emerge as the dual notion to local tensions. There is a close relationship between nowhere-zero flows and circuit covers of graphs as every nowhere-zero flow on a graph \(G\) determines a covering of \(G\) by circuits. This relationship is maintained for signed graphs, although a signed version of the definition of circuit is required.
Let \(G\) be a directed graph. A nowhere-zero flow on \(G\) is an assignment of non-zero integers to each edge of \(G\) such that for every vertex the Kirchhoff current law holds, which says that, the sum of the values of incoming edges is equal to the sum of the values of outgoing edges. A nowhere-zero \(k\)-flow is a nowhere-zero flow using edge labels with maximum absolute value \(k-1\). Since for a directed graph that admits nowhere-zero flows is independent of the choice of the orientation, therefore one may consider such concept over the underlying undirected graph. A celebrated conjecture of Tutte in 1954 says that every bridge less graph has a nowhere-zero 5-flow. Jaeger showed in 1979 that every bridgeless graph has a nowhere-zero 8-flow [2], and Seymour proved that every bridgeless graph has a nowhere-zero-6-flow [3]in 1981. However the original Tutte conjecture remains open, see for more result [4,5, 6].
As an analogous concept of a nowhere-zero flow for directed graphs, we consider zero-sum flow number for undirected graphs in this paper.Definition 1.1. For an undirected graph \(G\), a zero-sum flow is an assignment of non-zero integers to the edges such that the sum of the values of all edges incident with each vertex is zero. A zero-sum \(k\)-flow is a zero-sum flow whose values are integers with absolute value less than \(k\).
Note that from algebraic point of view finding such zero-sum flows is the same as finding nowhere zero vectors in the null space of the incidence matrix of the graph. Akbari et al. raised a conjecture for zero-sum flows similar to the Tutte $5$-flow Conjecture for nowhere-zero flows as follows:Conjecture 1. (Zero-Sum 6-Flow Conjecture) If \(G\) is a graph with a zero sum flow, then \(G\) admits a zero-sum \(6\)-flow.
It was proved in 2010 by Akbari et al. in [7] that the above zero-sum 6-flow Conjecture is equivalent to the Bouchet 6-flow Conjecture for bidirected graphs. In literatures a more general concept flow number, which is defined as the least integer \(k\) for which a graph may admit a \(k\)-flow, has been studied for both directed graphs and bi directed graphs. Wang and Hu in [8, 9] extend the concept in 2011 to the undirected graphs and call it zero-sum flow number, and also considered general constant-sum flows for regular graphs.
In the study of nowhere-zero flows of directed graphs (bidirected graphs) one considers a more general concept, namely, the least number of \(k\) for which a graph may admit a \(k\)-flow. In [9], Wang and Hu considered similar concepts for zero-sum \(k\)-flows. In the study of nowhere-zero flows of directed graphs(bidirected graphs) one considers a more general concept, namely, the least number of \(k\) for which a graph may admit a \(k\)-flow. In [9] Wang and Hu consider similar concepts for zero-sum \(k\)-flows.Definition 1.2. Let \(G\) be an undirected graph. The zero-sum flow number \(F(G)\) is defined as the least number of \(k\) for which \(G\) may admit a zero-sum \(k\)-flow. \(F(G) = Â\infty\) if no such \(k\) exists.
It is well known that grids are extremely useful in all areas of computer science. One of the main usage, for example, is as the discrete approximation to a continuous domain or surface. Numerous algorithms in computer graphics, numerical analysis, computational geometry, robotics and other fields are based on grid computations. In [10] and [11] the authors calculated the zero-sum flow number of triangular and hexagonal grids. In this paper, we calculate zero-sum flow number of Octagonal grid, generalized prism and book graph.
\(V (O_n^m ) = \{x_i^j ; 1 \leq i \leq 2n-1,\) \(i\) odd and \(1\leq
j \leq 3m + 1\} \cup\{ x_i^{3j-2}\) \(1 \leq i \leq 2n\); \(i\)
even and \(1 \leq j \leq m + 1\}\cup \{ x_{2n}^{3j-1},\
x_{2n}^{3j}; 1 \leq j \leq m\}\)
\begin{eqnarray*}
V (O_n^m ) &=& \{x_i^j ; 1 \leq i \leq 2n-1, \;i\;\textrm{odd and}\; 1\leq
j \leq 3m + 1\} \\
&\cup&\{ x_i^{3j-2} ; \;1 \leq i \leq 2n; \;i
\;\textrm{even and}\;1 \leq j \leq m + 1\}\\
&\cup& \{ x_{2n}^{3j-1},\ x_{2n}^{3j}; 1 \leq j \leq m\}\\
E(O_n^m ) &=& \{x_i^j x_i^{j+1} ; 1
\leq i \leq 2n-1; \;i\; \textrm{odd and} \;1 \leq j \leq
3m\} \\
&\cup & \{x_i^{3j-2}x_{i+1}^{3j-2}; \; 1 \leq i \leq 2n-1;
\;i\; \textrm{odd and} \;1 \leq j \leq m + 1\} \\
&\cup & \{x_i^{3j-2}
x_{i+1}^{3j-1}; 1 \leq i \leq 2n-2; \;i\; \textrm{even and} \;1 \leq j
\leq m\} \\
&\cup & \{ x_i^{3j}x_{i-1}^{3j+1}; 3 \leq i \leq 2n -1;
\;i\;\textrm{odd and} \; 1 \leq j \leq m\} \\
&\cup & \{ x_{2n}^j
x_{2n}^{j+1}; 1 \leq j \leq 3m\}
\end{eqnarray*}
$$|V(O_{n}^{m})|=(4m+2)n+2m\,\, \ and\, \,\ |E(O_{n}^{m})|=(6m+1)n+m$$
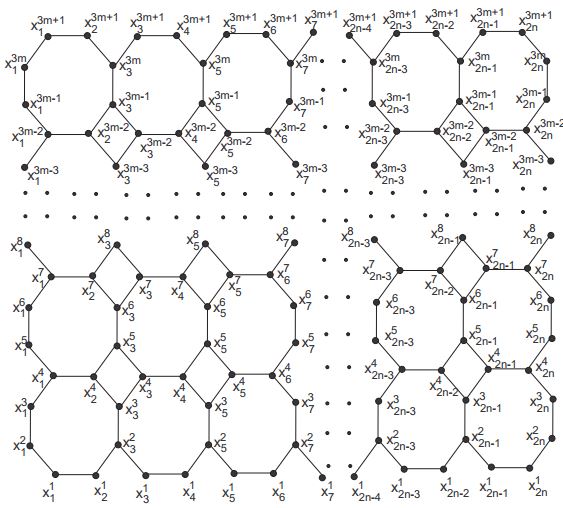
Theorem 2.1. The zero-sum flow number \(F(O_n^m)\) of \(O_n^m\) is \(3\) for all \(n,m\geq2\).
Proof. Note that there are \(4n+4m\) vertices of degree 2 and \(4mn-2n-2m\) vertices of degree \(3\) in \(O_n^m\), so a zero-sum flow edge assignment from \(\{-1,1\}\) is not possible. Therefore \(F(O_n^m)\) is at least \(3\). To prove the converse inequality we will consider the following edge labeling \(\varphi:E(O_n^m)\rightarrow\{1,-1,2\}\). $$ \varphi(x_i^{3j-2}x_{i+1}^{3j-2})=\left\{ \begin{array}{ll} 1, & \hbox{\(j=1,\ m+1\), \(i\) is odd and \(1\leq i\leq2n-1\)} \\ 2, & \hbox{\(2\leq j\leq m\), \(i\) is odd and \(1\leq i\leq2n-1\)} \end{array} \right.$$ $$ \varphi(x_i^{3j-1}x_{i}^{3j})=\left\{ \begin{array}{ll} 1, & \hbox{\(i=1,\ 2n\), \(1\leq j\leq m\)} \\ 2, & \hbox{\(1\leq j\leq m\), \(i\) is odd and \(3\leq i\leq2n-1\)} \end{array} \right.$$ For \(i\) odd, \(1\leq i\leq2n-1\) and \(1\leq j\leq m\), $$\varphi(x_i^{3j}x_{i}^{3j+1})=\varphi(x_i^{3j-2}x_{i}^{3j-1})= -1,$$ For \(i\) even, \(1\leq i\leq2n\) and \(1\leq j\leq m\), $$\varphi(x_i^{3j-2}x_{i+1}^{3j-1})= -1,$$ For \(i\) odd, \(3\leq i\leq2n\) and \(1\leq j\leq m\), $$\varphi(x_i^{3j}x_{i-1}^{3j+1})= -1,$$ We can see that \(\varphi\) is an edge labeling from \(E(O_n^m)\) to \(\{1,-1,2\}\). Now we will find the weight of each vertex and the weight of a vertex is the sum of all labels of edges adjacent to it. \begin{eqnarray*} wt(x_i^{3j-2}) &=& \varphi(x_i^{3j-2}x_{i+1}^{3j-2})+\varphi(x_i^{3j-2}x_{i}^{3j-1}) \\ &=& 0, \quad\quad \textrm{for}\;\; 1\leq i\leq 2n-1,\; \textrm{and} \;i \;\textrm{odd}, j=1\\ wt(x_i^{3j-2}) &=& \varphi(x_i^{3j-2}x_{i+1}^{3j-2})+\varphi(x_i^{3j-2}x_{i+1}^{3j-1}) \\ &=& 0, \quad\quad \textrm{for} \;1\leq i\leq 2n,\; \textrm{and} \;i\; \textrm{even}, \;j=1 \\ wt(x_i^{3j-1}) &=& \varphi(x_i^{3j-1}x_{i}^{3j})+\varphi(x_i^{3j-2}x_{i+1}^{3j-1}) \\ &=& 0, \quad \quad \textrm{for} \;\;i=1,2n, \;\;1\leq j\leq m\\ wt(x_i^{3j}) &=& \varphi(x_i^{3j-1}x_{i}^{3j})+\varphi(x_i^{3j}x_{i}^{3j+1})\\ &=& 0, \quad \quad \textrm{for} \;i=1,2n,\; 1\leq j\leq m \end{eqnarray*} \begin{eqnarray*} wt(x_i^{3m+1}) &=& \varphi(x_i^{3m}x_{i}^{3m+1})+\varphi(x_i^{3m+1}x_{i+1}^{3m+1}) \\ &=& 0, \quad \textrm{for}\; 1\leq i\leq 2n-1,\; \textrm{and} \;i\; \textrm{odd}.\\ wt(x_i^{3m+1}) &=& \varphi(x_{i-1}^{3m+1}x_{i}^{3m+1})+\varphi(x_i^{3m+1}x_{i+1}^{3m}) \\ &=& 0, \quad \quad \;\textrm{for} \;1\leq i\leq 2n,\; \textrm{and} \;i\; \textrm{even} \\ wt(x_i^{3j+1}) &=& \varphi(x_{i-1}^{3j+1}x_{i}^{3j+1})+\varphi(x_i^{3j+1}x_{i+1}^{3j+2})+\varphi(x_i^{3j+1}x_{i+1}^{3j}) \\ &=& 0, \quad \quad \;\textrm{for} \;1\leq i\leq 2n,\; \textrm{and} \;i\; \textrm{even}, \;1\leq j\leq m-1\\ wt(x_{2i+1}^{3j-1}) &=& \varphi(x_{i+1}^{3j-2}x_{i+2}^{3j-1})+\varphi(x_{2i+1}^{3j-2}x_{2i+1}^{3j-1})+\varphi(x_{2i+1}^{3j-1}x_{2i+1}^{3j}) \\ &=& 0 , \quad\quad \textrm{for} \;1\leq i\leq n-1, \;1\leq j\leq m\\ wt(x_{2i+1}^{3j}) &=& \varphi(x_{2i+1}^{3j-1}x_{2i+1}^{3j})+\varphi(x_{2i}^{3j+1}x_{2i+1}^{3j})+\varphi(x_{2i+1}^{3j}x_{2i+1}^{3j+1}) \\ &=& 0, \quad \quad \textrm{for}\; 1\leq i\leq n-1\;, \;1\leq j\leq m\\ wt(x_{2i-1}^{3j+1}) &=& \varphi(x_{2i-1}^{3j+1}x_{2i-1}^{3j+2})+\varphi(x_{2i-1}^{3j+1}x_{2i-1}^{3j})+\varphi(x_{2i-1}^{3j+1}x_{2i}^{3j+1}) \\ &=& 0, \quad \quad \textrm{for} \;1\leq i\leq n,\; 1\leq j\leq m-1 \end{eqnarray*} These computations shows that that \(\varphi\) is indeed a zero-sum 3-flow and we get \(F(O_n^m)\leq3\). This concludes the result.
The cartesian product \(G \times H\) of graphs \(G\) and \(H\) is a graph such that the vertex set of \(G\times H\) is the cartesian product \(V (G)\times V (H)\) and any two vertices \((u,u’)\) and \((v,v’)\) are adjacent in \(G \times H\) if and only if either \(u = v\) and \(u’\) is adjacent to \(v’\) in \(H\) , or \(u’ = v’\) and \(u\) is adjacent to \(v\) in \(G\).
The generalized prism \(P_n^m\) can be defined as the cartesian product \(C_n\times P_m\) of a cycle on \(n\) vertices with a path on \(m\) vertices. If we consider a cycle \(C_n\) with \(V(C_n)=\{x_i:\ 1\leq i\leq n\}\), \(E(C_n)=\{x_ix_{i+1}:\ 1\leq i\leq n-1\}\cup\{x_nx_1\}\) and a path \(P_m\) with \(V(P_m)=\{y_j:\ 1\leq j\leq m\}\), \(E(P_m)=\{y_jy_{j+1}:\ 1\leq j\leq m-1\}\), then \(V(P_n^m)=V(C_n\times P_m)=\{(x_i,y_j):\ 1\leq i\leq n,\ 1\leq j\leq m\}\) is the vertex set of the graph \(P_n^m\) and
\begin{eqnarray*} % \nonumber to remove numbering (before each equation) E(P_n^m) &=&E(C_n\times P_m) =\{(x_i,y_j)(x_{i+1},y_j):\ 1\leq i\leq n-1,\ 1\leq j\leq m\}\\ & \cup & \{(x_n,y_j)(x_1,y_j):\ 1\leq j\leq m\}\\ & \cup &\{(x_i,y_j)(x_i,y_{j+1}):\ 1\leq i\leq n,\ 1\leq j\leq m-1\} \end{eqnarray*} is the edge set of \(P_n^m\) . So, \(|V(P_n^m)|=nm\) and \(|E(P_n^m)|=n(2m-1)\).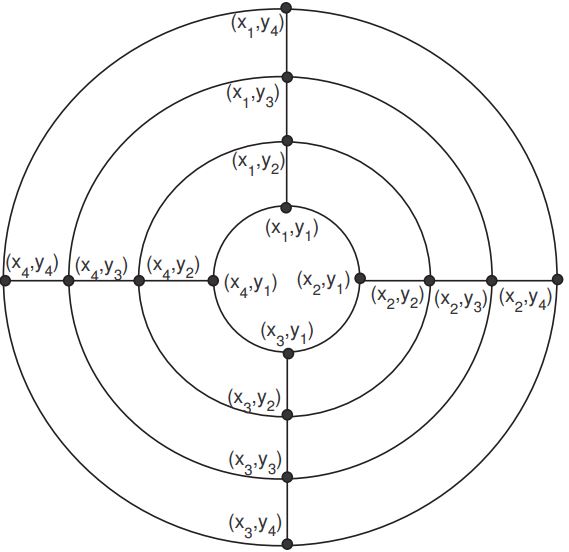
The generalized prism \(P_n^m\) has been studied extensively in recent years. Kuo et al. in [13] and Chiang et al. in [14] studied distance-two labelings of \(P_n^m\). Deming et al. in [15] gave complete characterization of the cartesian product of cycles and paths for their incidence chromatic numbers. Gravier et al. in [16] showed the link between the existence of perfect Lee codes and minimum dominating sets of \(P_n^m\). Lai et al. in [17] determined the edge addition number for the cartesian product of a cycle with a path. Chang et al. in [18] established upper bounds and lower bounds for global defensive alliance number of \(P_n^m\) and showed that the bounds are sharp for certain \(n,m\). In [19], Bača, et al. compute the exact value of total edge irregularity strength for generalized prism \(P_n^m\).
In following theorem we determine the exact zero-sum flow number \(F(P_n^m)\) of \(P_n^m\).Theorem 3.1. The zero-sum flow number \(F(P_n^m)\) of \(P_n^m\) is \(3\) for all \(n\geq3\) and \(m\geq2\).
Proof. Since there are \(mn-2n\) vertices of degree \(4\) and \(2n\) vertices of degree 3 in \(P_n^m\) so \(\{-1,1\}\) assignment for the edges is not possible for the zero sum flow therefore \(F(P_n^m)\geq3\). Now we will show that \(F(P_n^m)\leq3\) and for this purpose we shall consider the following labeling \(\varphi:E(P_n^m)\rightarrow \{-1,-2,2\}\) on the edges of \(P_n^m\) graph. $$\varphi((x_i,y_j)(x_{i+1},y_j))= \left\{ \begin{array}{ll} -1, & \hbox{\(1\leq i\leq n-1,\ j=1,m;\)} \\ -2, & \hbox{\(1\leq i\leq n-1,\ 2\leq j\leq m-1\).} \end{array} \right.$$ $$\varphi((x_n,y_j)(x_{1},y_j))= \left\{ \begin{array}{ll} -1, & \hbox{\(\ j=1,m;\)} \\ -2, & \hbox{\(\ 2\leq j\leq m-1.\)} \end{array} \right.$$ $$\varphi((x_i,y_j)(x_{i},y_{j+1}))= 2,\quad 1\leq i\leq n,\ 1\leq j \leq m-1$$ Now, using this assignment we will prove that the sum of flow at each vertex is zero. For this purpose we will find the weight of each vertex and the weight of a vertex is the sum of all labels of edges adjacent to it. The weight for each vertex is calculated below: \begin{eqnarray*} wt(x_i,y_1) &=& \varphi((x_i,y_1)(x_{i+1},y_1))+\varphi((x_i,y_1)(x_i,y_2))\\ &\ & +\varphi((x_{i-1},y_1)(x_i,y_1)) \\ &=& 0, \quad\quad\quad\quad\quad\quad\quad \textrm{for}\; 2\leq i \leq n-1 \end{eqnarray*} \begin{eqnarray*} wt(x_1,y_1) &=&\varphi((x_1,y_1)(x_2,y_1))+\varphi((x_n,y_1)(x_1,y_1))\\ &\ &+\varphi((x_1,y_1)(x_1,y_2))\\ &=& 0,\\ wt(x_n,y_1) &=&\varphi((x_n,y_1)(x_{n-1},y_1))+\varphi((x_1,y_1)(x_n,y_1))\\ &\ & +\varphi((x_n,y_1)(x_n,y_2))\\ &=& 0,\\ wt(x_i,y_m) &=&\varphi((x_i,y_m)(x_{i+1},y_m))+\varphi((x_i,y_m)(x_i,y_{m-1}))\\ &\ & +\varphi((x_{i-1},y_m)(x_i,y_m))\\ &=& 0, \quad\quad\quad\quad\quad\quad\quad \textrm{for}\; 2\leq i \leq n-1\\ wt(x_1,y_m) &=&\varphi((x_1,y_m)(x_2,y_m))+\varphi((x_n,y_m)(x_1,y_m))\\ &\ & +\varphi((x_1,y_m)(x_1,y_{m-1}))\\ &=& 0,\\ wt(x_n,y_m) &=&\varphi((x_n,y_m)(x_{n-1},y_m))+\varphi((x_n,y_m)(x_1,y_m))\\ &\ & +\varphi((x_n,y_m)(x_n,y_{m-1}))\\ &=& 0. \end{eqnarray*} for \(2\leq j\leq m-1\) and \(2\leq i\leq n-1\) \begin{eqnarray*} wt(x_i,y_j) &=&\varphi((x_i,y_j)(x_{i+1},y_j))+\varphi((x_i,y_j)(x_{i-1},y_j))\\ &\ & +\varphi((x_{i},y_j)(x_i,y_{j+1}))+\varphi((x_{i},y_j)(x_i,y_{j-1}))\\ &=& 0,\\ wt(x_1,y_j) &=&\varphi((x_1,y_j)(x_{2},y_j))+\varphi((x_1,y_j)(x_{n},y_j))\\ &\ &+\varphi((x_{1},y_j)(x_1,y_{j+1}))+\varphi((x_{1},y_j)(x_1,y_{j-1}))\\ &=& 0,\\ wt(x_n,y_j) &=&\varphi((x_n,y_j)(x_{1},y_j))+\varphi((x_n,y_j)(x_{n-1},y_j))\\ &\ &+\varphi((x_{n},y_j)(x_n,y_{j+1}))+\varphi((x_{n},y_j)(x_n,y_{j-1}))\\ &=& 0, \end{eqnarray*} By above computations we can see that \(\varphi\) give us a zero-sum 3-flow. So we get \(F(P_n^m)\leq3\). This concludes the result.
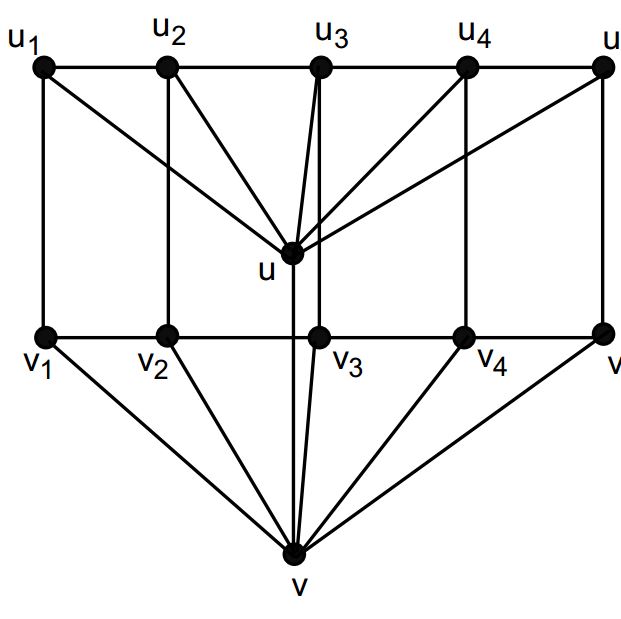
Theorem 4.1. The zero-sum flow number \(F((P_n + P_1) \times P_2)\) of \((P_n + P_1) \times P_2\) is \(3\) for all \(n\geq3\).
Proof. Note that the degree of vertices \(u_1,\ u_n,\ v_1\) and \(v_n\) is 3, so \(\{-1,1\}\) assignment for the edges will not give us a zero-sum flow therefore \(F((P_n + P_1) \times P_2)\geq3\). Now we will show that \(F((P_n + P_1) \times P_2)\leq3\) and for this purpose we shall consider the labeling \(\varphi:E((P_n + P_1) \times P_2)\rightarrow \{1, -1,-2\}\) on the edges of \((P_n + P_1) \times P_2\) graph. \(\varphi(uv)=\left\{ \begin{array}{ll} -1, & \hbox{if $n$ is odd;} \\ -2, & \hbox{if $n$ is even.} \end{array} \right. \) \(\varphi(uu_i)=\varphi(vv_i)=\left\{ \begin{array}{ll} 1, & \hbox{if $i=1,\ n$;} \\ (-1)^i, & \hbox{$n$ is even, $2\leq i\leq n-1$;} \\ (-1)^{i+1}, & \hbox{$n$ is odd, $2\leq i\leq n-1$.} \end{array} \right.\) \(\varphi(u_iv_i)=\left\{ \begin{array}{ll} -2, & \hbox{if $i=1,\ n$;} \\ (-1)^{i+1}, & \hbox{$n$ is even, $2\leq i\leq n-1$;} \\ -1, & \hbox{$n$ is odd, $i=2$;}\\ (-1)^{i}, & \hbox{$n$ is odd, $3\leq i\leq n-1$;} \end{array} \right.\) \(\varphi(u_iu_{i+1})=\varphi(v_iv_{i+1})=\left\{ \begin{array}{ll} (-1)^{i+1}, & \hbox{$n$ is even, $1\leq i\leq n-1$;} \\ 1, & \hbox{$n$ is odd, $i=1$;} \\ (-1)^{i}, & \hbox{$n$ is odd, $2\leq i\leq n-1$.} \end{array} \right.\) We can see that \(\varphi\) is an edge labeling from \(E((P_n + P_1) \times P_2)\) to \(\{1,-1,-2\}\). Moreover it is easy to check that \begin{eqnarray*} % \nonumber to remove numbering (before each equation) wt(u)&=& \sum_{i=1}^n\varphi(uu_i)+\varphi(uv)=0,\\ wt(v)&=& \sum_{i=1}^n\varphi(vv_i)+\varphi(uv)=0,\\ wt(u_1)&=& \varphi(uu_1)+ \varphi(u_1u_2)+\varphi(u_1v_1)=0,\\ wt(u_n)&=& \varphi(uu_{n})+ \varphi(u_nu_{n-1})+\varphi(u_nv_n)=0,\\ wt(v_1)&=& \varphi(vv_{1})+ \varphi(v_1v_{2})+\varphi(u_1v_1)=0,\\ wt(v_n)&=& \varphi(vv_{n})+ \varphi(v_nv_{n-1})+\varphi(u_nv_n)=0, \end{eqnarray*} For \(2\leq i\leq n-1\), \begin{eqnarray*} % \nonumber to remove numbering (before each equation) wt(u_i)&=& \varphi(uu_{i})+ \varphi(u_iu_{i-1})+\varphi(u_iu_{i+1})+\varphi(u_iv_i)=0 \end{eqnarray*} For \(2\leq i\leq n-1\), \begin{eqnarray*} % \nonumber to remove numbering (before each equation) wt(v_i)&=& \varphi(vv_{i})+ \varphi(v_iv_{i-1})+\varphi(v_iv_{i+1})+\varphi(u_iv_i)=0 \end{eqnarray*} So \(\varphi\) is a zero-sum 3-flow of \((P_n + P_1) \times P_2\). Therefore \(F((P_n + P_1) \times P_2)\leq3\). This conclude the statement of the theorem.